2. 湖南省交通建设质量安全监督管理局, 长沙 410116;
3. 湖南省永吉高速公路建设开发有限公司, 湖南 吉首 416000
2. Hunan Transportation Construction Quality and Safety Supervision and Management Administration, Changsha 410116, P. R. China;
3. Hunan Yongji Expressway Construction Development Co., Ltd., Jishou 416000, Hunan P. R. China
高效和无损的探地雷达(ground penetrating radar,GPR)技术已广泛应用于公路及铁路工程结构体厚度及缺陷的试验检测中[1-2],然而介质中雷达波速标定带来的误差常常严重影响试验检测的精度,使得高效无损的探地雷达技术未充分发挥其高分辨率优势,在公路及铁路工程的质量评定过程中仅作为辅助的参考手段,为提高试验检测效率和精度,规范波速校正的试验检测过程十分必要。相对介电常数和电导率是影响雷达波速的主要介电参数,探索它们之间的相关关系是解决该问题的关键,数值试验是细致研究介电参数特征和雷达波传播规律的有效途径,目前常用的数值实验工具主要为有限元法(finite element method,FEM)和有限差分法(finite difference method,FDM),基于麦克斯韦方程组的时域有限差分法以其节约计算时间和存储空间、直接时域范围计算、计算程序通用性强等优点[1-2],在模拟雷达波传播中得到了广泛的应用,Teixeira等[3]在完全匹配层吸收边界条件下利用FD法对各向异性的良导介质进行了三维GPR数值模拟,Levent Gürel等[4]在复杂介质中进行了三维GPR数值模拟,何兵寿等[5]对矿井地电模型进行了GPR数值模拟,李静等[6]研究了探地雷达的高阶FD数值模拟,底青云等[7]推导了含衰减项的探地雷达有限元方程,实现了复杂介质的探地雷达有限元数值模拟,冯德山等[8-9]研究了基于时域多分辨法的三维GPR数值模拟,刘新荣等[10]研究了隧道衬砌空洞三维探地雷达正演模拟,为雷达图谱的解释提供了依据,王绪本等[11]对岩溶洞穴进行了GPR物理模拟,宋华等[12]采用探地雷达对海堤模型进行了物理模拟试验,Giannopoulos[13]编写了基于Yee氏网格的Gprmax探地雷达数值模拟工具,张彬等[14]利采用旋转交错网格FD方法模拟了雷达波在衰减夹层介质中的传播情况,提高了模拟效率的同时改善了对低频隐失波的有效吸收,田钢等[15]则将FD算法应用于存在反射干扰特征的探地雷达数值模拟,为电磁反射抗干扰研究提供了理论依据。
文中采用二阶精度的FD方法,对不同电导率和不同相对介电常数的钢筋混凝土双介电参数进行了数值实验,着重研究了钢筋混凝土介质的相对介电常数、电导率和波速三者之间的相关关系,总结了双介电参数对雷达波速校正的经验性结果,为减少波速校正带来的误差和规范公路及铁路工程的探地雷达试验检测过程提供参考。
1、 FD法及TMz差分格式时域有限差分法于1966年由Yee首次提出[16],通过将电场分量E、磁场分量H在时间和空间上进行交替离散化,即每一个电磁E(或H)分量周围由4个电磁场H(E)分量环绕,如图 1所示,并在每个离散点上使用差商来代替微商,将求解包含时间变量的2个麦克斯韦旋度方程和2个散度方程转化为求解6个有限差分方程组,并通过时间轴的推进逐步求取空间上的电磁场值,而实际上,麦克斯韦方程组中2个散度方程可以由2个旋度方程导出,故在数值试验的计算中以旋度方程为基础。

|
图 1 FD网格中的场分量分布 Figure 1 Layout of field components in FD grid |
在无源场区域,麦克斯韦方程组中的2个旋度方程表示为如下的形式[17]:
| ∇×E=−μ∂H∂t−σmH, | (1) |
| ∇×H=ε∂E∂t+σeE, | (2) |
其中:ε为相对介电常数;σm为等效磁阻率,Ω/m,在TMz极化模式下,只含Ez、Hx和Hy分量的独立方程组为
| ∂Ez∂t=1ε(∂Hy∂x−∂Hx∂y−σeEz), | (3) |
| ∂Hx∂t=−1μ(∂Ez∂y+σmHx), | (4) |
| ∂Hy∂t=1μ(∂Ez∂x−σmHy)∘ | (5) |
采用二阶空间精度的中心差商代替微商,得到二维时域差分方程,即为TMZ模式下的FDTD更新方程组:
| ˜En+1z(i,j)=CA(i,j)⋅˜Enz(i,j)+CD⋅CB(i,j)⋅[Hn+12y(i+12,j)−Hn+12y(i−12,j)+Hn+12x(i,j−12)−Hn+12x(i,j+12)], | (6) |
| Hn+12x(i,j+12)=Hn+12x(i,j+12)+CD⋅[˜Enz(i,j)−˜Enz(i,j+1)], | (7) |
| Hn+12x(i,j+12)=Hn+12x(i,j+12)+CD⋅[˜Enz(i+1,j)−˜Enz(i,j)], | (8) |
其中系数项
从更新方程可以看出,电场分量Ez在(n+1)Δt时刻获取更新,而磁场分量Hx和Hy则均在(n+0.5)Δt时刻获取更新,在各个边界处理上,采用了完全匹配层 (PML) 吸收边界条件[18-19],详细的介电参数数值实验流程如图 2所示。
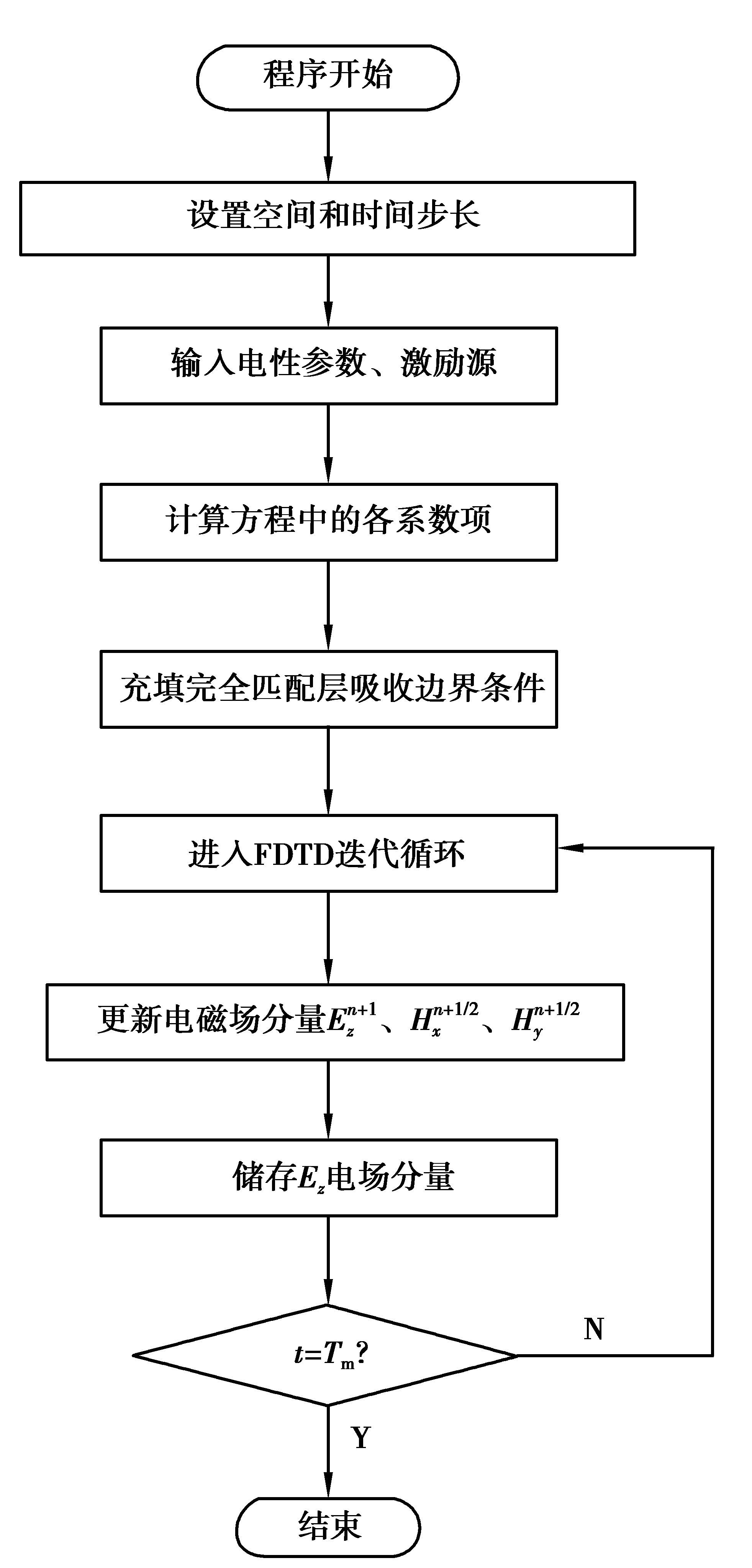
|
图 2 介电参数数值实验流程图 Figure 2 Flow chart of dielectric parameters simulation experiment |
不同钢筋埋深的混凝土介质模型如图 3所示,模型中设置钢筋的横纵向间距分别为10 cm和5 cm,最上部的钢筋深度为10 cm,最底部的钢筋深度为35 cm,模拟时采用天线中心频率为800 MHz,设置混凝土的相对介电常数ε1为9.0,电导率σ1为0.000 1 S/m,钢筋为导电属性的理想电导体(PEC)介质,直径均为0.02 m,网格的横向空间迭代步长为0.003 m,纵向空间步长为0.001 5 m,时间步长均为0.005 ns,各钢筋占据8个网格,吸收边界区域设置为5个网格,共完成了40道数据的模拟采集。
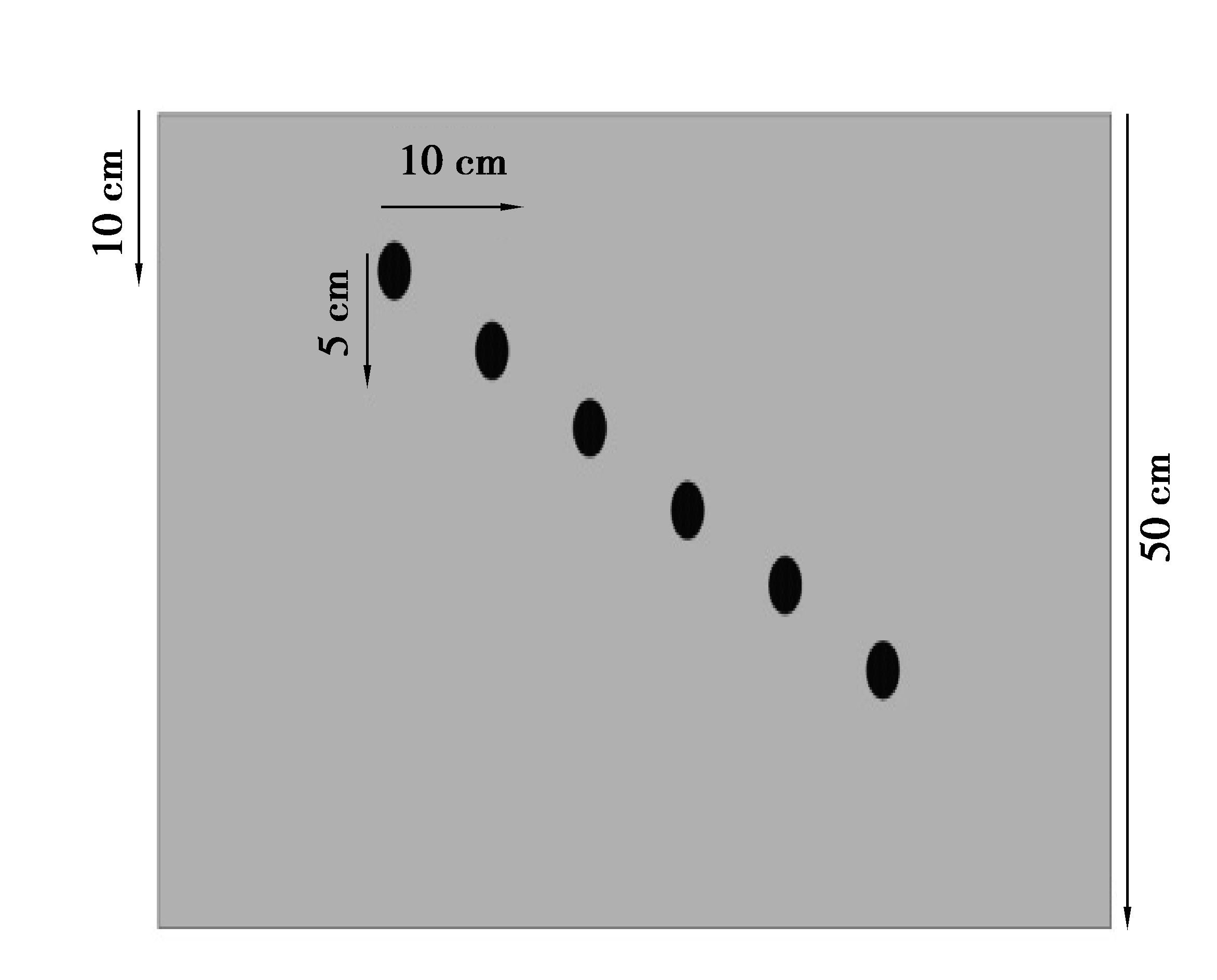
|
图 3 钢筋混凝土介质模型 Figure 3 Reinforced concrete medium model |
数值实验的模拟剖面结果如图 4所示,图中可见绕射波同相轴呈双曲形状,双曲线的曲率随钢筋异常体埋深的增大而减小,同样,绕射波的能量随钢筋异常体埋深的增加而减小,最底部钢筋的双曲线形态难以分辨,其中因多次反射波和绕射波的产生,深部的绕射信号难以分辨,该模拟剖面真实地反映了钢筋混凝土模型中不同钢筋埋深的基本特征。
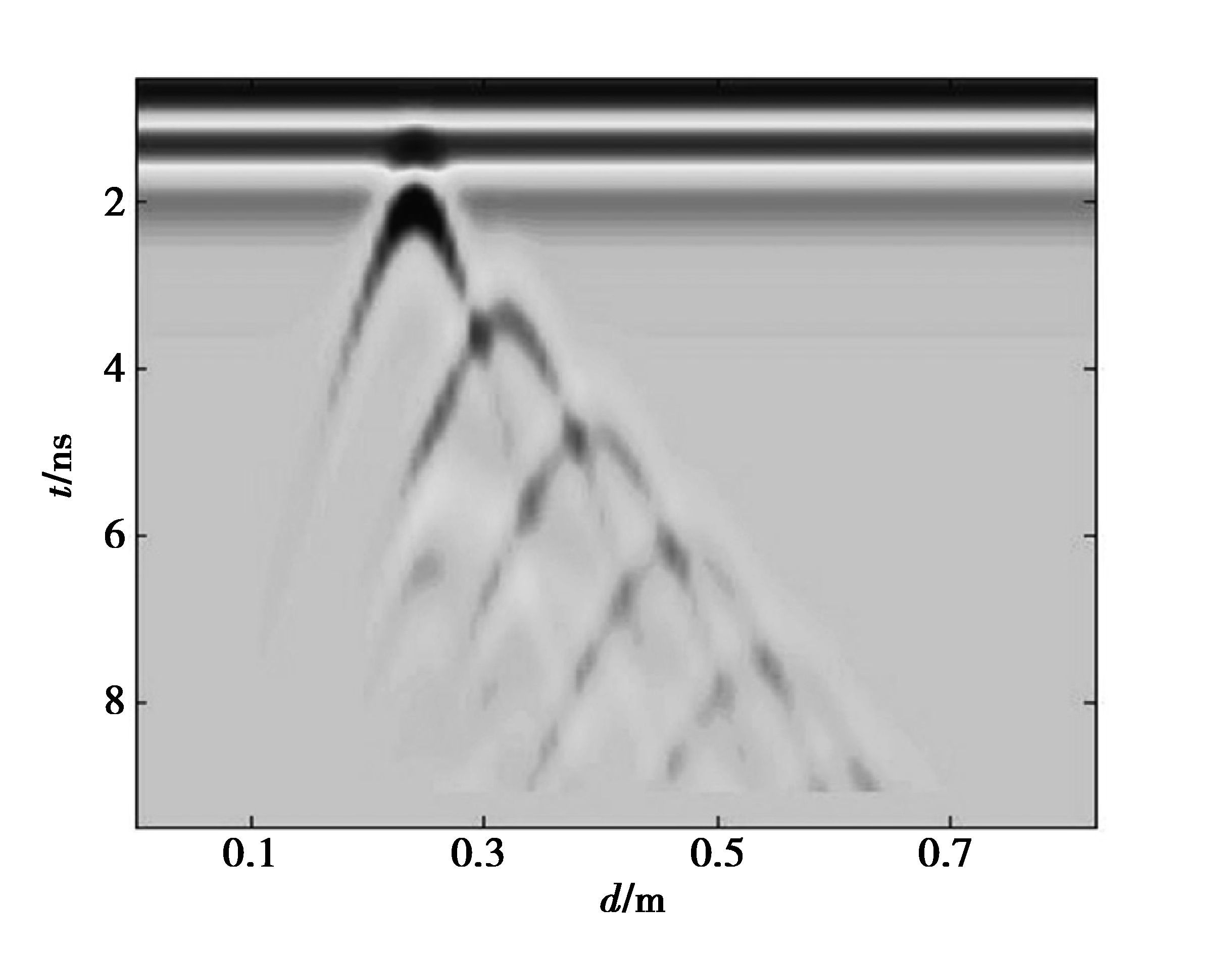
|
图 4 钢筋混凝土介质模型的模拟剖面 Figure 4 Simulation sections of the reinforced concrete medium model |
图 5为该模拟数据的第20道单道波的电场分量Ez,图 6为Ez电场分量在不同传播时刻的波场快照,4个时刻的能量显示已作均一化处理,从模拟剖面、单道波信号和波场快照结果可以看出,钢筋介质的电导率严重影响了雷达波能量继续往深部传播,成为了制约雷达波波速的主要因素。
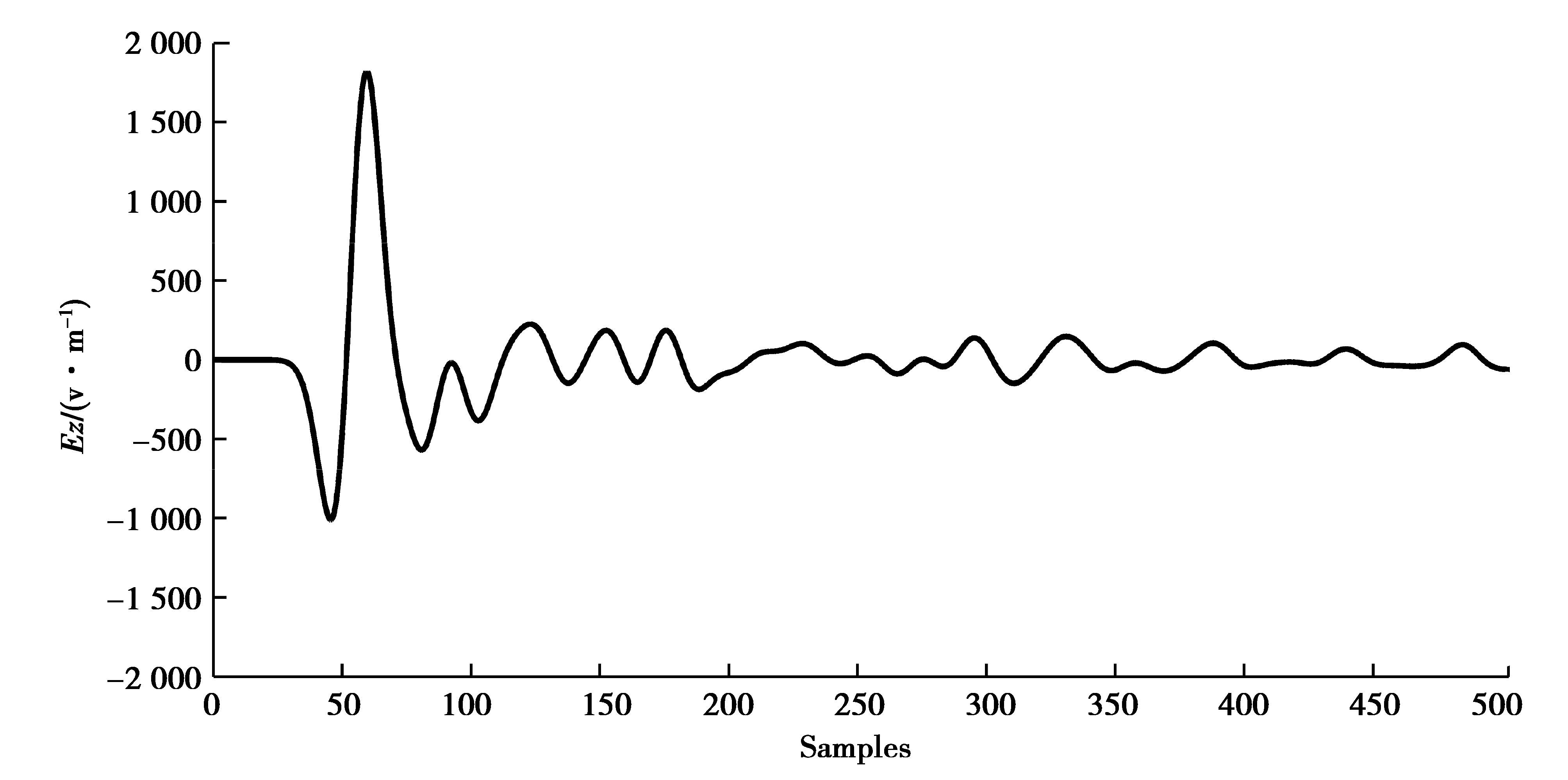
|
图 5 第20道探地雷达数据的单道信号 Figure 5 Single signal of the twentieth GPR scan |

|
图 6 Ez电场分量不同传播时刻的波场快照 Figure 6 Snapshots of Ez electric field in different propagation moment |
从不同时刻的Ez分量波场快照可以看出,雷达波在相对介电常数为9.0的背景介质中传播时,因混凝土介质中钢筋埋深各异,雷达拟球面波在钢筋位置产生了绕射异常,并同时以拟球面波的形式向外扩散。从第20道信号的单道波振幅中看出,雷达波的能量衰减严重,且随深度增加,雷达波在钢筋混凝土介质内部的传播速度呈现递减趋势,根据均匀介质中雷达波速理论,在5.0 ns时刻,雷达拟球面波的波前面应传播至模型的下边界,从图 6所示的数值实验结果来看,在6 ns时刻,雷达波的波前面仅传播至第210个网格位置,即传播至210×0.001 5 m=0.315 m位置,波前面的扩散速度受到了电导介质(钢筋)的严重影响。
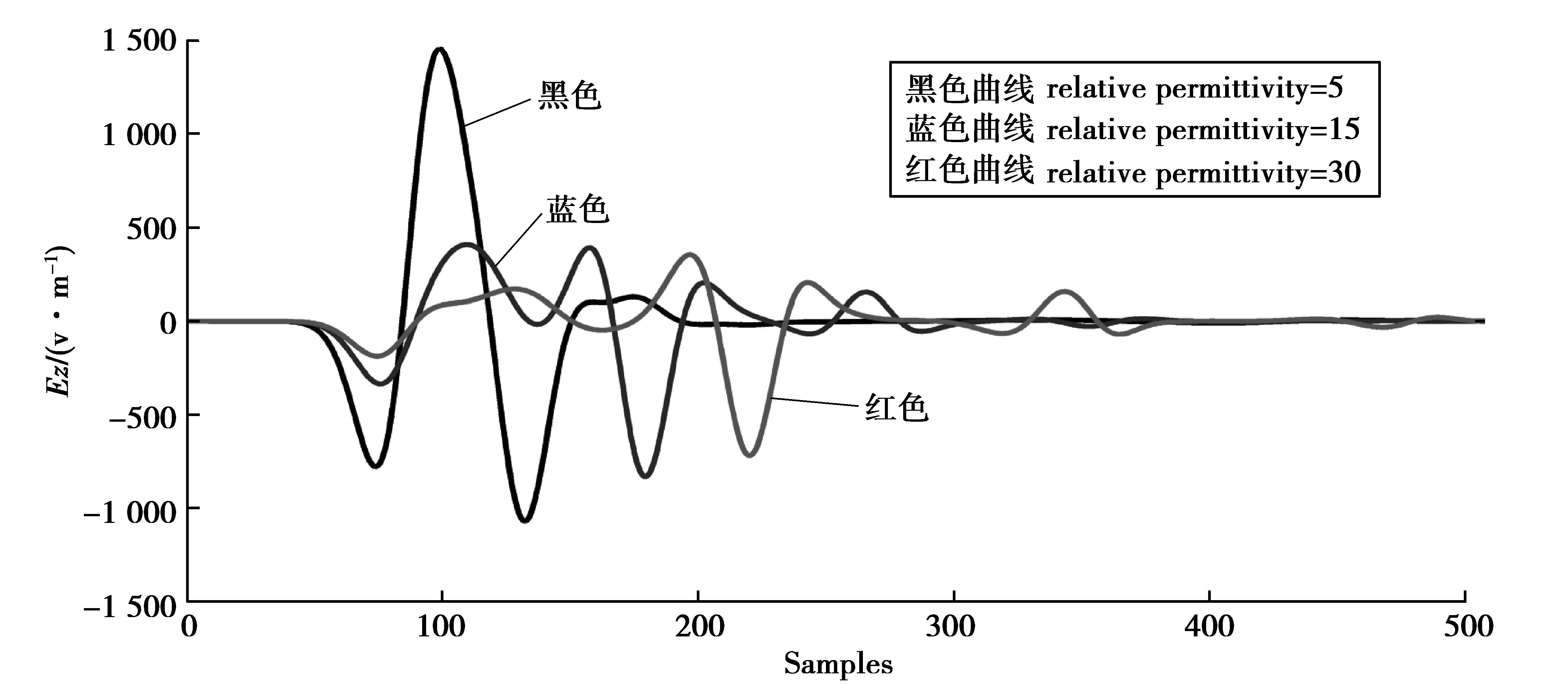
(3.2) 钢筋混凝土模型的双介电参数数值实验采用同样的方法进行了2组数值实验,针对相对介电常数为9.0的介质,对电导率分别为0.1 S/m、0.01 S/m的钢筋混凝土路面模型进行数值实验,其他参数保持一致,图 7为不同电导率混凝土模型的第20道单道波信号。同时,针对电导率为0.000 1 S/m的介质模型,对相对介电常数分别为30、15、5的钢筋混凝土模型进行相应的数值实验,图 8为不同介电常数混凝土模型的第20道单道波信号。

|
图 7 不同电导率介质模型的第20道探地雷达单道波信号 Figure 7 Single signal of the twentieth GPR scan with different conductivity medium model |
|
图 8 不同相对介电常数介质模型的第20道探地雷达单道波信号 Figure 8 Single signal of the twentieth GPR scan with different relative permittivity medium model |
如图 7中红色曲线所示,当钢筋混凝土介质的电导率为0.1 S/m时,Ez分量的单道波信号迅速衰减,且仅能观测到直达波信号,在第150个样点到第512个样点的深度区间,Ez分量的幅值保持为零,即在该情况下雷达波对混凝土模型中的钢筋异常体无绕射波产生,波形形态发生了严重畸变,电导介质对雷达波的传播速度影响较严重;相反,对于电导率为0.001 S/m的算例,雷达波在钢筋异常体位置的绕射波信号突出,易于识别,对后期的雷达波的衰减影响不大,雷达波的传播速度变化较小;由蓝色曲线可知当电导率为0.01 S/m时,传播后期的Ez分量具有较小的幅值,即电导介质对雷达波的传播速度产生了一定程度的影响。
如图 8所示,在混凝土介质模型的相对介电常数为5时,各个时刻雷达波的响应时间最早,见图中的黑色曲线,表明该情况下雷达波波速趋于常数
根据波场快照的能量图谱求取了对应的综合雷达波波速,并将该结果与统计的介电参数数值实验数据进行关联,三者的离散相关关系如表 1所示。
| 表 1 双介电参数与雷达波波速的相关关系 Table 1 Dual-dielectric parameter relative relationship with GPR Velocity |
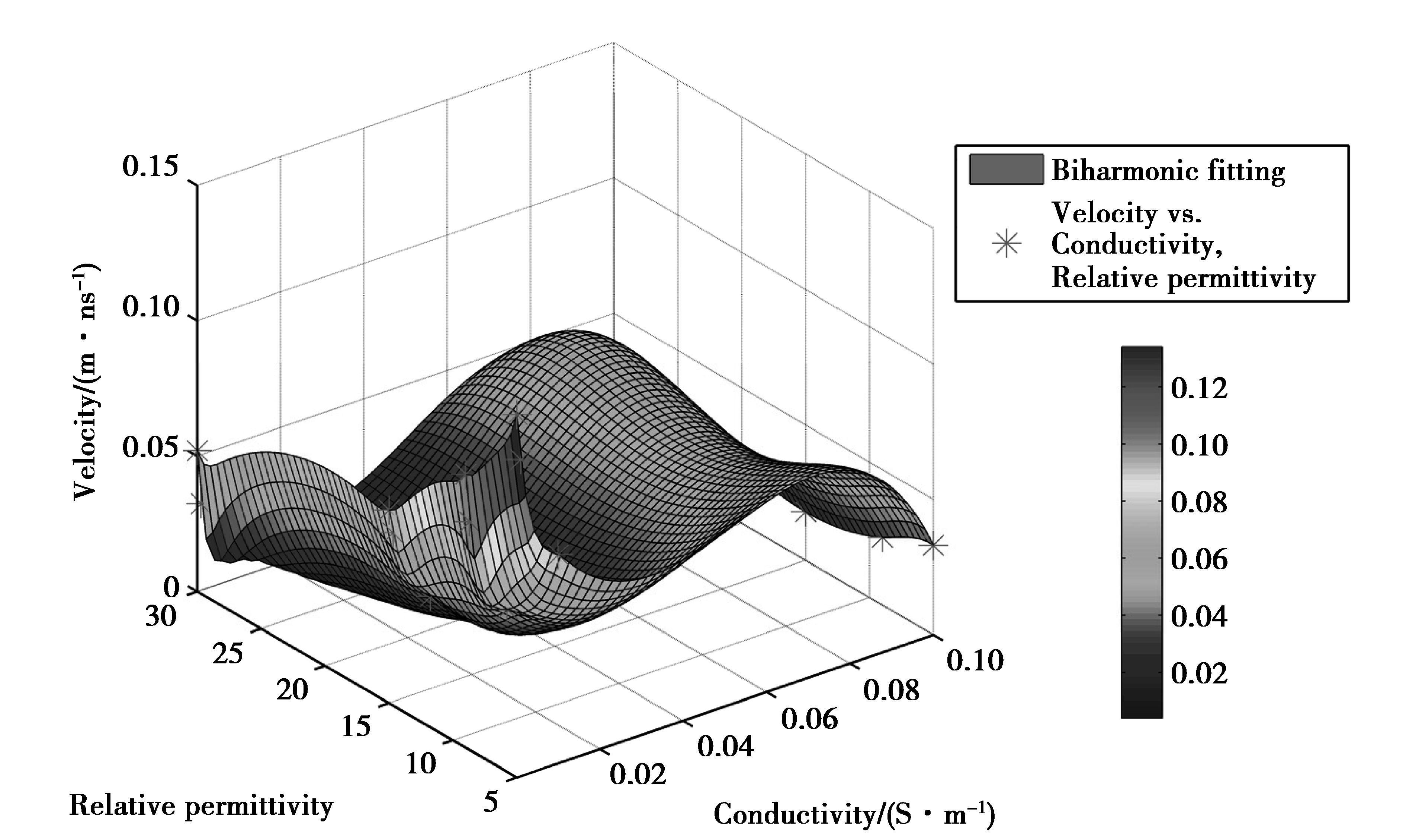
将上述相关关系的离散点进行统计,分别采用了三次插值和双调和样条插值的方法,将离散的三维曲面进行拟合,2种方法拟合的适合度信息如表 2所示。
| 表 2 三次插值和双调和样条插值拟合的适合度 Table 2 Goodness of fitting with Cubic and Biharmonic interpolation method |
从拟合的适合度信息表中看出,2种方法的均方根误差都为1,表明2种方法拟合的相关关系的变量对雷达波速都具有很强的解释能力,即拟合的适合度较高,而双调和样条插值方法的总平方误差小于三次插值的5个数量级,前者拟合的适合度更高。从图 9、图 10可以看出,其相关关系表现为一个分段的曲面,由三次插值和双调和样条插值的分段曲面可知,综合雷达波波速是相对介电常数和电导率共同影响的结果,如图 10所示,在电导率小于0.04 S/m和相对介电常数小于15的曲面内,雷达波速出现一个上升的缓冲区,数据的离散程度较小,即在该曲面范围内,钢筋混凝土介质的雷达波波速的校正可由

|
图 9 双介电参数与雷达波波速相关关系的三次插值拟合结果 Figure 9 Fitting results of the relative relationship between the dual-dielectric parameter with Velocity using Cubic interpolation method |
|
图 10 双介电参数与雷达波波速相关关系的双调和样条插值拟合结果 Figure 10 Fitting results of the relative relationship between the dual-dielectric parameter with Velocity using Biharmonic interpolation method |
2种插值方法拟合的介电参数与综合雷达波波速的相关关系曲面分别如图 9、图 10所示。
4、 结 论1)将双介电参数数值实验的结果应用于探地雷达试验检测中的波速校正,采用FD方法,对不同电导率和不同相对介电常数的钢筋混凝土模型进行了双介电参数数值实验,并从数值模拟剖面、单道波信号、电场分量波场快照3个方面,讨论了钢筋混凝土介质的相对介电常数、电导率和雷达波波速三者之间的关系;
2) 采用三次插值和双调和样条插值方法,拟合了双介电参数与雷达波波速之间的相关关系,得到了双介电参数对雷达波波速的相关关系校正的结论,为相关的探地雷达试验检测提供参考;
3) 双介电参数与雷达波波速的相关关系呈分段曲面分布,在电导率小于0.04 S/m和相对介电常数小于15的曲面内,雷达波波速的数据离散程度较小,采用
| [1] |
冯德山, 戴前伟.
高速公路路面厚度探地雷达检测[J]. 地球物理学进展 , 2008, 23 (1) : 289–294.
FENG Deshan, DAI Qianwei.
Application of ground penetrating radar in the survey of the pavement thickness in highway[J]. Progress in Geophysics , 2008, 23 (1) : 289–294.
( 2) 2)
|
| [2] |
周辉林, 姜玉玲, 徐立红, 等.
基于SVM的高速公路路基病害自动检测算法[J]. 中国公路学报 , 2013, 26 (2) : 42–47.
ZHOU Huilin, JIANG Yuling, XU Lihong, et al.
Automatic detection algorithm for expressway subgrade diseases based on SVM[J]. ChinaJournal of Highway and Transport , 2013, 26 (2) : 42–47.
( 2) 2)
|
| [3] |
Teixeira F L, Weng C C, Straka M, et al.
Finite-diference time-domain simulation of ground penetrating radar on dispersive,inhomogeneous,and conductive soils[J]. IEEE Transactions on Geoscience and Remote Sensing , 1998, 36 (6) : 1928–1937.
DOI:10.1109/36.729364 ( 1) 1)
|
| [4] |
Gürel L, Oguz U.
Three-dimensional FDTD modeling of a ground-penetrating radar[J]. IEEE Transactions on Geoscience and Remote Sensing , 2000, 38 (4) : 1513–1521.
DOI:10.1109/36.851951 ( 1) 1)
|
| [5] |
何兵寿, 魏修成.
矿井地质雷达超前探测正演模拟[J]. 煤田地质与勘探 , 2000, 28 (5) : 52–55.
HE Binshou, WEI Xiucheng.
The Forward modeling of drift GPR pulled ahead exploration[J]. Coal Geology&Exploration , 2000, 28 (5) : 52–55.
( 1) 1)
|
| [6] |
李静, 曾昭发, 吴丰收, 等.
探地雷达三维高阶时域有限差分法模拟研究[J]. 地球物理学报 , 2010, 53 (4) : 974–981.
LI Jing, ZENG Zhaofa, WU Fengshou, et al.
Study of three dimension high order FDTD simulation of GPR[J]. Chinese Journal of Geophys , 2010, 53 (4) : 974–981.
( 1) 1)
|
| [7] |
底青云, 王妙月.
雷达波有限元仿真模拟[J]. 地球物理学报 , 1999, 42 (6) : 818–825.
DI Qingyun, WANG Miaoyue.
2D finite element modeling for radar wave[J]. Chinese Journal of Geophysics , 1999, 42 (6) : 818–825.
( 1) 1)
|
| [8] |
冯德山, 戴前伟.
探地雷达时域多分辨法(MRTD)三维正演模拟[J]. 地球物理学进展 , 2008, 23 (5) : 1621–1625.
FENG Deshan, DAI Qianwei.
Application of the multi-resolution time domain method in three dimensional forward simulation of ground penetrating radar[J]. Progress in Geophysics , 2008, 23 (5) : 1621–1625.
( 1) 1)
|
| [9] |
冯德山, 戴前伟, 瓮晶波.
时域多分辨率法在探地雷达三维正演模拟中的应用[J]. 中南大学学报(自然科学版) , 2007, 38 (5) : 975–980.
FENG Deshan, DAI Qianwei, WENG Jinbo.
Application of multi-resolution time domain method in three dimensions forward simulation of ground penetrating radar[J]. Journal of Central South University (Science and Technology) , 2007, 38 (5) : 975–980.
( 1) 1)
|
| [10] |
刘新荣, 舒志乐, 朱成红, 等.
隧道衬砌空洞探地雷达三维探测正演研究[J]. 岩石力学与工程学报 , 2010, 29 (11) : 2221–2229.
LIU Xinrong, SHU Zhile, ZHU Chenghong, et al.
Study on forward simulation for ground penetrating radar three-dimensional detection of tunnel lining cavity[J]. Chinese Journal of Rock Mechanics and Engineering , 2010, 29 (11) : 2221–2229.
( 1) 1)
|
| [11] |
王亮, 李正文, 王绪本.
地质雷达探测岩溶洞穴物理模拟研究[J]. 地球物理学进展 , 2008, 23 (1) : 280–283.
WANG Liang, LI Zhengwen, WANG Xuben.
A study of Gedogical Radar to cavern detection and physical analogue[J]. Progress in Geophysics , 2008, 23 (1) : 280–283.
( 1) 1)
|
| [12] |
宋华, 王立忠.
海堤探地雷达探测模型试验研究[J]. 岩石力学与工程学报 , 2011, 30 (S1) : 2826–2833.
SONG Hua, WANG Lizhong.
Study of GPR model experiment for detecting coastal embankment[J]. Chinese Journal of Rock Mechanics and Engineering , 2011, 30 (S1) : 2826–2833.
( 1) 1)
|
| [13] |
Giannopoulos A.
Modelling ground penetrating radar by GprMax[J]. Construction and Building Materials , 2005, 19 (10) : 755–762.
DOI:10.1016/j.conbuildmat.2005.06.007 ( 1) 1)
|
| [14] |
张彬, 戴前伟, 尹小波.
基于旋转交错网格的探地雷达正演数值模拟[J]. 中国有色金属学报 , 2015, 25 (7) : 1943–1952.
ZHANG Bin, DAI Qianwei, YIN Xiaobo.
GPR simulation based on rotated staggered grid[J]. The Chinese Journal of Nonferrous Metals , 2015, 25 (7) : 1943–1952.
( 1) 1)
|
| [15] |
田钢, 林金鑫, 王帮兵, 等.
探地雷达地面以上物体反射干扰特征模拟和分析[J]. 地球物理学报 , 2011, 54 (10) : 2639–2651.
TIAN Gang, LIN Jinxing, WANG Bangbin, et al.
Simulation and analysis reflections interference from above surface objects of ground penetrating radar[J]. Chinese Journal of Geophysics , 2011, 54 (10) : 2639–2651.
( 1) 1)
|
| [16] |
Yee K S.
Numerical solution of initial boundary value problems involving Maxwell's equations in isotropic media[J]. IEEE Transactions on Antennas and Propagation , 1966, 14 (3) : 302–307.
DOI:10.1109/TAP.1966.1138693 ( 1) 1)
|
| [17] |
Atef E, Veysel D. The finite-difference time-domain method for electromagnetic with MATLAB simulations[M]. Hertfordshire: SciTech Publishing, 2009 .
( 1) 1)
|
| [18] |
Bérenger J P.
Numerical reflection of evanescent waves by PMLs:origin and interpretation in the FDTD case.Expected consequences to other finite methods[J]. International Journal of Numerical Modelling Electronic Networks Devices and Fields , 2000, 13 (2/3) : 103–114.
( 1) 1)
|
| [19] |
Park H,Lee J,Lee K.A split formulation of the nearly perfectly matched layer for an acoustic wave equation using the discontinuous Galerkin method[C]//2014 SEG Annual Meeting,26-31 October,2014,Denver,Colorado,USA.2014:3344-3348.
( 1) 1)
|
 2016, Vol. 39
2016, Vol. 39


