2. 重庆大学 土木工程学院, 重庆 400045
2. College of Civil Engineering, Chongqing University, Chongqing 400045, P. R. China
由于建筑已到使用寿命、使用功能改变、设计或施工错误以及偶然事件如地震等原因需要对建筑或路桥结构进行加固。复合纤维材料如碳纤维有强度高、耐腐蚀等优点广泛应用于结构加固领域。而直接将碳纤维粘贴于构件受拉侧对构件进行加固的方法存在公认的缺陷如碳纤维强度不能充分发挥、碳纤维应力增量滞后等,为克服这些缺陷国内外许多机构纷纷对碳纤维施加预应力后对结构进行加固。目前国内外对CFRP布施加的方法有4种:反拱法[1];利用外加辅助框架的外部张拉CFRP布法[2];在试验梁上直接纵向张拉CFRP布法[3];在试验梁上直接纵向张拉CFRP板法[4]。前3种张拉方法采用粘结CFRP材料U型箍锚固张拉的CFRP材料,再加上是层层张拉后渍胶粘贴施工时间长,CFRP的U型箍耗量大、成本高,构件表面需要打磨,以上原因致使其无法快速加固。在加载过程中第4种方法端部CFRP材料的锚固处混凝土易局部压碎。为此,文中研制出了一套利用波形齿对碳纤维进行横向张拉的预应力碳纤维加固施工技术。该法不用粘贴,省掉打磨、清洁、涂刷界面胶和打底胶等工序,提高了加固的效率 ,且波形齿锚具有能彻底解决预应力CFRP的锚固问题。因此,深入研究用波形齿对CFRP材料的横向张拉的预应力加固法具有学术及工程应用价值。
体外碳纤维带预应力加固施工技术如下:利用具有可靠受力性能的波形齿[5]先将CFRP带的两端锚固于受弯构件体外后再用中间波形齿对该CFRP带进行横向张拉的预应力加固技术。文中主要对3根足尺T形梁分别在梁两侧(适合于宽度窄、钢筋布置密集在底部无法打孔放置螺栓的情况)、梁底部(适合底部钢筋布置较少并能打孔放置螺栓的情况)布置CFRP带的体外预应力进行加固,并对加固后的T形梁进行试验研究及受弯性能分析。
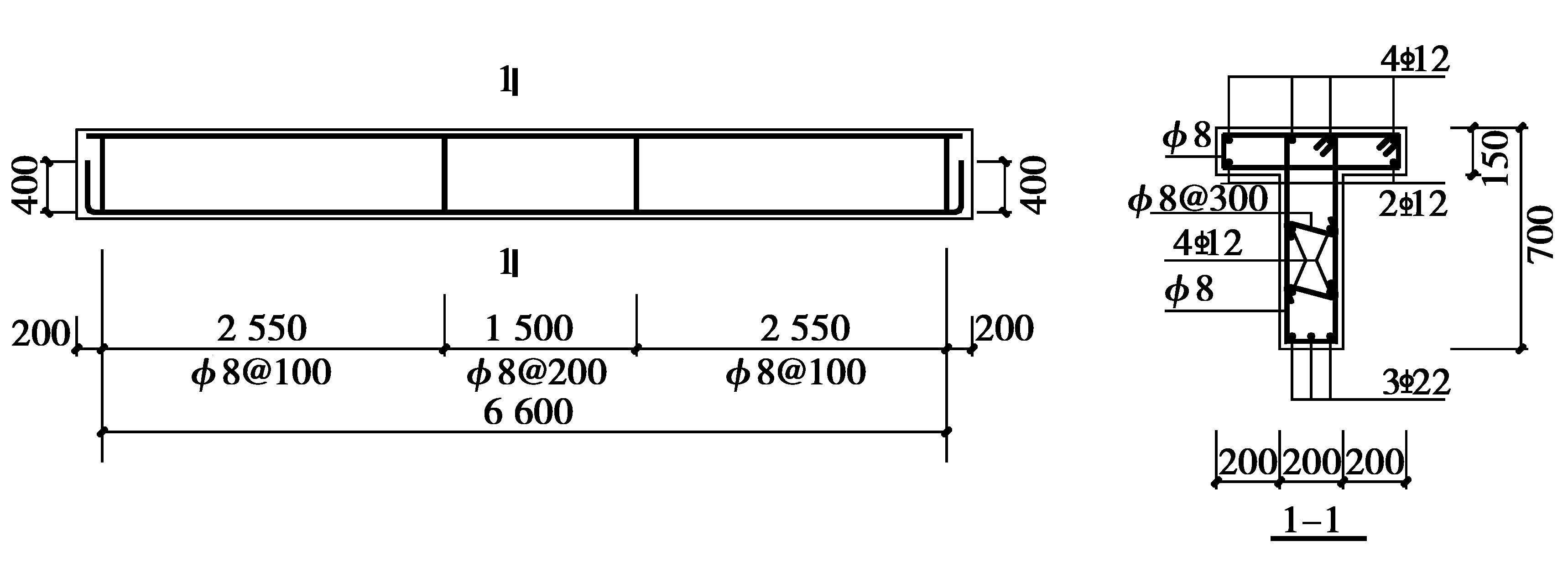
1、 试验基本情况 (1.1) 加固前的试验梁加固前的试验梁是4根长度、截面及配筋率等完全相同的T形截面钢筋混凝土梁,并且其混凝土为同车商品混凝土,混凝土为C30,其配筋3根22钢筋,如图 1所示。
|
图 1 加固前的试验梁(单位:mm) Figure 1 Test beam before strengthened |
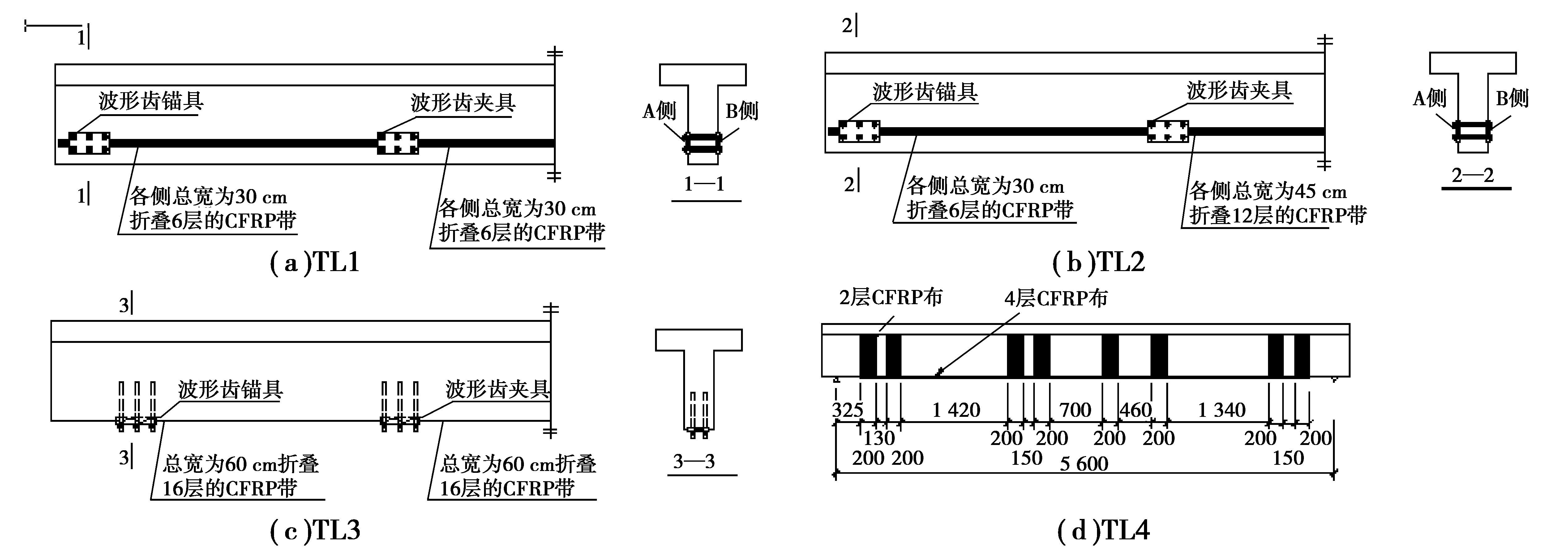
TL1、TL2为CFRP带在梁的两侧面进行体外预应力加固;TL3则为在梁底用CFRP带进行体外预应力加固;TL4为梁底用普通粘贴CFRP片材加固的试验对比梁。为了对比方便,TL1、TL3加固量相同,而TL2中段的加固量是根据TL1试验过程中段先断,左右两端碳纤维强度没有充分利用,两端的锚具锚固还十分可靠的情况设计的。TL2的加固量的设计是为了发挥左、右两段CFRP带的强度而增加中间段的加固量。TL1、TL2和TL3的加固量及加固方案如图 2所示。
|
图 2 试验梁的加固方式 Figure 2 Strengthening schemes of specimen |
碳纤维带采用如图 3所示的机具进行横向张拉[6]。试验梁中的钢筋、碳纤维片材以及混凝土材料实测参数分别如表 1和表 2所示。

|
图 3 横向张拉CFRP带示意图 Figure 3 sketch of lateral prestressing CFRP sheet |
| 表 1 试验材料力学性能参数 Table 1 Parameter of material mechanical performance |
| 表 2 试验加固方案及参数 Table 2 Strengthed Program and Parameter of beams |
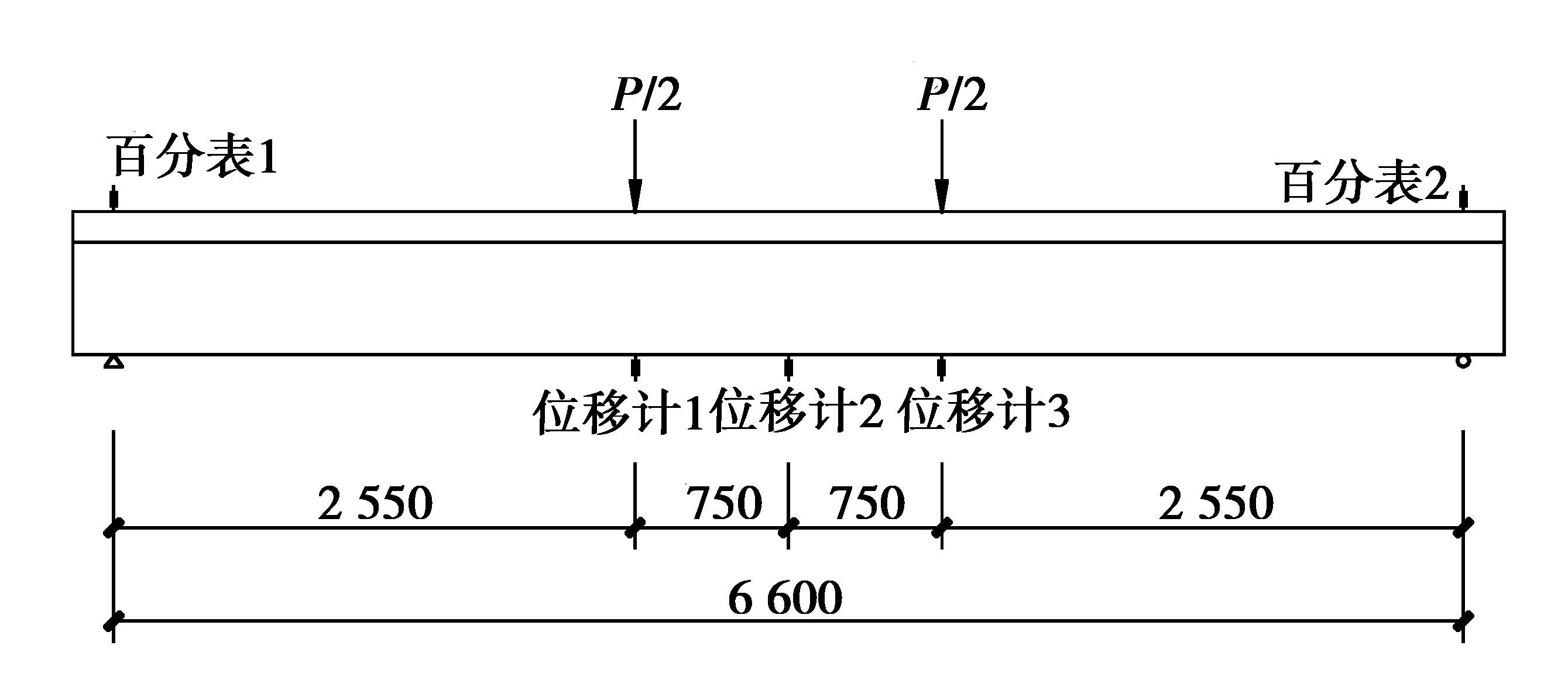
采用两点加载的方式对4根梁进行试验,为实现两点对称集中荷载分级加载在分配梁上布置液压千斤顶来。加载的两点间距为1.5 m(即纯弯矩区段长度)。通过压力传感器测得千斤顶的压力值。在正式加载过程中,均两次先预加载至25 kN(液压千斤顶的压力值)卸载后才实行单调逐级加载,在与理论计算的开裂荷载、屈服荷载、极限荷载接近时,减慢加载速率,直至构件破坏,试验加载如图 4所示,图 5是文中的加载照片。主要测量的试验数据有:受拉钢筋、纯弯段的混凝土的应变以及CFRP带沿梁长度方向左、中、右三段的应变,加固后梁的加载点、支座、跨中下挠度,以及裂缝宽度的测量。试验梁的参数如表 2所示。
|
图 4 加载示意图(单位:mm) Figure 4 Schematic illustration of test load |

|
图 5 梁试验加载图 Figure 5 Illustration of loading on testing beam |
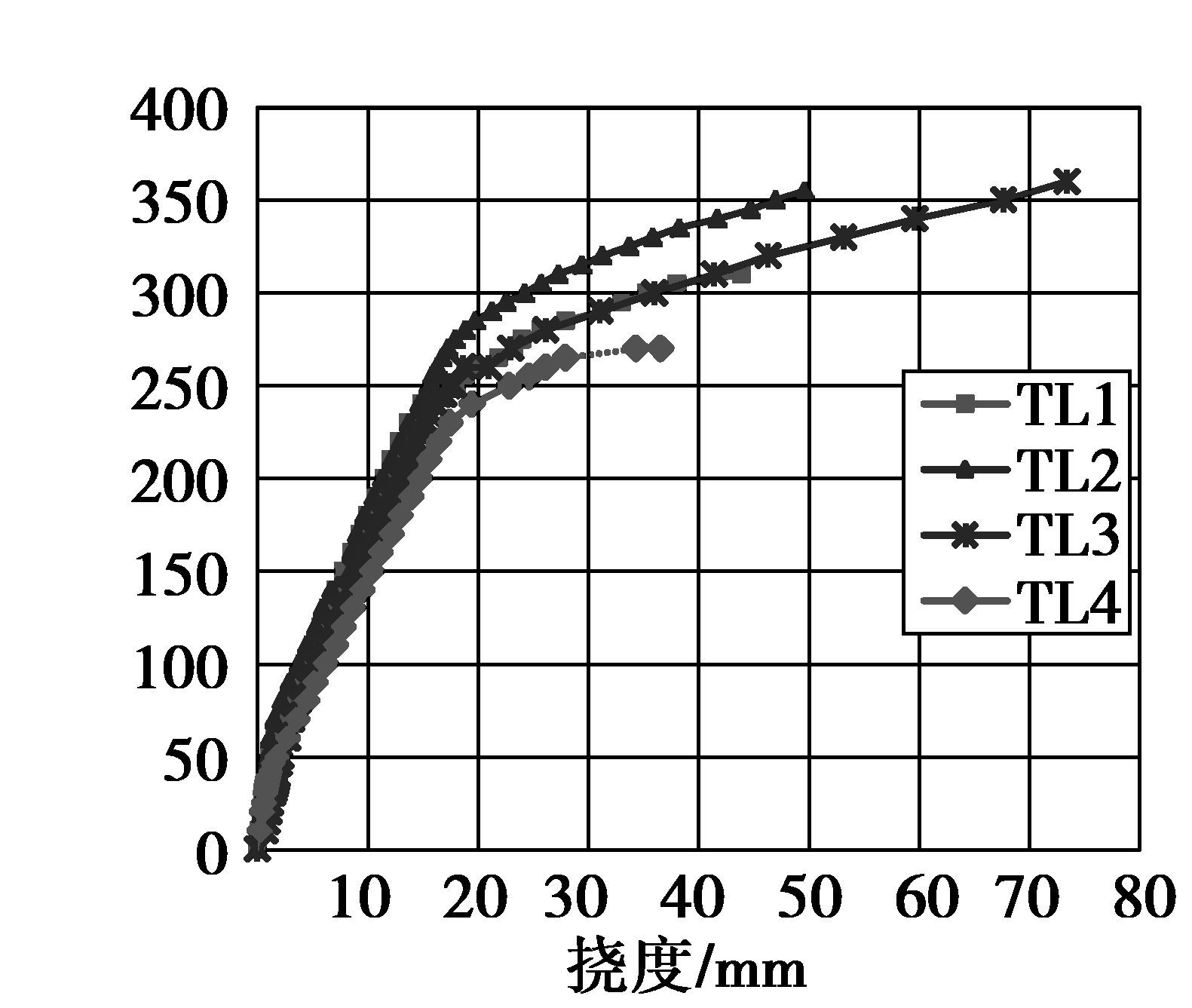
从图 6和表 3来看,在加载的前期TL1、TL2、TL3荷载-挠度曲线与TL4相比其刚度略有提高,而极限承载能力及变形能力的提高幅度较大。TL1的承载力及刚度方面与TL4有较大的改善,但TL1的CFRP片材有效高度比TL4小0.15 m。可见,梁侧CFRP体外预应力对称加固的方式与非预应力CFRP相比截面刚度、极限承载力及变形性能均有较大的改善。TL1与TL3的荷载-跨中挠度曲线是重合的,可以看出以波形齿为基础的预应力碳纤维加固技术梁侧与梁底的抗弯刚度没有明显区别;从TL1、TL2、TL3的曲线走向可以看出,只增加跨中段的加固量就可以提高加固梁的承载力和改善其变形能力,以波形齿为基础的预应力碳纤维加固技术可以随弯矩大小及位置调整加固量及波形齿布置。从表 3可以看,TL3无论是承载力还是变形能力均与总加固量相同的TL1有不少提高,说明梁底加固的极限抗弯和变形能力较梁侧加固好,因此在条件允许的情况下优先选择在梁底进行加固;从TL1~TL3的极限荷载值来看,在相同加固量的情况下梁侧加固的极限承载力提高的幅度比梁底小;各构件的延性系数均在3以上,能满足规范对梁抗震的延性需求;从破坏情况来看,无论CFRP片材在梁的跨中段或者是两端头段拉断,波形齿都能可靠地锚固住CFRP片材无滑移。由此可见波形齿具有可靠的工作性能。
|
图 6 试验梁的荷载-跨中挠度 Figure 6 Load-midspan deflection curves of beams |
| 表 3 试验梁的荷载及挠度 Table 3 Load and deflection of the test beams |
无粘结体外预应力加固中的CFRP片材除在锚固、张拉处外与试验梁的截面之间的变形不再协调,因此,试验梁的极限承载力不能仅用平截面假定的方法来确定,而预应力CFRP带的应力增量(Δfcf)只能通过张拉点与张拉点或锚固点和张拉点之间的总变形获得。加固的试验梁加载后会产生二次影响,其原因是梁的挠度会使CFRP带的有效偏心距变小,减小体外预应力CFRP片材的抗弯作用;因其挠度较小,一般的试验梁未开裂二次影响较小可忽略。体外预应力CFRP片材自由长度较大的加固梁理论计算时必须考虑二次影响,原因是极限受力状态下梁的挠度大,二次影响也随之加大。文中的理论计算借鉴牛斌的体外预应力计算理论[8]。理论计算的基本假定详见文献[9]。
(3.1) 加固梁的破坏形态依据混凝土、钢筋及 CFRP片材的应变关系,加固梁的破坏形态如下:
少筋破坏:εs>εy,εcf>εcfu,εc>εcu。
适筋破坏:εs>εy,εcf<εcfu,εc=εcu;或者εs>εy,εcf≥εcfu,εc<εcu。
超筋破坏:εs<εy,εcf<[εcfu],εc=εcu。
在设计时通过限制混凝土受压区高度来控制加固后的梁出现适筋破坏形态。
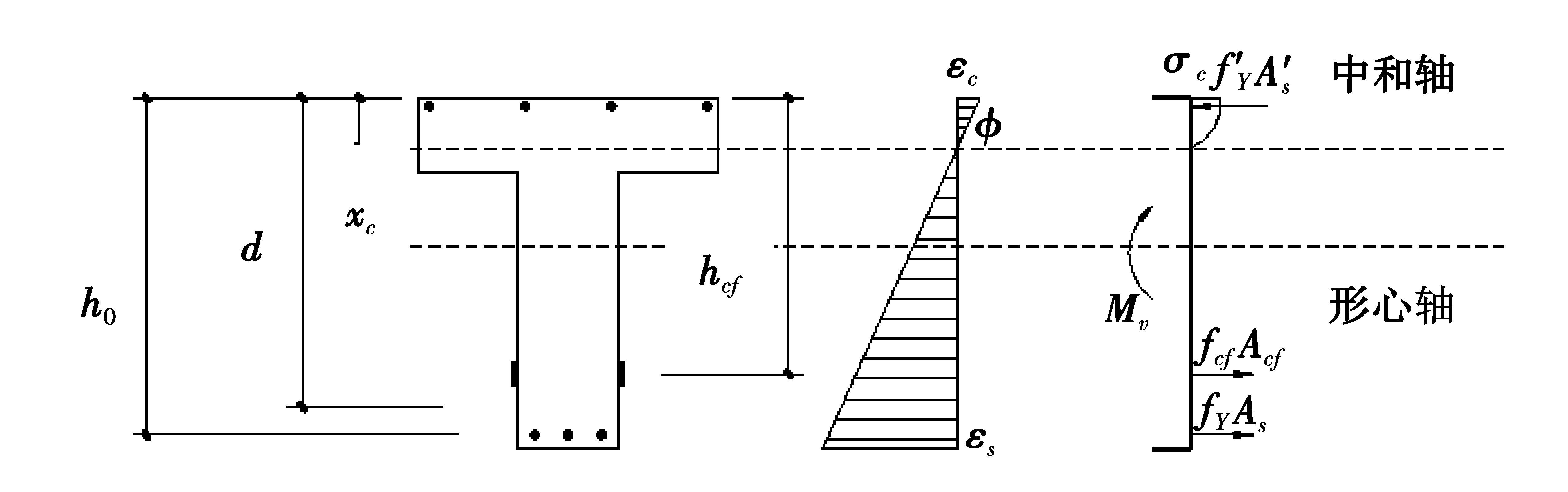
(3.2) 极限承载力计算如图 7所示,加固后的梁极限状态下弯矩:
| ${{M}_{u}}={{A}_{s}}{{f}_{y}}\left( {{h}_{0}}-\frac{x}{2} \right)+A{{\prime }_{s}}f{{\prime }_{y}}\left( \frac{x}{2-a{{\prime }_{s}}} \right)+{{A}_{cf}}{{f}_{cf}}\left( {{h}_{cf}}-\frac{x}{2} \right)\circ $ | (1) |
|
图 7 梁破坏状态的平截面假定 Figure 7 The section assumption of undermine state of beam |
考虑二次影响,式(1)修正为
| ${{M}_{u}}={{A}_{s}}{{f}_{y}}\left( {{h}_{0}}-\frac{x}{2} \right)+A{{\prime }_{s}}f{{\prime }_{y}}\left( \frac{x}{2-a{{\prime }_{s}}} \right)+{{A}_{cf}}{{f}_{cf}}\left( {{h}_{cf}}-\frac{x}{2}-\Delta \right)$ | (2) |
其中:Δ为梁计算截面(即试验梁的跨中截面)的挠度与体外CFRP带锚固点挠度的差值。
极限状态下CFRP带对应的应力值为
| $\left\{ \begin{align} & {{f}_{cf}}\text{=}{{f}_{cfe}}+\Delta {{f}_{cf}}; \ & \Delta {{f}_{cf}}=\frac{\Delta {{L}_{1}}{{E}_{cf}}}{{{L}_{1}}} \ \end{align} \right.$ | (3) |
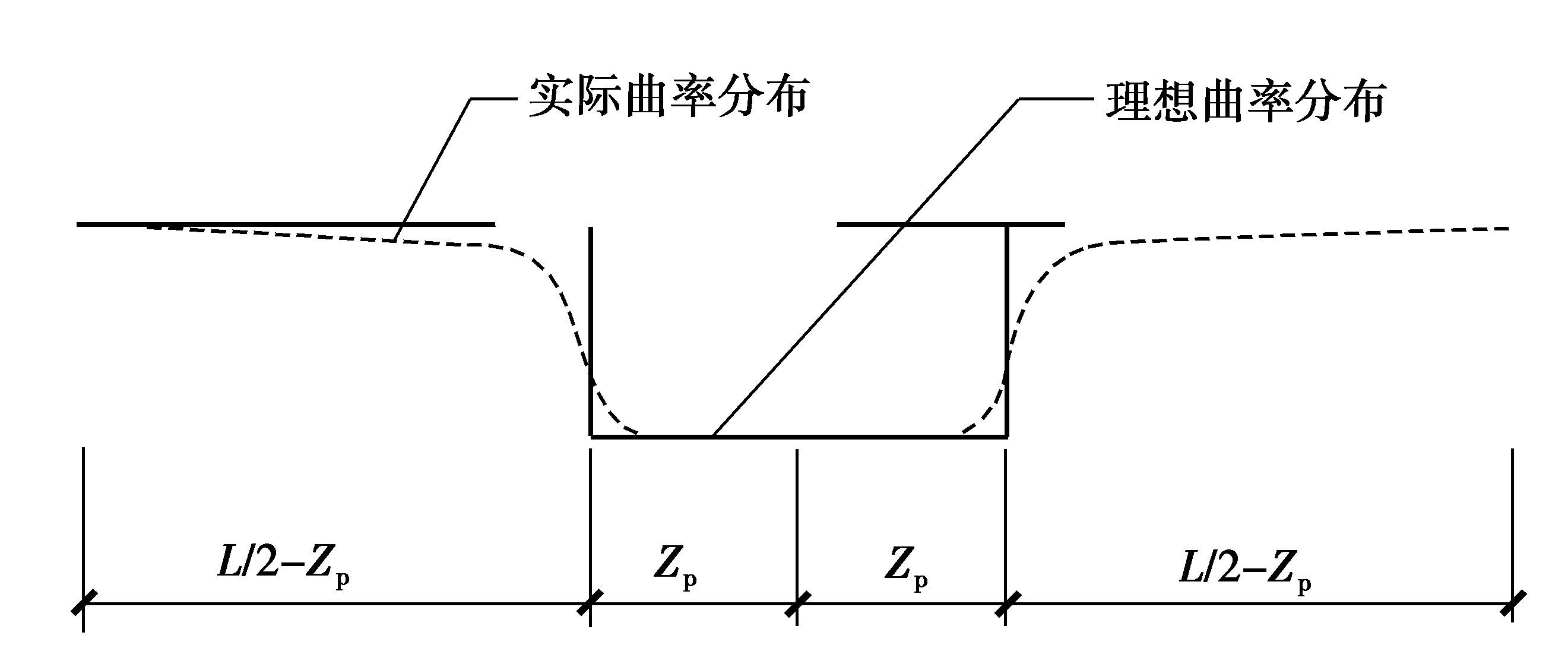
假定试验梁中普通受拉纵筋屈服后,变形主要集中在如图 8所示的塑性铰区内,则CFRP带加固试验T形梁的极限状态下的跨中挠度、曲率和转角的关系如式(4)所示。
|
图 8 体外预应力梁极限状态曲率 Figure 8 The curvature distribution of the vitro prestressed beams in limit state |
| $\begin{array}{*{35}{l}} {{\varphi }_{u}}=\frac{{{\varepsilon }_{c}}}{{{x}_{c}}} \ {{\theta }_{u}}={{Z}_{p}}{{\varphi }_{u}} \ {{\Delta }_{u}}={{Z}_{p}}{{\varphi }_{u}}\frac{L}{2} \ {{\Delta }_{d}}={{Z}_{p}}{{\theta }_{u}}=Z_{p}^{2}{{\varphi }_{u}} \ \Delta ={{\Delta }_{u}}-{{\Delta }_{d}}={{Z}_{p}}{{\varphi }_{u}}(L/2-{{Z}_{p}}) \ \end{array}$ | (4) |
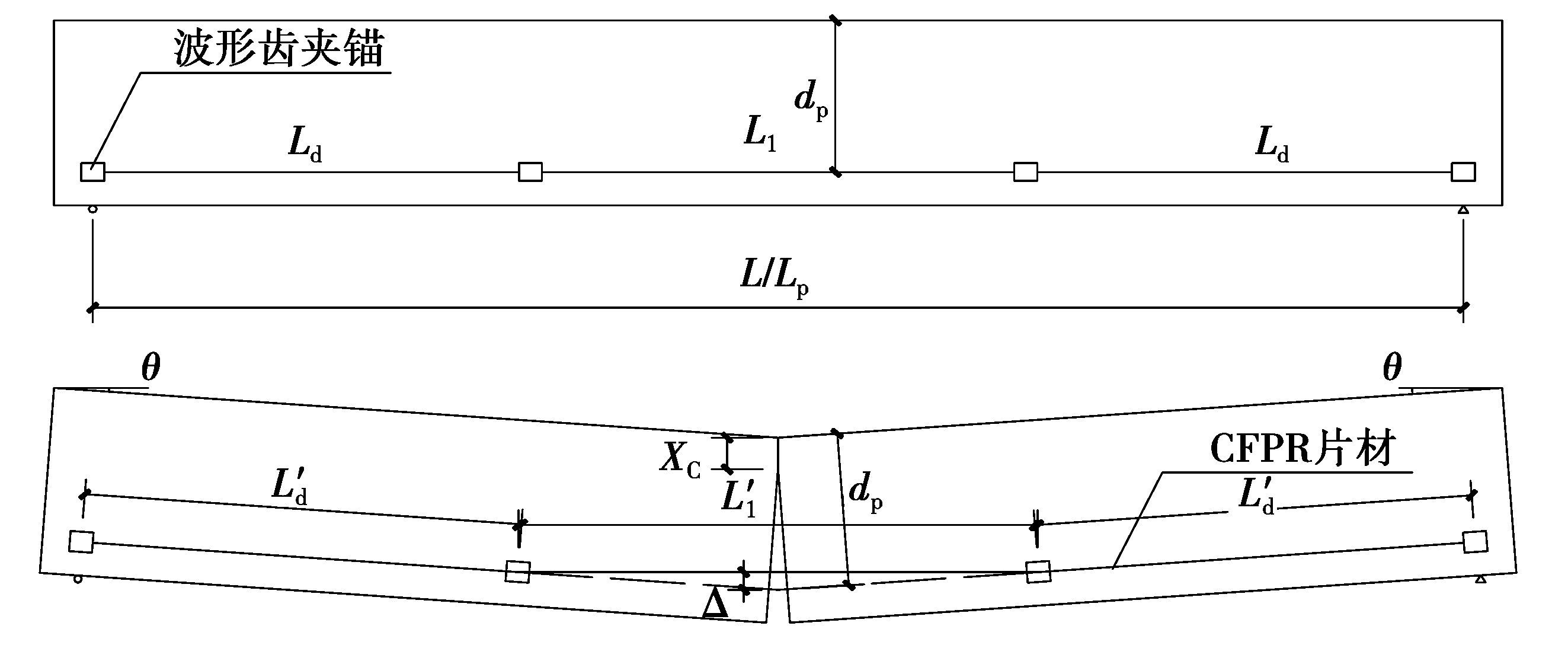
依据体外预应力片材的锚固点布置、线型及外荷载形式均与体外无粘结预应力试验梁的极限弯矩有关,因此应根据图 9所示的关系及CFRP片材加固的部位分别进行分析。
|
图 9 体外预应力CFRP带加固梁示意图 Figure 9 The beam strengthened of the vitro prestressed CFRP |
1)对称直线布置CFRP带在梁两侧面
梁两侧面对称直线布置CFRP带加固后的梁的极限弯矩值为式(2)。
依据图 9所示,试验梁极限状态下中间锚固点(即张拉点)之间的CFRP带长度为
| $L{{\prime }_{1}}=2~\text{sin}~{{\theta }_{u}}({{d}_{p}}-{{x}_{c}})+{{L}_{1}}~\text{cos}~{{\theta }_{u}}$ | (5) |
加固后的梁受弯后,其中性轴将产生弓形缩短,其值约为L1(1-cos θu),则极限状态时CFRP片材中间锚固点(即张拉点)间的伸长值为
| $\Delta {{L}_{1}}=2\text{sin}~{{\theta }_{u}}({{d}_{p}}-{{x}_{c}})+{{L}_{1}}\text{cos}~{{\theta }_{u}}-{{L}_{1}}(1-\text{cos}~{{\theta }_{u}})=2({{d}_{p}}-{{x}_{c}}){{\theta }_{u}}-{{L}_{1}}{{\theta }_{u}}^{2}$ | (6) |
2)直线布置CFRP带在梁底
在梁底直线布置CFRP带加固后的梁的极限弯矩值为式(1)。
依据图 9所示关系,则有:
| $L{{\prime }_{1}}=2\text{sin}{{\theta }_{u}}({{d}_{p}}-{{x}_{c}})+{{L}_{1}}$ | (7) |
| $\Delta {{L}_{1}}=2({{d}_{p}}-{{x}_{c}}){{\theta }_{u}}-{{L}_{1}}\frac{\theta _{u}^{2}}{2}$ | (8) |
将式(6)或式(8)代入式(3)可以得到Δfcf。
根据加固后的试验截面的内力平衡有:
第1类T形截面:
| ${{\alpha }_{1}}{{\beta }_{1}}{{f}_{c}}{{b}_{f}}x={{A}_{s}}{{f}_{y}}-A{{\prime }_{s}}f{{\prime }_{y}}+{{A}_{cf}}{{f}_{cf}}+\Delta {{f}_{cf}}$ | (9) |
第2类T形截面:
| ${{\alpha }_{1}}{{\beta }_{1}}{{f}_{c}}(bx+({{b}_{f}}-b){{h}_{f}})={{A}_{s}}{{f}_{y}}-A{{\prime }_{s}}f{{\prime }_{y}}+{{A}_{cf}}({{f}_{cf}}+\Delta {{f}_{cf}})$ | (10) |
将Δfcf代入式(9)或式(10)可获得混凝土受压区高度x,再将所求得的x代入式(1)或式(2)求解出加固梁的抗弯承载力理论值。
依据文献[8],加固梁的塑性铰区长度为
| ${{Z}_{p}}=0.5{{d}_{p}}+0.05Z$ | (11) |
其中:L0为等弯矩区的长度;Z为剪跨长度。
按上述方法对TL1-TL3进行计算,其混凝土极限压应变取0.033,纵向钢筋极限拉应变为1%,CFRP片材极限拉应变为1%(若按式(3)计算出的CFRP应变值大于1%则取1%进行承载力计算),表 4为TL1~TL3的理论计算结果。
| 表 4 加固后的梁的试验值与理论值 Table 4 Theoretical and actual value of beams strengthened |
图 6为加固试验梁的荷载-挠度曲线,有明显三折线特征,考虑“二次影响”的有效惯性矩法计算加固梁的挠度。
将CFRP带上的预应力作为外力采用共轭梁法,可得反拱挠度值
| ${{f}_{L}}=\frac{{{A}_{cf}}{{f}_{cfe}}el}{2{{E}_{c}}{{I}_{e}}}\left( \lambda +\frac{1}{4} \right)$ | (12) |
加固梁在外荷载和预应力作用下的跨中挠度则为
| $f=\frac{SM{{L}^{2}}}{{{E}_{c}}{{I}_{e}}}-\frac{{{A}_{cf}}{{f}_{cfe}}el}{2{{E}_{c}}{{I}_{e}}}\left( \lambda +\frac{1}{4} \right)$ | (13) |
考虑二次效应:
| $f=\frac{\frac{SM{{L}^{2}}}{{{E}_{c}}{{I}_{e}}}-\frac{{{A}_{cf}}{{f}_{cfe}}l}{2{{E}_{c}}{{I}_{e}}}\left( \lambda +\frac{1}{4} \right)\left( {{e}_{p}}+\Delta d \right)}{1-\frac{{{A}_{cf}}{{f}_{cfe}}l}{2{{E}_{c}}{{I}_{e}}}\left( \lambda +\frac{1}{4} \right)}$ | (14) |
其中:
| $S=\frac{1}{8}\left( 1-\frac{4{{a}^{2}}}{3{{L}^{2}}} \right),$ |
| ${{\Delta }_{d}}=\frac{M\lambda L}{6{{E}_{c}}{{I}_{e}}}\left[ 3-3{{\left( \frac{a}{L} \right)}^{2}}-\frac{{{\lambda }^{2}}}{aL} \right]-\frac{{{f}_{cfe}}{{A}_{cf}}el\lambda }{2{{E}_{c}}{{I}_{e}}}\circ $ |
式中:Δd是中间锚固点的位移量;梁底CFRP片材加固时,预应力CFRP片材的偏心距不变;λ是中间锚具中心到支座的距离;a为剪跨比;Ie按Branson建议的公式计算[10],其为控制截面的有效惯性矩。
| ${{I}_{e}}={{\left( \frac{{{M}_{cr}}}{M} \right)}^{3}}{{I}_{0}}+\left[ 1-{{\left( \frac{{{M}_{cr}}}{M} \right)}^{3}} \right]{{I}_{cr}},$ |
| ${{M}_{cr}}={{f}_{cfe}}{{A}_{cf}}{{e}_{p}}+\frac{{{f}_{cfe}}{{A}_{cf}}{{I}_{0}}}{{{A}_{y}}}+\frac{{{f}_{t}}{{I}_{0}}}{y}$ |
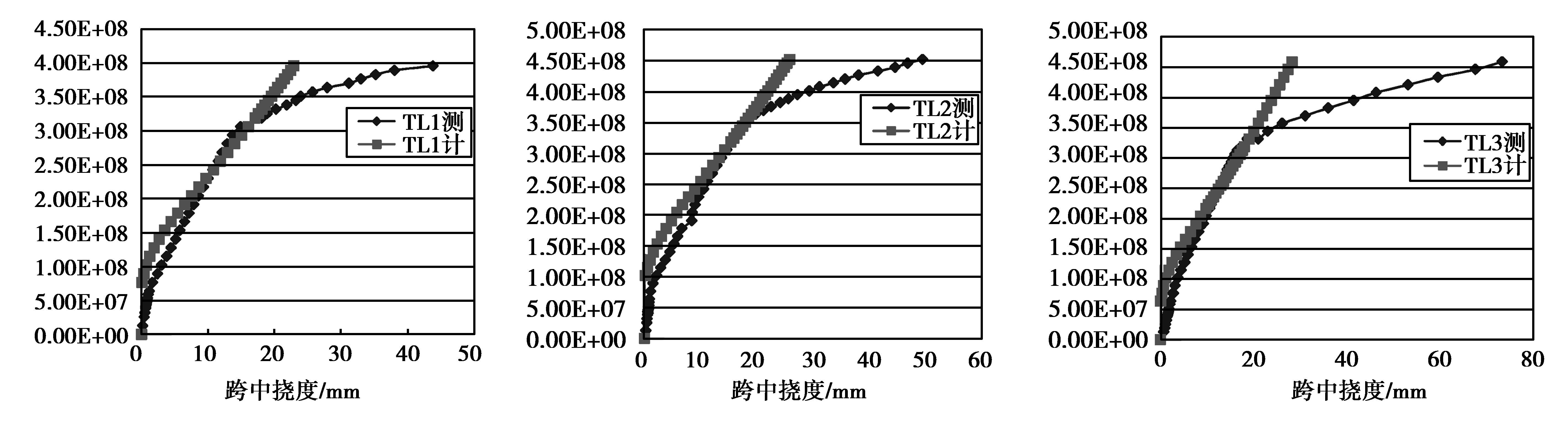
图 10为各试验梁按公式(14)计算结果与试验结果的比较。其余试件的对比情况类似。结果表明加固试验梁屈服前理论计算值与试验值曲线吻合度较好,具有一定程度的参考价值(对于结构构件来说,在正常使用阶段才需要计算挠度)。
|
图 10 试验梁挠度理论计算与试验值 Figure 10 Theoretical and experimental results of the test beams |
1)波形齿横向张拉CFRP片材在构件底部或构件两侧对称加固法与直接粘贴的非预应力CFRP材料相比在极限荷载、屈服荷载、开裂荷载均有较大幅度的提高,且变形性能也有较大改善。同时能解决预应力CFRP材料加固中的锚固问题。
2)在梁底与梁侧进行体外预应力波形齿横向张拉CFRP带的加固方法对提高梁的抗弯刚度区别不大。
3)多点锚固无粘结预应力CFRP片材能根据构件受力情况来调整各段的加固量从而能更充分利用材料的高强性能。
4)多点锚固体外无粘结预应力CFRP片材加固梁的延性能满足规范对梁的延性需求的规定。
5)文中的理论抗弯承载能力的计算公式、跨中挠度(钢筋屈服前)理论计算公式均与试验值较为吻合,可供设计参考使用。
| [1] |
赵启林, 王景全, 金广谦, 等.
碳纤维加固的"反拱预应力技术"及其提高钢结构承载能力的分析[J]. 钢结构 , 2002, 17 (3) : 51–54.
ZHAO Qilin, WANG Jingquan, JIN Guangqian, et al.
Analysis on the "revrse-arch prestressed technique" and the improved bearing capacity for steel structure strengthened by carbon-fibre[J]. Steel Construction , 2002, 17 (3) : 51–54.
( 0) 0)
|
| [2] |
Yu P,Silva P F,Nanni A.Flexural performance of RC beams strengthened with prestressed CFRP belts[C]//Materials and Processing Technology-60 Years of SAMPE Progress,May16-20,2004,Long Beach,CA,2004.
( 0) 0)
|
| [3] |
彭晖, 尚守平, 王海东, 等.
用预应力CFRP对RC梁的加固工艺研究[J]. 建筑技术开发 , 2003, 30 (5) : 21–23.
PENG Hui, SHANG Shouping, WANG Haidong, et al.
With the prestressed CFRP to the RC beam reinforcement technology research[J]. Building Techinque Development , 2003, 30 (5) : 21–23.
( 0) 0)
|
| [4] |
Basler M,Clenin R.Bridge strengthening with prestressed CFRP plate systems[C]//Proceedings of IABSE Symposium Shanghai,July 20-23,2004,Alberta,2004:1-8.
( 0) 0)
|
| [5] |
卓静.高强度复合材料FRP片材波形夹具锚锚固系统及应用研究[D].重庆:重庆大学,2004.
ZHUO Jing.Anchorage systems of high strength fiber reinforced polymer and the applications in strengthened structure[D].Chongqing:Chongqing University,2004.(in Chinese)
http://www.oalib.com/references/16933071 ( 0) 0)
|
| [6] |
陈小英, 李唐宁, 陈明政, 等.
波形齿锚具锚固CFRP片材的力学性能试验研究及锚具体系设计[J]. 工程力学 , 2009, 26 (6) : 184–192.
CHEN Xiaoying, LI Tangning, CHEN Mingzheng, et al.
Experimental research on mechanical property of anchor CFRP sheet with the wave-shaped-teeth anchor and design of anchor system[J]. Engineering Mechanics , 2009, 26 (6) : 184–192.
( 0) 0)
|
| [7] |
陈小英, 李唐宁.
波形齿体系张拉并锚固CFRP片材的预应力损失[J]. 土木建筑与环境工程 , 2009, 31 (3) : 18–24.
CHEN Xiaoying, LI Tangning.
Experimental analysis of pre-stress loss on tensioning and anchoring CFRP sheet with wave-shaped-gear[J]. Journal of Chongqing Jianzhu University , 2009, 31 (3) : 18–24.
( 0) 0)
|
| [8] |
牛斌.
体外预应力混凝土梁极限状态分析[J]. 土木工程学报 , 2000, 33 (6) : 7–15.
NIU Bin.
Ultimate analysis of externally prestressed concrete beams[J]. China Civil Engineering Journal , 2000, 33 (6) : 7–15.
( 0) 0)
|
| [9] |
张龙生.预应力CFRP片材体外快速加固混凝土梁试验研究与分析[D].重庆:重庆大学,2008.
ZHANG Longsheng.The analyse and test research the beam reinforced concrete strengthened fast by prestressing CFRP sheets out of beam's body[D].Chongqing:Chongqing University,2008.(in Chinese)
( 0) 0)
|
| [10] |
Branson D E.
Trost H.Application of the i-effective method in calculation deflections of partially prestressed members[J]. PCI Journal , 1982, 27 (5) : 62–77.
DOI:10.15554/pcij ( 0) 0)
|
 2016, Vol. 39
2016, Vol. 39

