2. 重庆大学重庆市冶金工程重点实验室, 重庆 400044;
3. 重庆大学化学化工学院, 重庆 400044
2. Chongqing Provincial Key Laboratory of Metallurgical Engineering, Chongqing University, Chongqing 400044, P. R. China;
3. School of Chemistry and Chemical Engineering, Chongqing University, Chongqing 400044, P. R. China
以CO、H2和固体碳等为能源和还原剂,将固态情形下矿石还原而获得的金属铁,称为直接还原铁(direct reduction iron,DRI)。它是一种非常理想的熔炼原材料[1],在电炉炼钢中可替代部分甚至全部废钢,在转炉炼钢中可以作冷却剂,可以加入高炉代替部分氧化球团等。尽管以H2还原为主的MIDREX竖炉工艺目前是生产DRI的重要途径之一[2-5],但驱动氢还原竖炉工艺推广的力量一直有限,氢还原竖炉工艺的研究一直没有得到足够重视[1, 6]。随着环保压力的逐渐增大和人类对氢能等清洁能源持继不断地开发,今后更广范围应用MIDREX工艺以满足日益增长的DRI商业需求不会是遥远的事情[6]。因此,对氢还原竖炉工艺进行研究具有重要意义。
竖炉还原工艺中,入炉气体提供还原性气体的同时,还提供还原所需要的热量。MIDREX工艺在实际操作时,一般向入炉气体中兑入氮气来保证还原的热量需求[2-5];氮气兑入的多少影响到还原性气体和热量的利用程度。CO还原矿石是弱放热反应,而H2还原矿石是吸热反应;因此,入炉气体中CO的配入量也影响煤气的需要量。总之,入炉煤气的成分对整个工艺有很大的影响。
量化消耗量、生成量等与工艺参数的关系以及工艺参数之间的限制关系已成为工艺分析、完善流程设计工艺系统优化的重要手段[7-15],是工艺系统控制的核心部分,可为生产中工艺控制系统设计奠定基础。笔者基于物料平衡与热量平衡建立可计算氢还原竖炉入炉煤气量等的模型,在一定条件下,确定消耗量和生成量随N2兑入成分、CO的配入量等工艺参数的定量变化规律,寻找煤气最佳利用的操作点,探索操作参数之间的影响规律和氢还原竖炉工艺的节能减排潜力,对工艺的设计和开发提供有用的信息。
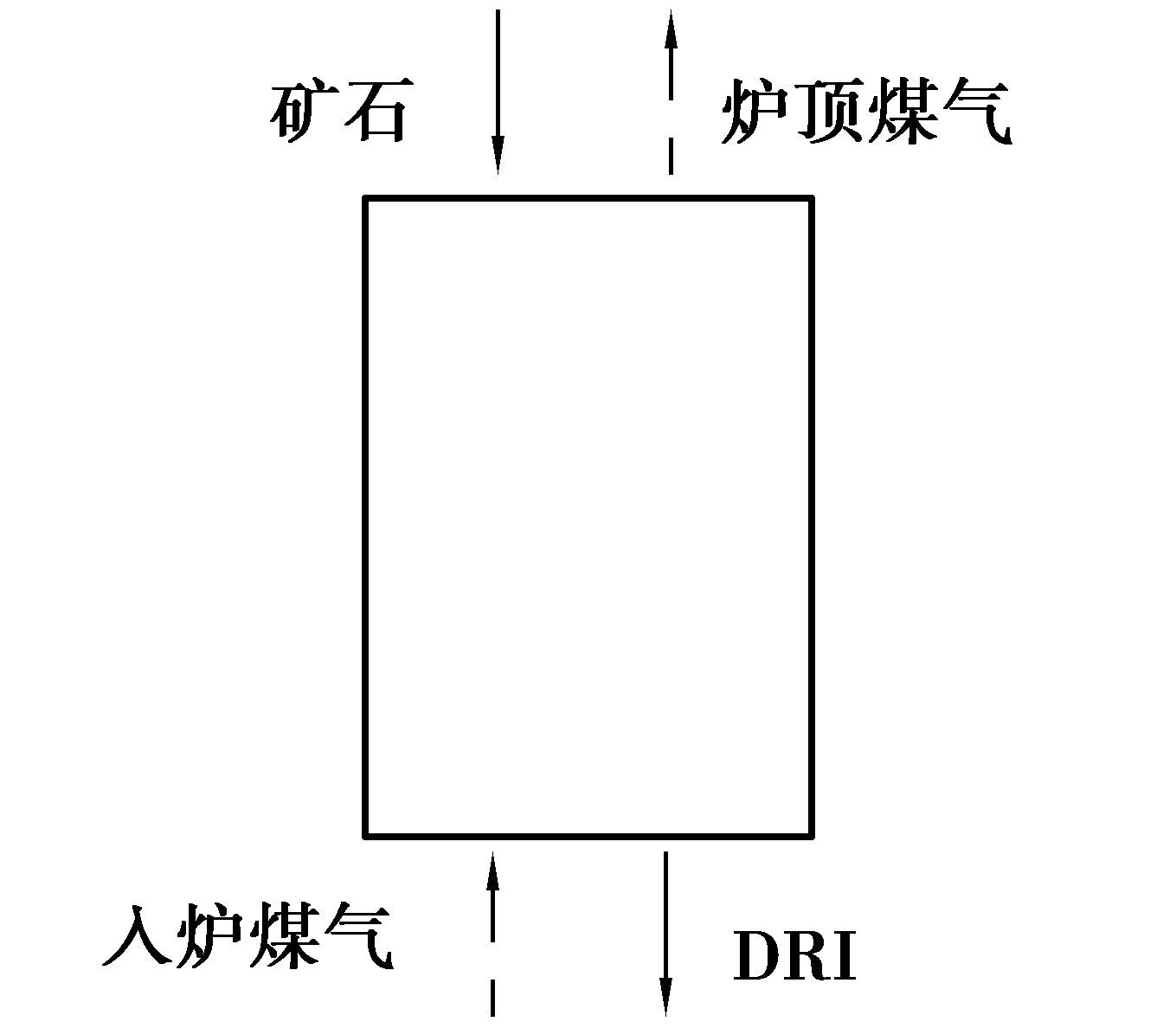
1、 氢还原竖炉模拟计算模型 (1.1) 模型建立的基本条件竖炉反应器及其物料流向示意图见图 1。向下流动质量为more的矿石和向上流动体积为Vingas的入炉煤气在炉内反应生成DRI和炉顶煤气。影响Vingas的因素有:N2的体积分数φN2(ingas)、CO和H2含量的比值φCO(ingas)/φH2(ingas)、入炉煤气的温度Tingas、DRI的金属化率MRDRI、DRI的温度TDRI、炉顶煤气的温度Toutgas、炉顶煤气还原势Routgas等。这里,Routgas定义为
| ${{R}_{\text{outgas}}}\text{=}\frac{{{\varphi }_{\text{CO}}}_{\left( \text{outgas} \right)}+{{\varphi }_{{{\text{H}}_{\text{2}}}}}_{\left( \text{outgas} \right)}}{{{\varphi }_{\text{CO}}}{{_{_{2}}}_{\left( \text{outgas} \right)}}+{{\varphi }_{{{\text{H}}_{\text{2}}}\text{O}}}_{\left( \text{outgas} \right)}},$ | (1) |
符号φi(ingas)、φi(outgas)分别表示i组分在入炉煤气和炉顶煤气中的体积分数;为方便,后文记φCO(ingas)/φH2(ingas)为q。根据竖炉操作原理[1-5]和已有操作经验,确定以上各参数的取值范围见表 1。
|
图 1 竖炉工艺物料流向示意图 Figure 1 The input and output materials of shaft furnace |
| 表 1 参数取值范围 Table 1 The values for process parameters |
本模拟计算以生产1 t DRI为基础。为简化,入炉煤气中的气体主要考虑H2、CO和N2,炉内反应主要考虑铁氧化物的还原,炉顶煤气中的炉尘不作考虑。入炉矿石为氧化性球团,矿石中铁全以Fe2O3形式存在。计算所选用矿石的成分见表 2。
| 表 2 矿石成分 Table 2 The ore content |
DRI中的金属铁量(kg)为:more·wTFe(ore)·MRDRI。其中wTFe(ore)为矿石中全铁的质量分数,DRI中的FeO量(kg)为:more·mTFe(ore)·(1-MRDRI)÷56×72。DRI中的脉石量(kg)为:more-more·wTFe(ore)÷112×160。由此得产生1 t DRI需要的矿石量(kg)为
| ${{m}_{\text{ore}}}=\frac{1000}{{{w}_{TFE\left( \text{ore} \right)}}\cdot M{{R}_{\text{DRI}}}+{{w}_{TFe(ore)}}\cdot \left( 1-M{{R}_{\text{DRI}}} \right)\div 56\times 72+\left( 1-{{w}_{\text{TFe(ore)}}} \right)\div 112\times 160}\circ $ | (2) |
当Fe2O3还原至FeO时,矿石所失去的氧(kg)为
| $O_{\text{loss}}^{1}={{m}_{\text{ore}}}\cdot {{w}_{\text{TFe(ore)}}}\div 112\times 16$ | (3) |
当FeO还原至Fe时,矿石所失去的氧(kg)为
| $O_{\text{loss}}^{2}={{W}_{\text{ore}}}\cdot {{\gamma }_{\text{TFe(ore)}}}\cdot M{{R}_{\text{DRI}}}\div 56\times 16$ | (4) |
假设矿石因反应而分别被H2、CO夺去的氧量与它们在入炉煤气中的量成正比,则H2还原矿石而产生的水量(N·m3)为
| $V_{{{\text{H}}_{\text{2}}}\text{O}}^{r}=\frac{O_{\text{loss}}^{1}+O_{\text{loss}}^{2}}{16}\cdot \frac{{{\varphi }_{{{\text{H}}_{\text{2}}}}}_{\left( \text{ingas} \right)}}{{{\varphi }_{\text{CO}}}_{\left( \text{ingas} \right)}+{{\varphi }_{{{\text{H}}_{\text{2}}}}}_{\left( \text{ingas} \right)}}\times 22.4$ | (5) |
CO还原矿石产生的CO2量(N·m3)为
| $V_{\text{C}{{\text{O}}_{\text{2}}}}^{\text{r}}=\frac{O_{\text{loss}}^{1}+O_{\text{loss}}^{2}}{16}\cdot \frac{{{\varphi }_{\text{CO}}}_{\left( \text{ingas} \right)}}{{{\varphi }_{\text{CO}}}_{\left( \text{ingas} \right)}+{{\varphi }_{{{\text{H}}_{\text{2}}}}}_{\left( \text{ingas} \right)}}\times 22.4$ | (6) |
炉顶煤气量等于入炉煤气量,即
| ${{V}_{\text{outgas}}}={{V}_{\text{ingas}}}$ | (7) |
炉顶煤气中各组分的体积分数分别为
| ${{\varphi }_{\text{CO}}}_{\left( \text{outgas} \right)}=\frac{{{V}_{\text{ingas}}}\cdot {{\varphi }_{\text{CO}}}_{\left( \text{ingas} \right)}-V_{\text{C}{{\text{O}}_{\text{2}}}}^{\text{r}}}{{{V}_{\text{outgas}}}},$ | (8) |
| ${{\varphi }_{{{\text{H}}_{\text{2}}}}}_{\left( \text{outgas} \right)}=\frac{{{V}_{\text{ingas}}}\times {{\varphi }_{{{\text{H}}_{\text{2}}}}}_{\left( \text{ingas} \right)}-V_{{{\text{H}}_{\text{2}}}\text{O}}^{\text{r}}}{{{V}_{\text{outgas}}}},$ | (9) |
| ${{\varphi }_{{{\text{H}}_{\text{2}}}\text{O}}}_{\left( \text{outgas} \right)}=\frac{V_{{{\text{H}}_{\text{2}}}\text{O}}^{\text{r}}}{{{V}_{\text{outgas}}}},$ | (10) |
| ${{\varphi }_{\text{CO}}}{{_{_{2}}}_{\left( \text{outgas} \right)}}=\frac{V_{\text{C}{{\text{O}}_{\text{2}}}}^{\text{r}}}{{{V}_{\text{outgas}}}},$ | (11) |
| ${{\varphi }_{\text{N}}}{{_{_{2}}}_{\left( \text{outgas} \right)}}={{\varphi }_{\text{N}}}{{_{_{2}}}_{\left( \text{ingas} \right)}}$ | (12) |
入炉煤气带入显热(kJ)为
| ${{Q}_{\text{in}}}=\sum\limits_{i}{{{V}_{\text{ingas}}}\cdot {{\varphi }_{i}}_{\left( \text{ingas} \right)}}\cdot {{H}_{i}}{{|}_{{{T}_{\text{ingas}}}}},$ | (13) |
式中:HiTingas是1 N·m3i气体在温度为Tingas时的显热,kJ/(N·m3),i=(H2,CO,N2)。矿石的反应热Qoutr由Fe2O3与CO的反应热QCO1、FeO与CO的反应热QCO2、Fe2O3与H2的反应热QH21、FeO与H2的反应热QH22组成,即
| $Q_{\text{out}}^{\text{r}}=Q_{\text{CO}}^{\text{1}}+Q_{\text{CO}}^{\text{2}}+Q_{{{\text{H}}_{\text{2}}}}^{\text{1}}+Q_{{{\text{H}}_{\text{2}}}}^{\text{2}},$ | (14) |
其中:
| $Q_{\text{CO}}^{\text{1}}=\frac{O_{\text{loss}}^{1}}{16}\cdot \frac{{{\varphi }_{\text{CO}}}_{\left( \text{ingas} \right)}}{{{\varphi }_{\text{CO}}}_{\left( \text{ingas} \right)}+{{\varphi }_{{{\text{H}}_{\text{2}}}}}_{\left( \text{ingas} \right)}}\times \left( -1600 \right),$ | (15) |
| $Q_{\text{CO}}^{\text{2}}=\frac{O_{\text{loss}}^{2}}{16}\cdot \frac{{{\varphi }_{\text{CO}}}_{\left( \text{ingas} \right)}}{{{\varphi }_{\text{CO}}}_{\left( \text{ingas} \right)}+{{\varphi }_{{{\text{H}}_{\text{2}}}}}_{\left( \text{ingas} \right)}}\times \left( -10980 \right),$ | (16) |
| $Q_{{{\text{H}}_{\text{2}}}}^{\text{1}}=\frac{O_{\text{loss}}^{1}}{16}\cdot \frac{{{\varphi }_{{{\text{H}}_{\text{2}}}}}_{\left( \text{ingas} \right)}}{{{\varphi }_{\text{CO}}}_{\left( \text{ingas} \right)}+{{\varphi }_{{{\text{H}}_{\text{2}}}}}_{\left( \text{ingas} \right)}}\times 38960,$ | (17) |
| $Q_{{{\text{H}}_{\text{2}}}}^{\text{2}}=\frac{O_{\text{loss}}^{2}}{16}\cdot \frac{{{\varphi }_{{{\text{H}}_{\text{2}}}}}_{\left( \text{ingas} \right)}}{{{\varphi }_{\text{CO}}}_{\left( \text{ingas} \right)}+{{\varphi }_{{{\text{H}}_{\text{2}}}}}_{\left( \text{ingas} \right)}}\times 29580$ | (18) |
随DRI输出的显热(kJ)为
| $Q_{\text{out}}^{\text{DRI}}=\sum\limits_{i}{{{m}_{i}}}\cdot {{H}_{i}}{{|}_{{{T}_{\text{DRI}}}}}$ | (19) |
式中:mi为i物质的质量(kg);HiTDRI为1 kg i物质在温度TDRI时的显热,kJ/kg,i=(Fe,FeO,gangue)。假设竖炉热损失(kJ)是其热收入的5%,即
| $Q_{\text{out}}^{\text{loss}}=0.05\times {{Q}_{\text{in}}},$ | (20) |
根据输入热等于输出热的关系得随炉顶煤气输出的显热(kJ)为
| $Q_{\text{out}}^{\text{outgas}}={{Q}_{\text{in}}}-Q_{\text{out}}^{\text{r}}-Q_{\text{out}}^{\text{DRI}}-Q_{\text{out}}^{\text{loss}},$ | (21) |
而Qoutoutgas又可表达为
| $Q_{\text{out}}^{\text{outgas}}=\sum\limits_{i}{{{V}_{\text{outgas}}}\cdot {{\varphi }_{i}}_{\left( \text{outgas} \right)}}\cdot {{H}_{i}}{{|}_{{{T}_{\text{outgas}}}}},$ | (22) |
式中:i=(CO,H2,CO2,N2,H2O)。因此,在Qin、Qoutr、QoutDRI、Qoutloss、φioutgas、Vi(outgas)已知的情况下,通过数值迭代,可计算出Toutgas。
(1.4) 计算流程图 2是模拟计算的具体流程图。首先给定入炉煤气成分和温度、DRI金属化率和温度、炉顶煤气温度最低限值Toutgas|min和炉顶煤气还原势最低限值Routgas|min,然后根据给定的矿石成分计算生产1 t DRI需要的矿石量;接着通过迭代计算确定竖炉入炉煤气量,入炉煤气带入的还原性气体(CO+H2)和热量在满足竖炉物料和热量平衡的同时,还要满足3个约束条件:①让炉顶煤气温度不小于Toutgas|min;②让炉顶煤气还原势不低于Routgas|min;③让Routgas-Routgas|min≥10-4满足的同时,不能让Toutgas-Toutgas|min≥10-3℃也满足。

|
图 2 计算流程图 Figure 2 The flow chart for calculation |
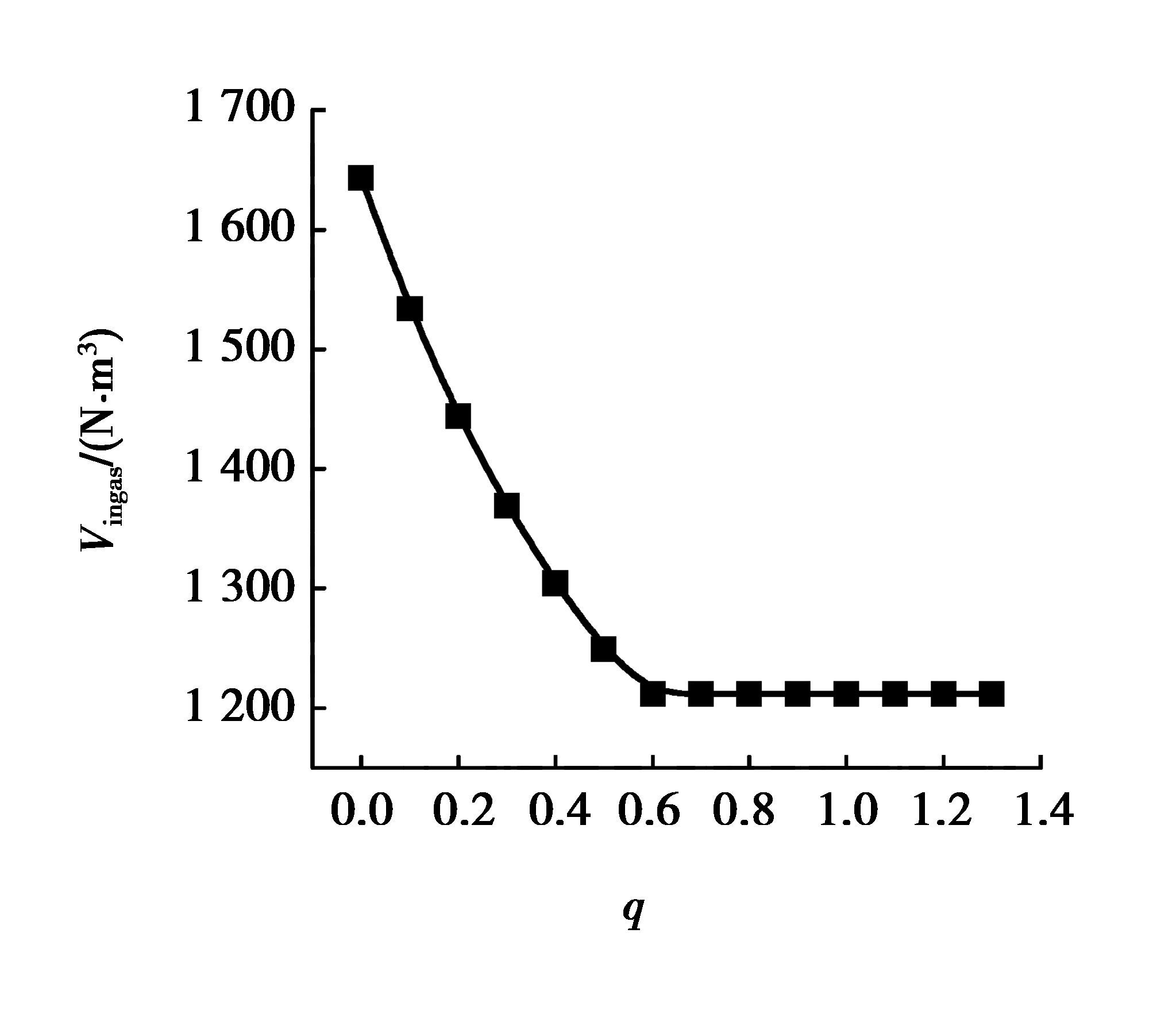
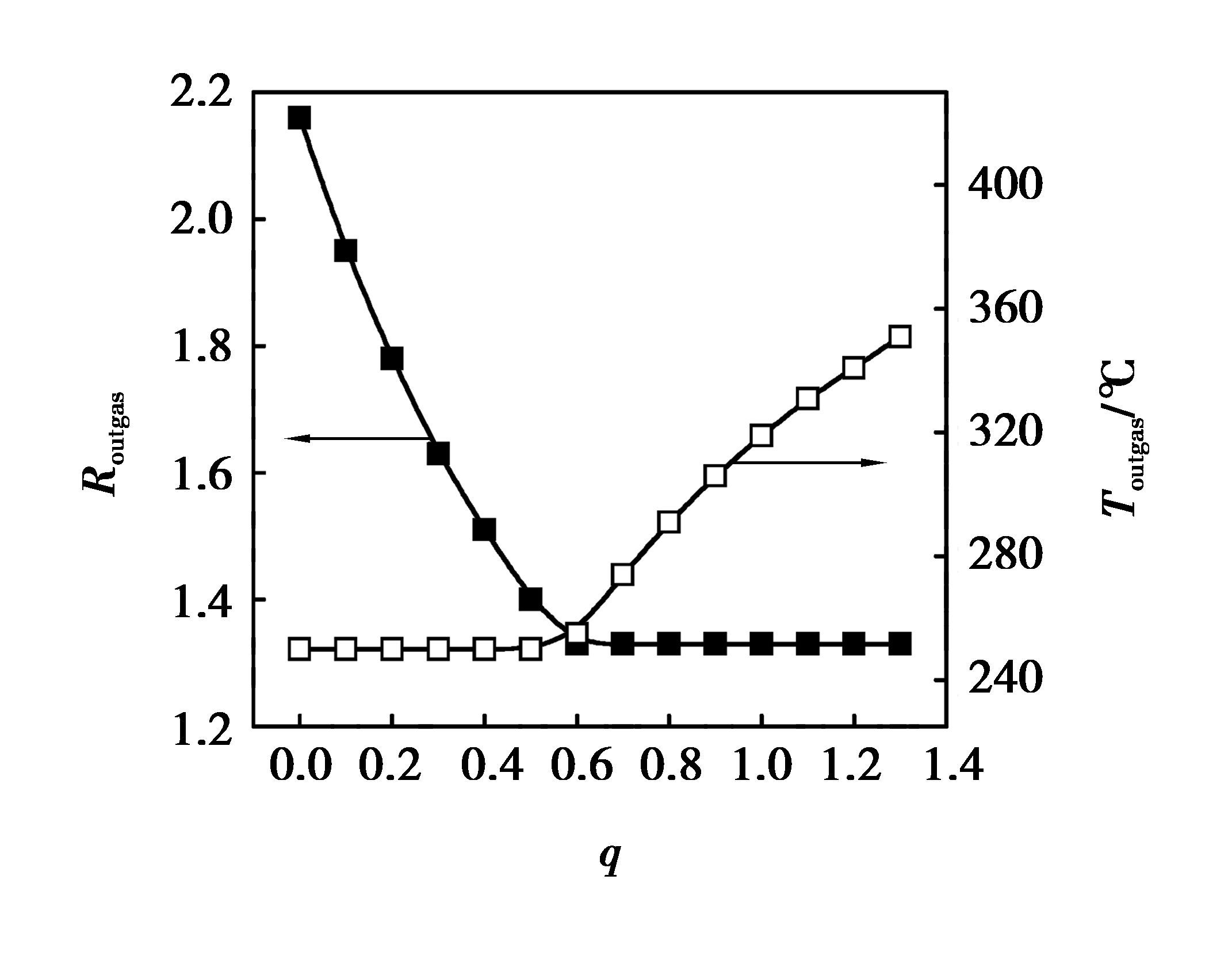
当φN2(ingas)=0、Tingas=900 ℃、MRDRI=0.9、TDRI=800 ℃时,入炉煤气量的计算结果随q的变化如图 3所示;炉顶煤气还原势和炉顶煤气温度随q的变化见图 4。由图看出:当q的值从0逐渐增加到0.6左右时,Vingas从1 650 N·m3左右下降到1 200 N·m3左右;Routgas不断下降而Toutgas基本维持在最低的250 ℃。此变化的原因是由于氢气还原矿石是吸热反应,当q的值越小时,还原气中氢气的量越多,还原矿石所需的热量越多。因此,当炉顶煤气达到最低温度时,所需入炉煤气带入的热量越多;在Tingas不变时,所需要的Vingas值越大;在MRDRI不变时,即在还原所消耗CO和H2的量不变时,炉顶煤气还原势也就越高。
|
图 3 Vingas随q的变化 Figure 3 Vingasvaries with q |
|
图 4 Routgas,Toutgas随q的变化 Figure 4 Routgas,Toutgasvary with q |
由图 3和图 4看出:当q的值从0.6左右逐渐增大时,入炉煤气量基本不发生变化,炉顶煤气还原势基本维持在最低值1.33,而炉顶煤气温度逐渐升高。此变化的原因是:当q逐渐增大时,还原煤气中CO的量逐渐增加,而H2的量逐渐减少,还原矿石所吸收的热量逐渐减少。因此,当炉顶煤气还原势达到最低值时,在入炉煤气所带入的热量中,用于增加炉顶煤气温度的那部分热量逐渐增多,炉顶煤气温度逐渐升高;在还原所消耗CO和H2的量不变(MRDRI不变)时,入炉煤气量不随q增大而发生变化。
当q从0.6左右减少时,炉顶煤气还原势增加,还原势增加意味着煤气中含有的化学能增加,竖炉能量利用率变低;当q从0.6左右增大时,炉顶煤气温度升高,温度增加意味着煤气中含有的显热增加,能量利用率也变低。由图 4可知:当q维持在0.6左右时,炉顶煤气还原势和温度都最低,竖炉能量利用最佳。
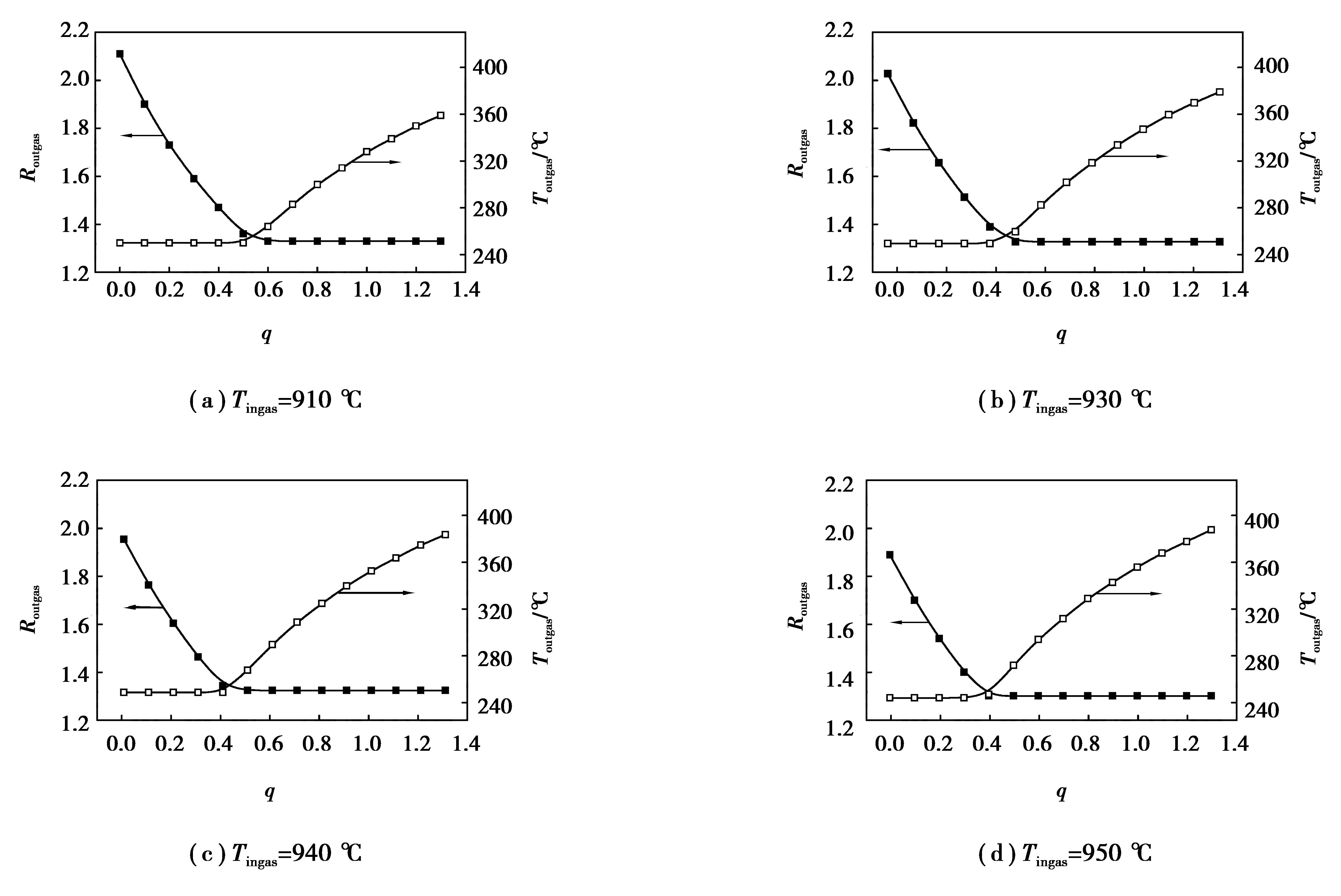
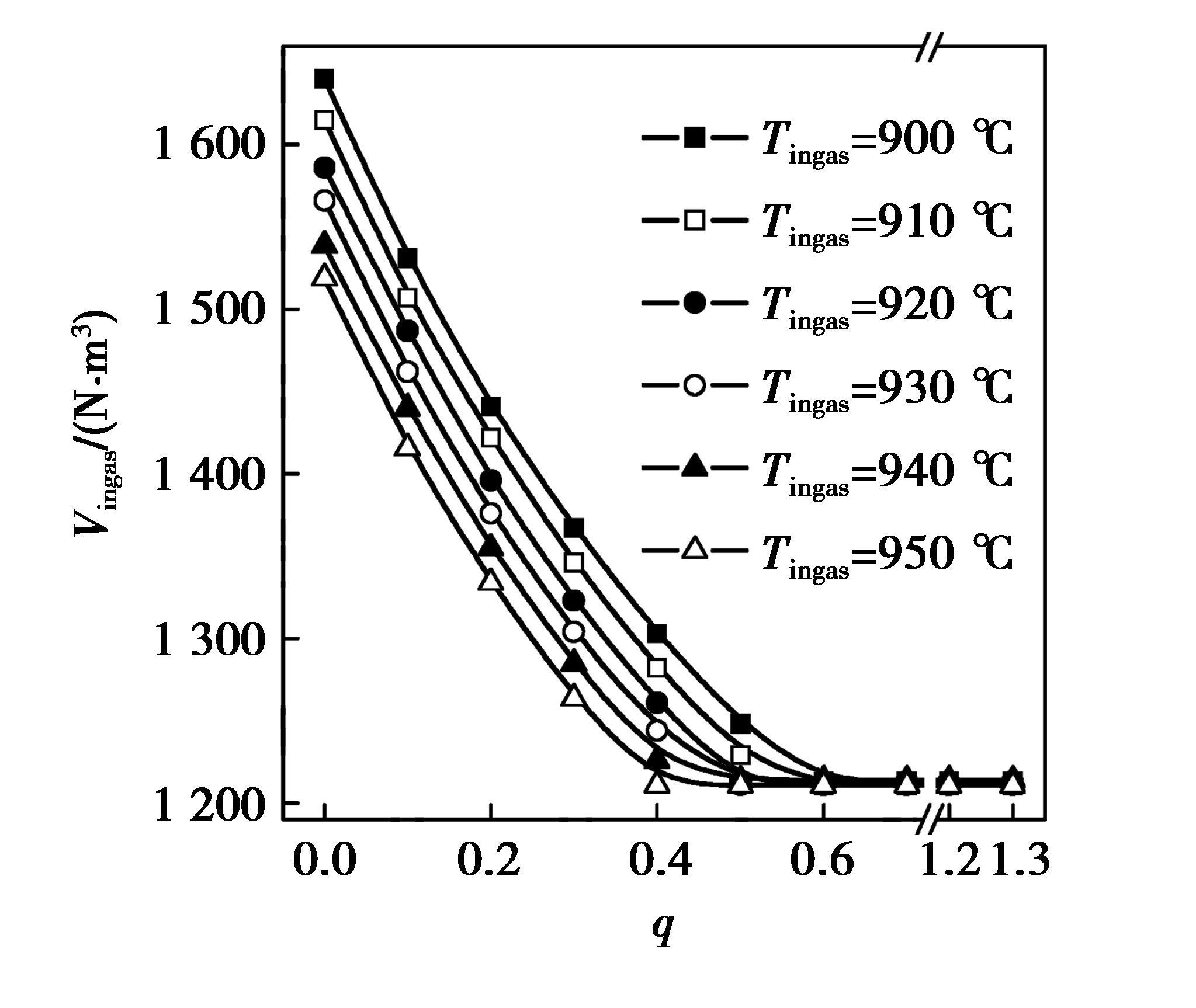
(2.2) 入炉煤气温度的影响在φN2(ingas)=0、TDRI=800℃、MRDRI=0.9的条件下,Tingas从900 ℃变化到950 ℃时,计算的炉顶煤气还原势和炉顶煤气温度随q的变化见图 5,入炉煤气量随q的变化见图 6。由图 5中(a)~(d)各图看出:当q=0、入炉气体温度逐渐增大时,炉顶煤气还原势的值逐渐有所降低;当q=1.3、入炉气体温度逐渐增大时,炉顶煤气温度逐渐有所增加。入炉气体温度逐渐增大时,能量利用最佳点对应的q值逐渐左移,即入炉煤气中适宜的CO兑入成分逐渐减少。在能量利用最佳点之左,热量需求决定着入炉煤气量,因此,随入炉煤气温度升高,入炉煤气量有所降低,在还原性气体(CO+H2)用量不变的前提下,炉顶煤气还原势有所降低;在能量利用最佳点之右,还原性气体需求决定着入炉煤气量,在金属化率一定的情况下,所需入炉煤气量是不变的,而随入炉煤气温度升高,即随入炉煤气带入热量的增加,炉顶煤气温度逐渐有所增加。图 6清晰地示出:在能量利用最佳点之左,随入炉煤气温度升高,入炉煤气量逐渐有所降低;而在能量利用最佳点之右,随入炉煤气温度升高,入炉煤气量基本不变。
|
图 5 不同入炉煤气温度条件下,Routgas,Toutgas随q的变化 Figure 5 Routgas,Toutgasvary with q and Tingas |
|
图 6 入炉煤气量随Tingas和q的变化 Figure 6 Vingasvaries with Tingasand q |
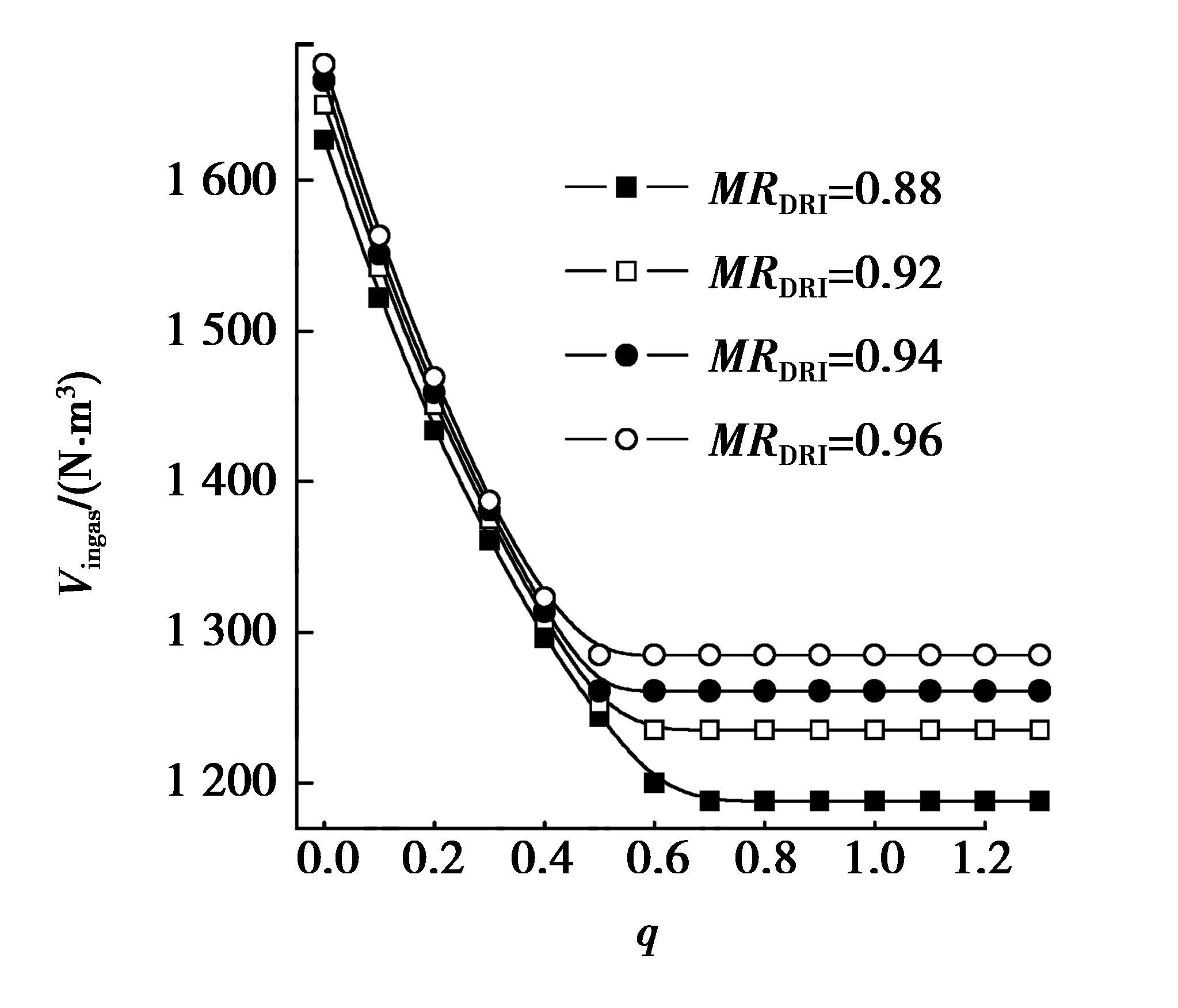
在φN2(ingas)=0、TDRI=800 ℃、Tingas=900 ℃的条件下,MRDRI从0.88变化到0.96时,入炉煤气量随q的变化见图 7,炉顶煤气还原势和炉顶煤气温度随q的变化见图 8。当金属化率增加时,矿石还原量增加,毫无疑问所需的入炉气体量增加。图 7清楚地示出了这种变化趋势。当q为0时,随着金属化率的增加,煤气用量约由1 635 N·m3变化到1 685 N·m3;当q为1.0时,随着金属化率的增加,煤气用量约由1 190 N·m3变化到1 290 N·m3。在能量利用最佳点之左,入炉气体量增加的幅度较小;在能量利用最佳点之右,入炉气体量增加的幅度较大。在能量利用最佳点之左,煤气需要量由热平衡控制;由于入炉煤气温度并不算低,因此,Vingas随金属化率的变化幅度不太大。金属化率的增加,H2和CO的消耗量增加,H2O和CO2的生成量增加,煤气还原势因H2和CO的消耗而降低的值增加,因H2O和CO2生成而降低的值也增加。因此,Routgas随金属化率变化而改变的相对幅度大;相反地,要维持还原势不变,入炉煤气量变化幅度应较大。在煤气需要量由还原势控制的能量利用最佳点之右,随着金属化率的增加,Vingas增加的幅度较大。
|
图 7 Vingas随q和金属化率的变化 Figure 7 Vingasvaries with q and MRDRI |
|
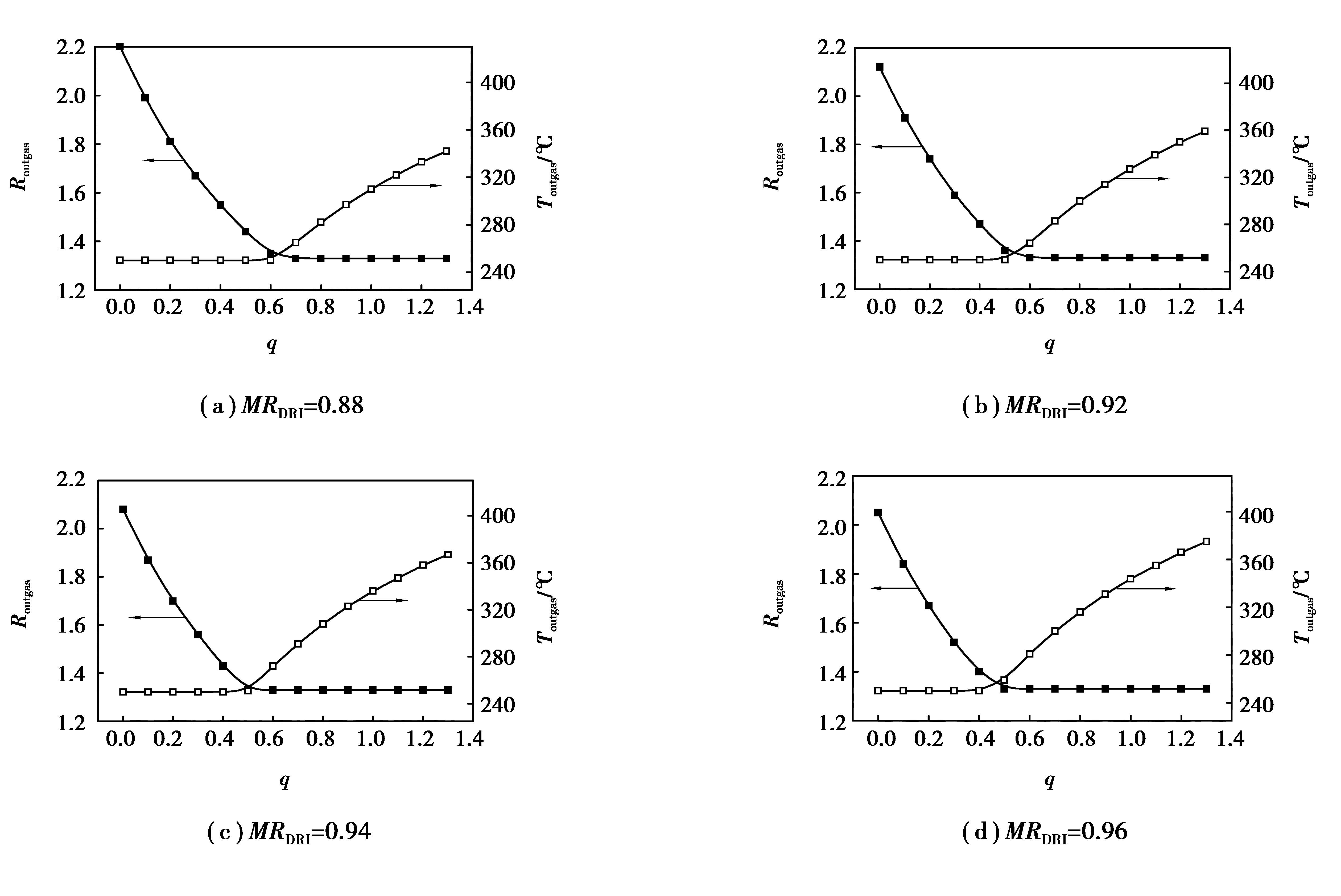
图 8 不同金属化率条件下,Routgas、Toutgas随q的变化 Figure 8 Routgas、Toutgasvary with q and MRDRI |
由图 8可知:当金属化率逐渐增大时,在能量利用最佳点之左,炉顶煤气还原势的值有所降低,在能量利用最佳点之右,炉顶煤气温度的值有所增加;能量利用最佳点逐渐左移,即入炉煤气中适宜CO兑入成分逐渐减少。在能量利用最佳点之左,金属化率增加,反应消耗还原性气体(CO+H2)的量增加,而入炉气体量增加的幅度较小,因此,还原势降低;在能量利用最佳点之右,随金属化率增加,入炉煤气量增加幅度较大,带入的热量增加,炉顶煤气温度逐渐有所增加。
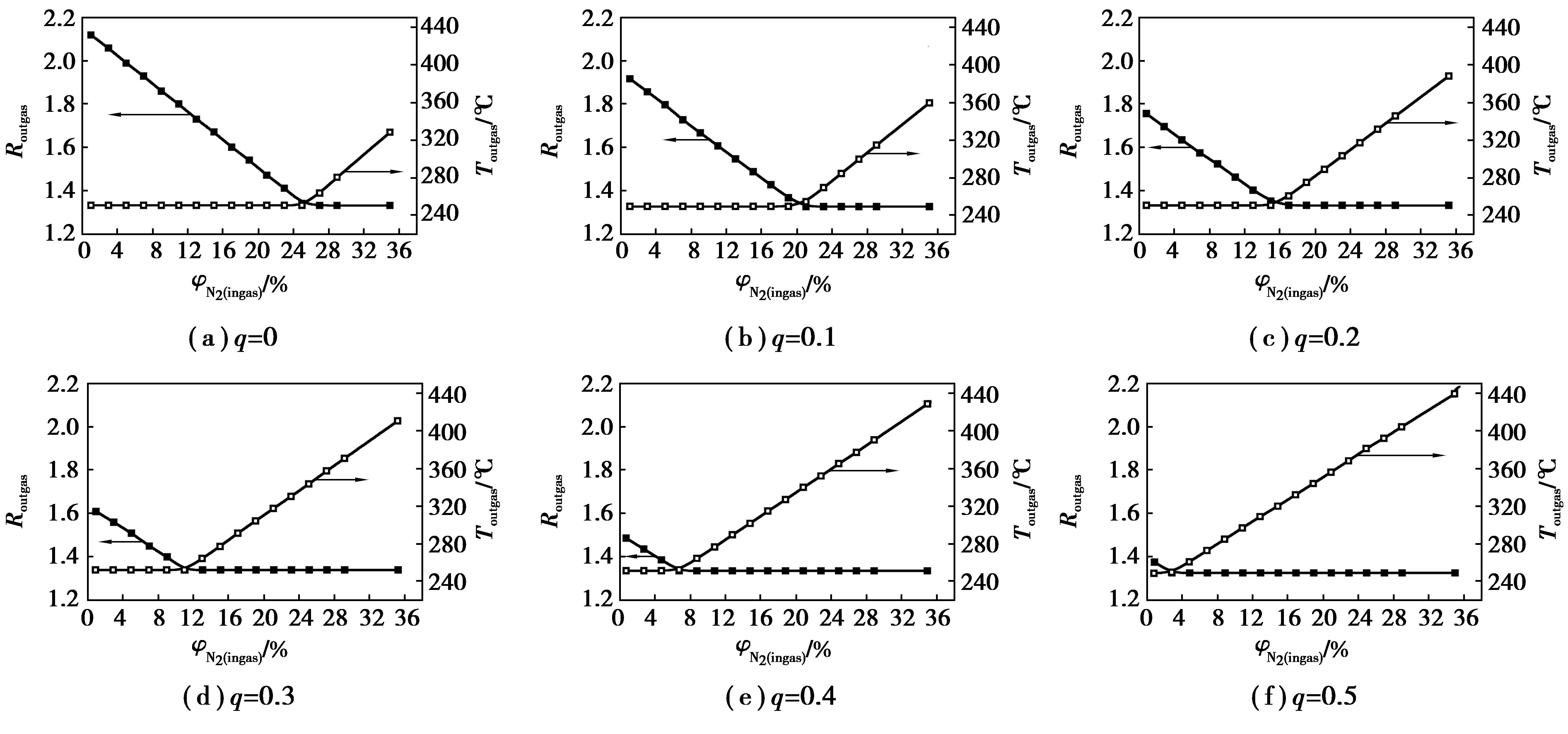
(2.4) 兑入N2的计算结果当其他条件不变,q的值取0、0.1、0.2、0.3、0.4、0.5时所计算的炉顶煤气还原势、炉顶煤气温度随氮气含量变化的关系分别见图 9(a)~(f)。由图 9(a)看出:随着氮气成分的逐渐增大,Routgas首先不断下降,当φN2(ingas)≈25%时,还原势达到最小值,然后随着氮气成分继续增大,Routgas基本维持在Routgas|min;而炉顶煤气温度首先保持不变,维持在Toutgas|min,当φN2(ingas)>25%时,随着氮气成分的增大,Toutgas逐渐增大。当φN2(ingas)<25%时,入炉煤气中氢气量多,当入炉煤气所带入的热量刚好保证炉顶煤气温度等于最低温度(即满足Toutgas=Toutgas|min)的时候,它所带入的H2早已保证Routgas>Routgas|min了;φN2(ingas)越小,当Toutgas=Toutgas|min时,Routgas与Routgas|min的差值越大。当φN2(ingas)>25%时,入炉煤气中H2的量相对地减少,还原一定量的矿石需要更多量的煤气。当入炉煤气所带入的H2刚好保证Routgas=Routgas|min的时候,所带入的热量早已保证Toutgas>Toutgas|min了;φN2(ingas)越大,当Routgas=Routgas|min时,Toutgas与Toutgas|min的差值越大。
|
图 9 不同q条件下,Routgas,Toutgas随氮气兑入成分的变化 Figure 9 Routgas,Toutgasvary with q and the N2 composition |
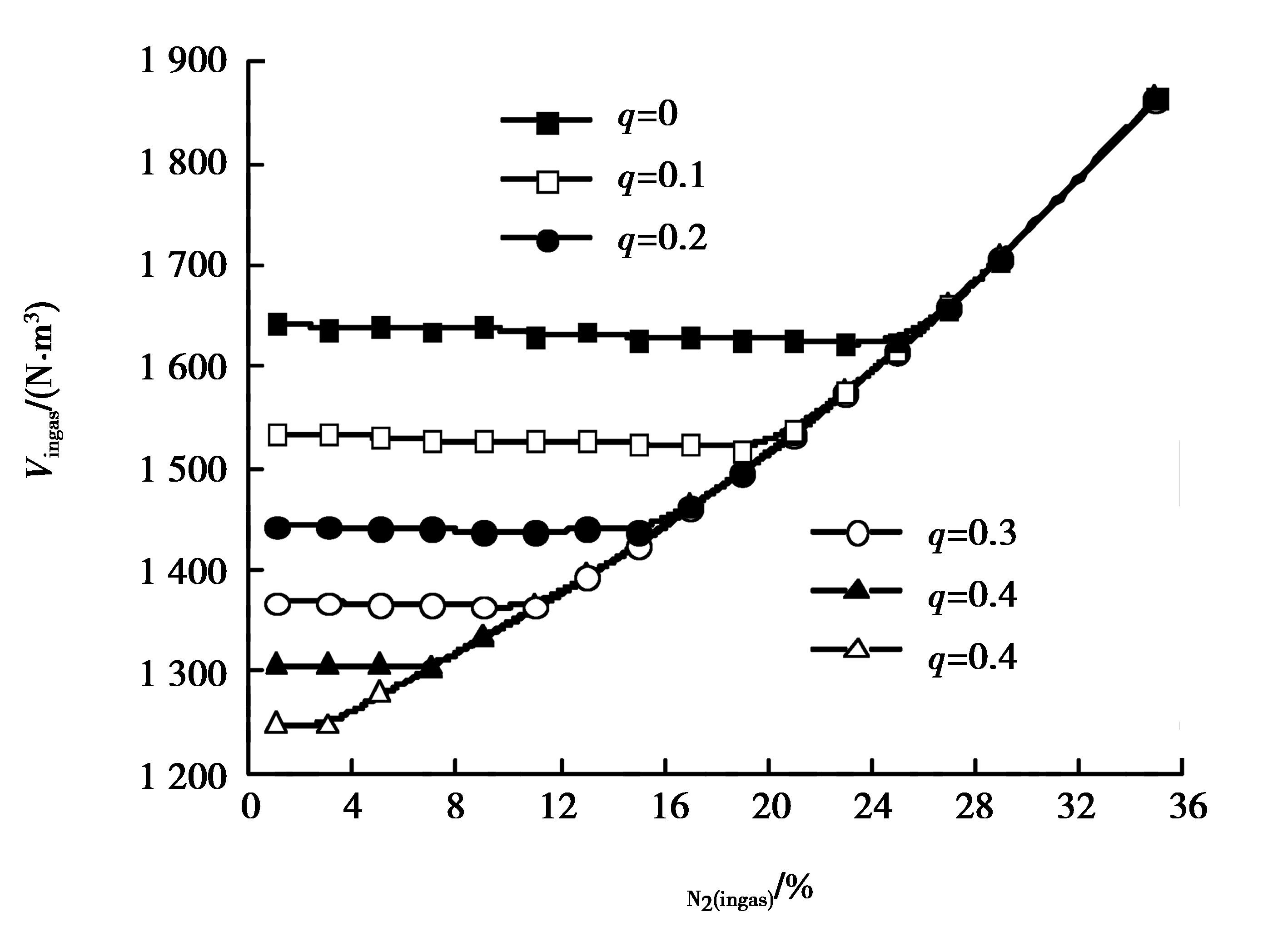
当其他条件不变,q的值分别取0、0.1、0.2、0.3、0.4、0.5时,所计算的入炉煤气量随氮气含量变化的关系见图 10。由图 10看出:当q=0时,随着氮气成分的逐渐增大,入炉煤气量首先保持基本不变,维持在1 650 N·m3左右,当φN2(ingas)>25%时,随着氮气成分的增大,入炉煤气量逐渐增大。当q=0时,在矿石还原量一定的条件下,所需要的热量是一定的;H2、N2都是双原子分子,若将它们看作理想气体,它们的热容都是相同的,当氮气成分逐渐增大时,单位体积入炉煤气中H2的量相对减少,但单位体积中双原子分子数没有变化,因此,当氮气成分变化时,单位体积入炉煤气的热容量不变;所以,当q=0、φN2(ingas)<25%时,入炉煤气量是基本不变的。当q=0、φN2(ingas)>25%时,还原煤气中H2的量少,决定入炉煤气量的不再是热量需求,而是还原性气体H2的需求;随着氮气成分的增加,H2的成分减少,还原一定量的矿石就需要更多的入炉煤气量。
|
图 10 Vingas随CO/H2和氮气兑入成分的变化 Figure 10 Vingasvaries with CO/H2 and the N2 composition |
图 9(a)示出:当φN2(ingas)≈25%时,竖炉能量利用最佳。在图 10可知:当q=0时,能量最佳利用所需要的煤气量约为1 650 N·m3。综合图 9和图 10可知:不同q值条件下,能量最佳利用时所对应的N2的成分是不同的、所需要的入炉煤气量是不同的。将能量最佳利用时所需要的入炉煤气量、所对应的氮气兑入成分,与q值的关系见表 3。
| 表 3 能量最佳利用所对应氮气成分、所需入炉煤气量随q的变化 Table 3 The N2 composition and Vingas needed under the condition of optimal energy utilization vary with q |
表 3说明:当q值在0~0.6范围内,可以通过兑入氮气达到改善煤气利用的目的;当入炉煤气中氢气比重越大时,若要能量利用最佳,需兑入的氮气越多,所需要的入炉煤气量越多。将表 3中不同q值所对应的入炉煤气量与图 3中不同q值对应的入炉煤气量相比较,可以发现同一个q值对应的两个入炉煤气量基本是相同的,尽管图 3中的入炉煤气不含有氮气,表 3中各能量利用最佳点所对应的入炉煤气各含有不同程度的氮气。这个现象表明:当通过兑入氮气以提高氢气还原的能量利用率时,可以减少入炉氢气的量,但不能减少入炉气体的总量;伴随着一定氢气量的减少,需有相应量氮气的增加。
3、 结 论1)利用一组物料、热量守衡式及其他有关约束关系式,建立了氢还原竖炉模拟模型。其可计算物料消耗量、入炉煤气量和各种相关量,能确定它们和氮气与CO兑入成分、DRI金属化率、入炉煤气温度等的关系,可为氢还原竖炉工艺的设计、操作和节能等提供参考信息。
2)纯氢还原需要最多的入炉煤气量,且炉顶煤气化学势最高,化学能利用最不充分;随着H2中CO兑入成分的逐渐增加,入炉煤气量和炉顶煤气化学势都逐渐降低。算例表明:兑入CO可使入炉煤气量从纯氢还原的1 650 N·m3左右下降到1 200 N·m3左右;当q的值约为0.6时,竖炉能量利用最佳。
3)当入炉煤气温度增大时,氢还原竖炉入炉煤气量、炉顶煤气还原势都降低,CO兑入量可减少;当DRI金属化率增大时,入炉煤气量增加、而炉顶煤气还原势通常会降低,CO兑入量可减少。
4)兑入氮气可以减少入炉氢气的量,但不能减少入炉气体的总量;伴随着一定氢气量的减少,需有相应量氮气的增加。算例表明:当氮气兑入成分约为25%时,纯氢还原竖炉能量利用最佳;当q=0.3时,最佳氮气兑入成分约为11%。
| [1] |
陈津, 林万明, 赵晶. 非焦煤冶金技术[M]. 北京: 化学工业出版社, 2007 : 230 -251.
CHEN Jin, LIN Wanming, ZHAO Jin. Metallurgical technologies by non-coking coal[M]. Beijing: Chemical Industry Press, 2007 : 230 -251.
( 0) 0)
|
| [2] |
王兆才, 陈双印, 储满生, 等.
煤制气[XC半字线.TIF,JZ]竖炉生产直接还原铁浅析[J]. 中国冶金 , 2013, 23 (1) : 20–25.
WANG Zhaocai, CHEN Shuangyin, CHU Mansheng, et al.
Tentative study on direct reduction iron production by gasification-shaft furnace[J]. China Metallurgy , 2013, 23 (1) : 20–25.
( 0) 0)
|
| [3] |
储满生, 赵庆杰, 王兆才, 等.
我国非高炉炼铁发展新热潮的浅析[J]. 中国废钢铁 , 2009 (4) : 8–15.
CHU Mansheng, ZHAO Qingjie, WANG Zhaocai, et al.
A brief analysis on new development of non-blast furnace ironmaking in china[J]. Iron&Steel Scrap of China , 2009 (4) : 8–15.
( 0) 0)
|
| [4] |
郭廷杰.MIDREX工艺最新发展动向[N].世界金属导报,2011-02-01(010).
GUO Tingjie.New advances of MIDREX process[N].World Metal News,2011-02-01(010).
( 0) 0)
|
| [5] |
徐辉, 邹宗树, 余艾冰.
Midrex还原竖炉反应的数值模拟[J]. 钢铁 , 2008, 43 (5) : 12–17.
XU Hui, ZOU Zongshu, YU Aibing.
A preliminary numerical simulation of Midrex reduction shaft furnace[J]. Iron&Steel , 2008, 43 (5) : 12–17.
( 0) 0)
|
| [6] |
徐匡迪.
低碳经济与钢铁工业[J]. 钢铁 , 2010, 45 (3) : 1–12.
XU Kuangdi.
Low carbon economy and iron and steel industry[J]. Iron&Steel , 2010, 45 (3) : 1–12.
( 0) 0)
|
| [7] |
齐渊洪, 严定鎏, 高建军, 等.
氧气高炉工业化试验研究[J]. 钢铁 , 2011, 46 (3) : 6–8.
QI Yuanhong, YAN Dingliu, GAO Jianjun, et al.
Study on industrial test of the oxygen blast furnace[J]. Iron&Steel , 2011, 46 (3) : 6–8.
( 0) 0)
|
| [8] |
高建军, 郭培民, 齐渊洪, 等.
工艺参数对氧气高炉能耗的影响规律[J]. 钢铁研究学报 , 2011, 23 (7) : 14–17.
GAO Jianjun, GUO Peimin, QI Yuanhong, et al.
Effect of process parameters on energy consumption of the oxygen blast furnace[J]. Journal of Iron and Steel Research , 2011, 23 (7) : 14–17.
( 0) 0)
|
| [9] |
韩毅华, 王静松, 李燕珍, 等.
炉顶煤气循环--氧气鼓风高炉综合数学模型[J]. 北京科技大学学报 , 2011, 33 (10) : 1280–1286.
HAN Yihua, WANG Jingsong, LI Yanzhen, et al.
Comprehensive mathematical model of top gas recycling-oxygen blast furnaces[J]. Journal of University of Science and Technology Beijing , 2011, 33 (10) : 1280–1286.
( 0) 0)
|
| [10] |
QU Yingxia, ZOU Zongshu, XIAO Yanping.
A comprehensive static model for COREX process[J]. Transactions of the Iron and Steel Institute of Japan , 2012, 52 (12) : 2186–2193.
DOI:10.2355/isijinternational.52.2186 ( 0) 0)
|
| [11] |
郭培民, 高建军, 赵沛.
氧气高炉多区域约束性数学模型[J]. 北京科技大学学报 , 2011, 33 (3) : 334–338.
GUO Peimin, GAO Jianjun, ZHAO Pei.
Multi-zone constrained mathematical model of oxygen blast furnaces[J]. Journal of University of Science and Technology Beijing , 2011, 33 (3) : 334–338.
( 0) 0)
|
| [12] |
Kadrolkar A, Roy S K, Sen P K.
Minimization of exergy losses in the COREX process[J]. Metallurgical and Materials Transactions B , 2012, 43 (1) : 173–185.
DOI:10.1007/s11663-011-9586-2 ( 0) 0)
|
| [13] |
王成善, 肖兴国, 王文忠.
COREX工艺系统模拟的数学模型[J]. 重庆大学学报 , 2009, 32 (8) : 869–875.
WANG Chengshan, XIAO Xingguo, WANG Wenzhong.
System simulation for COREX process:model descrip-tions[J]. Journal of Chongqing University , 2009, 32 (8) : 869–875.
( 0) 0)
|
| [14] |
王臣, 李晓清, 徐万仁.
COREX工艺燃料消耗影响因素分析及优化方向[J]. 宝钢技术 , 2011 (6) : 37–43.
WANG Chen, LI Xiaoqing, XU Wanren.
Analysis of influencing factors of fuel consumption in COREX process and its optimization direction[J]. Bao-Steel Technology , 2011 (6) : 37–43.
( 0) 0)
|
| [15] |
曲迎霞, 王臣, 邹宗树, 等.
COREX工艺模型及应用分析[J]. 过程工程学报 , 2008, 8 (z1) : 68–72.
QU Yingxia, WANG Chen, ZOU Zongshu, et al.
Process modeling of COREX and its application analysis[J]. The Chinese Journal of Process Engineering , 2008, 8 (z1) : 68–72.
( 0) 0)
|
 2016, Vol. 39
2016, Vol. 39

