2. 西南大学 电子信息工程学院, 重庆 400715;
3. 重庆大学 计算机学院, 重庆400044
2. College of Electronic and Information Engineering, Southwest University, Chongqing 400715, P. R. China;
3. College of Computer Science, Chongqing University, Chongqing 400044, P. R. China
图像的边缘是图像最基本的特征,图像边缘提取是理解图像、识别图像的重要基础,也是计算机视觉的中心任务,是图像处理和计算机视觉领域经典的研究课题之一。
1988年美国华裔科学家蔡少棠和杨林等[1]结合神经网络和细胞自动机的优点,提出细胞神经网络(cellular neural network,CNN)。CNN是一种局部互联的神经网络变体,整个网络由大规模非线性模拟电路组成,其局部互联的特性使得它具有高速并行处理的能力,在图像处理领域得到广泛的应用。CNN用于图像边缘提取的关键是找到一组能够满足处理任务的细胞之间相互的连接的权重(称为模板)[2]。文献[3-4]根据待处理图片的本身特性设计自适应性的CNN模板,这类算法设计的模板对指定图片具有很好的边缘提取能力,但由于模板取值是根据处理图片计算得出,缺乏推广性。文献[5]将样本空间看作约束条件建立线性矩阵不等式,通过求解矩阵得出模板的取值范围,该方法对样本选择和过程控制要求都非常高,同时,设计出的模板解决问题能力容易依赖样本空间。文献[6-9]将模板设计过程看作优化问题,用进化算法对解空间进行搜索:文献[6]采用遗传算法、文献[7]采用蚁群算法、文献[8-9]采用粒子群算法对模板进行优化,进化算法模拟生物特性,对参数空间给出一种编码方案,不直接对问题的具体参数进行处理,不是从某个单一的初始点开始搜索,而是从一组初始点搜索,搜索空间更广泛,搜索过程更加智能,因而得到广泛的应用。
粒子群算法相对于遗传算法、蚁群算法结构更为简单、易于实现、能保留个体和全局的最优信息、具有记忆功能,且利用个体和全局信息协同搜索。但是粒子群算法在解决复杂的多峰值问题时,由于收敛过于迅速,粒子容易聚集到一个较小的解空间内,从而失去粒子种群多样性,出现早熟现象陷入局部最优解。模拟退火算法在退火过程中不但接受好的解,还以一定概率接受差的解,这种概率受温度参数的控制[10-11]。文中结合粒子群算法和模拟退火算法的优点,在粒子群算法基础上引入模拟退火思想,用退火温度调节粒子的突跳概率,结合轮盘赌策略确定全局最优的某个替代值,形成SA-PSO(simulated annealing-particle swarm optimization)算法对CNN边缘提取模板进行设计,能有效避免PSO(particle swarm optimization)算法陷入局部最优解。
进化算法用于CNN模板设计的研究中[6-9],并未考虑粒子在计算适应值时将信息代入CNN模拟器时对CNN本身稳定性的影响。模板设计过程中通常是将每轮搜索产生的解作为模板输入CNN处理器中,评价当前解的优劣情况,而进化算法产生解的过程并未考虑到CNN本身的动力学特性,如果对粒子的解空间不加约束,可能导致在搜索过程产生的解使细胞没有稳定输出,使得算法在此轮搜索无法产生当前解的适应值,从而导致搜寻过程不能顺利进行。针对这一问题,笔者利用参考文献[12]得出的关于CNN反馈模板的研究结论对粒子的SA-PSO中粒子的解空间进行约束,保证在约束后的解空间产生的解均能使CNN有大于1的稳定输出,从而能计算出每轮解的适用值,为搜索顺利进行提供必要的条件。
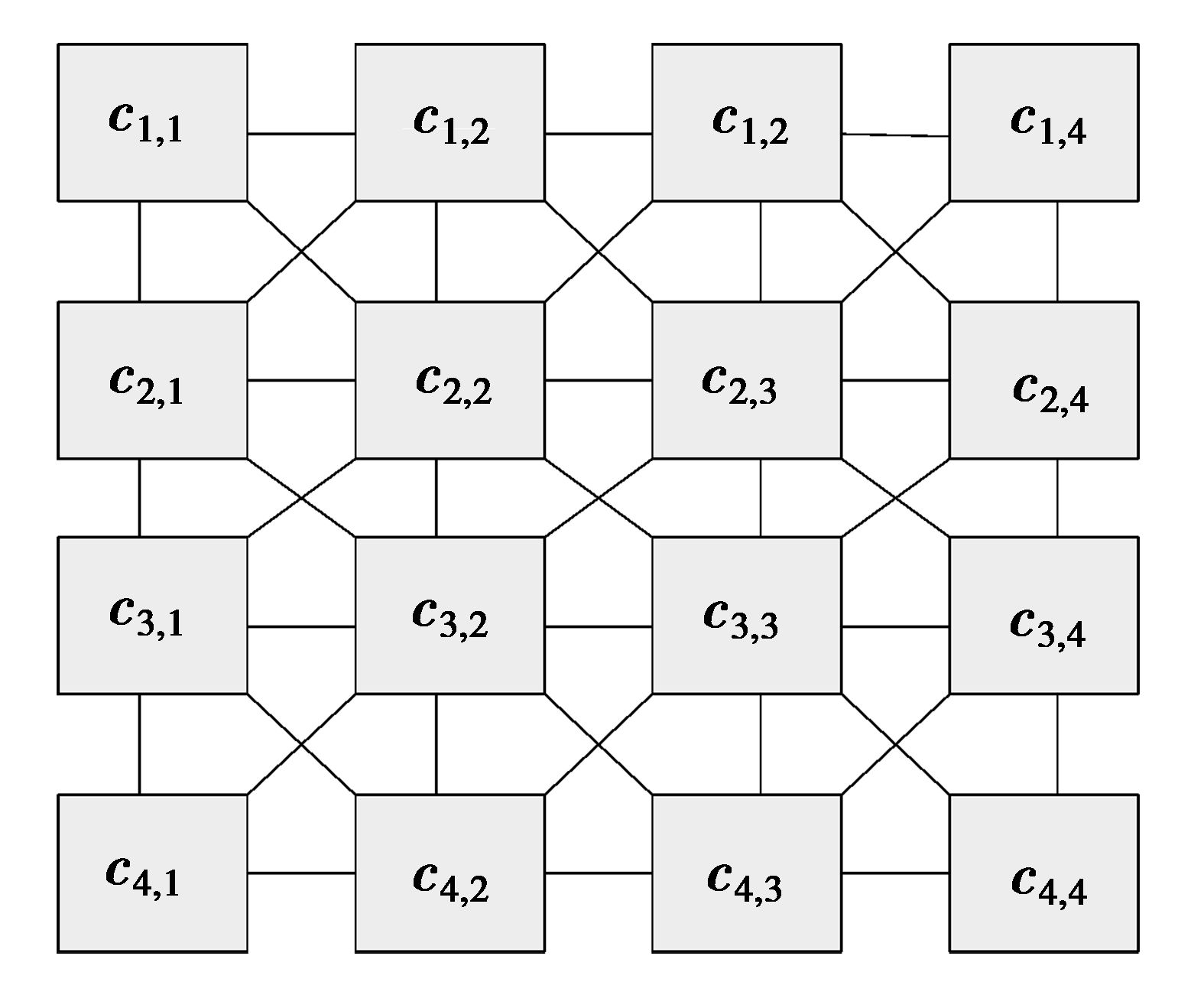
1、 CNN结构及基于CNN的边缘提取 (1.1) CNN基本结构在细胞神经网络中的每一个神经元被称为一个细胞(cell),它是由一组线性和非线性的电路组成。细胞与周围相邻的细胞直接联系,细胞之间发生互联的距离称为r。在一个二维的细胞神经网络中,有限个细胞排成M行和N列的M×N的CNN网络。细胞ci, j代表第i行和第j列的细胞。这个细胞与周围直接发生互联的细胞的最远距离称为R[13]。4×4的CNN网络结构图如图 1所示。
|
图 1 4×4的CNN网络结构图 Figure 1 4×4 CNN networks |
每个细胞的电路状态可以被一组线性和非线性的合方程式表示,CNN的状态方程为
| $\begin{align} & \frac{{{x}_{i,j}}\left( t \right)}{\text{d}t}=-{{x}_{i,j}}+\sum\limits_{Ci+k,j+l\in Sr\left( i,j \right)}{{{a}_{k,l}}}\left( i,j,t \right){{y}_{i+k,j+l}}+ \\ & \sum\limits_{Ci+k,j+l\in Sr\left( i,j \right)}{{{b}_{k,l}}}\left( i,j,t \right){{u}_{i+k,j+l}}+{{z}_{i,j}}\left( i,j,t \right)=-{{x}_{i,j}}+ \\ & \sum\limits_{k=-r}^{r}{\sum\limits_{l=r}^{r}{{{a}_{k,l}}}}{{y}_{i+k,j+l}}+\sum\limits_{k=-r}^{r}{\sum\limits_{l=r}^{r}{{{b}_{k,l}}}}{{u}_{i+k,j+l}}+{{z}_{i,j}} \\ \end{align}$ | (1) |
| ${{s}_{r}}\left( i,j \right)=\left\{ c \right.\left( k,l \right)\left| \underset{1\le k\le M,1\le l\le N}{\mathop{\max }}\, \right.\left\{ \left\{ \left| k-i \right| \right. \right.,\left. \left. \left| l-j \right| \right\} \right\}\le \left. r \right\},$ | (2) |
输出方程为
| $\begin{align} & {{y}_{i,j}}=f\left( {{x}_{i,j}} \right)=\frac{1}{2}\left( \left| {{x}_{i,j}}-1 \right|-\left| {{x}_{i,j}}+1 \right| \right), \\ & i=1.2,\cdots ,M,j=1,2,\cdots ,N, \\ \end{align}$ | (3) |
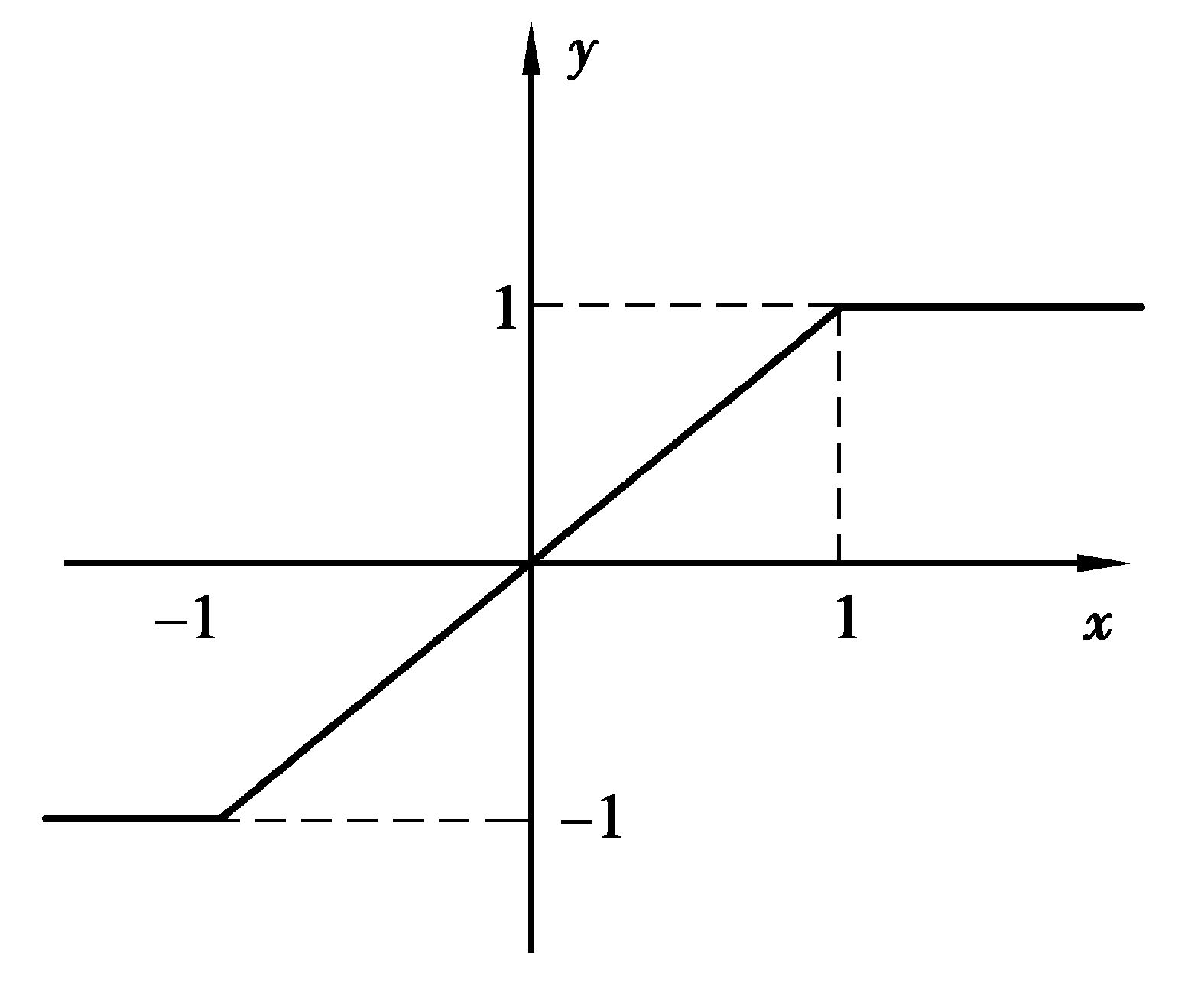
式中:ak, l,bk, l,z分别为CNN系统的反馈模板,控制模板和偏移,共同决定CNN系统的动力学特性;xi, j,yi, j,ui, j分别表示细胞Ci, j的状态,输出和输入。图 2为CNN的输出函数。
|
图 2 CNN输出的函数图 Figure 2 CNN output curve |
CNN的模型是基于连续时间的,而图像处理中时间域和空间域都是离散,所以用一个差分方程来近似取代式(1) [14]。令t=nh,n为正数,h为常数步长,用其对应的差分无限逼近于
| $\begin{align} & {{x}_{i,j}}\left( t+h \right)=h[-{{x}_{i,j}}\left( t \right)+\sum\limits_{Ci+k,j+l\in Sr\left( i,j \right)}{{{a}_{k,l}}}\left( i,j \right){{y}_{i+k,j+l}}\left( t \right)+ \\ & \sum\limits_{Ci+k,j+l\in Sr\left( i,j \right)}{{{b}_{k,l}}}\left( i,j \right){{u}_{i+k,j+l}}+{{z}_{i,j}}\left( i,j \right)+{{x}_{i,j}}\left( t \right) \\ \end{align}。$ | (4) |
| $\begin{align} & {{y}_{i,j}}\left( t+h \right)=f\left( {{x}_{i,j}}\left( t+h \right) \right)=\frac{1}{2} \\ & \left( \left| {{x}_{i,j}}\left( t+h \right)-1 \right|-\left| {{x}_{i,j}}\left( t+h \right)+1 \right| \right) \\ \end{align}。$ | (5) |
为了讨论简单,令h=1,状态方程式则为
| $\begin{align} & {{x}_{i,j}}\left( t+1 \right)=\sum\limits_{Ci+k,j+l\in Sr\left( i,j \right)}{{{a}_{k,l}}}\left( i,j \right){{y}_{i+k,j+l}}\left( t \right)+ \\ & \sum\limits_{Ci+k,j+l\in Sr\left( i,j \right)}{{{b}_{k,l}}}\left( i,j \right){{u}_{i+k,j+l}}+{{z}_{i,j}}\left( i,j \right) \\ \end{align}$ | (6) |
由式(1) 可以得出ak, l,bk, l,z控制着CNN的动力学特性,所以寻找一组合理的模板完成指定的任务至关重要。
一个二维灰度8比特图像里,它的任意一点pi, j取值为[0,255], 而在CNN系统里,每个细胞输入ui, j∈[-1,1], 输出yi, j∈[-1,1]。CNN在图像领域的应用中,一般方法是将图像的点映射为CNN网络中的细胞,所以,用式(7) 将像素值映射到CNN网络中。此外,在文中规定细胞稳定输出值yi, j=1为非边缘, yi, j=-1为边缘。
| ${{u}_{i,j}}=2\times \frac{{{p}_{i,j}}}{255}-1$ | (7) |
粒子群优化算法(PSO)是源于对鸟群捕食行为研究而提出的一种进化计算,在PSO算法中每个优化问题的解被抽象成没有质量和体积的微粒。离子在N维空间里的位置表示为一个矢量,每个离子的飞行速度也表示为一个矢量。PSO算法首先初始化一群随机粒子,然后粒子们就追随当前的最优粒子在空间中搜索,通过迭代找到最优解。假设在d搜索空间中第i个粒子的位置和速度分别为:Qi=(qi, 1, qi, 2…qi, d),Vi=(vi, 1, vi, 2…vi, d)。在每次迭代中,粒子通过跟踪两个最优解来更新位置,第一个就是粒子本身所找到的最优解,即个体极值pbest, P=(pi, 1, pi, 2…pi, d);另一个是整个种群目前找到的最优解,即全局优解gbest, Pg。在找到这两个最优值时,粒子根据如下公式来更新最近的速度和新的位置。
| $\begin{align} & {{v}_{i,j}}\left( t+1 \right)=\omega {{\nu }_{i,j}}\left( t \right)+{{c}_{1}}*rand\left( 1 \right)\left[ {{p}_{i,j}}-{{q}_{i,j}}\left( t \right) \right] \\ & +{{c}_{2}}*rand\left( 1 \right)\left[ {{p}_{i,j}}-{{q}_{i,j}}\left( t \right) \right], \\ \end{align}$ | (8) |
| ${{q}_{i,j}}\left( t+1 \right)={{q}_{i,j}}\left( t \right)+{{v}_{i}}\left( t+1 \right),j=1,2\cdots ,d,$ | (9) |
式中:w为惯性权重;c1,c2正的学习因子;rand(1) 为0~1之间的随机数。
(2.2) 模拟退火PSO在基本粒子群算法中,粒子群通过跟踪两个“极值”来更新自己,算法结果简单,运行速度快,但是在问题解空间中随机搜索过程中,依然存在着早熟收敛和收敛较慢的两个难题,并且具有种群多样性随代数增加下降过快,有可能不收敛于全局最优解等缺点。模拟退火算法在退火过程中不但接受好的解,而且还以一定的概率接受差的解,同时,这种概率受到温度参数的控制,其大小随着温度的下降而减少,所以,具有概率突跳的能力,能够有效避免基本PSO搜索过程中陷入局部极小解的问题。引入模拟退火的粒子群算法(SA-PSO)的步骤如下[15-16]:
Step1.随机初始化种群中各微粒的位置和速度;
Step2.评价每个微粒的适应度,将当前各微粒的位置和适应值存储在各微粒的pi中,将所有的pbest中的适应值最优个体的位置和适应值存储于pg中;
Step3.确定初始温度T(0) ;
Step4.根据以下公式确定当前各温度下的pi的适配值:
Step5.采用轮盘策略从所有pi中确定全局最优的某个替代值p′g [17],然后根据式(10) 更新各微粒的速度和位置,
| $\begin{align} & {{v}_{i,j}}\left( t+1 \right)=\omega \{{{\nu }_{i,j}}\left( t \right)+{{c}_{1}}*rand\left( 1 \right)\left[ {{p}_{i,j}}-{{q}_{i,j}}\left( t \right) \right] \\ & +{{c}_{2}}*rand\left( 1 \right)\left[ {{{{p}'}}_{i,j}}-{{q}_{i,j}}\left( t \right) \right]\}, \\ & {{q}_{i,j}}\left( t+1 \right)={{q}_{i,j}}\left( t \right)+{{v}_{i}}\left( t+1 \right),j=1,2\cdots ,d, \\ \end{align}$ | (10) |
其中,
Step6.计算各微粒新的目标值,更新各微粒的pi值及群体的pg值;
Step7.进行退温操作T(k+1) =λT(k);
Step8.若满足停止条件,搜索停止,输出结果,否则转step4。
3、 算法结构及参数设定 (3.1) 算法流程使用SA-PSO算法训练边缘提取CNN模板的流程如下:
Step1.按照式(4) 、式(5) 将CNN系统离散化,并按照式(7) 将算法涉及图片的像素点值映射为CNN每个细胞的输入ui, j;
Step2.随机初始化粒子种群的速度、位置,初始温度等参数,初始化CNN状态xi, j;
Step3.将粒子的位置信息映射为CNN模板,将模板和ui, j输入CNN处理器中进行边缘提取;
Step4.边缘提取的结果与理想边缘做对比,根据适应度函数(第4节将给出定义)计算出本次迭代的适应值;
Step5.本次迭代适应值返回SA-PSO算法,更新各微粒位置、速度等信息;
Step6.根据适应值计算本轮迭代的pi,pg,进行退温操作Tk+1=λTk;
Step7.判断是否满足给定迭代停止条件,是则输出当前粒子状态,否则进行step3。
(3.2) 参数约束仔细观察上述算法流程,不难得出,在step3中,将SA-PSO算法中的粒子的位置信息当成CNN的模板输出到CNN模拟器时,并未考虑到模板本身对CNN动力学特性的影响。然而事实上,模板控制着CNN的动力学行为,粒子在寻找最优解时相对独立于CNN本身的性质。这样,当前迭代产生的最优解有可能不能使整个细胞神经网络完全收敛,导致step3无法得到稳定输出,影响后面流程进行。为了有效地避免这一情况的产生,文中对粒子解空间进行约束,使粒子在保证细胞神经网络完全收敛的解空间进行搜索。
引理1:保证CNN能收敛于稳定的平衡点的充分条件为:反馈模板A为对称矩阵[12]。
引理2:反馈模板的中心元素A0, 0>1,所有细胞将稳定的输出到绝对值大于1,yi, j>1[12]。
定义一个影响半径r=1的无耦合CNN系统,模板选取如下
| $A=\left[ \begin{matrix} 0 & 0 & 0 \\ 0 & a & 0 \\ 0 & 0 & 0 \\ \end{matrix} \right],A=\left[ \begin{matrix} {{b}_{-1,-1}} & {{b}_{-1,0}} & {{b}_{-1,1}} \\ {{b}_{0,-1}} & {{b}_{0,0}} & {{b}_{0,1}} \\ {{b}_{1,-1}} & {{b}_{1,0}} & {{b}_{1,1}} \\ \end{matrix} \right],Z=z$ | (11) |
对粒子群算法的粒子的位置信息作约束,将(10) 式转化为粒子解向量
| $p=\left( a,{{b}_{-1,-1}},{{b}_{-1,0}},{{b}_{-1,1}},{{b}_{0,-1}},{{b}_{0,0}},{{b}_{0,1}},{{b}_{1,-1}},{{b}_{1,0}},{{b}_{1,1}},z \right)。$ | (12) |
为了保证CNN能收敛到稳定的平衡点,根据引理1,令
| ${{b}_{-1,0}}={{b}_{0,-1}},{{b}_{-1,1}}={{b}_{1,-1}},{{b}_{0,1}}={{b}_{1,0}}。$ | (13) |
为了保证能够step3能够输出边缘结果,即每次迭代的CNN输出|yi, j|>1,令(11) 式中
| $a>1$ | (14) |
在SA-PSO算法中对粒子的位置信息作如上的两点约束就能保证算法在寻找最优解的过程中产生的位置信息均能保证细胞神经网络稳定且输出的绝对值大于1。从而使step3能够输出边缘,保证每轮迭代产生适应值,使SA-PSO能顺利地进行每一轮搜索。
4、 仿真结果及稳定性分析 (4.1) 模拟学习为了验证文中提出算法的有效性,文中在MATLAB 7.0平台下进行模拟仿真。图 3为训练样本,其中图 3 (a)为原图,图 3(b)为理想输出图片。
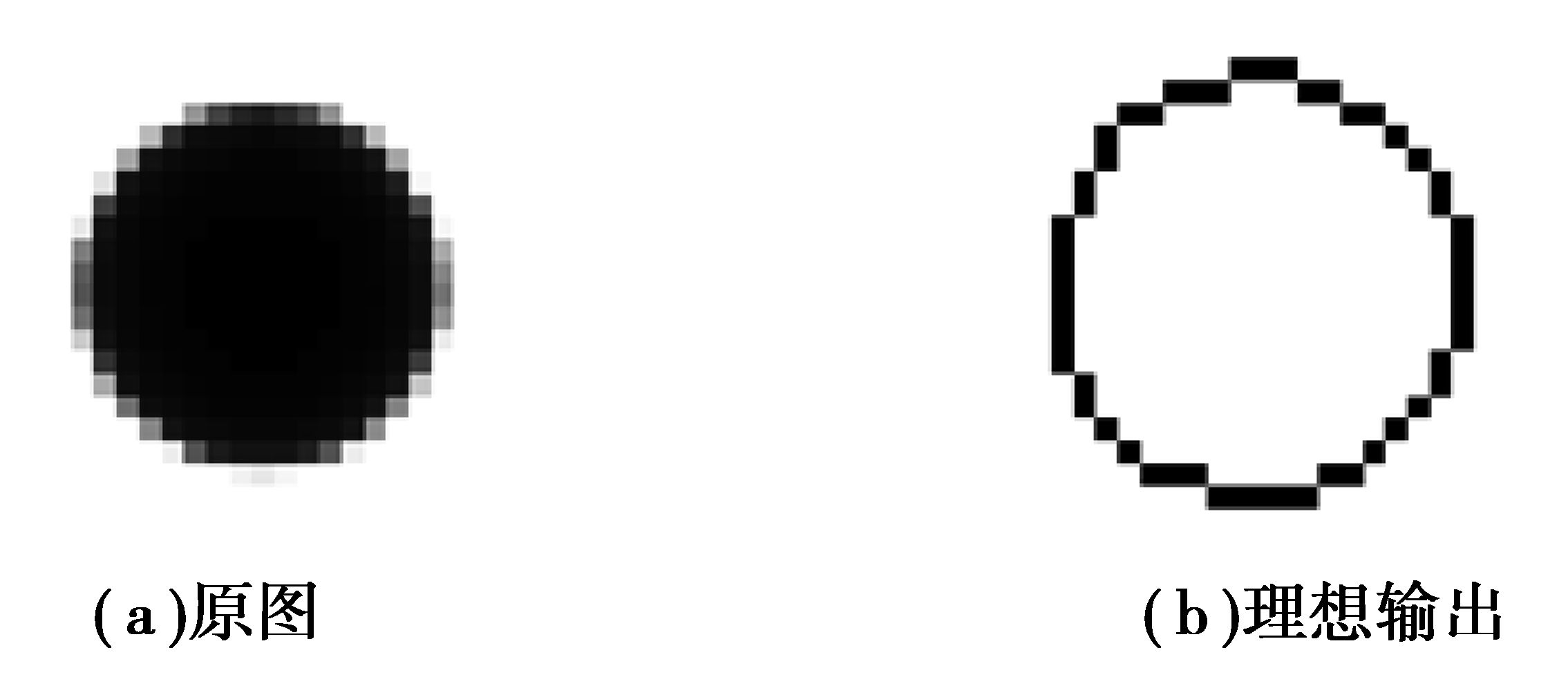
|
图 3 训练样本 Figure 3 Training sample |
用式(13) 、式(14) 对粒子的解空间式(12) 进行约束得到新的解空间p=(a, b-1, -1, b-1, 0, b-1, 1, b-1, 0, b-1, 0, b0, 0, b0, 1, b-1, 1, b1, 0, z),其中a>1。
定义适应度函数为
| $f\left( p \right)=\sum\limits_{i=1}^{k}{{{\left( y_{i}^{d}-{{y}_{i}}\left( \infty \right) \right)}^{2}}},$ | (15) |
式中:k为网络中细胞的个数,yid是第i个像素的理想输出,yi(∞)表示第i个CNN细胞的最终输出。令所有细胞的初始状态为xi, j(0) =0。在SA-PSO算法中,学习因子取值c1=2.05和c2=2.05, 退火常数为λ=0.5,初始温度为T0=f(pg)/ln 5;粒子数选取40,经过200次迭代,整理后得最优解
| $p=\left( 6,-1,-1.3,-1,-1.3,8.75,-1.2,-1,-1.2,-1,-0.5 \right)。$ | (16) |
将式(16) 的解映射为CNN的模板为
| $A=\left[ \begin{matrix} 0 & 0 & 0 \\ 0 & 6 & 0 \\ 0 & 0 & 0 \\ \end{matrix} \right],B=\left[ \begin{matrix} -1 & -1.3 & -1 \\ -1.3 & 8.75 & -1.2 \\ -1 & -1.2 & -1 \\ \end{matrix} \right],z=-0.5。$ | (17) |
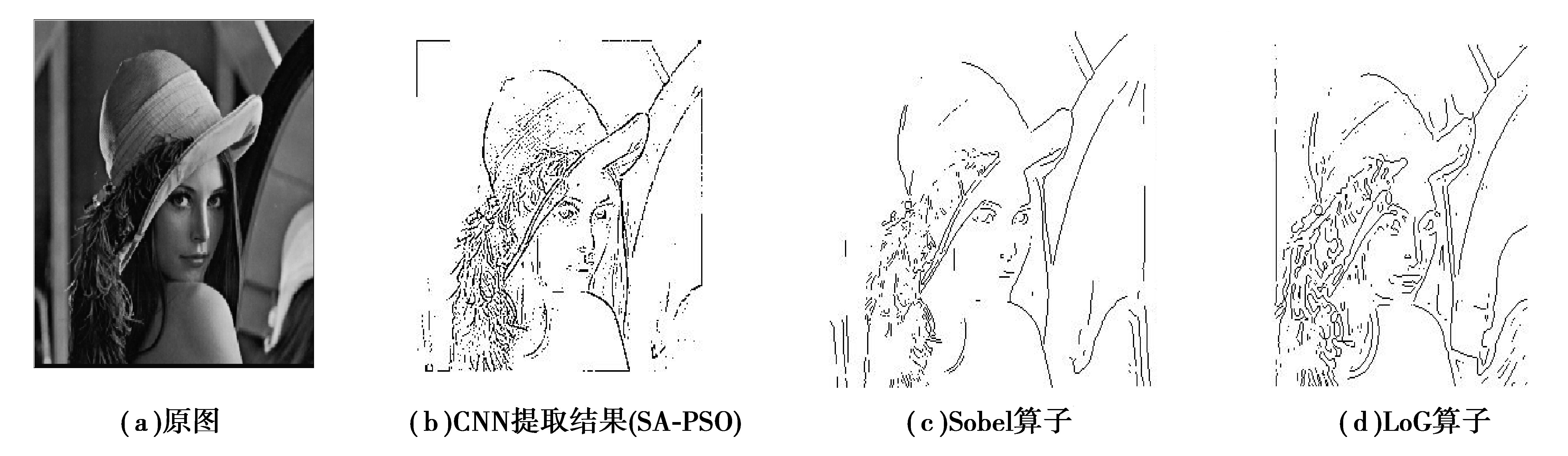
用CNN模板式(17) 对灰度图像图 4(a)lena图进行边缘提取。边缘检测评价性能要求为[17]:正确检测、准确定位边缘、边缘具有连续性。因为数字图像的复杂多样性,边缘检测的评价大多数仍然采用直观评价的方式。为了更加清楚说明文中算法的效果,采用经典的算法Sobel, LoG算子对lena图进行边缘提取。图 4(b)、(c)、 (d)分别为CNN、Sobel算子、LoG算子边缘提取结果。从对比中,可以看出CNN提取的边缘更加连续,在人物的面部细节的边缘检测和定位上好于Sobel, LoG算子,更符合人类视觉习惯。
|
图 4 Lena边缘提取效果图 Figure 4 Edge detection results |
CNN在图像领域应用的明显优势在于高速的并行处理能力。在文中,CNN模板一旦确认,CNN每个细胞的状态方程式(1) 的控制和偏移部分将作为一个常数输入到状态方程式中,在状态的演化过程中, 每个细胞相互独立,并行演化。因为每个细胞对应着图像的像素信息,所以用CNN处理图像能真正 实现图像的并行处理,处理速度与图像的大小无关。同时,为了证明文中设计的模板的在收敛速度方面的性能,定义收敛速率(convergence rate, CR)为
| ${{C}_{R}}=\frac{n}{N},$ | (18) |
式中:N为处理图像的像素个数,n为像素收敛的个数。图 5为本文中提出算法的收敛速率图。从图中可以看出,设计出的模板在对lena图进行边缘检测时经过70步迭代已经使所有细胞完全收敛。从实验结果来看,当硬件水平达到一定水平时,该模板在边缘提取速度极快。

|
图 5 收敛速率图 Figure 5 Convergence rate |
提出了一种用SA-PSO算法对CNN边缘提取模板进行求解的方法,并对该方法设计出的模板在边缘提取的效果和收敛性能上进行检测。从实验结果来看,设计出的CNN模板不仅具有良好的边缘检测能力,还有较快的处理速度。
| [1] |
Chua L O, Yang L.
Cellular neural networks:theory and applications[J]. IEEE International Symposium on Circuits and Systems , 1988, 35 : 1257–1272.
( 0) 0)
|
| [2] |
Deng S J, Tian Y, Hu X P, et al.
Application of new advanced CNN structure with adaptive thresholds to color edge detection[J]. Communications in Nonlinear Science&Numerical Simulation , 2012, 17 (4) : 1637–1648.
( 0) 0)
|
| [3] |
张莹, 王太勇, 黄国龙, 等.
基于参数自适应CNN的灰度图像边缘检测[J]. 计算机工程与应用 , 2008, 44 (18) : 160–162.
ZHANG Ying, WANG Taiyong, HUANG Guolong, et al.
Edge detection of gray-scale images based on self-adaptive CNN[J]. Computer Engineering&Applications , 2008, 44 (18) : 160–162.
( 0) 0)
|
| [4] |
王平, 田袁, 胡锡鹏.
阈值自适应CNN的彩色图像边缘提取[J]. 计算机工程与应用 , 2014, 50 (21) : 189–194.
Wang Ping, Tian Yuan, Hu Xipeng.
Color edge detection based on CNN with adaptive threshold[J]. Computer Engineering and Applications , 2014, 50 (21) : 189–194.
( 0) 0)
|
| [5] |
Li H Q, Liao X F, Li C D.
Edge detection of noisy images based on cellular neural networks[J]. Communications in Nonlinear Science&Numerical Simulation , 2011, 16 (9) : 3746–3759.
( 0) 0)
|
| [6] |
任鲁涌.
一种基于遗传算法的细胞神经网络模板设计算法[J]. 山东工程学院学报 , 2001, 15 (4) : 48–52.
Ren Luyong.
A New algorithm for CNN template design based genetic algorithm[J]. Journal of Shangdong Institute of Technology , 2001, 15 (4) : 48–52.
( 0) 0)
|
| [7] |
Nagy E.
CNN template optimization by adaptive simulated annealing[J]. leice , 1996 .
( 0) 0)
|
| [8] |
卢珊萍, 于盛林.
基于粒子群算法的细胞神经网络模板参数设计[J]. 计算机技术与发展 , 2009, 19 (4) : 83–86.
LU Shanping, YU Shenglin.
A Template Design Method for Cellular Neural Network Based on Particle Swarm Optimizer Algorithm[J]. Computer Technology and Development , 2009, 19 (4) : 83–86.
( 0) 0)
|
| [9] |
Fornarelli G, Giaquinto A.
Adaptive particle swarm optimization for CNN associative memories design[J]. Neurocomputing , 2009, 72 (16-18) : 3851–3862.
DOI:10.1016/j.neucom.2009.05.004 ( 0) 0)
|
| [10] |
焦巍, 刘光斌, 张艳红.
求解约束优化的模拟退火PSO算法[J]. 系统工程与电子技术 , 2010, 32 (7) : 1532–1536.
JIAO Wei, LIU Guangbin, ZHANG Yanhong.
Particle swarm optimization based on simulated annealing for solving constrained optimization problems[J]. Systems Engineering and Electronics , 2010, 32 (7) : 1532–1536.
( 0) 0)
|
| [11] |
傅文渊, 凌朝东.
布朗运动模拟退火算法[J]. 计算机学报 , 2014, 37 (6) : 1301–1308.
FU Wenyuan, LING Chaodong.
Brownian motion based simulated annealing algorithm[J]. Chinese Journal of Computers , 2014, 37 (6) : 1301–1308.
( 0) 0)
|
| [12] |
Crounse K R, Chua L O.
Methods for image processing and pattern formation in Cellular Neural Networks:a tutorial[J]. IEEE Transactions onCircuits&Systems I Fundamental Theory&Applications , 1995, 42 (10) : 583–601.
( 0) 0)
|
| [13] |
Chua L O, Yang L.
Cellular neural networks:applications[J]. IEEE Transactions on Circuits&Systems , 1988, 35 (10) : 1273–1290.
( 0) 0)
|
| [14] |
Harrer H, Nossek J A, Stelzl R.
An analog implementation of discrete-time cellular neural networks[J]. IEEE Transactions on Neural Networks , 1992, 3 (3) : 466–476.
DOI:10.1109/72.129419 ( 0) 0)
|
| [15] |
龚纯, 王正林. 精通MATLAB最优化计算[M]. 北京: 电子工业出版社, 2009 .
GONG Chun, WANG Zhenglin. Proficient in MATLAB optimization calculation[M]. Beijing: Publishing House of Electronics Industry, 2009 .
( 0) 0)
|
| [16] |
王凌, 刘波. 微粒群优化与调度算法[M]. 北京: 清华大学出版社, 2008 : 45 -46.
WANG Ling, LIU Bo. Particle swarm optimization and scheduling algorithm[M]. Beijing: Tsinghua University Press, 2008 : 45 -46.
( 0) 0)
|
| [17] |
Zhu Q M.
Efficient evaluation of edge connectivity and width uniformity[J]. Image and Vision Computing , 1996, 14 (1) : 21–34.
DOI:10.1016/0262-8856(95)01036-X ( 0) 0)
|
 2016, Vol. 39
2016, Vol. 39

