2. 西门子中国研究院, 北京 100102
2. Siemens Ltd. China Corporate Technology, Beijing 100102, P.R.China
结构非线性问题分为几何非线性问题、材料非线性问题、状态非线性问题[1]。接触问题是典型的状态非线性问题,即接触区域的大小和位置未知,同时,随着接触状态的改变,接触表面的法向和切向刚度也发生改变。另外,接触问题很多时候伴随有由大变形引起的几何非线性和材料非线性问题[2]。因此,在高度非线性接触问题的数值模拟过程中经常发生收敛性困难这一问题[3-8]。
通过使用ANSYS Workbench有限元软件对法兰连接这一实际工程问题进行了数值模拟,分析了模拟过程中影响计算收敛性的各个因素,并对与之对应的ANSYS软件中各个参数进行合理设置。在建立有限元模型过程中,网格划分采用了接触单元尺寸,使接触区的网格形状近似;在模拟螺栓连接时,用非对称绑定接触模拟螺母和螺栓的连接,非对称摩擦接触模拟螺母与法兰,以及法兰之间的连接,用多个子步施加螺栓预紧力的加载方式来模拟拧紧的螺栓。在数值计算过程中,对绑定接触采用罚函数法,对摩擦接触采用增广拉格朗日乘子法;绑定接触的罚刚度可采用一个较大值,摩擦接触的罚刚度通过试算来确定,在试算过程中初始给一个较小的罚刚度值保证收敛,再逐步增大直至计算收敛[9-11]。
1 建立接触对机械工程中的法兰连接件通常使用螺栓来实现连接,有限元软件能够有效地实现该连接方式的模拟。合理地建立各装配体的接触对,即确定接触面和目标面,并定义接触对的接触类型,有利于避免产生较大的穿透量,以及加快收敛速度。
1.1 螺栓接触对有限元软件分析中定义了接触面不能穿透目标面,且螺母内表面相对于螺栓来说是凹面,因此,定义螺母内表面和法兰螺栓孔为目标面,螺栓的表面为接触面;螺母上与法兰接触的面积远小于与之相对应的法兰上的接触面积,因此,定义螺母接触侧为接触面,法兰接触侧为目标面。另外,由于螺栓与螺母之间的螺纹副通过内、外螺纹旋合的形式连接,故近似认为二者之间无相对滑移和相对分离,因此,对螺母和螺栓的接触对采用绑定接触类型;为了真实模拟实际工作情况,对螺母与法兰接触对和螺栓与法兰螺栓孔接触对采用摩擦接触类型。螺栓接触对如图 1所示。

|
图 1 螺栓接触对 Figure 1 Contact pairs on the bolt |
法兰上的凸面定义为接触面,机体的凹面定义为目标面。实际工作情况中,法兰与机体之间可能有相对滑移或是间隙,因此,法兰接触对采用摩擦接触类型, 摩擦系数取0.12。
2 网格划分计算模型均采用20节点的六面体单元(SOLID186)进行划分。远端质量点采用MASS21单元,远端力与远端质量点作用面采用SURF154单元。螺栓上采用预紧力单元PRETS179。各个接触体均采用相同尺寸划分,同时,在接触面上使用接触尺寸这一局部尺寸功能,这样会在接触面上产生大小与形状近似的单元。在目标面上的接触单元为TARGET170, 接触面上的接触单元为CONTACT174(8-node)。为了避免接触体产生刚体运动,在接触区添加了弱弹簧并采用COMBIN14单元。模型的有限元单元数如表 1所示,局部接触区有限元模型如图 2所示。

|
图 2 局部接触区网格 Figure 2 Grids in the local contact zone |
| 表 1 有限单元数 Table 1 The number of elements |
实际接触体之间不发生相互穿透,有限元程序进行模拟时需要在接触面之间建立一种关系来防止它们在分析时相互穿过,这种方式称为强制接触协调。接触非线性算法是基于约束变分原理,将附加约束条件引入最小位能原理,则变分求驻值变为无附加约束条件的问题[4-5, 12-15]。
3.1 罚函数法所谓罚函数法,就是在接触面之间用“弹簧”建立强制接触协调关系。当接触面分开时,弹簧不起作用;当接触面穿透时,弹簧起作用。弹簧偏移量满足平衡方程
| $ F=K\Delta, $ | (1) |
式中:K为弹簧刚度,在这里指罚刚度(或接触刚度); Δ为弹簧偏移量,接触问题中的穿透量。在数学上要求有限小的穿透量才能在接触面上产生接触力,而实际接触体不相互穿透,要求在接触面处产生最小的穿透量,才能给出最大的精度。因此,要与实际接触情况更接近,就意味着罚刚度要足够大才能产生较真实的接触力。然而,罚刚度太大会引起收敛困难(具体表现在罚刚度太大会引起下一次迭代过程中接触体出现弹开现象)。
罚函数法的无约束变分问题表述为
| $ \begin{array}{l} min\prod {^*} \left(U \right)=\prod {\left(U \right)}+\prod {_P} \left(U \right)=\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{1}{2}{U^{\rm{T}}}\boldsymbol{K}U - {U^{\rm{T}}}F+\frac{1}{2}{P^{\rm{T}}}{E_P}P. \end{array} $ | (2) |
式中:U为节点位移;K为系统刚度矩阵;F为接触力;P为穿透深度,是u的函数;EP为罚因子。
由于绑定接触类型不允许接触体之间有分离和滑动,即接触状态不会随时间发生改变,属于线性情况,因此,对螺母与螺栓的非对称绑定接触采用罚函数法计算。
3.2 增广拉格朗日乘子法增广拉格朗日乘子法,就是在罚函数的基础上增加一个附加自由度(接触压力)来实现强制接触协调关系,即在迭代的刚开始,接触协调基于罚刚度确定,一旦达到平衡,检查穿透容差,如果穿透值太大,接触压力增加(减小穿透量),迭代继续。
增广拉格朗日法的无约束变分问题表述为
| $ \begin{array}{l} min\prod {^*} \left({U, \lambda } \right)=\prod {\left(U \right)}+\prod {_P} \left(U \right)+\prod {_c} \left(U \right)=\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{1}{2}{U^{\rm{T}}}KU - {U^{\rm{T}}}F+\frac{1}{2}{P^{\rm{T}}}{E_P}P+{g^{\rm{T}}}\lambda. \end{array} $ | (3) |
式中:g为间隙函数;λ为拉格朗日乘子。
由于附加自由度的引入,增广拉格朗日法对罚刚度不再敏感,通过不断更新接触刚度使穿透值在容限范围内,从而使迭代继续。因此,所有非对称摩擦接触均采用增广拉格朗日乘子法计算。
另外,在计算过程中通过查看软件的求解信息来观察迭代的收敛情况,根据其迭代收敛情况增大或减小罚刚度以使其收敛。
4 初始界面调整有限元模型中均采用了带有中间节点的单元,故采用高斯节点进行接触状态的探测,这样可以减小穿透量,有助于收敛。对于绑定接触类型,程序默认填充所有的几何间隙,忽略所有的初始渗透。对于摩擦接触类型,通过界面修正来调整几何间隙,使其建立初始闭合的接触状态,从而防止刚体运动以及减少迭代次数。另外,通过初始接触状态检查所提供的穿透量和间隙值来调整Pinball半径。这样,所有接触均为闭合接触状态,减少了迭代次数并快速找到稳定的接触状态。调整后的初始接触状态如表 2所示。
| 表 2 初始接触状态 Table 2 Initial contact status |
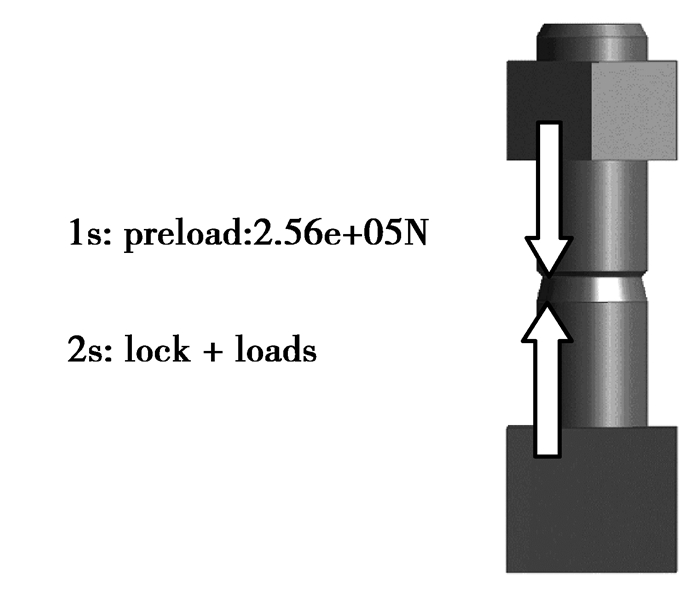
1)ANSYS使用螺栓预紧力来模拟螺栓拧紧过程[16-18],第一个荷载步是施加预紧力,第二步是锁住,即保持预紧力在各个螺栓上产生的位移,同时施加载荷。按VDI2230[19]附录表A2计算螺栓预紧力,该法兰连接结构采用M27、强度等级为10.9的高强螺栓,摩擦系数为0.12,计算螺栓预紧力为256 kN。
考虑避免因穿透量过大而引起收敛困难,用线性加载的方式来施加预紧力,在开始加载时给一个很小的载荷增量(算例中initial substep=100)。同时打开自动时间步,程序自动调整荷载增量,用较少的资源获得有效解。这样给螺栓施加一个很小的初始荷载,程序能够通过少量迭代找到一个稳定的接触状态,在此稳定的接触状态基础上,程序根据收敛情况自动调整后续荷载子步步长来施加载荷(total substeps=11),通过此方式来使计算收敛。
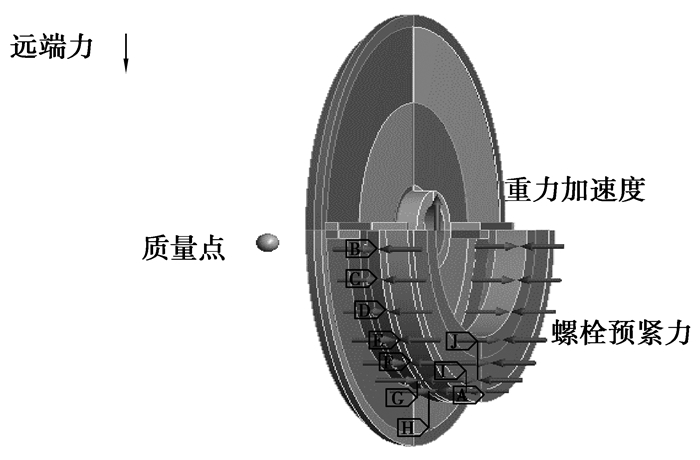
2)在压缩机叶轮的装配过程中提升设备作用在蜗壳上,提升设备自重用大小为19.6 kN作用在法兰盘上的远端力来等效。另外,用远程质量点来模拟涡壳与法兰盘的连接,远程质量点的位置由蜗壳的质心位置确定,质量点与法兰的约束用MPC(多点约束方程)来建立连接。远端力、远程质量点以及法兰的重力加速度均在第二步施加。假如收敛困难,同样给定一个较大的初始荷载子步数来解决该问题。模型边界条件如图 3、4所示。
|
图 3 螺栓预紧力 Figure 3 Bolt pretension |
|
图 4 第2 s时的边界条件 Figure 4 Boundary condition in the 2nd second |
材料在常温下的力学性能参数如表 3所示。
| 表 3 材料参数(20 ℃) Table 3 Material parameters (20 ℃) |
前面对影响计算收敛性的各个因素进行了详细分析,并对相关参数进行了设置。但影响计算精度和收敛性的重要参数罚刚度是需要根据接触计算的迭代情况来进行一系列试算才能找到合适的值[20]。本次分析中,先估算一个罚刚度,在此基础上对罚刚度进行调整。计算方法如下:
| $ {K_n}=fEh \approx fE, $ | (4) |
| $ {K_t}=0.01{K_n}, $ | (5) |
式中:f为调整系数,大面积实体接触取值为0.1~10,弯曲为主的体接触取值为0.01~0.1。
由于模型中螺栓与螺母的绑定接触对均采用了罚函数接触算法,考虑到能更真实地模拟其接触情况,初始罚刚度系数FKN为1.0,即大罚刚度值产生小的穿透量,穿透量越小越符合真实接触情况。非对称摩擦接触对采用了增广拉格朗日接触算法,为避免罚刚度太大引起接触力振荡,导致收敛困难,初次计算采用一个较小的罚刚度系数FKN为0.1。若计算收敛,则逐步增大摩擦接触和绑定接触的罚刚度,直到某项重要的结果项(算例中取接触摩擦应力)不再变化。若计算不收敛,减小罚刚度直至收敛。
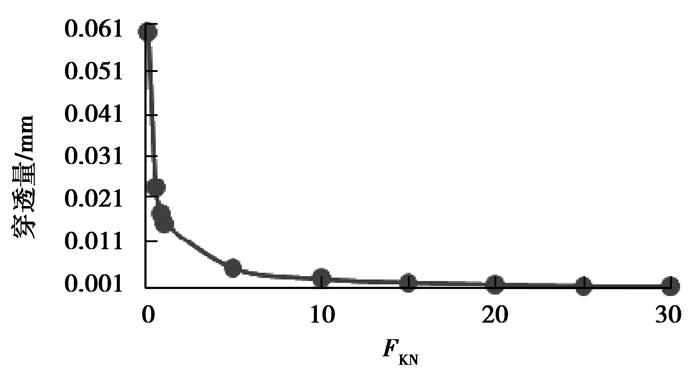
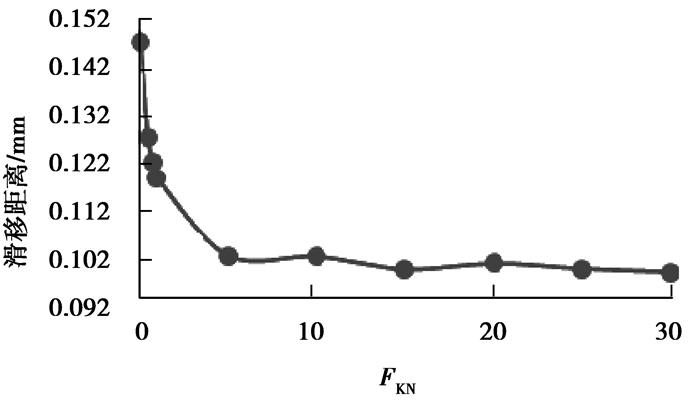
从计算结果可以看出,随着罚刚度的增大,穿透量与滑移距离逐渐减小,最大接触摩擦应力逐渐增大。FKN=20时,该计算趋于收敛,此时罚穿透量为0.001 75 mm,远小于实体单元厚度(8 mm),表明计算结果有较好的计算精度。不同罚刚度对计算结果的影响如表 4、图 5、图 6、图 7所示。
| 表 4 罚刚度对计算结果的影响 Table 4 Influence of FKN on result |
|
图 5 罚刚度对穿透量的影响 Figure 5 Influence of FKN on penetration |
|
图 6 罚刚度对滑动距离的影响 Figure 6 Influence of FKN on sliding distance |

|
图 7 罚刚度对最大摩擦应力的影响 Figure 7 Influence of FKN on max frictional stress |
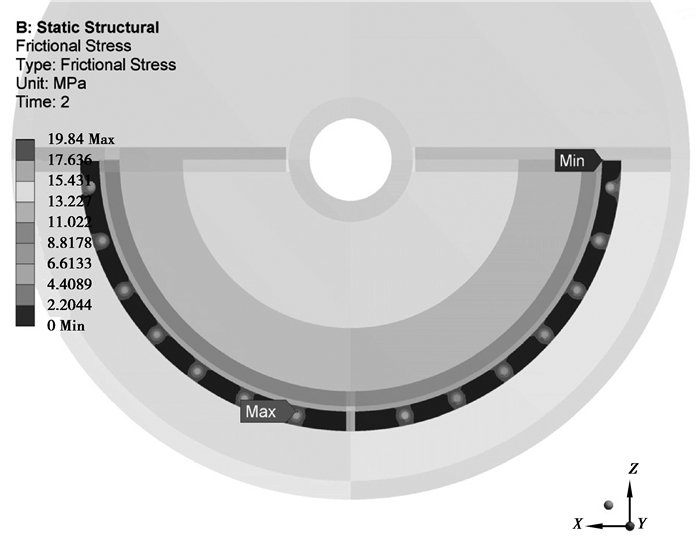
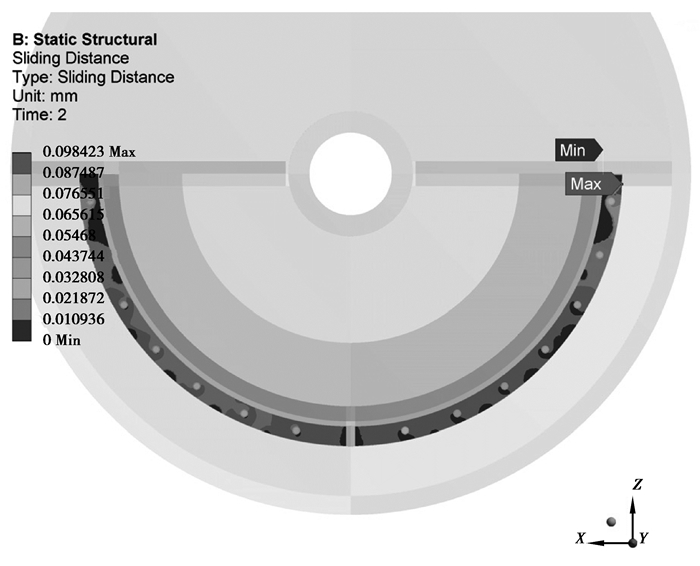
另外,由图 8可知摩擦力在接触面上分布不均匀,主要分布在栓孔周围,且呈环状由栓孔向周围递减,与螺栓在预紧力作用下接触面上压应力的分布相符合。由图 9可知法兰盘接触良好,仅有非常小的滑移,表明在外力作用下对该法兰连接无影响,满足工程使用要求。
|
图 8 接触面摩擦应力云图 Figure 8 Frictional stress on the contact surface |
|
图 9 接触面滑移量 Figure 9 Sliding distance on the contact surface |
收敛困难是非线性接触问题数值模拟过程中难以解决的问题之一。使用ANSYS Workbench对该问题进行数值模拟时,需要充分理解问题的特性和建立合理的计算模型。模型简化、接触对建立、网格划分、初始界面调整、接触算法选择、边界条件施加,以及罚刚度选取等都对计算收敛有重要影响。以螺栓连接法兰为例详细分析了这些影响因素,主要做了以下工作:
1) 对模型做了适当简化,对非主要分析对象蜗壳采用依附在法兰盘上的质量点模拟;另外,采用作用在法兰盘上的远端力模拟原本直接作用在蜗壳上的荷载。这样减少了单元和接触对的数量,在螺栓与螺母的接触类型选择上采用了绑定接触类型,相对降低了整个模型的非线性程度,有利于最终结果的收敛。
2) 整个模型采用六面体单元进行网格划分,减小了有限元模型并提高了计算的精度。在接触面上使用接触尺寸功能获得了形状与大小近似的接触单元,有利于减小接触发生时的穿透量。为了避免发生刚体运动,在模型上添加了弱弹簧单元。
3) 螺栓与螺母的绑定接触采用了罚函数法,并使用了大罚刚度系数;所有摩擦接触采用了增广拉格朗日乘子法,在一开始采用一个较小的罚刚度系数,然后,逐渐增大罚刚度系数来避免计算一开始就不收敛。同时,计算过程中观察N-R残差。若发生振荡,可适当减小罚刚度。
4) 通过对摩擦接触类型进行界面修正和根据初始接触信息来调整Pinball半径值,消除了几何模型中的间隙和穿透,有利于减小迭代次数。
5) 使用线性加载的方式施加螺栓预紧力来模拟螺栓拧紧过程,在开始加载时给一个很小的载荷增量,这样有利于计算收敛;同时打开自动时间步,用较少的资源获得有效解。
| [1] |
王新敏. ANSYS工程结构数值分析[M]. 北京: 人民交通出版社, 2007 .
WANG Xinmin. Numerical analysis of engineering structure[M]. Beijing: China communication press, 2007 . (in Chinese) |
| [2] |
苏春峰, 艾延延, 娄小宝.
接触非线性仿真中接触刚度因子选取的方法研究[J]. 沈阳航空工业学院学报 , 2009, 26 (3) : 5–9.
SU Chunfeng, AI Yanting, LOU Xiaobao. Study on contact stiffness factor selection methed in contact non-linear simulation[J]. Journal of shenyang institute of aeronautical engineering , 2009, 26 (3) : 5–9. (in Chinese) |
| [3] |
陈万吉, 胡志强.
三维摩擦接触问题算法精度和收敛性研究[J]. 大连理工大学学报 , 2003, 43 (5) : 541–547.
CHEN Wanji, HU Zhiqiang. Study of convergence of exact algorithm to solve three-dimensional frictional contact problems[J]. Journal of dalian university of technology , 2003, 43 (5) : 541–547. (in Chinese) |
| [4] | Fredriksson B. Finite element solution of surface nonlinearities in structural mechanics with emphasis to contact and fracture mechanics problems[J]. Computers & Structures , 1976 (6) : 281–290. |
| [5] | Okamoto N, Nakazawa M. Finite element incremental contact analysis with various frictional conditions[J]. International journal for numerical methods in engineering , 1979 (14) : 337–357. |
| [6] | Reid J D, Hiser N R. Detailed modeling of bolted joints with slippage[J]. Finite elements in analysis and design , 2005 (41) : 547–562. |
| [7] | Girao Coelho A M, da Silva L S, Bijlaard F S K. Finite-element modeling of the nonlinear behavior of bolted tstub connections[J]. Journal of structural engineering , 2006 : 918–928. |
| [8] | Diaz C, Marti P, Victoria M, et al. Review on the modelling of joint behavior in steel frames[J]. Journal of constructional steel research , 2011, 67 (5) : 741–758. DOI:10.1016/j.jcsr.2010.12.014 |
| [9] |
许京荆. ANSYS13.0 Workbench数值模拟技术[M]. 北京: 中国水利水电出版社, 2012 .
Xu Jingjing. ANSYS13.0 Workbench of numerical simulation[M]. Beijing: China water power press, 2012 . (in Chinese) |
| [10] |
朱红钧.ANSYS15.0几何建模与网格划分实战指南[M].北京:人民邮电出版社, 2014. ZHU Hongjun.A guide to the practice of geometry modeling and mesh generation of ANSYS15.0[D].Beijing: Posts and telecommunications press, 2014.(in Chinese) |
| [11] |
龚国伟.风电机组法兰螺栓连接建模与仿真技术研究[D].重庆:重庆大学, 2014. GONG Guowei. Modeling and simulink research about the flange bolts connection of wind turbine [D]. Chongqing: Chongqing university, 2014. (in Chinese) http://cdmd.cnki.com.cn/article/cdmd-10611-1014045802.htm |
| [12] | Peter Wriggers. Computational contact mechanics[M]. Springer-verlag berlin heidelberg: 2006 . |
| [13] | Zienkiewicz O C, Taylor R L, Zhu J Z. The finite element method: Its basis and fundamentals[M]. Sixth edition: 2008 . |
| [14] |
王晓慧, 樊思思, 李人杰, 等.
改进的螺栓连接结构建模方法及其在导弹设计中的应用[J]. 固体火箭技 , 2014, 37 (5) : 694–698.
WANG Xiaohui, FAN Sisi, LI Renjie, et al. A modified modeling method of bolted connection and its application to the missile design[J]. Journal of solid rocket technology , 2014, 37 (5) : 694–698. (in Chinese) |
| [15] |
许超, 余绍蓉, 郑晓亚, 等.
机械螺栓法兰连接的有限元力学模型比较研究[J]. 机械设计与制造 , 2009 : 37–39.
XU Chao, Yu Shaorong, ZHENG Xiaoya, et al. Comparative evaluation of finite element models for mechanical structures with bolted joints[J]. Machinery design & manufacture , 2009 : 37–39. (in Chinese) |
| [16] |
郭然, 施惠基, 郁向东.
, 多层圆柱结构接触预紧力失效分析[J]. 工程力学 , 2003, 20 (4) : 192–198.
GUO Ran, SHI Huiji, Yu Xiangdong. Failure Analysis of the Multi-layer Cylindrical Structure by Pre-stressed Contact Load[J]. Engineering Mechanics , 2003, 20 (4) : 192–198. (in Chinese) |
| [17] |
高旭, 曾国英.
螺栓法兰连接结构有限元建模及动力学分析[J]. 润滑与密封 , 2010, 35 (4) : 68–71.
GAO Xu, ZENG Guoying. The finite element modeling and dynamics analysis of bolts-flanges connection structure[J]. Lubrication engineering , 2010, 35 (4) : 68–71. (in Chinese) |
| [18] |
黄永辉, 王荣辉, 刘长海, 等.
高强螺栓拼接接头传力特性的有限元模拟与试验研究[J]. 铁道学报 , 2011, 33 (11) : 93–98.
HUANG Yonghui, WANG Ronghui, LIU Changhai, et al. Experimental study and finite element analysis on friction high-strength bolt connections[J]. Journal of the china railway society , 2011, 33 (11) : 93–98. (in Chinese) |
| [19] |
VDI 2230第一部分高强度螺栓连接的系统计算单个圆柱螺栓连接[S].2003. VDI 2230, part1, Systematic calculation of high-strength bolted joints[S].2003. (in Chinese) |
| [20] |
高霄汉, 汪玉, 杜俭业, 等.
基于ANSYS软件模拟冲击接触问题的讨论[J]. 噪声与振动控制 , 2012, 2 (6) : 130–133.
GAO Xiaohan, WANG Yu, DU Jianye, et al. Simulation of impact contact based on ansys software[J]. Noise and vibration control , 2012, 2 (6) : 130–133. (in Chinese) |
 2016, Vol. 39
2016, Vol. 39


