2. 河海大学 工程力学系, 南京 210098
2. Department of Engineering Mechanics, Hohai University, Nanjing 210098, P.R.China
近场动力学(Peridynamics,PD)思想由美国Sandia国家实验室的Silling教授于2000年首次提出[1],它结合分子动力学方法、无网格法和有限元法的优点,区别于传统局部模型的位移偏微分方程求解模式。基于传统连续介质力学理论的数值方法,均以连续的位移场作为基本未知量,在处理不连续问题时,必须预先知道裂纹的存在与否及其位置和方向,裂纹变化后还要重新划分网格。而近场动力学方法采用基于非局部思想的直接积分形式的运动方程,通过积分计算在一定近场范围(horizon)内具有一定影响域的材料点之间的相互作用力,而不论位移场的连续与否。由于微观结构特征包含在PD的本构函数内,材料的内部响应在“点对”尺度上计算,裂纹自然萌生和扩展,不受连续性和网格约束。
近场动力学理论提出了解决连续理论和不连续问题之间根本矛盾的一种有效途径,避免了传统连续介质力学方法在求解不连续问题时的奇异性,自提出以来,在国际上引起了广泛的关注[2-4],国内研究尚处于起步阶段[5-9]。已有PD算法和应用研究主要集中在动力破坏[10-12]和裂纹扩展形态模拟[13-14]方面,外部荷载往往以物质点位移或速度的形式施加在模型上进行处理,很少进行类似于传统方法的定量变形计算和准静态力学分析。笔者在近场动力学理论框架下,对反映物质点长程力基本特性的本构力函数进行改进,通过引入人工阻尼、构建分级加载算法和系统失衡判断准则,使近场动力学方法能适用于定量的准静态变形计算的分析。
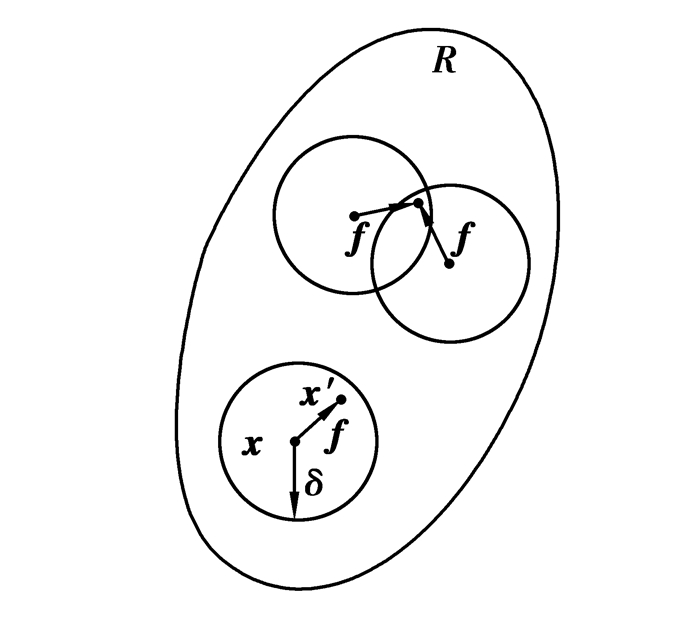
1 近场动力学基本理论近场动力学假定占据某一空间R的任一物质点x,在某一时刻t, 与其周围空间一定范围δ内的所有物质点存在相互作用力f(如图 1所示)。根据牛顿第二定律,其运动方程为
| $ \begin{array}{l} \rho \frac{{{\partial ^2}\boldsymbol{u}}}{{\partial {t^2}}}\int_H {\boldsymbol{f}\left({\boldsymbol{u}\left({\boldsymbol{x'}, t} \right), \boldsymbol{u}\left({\boldsymbol{x}, t} \right), \boldsymbol{x'}, \boldsymbol{x}, t} \right){\rm{d}}} {V_{x'}}+\boldsymbol{b}\left({\boldsymbol{x}, t} \right), \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\forall \boldsymbol{x} \in R, t \ge 0, \end{array} $ | (1) |
|
图 1 物质点间的相互作用力 Figure 1 Pairwise interaction of a material point with its neighboring points |
式中:x′∈R;丨x′-x丨≤δ,δ为近场范围尺寸;u为物质点的位移;f为物质点x与x′之间的相互作用力函数;即本构力函数;ρ为物质点密度;b代表单位体积物质所受的外载荷,即外载荷密度。
近场动力学方法的关键在于找到合适的本构力函数f,理论上任何满足线性容许条件和角动量守恒的函数,均可视为本构力函数。
对于均匀材料,可以定义本构力函数f为
| $ \boldsymbol{f}=\boldsymbol{f}\left({\boldsymbol{u}' - \boldsymbol{u}, \boldsymbol{x}' - \boldsymbol{x}} \right)=\boldsymbol{f}\left({\boldsymbol{\eta}, \boldsymbol{{\rm{\xi }}} } \right), $ | (2) |
式中:ξ=x′-x,η=u′-u,ξ、η为近场范围δ内的物质点对之间的相互作用力在参考构型中的相对位置和相对位移。根据牛顿第三定律得
| $ \boldsymbol{f}\left({ - \boldsymbol{\eta}, - \boldsymbol{{\rm{\xi }}} } \right)=- \boldsymbol{f}\left({\boldsymbol{\eta}, \boldsymbol{{\rm{\xi }}} } \right), $ | (3) |
由此可写出均匀材料的本构力函数f一般式
| $ \boldsymbol{f}\left({\boldsymbol{\eta}, \boldsymbol{{\rm{\xi }}} } \right)=F\left({\boldsymbol{\eta}, \boldsymbol{{\rm{\xi }}} } \right)\left({\boldsymbol{\eta}+\boldsymbol{{\rm{\xi }}} } \right), $ | (4) |
其中F(η, ξ)为标量函数,且满足
| $ F\left({\boldsymbol{\eta}, \boldsymbol{{\rm{\xi }}} } \right)=F\left({ -\boldsymbol{ \eta}, - \boldsymbol{{\rm{\xi }}} } \right). $ | (5) |
材料的特性均包含在函数f(η, ξ)中,该函数表示了一个由物质点ξ产生的变形η到力密度之间的映射。
近场动力学方法中,没有使用“应变”的概念,因而避免了对位移场的求导。在本构模型中使用“伸长率(Bond Stretch)”的概念来描述材料的破坏特征。伸长率用s表示,Silling等[5]将其定义为
| $ s\left({\boldsymbol{\eta}, \boldsymbol{{\rm{\xi }}}} \right)=\frac{{\left| {\boldsymbol{\eta}+\boldsymbol{{\rm{\xi }}} } \right| - \left| \boldsymbol{{\rm{\xi }}} \right|}}{{\left| \boldsymbol{{\rm{\xi }}} \right|}}. $ | (6) |
当物质点对之间的伸长量超越了某给定的限值,则它们之间生成的“键”将发生永久性断裂。一旦“键”发生断裂,便永远不可恢复。该给定的限值称为“临界伸长率(Critical Stretch)”,记为s0。它表示在一个物质点对内,相互作用的两个物质点经过一定的相对位移后,当点对的伸长率超过s0时,该点对破坏,两物质点间不再发生相互作用。
为了描述“键”的破坏情况,引入一个与时间t相关的标量布尔函数μ(ξ, t):
| $ \mu \left({\boldsymbol{{\rm{\xi }}}, t} \right)=\left\{ \begin{array}{l} 1, s\left({t', \boldsymbol{{\rm{\xi }}} } \right)<{s_0}, 0 <t' <t;\\ 0, \;\;\;其他. \end{array} \right. $ | (7) |
根据对本构模型中物质点对间的“键”破坏定义以及基于“临界伸长率”的破坏准则,可以得到材料内部某物质点x在t时刻的损伤为[1, 5]
| $ \varphi \left({\boldsymbol{x}, t} \right)=1 - \frac{{\int_{{H_x}} {\mu \left({t, \boldsymbol{{\rm{\xi }}} } \right){\rm{d}}{V_{x'}}} }}{{\int_{{H_x}} {{\rm{d}}{V_{x'}}} }}. $ | (8) |
由式(6)~(8)可见,PD模型的本构力函数中包含了损伤和断裂描述,不需要另外的断裂准则如传统的临界应力强度因子等,因而在分析破坏问题时不再需要传统的开裂判断或裂纹路径等分析,裂纹将自然萌生、扩展,材料的损伤和不连续作为积分方程解的一部分。
从PD方法的基本方程可见,材料的内力通过物质点之间的相互作用表征。材料内某一物质点的变形位置取决于近场范围内与之发生相互作用的点的力的总和。物质点间的相互作用力函数f包含了材料的物质属性,即传统理论中的本构信息。PD方法将固体材料或结构离散为空间域内含有物质特性的物质点,不需要假设位移场的连续性,求解时不存在空间求导。近场动力学的基本方程也不再以传统的应力-应变关系等形式出现,位移场的连续与否并不影响方程的求解,因此不会出现传统连续性模型求解时出现的病态特征。PD模型是一个典型的计入远程作用的新型非局部模型,是对基于偏微分方程求解的传统连续介质力学模型和传统局部模型的有益补充。
2 本构力函数的改进本构力函数f的构建是近场动力学方法建模的核心和关键,它包含了材料的本构信息。由相关文献[1, 4-5, 15]可知,均匀各向同性微观线弹性材料的本构力函数f为
| $ \boldsymbol{f}=\boldsymbol{f}\left({\boldsymbol{\eta}, \boldsymbol{{\rm{\xi }}} } \right)=\frac{{\boldsymbol{{\rm{\xi }}}+\boldsymbol{\eta} }}{{\left| {\boldsymbol{{\rm{\xi }}}+\boldsymbol{\eta} } \right|}}sc\left({\boldsymbol{{\rm{\xi }}}, \delta } \right), $ | (9) |
式中:c(ξ, δ)称为微观弹性模量函数,表征物质点对的刚度,它由集中函数c(0, δ)和本构力核函数g(ξ, δ)构成,且c(ξ, δ)=c(0, δ)g(ξ, δ)。集中函数c(0, δ)用来描述两物质点在无限靠近时的点对刚度,本构力核函数g(ξ, δ)用以反映物质点间长程力的强度随两物质点间距离的变化规律。
根据本构力核函数的性质,可构造适当的本构力函数,Silling等[4]在初始微观弹脆性模型(PMB)中首先给出了一个最为简单的本构力核函数
| $ g\left({\boldsymbol{{\rm{\xi }}}, \delta } \right)=\left\{ \begin{array}{l} 1, \boldsymbol{{\rm{\xi }}} \le \delta {\rm{;}}\\ 0, \boldsymbol{{\rm{\xi }}} > \delta. \end{array} \right. $ | (10) |
即将物质点对的刚度系数设为常数,此时微观弹性模量函数c(ξ, δ)就简化为
| $ c\left({{\boldsymbol{\rm{\xi }}}, \delta } \right)=c\left({0, \delta } \right)c\left(\delta \right)=\frac{{9E}}{{\pi {\delta ^3}}}, $ | (11) |
该函数很好地体现了“近场”的思想,对于任一物质点,只与近场范围内的物质点发生相互作用。对近场范围外的点,其作用为0。但是该函数过于简单,且存在计算精度方面的问题。考虑到物质点对间相互作用力的强度随间距变化的特点,笔者构造二次多项式型本构力核函数,其形式为
| $ g\left({{\boldsymbol{\rm{\xi }}}, \delta } \right)=\left\{ \begin{array}{l} 1 - {\left({\frac{{\boldsymbol{\rm{\xi }}}}{\delta }} \right)^2}, \boldsymbol{{\rm{\xi }}} \le \delta;\\ 0, \boldsymbol{{\rm{\xi > }}}\delta. \end{array} \right. $ | (12) |
该函数充分考虑了近场范围尺寸δ对本构力函数的影响,且计算精度较式(10)有所提高。
3 计算方法根据PD思想,对式(1)进行空间离散,将其离散为节点,每个节点占据一定的体积,节点之间没有单元或者其他几何联系,PD方法的运动方程(1)的解可以转化为求解有限和的形式
| $ \rho {\boldsymbol{{\ddot u}}_i}=\sum\limits_p {\boldsymbol{f}\left({\boldsymbol{u}_p^n - \boldsymbol{u}_i^n, {\boldsymbol{x}_p} - {\boldsymbol{x}_i}} \right){V_p}}+\boldsymbol{b}_i^n, $ | (13) |
式中:n为时间步号;Vp为节点p处的体积;xi为第i个配置点处的位矢。
根据线性化理论[1],式(13)可转化为
| $ \rho {\boldsymbol{{\ddot u}}_i}=\sum\limits_p {\boldsymbol{C}\left({\boldsymbol{u}_p^n - \boldsymbol{u}_i^n} \right)\left({{\boldsymbol{x}_p} - {\boldsymbol{x}_i}} \right){V_p}}+\boldsymbol{b}_i^n, $ | (14) |
其中C为一二阶张量,其定义为
| $ \boldsymbol{C}\left(\boldsymbol{{\rm{\xi }}} \right)=\frac{{\partial \boldsymbol{f}}}{{\partial \boldsymbol{\eta} }}\left({0, \boldsymbol{{\rm{\xi }}}} \right). $ | (15) |
近场动力学方法基于非局部作用思想建立模型,并通过求解运动方程来描述物质的力学行为, 其最初的思想是假设物质点自始至终处于绝对运动状态, 所描述的问题也仅局限于动力破坏问题。为了能使其描述静力问题, 可以模仿有限元法形成总体刚度矩阵, 然后通过求解非线性方程组得到问题解, 然而这样处理一方面要求计算机具有庞大的内存(近场动力学方法要求将求解构型离散为足够细小的物质点);另一方面由于目前现有的求解非线性方程组方法对于大变形、破坏等强非线性问题显得并不是十分有效,体现不出近场动力学方法在处理此类问题的优势。
为了充分利用PD方法求解强非线性和不连续问题的优势来模拟准静态问题,笔者借鉴经典动力学中求解静力问题的动态松弛法,在近场动力学的基本方程上通过引入人工阻尼,使得物质点在外荷载作用下达到平衡状态,此时物质点的控制方程为
| $ \rho \left(x \right)\boldsymbol{\ddot u}\left({\boldsymbol{x}, t} \right)+C\boldsymbol{\dot u}=\int_H {\boldsymbol{f}\left({\boldsymbol{u}\left({\boldsymbol{x}, t} \right)- \boldsymbol{u'}\left({\boldsymbol{x}, t} \right), \boldsymbol{x'} - \boldsymbol{x}} \right)} {\rm{d}}V', $ | (16) |
式中:ρ为物质密度; C为人工阻尼系数,是一个正实数,其大小将影响静力学求解的收敛速度和收敛方式。式(16)可以简记为
| $ \rho \left(\boldsymbol{x} \right)\boldsymbol{\ddot u}\left({\boldsymbol{x}, t} \right)+C\boldsymbol{\dot u}=\boldsymbol{L}u\left({\boldsymbol{x}, t} \right)+\boldsymbol{b}\left({\boldsymbol{x}, t} \right), $ | (17) |
其中
| $ \boldsymbol{L}u\int_H {\boldsymbol{f}\left({\boldsymbol{u}\left({\boldsymbol{x}, t} \right)- \boldsymbol{u'}\left({\boldsymbol{x}, t} \right), \boldsymbol{x'} - \boldsymbol{x}} \right)} {\rm{d}}V'=\int_H {\boldsymbol{k}\left({\boldsymbol{x'} - \boldsymbol{x}} \right)\left({\boldsymbol{u}\left({\boldsymbol{x}, t} \right)- \boldsymbol{u'}\left({\boldsymbol{x}, t} \right)} \right)} {\rm{d}}V'. $ | (18) |
为了模拟结构的静力破坏,笔者采用外力分级加载方式,提出了失衡判断准则。在近场动力学方法模拟时,最容易出现的情况就是物质点在加载初期,由于瞬间加速度过大而散开,导致运算无法继续进行。为了克服这一弊端,需要对外荷载进行分级加载。在此引入一个荷载分级因子λ,对外荷载b进行分级。将λ分成m个增量:
| $ 0={\lambda _0} <{\lambda _1} <{\lambda _2} <\cdots <{\lambda _m}=1, $ | (19) |
| $ \Delta {\lambda _m}={\lambda _m} - {\lambda _{m - 1}}, $ | (20) |
则每一级荷载增量为Δλmb=(λm-λm-1)b。
在计算时,将一个外荷载增量施加到物质点上,经过一段时间达到平衡后,再施加下一个增量。为避免由于所施加的外荷载增量过大而导致结构过早地破坏,尤其是结构在第一级荷载增量作用下发生破坏的情况,应对Δλm做出限制:
| $ \frac{1}{2}\frac{{\Delta {\lambda _m}\boldsymbol{b}}}{\rho }\Delta {t^2} <{s_0}\Delta x, $ | (21) |
即
| $ \Delta {\lambda _m}\boldsymbol{b} <\frac{{2\rho {s_0}\Delta x}}{{\Delta {t^2}}}, $ | (22) |
式中:s0为临界伸长率;Δt为时间步长;Δx为物质点的间距。若某时刻结构出现一定程度的损伤并开始破坏,此时荷载将不再增加,保持该级荷载作用直至结构整体破坏。当m越大时表示加载速率越缓慢,所得到的极限破坏荷载精度越高,所耗费的时间越长。在时间轴上做中心差分列式,得到位移对时间步长Δt的显式表达式:
| $ \left\{ \begin{array}{l} {\boldsymbol{{\dot u}}^{n+\frac{1}{2}}}=\left({\left({\rho/\Delta t - C/2} \right){\boldsymbol{{\dot u}}^{n - \frac{1}{2}}}+\left({{\lambda _m}\boldsymbol{b} - \boldsymbol{L}_\boldsymbol{u}^n} \right)} \right)\left({\rho/\Delta t - C/2} \right), \\ {\boldsymbol{u}^{n+1}}={\boldsymbol{u}^n}+{\boldsymbol{{\dot u}}^{n+\frac{1}{2}}}\Delta t. \end{array} \right. $ | (23) |
上述中心差分格式的求解是条件稳定的,而对于被离散为众多物质点的多自由度结构系统,可以采用以单一物质点的失衡力来判断该算法的稳定性。因此,笔者构建物质点系统的失衡判断准则为
| $ \left\| {\boldsymbol{\psi} \left(\boldsymbol{u} \right)} \right\| \le \beta \left\| \boldsymbol{b} \right\|, $ | (24) |
或
| $ \frac{{\sqrt {\sum\limits_{j=1}^N {{{\left({\boldsymbol{\psi} _j^i} \right)}^2}} } }}{{\sum\limits_{j=1}^N {{{\left({{\boldsymbol{b}_j}} \right)}^2}} }} \le \beta, $ | (25) |
式中:N为结构的自由度总数;ψji=Luji+bji表示第j个自由度在第i次迭代时的失衡力;β是失衡判断指标,即失衡力与外荷载之比大于该值时,系统将无法维持平衡,若小于该值,则该荷载步迭代收敛,施加下一级荷载。当结构出现细微损伤时,若迭代仍能收敛,则继续施加下一级荷载。β越小,所得到的结果越精确,但计算量也越大。合理的选取失衡判断指标,有利于近场动力学方法应用到工程结构的极限荷载的定量计算。
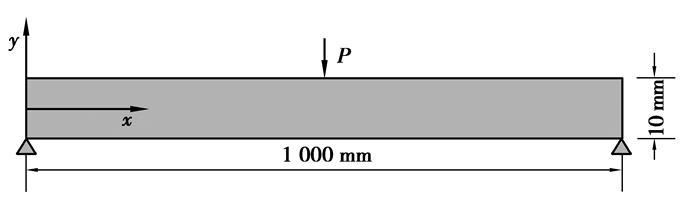
4 算例分析考虑长度为1 m,高度为0.1 m的矩形简支梁,梁上边缘中点承受大小为1 kN,方向竖直向下的荷载作用,如图 2所示。
|
图 2 简支梁受集中力作用的近场动力学模型 Figure 2 Peridynamics model of a simply supported beam under concentrated force |
材料密度为2 400 kg/m3,弹性模量E=20 GPa。构造简单的正方形晶格,晶格常数Δx=0.002 m,离散的物质点数为25 551,时间步长Δt=1×10-6 s,人工阻尼系数C=5×106,失衡判断指标β=1×10-5。
计算时,以水平方向为x轴,竖向为y轴。为比较分析,选取其竖向位移为参考,采用有限元软件ANSYS对同样的结点数及间距、弹性参数的构型进行计算,施加相同的边界条件,按静力问题求解,其中近场动力学方法计算得到的位移云图见图 3(a),ANSYS求解的位移云图见图 3(b)。

|
图 3 位移云图 Figure 3 Displacement image |
由位移云图可以看出,在计算静力问题时,近场动力学方法与有限元计算的结果相一致,其数值及形态吻合较好。梁的底部受拉,竖向位移的最大值在梁的中部,PD计算的竖向位移最大值为1.241×10-5 m,方向向下。有限元计算的竖向位移最大值为1.317×10-5 m,二者计算的结果相差很小。计算结果产生差异的原因在于两种方法本身的区别,以及加载方式和求解体系的不同。
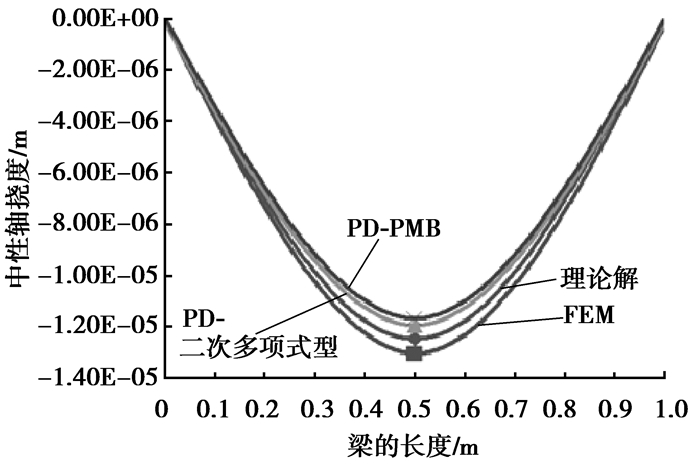
为了更进一步验证计算结果的准确性,选取中性轴上的一排粒子,根据材料力学原理,对其竖向位移求出理论解,并与计算的结果相比较,结果如图 4所示。
|
图 4 中性轴挠度曲线 Figure 4 Deflection curve of neutral axis |
图 4中显示了用有限元方法、近场动力学方法计算的结果以及理论解。其中采用近场动力学方法计算时,分别给出了未对本构力核函数改进的PD方法(即PMB模型)和采用二次多项式型本构力核函数改进的PD方法计算的结果。从图中结果可以看出,改进后的PD本构力核函数计算的结果较未改进时更接近理论解。因此也说明笔者对本构力核函数的改进是有效的。在梁的两侧附近,由于变形比较小,因此PD的结果和FEM的结果均与理论解吻合较好。在梁的中部,由于变形较大,二者的结果均与理论解有一定的偏差。PD计算的结果较理论解略小,而FEM的结果略大。挠度最大值发生在中性轴的中点,比较该点的竖向位移,PD的结果为1.1978×10-5 m,FEM的为1.3072×10-5 m,而理论解为1.25×10-5 m,方向均向下。二者的结果与理论解的误差PD为4.17%,FEM为4.58%。由此可以看出,近场动力学方法在处理静力问题时,其结果是准确可靠的。
5 结论为了使近场动力学方法能够适用于定量的准静态变形计算和分析,笔者通过构造二次多项式型PD本构力核函数,采用动态松弛法,构建了分级加载算法和系统失衡判断准则。算例结果表明,近场动力学方法在准静态变形计算和定量分析中,其结果是准确可靠的。采用的分级加载算法和系统失衡判断准则,也有利于将近场动力学方法应用到工程结构极限荷载的定量计算。今后需进一步研究传统理论中应力、应变、弹性常数以及其他物性参数在近场动力学模型中的描述和使用,以便对已知传统物性参数的材料和结构进行近场动力学建模和计算分析。
| [1] | Silling S A. Reformulation of elasticity theory for discontinuities and long-range forces[J]. Journal of the Mechanics and Physics of Solids , 2000, 48 (1) : 175–209. DOI:10.1016/S0022-5096(99)00029-0 |
| [2] | Weckner O, Abeyaratne R. The effect of long-range forces on the dynamics of a bar[J]. Journal of the Mechanics and Physics of Solids , 2005, 53 (3) : 705–728. DOI:10.1016/j.jmps.2004.08.006 |
| [3] | Silling S A, Epton M, Weckner O, et al. Peridynamic states and constitutive modeling[J]. Journal of Elasticity , 2007, 88 (2) : 151–184. DOI:10.1007/s10659-007-9125-1 |
| [4] | Silling S A, Askari E. A meshfree method based on the peridynamic model of solid mechanics[J]. Computers & Structures , 2005, 83 (17/18) : 1526–1535. |
| [5] |
黄丹, 章青, 乔丕忠, 等.
近场动力学方法及其应用[J]. 力学进展 , 2010, 40 (4) : 448–459.
HUANG Dan, ZHANG Qing, QIAO Pizhong, et al. A review on peridynamics method and its applications[J]. Advances in Mechanics , 2010, 40 (4) : 448–459. (in Chinese) |
| [6] |
沈峰, 章青, 黄丹, 等.
冲击荷载作用下混凝土结构破坏过程的近场动力学模拟[J]. 工程力学 , 2012, 29 (s1) : 12–15.
SHEN Feng, ZHANG Qing, HUANG Dan, et al. Peridynamics modeling of failure process of concrete structure subjected to impact loading[J]. Engineering Mechanics , 2012, 29 (s1) : 12–15. (in Chinese) |
| [7] | Shen F, Zhang Q, Huang D. Damage and failure process of concrete structure under uniaxial compression based on peridynamics modeling[J]. Mathematical Problems in Engineering , 2013 (1) : 206–232. |
| [8] |
沈峰, 章青, 黄丹, 等.
基于近场动力学理论的混凝土轴拉破坏过程模拟[J]. 计算力学学报 , 2013, 30 (z1) : 79–83.
SHEN Feng, ZHANG Qing, HUANG Dan, et al. Damage and failure process of concrete structure under uni-axial tension based on peridynamics modeling[J]. Chinese Journal of Computational Mechanics , 2013, 30 (z1) : 79–83. (in Chinese) |
| [9] |
胡祎乐, 余音, 汪海.
基于近场动力学理论的层压板损伤分析方法[J]. 力学学报 , 2013, 45 (4) : 624–628.
HU Yile, YU Yin, WANG Hai. Damage analysis method for laminates based on peridynamic theory[J]. Chinese Journal of Theoretical and Applied Mechanics , 2013, 45 (4) : 624–628. (in Chinese) |
| [10] | Dayal K, Bhattacharya K. Kinetics of phase transformations in the peridynamic formulation of continuum mechanics[J]. Journal of the Mechanics and Physics of Solids , 2006, 54 (9) : 1811–1842. DOI:10.1016/j.jmps.2006.04.001 |
| [11] | Kilic B, Madenci E. Structural stability and failure analysis using peridynamic theory[J]. International Journal of Non-Linear Mechanics , 2009, 44 (8) : 845–854. DOI:10.1016/j.ijnonlinmec.2009.05.007 |
| [12] | Weckner O, Emmrich E. Numerical simulation of the dynamics of a nonlocal, inhomogeneous, infinite bar[J]. Journal of Computational and Applied Mechanics , 2005, 6 (2) : 311–319. |
| [13] | Silling S A, Weckner O, Askari E, et al. Crack nucleation in a peridynamic solid[J]. International Journal of Fracture , 2010, 162 (1/2) : 219–227. |
| [14] | Huang D, Lu G, Liu Y. Nonlocal peridynamic modeling and simulation on crack propagation in concrete structures[J]. Mathematical Problems in Engineering , 2015, 2015 : 1–11. |
| [15] | Lai X, Liu L S, Liu Q W, et al. Slope stability analysis by peridynamic theory[J]. Applied Mechanics and Materials , 2015, 744/745/746 : 584–588. |
 2016, Vol. 39
2016, Vol. 39


