蜂窝材料凭借其优越的性能,在航空航天、机械、交通等诸多领域获得了广泛应用。近几十年来,有关蜂窝材料结构及其力学性能的研究,一直是学者们关注的焦点之一[1]。其中六边形结构作为较常见的蜂窝结构之一,其相关研究也较为充分。在小变形情况下,目前仅能由经典梁理论给出该结构面内等效弹性参数的解析公式[1-6],其中,Gibson等[2]在1982年提出的解析式,由于形式简单而被广泛采用。1988年Gibson等[1]又对该公式进行了修正,使之更准确、适用范围更广。然而,Gibson等的结果随着蜂窝结构相对密度和变形程度的增大将逐渐失效。随着研究的不断深入,均匀化理论和有限元法的结合成为研究高密度蜂窝材料力学特性的一种有效途径[7-8]。基于均匀化理论衍生出来的三点边界法(three-point bounds)[9]和三点近似法(three-point approximations)[10]也为求解高密度蜂窝材料等效参数提供了便利的工具。然而此类解法未能给出便于应用的解析表达式。
对于六边形蜂窝结构几何大变形情况的研究目前也仅局限于低密度情况,其中,Warren等[11]通过分析代表性单元的几何非线性行为给出了宏观结构的几何非线性本构;Zhu等[12]采用椭圆积分法,研究了六边形蜂窝结构几何非线性本构;Lan等[13]也采用椭圆积分方法研究蜂窝材料几何大变形问题,对面内等效杨氏模量、等效剪切模量与相对密度的关系进行了详细的论述。然而,Warren等的结果在变形较大时精度较差;Zhu等和Lan等的结果不具备显示表达式,不便于实际应用。此外,不少学者侧重于研究单轴或双轴压缩情况下蜂窝材料的弹性屈曲模式[14-16]。到目前为止,尚未总结出能反应相对密度(或者细长比)影响、具有解析形式的几何非线性应力-应变关系。
笔者采用ANSYS软件对几组不同相对密度的等壁厚正六边形蜂窝结构进行计算分析。定义了Gibson公式的非线性因子,在数值结果的基础上得到了适用于描述低密度蜂窝在弹性大变形情况下的本构关系。为将此本构推广到高密度情况,笔者又基于数值结果引入另一个修正因子对低密度蜂窝弹性大变形本构关系进行修正,建立了适用于应变和密度在较大变化范围的等壁厚正六边形蜂窝材料弹性大变形本构关系。
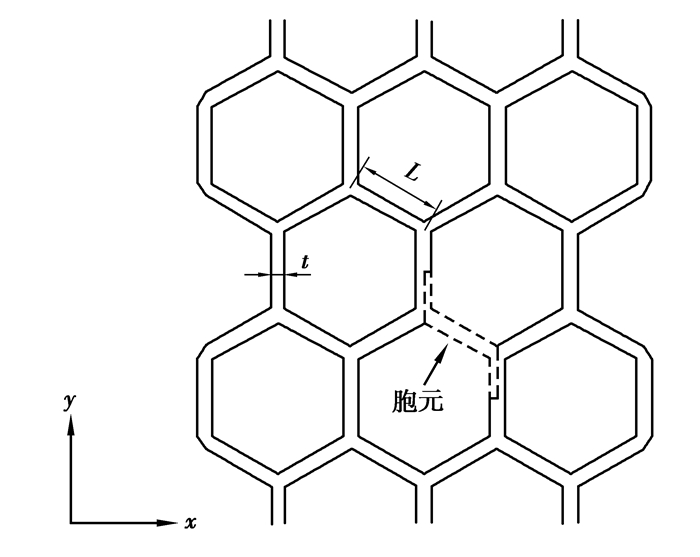
1 Gibson公式及其非线性修正因子对于低密度等壁厚正六边形蜂窝材料,胞壁可以等效为梁模型,如图 1所示。Gibson等[1](1988)基于铁木辛柯梁理论,同时考虑了胞壁的弯曲、剪切和伸缩,得出了等壁厚正六边形蜂窝材料等效杨氏模量的表达式
| $ {E^*}{\rm{=}}\frac{{4{E_{\rm{s}}}}}{{\sqrt 3 }}\frac{{{t^3}}}{{{L^3}}} \cdot \frac{1}{{1+\left({5.4+1.5{v_{\rm{s}}}} \right)\cdot {{\left({\frac{t}{L}} \right)}^2}}}, $ | (1) |
|
图 1 等壁厚正六边形蜂窝 Figure 1 Right hexagonal honeycomb with the uniform thickness faces 注:虚线框内区域为笔者选取的胞元 |
式中:Es为基体材料的杨氏模量,νs为基体材料的泊松比,t为胞壁厚度,L为细胞壁长度。本文后续的讨论均基于式(1),为叙述方便,将其称为Gibson公式。为更好地描述蜂窝材料几何非线性本构,与文献[13]不同的是,这里采用切线模量定义Gibson公式的非线性修正因子
| $ m=\frac{1}{{{E^*}}}\frac{{{\rm{d}}\sigma }}{{{\rm{d}}\varepsilon }}, $ | (2) |
式中:σ为工程应力,ε为工程应变,当然也可以采用其他的应力-应变组合。
2 有限元模型在蜂窝材料的等效分析中,通常通过对胞元的分析来进行简化。由于细长比很小时,胞壁交结区域的影响是可以忽略的,但随着细长比的增大,该区域的影响越来越显著,此时Gibson等所截取的胞元就不再适用了,笔者根据蜂窝结构的周期性和变形所具有的对称性,截取与文献[6]相似的胞元,其尺寸和边界条件如图 2所示。所截取的胞元考虑了胞壁交结区域(△D1E1H1)的影响,而且各截面都是对称面,可以认为该截面上的剪应力为0,便于有限元分析中边界条件施加。图 2(a)中,边A1B1上的所有节点位移在y方向上耦合,使其在变形后仍保持水平状态;图 2(b)中,边I1A1上的所有节点位移在x方向上耦合,使其在变形后仍保持竖直状态。在有限元分析中,选取平面应力单元PLANE82,基体材料参数为Es=70 GPa, νs=0.33。笔者选取细长比

|
图 2 胞元及其边界条件 Figure 2 Unit cell and its boundary conditions |
对于蜂窝材料的单向拉压问题。假设图 2(a)中边I1A1上的反力为FRx, 此时x方向单向受载时的等效工程应力、应变为
| $ \sigma x=\frac{{2{F_{Rx}}}}{{3L}}, \varepsilon x=\frac{{2\bar u}}{{\sqrt 3 L}}. $ | (3) |
通过式(3)可得出每一加载步对应的等效工程应力、应变值。同理,也可求得y方向加载时对应的结果。由于数值结果中的应力-应变关系是离散的数据点,因此,计算某一点处的斜率(切线模量)均采用差商的形式。由于位移加载的步长很小,所以假设第k时刻到第k+1时刻这一加载步内的应力和应变近似呈线性规律,这里取第k点对应的斜率为该点前后两个相邻加载步斜率的平均值
| $ \frac{{{\rm{d}}\sigma }}{{{\rm{d}}\varepsilon }}\left| {_{\varepsilon=\varepsilon k}} \right.=\frac{1}{2}\left({\frac{{{\sigma _{k+1}} - {\sigma _k}}}{{{\varepsilon _{k+1}} - {\varepsilon _k}}}+\frac{{{\sigma _k} - {\sigma _{k+1}}}}{{{\varepsilon _k} - {\varepsilon _{k+1}}}}} \right)=\frac{1}{2}\left({E_k^{k+1}+E_{k - 1}^k} \right) $ | (4) |
式中:σk,σk+1分别为k和k+1时刻对应的等效工程应力;εk,εk+1分别为k和k+1时刻对应的等效工程应变。
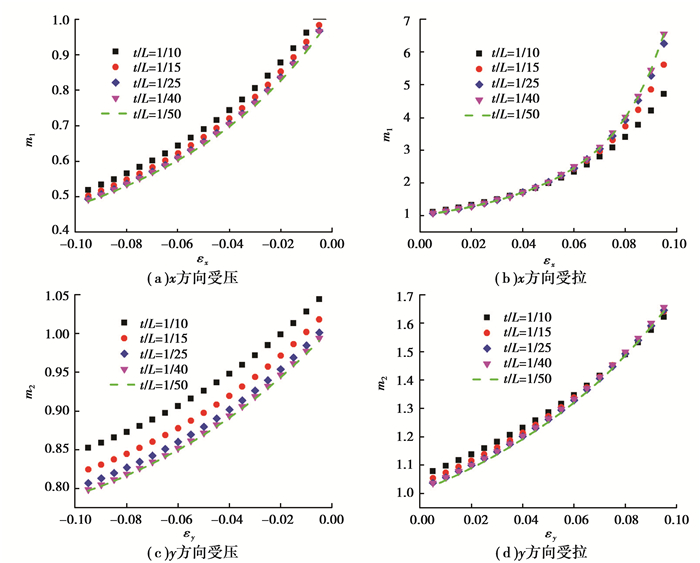
由式(4)和Gibson公式非线性因子的定义可分别计算出x和y方向的非线性因子m1, m2。具体数值结果如图 3所示。
|
图 3 非线性修正因子-应变关系 Figure 3 Nonlinear modified factors-strain curves |
图 3中,细长比为1/50,1/40,1/25对应的非线性因子与应变关系曲线非常接近(基本重合),但随着细长比的增大,对应的曲线将逐渐偏离。所以,由数值结果可知,当等壁厚正六边形蜂窝材料细长比(密度)很小时,非线性因子m1, m2只与应变值有关,而与细长比无关,而且其形状与指数函数类似, 这也印证了Lan等[13]的结论。为此可假设
| $ {m_1}\left({{\varepsilon _x}} \right)={{\rm{e}}^{{A_{1\varepsilon x}}}}\left({1+{B_1}{\varepsilon _x}+{C_1}\varepsilon _x^2+{D_1}\varepsilon _x^3+{E_1}\varepsilon _x^4} \right), $ | (5a) |
| $ {m_2}\left({{\varepsilon _y}} \right)={{\rm{e}}^{{A_{2\varepsilon y}}}}\left({1+{B_2}{\varepsilon _y}+{C_2}\varepsilon _y^2+{D_2}\varepsilon _y^3+{E_2}\varepsilon _y^4} \right). $ | (5b) |
针对细长比t/L=1/50的蜂窝结构在应变值为-0.1~0.1范围内,对于x和y方向单向受载情况各选取40对工程应变和非线性因子的数据点,通过最小二乘法分别求出了m1(εx),m2(εy)中各个待定系数的值,如表 1所示。
| 表 1 式(5)中的待定系数 Table 1 The values of undetermined coefficients in Eq.(5) |
对式(5)进行积分,可得到x和y方向的几何非线性应力应变关系:
| $ {\sigma _x}={E^*} \cdot \int_0^{\varepsilon x} {{m_1}\left({{\varepsilon _x}} \right){\rm{d}}{\varepsilon _x}, } $ | (6a) |
| $ {\sigma _y}={E^*} \cdot \int_0^{\varepsilon y} {{m_2}\left({{\varepsilon _y}} \right){\rm{d}}{\varepsilon _y}}. $ | (6b) |
对于高密度蜂窝,由于等效梁理论的失效以及胞壁交节区域的显著影响,此时前述基于低密度蜂窝建立的几何非线性应力应变关系式(6)也将不再适用。为此引入另一个非线性修正因子,对式(6)做出如下修正:
| $ {\sigma _x}={E^*} \cdot \left[{\int_0^{\varepsilon x} {{m_1}\left({{\varepsilon _x}} \right){\rm{d}}{\varepsilon _x}} } \right] \cdot {f_1}\left({{\varepsilon _x}, \frac{t}{L}} \right), $ | (7a) |
| $ {\sigma _y}={E^*} \cdot \left[{\int_0^{\varepsilon y} {{m_2}\left({{\varepsilon _y}} \right){\rm{d}}{\varepsilon _y}} } \right] \cdot {f_2}\left({{\varepsilon _y}, \frac{t}{L}} \right). $ | (7b) |
假设采用三次多项式(常数项取1)描述此修正因子, 即
| $ \begin{array}{l} {f_1}\left( {{\varepsilon _x},\frac{t}{L}} \right) = {a_{30}}\varepsilon _x^3 + {a_{21}}\varepsilon _x^2\frac{t}{L} + {a_{12}}{\varepsilon _y}{\left( {\frac{t}{L}} \right)^2} + {a_{03}}{\left( {\frac{t}{L}} \right)^3} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{a_{20}}\varepsilon _x^2 + {a_{11}}{\varepsilon _x}\frac{t}{L} + {a_{02}}{\left( {\frac{t}{L}} \right)^2} + {a_{10}}{\varepsilon _x} + {a_{01}}\frac{t}{L} + 1, \end{array} $ | (8a) |
| $ \begin{array}{l} {f_2}\left( {{\varepsilon _y},\frac{t}{L}} \right) = {b_{30}}\varepsilon _y^3 + {b_{21}}\varepsilon _y^2\frac{t}{L} + {a_{12}}{\varepsilon _y}{\frac{t}{L}^2} + {b_{03}}{\left( {\frac{t}{L}} \right)^3} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{b_{20}}\varepsilon _y^2 + {b_{11}}{\varepsilon _y}\frac{t}{L} + {b_{02}}{\left( {\frac{t}{L}} \right)^2} + {b_{10}}{\varepsilon _y} + {b_{01}}\frac{t}{L} + 1. \end{array} $ | (8b) |
在工程应变值为-0.1~0.1范围内,针对细长比为
| 表 2 式(8)的待定系数 Table 2 The values of undetermined coefficients in Eq.(8) |
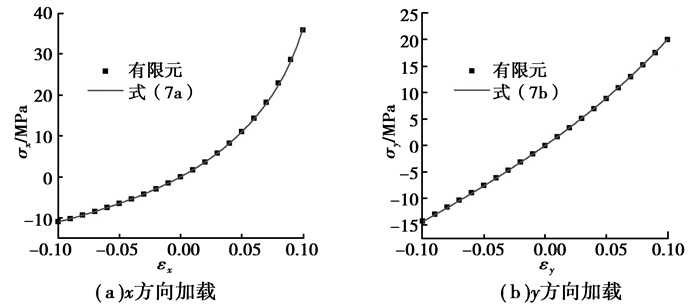
图 4为当等壁厚正六边形蜂窝细长比为1/10时,式(7)与有限元结果在应变值为-0.1~0.1范围内的应力应变关系对比情况,从图中可以看出式(7)在一定范围内与有限元结果十分吻合(其中x方向最大相对误差为1.83%,y方向最大相对误差为0.90%)。本文中相对误差指的是在相同应变下,数值仿真与式(7)得到的应力值之间的相对误差δ。即
| $ \delta=\left| {\frac{{{\sigma _{{\rm{Eq}}{\rm{.}}\left({\rm{7}} \right)}} - {\sigma _{{\rm{simulation}}}}}}{{{\sigma _{{\rm{simulation}}}}}}} \right|. $ | (9) |
|
图 4 等壁厚正六边形蜂窝结构应力-应变曲线(Es=70 GPa, vs=0.33, t/L=1/10) Figure 4 Stress as a function of strain for the right hexagonal honeycombs with uniform cells (Es=70 GPa, vs=0.33, t/L=1/10) |
然而,图 4所表现的仅为特定细长比下一定应变范围内式(7)的精度。为了反映式(7)对于不同细长比(密度)等壁厚正六边形蜂窝材料在较大应变范围内的精度,以应变为横坐标,细长比为纵坐标,绘制了能反映在不同应变值和细长比时对应的式(7)与有限元数值结果相对误差δ的等值线图。通过相对误差等值线图,可以直观地评估式(7)的适用性。图 5为式(7)与仿真结果的相对误差等值线图。从图 5可以看出,虽然式(7)是利用1/25≤t/L≤1/4,-0.1≤ε≤0.1范围内的数据拟合的,但式(7)在此区域以外的较大范围内仍然具有较高精度。因此,可认为式(7)是一种有效的本构关系。

|
图 5 应力误差等值线 Figure 5 Relative error contour |
1)定义了Gibson公式的非线性修正因子(式(2)),通过ANSYS对不同密度的等壁厚正六边形蜂窝进行分析, 数值结果表明,对于正六边形蜂窝材料,当细长比(密度)很小时,非线性因子与细长比本身无关,而只与变形程度有关,且该非线性因子随应变的变化曲线形状与指数函数形状类似。从而可方便地描述一类低密度等壁厚正六边形蜂窝材料的几何非线性本构关系。
2)所给出的拟合公式(式(7))是在经典Gibson公式基础上加以修正、推广而来,其形式简单,拟合精度高,对于细长比和应变值在一定变化范围内的等壁厚正六边形蜂窝材料具有良好的适用性。本文方法可以推广到普通六边形蜂窝材料。
| [1] | Gibson L J, Ashby M F. Cellular solids: structure and properties[M]. Cambridge: Cambridge University Press, 1988 . |
| [2] | Gibson L J, Ashby M F, Schajer G S, et al. The mechanics of two-dimensional cellular materials[J]. Proceedings of the Royal Society A , 1982, 382 (1782) : 25–42. DOI:10.1098/rspa.1982.0087 |
| [3] | Warren W E, Kraynik A M. Foam mechanics: the linear elastic response of two-dimensional spatially periodic cellular materials[J]. Mechanics of Materials , 1987, 6 (1) : 27–37. DOI:10.1016/0167-6636(87)90020-2 |
| [4] |
富明慧, 尹久仁.
蜂窝芯层的等效弹性参数[J]. 力学学报 , 1999, 31 (1) : 113–118.
FU Minghui, YIN Jiuren. Equivalent elastic parameters of the honeycomb core[J]. Acta Mechanics Sinica , 1999, 31 (1) : 113–118. (in Chinese) |
| [5] | Masters I G, Evans K E. Models for the elastic deformation of honeycombs[J]. Composite Structures , 1996, 35 (4) : 403–422. DOI:10.1016/S0263-8223(96)00054-2 |
| [6] | Kim H S, Al-hassani S T S. Effective elastic constants of two-dimensional cellular materials with deep and thick cell walls[J]. International Journal of Mechanical Sciences , 2003, 45 (12) : 1999–2016. DOI:10.1016/j.ijmecsci.2004.02.002 |
| [7] |
庄守兵, 吴长春, 冯淼林, 等.
基于均匀化方法的多孔材料细观力学特性数值研究[J]. 材料科学与工程 , 2001, 19 (4) : 9–13.
ZHANG Shoubing, WU Changchun, FENG Miaolin, et al. Microscopic investigation of cellular materials mechanical properties based on homogenization theory[J]. Materials Science & Engineering , 2001, 19 (4) : 9–13. (in Chinese) |
| [8] |
王飞, 庄守兵, 虞吉林.
用均匀化理论分析蜂窝结构的等效弹性参数[J]. 力学学报 , 2002, 34 (6) : 914–923.
WANG Fei, ZHUANG Shoubing, YU Jilin. Application of homogenization FEM to the equivalent elastic constants of honeycomb structures[J]. Acta Mechanics Sinica , 2002, 34 (6) : 914–923. (in Chinese) |
| [9] | Gibiansky L V, Torquato S. Geometrical-parameter bounds on the effective moduli of composites[J]. Journal of the Mechanics & Physics of Solids , 1995, 43 (10) : 1587–1613. |
| [10] | Torquato S. Effective stiffness tensor of composite media: II Applications to isotropic dispersions[J]. Journal of the Mechanics and Physics of Solids , 1998, 46 (8) : 1411–1440. DOI:10.1016/S0022-5096(97)00083-5 |
| [11] | Warren W E, Kraynik A M, Stone C M. A constitutive model for two-dimensional non-linear elastic foams. Journal of the mechanics and physis of solids[J]. 1989, 37(6): 717-733. |
| [12] | Zhu H X, Mills N J. The in-plane non-linear compression of regular honeycombs[J]. International Journal of Solids and Structure , 2000, 37 (13) : 1931–1949. DOI:10.1016/S0020-7683(98)00324-2 |
| [13] | Lan L H, Fu M H. Nonlinear constitutive relations of cellular materials[J]. AIAA Journal , 2009, 47 (1) : 264–270. DOI:10.2514/1.39531 |
| [14] | Hutzler S, Weaire D. Buckling properties of 2D regular elastic honeycombs. Journal of Physics: Condensed Matter[J]. 1997, 9(22): 323-329. |
| [15] | Chuang C H, Huang J S. Effects of solid distribution on the elastic buckling of honeycombs[J]. International Journal of Mechanical Sciences , 2002, 44 (44) : 1429–1443. |
| [16] | Yang M Y, Huang J S. Elastic buckling of regular hexagonal honeycombs with plateau borders under biaxial compression[J]. Composite Structures , 2005, 71 (2) : 229–237. DOI:10.1016/j.compstruct.2004.10.014 |
 2016, Vol. 39
2016, Vol. 39


