颗粒增强复合材料在宏观上具有均匀性。从复合材料细观结构预测其宏观性能一般有两种方法，即解析法和有限元法。解析法中较成熟的有Eshelby等效夹杂理论、变分法、自洽法、Mori-Tanaka法等，在分析几何体简单、夹杂体积分数小的模型时，估计的材料宏观等效性能较为合理有效，但无法描述微结构的应力应变演化，也不能处理含任意微结构的问题。为了克服这种局限性，基于单胞模型的有限元计算方法越来越流行。这种方法通过细化微结构上的代表性体积单元(representative volume element，RVE)得到等效材料的响应和演化。廖光开等^[1]建立了计算钨丝增强锆基块体非晶复合材料等效弹性常数的理论模型，结合有限元法对该复合材料等效弹性常数进行了数值计算。谢桂兰等^[2]利用均匀化有限元方法，预测了碳纳米管和纳米薄层各参数对复合材料层合板的宏观弹性模量的影响。李涛等^[3]建立了非连续长玻纤增强复合材料的代表性体积单元，研究了采用均匀化方法预测长玻纤增强聚丙烯注塑件的弹性力学性能的可行性。

基于单胞模型来预测复合材料宏观等效性能的研究很多，但是，大多研究都采用含单个夹杂的简单单胞模型。而实际夹杂微结构的大小、形状、空间分布大多是随机的，因此，需要采用能够反映随机微结构的单胞模型。1991年，Ghosh等^[4]提出了Voronoi单元有限元法(voronoi cell finite element method，VCFEM)。VCFEM法是在材料横截面扫描图基础上划分常规的Voronoi网格图，能够准确地描述材料微结构大小、形状和空间分布的随机性。VCFEM法在计算多相复合材料时具有单元数量少计算效率高等优越性。2000年，Moorthy和Ghosh进一步研究了VCFEM的单元适应性和收敛性问题^[5]，验证了VCFEM解的正确性。VCFEM法已经推广到许多复杂复合材料的研究中。2012年，Dong等^[6]发展了适用于复合材料和多孔材料的细观力学模型的T-trefftz Voronoi单元有限元法。2013年，Ghosh等^[7]通过LE-VCFEM法对非均质的铝合金的局部韧性断裂进行了分析。徐佳丽^[8]基于VCFEM法对颗粒复合增强材料的研究引入传统有限元计算方法，实现了两种单元的混合运算。郭隽^[9]结合危险区域自检技术在危险区域进行了Voronoi网格的重生成。

笔者把能反映界面脱层的VCFEM方法和直接均匀化方法结合起来研究颗粒增强复合材料的有效弹性模量。采用VCFEM方法对代表性体积单元进行细观结构分析，得到细观应力场，然后进行平均化，得到平均应力应变曲线和材料的有效宏观弹性模量。此方法得到的平均应力应变曲线可以反映夹杂基体界面脱层对材料有效性能的影响。对多个模型进行了数值模拟，分析了夹杂微结构的形状、体积分数、空间分布等因素对材料有效弹性模量的影响。

1 考虑界面脱层的Voronoi单元原理

Ghosh等^[4]基于卞学璜提出的应力杂交元法提出了Voronoi单元的构造原理。郭然^[10]改进了应力函数的选取和积分区域的划分并给出了考虑界面脱层的Voronoi单元构造方法。笔者采用郭然提出的考虑界面脱层的Voronoi单元有限元法。

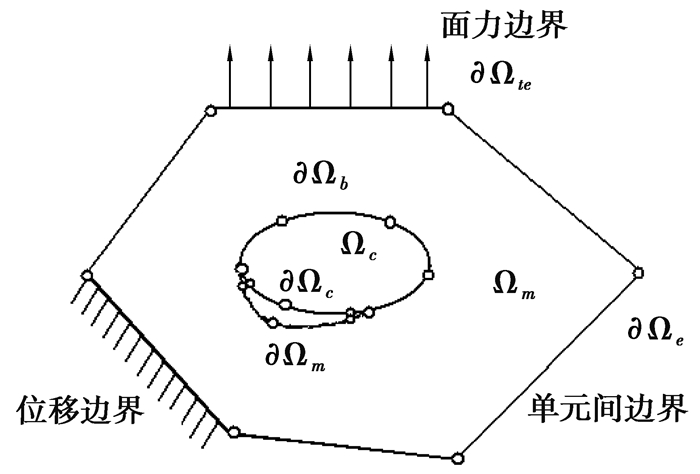
夹杂颗粒随机分布的代表性体积单元的Voronoi单元划分如图 1所示^[4]。若考虑界面脱层，则每个Voronoi单元如图 2所示^[10]。其中，Ω_m为基体部分，Ω_c为夹杂部分，∂Ω_te为面力边界，∂Ω_e为单元间边界，∂Ω_b为基体夹杂界面未脱层边界，∂Ω_m为脱粘部分基体侧边界，∂Ω_c为脱粘部分夹杂侧边界；单元外边界上外法线向量为n^e，基体夹杂未脱层边界处指向基体侧的法向向量为n^b，基体夹杂脱层处基体边缘的法向向量为n^m，基体夹杂脱层处夹杂边缘的法向向量为n^c。

在未脱粘界面上，面力连续条件为

${n^b} \cdot \left( {{\sigma ^m}-{\sigma ^c}} \right) = 0, \left( {在\partial {\Omega _b}上} \right)$

(1)

在脱粘界面上，两侧面力均为零：

${n^m} \cdot {\sigma ^m} = 0, \left( {在\partial {\Omega _m}上} \right)$

(2)

${n^c} \cdot {\sigma ^c} = 0, \left( {在\partial {\Omega _c}上} \right)$

(3)

考虑边界面力条件的应力杂交元的余能泛函为

${\varPi _{mc}}\sum\limits_e {\left( {\int_{{\Omega _e}} {\frac{1}{2}\sigma :S:\sigma {\rm{d}}\Omega-\int_{\partial {\rm{d}}\Omega } {\partial {\rm{d}}\Omega + \int_{\partial {\Omega _{te}}} {\bar T \cdot u{\rm{d}}\partial \Omega } } } } \right)} .$

用Lagrange乘子法把式(1)-(3)的边界条件引入到上式的余能泛函中，得到修正后的增量形式的余能泛函为

$\begin{array}{l} \varPi _{mc}^e\left( {\Delta \sigma, \Delta u} \right) = \int_{{\Omega _e}} {\Delta B\left( {\sigma, \Delta \sigma } \right)} {\rm{d}}\Omega {\rm{ + }}\int_{{\Omega _e}} {\varepsilon :\Delta \sigma {\rm{d}}\Omega }-\\ \int_{\partial {\Omega _e}} {{n^e} \cdot \left( {\sigma + \Delta \sigma } \right) \cdot \left( {u + \Delta u} \right){\rm{d}}\partial \Omega {\rm{ + }}\int_{\partial {\Omega _{te}}} {\left( {\bar f + \Delta \bar f} \right) \cdot \left( {u + \Delta u} \right){\rm{d}}\partial \Omega {\rm{ + }}} } \\ \int_{\partial {\Omega _b}} {{n^b} \cdot \left( {{\sigma ^m} + \Delta {\sigma ^m}-{\sigma ^c}-\Delta {\sigma ^c}} \right) \cdot \left( {{u^b} + \Delta {u^b}} \right){\rm{d}}\partial \Omega } \\ - \int_{\partial {\Omega _m}} {{n^m} \cdot \left( {{\sigma ^m} + \Delta {\sigma ^m}} \right) \cdot \left( {{u_m} + \Delta {u^m}} \right){\rm{d}}\partial \Omega } - \\ \int_{\partial {\Omega _c}} {{n^c} \cdot \left( {{\sigma ^c} + \Delta {\sigma ^c}} \right) \cdot \left( {{u^c} + \Delta {u^c}} \right){\rm{d}}\partial \Omega {\rm{.}}} \end{array}$

系统的总能量：$\prod\nolimits_{mc} { = \sum\limits_e {\Pi _{mc}^e} } $。

单元能量对应力增量求一阶变分可得到单元内的欧拉方程：

$\Delta \varepsilon = \frac{1}{2}\left[{\nabla \left( {\Delta u} \right) + \left( {\Delta u} \right)\nabla } \right], \;\;\;\;\;\left( {在{\Omega _e}内} \right)$

系统总能量Π_mc对位移增量Δε求一阶变分可得到单元内的力协调条件：

$\begin{array}{l} {n^e} \cdot \left( {\sigma + \Delta \sigma } \right) = \bar f + \Delta \bar f, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {给定单元面力边界} \right)\\ {n^{e-}} \cdot \left( {\sigma + \Delta \sigma } \right) + {n^{e + }} \cdot \left( {\sigma + \Delta \sigma } \right) = 0, \;\;\;\;\;\;\;\left( {单元间} \right)\\ {n^b} \cdot \left( {{\sigma ^c} + \Delta {\sigma ^c}} \right) = {n^b} \cdot \left( {{\sigma ^m} + \Delta {\sigma ^m}} \right), \;\;\;\;\;\;\left( {界面未脱层处} \right)\\ {n^c} \cdot \left( {{\sigma ^c} + \Delta {\sigma ^c}} \right) = 0, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {界面脱层处基体侧} \right)\\ {n^m} \cdot \left( {{\sigma ^m} + \Delta {\sigma ^m}} \right) = 0, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {界面脱层处夹杂侧} \right) \end{array}$

对于二维问题，平衡应力场为：

${\left[{\Delta \sigma } \right]^m} = {P^m}\Delta {\beta ^m}, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {在{\Omega _m}内} \right)$

(4)

${\left[{\Delta \sigma } \right]^c} = {P^c}\Delta {\beta ^c}, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {在{\Omega _c}内} \right)$

(5)

单元边界位移场由线性插值函数插值得到：

$\left[u \right] = \left\{ \begin{array}{l} {u_1}\\ {u_2} \end{array} \right\} = L\left\{ q \right\} = \left[{\begin{array}{*{20}{c}} {1-a/{l_i}}&0&{a/{l_i}}&0\\ 0&{1-a/{l_i}}&0&{a/{l_i}} \end{array}} \right]\left\{ \begin{array}{l} {q_{2i -1}}\\ {q_{2i}}\\ {q_{2i + 1}}\\ {q_{2i + 2}} \end{array} \right\}.$

单元边界位移增量由各个边界段节点广义位移增量插值得到

$\left[{\Delta u} \right] = L\left\{ {\Delta q} \right\}.$

(6)

将式(4)-(6)代入修正后的增量形式的余能泛函中，可得单元余能泛函的弱形式。

修正余能的驻值条件为

$\frac{{\partial \prod\nolimits_{mc}^e {} }}{{\partial \left( {\Delta {\beta ^m}} \right)}} = 0, \frac{{\partial \prod\nolimits_{mc}^e {} }}{{\partial \left( {\Delta {\beta ^c}} \right)}} = 0.$

由此可得单元内的欧拉方程的弱表达式，其迭代表达式的矩阵形式为

$\left[{\begin{array}{*{20}{c}} {{H^m}}&0\\ 0&{{H^c}} \end{array}} \right]\left\{ \begin{array}{l} {\rm{d}}{\beta ^{mi}}\\ {\rm{d}}{\beta ^{ci}} \end{array} \right\} = \left[{\begin{array}{*{20}{c}} {{G_e}}&{-{G_{mb}}}&{{G_{nm}}}&0\\ 0&{{G_{cb}}}&0&{{G_{cc}}} \end{array}} \right]\left\{ \begin{array}{l} {\rm{d}}{q^{eu}}\\ {\rm{d}}{q^{bi}}\\ {\rm{d}}{q^{mi}}\\ {\rm{d}}{q^{ci}} \end{array} \right\}.$

其中：

$\begin{array}{l} {H^m} = \int_{\Omega m} {{P^{m\;{\rm{T}}}}{S_m}{P^m}{\rm{d}}\Omega, {H^c} = \int_{\Omega c} {{P^{c\;{\rm{T}}}}{S_c}{P^c}{\rm{d}}\Omega, {G_e} = \int_{\partial {\Omega _e}} {{P^{m\;{\rm{T}}}}{n^{b\;{\rm{T}}}}L\partial \Omega, } } } \\ {G_{mm}} = \int_{\partial {\Omega _m}} {{P^{m\;{\rm{T}}}}{n^{m\;{\rm{T}}}}{L^m}{\rm{d}}\partial \Omega {\rm{, }}} \\ {G_{cc}} = \int_{\partial {\Omega _c}} {{P^{c\;{\rm{T}}}}{n^{c\;{\rm{T}}}}{L^c}{\rm{d}}\partial \Omega {\rm{, }}{G_{mb}} = \int_{\partial {\Omega _b}} {{P^{m\;{\rm{T}}}}{n^{b\;{\rm{T}}}}{L^b}{\rm{d}}\partial \Omega {\rm{, }}{G_{cb}}} } = \int_{\partial {\Omega _b}} {{P^{c\;{\rm{T}}}}{n^{b\;{\rm{T}}}}{L^b}{\rm{d}}\partial \Omega } . \end{array}$

求解上式可得应力参数增量表达式为

${\rm{d}}{\beta ^i} = {H^{-1}}G{\rm{d}}{q^i}, $

(7)

其中：

$\boldsymbol{H} = \left[{\begin{array}{*{20}{c}} {{H^m}}&0\\ 0&{{H^c}} \end{array}} \right], G = \left[{\begin{array}{*{20}{c}} {{G_e}}&{-{G_{mb}}}&{{G_{mm}}}&0\\ 0&{{G_{cb}}}&0&{{G_{cc}}} \end{array}} \right], {\rm{d}}{\beta ^i} = \left\{ \begin{array}{l} {\rm{d}}{\beta ^{mi}}\\ {\rm{d}}{\beta ^{ci}} \end{array} \right\}, {\rm{d}}{q^i} = \left\{ \begin{array}{l} {\rm{d}}{q^{ei}}\\ {\rm{d}}{q^{bi}}\\ {\rm{d}}{q^{mi}}\\ {\rm{d}}{q^{ci}} \end{array} \right\}.$

系统总能量Π_mc分别对节点位移增量Δq^e、Δq^b、Δq^m和Δq^c求一阶变分，可得面力边界条件的弱表达式，其矩阵形式可简写为

$\sum\limits_e {{G^{\rm{T}}}{\rm{d}}{\beta ^i} = \sum\limits_e {\bar F-} } \sum\limits_e {{G^{\rm{T}}}\left\{ \begin{array}{l} {\beta ^m} + \Delta {\beta ^{mi}}\\ {\beta ^c} + \Delta {\beta ^{ci}} \end{array} \right\}, } $

(8)

其中：

$\bar F = \left[\begin{array}{l} {{\bar F}^e}\\ 0\\ 0\\ 0 \end{array} \right], {{\bar F}^{e\;{\rm{T}}}} = {\int_{\partial {\Omega _{tc}}} {\left( {\bar f + \Delta \bar f} \right)} ^{\rm{T}}}L{\rm{d}}\partial \Omega {\rm{, }}$

将式(7)代入式(8)可得：

$\sum\limits_e {{G^{\rm{T}}}{H^{-1}}G{\rm{d}}{q^i} = \sum\limits_e {\bar F}-\sum\limits_e {{G^{\rm{T}}}\left\{ \begin{array}{l} {\beta ^m} + \Delta {\beta ^{mi}}\\ {\beta ^c} + \Delta {\beta ^{ci}} \end{array} \right\}.} } $

(9)

系统的求解方程可写为

$\sum\limits_e {{K_e}{\rm{d}}{q^i} = \sum\limits_e {\bar F}-\sum\limits_e {{G^{\rm{T}}}\left\{ \begin{array}{l} {\beta ^m} + \Delta {\beta ^{mi}}\\ {\beta ^c} + \Delta {\beta ^{ci}} \end{array} \right\}} .} $

(10)

其中单元刚度矩阵为

${\boldsymbol{K}_e} = \left[{\begin{array}{*{20}{c}} {G_e^{\rm{T}}}&0\\ {-G_{mb}^{\rm{T}}}&{G_{cb}^{\rm{T}}}\\ {G_{mm}^{\rm{T}}}&0\\ 0&{G_{cc}^{\rm{T}}} \end{array}} \right]\left[{\begin{array}{*{20}{c}} {{H^{m-1}}}&0\\ 0&{{H^{c-1}}} \end{array}} \right]\left[{\begin{array}{*{20}{c}} {{G_e}}&{-{G_{mb}}}&{{G_{mm}}}&0\\ 0&{{G_{cb}}}&0&{{G_{cc}}} \end{array}} \right].$

由应力函数矩阵P求得H和矩阵G，然后可得单元刚度矩阵，由式(7)可得应力参数增量Δβ，由式(4)、式(5)可得基体和夹杂部分各点应力增量，累计到总量可得整个代表性体积单元的应力场。

2 均匀化方法

求解复合材料有效性能的方法^[11]很多：1) 以复合材料代表体元为基础的直接均匀化方法；2) 以单一夹杂理论为基础的各种近似模型及利用上述模型构造的各种数值方法，如自洽法、Mori-Tanaka法等；3) 微分法；4) 以变分原理为基础的上下限法；5) 双尺度渐近展开均匀化方法。

2.1 直接均匀化方法

直接均匀化法基于场量的表面或体积平均而直接计算有效应力和有效应变，根据宏观应力和应变二者之间的关系，求得宏观有效性能。可以用数值方法进行细观场量的直接平均，如有限元和边界元方法^[12-13]，而细观结构可以是任意的几何尺寸。

RVE的细观应力和应变的体积平均定义为

$\begin{array}{l} \left\langle {{\sigma _{ij}}} \right\rangle = \frac{1}{V}\int_V {{\sigma _{ij}}{\rm{d}}V = \frac{1}{{{V_m}}}\int_{{V_m}} {{\sigma _{ij}}{\rm{d}}{V_m} + \frac{1}{{{V_c}}}\int_{{V_c}} {{\sigma _{ij}}{\rm{d}}{V_c}, } } } \\ \left\langle {{\varepsilon _{ij}}} \right\rangle = \frac{1}{V}\int_V {{\varepsilon _{ij}}{\rm{d}}V = \frac{1}{{{V_m}}}\int_{{V_m}} {{\varepsilon _{ij}}{\rm{d}}{V_m} + \frac{1}{{{V_c}}}\int_{{V_c}} {{\varepsilon _{ij}}{\rm{d}}{V_c}} } } . \end{array}$

如果非均匀材料有均匀位移边界条件或均匀应力边界条件，可以证明平均应变等于边界上的常应变，平均应力等于边界上的常应力：

$\left[{{\varepsilon _{ij}}} \right] = \varepsilon _{ij}^0huo\left[{{\sigma _{ij}}} \right] = \sigma _{ij}^0.$

(11)

因此，当给定均匀位移边界条件时，复合材料的有效应变是已知的，为了计算复合材料的有效弹性模量，要先计算材料的有效应力场；当给定均匀应力边界条件时，复合材料的有效应力是已知的，为了计算复合材料的有效弹性模量要先计算材料的有效应变场。

2.2 双尺度渐近展开均匀化方法

双尺度渐近展开均匀化方法由Benssousan等^[14]和Sanchez-Palencia^[15]提出，与有限元法结合起来，在复合材料有效性能预报方面得到了广泛的应用。渐近均匀化理论有严格的数学理论推导。该方法同时引入均匀的宏观结构和非均匀的具有周期性分布的细观结构：将位移表示成关于宏观坐标和微细观坐标的函数，并用小参数渐近展开，用摄动技术得到一系列控制方程。对这些问题的求解给出了复合材料的宏观有效性能，并给出了微观应力场。

相关文献已经证明，渐近均匀化方法与直接平均法虽然数学表示不同，但它们的基本原理是共同的，它们预测的平均性能其结果也是一致的^[16-18]。本文中算例有均匀位移边界条件，VCFEM法对RVE进行模拟，可得整个RVE内的细观应力场，因此，采用直接均匀化方法。由均匀位移边界条件得平均应变，对RVE的细观应力场进行体积平均得到平均应力，由此得复合材料的有效弹性模量。

3 算例

下述算例应用郭然提出的考虑界面脱层的Voronoi单元有限元法分别对单夹杂和随机分布的多夹杂代表性体积单元进行了模拟，得到代表性体积单元内的应力场，

然后用Fortran语言编写的均匀化程序得到平均的应力应变，从而得到平均应力应变曲线和有效弹性模量。分析了夹杂形状、大小、空间分布等因素对复合材料有效弹性模量的影响。

3.1 算例1

本算例要模拟的模型是在20 mm×20 mm正方形的基体里包含一个半径为5 mm的圆形夹杂，夹杂位于正方形基体的中心位置，所占体积比为19.6%。所受边界条件和位移载荷如图 3所示，上下边竖直位移为0，左边水平位移为0，右端分载荷步施加水平位移载荷，每载荷步位移为0.001 mm，共40个载荷步。材料参数如表 1所示，基体部分(Al2024)为双线性弹塑性材料，夹杂部分(SiC)为线性弹性材料。

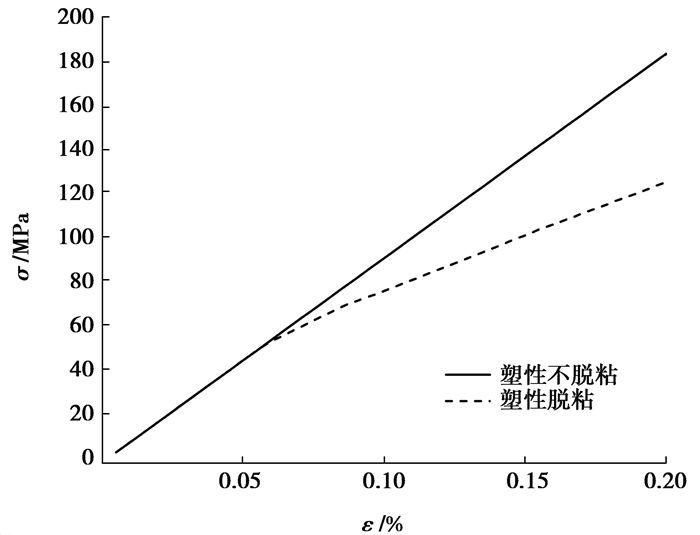
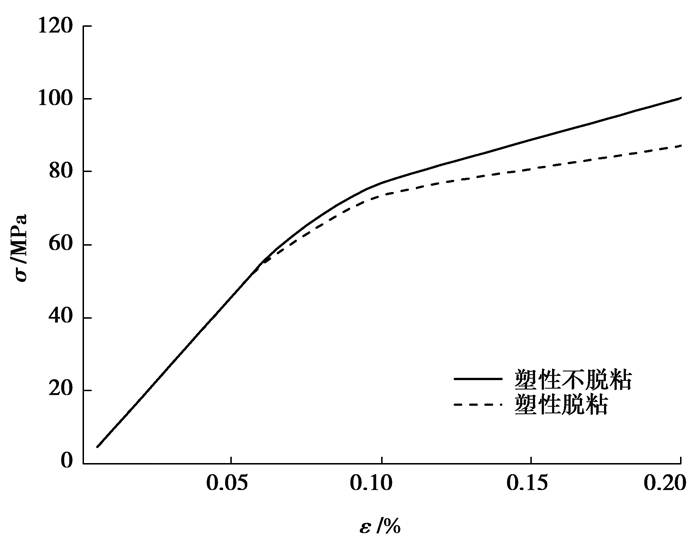
图 4给出了在第20载荷步时模型的水平应力云图，图 5和图 6分别给出了不考虑基体材料塑性和考虑基体材料塑性时模型的平均应力应变曲线。从图中可以看出，夹杂的加入提高了材料的刚度，但在界面处有较高的应力集中，容易发生界面脱层，界面的脱层降低了材料的刚度，这是因为脱层部分的夹杂不再传递载荷，使得材料的承载能力得到削弱。模拟得到的有效宏观弹性模量为91.8 GPa，由Eshelby等效夹杂理论计算得到的有效宏观弹性模量为95.3 GPa，相对误差为3.8%。而Eshelby等效夹杂理论是含有一夹杂物的无限大介质在无限远场处应力作用下的应力场，在体积分数较小的情况下能得到较准确的有效模量。因此，本文的结果可信。

3.2 算例2

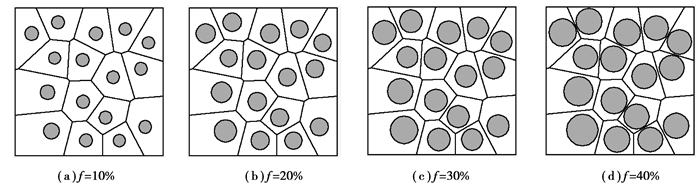
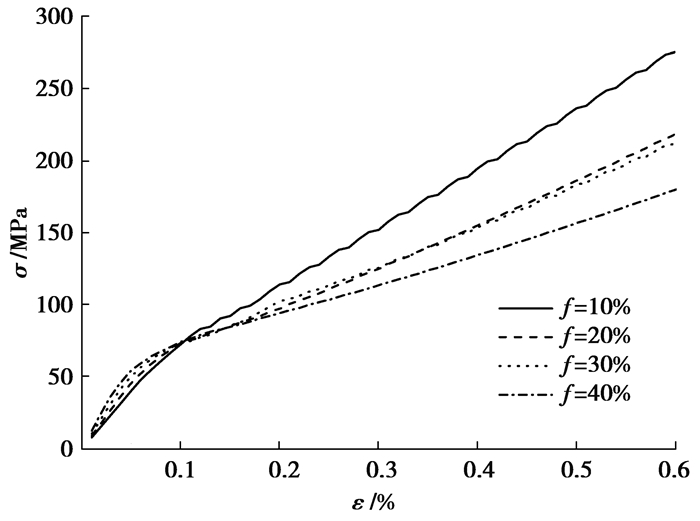
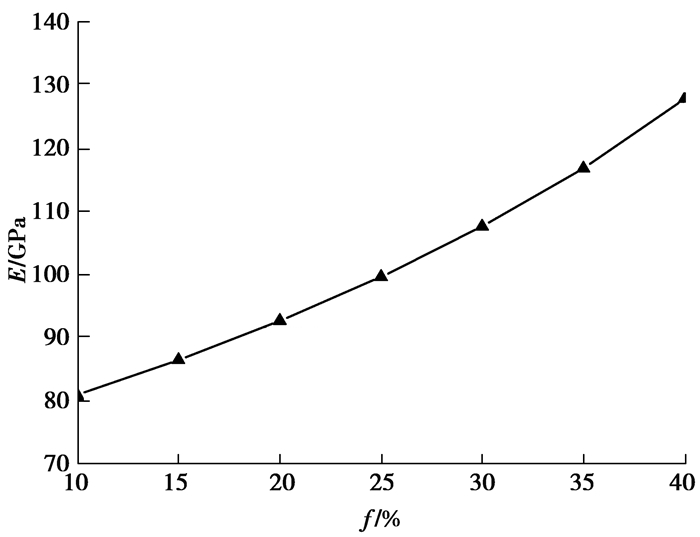
本算例中基体为2 mm×2 mm的正方形，基体中随机分布16个圆形夹杂颗粒。夹杂的形状、空间分布相同，研究不同体积分数的多夹杂随机分布的代表性体积单元的有效宏观模量。分布如图 7所示，(a)、(b)、(c)、(d)的体积分数f分别为10%、20%、30%、40%。边界条件和算例1相同：上下边固定竖直位移，左边固定水平位移，右端分载荷步施加水平位移载荷，每载荷步位移为0.000 2 mm，共30个载荷步。材料参数如表 1所示。图 8给出了不同体积分数的平均应力应变曲线，图 9给出了多夹杂随机分布的Voronoi单元的有效弹性模量随体积分数的变化曲线。从结果可以看出，材料的有效宏观弹性模量随夹杂体积分数的增大而变大，大的夹杂体积分数可以更有效地提高材料的总体刚度。这是因为夹杂为硬性夹杂，其弹性模量比基体的弹性模量大，当夹杂体积分数较大时材料的有效弹性模量就会较大。同时大的夹杂也提高了界面的应力集中，含有大的夹杂的模型较先出现界面脱层，而界面的脱层反而降低了材料的刚度。

3.3 算例3

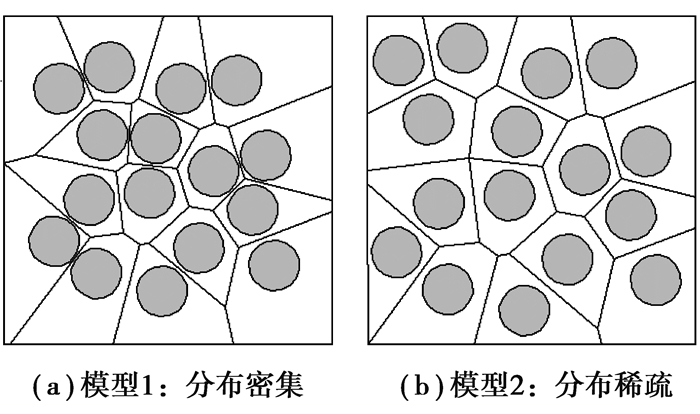
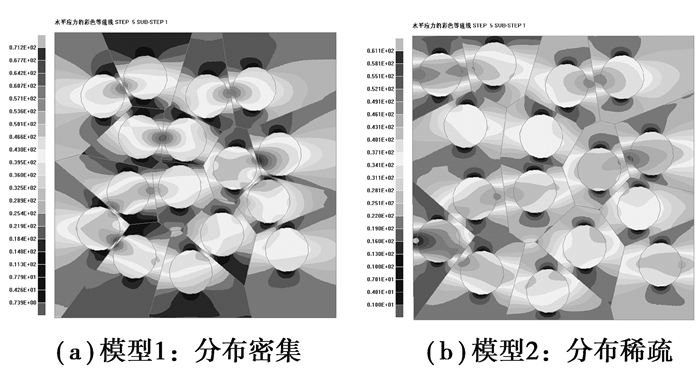
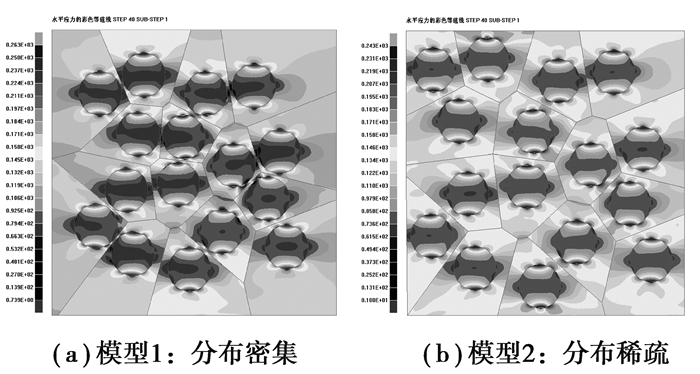
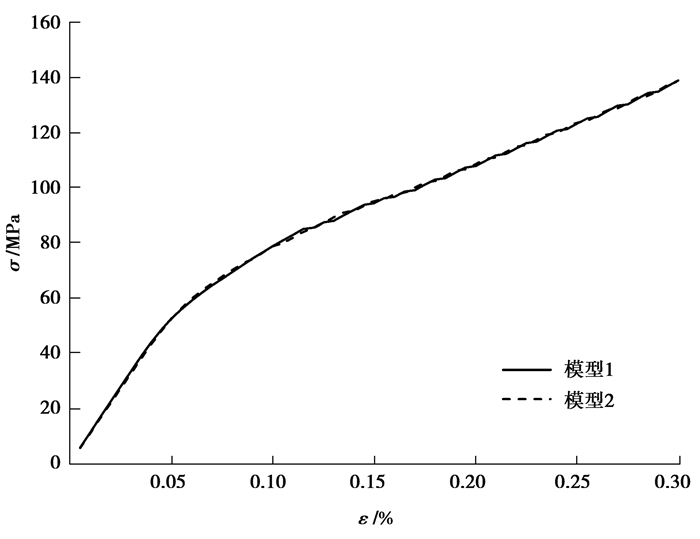
本算例中基体为2 mm×2 mm的正方形，基体中随机分布16个圆形夹杂颗粒，夹杂大小相同，体积分数均为30%，模型1中夹杂分布密集，模型2中夹杂分布稀疏，如图 10所示。边界条件和以上算例相同：上下边固定竖直位移，左边固定水平位移，右端分载荷步施加水平位移载荷，每载荷步位移为0.000 1 mm，共60个载荷步。材料参数如表 1所示。图 11给出了第5载荷步时模型的水平力云图，此时界面未发生脱层，图 12给出了第40载荷步时模型的水平应力云图，此时界面全部脱层。从图中可以看出夹杂分布集中时界面应力集中更明显。图 11给出了两个模型的平均应力应变曲线，(a)中模型1的有效弹性模量为110.90 GPa，(b)中模型2的有效弹性模量为107.96 GPa。夹杂的空间分布对材料的有效弹性模量有影响，夹杂分布较集中时材料有效弹性模量较大，对材料刚度的增强更明显。这是因为当夹杂分布较集中时，夹杂之间的互作用应力较大。

3.4 算例4

本算例中基体为2 mm×2 mm的正方形，基体中随机分布40个夹杂颗粒，夹杂的大小、形状不同，空间分布位置相同，体积分数均为30%，如图 13所示。图 14(a)、(b)、(c)、(d)、(e)中夹杂为椭圆形，大小、形状相同，方向不同，模型(a)中方向随机，模型(b)中夹杂长轴沿水平方向，模型(c)、(d)中夹杂长轴与水平方向夹角分别为30°和60°，模型(e)中夹杂长轴沿竖直方向，模型(f)中夹杂为半径相等的圆形，模型(g)中夹杂的大小、形状、方向均是随机的。边界条件和以上算例相同：上下边固定竖直位移，左边固定水平位移，右端分载荷步施加水平位移载荷，每载荷步位移为0.000 1 mm，共60个载荷步。材料参数如表 1所示。均匀化后不同模型的有效弹性模量分别为106.12、115.89、110.80、103.88、102.75、106.36、107.35 GPa。由模型(a)、(b)、(c)、(d)、(e)的结果可以看出夹杂的方向对有效弹性模量有影响，有效弹性模量随着夹杂长轴方向和载荷方向的夹角的增大而减小，夹杂长轴方向和载荷方向相同时材料的有效弹性模量最大，夹杂长轴方向和载荷方向垂直时材料的有效弹性模量最小。从结果中还可以看出，夹杂的形状对材料有效弹性模量也有影响。模型(g)的结果稍大于模型(a)和模型(f)，是因为模型(g)有较大的夹杂。

4 结论

基于Voronoi单元有限元法对颗粒增强复合材料的代表性体积单元进行了模拟，得到整个代表性体积单元内的应力场，并通过平均化方法得到材料的平均应力应变曲线和有效弹性模量，并对含单夹杂和随机分布的多夹杂的模型进行数值模拟，得到材料的有效弹性模量，分析了夹杂微结构的形状、体积分数、空间分布等因素对材料有效宏观弹性模量的影响。

1) 采用含任意夹杂的代表性体积单元，能反映颗粒增强复合材料的微结构的随机性。

2) 采用考虑夹杂基体界面脱层的Voronoi单元，直接均匀化后的平均应力应变曲线可以反映界面脱层对材料有效宏观性能的影响。

3) 得到复合材料的有效弹性模量后，可以在徐佳丽等研究的基础上对复合材料进行宏细观跨尺度模拟。首先对复合材料在宏观尺度上进行普通有限元计算，由自检技术和网格重生成技术在有可能破坏的危险区域划分Voronoi单元，然后进行VCFEM法和普通有限元法的混合运算。