隧道围岩在隧道开挖过程中处于复杂的应力状态,针对复杂应力状态下的围岩稳定性评价,国内外学者已经开展了许多有意义的研究[1-4]。其中,基于强度准则的应力判别方法在工程中经常被采用[5-7]。不同的学者依据不同的强度准则给出不同的评价指标,主要包括:简单的单轴应力强度指标和复杂应力状态下的强度指标。利用单轴应力强度指标来评价复杂应力状态下的隧道围岩是不合适的。参考近年来的研究文献,应力空间状态下的“屈服接近度”被较多地应用为工程结构稳定性、安全性定量评价的指标[8-10]。其中,具有代表性的是周辉等[8]提出的基于Mohr-Coulomb强度准则的屈服接近度。文献[11-13]也基于文献[8]提出的方法,针对不同的材料破坏准则提出了不同的屈服接近度。
周辉等[8]基于材料破坏准则在主应力空间的表达提出了屈服接近度的概念:空间应力状态下的一点沿最不利应力路径到屈服面的距离与相应的最稳定参考点在相同罗德角方向上沿最不利应力路径到屈服面的距离之比。由于该定义是基于经典的Mohr-Coulomb破坏准则提出的,而这种破坏准则的应力空间屈服面是平面型、子午线是直线型的,所以在主应力空间中,某应力点的屈服接近度可以等比例地反映到偏平面上(因为它们之间存在线性比例关系)。而对于在工程中应用效果较好的基于试验的破坏准则来说,其屈服面和子午线大都为曲面和曲线(例如Hoek-Brown、Willam-Warnke准则等),所以按照上述屈服接近度的定义,其屈服接近度函数很难求解。
另外,对于拉伸破坏的分析,文献[8]中也存在一些不妥,即图 1中的应力圆1与直线BC和直线BD同时相切,定义D点处的应力值为材料的轴心抗拉强度σL,而轴心抗拉强度的应力圆应该通过坐标原点,如图 1中的虚线应力圆所示。所以利用应力圆1来推导材料的拉伸屈服函数,其结果是不正确的。
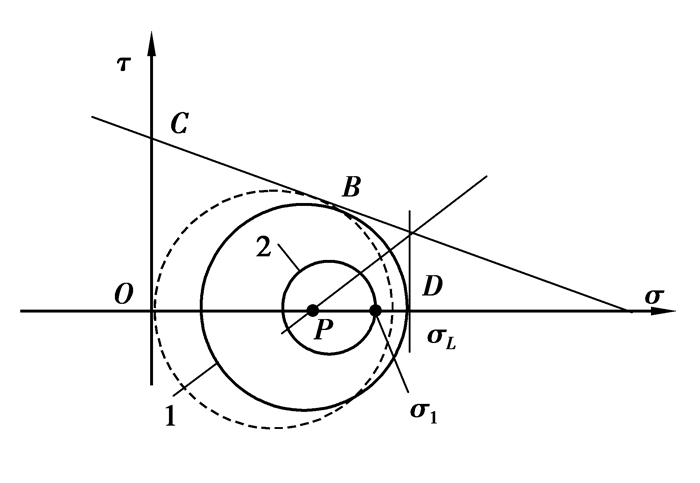
|
图 1 拉伸剪切破坏分析图 Figure 1 Plot of tension-shear failure |
基于上述两个原因,笔者对基于材料破坏准则的屈服接近度给出了新的定义,并重新推导了Mohr-Coulomb破坏准则在拉伸破坏下的屈服接近度公式。同时也对适用于不同材料的多个破坏准则推导了相应的屈服接近度函数,并给出了统一的表达式,以方便屈服接近度函数的程序编写。
1 Mohr-Coulomb屈服条件和屈服接近度概念材料的屈服条件是材料的受力状态由弹性进入塑性的边界条件。一般情况下,屈服条件与应力的6个分量有关,在不考虑应力主轴旋转的情况下与3个主应力分量或不变量有关,而且是它们的函数,即屈服函数[14]。屈服函数在主应力空间表示一个空间曲面,即屈服面。
文中借用了屈服函数的概念,即在主应力空间条件下,将材料的破坏准则,用主应力分量或不变量来表达,即推导其相应的“屈服函数”。再通过现时主应力分量处于“屈服函数”表达的屈服面(这里对应的是材料破坏准则的破坏面)的内部还是外部来判断材料是否发生破坏,或者接近这个屈服面的程度。
对于岩土材料,常用的破坏准则有广义Mises准则、广义Tresca准则、Hock-Brown准则等,还有应用最广和应用时间最长的破坏条件Mohr-Coulomb准则。
1.1 Mohr-Coulomb屈服条件当材料受力单元的某一受力状态的摩尔应力圆与Mohr-Coulomb剪切线相切,就认为材料将发生剪切塑性破坏。
Mohr-Coulomb准则的表达式为
| $\tau = c-\sigma \tan \varphi .$ | (1) |
假设应力方向以拉为正、压为负,由应力摩尔圆和Mohr-Coulomb准则(如图 3所示)可以得出满足Mohr-Coulomb准则的屈服条件函数为
| $F\left( {{I_1}, {J_2}, {\theta _\sigma }} \right) = \frac{1}{3}{I_1}\sin \varphi + \left( {\cos {\theta _\sigma }-\frac{1}{{\sqrt 3 }}\sin {\theta _\sigma }\sin \varphi } \right)\sqrt {{J_2}}-c\cos \varphi, \left( {-{{30}^ \circ } \le {\theta _\sigma } \le {{30}^ \circ }} \right), $ | (2) |
式中,I1、J2、θσ分别为第一主应力不变量、第二偏应力不变量和应力罗德角,c、φ分别为岩土的内聚力和内摩擦角。
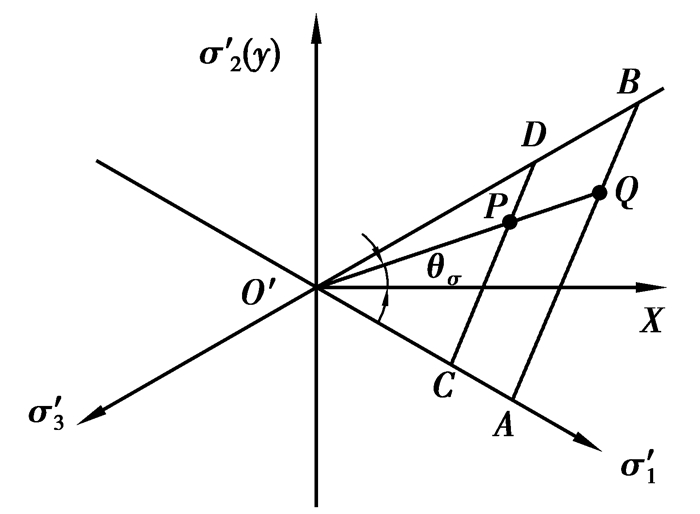
|
图 3 屈服接近度π平面示意图 Figure 3 Yielding approach index in π plane |
该函数代表主应力空间中的一个曲面,即屈服曲面。式(2)表达的屈服曲面是一个由6个形状相同的平面围成的三轴对称的不规则六棱锥面,如图 2(a)所示。屈服面在π平面上的几何图形为6个在60°的扇形区域内形状相同的倾斜直线段AB(屈服线),如图 2(b)所示。
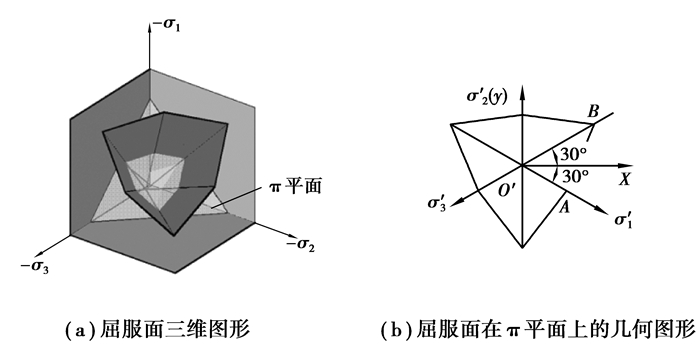
|
图 2 应力空间Mohr-Coulomb屈服面示意图 Figure 2 Mohr-Coulomb yield surface in principal stress space |
由于文献[8]是基于Mohr-Coulomb破坏准则定义的屈服接近度,只适用于屈服曲面是平面的情况,而对于多数屈服面是曲面的则求解难度较大。为了更方便地求解并广泛地适用于各种形状的应力空间屈服面,将屈服接近度进行了重新定义。空间应力状态下一点的屈服接近度为:沿π平面坐标原点与应力点的连线方向,该点到屈服边界线的距离与π平面坐标原点到屈服边界线的距离之比。
主应力空间的P点,由受力单元的3个主应力值确定,其在π平面的坐标值也可以由这3个主应力计算得到。σ1, σ2, σ3分别为P点的3个主应力。对于Mohr-Coulomb破坏准则,应力空间P点的屈服接近度可以表示为(AB为屈服边界,Q点为O′P延长线与AB的交点,如图 3所示)
| $Y = f\left( {{I_1}, {J_2}, {\theta _\sigma }} \right) = \frac{{PQ}}{{O'Q}} = 1-\frac{{O'P}}{{O'Q}}, $ | (3) |
式中,Y∈[0, 1],数值越小,表示越接近破坏,当Y=0表示应力点达到破坏。
2 基于Mohr-Coulomb破坏准则屈服接近度函数的建立 2.1 受力单元破坏形式分析事实上,Mohr-Coulomb破坏准则可以看作是受力单元在各种应力状态下破坏时极限应力圆的包络线,从工程应用的角度来看,这条外包线也可以近似看作是两种特殊受力情况下极限应力圆的公切线,即单轴压缩和单轴拉伸两种情况[15]。因为对于受力单元的破坏形式不同,将采取不同的破坏条件。所以,应先对要分析的受力单元将要发生的破坏形式进行判断。这里,采用带拉伸截断修正的Mohr-Coulomb破坏准则,如图 4所示。
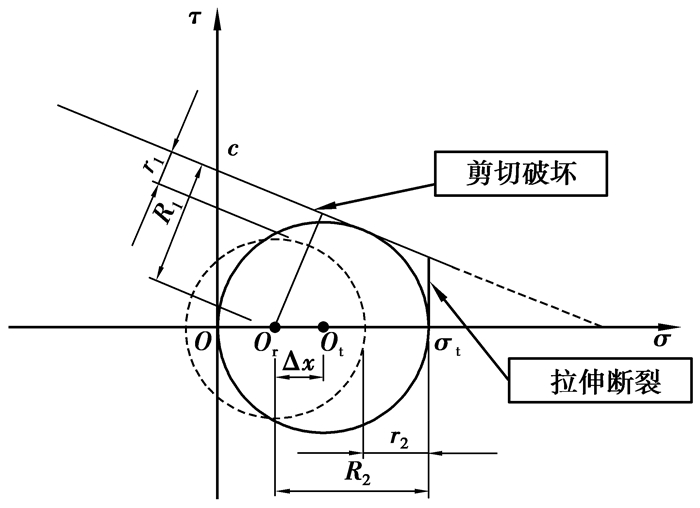
|
图 4 受力单元破坏形式分析图 Figure 4 Failure mode analysis |
选取单轴拉伸破坏极限应力圆(图 4中的实线圆)为参照,OOt=12σt(σt为岩土的单轴抗拉强度)。对于图 4中虚线应力圆,其圆心Or在Ot左侧,|OrOt|=Δx,讨论此时应力状态下可能的破坏形式。
通过对比
| $\left\{ \begin{array}{l} \frac{{{r_1}}}{{{R_1}}} = \frac{{R-r}}{R} = 1-\frac{r}{R}, \\ \frac{{{r_2}}}{{{R_2}}} = \frac{{{\sigma _t} + \Delta x-r}}{{{\sigma _t} + \Delta x}} = 1 - \frac{r}{{{\sigma _t} + \Delta x}}. \end{array} \right.$ | (4) |
很显然,两式总是存在
在图 3所示的π平面上,O′P为主应力空间点P(σ1, σ2, σ3)在π平面上的剪应力分量,记为τπP,可以表示为
| $\tau _\pi ^P = \frac{1}{{\sqrt 3 }}\sqrt {{{\left( {{\sigma _1}-{\sigma _2}} \right)}^2} + {{\left( {{\sigma _2}-{\sigma _3}} \right)}^2} + {{\left( {{\sigma _3}-{\sigma _1}} \right)}^2}} {\rm{ = }}\sqrt {2{J_2}}, $ | (5) |
式中,σ1,σ2,σ3为P点的3个主应力。O′Q为屈服线上Q点的剪应力分量,记为τπQ,可以用极坐标的形式表示为
| $\tau _\pi ^Q = \frac{{\sqrt 2 \left( {3c\cos \varphi-{I_1}\sin \varphi } \right)}}{{3\cos {\theta _\sigma }-\sqrt 3 \sin \varphi sin{\theta _\sigma }}}.$ | (6) |
将式(5)和式(6)代入式(3),得到
| $Y = f\left( {{I_1}, {J_2}, {\theta _\sigma }} \right) = 1-\frac{{\sqrt {{J_2}} }}{{k-\alpha {I_1}}}, $ | (7) |
其中,
| $\left\{ \begin{array}{l} k = \frac{{3c\cos \varphi }}{{3\cos {\theta _\sigma }-\sqrt 3 \sin \varphi \sin {\theta _\sigma }}}, \\ \alpha = \frac{{\sin \varphi }}{{3\cos {\theta _\sigma }-\sqrt 3 \sin \varphi \sin {\theta _\sigma }}}. \end{array} \right.$ | (8) |
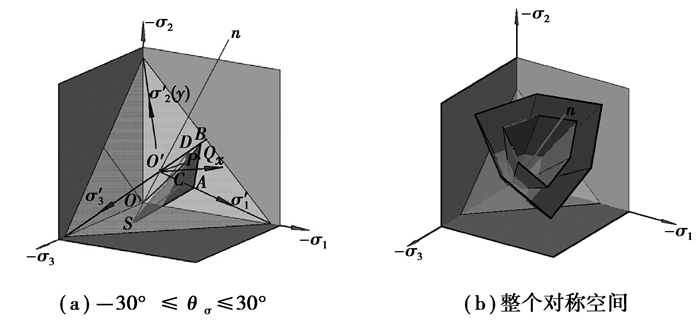
如果在π平面上,过P点作直线CD//AB(如图 3所示),则直线CD上所有点接近屈服曲线的程度都是相同的。将其扩展到空间,如图 5(a)所示,在-30°≤θσ≤30°空间区域内,平面SCD(S为不规则六棱锥面的锥顶)上的所有应力点的屈服接近度都相同,在其余5个对称空间也具有相同的情况,如图 5(b)图所示。
|
图 5 屈服接近度三维空间示意图 Figure 5 The diagram of YAI in three dimensional space |
当
| $Y = f\left( {{\sigma _1}, {\sigma _3}} \right) = \frac{{{\sigma _t}-{\sigma _1}}}{{{\sigma _t}-\frac{1}{2}\left( {{\sigma _1} + {\sigma _3}} \right)}}.$ | (9) |
如果用不变量来表示,可以表示为与式(7)相同的形式为
| $Y = f\left( {{\sigma _1}, {\sigma _3}} \right) = 1-\frac{{\sqrt {{J_2}} }}{{k-\alpha {I_1}}}, $ |
其中,
| $\left\{ \begin{array}{l} k = \frac{{3{\sigma _t} + \sqrt {3{J_2}} \sin {\theta _\sigma }}}{{3\cos {\theta _\sigma }}}, \\ \alpha = \frac{1}{{3\cos {\theta _\sigma }}}. \end{array} \right.$ | (10) |
综合上述内容,带拉伸截断的Mohr-Coulomb准则的屈服接近度可以统一表示为式(7)的形式,其中,对于剪切破坏、拉伸破坏时,系数k和α分别按照式(8)和(10)计算。
用同样的方法,推导了其他几种常见破坏准则[14, 16-18]下的屈服接近度公式,并采用了统一的表达形式,如表 1所示。
| 表 1 常见破坏准则下的屈服接近度函数统一表达形式 Table 1 Uniform YAI based on various material strengthcriterions |
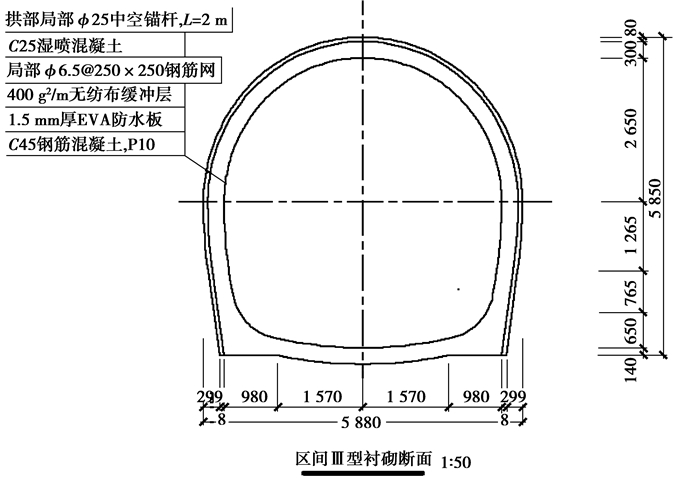
结合青岛市地铁一期工程(地铁3号线),选取了错埠岭站—清江路站区间段的隧道围岩(K11+190~K11+269)为研究对象,根据区间地质钻孔(QX11-04, QX11-06)资料(Ⅲ类围岩)以及该区间Ⅲ型衬砌断面设计图(如图 6所示),选用表 2所示的岩体与衬砌物理力学参数[19],并建立有限元模型。
|
图 6 隧道断面设计图 Figure 6 Tunnel section design drawing |
| 表 2 围岩及衬砌参数 Table 2 Parameters of surrounding rock and lining |
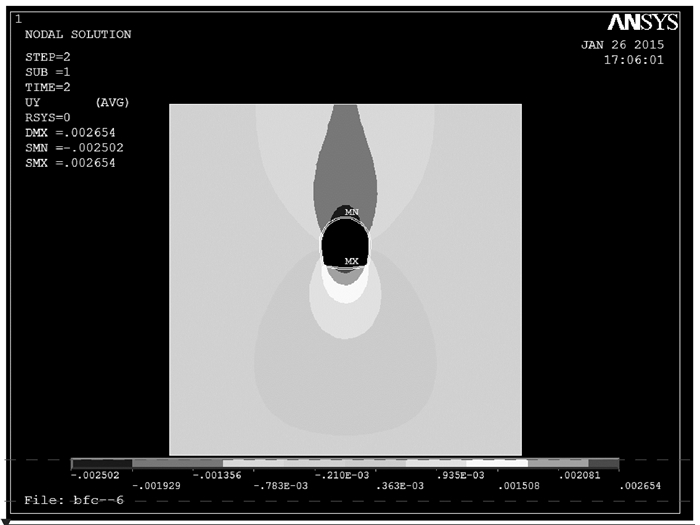
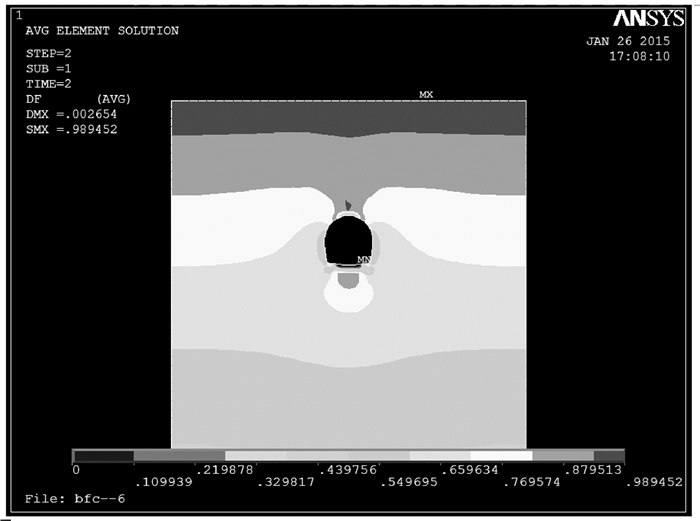
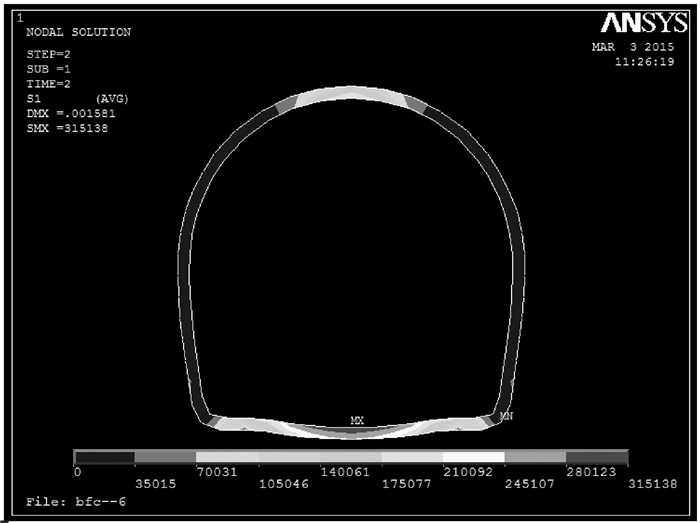
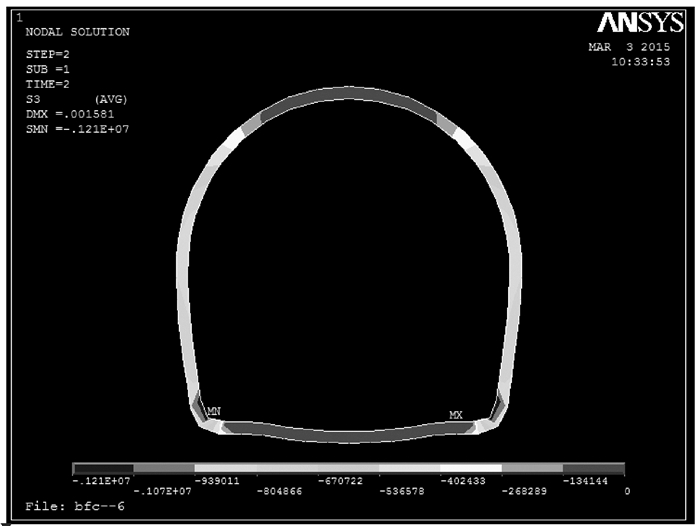
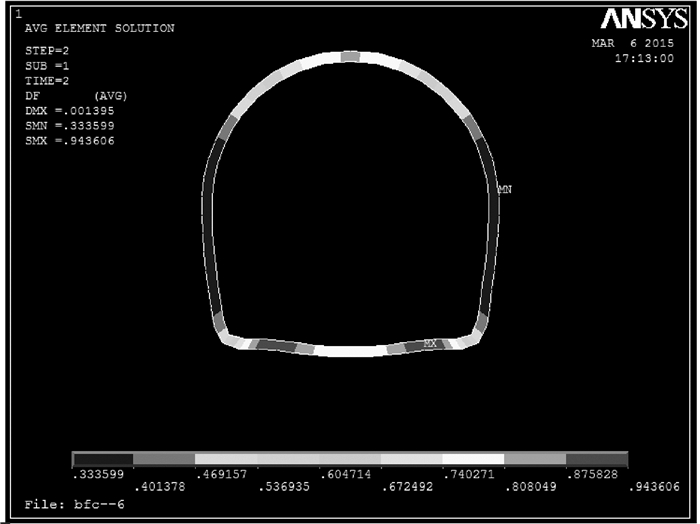
对模型施加初应力荷载以消除重力引起的位移场。利用生死单元技术,模拟隧道开挖。最后,在有限元的后处理阶段嵌入屈服接近度自编Matlab计算程序,实现隧道开挖围岩屈服接近度的等值线云图显示。图 7、图 8分别为隧道开挖后围岩的竖向位移和屈服接近度云图;图 9~11分别为衬砌的应力和屈服接近度云图。图 8中,围岩顶部和底部的局部区域的Y=0,显示围岩在洞顶和洞底的局部区域,出现了破坏,原因是这两处岩体在应力释放和应力重分布后出现了拉应力,使得岩体处于应力空间的不利位置,这与实际施工时,隧道洞顶有局部碎石冒落和洞底底鼓局部出现拉裂缝现象相一致;而隧道围岩的其他部位的Y值大约在0.5~1.0之间,表明其他部位围岩的应力状态相对其破坏屈服面较远,具有较好的安全性。从图 9可以看出围岩的最大竖向位移不超过3 mm,考虑到衬砌支护,可以认为该区间隧道开挖其围岩是安全、稳定的。图 9、图 10显示混凝土衬砌最大、最小主应力远未达到材料的抗压强拉和抗度强度标准值;从图 11整个云图显示,同时参照文献[20]的损伤预测标准,衬砌整体处于结构安全状态(Y=[0.2, 1.0]表示结构安全)。
|
图 7 隧道围岩竖向位移云图 Figure 7 Vertical displacement of surrounding rock |
|
图 8 隧道围岩屈服接近度云图 Figure 8 YAI of surrounding rock |
|
图 9 衬砌第一主应力云图 Figure 9 The first principal stress of lining |
|
图 10 衬砌第三主应力云图 Figure 10 The third principal stress of lining |
|
图 11 衬砌屈服接近度云图 Figure 11 YAI of lining |
笔者对基于力学强度理论的屈服接近度在已有研究成果的基础上进行了进一步研究,对周辉提出的屈服接近度概念进行了重新定义,使其可以更广泛地适用于各种材料的强度准则。同时,对金属、岩土、混凝土材料常见的8种破坏准则下的屈服接近度函数进行了推导,且给出了统一的表达式,以方便数值计算程序的编写。由于具有相同的等效应力的单元接近屈服面的程度会有所差别,仅通过围岩的等效应力的大小来判断其安全程度不尽合理。因此,屈服接近度可以直观、定量地反映隧道开挖后围岩在应力空间所处的危险程度,对工程人员合理判断围岩稳定及安全性评价具有重要的理论基础和工程实用价值。
| [1] | Zheng Y, Qiu C, Hong Z, et al. Exploration of stability analysis methods for surrounding rocks of soil tunnel[J]. Chinese Journal of Rock Mechanics & Engineering , 2008, 27 (10) : 1968–1980. |
| [2] | Andonov E. Evaluation of rock mass stability around tunnels of the irrigation system "Afrin"[J]. Journal of Mining Science , 2005, 41 (4) : 320–331. DOI:10.1007/s10913-005-0097-x |
| [3] |
宫凤强, 李夕兵, 高科.
地下工程围岩稳定性分类的突变级数法研究[J]. 中南大学学报(自然科学版) , 2008, 39 (5) : 1082–1086.
GONG Fengqiang, LI Xibing, GAO Ke. Catastrophe progression method for stability classification of underground engineering surrounding rock[J]. Journal of Central South University: Science and Technology , 2008, 39 (5) : 1082–1086. (in Chinese) |
| [4] | Mukhlisin M, Baidillah M R, Ibrahim A, et al. Effect of soil hydraulic properties model on slope stability analysis based on strength reduction method[J]. Journal of the Geological Society of India , 2014, 83 (5) : 586–594. DOI:10.1007/s12594-014-0087-1 |
| [5] | Duan Q M, BAI L F, Ren H L. Stability analysis of the surrounding rock of large-span multi-arch tunnels based on the hock-brown criterion[J]. Modern Tunnelling Technology , 2013, 50 (6) : 94–100. |
| [6] |
孙金山, 卢文波.
Hoek-Brown经验强度准则的修正及应用[J]. 武汉大学学报(工学版) , 2008, 41 (1) : 63–66.
SUN Jinshan, LU Wenbo. Modification of Hoek-Brown criterion and its application[J]. Engineering Journal of Wuhan University , 2008, 41 (1) : 63–66. (in Chinese) |
| [7] |
张传庆, 冯夏庭, 周辉.
岩石多轴与常规三轴强度的关系[J]. 固体力学学报 , 2011, 32 (3) : 228–234.
ZHANG Chuanqing, FENG Xiating, ZHOU Hui. Relationship between polyaxial strength and conventional triaxial strength for rock[J]. Chinese Journal of Solid Mechanics , 2011, 32 (3) : 228–234. (in Chinese) |
| [8] |
周辉, 张传庆, 冯夏庭, 等.
隧道及地下工程围岩的屈服接近度分析[J]. 岩石力学与工程学报 , 2005, 24 (17) : 3083–3087.
ZHOU Hui, ZHANG Chuanqing, FENG Xiating, et al. Analysis of rock mass stability in tunnel and underground engineering based on yield approach index[J]. Chinese Journal of Rock Mechanics and Engineering , 2005, 24 (17) : 3083–3087. (in Chinese) |
| [9] |
曹林卫, 彭向和, 杨春和, 等.
基于屈服接近度概念的尾矿坝静力稳定性分析及其与强度折减系数法的对比[J]. 西安建筑科技大学学报(自然科学版) , 2010, 42 (3) : 407–414.
CAO Linwei, PENG Xianghe, YANG Chunhe, et al. Analysis on the static stability of the tailings dam with the concept of yield approaching degree comparing to strength-reduction method[J]. Journal of Xi'an University of Architecture and Technology , 2010, 42 (3) : 407–414. (in Chinese) |
| [10] |
张传庆, 周辉, 冯夏庭, 等.
基于屈服接近度的围岩安全性随机分析[J]. 岩石力学与工程学报 , 2007, 26 (2) : 292–299.
ZHANG Chuanqing, ZHOU Hui, FENG Xiating, et al. Stochastic analysis method on safety of surrounding rock mass based on yielding approach index[J]. Chinese Journal of Rock Mechanics and Engineering , 2007, 26 (2) : 292–299. (in Chinese) |
| [11] |
孟丹, 朱崇钊.
地铁隧道钻爆法施工影响下混凝土结构损伤预测方法研究[J]. 岩石力学与工程学报 , 2007, 26 (2) : 292–299.
MENG Dan, ZHU Chongzhao. Damage prediction method of a concrete structure due to tunnel blasting excavations[J]. Journal of Vibration and Shock , 2007, 26 (2) : 292–299. (in Chinese) |
| [12] |
易小明, 张顶立, 李鹏飞.
隧道下穿时地表房屋变形开裂的定量评估[J]. 岩石力学与工程学报 , 2008, 27 (11) : 2289–2294.
YI Xiaoming, ZHANG Dingli, LI Pengfei. Quantitative evaluation of house deformation and cracks caused by tunnel-crossing[J]. Journal of Vibration and Shock , 2008, 27 (11) : 2289–2294. (in Chinese) |
| [13] |
汤福平, 肖明, 张雨霆.
基于破坏接近度的围岩稳定性研究[J]. 中国农村水利水电 , 2009 (4) : 87–90.
TANG Fuping, XIAO Ming, ZHANG Yuting. Research on rock mass stability based on failure approach index[J]. Journal of China Water Conservancy and Hydroelectric Power , 2009 (4) : 87–90. (in Chinese) |
| [14] |
郑颖人, 孔亮. 岩土塑性力学原理[M]. 北京: 中国建筑工业出版社, 2002 .
ZHENG Yingren, KONG Liang. Geotechnical plastic mechanics[M]. Beijing: China Architecture & Building Press, 2002 . (in Chinese) |
| [15] |
孙训方, 方孝淑, 关来泰. 材料力学[M]. 北京: 高等教育出版社, 2002 .
SUN Xunfang, FANG Xiaoshu, GUAN Laitai. Strength of materical[M]. Beijing: Higher Education Press, 2002 . (in Chinese) |
| [16] |
过镇海. 混凝土的强度和本构关系——原理与应用[M]. 北京: 中国建筑工业出版社, 2004 .
GUO Zhenhai. Strength and constitutive relation of concrete: principles and applications[M]. Beijing: China Architecture & Building Press, 2004 . (in Chinese) |
| [17] |
过镇海. 钢筋混凝土原理[M]. 北京: 清华大学出版社, 1999 .
GUO Zhenhai. Principles of reinforced concrete[M]. Beijing: Tsinghua University Press, 1999 . (in Chinese) |
| [18] |
中华人民共和国住房和城乡建设部.GB50010—2010混凝土结构设计规范[S].北京:中国建筑工业出版社, 2010. Ministry of Housing and Urban-Rural Development of the People's Republic of China. GB50010—2010 Code for design of concrete structures[S]. Beijing: China Architecture and Building Press, 2000.(in Chinese) |
| [19] | 青岛地铁集团有限公司.青岛地铁隧道围岩分级指南(试行)(Q/QD-JS-TJ-1002—2014)[Z]. |
| [20] |
孟丹.地铁隧道开挖影响建筑物损伤预测与安全控制研究[D].青岛:青岛理工大学, 2013. MENG Dan. Damage prediction and safety control of subway tunnel excavation effect buildings[D]. Qingdao: Qingdao Technological University, 2013.(in Chinese) |
 2016, Vol. 39
2016, Vol. 39

