2. 福州大学 土木工程学院, 福州 350002;
3. 西安建筑科技大学 土木工程学院, 西安 710000
2. College of Civil Engineering, Fuzhou University, Fuzhou 350002, P.R.China;
3. School of Civil Engineering, Xi'an University of Architecture and Technology, Xi'an 710000, P.R.China
以钢管混凝土为柱肢、空钢管为缀杆,截面尺寸由柱顶至柱底按一定坡度逐渐增大的变截面钢管混凝土格构柱,具有整体稳定性好、承压能力和结构刚度大、延性高、造型美观、节约材料等优点。与普通等截面钢管混凝土格构柱相比,变截面钢管混凝土格构柱由于降低了柱身重心高度,能更好隔离吸收和耗散地震能量,同时具有良好的力学性能和优美的立面造型,因此,在对抗震性能和外形美观要求高的超高桥墩结构、工业厂房、高层建筑、设备构架和大跨度钢管混凝土桁肋拱中具有广阔的应用前景[1]。然而对于工程应用日益广泛的变截面钢管混凝土格构柱,现行的钢管混凝土设计规程[2-5]中没有给出相关的计算方法。文献[6]采用等效截面法,将变截面钢管混凝土格构柱等效为高度不变,断面尺寸为中截面的等截面钢管混凝土格构柱,其承载力计算结果与有限元数值分析结果吻合,但该方法尚缺少试验的验证,是否合理有待深入研究。文献[7]进行了变截面钢管混凝土格构柱轴压和偏压试验研究,采用等效惯性矩法计算格构柱的极限承载力,但该方法计算过程和计算公式较繁琐,不方便工程应用。
为此,以文献[7]的试验构件为分析对象,对变截面钢管混凝土格构柱开展算法研究,借鉴国外相关规程和文献,在试验验证和有限元分析验证的基础上,提出适合工程应用的变截面钢管混凝土格构柱轴压极限承载力的实用算法。
1 变截面钢管混凝土格构柱轴压试验文献[7]轴压试件总数为6根,包括4根变截面钢管混凝土格构柱和2根等截面钢管混凝土格构柱。试件设计时,以四川雅安干海子大桥的四肢变截面钢管混凝土格构墩为原型,缩尺比例为1:8。
试验参数为柱高和柱肢坡度,参数取值时考虑了试验室设备加载条件和工程应用实例范围。试件具体参数见表 1,其中,试件高度为2 m和3.5 m,柱肢坡度1:n为1:40和1:20。表中长细比λ取试件中截面的尺寸代入计算。
| 表 1 变截面钢管混凝土格构柱试验参数及结果一览表 Table 1 Parameter and results of specimens |
各试件均为平缀管式钢管混凝土格构柱,其小头处截面尺寸均相同,面内柱肢间距a为0.3 m,面外柱肢间距c为0.5 m。大头截面处面内柱肢间距b根据试件高度和放坡确定。柱肢钢管直径ϕ=114 mm、壁厚t=2 mm。缀管规格为直径ϕ=48 mm、壁厚t=2 mm的空钢管。格构柱节间距离250 mm。变截面钢管混凝土格构柱试件的具体构造如图 1所示。

|
图 1 试件构造图(单位:mm) Figure 1 Configuration of specimens |
柱肢钢管钢材实测弹性模量为2.05×105 MPa,屈服强度为300 MPa,极限抗拉强度为444 MPa,泊松比为0.27。缀管钢材实测弹性模量为1.98×105 MPa,屈服强度为351 MPa,极限抗拉强度为488 MPa,泊松比为0.28。混凝土立方体抗压强度为38 MPa,弹性模量为32 500 MPa。此外,同批制作3根与试件柱肢相同的钢管混凝土单圆短柱(ϕ89×1.8 mm),高度为350 mm,轴压试验的结果其极限承载力平均值为580 kN。试验参数及结果如表 1所示。
从表 1试验结果比较可知,柱肢坡度和试件高度是影响变截面钢管混凝土格构柱轴压极限承载力的重要因素。对于小头截面尺寸相同的变截面钢管混凝土格构柱,试件高度越大,或柱肢坡度越小,试件的长细比越大,极限荷载越小。
2 极限承载力计算方法根据试验结果可知[7],四肢变截面钢管混凝土格构柱轴压构件的受力性能和破坏模式与四肢等截面钢管混凝土格构柱相似。因此,文中在计算变截面钢管混凝土格构柱的轴压极限承载力时,采用国家规范GB 50923—2013[2]中关于等截面钢管混凝土格构柱承载力的计算框架,如式(1)~(2)。
| ${N_{\rm{D}}} = \varphi \sum\limits_{i = 1}^n {{N_{oi}}, } $ | (1) |
| ${N_0} = {k_3}\left( {1.14 + 1.02{\xi _0}} \right)\left( {1 + {\rho _c}} \right){f_{{\rm{cd}}}}{A_{\rm{c}}}, $ | (2) |
式中:ND为钢管混凝土格构柱的轴压承载力;φ为稳定系数;N0为钢管混凝土单圆管截面轴心抗压强度设计值;k3为轴心抗压强度设计值换算系数;ξ0为钢管混凝土的约束效应系数设计值;ρc为钢管混凝土截面含钢率; fcd为混凝土轴心抗压强度设计值;Ac为钢管内混凝土的截面面积。
2.1 变截面钢管混凝土格构柱的等效长度由式(1)可见,变截面钢管混凝土格构柱的轴压极限承载力计算中,关键是稳定系数φ的确定。而稳定系数φ的计算核心是如何将变截面钢管混凝土格构柱转换成等效的等截面钢管混凝土格构柱。
目前的计算思路主要有以下3种:第1种是等效惯性矩形式,即构件长度不变,改变构件截面惯性矩[7];第2种是等效截面法,即构件长度不变,可取小头截面和大头截面的平均值为等效截面[6]。第3种是等效长度形式,即截面尺寸选取小头或大头,改变构件长度。文中拟采用第3种等效长度形式,参考国外变截面钢构件的计算思路,提出变截面钢管混凝土格构柱等效长度的计算方法。
文献[8]介绍了美国《建筑钢结构规范》AISC-LRFD[9]中变截面钢构件的稳定设计原理。对于线性渐变的变截面钢柱(如图 2所示),其柱高为l,柱肢坡度为θ,小头截面的柱宽为d0,大头截面的柱宽为dl=d0(1+γ),这里γ为截面增大系数,可按公式(3)计算。设计时,选取变截面柱的最小截面,将变截面柱等效为等截面柱,通过引入修正系数g(等效长度系数)来反映柱身截面变化对变截面柱承载力增大的效果。
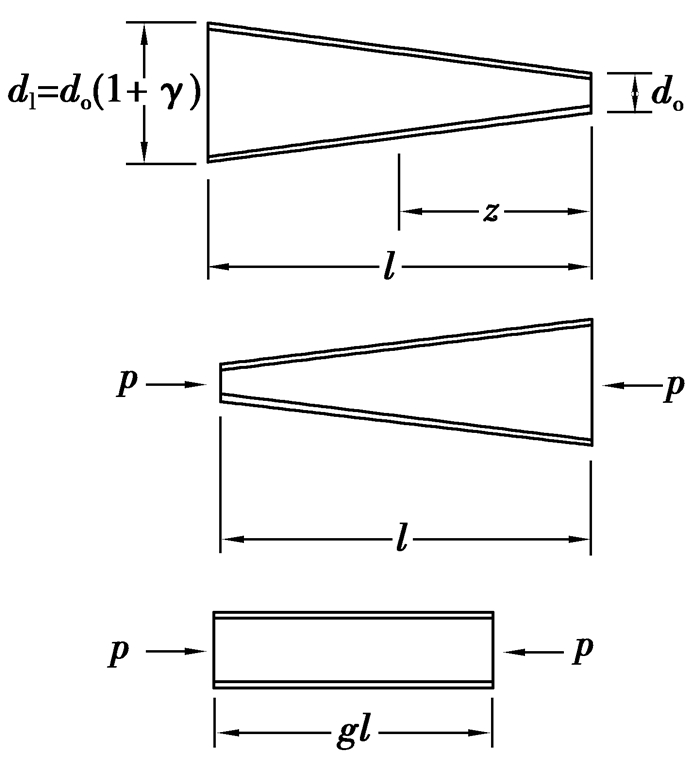
|
图 2 变截面柱等效长度系数g的示意图 Figure 2 Equivalent length factor (g) of variable cross-sectional column |
遵循这一计算原理,将长度为l的变截面钢管混凝土格构柱,等效成小头截面不变,长度为gl的等截面钢管混凝土格构柱,见式(4)。
| $\gamma = \left( {2*\theta *l} \right)/{d_0}, $ | (3) |
| $g = 1-0.375\gamma + 0.08{\gamma ^2}\left( {1-0.0775\gamma } \right).$ | (4) |
换算得到等效长度的等截面钢管混凝土格构柱之后,可借鉴文献[10]中平缀条钢格构柱的计算思路,采用放大系数法计算平缀管式钢管混凝土格构柱的换算长细比,见式(5)。
| ${\lambda ^*} = \frac{{KL}}{r} = \sqrt {{{\left( {\frac{L}{r}} \right)}^2} + \frac{{{\pi ^2}}}{{12}}{{\left( {\frac{a}{{{r_c}}}} \right)}^2}}, $ | (5) |
式中:λ*为换算长细比;K为换算长细比系数;L/r为构件长细比;a为平缀条间距;rc为柱肢半径。
2.3 钢管混凝土格构柱的稳定系数计算得到格构柱的换算长细比之后, 格构柱的稳定系数仍采用国家规范GB 50923—2013[2]的计算公式,见式(6)。柱相对长细比λn的计算见式(7)。
| ${\lambda _n} \le 1.5\;\;\;\;\varphi = {0.658^{\lambda \frac{2}{n}}}, $ | (6) |
| $\lambda > 1.5\;\;\;\;\;\varphi = \frac{{0.877}}{{\lambda _n^2}}.$ | (7) |
式中:Es为钢的弹性模量;Ec为混凝土的弹性模量;As为钢管的面积;Ac为混凝土的面积;fy为钢材的屈服强度;fck为混凝土立方体抗压强度标准值;ρc为钢管混凝土截面含钢率;φ为钢管混凝土格构柱的稳定系数。
3 变截面钢管混凝土格构柱轴压试验验证为探讨变截面钢管混凝土格构柱轴压极限承载力的计算方法是否合理、准确,以文献[7]的试验构件为分析对象,对变截面钢管混凝土格构柱进行算法的试验验证,计算结果见表 2。其中计算值1采用文中的等效长度法,计算值2采用文献[6]的等效截面法。单肢钢管混凝土短柱的承载力取试验值。试件的轴压极限承载力计算结果如表 2所示。
| 表 2 试件的轴压极限承载力计算值与试验值比较 Table 2 Comparison of calculation results and test results |
由表 2可见,等效截面法和等效长度法的轴压承载力计算结果十分接近,且均与试验值吻合较好。等效长度法计算值与试验值比值的均值为1.033,方差为0.021;等效截面法计算值与试验值比值的均值为1.033,方差为0.022。
4 有限元分析验证由于试验构件的数量有限,为扩大参数分析范围,应用ANSYS程序,在对试验构件计算验证的基础上,对变截面钢管混凝土格构柱轴压极限承载力进行参数影响的数值分析,对文中的等效长度法及文献[6]提出的等效截面法进行进一步的有限元分析验证。
4.1 有限元计算方法文中的有限元分析采用大型通用程序ANSYS。由文献[7]试验结果可知,变截面钢管混凝土轴压格构柱破坏时有较明显的面内弯曲,属整体破坏。因此有限元分析时,可采用杆系单元。柱肢钢管、管内混凝土、缀管均采用Timoshenko梁单元BEAM188模拟,端板采用BEAM4单元模拟。
钢管混凝土柱肢建模时采用由钢管单元和混凝土单元重合的双单元[11],材料本构关系采用一维的表达式。其中钢管本构关系采用四折线应力应变关系曲线[12]。对于管内核心混凝土,其材料本构关系选用以一维方式表达的考虑套箍效应的本构关系[13]。
材料非线性求解时,将试件的材料特性代入,按上述公式计算并输入相应的应力应变曲线。几何非线性求解时,采用大挠度非线性有限元方法计算,用newton-raphson法求解,通过设置柱长千分之一的初挠度来考虑初始几何缺陷的影响。
4.2 极限承载力计算结果比较图 3为各试件的极限承载力计算值与试验值比较的结果。极限承载力的试验值与计算值均指最大荷载。由图 3可见,有限元计算值与试验值吻合较好,二者比值的均值为1.010,方差为0.023。说明采用文中建立的有限元模型,能较准确地计算变截面钢管混凝土格构柱的轴压极限承载力。
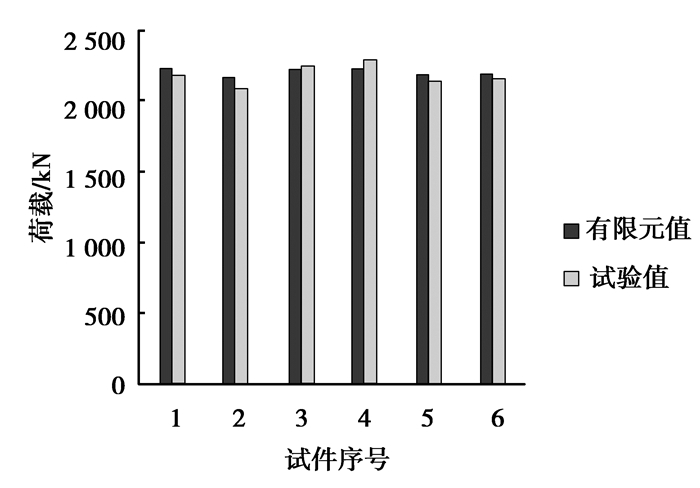
|
图 3 极限承载力计算值与试验值比较 Figure 3 Comparison of test results and calculation results results |
以文中试件为例,扩大试验参数范围,采用上述实用算法的极限承载力计算结果与有限元计算值的比较(见图 4)。其中柱高的变化范围为2~10 m(λ的变化范围为10~50),柱肢坡度的变化范围为1:60~1:20。单肢柱的轴心受压短柱承载力采用国家规范GB 50923—2013的计算公式。
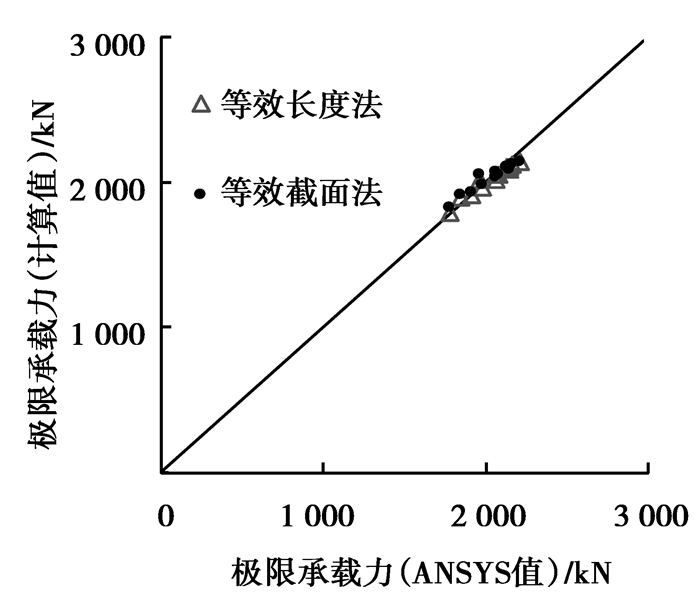
|
图 4 极限承载力计算结果比较 Figure 4 Calculation results of ultimate load carrying capacity |
从图 4可以看出,等效长度法的计算值与ANSYS计算结果吻合良好,均值为0.987,方差为0.011。(等效截面法的均值0.993,方差0.024)。该算例进一步验证了文中提出的等效长度法,对于变截面钢管混凝土格构柱是适用的。因此,在试验验证和有限元分析验证的基础上,文中提出变截面平缀管式钢管混凝土格构柱轴压极限承载力的实用算法,如表 3所示。
| 表 3 变截面钢管混凝土柱轴压极限承载力的实用算法 Table 3 Calculation methods of ultimate load of variable cross-sectional CFST columns on axial load |
1) 在计算变截面平缀管式钢管混凝土格构柱的轴压极限承载力时,采用国家规范GB 50923—2013的计算框架。其中关于格构柱的计算长度借鉴了国外变截面钢柱的计算思路[8-9],即采用等效长度法,将高度为l的变截面钢管混凝土格构柱等效为小头截面不变,高度为gl的等截面钢管混凝土格构柱。
2) 借鉴文献[10]中平缀条钢格构柱的计算方法,采用放大系数法计算变截面平缀管式钢管混凝土格构柱的换算长细比。
3) 对变截面钢管混凝土格构柱,分别进行了算法的试验验证和有限元分析验证。研究结果表明,计算值与试验结果和有限元数值计算结果均吻合良好。文中给出的四肢变截面钢管混凝土格构柱轴压极限承载力的计算方法思路清晰、计算简捷、结果准确且偏于安全,可供工程应用和钢管混凝土设计规程修订时参考。
| [1] | Zhijing O. The practice of concrete filled steel tube piers to bridges: a review[J]. Applied Mechanics and Materials , 2013 (405/408) : 1602–1604. |
| [2] |
福州大学, 中建海峡建设发展有限公司.钢管混凝土拱桥技术规范:GB 50923—2013[S].北京:中国计划出版社, 2013. Fuzhou University, CSCEC Strait Construction and Development Co, LTD. Technical code for concrete filled steel tubular structures: GB 50923—2013[S]. Beijing: China Planing Press, 2013. |
| [3] |
哈尔滨建筑工程学院, 中国建筑科学研究院.钢管混凝土结构设计与施工规程:CECS 28:90[S].北京:中国计划出版社, 1992. Harbin College of Civil Engineering and Architecture, China Academy of Building Research. Specification for design and construction of concrete filled steel tubular structures: CECS 28:90[S]. Beijing: China Planing Press, 1992. (in Chinese) |
| [4] |
苏州混凝土水泥制品研究院, 中国船舶总公司第九设计研究院.钢管混凝土结构设计与施工规程:JCJ 01-89[S].上海:同济大学出版社, 1990. Suzhou Concrete and Cement Products Research Institute, The Ninth Design and Research Institute of China State Shipbuilding Corporation. Specification for design and construction of concrete filled steel tubular structures: JCJ 01-89[S]. Shanghai: Tongji University Press, 1990. (in Chinese) |
| [5] |
华北电力设计院.钢管混凝土组合结构设计规程: DL/T 5085—1999[S].北京:电力出版社, 1999. North China Electric Power Design Institute. Code for design of steel-concrete structures: DL/T 5085—1999[S]. Beijing: China Electric Power Press, 1999. (in Chinese) |
| [6] | Ou Z J, Huang L, Yan Q L. Research on calculation method of the stability factor of variable cross-sectional concrete filled steel tubular laced columns[J]. Applied Mechanics and Materials , 2014 : 1420–1423. |
| [7] |
黄蕾.变截面钢管混凝土格构柱极限承载力研究[D].福州:福州大学, 2015. Huang Lei. Research on ultimate load-carrying capacity of concrete filled steel tubular battened columns with variable cross-section[D]. Fuzhou: Fuzhou University, 2015. (in Chinese) |
| [8] | Galambos TV. Guide to stability design criteria for metal structures[M]. New York: John Wiley &Sons, Inc, 1998 : 83 -87. |
| [9] | LRFD. Specification for structural steel buildings[S]. Chicago: American institute of steel construction (AISC), 1999. |
| [10] | Bleich, F. Buckling strength of metal structures[M]. McGraw-Hill, New York: 1952: 174-179. |
| [11] |
陈宝春, 欧智菁.
钢管混凝土格构柱极限承载力计算方法研究[J]. 土木工程学报 , 2008, 41 (1) : 55–63.
Chen Baochun, Ou Zhijing. Research on calculation method of the ultimate load carrying capacity of concrete filled steel tubular laced columns[J]. China Civil Engineering Journal , 2008, 41 (1) : 55–63. (in Chinese) |
| [12] |
陈宝春, 秦泽豹, 彦坂熙, 等.
钢管混凝土拱(单圆管)面内受力双重非线性有限元分析[J]. 铁道学报 , 2003, 25 (4) : 80–84.
Chen Baochun, Qin Zebao, Yan Banxi, et al. Analysis of concrete filled steel tubular (single tube) arch subjected to in-plane loads by nonlinear finite element method[J]. Journal of the China Railway Society , 2003, 25 (4) : 80–84. (in Chinese) |
| [13] |
韩林海. 钢管混凝土结构理论与实践[M]. 北京: 科学出版社, 2004 .
Han Linhai. The concrete filled steel tubular structures from theory to practice[M]. Beijing: Science Press, 2004 . (in Chinese) |
 2016, Vol. 39
2016, Vol. 39

