2. 中石油渤海钻探工程技术研究院, 天津 300457
2. Research Institute of Bohai Drilling Engineering Technology, CNPC, Tianjin 300000, P.R.China
钻井过程中,在拉压、扭转、弯曲、冲击载荷、摩擦以及循环介质携岩的冲腐蚀作用下,井下钻具易发生断裂失效。图 1为钻井过程中上提204T钻柱时,钻具的断裂图。目前,国内外学者对钻柱失效的研究主要集中在理论分析和实验研究两个方面。根据钻柱所处的力学环境建立其相应的数学模型,然后在一定的边界条件下,运用数值分析算法进行求解,得到影响钻柱使用寿命的各个参数表达式,进而从结论出发,提出预防钻柱提前失效的措施并进行检验[1-4]。

|
图 1 钻杆管体断裂 Figure 1 Drill pipe fracture failure |
扩展有限元(extended finite element method, XFEM)是1999年以美国西北大学Belytschko教授[5]为代表的研究组首先提出,随后得到飞速发展。XFEM对于结构内的几何或物理界面并不需要进行网格划分,是迄今为止求解含有夹杂物等不连续力学问题最有效的数值方法,它既避免了常规有限元在裂纹尖端等高应力区或变形集中区需要进行高密度细化网格的做法,又避免了在模拟裂纹扩展时需要满足的网格重划分、裂纹面与单元边界一致性要求[6]。Stolarska等[7]将水平集法(level set method, LSM)引入扩展有限元分析方法中,其中水平集用来表示裂纹和裂纹尖端的位置,XFEM用来求取应力和位移,计算裂纹扩展率。Dolbow等[8]将XFEM应用于细观结构材料断裂的有效特性分析中,降低了细观结构分析时对网格重构的要求。
细观力学的研究起源于Taylor等在细观塑性理论方面的成就,在此基础之上,20世纪50年代就提出了细观损伤力学理论,并在20世纪70年代蓬勃发展起来。到了20世纪80年代,细观力学的研究方法涉及到了各种工程材料,譬如金属与合金材料、混凝土材料、岩石材料、陶瓷材料、高分子材料、微电子元件材料以及其他各种复合材料等。从20世纪90年代开始,研究人员开始使用细观力学方法预测和设计各种性能的材料,并取得了巨大成功[9-11]。材料的特性取决于材料的原子结构与微观结构,要深入了解和研究材料的变形与破坏特性,就不能停留在宏观尺度上,而应该开展多尺度分析,使宏观、细观分析与微观尺度甚至原子尺度的分析结合起来,在较深的层次上找出问题出现的根源及变形与破坏机制。
文中采用细观力学分析方法,结合断裂力学算法——扩展有限元法,对细观尺度下的微裂纹扩展过程以及相应的应力应变分布进行研究,并通过细观力学的“均匀化”方法评价微裂纹的扩展对材料宏观性能的影响,为探索钻柱材料断裂机理提供新的方法。
1 细观力学基本原理 1.1 分析流程金属是由数以百万计的颗粒和杂乱无章的结晶组成,在电子显微镜下,对于同一金属试件相邻的两个1 mm2的影像都是不相同的。对于金属材料的细观结构分布,在足够大的参考体积中分析细观场的空间变化已远远超过计算机的分析能力,显然这种方法是不可取的,因此可采用近似的方法,即采用代表性体积单元(representative volume element, RVE)来表征这种非均匀、无序材料的集合[12]。
代表性体积单元RVE在尺度上具有二重性:1) 使代表性体积单元RVE的尺寸在宏观尺度上相对于结构的特征尺寸足够小,可以看作一个物质点,从而满足连续介质力学的基本假设,进而可以采用等效均匀介质来代替实际的非均匀材料,通过对等效介质的结构计算获得宏观应力场和应变场,即细观尺度上局部场的平均值,同时,可以获得非均匀材料细观尺度下的不规则应力场和应变场,以及代表性体积单元中的平均场;2) 使代表性体积单元RVE的尺寸在细观尺度上足够大,保证代表性体积单元RVE尺寸要远大于非均匀材料组分(夹杂或加强物)的特征尺寸(即细观尺寸),从而在包含足够多细观组织结构信息的基础上,可以准确表征局部连续介质的统计学平均性质。由代表性体积单位构成的材料即为统计均匀材料,统计均匀材料在均匀边界条件作用下形成的场分布为统计均匀场[13]。
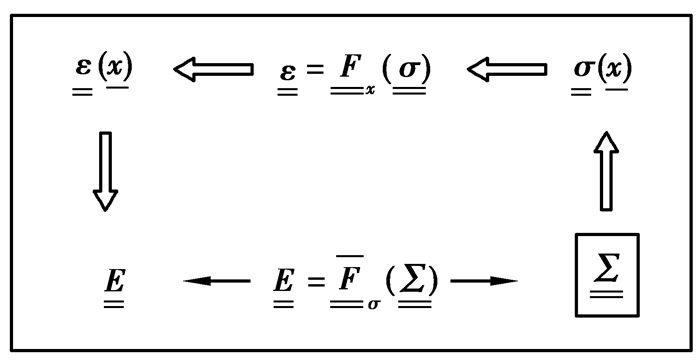
当代表性体积单元边界上存在均匀应力情况时的总体分析流程见图 2所示[14]。其中,
|
图 2 细观力学分析流程 Figure 2 Mesomechanics analysis process |
Voronoi图又称泰森多边形或Dirichlet图,早在1850年Dirichlet和1908年Voronoi就对Voronoi图作过详细的讨论。如果在一片草地上,随机放置若干个火源,假定这些火源同时被点燃,并且以相同的燃烧速度向各个方向蔓延,那么当相邻火源燃烧相遇时,燃烧熄灭处所形成的图形即为Voronoi图,其中每一个Voronoi多边形中只含有一个且只能包含一个火源[15]。而在金属材料的形成过程中,晶体结晶是以晶核为始点,然后向四周扩展的,与Voronoi图生成具有相似性。正因为此种相似性,笔者将使用随机函数生成的点坐标来代表晶核、Voronoi多边形代表形成的晶体,用晶体来模拟细观力学中的代表性体积单位,并在Abaqus软件平台上完全采用Python脚本语言二次开发了快速建立任意数目晶粒的建模程序。
1.3 “均匀化”根据细观力学从宏观微观宏观的分析思路,结合Abaqus软件输出数据库中各对象的层次关系,采用Python语言编制Abaqus软件面积加权平均后处理程序,实现对模型中每个单元的应力、应变和位移进行“均匀化”处理,用来分析微裂纹的扩展对材料宏观性能的影响。
2 扩展有限元基本原理扩展有限元基本思想就是在裂纹影响区域,通过引入加强函数来改进传统有限元位移空间。主要基于插值函数单元分解的思想,建立了适合于描述含裂纹面的近似位移插值函数[16-18]
| $u\left( x \right) = \sum\limits_{i \in N} {{N_i}\left( x \right){u_i}} + \sum\limits_{j \in {N_{{\rm{disc}}}}} {{N_j}H\left( x \right){a_j} + \sum\limits_{k \in {N_{{\rm{asy}}}}} {{N_k}\left( {\sum\limits_{\alpha = 1}^4 {{\varphi _\alpha }\left( x \right)b_k^\alpha } } \right), } } $ | (1) |
式中:N是所有常规单元节点的集合;Ndisc是裂纹面贯穿的单元内节点的集合;Nasy是裂纹尖端所在单元内节点的集合;ui、aj、bkα分别表示常规单元节点、贯穿单元节点和裂尖单元节点的位移;H(x)为跳跃函数;φα(x)为裂尖渐进位移场附加函数,反映裂尖的应力奇异性。
利用节点变分的任意性,XFEM离散线性方程组与常规有限元一样可表示为
| $\mathit{\boldsymbol{Kd = F}}$ | (2) |
式中:K为整体刚度矩阵;d为节点位移列向量;F为等效节点力列向量。
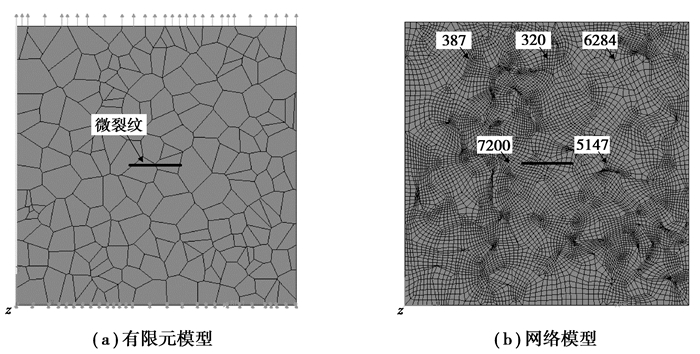
3 断裂力学的细观有限元分析 3.1 有限元模型建立在Abaqus平台下调用所开发的任意数目晶粒的建模程序,建立含有微裂纹的200晶粒的扩展有限元模型,见图 3(a)所示,图中晶粒模型为Voronoi多边形,其中晶核为随机分布。整个正方形模型的长度为1 mm,裂纹贯穿两个晶粒,裂纹尺寸2a=0.167 604 mm,裂纹在模型中心左侧0.084 619 mm,在模型中心右侧0.082 985 mm。在全局坐标系下y轴方向承受拉力σy=1 000 MPa,由于整个分析步设置时间为1 s,载荷是Ramp坡状线性加载,所以,在整个分析过程中载荷是逐渐施加的,直到1 000 MPa。划分的网格以及部分节点编号见图 3(b)所示。
|
图 3 200晶粒的扩展有限元模型和网格模型 Figure 3 Extended finite element model containing 200 grains and mesh model |
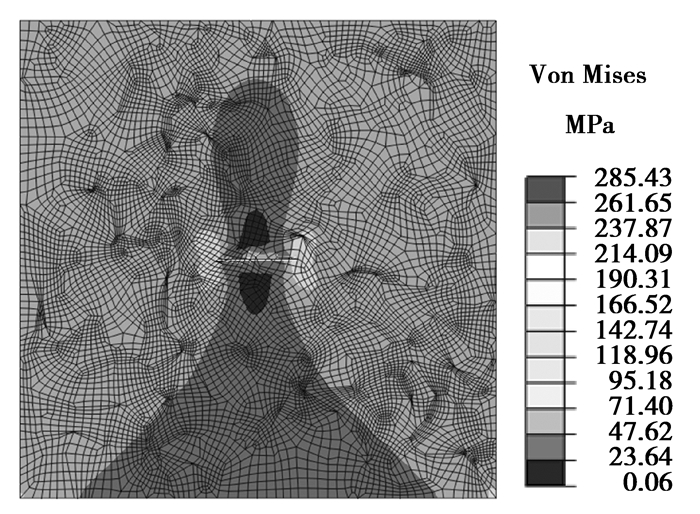
图 4~图 11为200晶粒的扩展有限元模型断裂过程的Von Mises应力分布云图。图 4为增量步0.05 s时的Von Mises应力分布云图,由于裂纹的存在,在裂纹的尖端区域产生了应力集中,裂纹尖端Von Mises应力为285.43 MPa,而由于外载为坡状加载,此时模型承受的外载拉力为50 MPa均匀分布力,同时,在远离裂纹区域处,Von Mises应力为50 MPa左右,与外载拉力大小相当。随着增量步的增大,在0.109 4 s时的Von Mises应力分布云图见图 5所示,此时外载作用为109.4 MPa,而裂纹尖端的Von Mises应力增大为611.92 MPa,但远离裂纹的区域处的Von Mises应力在105 MPa左右,与外载相当。
|
图 4 增量步为0.05 s时的应力云图 Figure 4 Stress contour at 0.05 s |

|
图 5 增量步为0.109 4 s时的应力云图 Figure 5 Stress contour at 0.109 4 s |

|
图 6 增量步为0.201 6 s时的应力云图 Figure 6 Stress contour at 0.201 6 s |
|
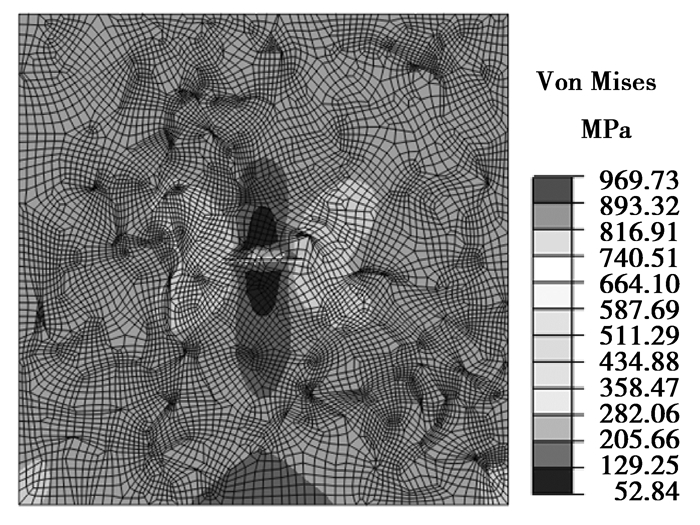
图 7 增量步为0.251 6 s时的应力云图 Figure 7 Stress contour at 0.251 6 s |

|
图 8 增量步为0.301 6 s时的应力云图 Figure 8 Stress contour at 0.301 6 s |

|
图 9 增量步为0.351 6 s时的应力云图 Figure 9 Stress contour at 0.351 6 s |

|
图 10 增量步为0.354 7 s时的应力云图 Figure 10 Stress contour at 0.354 7 s |

|
图 11 断裂时的裂纹形状 Figure 11 Crack shape when material is broken |
在0.201 6 s增量步时,裂纹尖端应力超过了S135材料4337钢的最小屈服强度,材料发生屈服,并产生一定塑性应变,见图 6。在图 7所示的0.251 6 s增量步时,裂纹尖端的Von Mises应力为969.73 MPa,与0.201 6 s增量步时的Von Mises应力值967.56 MPa相近,此时模型材料进入应力增长缓慢、塑性应变增长的阶段,即材料的屈服阶段。
图 8所示的增量步为0.301 6 s时的Von Mises应力云图,此时裂尖区域材料不断发生屈服,裂尖区域的应力缓慢增大,直到图 9所示的0.351 6 s增量步时,裂尖的能量积累到一定程度,应力超过S135钢材的抗拉强度,从而导致裂纹发生扩展,裂纹尖端扩展了两个单元。由于裂纹的扩展,能量得到了释放,在图 10中,裂纹尖端最大应力值(971.89 MPa)区域相对于图 9中0.351 6 s增量步时的最大应力值(974.14 MPa)区域明显减小。
在后期的计算中,随着增量步的增加,载荷的加大,裂纹尖端区域不断发生严重的应力集中现象,并且能量不断积累、最大应力值区域不断增大,直到在裂纹尖端发生裂纹扩展,应力得到释放,进入下一个应力积累、裂纹扩展和应力释放的循环过程中,最终整个模型被拉断破坏,见图 11所示。
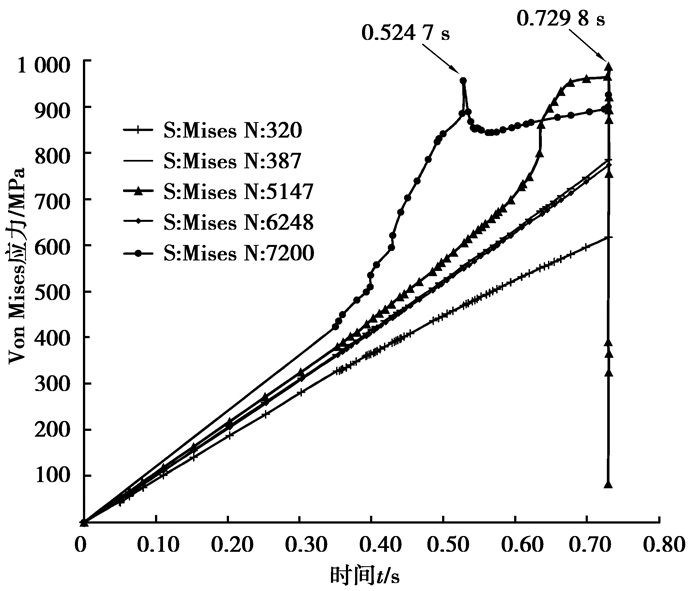
图 12和图 13为5个节点上的Von Mises应力和最大主应力在分析过程中随增量步的变化曲线,其中5个节点的具体位置见图 3(b)所示的网格模型,数字代表节点的编号。387号节点位于模型的左上侧,320号节点在模型的中上方,6284号节点在模型的右上侧,7200号和5147号节点分别在初始裂纹的左右两侧,且在裂纹扩展路径的附近,属于裂纹扩展路径所贯穿单元的节点之一。
|
图 12 结点上Von Mises应力随增量步的变化 Figure 12 Von Mises stress of different nodes |
|
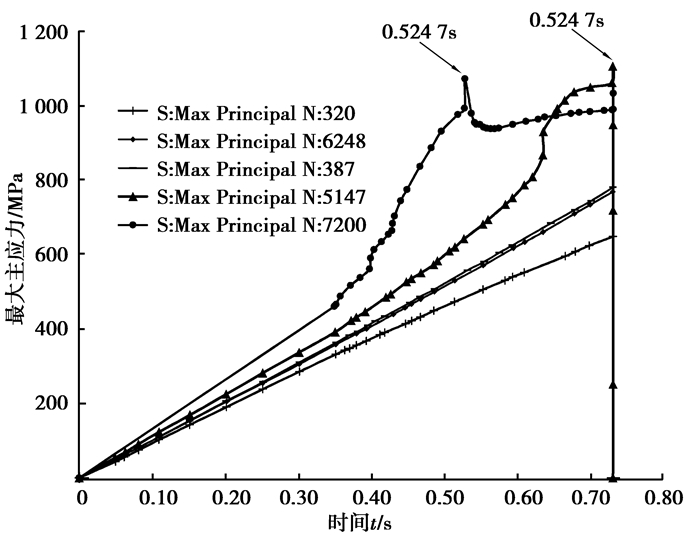
图 13 结点上最大主应力随增量步的变化 Figure 13 Maximum principal stress of different nodes |
由图 12和图 13中的曲线分布可知,387号、320号和6284号3节点的Von Mises应力和最大主应力与外载的大小相差无几,在这些远离裂纹区域的节点上不存在应力集中现象,也很难达到屈服状态。387号和6284号两节点近似处于对称位置,在整个分析过程中,Von Mises应力和最大主应力大小也近似相等。7200号节点在初始裂纹的左侧,在0.524 7 s增量步时,Von Mises应力为952 MPa,超过了S135材料的屈服强度,材料发生了屈服,产生塑性应变,对应的最大主应力超过了S135材料的抗拉强度1 000 MPa,此时裂纹尖端刚好要扩展到该节点所在的单元之一。随着裂纹的扩展,7200号节点上的应力得到释放,应力值下降。5147号节点在裂纹的右侧,在0.729 8 s增量步时,裂纹尖端扩展到该节点所在单元之一,此时对应的最大主应力也超过了S135材料的抗拉强度1 000 MPa,最终裂纹尖端穿过该节点所在单元开裂,该节点上的应力值由1 109 MPa急剧下降,最大主应力下降为几乎为零的地步,这主要是因为5147号节点距离裂纹扩展路径较近的缘故。
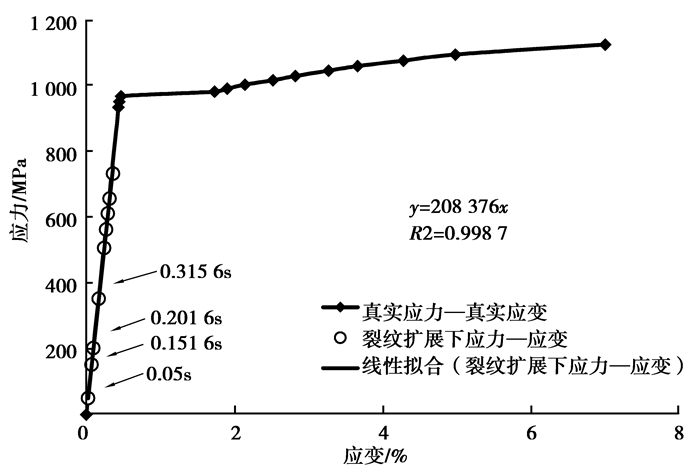
3.3 “均匀化”分析在不同增量步下,运用开发的Abaqus软件加权平均后处理代码程序,对裂纹扩展过程中的应力、应变和位移进行面积加权,从而得到单向受拉模型整体反映的应力应变曲线。图 14为裂纹扩展过程中,不同增量步下的应力应变值与模型输入真实应力真实应变值的对比。由于计算的复杂性和耗时性,主要取0.73 s以内增量步的结果进行加权处理,因此施加在模型中的最大均布外载则为730 MPa,此时经过面积加权平均得到的最大均布外载为731.6 MPa,面积加权平均出来的外载值与真实施加的外载值近似相等,符合细观力学计算特征。同时,由于所加外载都在S135材料宏观屈服强度931 MPa以内,所以在图 14中,不同增量步下
|
图 14 裂纹扩展过程中的宏观应力应变 Figure 14 Macro stress-strain with crack propagation |
加权平均出来的应力应变值仍落在材料的弹性阶段,而在细观尺度下,由于裂纹的存在,导致了局部区域应力集中,超过了材料的屈服强度而发生塑性应变,这进一步说明了在交变载荷作用下,塑性应变不断积累,在一定程度下形成疲劳裂纹的扩展而导致钻柱的断裂或刺漏。同时,对整个分析过程中材料整体处于弹性阶段的应力应变值进行线性拟合,得到的弹性模量为2.083 76×105MPa,与初始设置的弹性模量2.1×105MPa相当,充分反映了在宏观尺度下性能稳定的材料,在细观尺度下由于微裂纹的存在,局部区域的材料仍会因应力集中超过屈服强度而发生塑性应变。
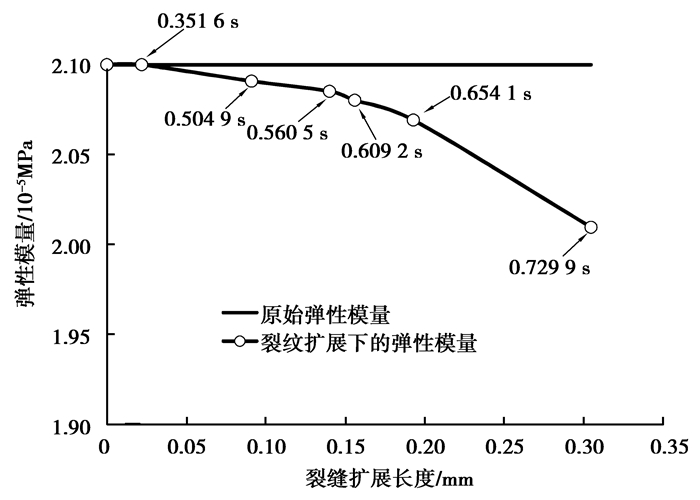
由于模型材料整体上仍处于弹性阶段,现将每一增量步下加权平均出来的应力应变直接求比值,相当于随着裂纹的扩展模型整体反映出来的弹性模量,裂纹扩展不同长度下的弹性模量分布曲线见图 15所示,初始裂纹为0.167 604 mm。虽然在0.201 6 s增量步时,裂纹尖端已经出现塑性区,但在裂纹发生扩展的0.351 6 s增量步以前,得到的弹性模量仍为2.1×105MPa,在0.351 6 s增量步以后随着裂纹的扩展,得到的弹性模量不断降低。这也从一个侧面说明了弹性模量是材料整体性能的反映,包括材料内夹杂和微裂纹的作用,只要裂纹不发生扩展,弹性模量是恒定的,尽管局部区域发生了塑性应变。
|
图 15 裂纹扩展过程中的弹性模量变化 Figure 15 The change of elasticity modulus with crack propagation |
1) 即使在低应力作业下,裂纹尖端区域也会发生严重的应力集中,随着能量不断积累、最大应力值区域不断增大,最终在裂纹尖端发生裂纹扩展,进而应力得到释放,从而进入下一个应力积累、裂纹扩展和应力释放的循环过程中,直到整个模型断裂破坏。
2) 当不同增量步下加权平均出来的应力应变值落在材料的弹性阶段时,在细观尺度下,由于裂纹的存在,导致了局部区域应力集中,仍会超过材料的屈服强度而发生塑性应变。
3) 在弹性阶段的外载作用下,即使裂纹尖端区域屈服产生塑性应变,但只要裂纹不扩展,模型整体表现出来的弹性模量是恒定不变的;当裂纹扩展时,模型整体表现出来的弹性模量是逐渐降低的。
| [1] |
章扬烈. 钻柱运动学与动力学[M]. 北京: 石油工业出版社, 2001 .
ZHANG Yanglie. Drill string of kinematics and dynamics[M]. Beijing: Petroleum Industry Press, 2001 . (in Chinese) |
| [2] | Ghasemloonia A, Rideout D G, Butt S D. Analysis of multi-mode nonlinear coupled axial-transverse drillstring vibration in vibration assisted rotary drilling[J]. Journal of Petroleum Science and Engineering , 2014, 116 (2) : 36–49. |
| [3] | Moradi S, Ranjbar K. Experimental and computational failure analysis of drillstrings[J]. Engineering Failure Analysis , 2009, 16 (3) : 923–933. DOI:10.1016/j.engfailanal.2008.08.019 |
| [4] | Dao N H, Sellami H. Stress intensity factors and fatigue growth of a surface crack in a drill pipe during rotary drilling operation[J]. Engineering Fracture Mechanics , 2012, 96 : 626–640. DOI:10.1016/j.engfracmech.2012.09.025 |
| [5] | Belytschko T, Black T. Elastic crack growth in finite elements with minimal remeshing[J]. International Journal for Numerical Methods in Engineering , 1999, 45 (5) : 601–620. DOI:10.1002/(ISSN)1097-0207 |
| [6] | Sharma K, Singh I V, Mishra B K, et al. Numerical modeling of part-through cracks in pipe and pipe bend using XFEM[J]. Procedia Materials Science , 2014, 6 : 72–79. DOI:10.1016/j.mspro.2014.07.009 |
| [7] | Stolarska M, Chopp D L, Moës N, et al. Modelling crack growth by level sets in the extended finite element method[J]. International Journal for Numerical Methods in Engineering , 2001, 51 (8) : 943–960. DOI:10.1002/nme.201 |
| [8] | Dolbow J E, Nadeau J C. On the use of effective properties for the fracture analysis of microstructured materials[J]. Engineering Fracture Mechanics , 2002, 69 (14) : 1607–1634. |
| [9] |
张研, 韩林. 细观力学基础[M]. 北京: 科学出版社, 2014 .
ZHANG Yan, HAN Lin. Foundation of mesomechanics[M]. Beijing: Science Press, 2014 . (in Chinese) |
| [10] |
杨卫.
细观力学和细观损伤力学[J]. 力学进展 , 1922, 22 (1) : 1–9.
YANG Wei. Mesomechanics and meso-damage mechanics[J]. Advances in Mechanics , 1922, 22 (1) : 1–9. (in Chinese) |
| [11] | Taya M, Dunn M, Derby B, et al. Thermal residual stress in a two-dimensional in-plane misoriented short fiber composite[J]. Applied Mechanics Reviews , 1990, 43 (5S) : 294–303. DOI:10.1115/1.3120831 |
| [12] |
范镜泓. 材料变形与破坏的多尺度分析[M]. 北京: 科学出版社, 2008 .
FAN Jinghong. Multiscale analysis for deformation and failure of materials[M]. Beijing: Science Press, 2008 . (in Chinese) |
| [13] |
何凤兰, 李旭东, 王国栋.
基于DEFORM三维多晶体材料微结构的有限元分析[J]. 甘肃科技 , 2009, 25 (14) : 10–12.
HE Fenglan, LI Xudong, WANG Guodong. Finite element analysis of 3D polycrystal material microstructure basing on DEFORM[J]. Gansu Science and Technology , 2009, 25 (14) : 10–12. (in Chinese) |
| [14] |
张研, 张子明. 材料细观力学[M]. 北京: 科学出版社, 2008 .
ZHANG Yan, ZHANG Ziming. Mesomechanics of materials[M]. Beijing: Science Press, 2008 . (in Chinese) |
| [15] |
周培德. 计算几何算法设计与分析[M]. 北京: 清华大学出版社, 2008 .
ZHOU Peide. Computation geometry: the design and analysis of algorithm[M]. Beijing: Tsinghua University Publishing Press, 2008 . (in Chinese) |
| [16] |
陈金龙, 战楠, 张晓川.
基于扩展有限元法的裂尖场精度研究[J]. 计算力学学报 , 2014, 31 (4) : 425–429.
CHEN Jinlong, ZHAN Nan, ZHANG Xiaochuang. Numerical study on the accuracy of crack tip field by extened finited element method[J]. Chinese Journal of Computational Mechanics , 2014, 31 (4) : 425–429. (in Chinese) |
| [17] | Chopp D L, Sukumar N. Fatigue crack propagation of multiple coplanar cracks with the coupled extended finite element/fast marching method[J]. International Journal of Engineering Science , 2003, 41 (8) : 845–869. DOI:10.1016/S0020-7225(02)00322-1 |
| [18] |
林铁军, 练章华, 曾晓健, 等.
应用XFEM模拟研究钻杆裂纹扩展过程[J]. 重庆大学学报 , 2010, 33 (7) : 123–128.
LIN Tiejun, LIAN Zhanghua, ZENG Xiaojian, et al. Simulation on crack growth of drill pipe with XFEM[J]. Journal of Chongqing University , 2010, 33 (7) : 123–128. (in Chinese) |
 2016, Vol. 39
2016, Vol. 39


