在高速PCB(print circuit board)中,电源分配网络负责为芯片提供稳定可靠的电源供应。由于芯片供电电压的降低,电流增大,为保证更低的电源噪声,设计时PDN阻抗在一定的频段内要足够小[1-2]。
电源板建模是PDN阻抗分析中最重要的部分。文献[3-4]采用谐振腔模型得到电源板阻抗的解析式,这种方法精度高、计算快,但仅适用于矩形的电源板。对于任意形状的电源板,文献[5-7]采用了数值方法,如时域有限差分法、矩量法、有限元法等,计算精度很高,但计算过程复杂。等效电路模型也较为常见,但也存在计算量巨大的问题。文献[8-9]将电源板分割成多个矩形部分以及较小的任意结构,其中矩形部分通过解析式求解,从而有效地减小剖分区域,提高计算效率。然而对于电源板存在过孔或细缝的情况,分割法并不适用。因此,笔者将带有过孔等的电源板缝补回完整的矩形,结合解析式与有限差分法形成其互补模型,进而求得电源板的节点阻抗矩阵。
电源板的PDN阻抗较大且存在多个谐振点,工程中通常在电源板间添加去耦电容以降低PDN阻抗。文献[10-11]根据经验公式确定去耦电容的数目,而电容的安装位置主要依赖于设计者的经验。文献[12-13]则采用遗传算法、粒子群算法等自动选取电容及安装位置,使单电源端口PDN满足要求。比较两种算法,PSO较为简单且全局寻优能力更强。实际PCB存在多个受电电源端口,而这种单端口的设计没有考虑各端口间的相互影响,因此,笔者以多输入阻抗作为优化目标,通过PSO自动选取去耦电容及其位置,从而达到目标值要求。
1 电源分配网络阻抗分析目标阻抗法指出,要将电源噪声限制在系统的噪声容限内,芯片受电电源端口的输入阻抗必须在一定频率范围内小于目标阻抗,而目标阻抗
| ${{Z}_{target}}=\frac{{{V}_{dd}}\times {{C}_{ripple}}}{{{I}_{t}}},$ | (1) |
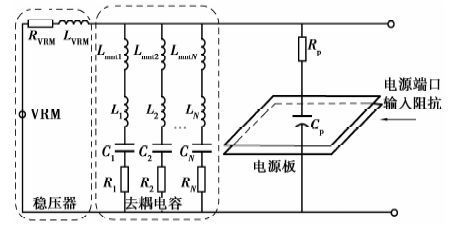
式中:Vdd为工作电压,It是最坏情况下的瞬变电流的平均值,Cripple指可容许纹波系数,一般取5%。受电电源端口的输入阻抗是电源EMI的关键参数。图 1是典型PDN的构成,其中,稳压器、电容器的模型分别是RL串联支路、RLC串联支路,而电源板的建模最为复杂。
|
图 1 PDN的构成 Figure 1 Composition of PDN |
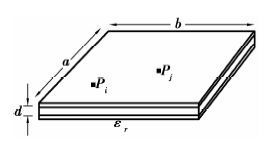
当电源板为图 2所示的长方体结构时,采用谐振腔理论得到板上任意两个端口i和j间互阻抗Zij的表达式,即
| $\begin{align} & {{Z}_{ij}}=j\omega \mu d\sum\limits_{m=0}^{\infty }{\sum\limits_{m=0}^{\infty }{\frac{{{C}_{m}}{{C}_{n}}}{ab({{k}^{2}}_{xm}+{{k}^{2}}_{yn}-{{k}^{2}})}}}\times cos({{k}_{xm}}{{x}_{i}})cos({{k}_{yn}}{{y}_{i}})cos({{k}_{xm}}{{x}_{j}})\times \\ & cos({{k}_{yn}}{{y}_{j}})sin~c\left( \frac{{{k}_{xm}}d{{x}_{i}}}{2} \right)sin~c\left( \frac{{{k}_{yn}}d{{y}_{i}}}{2} \right)\times sin~c\left( \frac{{{k}_{xm}}d{{x}_{j}}}{2} \right)sin~c\left( \frac{{{k}_{yn}}d{{y}_{j}}}{2} \right), \\ \end{align}$ | (2) |
|
图 2 电源板 Figure 2 Plane pair structure |
式中:kxm=mπ/a,kyn=nπ/b,(xi,yi),(xj,yj)分别为是端口i和j的坐标,(dxi,dyi),(dxj,dyj)则为端口i、j的尺寸,数值远小于波长。当m=n=0时,CmCn=1;当m,n中有且仅有一个等于0时,CmCn=2;当m,n均大于0时,CmCn=4。复波数k=ω$\sqrt{\varepsilon \mu }$(1-j(tan δ+di/d)/2),而d1和d分别为金属板的趋肤深度和厚度。μ为基板的磁导率,ε是基板的介电常数。解析法计算快速且精度很高,但实际电源板常常存在通孔、狭缝、分割等结构,此时解析式不再适用,而数值方法如有限差分法能很好地解决这一问题。
1.2 等效电路模型由于电源板间电位差分布满足二维赫姆赫兹方程
| $({{\nabla }^{2}}+{{k}^{2}})\varphi \left( x,y \right)=j\omega \mu d{{J}_{z}}\left( x,y \right),$ | (3) |
式中:φ为电源板的电位差;J0为注入电源板的电流。电源板边界满足
| $\partial \varphi /\partial n=0。$ | (4) |
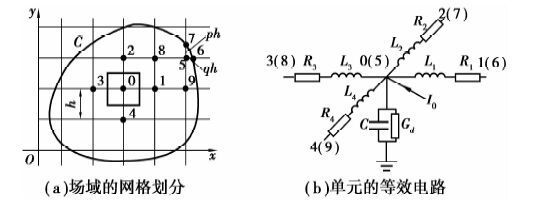
因此,求解电源板的阻抗转换为式(3)和(4)的定解问题。采用有限差分法求解时,首先对场域进行网格划分,形成正方形子块,如图 3(a),由于子块的边长远小于λ,因此每个子块等效为一个节点。其次将式(3)离散成差分方程,根据差分方程构造图 3(b)的等效电路,其中,内部子块0的参数
| ${{R}_{1}}=0,{{L}_{1}}=\mu d,C=\varepsilon {{h}^{2}}/d,{{G}_{d}}=\omega Ctan~\delta ,$ | (5) |
|
图 3 电源板的电路模型 Figure 3 Circuit model of power plane |
式中:R2=R3=R4=R1,L2=L3=L4=L1。而紧邻边界的子块5,由于p,q为小于1的正数,等效电路的电感参数发生变化,即
| $\begin{align} & {{L}_{1}}=p\left( p+1 \right)\mu d/2,{{L}_{2}}=q\left( q+1 \right)\mu d/2, \\ & {{L}_{3}}=\left( p+1 \right)\mu d/2,{{L}_{4}}=\left( q+1 \right)\mu d/2。 \\ \end{align}$ | (6) |
此外,等效电路中边界上的节点6和7做悬空处理。最后将所有子块的等效电路根据位置关系进行相应的电气连接,形成分布参数电路,进而求得任意节点的阻抗。
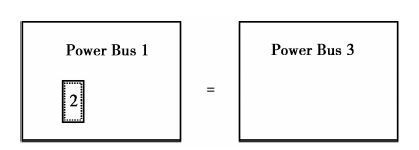
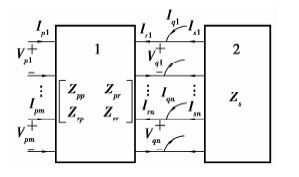
1.3 互补模型在不规则的电源板中,为实现解析式的应用,尽可能地构造矩形部分的场域。如分割方法将电源板分割为若干矩形部分,与之类似,互补模型则寻找某电源板1的互补结构2,通过设置虚拟节点将两者连接成完整的矩形电源板3,如图 4所示。假设电源板1上有m个待求端口,记为p类,在1、2边界上设置n个虚拟节点,记为r类,与之对应电源板2上虚拟节点记为s类,如图 5所示。
|
图 4 互补模型示意图 Figure 4 Complementation model |
|
图 5 虚拟节点的设置 Figure 5 Setup of virtual nodes |
电源板1和2的节点电压电流
| $\left[ \begin{matrix} {{V}_{p}} \\ {{V}_{r}} \\ \end{matrix} \right]=\left[ \begin{matrix} {{Z}_{pp}} & {{Z}_{pr}} \\ {{Z}_{rp}} & {{Z}_{rr}} \\ \end{matrix} \right]\left[ \begin{matrix} {{I}_{p}} \\ {{I}_{r}} \\ \end{matrix} \right],$ | (7) |
| ${{V}_{s}}={{Z}_{s}}{{I}_{s}},$ | (8) |
式中:Zpp、Zpr、Zrp及Zrr是未知量,Zs采用解析式或路模型求解,即为已知量。由于r类端口和s类端口连接后形成端口q,显然q类端口的数目也为n,电压电流存在如下关系:
| ${{V}_{q}}={{V}_{r}}={{V}_{s}},{{I}_{q}}={{I}_{r}}+{{I}_{s}}。$ | (9) |
联立式(7)、(8)和(9)得电源板3的Z参数矩阵
| $\left[ \begin{matrix} Z{{\prime }_{pp}} & Z{{\prime }_{pq}} \\ Z{{\prime }_{qp}} & Z{{\prime }_{qq}} \\ \end{matrix} \right]={{\left[ \begin{matrix} {{E}_{m\times m}} & {{Z}_{pr}}{{Z}^{-1}}_{s} \\ 0 & {{E}_{n\times n}}+{{Z}_{rr}}{{Z}^{-1}}_{s} \\ \end{matrix} \right]}^{-1}}\left[ \begin{matrix} {{Z}_{pp}} & {{Z}_{pr}} \\ {{Z}_{rp}} & {{Z}_{rr}} \\ \end{matrix} \right]。$ | (10) |
对式(10)进行代数变换得到电源板1的待求量
| ${{Z}_{pp}}=Z{{\prime }_{pp}}+Z{{\prime }_{pq}}{{({{Z}_{s}}-Z{{\prime }_{qq}})}^{-1}}Z{{\prime }_{qp}}。$ | (11) |
与数值方法相比,互补模型的剖分区域从较大的电源板1转化成较小的电源板2,在保证精度的同时可以极大地减少计算量,尤其适用于带有孔缝等细小结构的电源板。
最后将电源板模型与电容器、稳压器等其他元件的模型相连,并将电压源置0,形成新的节点阻抗矩阵。电源板1上某电源端口j的输入阻抗
| ${{Z}_{j}}=\frac{{{V}_{j}}}{{{I}_{j}}}=\frac{1}{{{I}_{j}}}\sum\limits_{l=1}^{n}{{{Z}_{jl}}{{I}_{l}}}。$ | (12) |
式中:n为电源端口的数目,Vj、Ij分别为端口j的电压、电流。Zj考虑了其他受电电源端口的影响,又称为多输入阻抗。
2 电源去耦网络的优化当电源端口的输入阻抗不满足目标阻抗时,需要为PDN设计合适的去耦网络以获得平坦的低输入阻抗,从而降低电源噪声。PDN去耦网络设计的关键是确定去耦电容的种类及其安装位置。由于去耦电容种类繁多,各电容去耦性能各异,选用不同电容,安装在不同位置都会得到不同的PDN阻抗。设计时,在允许安装去耦电容的区域上设置若干电容端口,用于表征位置信息。假设某PDN有a个电源端口,b个电容端口,Z参数矩阵根据电源端口、电容端口进行分块
| $\left[ \begin{matrix} {{V}_{ic}} \\ {{V}_{cap}} \\ \end{matrix} \right]=\left[ \begin{matrix} A & B \\ C & D \\ \end{matrix} \right]\left[ \begin{matrix} {{I}_{ic}} \\ {{I}_{cap}} \\ \end{matrix} \right]。$ | (13) |
1个电容端口只能安装1个电容,当电容端口k(k=a+1,a+2,…,a+b)有去耦电容时,电压Vk与电流Ik关系
| $-{{\dot{I}}_{k}}={{Y}_{k}}{{\dot{V}}_{k}},$ | (14) |
式中Yk是并联电容的导纳值,而该端口悬空时,Yk数值为0。如果去耦电容及对应的端口均已知,那么b个电容端口的电压电流
| ${{I}_{cap}}={{Y}_{C}}{{V}_{cap}},$ | (15) |
式中YC=-diag(Ya+1,Ya+2, …,Ya+b)。结合式(13)和式(15)可以消去所有的电容端口,从而得到添加电容后a个电源端口的Z参数矩阵
| $Z=A+B{{(I-{{Y}_{C}}D)}^{-1}}{{Y}_{C}}C。$ | (16) |
当电容种类或位置发生改变时,YC发生变化,而Z与YC存在复杂的非线性关系。此外,工程可选用的电容种类繁多,如表贴电容就达到几千种,因此,去耦电容的选取是一个复杂非线性的全局寻优问题。针对这类工程问题,粒子群算法具有实现容易、精度较高、收敛快速的优点。PSO模拟鸟群飞行觅食的行为,从随机解出发,通过适应值来评价解的品质,追随当前搜索到的最优值来寻找全局最优。
PSO确定去耦电容时,根据自谐振频率对可选电容器进行排序并组成电容库C={c1,c2,…,cr},对可安装端口进行编号并组成端口库P={p1,p2,…,ps}。设m个粒子组成种群X={x1,x2,…,xm},其中,每个粒子所处的位置xi={c1,p1,c2,p2,…,cn,pn}表示电容c1~cn分别安装在端口p1~pn上。迭代时,粒子不断地调整自己的位置xi,可以表示搜索新的电容安装方案。粒子能记住自己找到的最优解xl及整个种群的最优解xg。此外粒子都有一个速度vi={v1,v2,…,vm},每次迭代后,粒子的速度、位置会得到更新[14-15]:
| $\begin{align} & {{v}_{id}}\left( t+1 \right)=\omega \left( t \right){{v}_{id}}\left( t \right)+{{p}_{1}}{{r}_{1}}\left( {{x}_{ld}}-{{x}_{id}} \right)+{{p}_{2}}{{r}_{2}}\left( {{x}_{gd}}-{{x}_{id}} \right){{x}_{id}}\left( t+1 \right)= \\ & {{x}_{id}}\left( t \right)+{{v}_{id}}\left( t+1 \right)\omega \left( t \right)=({{\omega }_{i}}-{{\omega }_{f}})\frac{{{t}_{max}}-t}{{{t}_{max}}}+{{\omega }_{f}}。 \\ \end{align}$ | (17) |
式中:xid(t+1)、vid(t+1)分别表示粒子i在t+1次迭代中第d维上的位置和速度,r1和r2是0~1之间的随机数,ωi和ωf分别是权重ω的起始值和最终值,p1和p2为加速系数,tmax是迭代的最大次数。
电容个数的减少不仅可以降低设计的成本,而且占用更少的空间,从而增加其他元件布局布线的灵活性。因此,将电容个数作为适应度函数的重要部分。优化过程存在约束条件,即每个电源端口均要满足目标阻抗的要求
| $max({{Z}_{i}}\left( f \right))\le {{Z}_{itarget}},i=1,2,\ldots ,m,$ | (18) |
式中:Zi(f)为频域下电源端口i的输入阻抗幅值,Zitarget是电源端口i的目标值,m为电源端口数目。此时适应值
| ${{V}_{fit}}={{N}_{C}}+\sum\limits_{i=1}^{m}{(m}ax({{Z}_{i}}\left( f \right))-{{Z}_{itarget}}),$ | (19) |
式中,NC为去耦使用的电容数,右端第2项不大于0,因此Vfit≤NC。当约束条件不成立时,适应值
| ${{V}_{fit}}={{N}_{C}}+\sum\limits_{i=1}^{m}{(m}ax({{Z}_{i}}\left( f \right))-{{Z}_{itarget}})+50\sum\limits_{i=1}^{m}{max}({{Z}_{i}}\left( f \right))。$ | (20) |
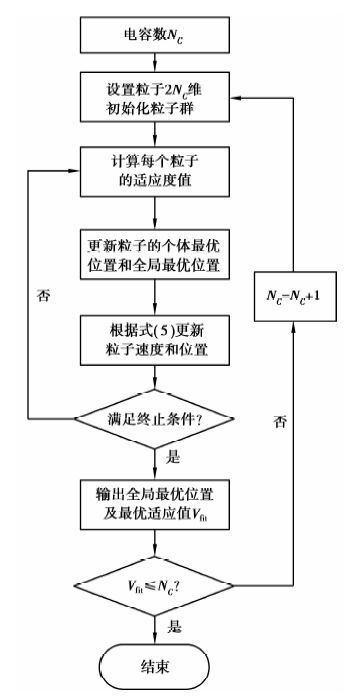
式中,右端第3项是罚函数,VfitNC。整个过程进行最小值搜索,计算流程图如图 6所示,最后采用最少的去耦电容达到目标阻抗要求。
|
图 6 去耦电容优化流程图 Figure 6 Optimization flow chart |
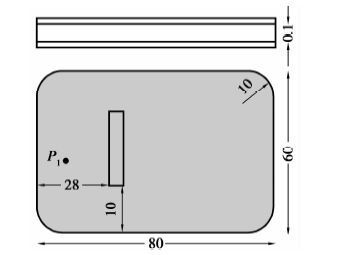
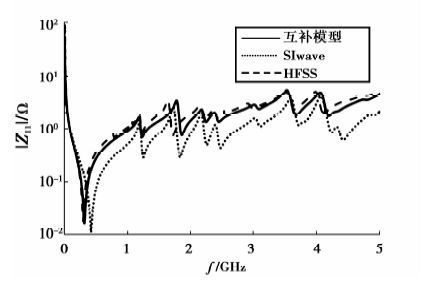
为验证互补模型的正确性,选择某2层电源板作为分析实例。电源板外轮廓为圆角矩形,内部有一条长30 mm、宽2 mm的长方体孔缝,设置某端口P1的位置为(10,15),如图 7所示。计算频带为1~5 GHz,扫频点数为1 000。图 8对互补模型、ANSYS SIwave、HFSS的结果进行了对比,可以发现,互补模型的结果在大部分频段内与HFSS的基本吻合,而SIwave仿真值在频率较高时存在较大的误差。这是因为HFSS采用的是三维有限元法,在细小孔缝的附近进行精细的剖分以保证精度,而SIwave采用的是二维有限元法,计算时忽略了细小孔缝。在计算时间上,HFSS用了2 338 s,互补模型则只需75 s,因此,对于存在孔缝的不规则电源板的计算,互补模型能在保证精度的同时大幅地缩减计算时间。
|
图 7 电源板 Figure 7 Diagram of arbitrary shaped power plane |
|
图 8 电源板的阻抗曲线 Figure 8 Comparison of self and mutual impedance |
实验设计了一块4层PCB,如图 9所示,该板顶层、底层是布线层,中间的电源平面和地平面构成电源板,其中铜皮厚0.036 mm,基板厚度为0.486 6 mm。

|
图 9 实验电路板 Figure 9 Practical board for case study |
在底层设置电容端口P4~P19,在顶层设置电源端口P1、P2和P3,工作电压为3.3 V,可容许纹波为5%,汲取的最大电流分别为60,50,40 mA,因此,P1、P2和P3的目标阻抗分别为2.750,3.300,4.125 Ω。
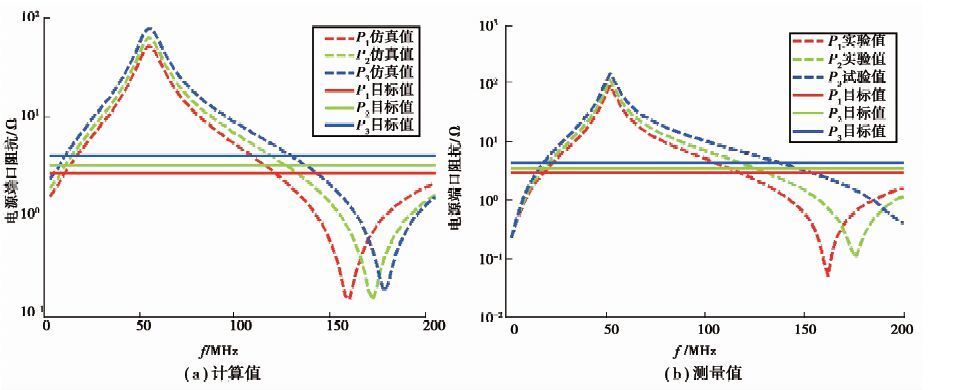
仿真模型中,稳压器等效参数Rvrm=50 mΩ,Lvrm=5 nH,计算PDN的节点阻抗矩阵,并根据式(12)求得端口P1、P2和P3的多输入阻抗。实验采用E5061B网络分析仪测量端口阻抗,同样地,将测量值转换成多输入阻抗。图 10中对仿真、实验结果进行对比,可以发现,两者在趋势上基本一致,数值较为接近。然而,3个受电端口的输入阻抗在很宽的频域范围内大于目标值。
|
图 10 去耦前电源端口的阻抗 Figure 10 PDN impedance without decoupling capacitor |
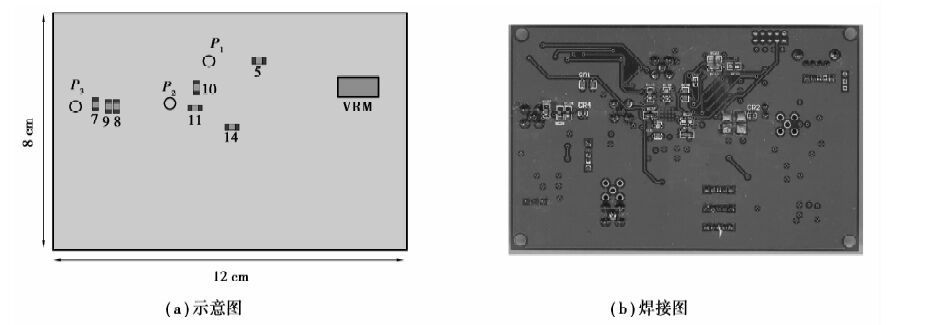
为此,采用PSO确定去耦电容种类及安装端口,如表 1所示。图 11(a)、(b)分别为电容安装位置的示意图及焊接图。
|
图 11 去耦电容的安装 Figure 11 Diagram of mounting capacitor |
| 表 1 PSO给出的电容方案 Table 1 Values and positons of decoupling capacitors |
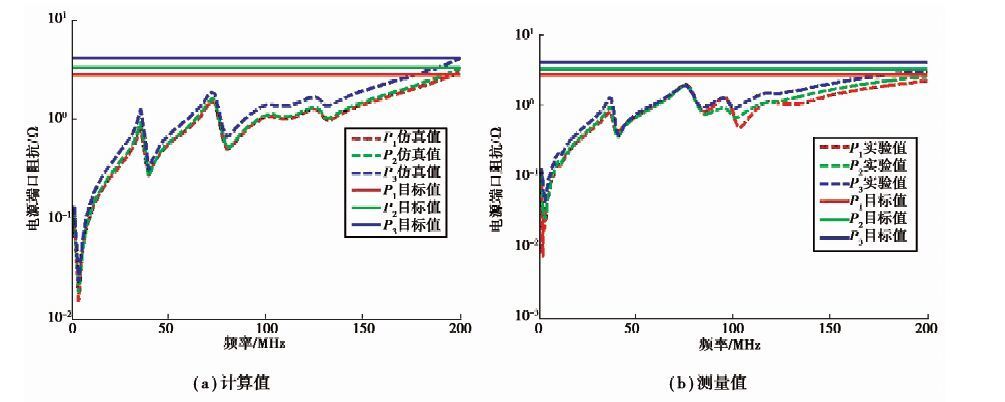
图 12(a)为安装电容后各电源端口多输入阻抗的仿真曲线,与图 10(a)比较,去耦后超标频段的阻抗值有了很大的下降,曲线较为平坦并满足目标阻抗要求,而图 12(b)的实验曲线,其趋势与图 12(a)大致相同,谐振点有些偏移,基本满足各自的目标值,这说明该电容方案是有效的。
|
图 12 去耦后电源端口的阻抗 Figure 12 PDN impedance with decoupling capacitor |
对于电源板的建模,通过设置其互补部分及虚拟节点,使解析表达式得以应用。当互补部分形状不规则时,应用有限差分法获得其阻抗特性。在互补部分较小时,与三维有限元法相比,互补模型在保证精度的同时大幅减少计算量,提高计算效率。
在此基础上将节点阻抗矩阵的求解过程嵌入到粒子群算法中,为PDN多个电源端口进行去耦电容的优化,同时,以实验板的3个受电电源端口为例,验证了这种方法在电源分配网络去耦设计中的有效性。
| [1] | Swaminathan M, Kim J, Novak I, et al. Power distribution networks for system-on-package:status and challenges[J]. IEEE Transactions on Advanced Packaging, 2004, 27(2): 286–300. DOI:10.1109/TADVP.2004.831897 |
| [2] |
冯利民, 钱照明.
电源去耦方式对数字电路板级EMC性能的影响[J]. 电工技术学报, 2007, 22(4): 14–20.
FENG Limin, QIAN Zhaoming. Influence of decoupling approach of power network on EMC performance of digital PCB[J]. Transactions of China Electrotechnical Society, 2007, 22(4): 14–20. (in Chinese) |
| [3] | Fizesan R, Pitica D. Power integrity design tips to minimize the effects of mounting inductance of decoupling capacitors[C]//13th International Conference on Optimization of Electrical and Electronic Equipment (OPTIM),2012.:IEEE, 2012:36-41. |
| [4] | Guan S W, Kuo C W, Wang C C. A novel decoupling capacitor for power integrity of quad flat nonlead (QFN) package[C]//Microwave Conference Proceedings (APMC), 2011 Asia-Pacific, Melbourne.:IEEE, 2011:1913-1916. |
| [5] | Ye X, Ko L, Li M, et al. DC power-bus design using FDTD modeling with dispersive media and surface mount technology components[J]. IEEE Transactions on Electromagnetic Compatibility, 2001, 43(4): 579–587. DOI:10.1109/15.974638 |
| [6] | Engin A, Bharath K, Swaminathan M. Multilayered finite-difference method (M-FDM) for modeling of package and printed circuit board planes[J]. IEEE Transactions on Electromagnetic Compatibility, 2007, 49(1): 441–447. |
| [7] | W u, Shiue G H, Guo W D, et al. Delaunay-Voronoi modeling of power-ground planes with source port correction[J]. IEEE Transactions on Advanced Packaging, 2008, 31(2): 303–310. DOI:10.1109/TADVP.2008.920326 |
| [8] | Youchul J, Aabert C. Hybrid analytical modeling method for split power bus in multilayered package[J]. IEEE Transactions on Electromagnetic Compatibility, 2006, 48(1): 82–94. DOI:10.1109/TEMC.2006.870701 |
| [9] | Chuntian Liu, Junfa Mao. Analysis of power-ground plane with combination of rectangle and triangle segmentation[C]//Microwave Conference, Proceedings (APMC), 2009 Asia-Pacific, Singapore.:APMC, 2009:2424-2427. |
| [10] | Siming P, Brice A. Optimization of power delivery network design for multiple supply voltages[C]//2013 IEEE International Symposium on Electromagnetic Compatibility (EMC).:IEEE, 2013:333-337. |
| [11] | Pan BH, Chu X Q, Zhang S S, et al. Fast algorithm based on self-resonant frequency for decoupling capacitor selection[J]. Electronics Letters, 2013, 49(18): 1176–1178. DOI:10.1049/el.2012.3744 |
| [12] | Shibasaka K, Kanazawa K, Yasunaga M. Decoupling-capacitor allocation problem solved by genetic algorithm[C]//Electrical Design of Advanced Packaging and Systems Symposium (EDAPS), 2013 IEEE, Nara.2012:IEEE, 2013:225-228. |
| [13] | Tripathi N, Mukherjee J, Apte R, et al. Selection and placement of decoupling capacitors in high speed systems[J]. IEEE Transactions on Electromagnetic Compatibility, 2013, 2(4): 72–78. |
| [14] |
李鑫滨, 朱庆军.
一种改进粒子群优化算法在多目标无功优化中的应用[J]. 电工技术学报, 2010, 25(7): 137–143.
LI Xinbin, ZHU Qingjun. Application of improved particle swarm optimization algorithm to multi-objective reactive power optimization[J]. Transactions of China Electrotechnical Society, 2010, 25(7): 137–143. (in Chinese) |
| [15] |
吕干云, 方奇品, 蔡秀珊.
一种基于粒子群优化算法的间谐波分析方法[J]. 电工技术学报, 2009, 24(12): 156–161.
LYU Ganyun, FANG Qipin, CAI Xiushan. A method for inter-harmonics analysis based on PSO[J]. Transactions of China Electrotechnical Society, 2009, 24(12): 156–161. (in Chinese) |
 2016, Vol. 39
2016, Vol. 39

