基于磁耦合谐振的无线电能传输技术具有传输距离大、穿透性能好、传输功率和效率高等优点,因此无线电能传输技术在工业领域受到越来越多的关注[1-2]。但是现阶段磁耦合谐振式无线电能传输技术仍存在一些亟待解决的问题,其中较关键的一个问题是传输效率。阻抗匹配网络可以有效地提高无线电能传输效率,针对这一问题国内外做了大量研究。文献[3]提出了在发射线圈和接收线圈之间加入多个中继线圈,通过改变中继线圈的相对位置,实现阻抗匹配。文献[4]分析了在多个接收线圈的情况下,交叉耦合对无线电能传输效率的影响,设计采用单匝电源线圈进行阻抗匹配。文献[5]分别在发射端和接收端采用三线圈结构,通过调节线圈间距,达到阻抗匹配和频率跟踪的效果。文献[6]通过匹配网络使整个系统的谐振频率保持不变,从而保证能量高效率传输。文献[7]随着线圈距离的改变不断调整射频源的频率,确保较高效率传输能量。文献 [8]通过升压降压变换器调节输入阻抗,减小功率反射,提高系统能量传输效率。
上述工作为阻抗匹配做了大量有益的研究,为提高传输效率提供了有益的参考,但是针对传输距离改变进行自动匹配的研究还很少,而无线电能传输在移动物体中的应用更为广泛,因此该方面的研究具有较大的现实意义。笔者针对无线电能传输过程中随着传输距离的改变,射频源输出阻抗失配的问题提出一种自动阻抗匹配的方法。在射频源和发射线圈之间加入自动阻抗匹配网络来保证射频源输出负载的稳定性。
为了提高阻抗匹配的精度和速度,提出了一种改进的粒子群算法。首先分析了自动阻抗匹配系统的结构,接着论述了改进的粒子群算法的优化思路和实现步骤,并将改进算法和传统算法进行仿真实验比较,证明了改进算法在匹配速度和匹配精度方面的优越性。最后通过实验验证了基于改进的粒子群算法的自动阻抗匹配系统,有效地提高了无线电能传输系统的效率。
1 自动阻抗匹配系统在无线电能传输系统中,线圈之间距离的改变导致系统输入阻抗发生变化。射频源采用是信号源加E类功率放大器构成。如果输入阻抗与射频源内阻不匹配的话,整个系统负载网络反射系数会很高,很容易导致功率输出低,严重的甚至可能烧坏功放。所以对磁耦合谐振式无线电能传输系统来说,阻抗匹配不仅可以保护射频源,还可以提高射频源的输出效率[9-11]。
研究系统中采用反射系数检测器检测到入射电压和反射电压并将其送进DSP控制系统的中央处理单元,经过改进粒子群算法得到电感和电容值,通过继电器开关阵列控制电容电感到达阻抗匹配。如图 1为设计的自动阻抗匹配器结构图。
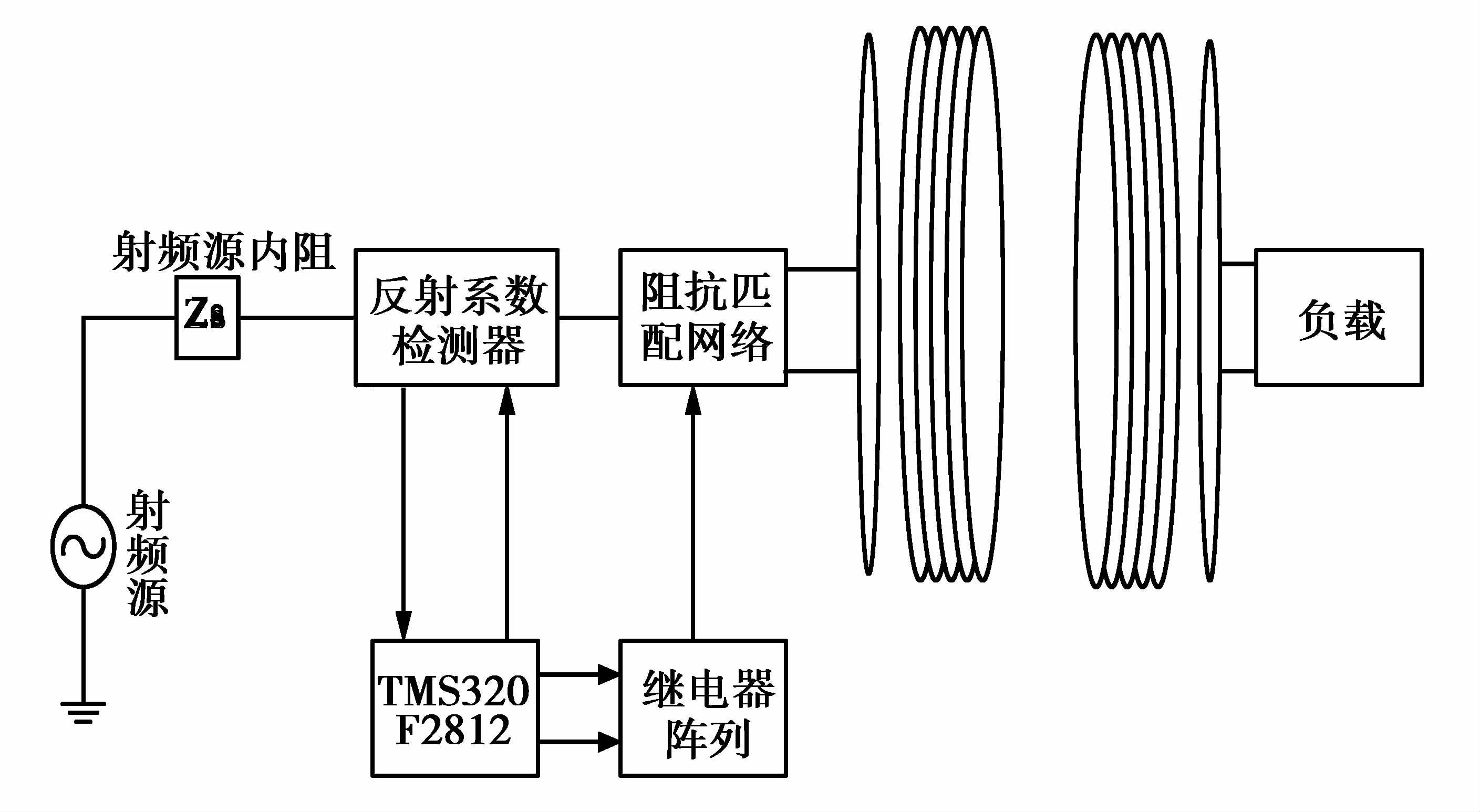
|
图 1 整体匹配装置示意图 Figure 1 The overall matching device schematic diagram |
匹配的电路有很多种结构,但Г型和反Г型比较常见,其结构也比较简单,工作也比较稳定,匹配速度快,易于操作,成本也低,笔者也采用反Г结构进行匹配。
根据图 2,分别计算各相关阻抗值
| Z1=R+jX1+jωCPR−ωCPX, | (1) |
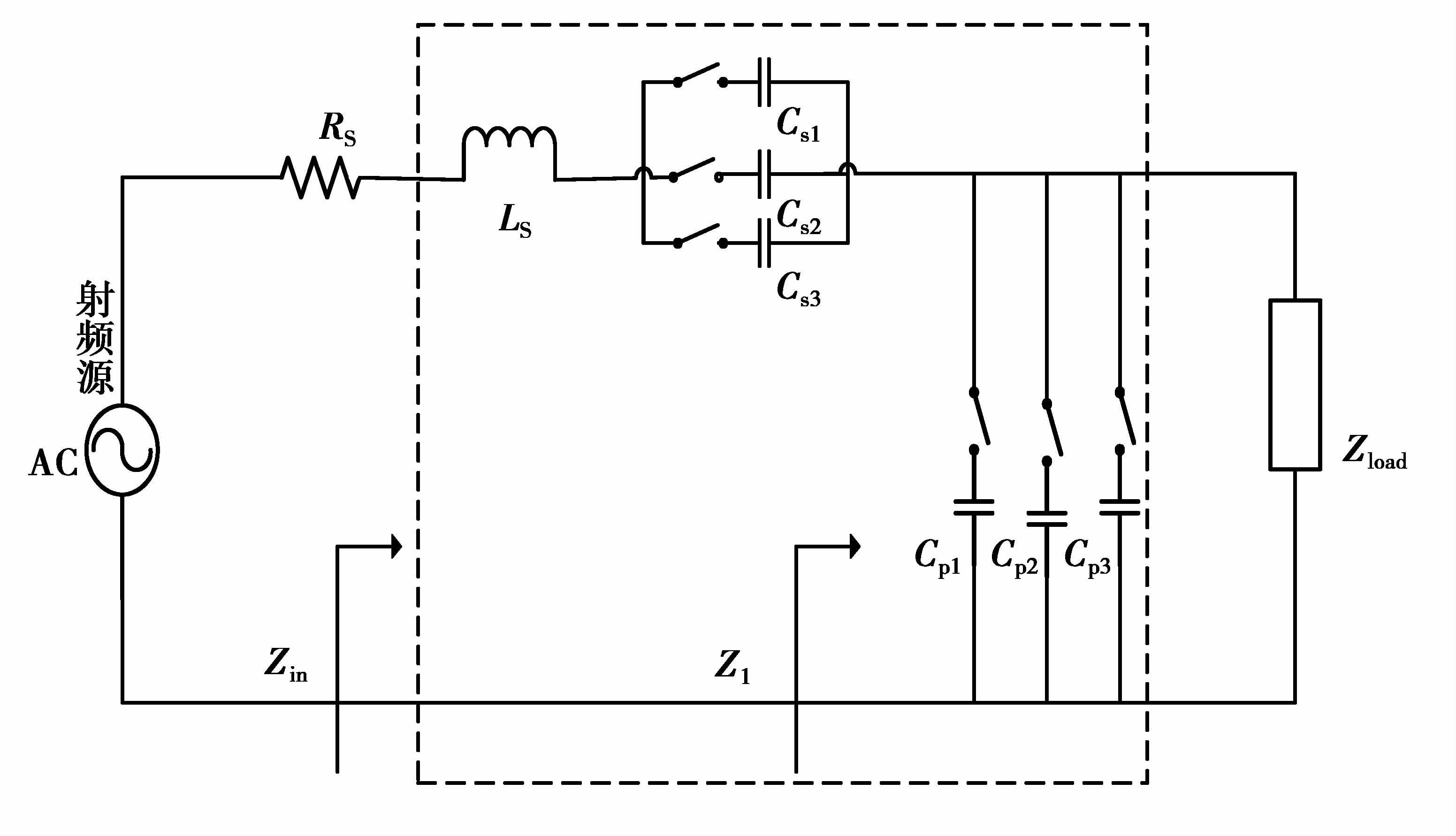
|
图 2 匹配网络原理图 Figure 2 The principle diagram of the matching network |
式中:R为负载阻抗实部值;X为负载阻抗虚部值;ω为工作频率;CP为并联臂上的电容总值。
| Zin=Z1+jωLS+1jωCS, | (2) |
式中:Zin为系统的输入阻抗;ω为工作频率;LS为串联臂上的电感值;CS为串联臂上的电容值。
将式(1)代入式(2)得输入阻抗Zin。
由以上各式可得电路反射系数
| Γ=Zin−RSZin+RS, | (3) |
式中:Γ为反射系数;RS为射频源内阻值。在理想匹配情况下反射系数接近于0。
2 改进粒子群算法研究粒子群优化算法(particle swarm optimization,PSO)是一种进化计算技术,由Eberhart博士和Kennedy博士发明,源于对鸟群捕食的行为研究。传统粒子群算法由于所有粒子的飞行方向是根据自身和全体经验决定,进化后期收敛速度明显减慢,容易陷入局部最优,将会降低自动阻抗匹配的速度和精度。针对传统粒子群算法收敛速度缓慢且容易陷入局部最优解的缺点进行了如下改进:首先传统算法的权重值是固定的,研究的权重值根据粒子的分布可以自动调节。然后将混沌算法与传统粒子群算法相结合,对局部最优粒子进行混沌搜索。最后针对越界粒子提出了采用惩罚函数的方案,始终不超出规定的自变量范围[12-15]。
将上述改进粒子群算法应用到无线电能传输系统时,结合无线电能传输装置中阻抗匹配的特点,每个粒子代表当前匹配网络的状态,笔者采用二维匹配网络,结构简单,匹配速度快。用P来表示每个粒子,那么任何一个粒子可以用下式表示
| Pi=(Csi,Cpi)。 | (4) |
该式子将粒子群算法和阻抗匹配相结合,Pi代表一个二维粒子,Csi和Cpi分别代表串联臂和并联臂的电容总值,即需要求解的未知变量。
PSO算法首先初始化一群随机粒子(随机解),然后粒子们就追随当前的最优粒子在解空间中搜索,即通过迭代找到最优解。假设该二维搜索空间中第i个粒子的位置和速度分别为Xi=(xi,1xi,2)和Vi=(vi,1vi,2),将改进的粒子群算法和阻抗匹配的实际模型相结合,二维粒子的位置坐标和阻抗匹配的串联并联电容值二者存在一一对应的关系。即
| Pi=Xi且Csi=xi,1,Cpi=xi,2, | (5) |
Csi,Cpi和系统输入阻抗的关系如下
| Zin=R+jX1+jωCpiR−ωCpiX+jωLS+1jωCsi。 | (6) |
根据最大功率传输定理,即当负载发生变化时,实时调节CS,CP的值从而实现射频源内阻和系统输入阻抗Zin之间的共轭匹配,因此可得阻抗匹配的适应值函数fitness
| fitness=|real(Zin−RS)|2+|imag(Zin)|2, | (7) |
式中:Zin为系统输入阻抗;RS为射频源内阻(RS=50 Ω)。理想匹配结果Zin实部为50 Ω,虚部为0 Ω。
在每一次迭代中,粒子根据如下的公式来更新自己的速度和位置,从而不断调整串联并联的电容值大小。
| {vi,j(t+1)=ωvi,j(t)+c1r1(pi,j−xi,j(t))+c2r2(pg,j−xi,j(t));xi,j(t+1)=xi,j(t)+vi,j(t+1),i,j=1,2, | (8) |
式中:w为惯性权重;c1和c2为正的学习因子;r1和r2为0到1之间均匀分布的随机数;pi,j为粒子自身的最优位置;pg,j为全局最优位置;xi,j(t)为粒子的当前位置。
传统粒子群算法的权重值是固定的,当各粒子的目标值趋于一致或趋于局部最优时,将使惯性权重增加,有利于提高算法的全局寻优能力,而各微粒的目标值比较分散时,将使权重减小,提高局部寻优能力。权重改进公式如下
| w={wmin−(wmax−wmin)∗(f−fmin)(favg−fmin),f≤favg;wmax,f>favg, | (9) |
式中:wmax和wmin分别表示w的最大值和最小值;f表示粒子当前的目标函数值;favg和fmin分别表示当前所有微粒的平均目标值和最小目标值。
接着将混沌算法和传统粒子群算法相结合,根据粒子群搜索结果判断是否陷入局部最优,如果陷入则对适应值函数最好的20%的微粒执行混沌局部搜索,并更新pbest和gbest。混沌搜索公式如下
| {sk + 1j = 4skj (1−skj ),j = 1,2,…,n;xk + 1j =xmin ,j + sk + 1j (xmax,j −xmin,j ),j=1,2,...,n。 | (10) |
式中:skj为xkj映射到0到1之间的混沌变量。
最后在传统粒子群算法的基础上加入惩罚函数。对于越界的粒子进行处理,增加目标函数值,继续搜索。惩罚函数公式如下
| {ifxi,j<xmin,j;result=result+(xi,j-0)2;ifxi,j>xmax,j;result=result+(xi,j-0)2 | (11) |
式中:xmin和xmax分别为x的下限值和上限值。
综上所述,改进的粒子群算法流程图如图 3。
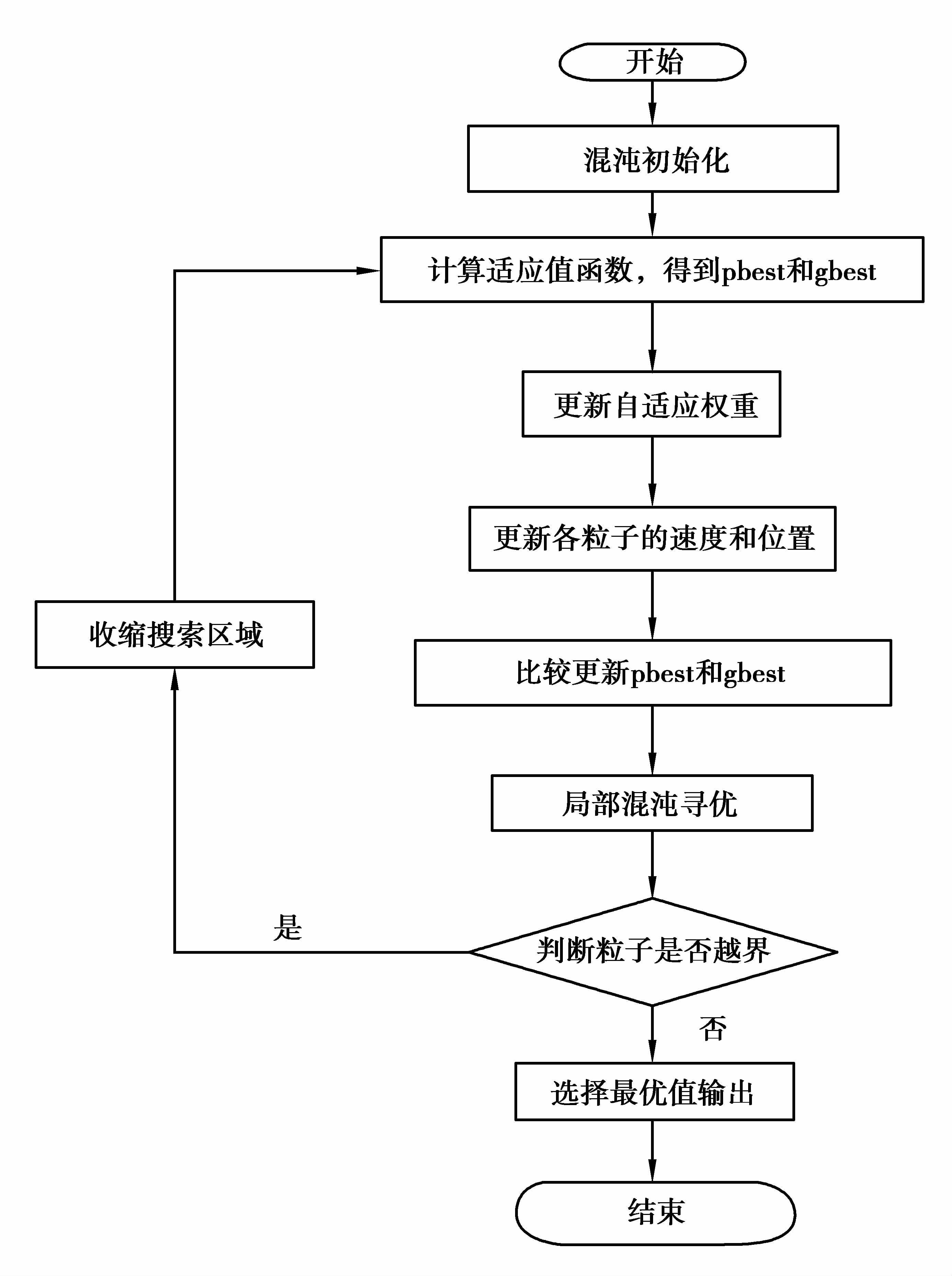
|
图 3 改进粒子群算法流程图 Figure 3 Improved particle swarm algorithm flow chart |
为了使改进粒子群算法(GPSO)和基本粒子群算法(PSO)在相同条件下比较,表 1对参数设置如下:
| 表 1 参数设置 Table 1 Parameter settings |
将射频源频率设定为3.22 MHz,该频率为线圈的谐振频率,设定相应的初始区间相同CS=[1E-12,1E-2],CP=[1E-12,1E-2]。迭代次数为100、200、300,学习因子c1=c2=2。在matlab上进行程序仿真试验。
随着迭代次数的增加,阻抗匹配的精度逐渐增加,在迭代次数相同的情况下,横向对比,改进的粒子群算法相对基本粒子群算法的阻抗匹配精度高104,最高可达到108,表明改进的粒子群算法的精度远远超过基本粒子群算法,由此得出结论:GPSO和PSO相比更满足无线电能传输系统Γ型匹配网络的精确性。
无线电能传输的阻抗匹配网络不仅要求精度高而且具有实时性,随着传输距离的改变,快速跟踪调节。为了更形象地对比2种算法,以线圈距离23 cm,用ZV-Z170矢量网络分析仪测得Zload为34+j82 Ω,图 4给出了2种算法的收敛对比曲线。
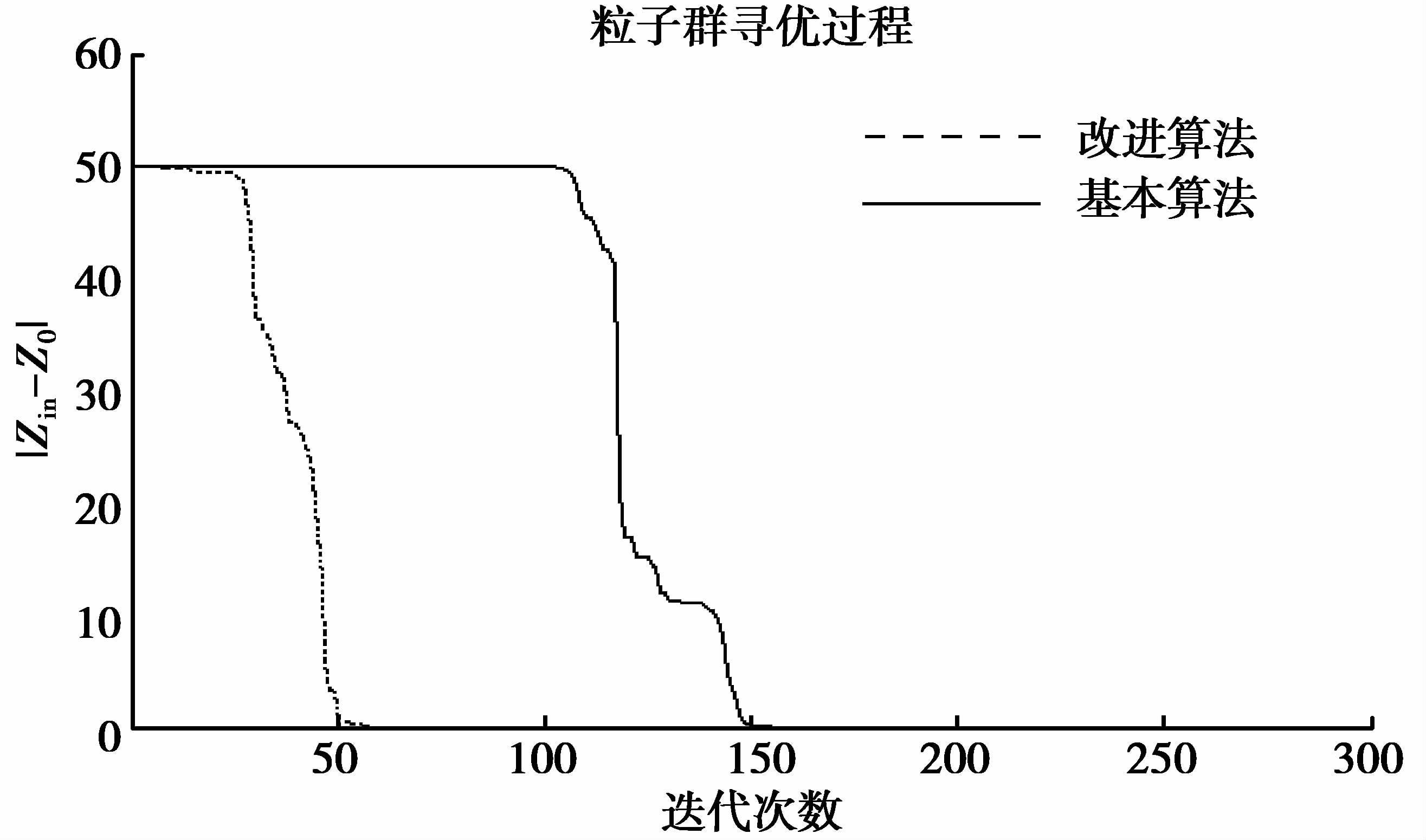
|
图 4 改进算法与基本算法的迭代次数对比曲线 Figure 4 The convergence speed comparison curve of the improved algorithm and the traditional algorithm |
从图中比较可知,GPSO一开始的下降速度就比PSO要快些,并至少比PSO提前100步收敛。
从表 2可以看出改进粒子群算法的精度提高,图 4反映了改进粒子群算法的收敛速度加快,从而验证了上节所提改进优化措施的有效性。
| 表 2 固定频率点线圈距离变化时的阻抗匹配对比情况 Table 2 Comparison of fixed frequency point impedance matching coil when distance changing |
为了反映改进粒子群算法的优越性,图 5描绘了粒子寻优的动态过程,开始种群相对分散,随着迭代次数的增加,不断进行自我学习和种群交流,逐渐向目标值聚集靠拢。
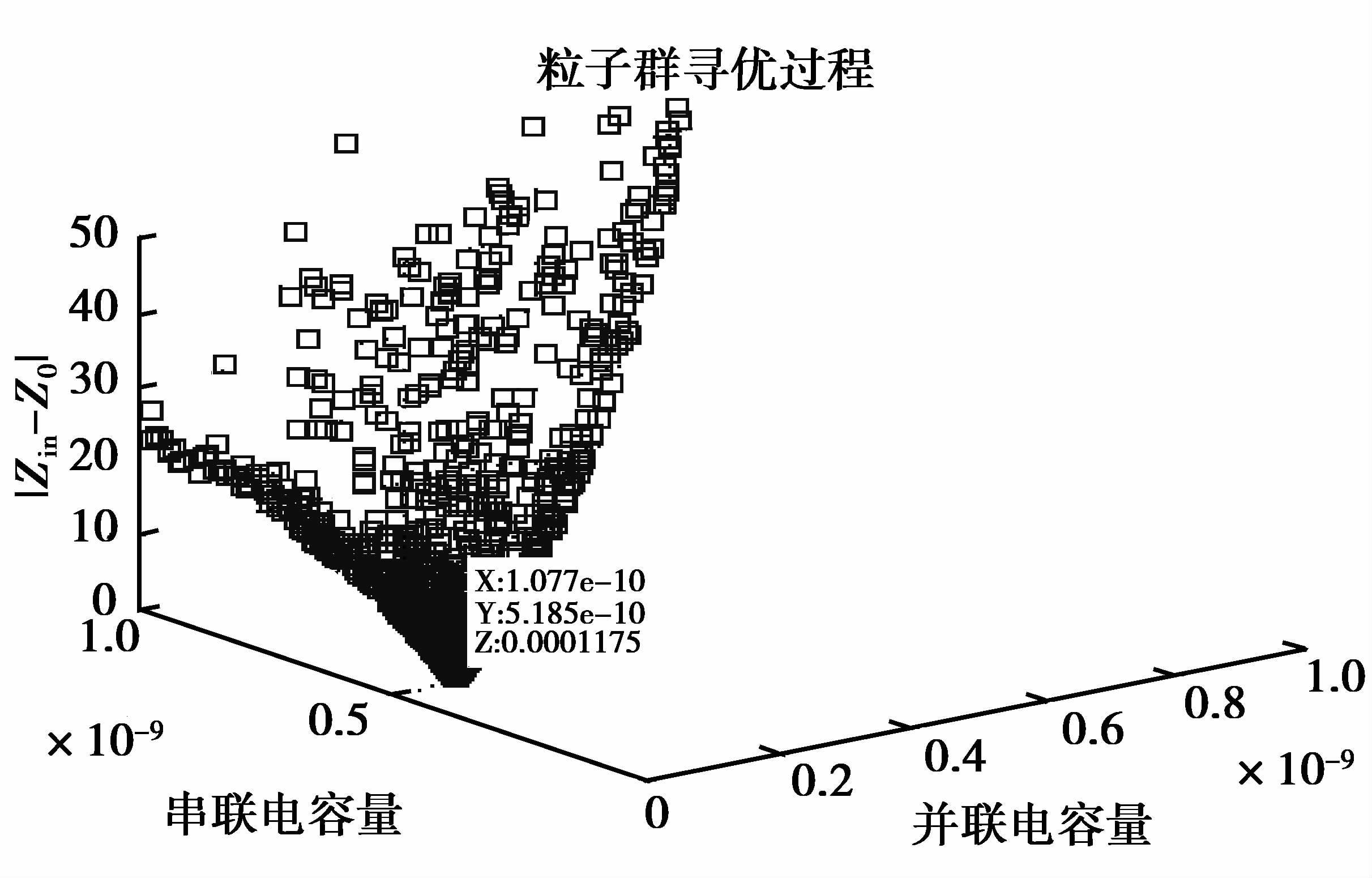
|
图 5 整体迭代寻优过程 Figure 5 Global iterative optimization process |
最终所有粒子寻优结果趋于稳定,每个粒子对应的串联臂和并联臂上的电容值结果如图 6 所示。
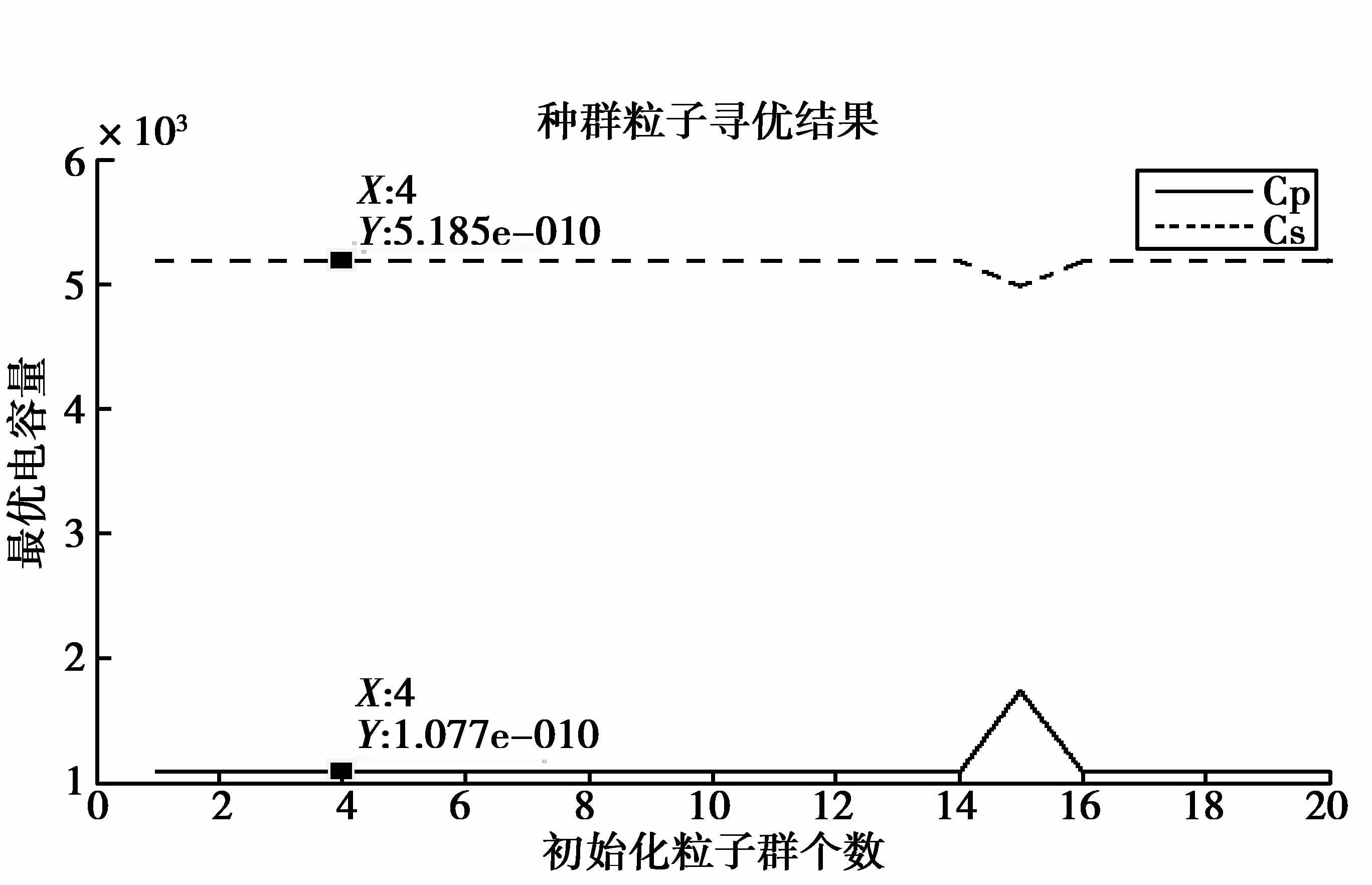
|
图 6 改进算法寻优结果 Figure 6 The result of improved algorithm optimizatio |
将上述改进的粒子群算法嵌入阻抗匹配网络,流程图如图 7所示。匹配网络的各项参数通过检测模块传输给优化适应值函数,通过计算适应度来判断是否达到要求,如果没有达到要求,则将各项参数和适应值都放到改进粒子群算法中,得到新的串并联电容值。如果达到要求则不用更新电容值。
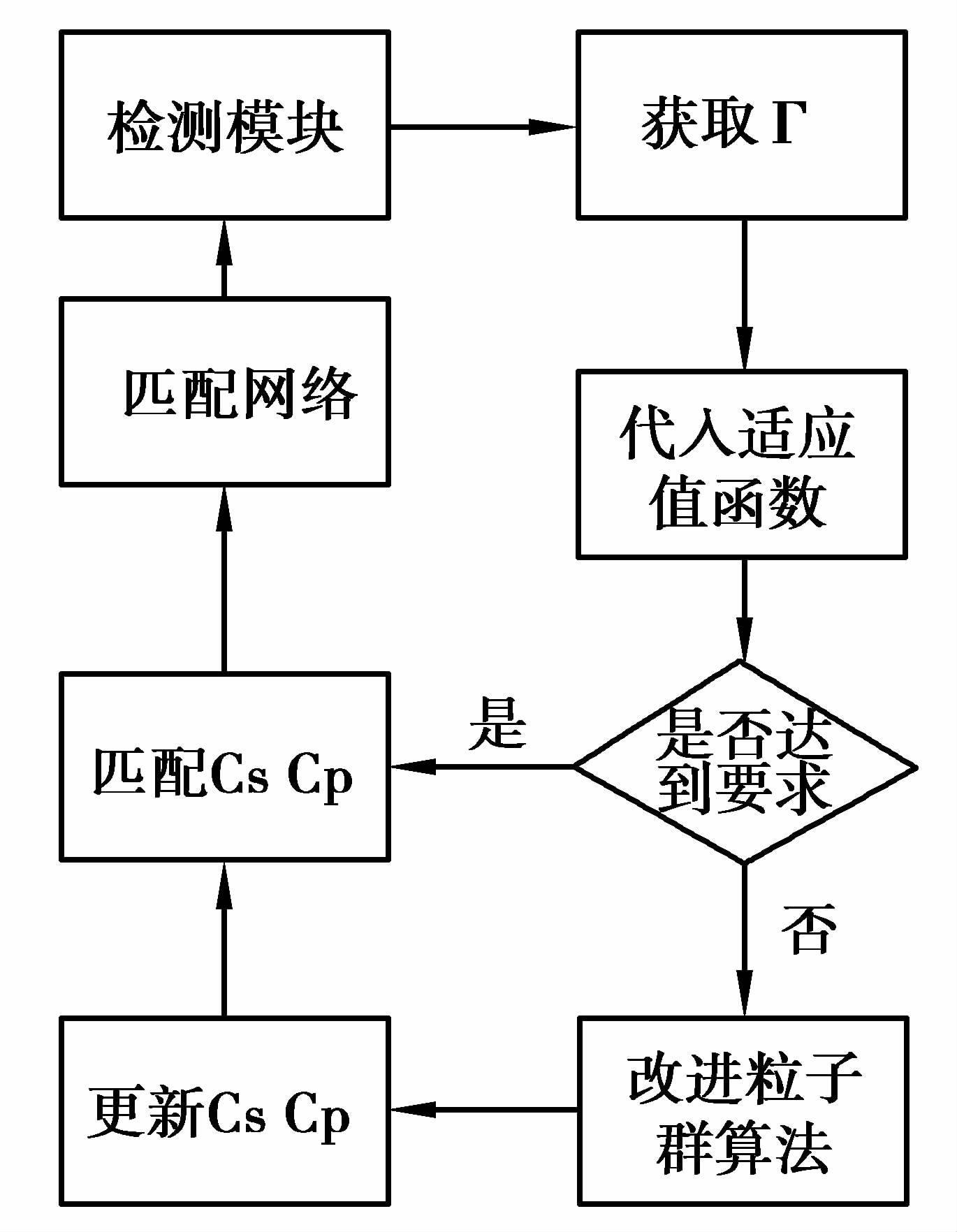
|
图 7 算法嵌入流程图 Figure 7 Algorithm embedding flow chart |
将自动阻抗匹配网络置于射频源和发射线圈之间,通过继电器阵列控制接入的电容电感量实现自动匹配(如图 8所示),将反射能量降到最低。为了得到系统的传输效率,在射频源和感应线圈之间接入通过式功率计,同时检测得到射频源的输出功率值和反射功率值,由式(12),计算系统的传输效率。
| η=1P反P入 | (12) |

|
图 8 自适应阻抗匹配器 Figure 8 Adaptive impedance matching |
调节信号源的输出频率和幅值,保持输出频率为3.24 MHz不变,输出电压峰值为3 V保持不变。逐步增加2个谐振线圈之间的传输距离d,利用通过式功率计检测无线电能传输装置在不同距离下的入射功率和反射功率,计算得到射频源的输出效率。阻抗匹配前后接受效率对比如图 9所示。
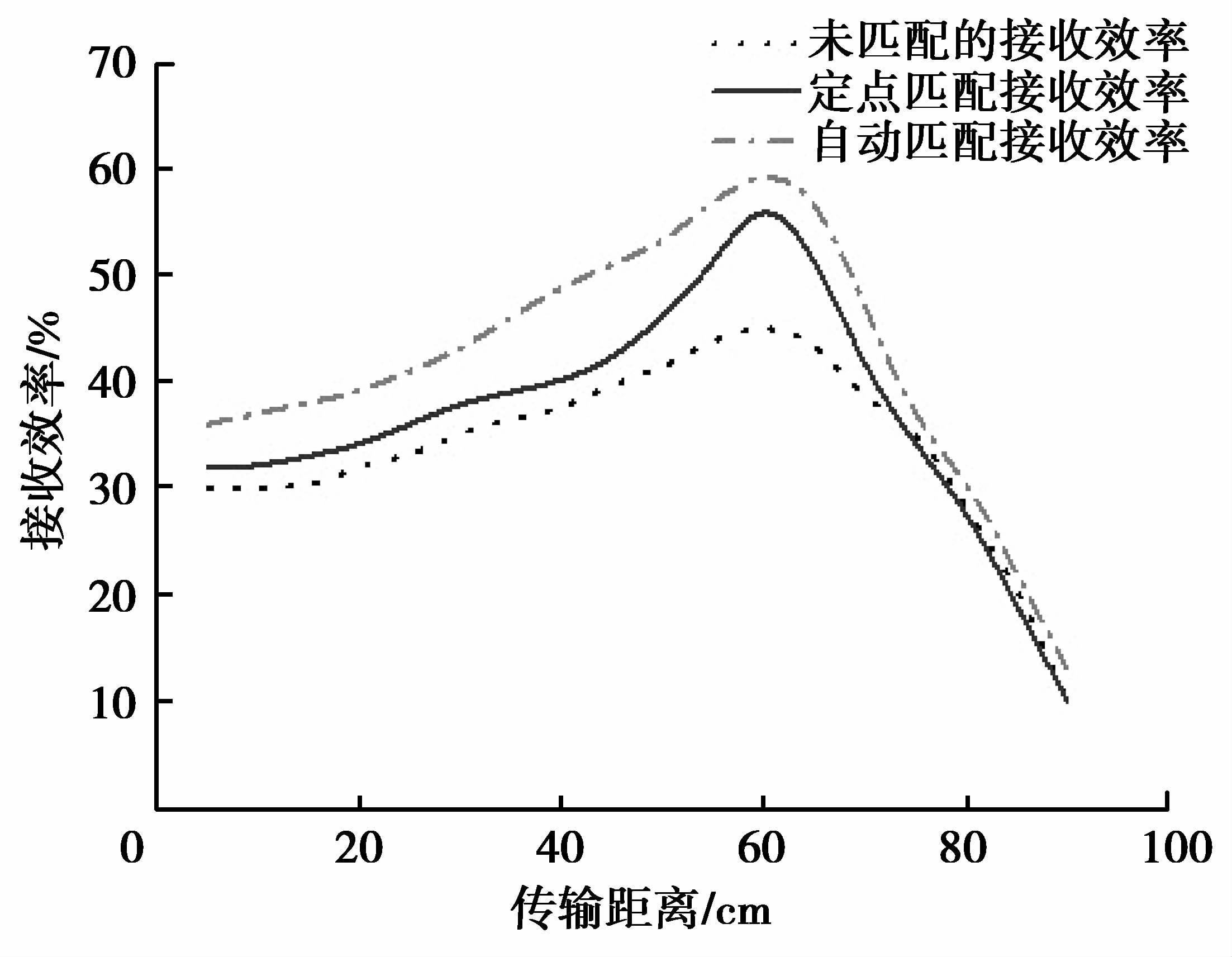
|
图 9 自适应阻抗匹配距离实验 Figure 9 Adaptive impedance matching distance experiment |
从图 9可以看出,自适应阻抗匹配装置整体的传能效果比未匹配和定点匹配装置的传能效果都好。当线圈距离大于70 cm时,处于欠耦合状态,能量传输效率都明显降低;当线圈距离在60 cm左右时,处于临界耦合状态,自动匹配的效率明显高于未匹配和定点匹配装置;当线圈距离低于50 cm,处于欠耦合状态由于频率分裂使系统效率降低,但自动匹配装置的传输效率最高,定点匹配其次。实验结果证明随着距离的改变,自动阻抗匹配系统有效地提高了系统的传输效率。
4 结 论通过仿真结果可知改进粒子群算法无论在匹配精度还是匹配速度方面均优于基本粒子群算法,接着将改进算法嵌入到自动阻抗匹配系统中,通过对比可知,自动阻抗匹配的效果最好,提高了系统的效率。由于反Γ型匹配网络存在匹配禁区,下一步将研究Π和Τ匹配网络,并将其嵌入到自动阻抗匹配系统中。本研究结果将为磁耦合谐振式无线电能传输相关产品的研究提供理论和实验依据。
| [1] |
赵争鸣, 张艺明, 陈凯楠.
磁耦合谐振式无线电能传输技术新进展[J]. 中国电机工程学报, 2013, 33(3): 1–13.
ZHAO Zhengming, ZHANG Yiming, CHEN Kainan. New progress of magnetically-coupled resonant wireless power transfer technology[J]. Proceedings of the CSEE, 2013, 33(3): 1–13. (in Chinese) |
| [2] |
黄学良, 吉青晶, 谭林林, 等.
磁耦合谐振式无线电能传输系统串并式模型研究[J]. 电工技术学报, 2013, 28(3): 171–187.
HUANG Xueliang, JI Qingjin, TAN Linlin, et al. Study on series-parallel model of wireless power transfer[J]. Transactions of China Electrotechnical Society, 2013, 28(3): 171–187. (in Chinese) |
| [3] | Lee J, Lim Y, Ahn H, et al. Impedance-matched wireless power transfer systems using an arbitrary number of coils with flexible coil positioning[J]. IEEE Antennas & Wireless Propagation Letters, 2014, 13(6): 1207–1210. |
| [4] | Kim J,Son H C,Kim D H,et al. Impedance matching considering cross coupling for wireless power transfer to multiple receivers[C]//Wireless Power Transfer:IEEE, 2013:226-229. |
| [5] | Ricketts D S, Chabalko M, Hillenius A. Tri-Loop impedance and frequency matching with high-resonators in wireless power transfer[J]. IEEE Antennas & Wireless Propagation Letters, 2014, 13(13): 341–344. |
| [6] | Beh T C, Kato M, Imura T, et al. Automated impedance matching system for robust wireless power transfer via magnetic resonance coupling[J]. IEEE Transactions on Industrial Electronics, 2013, 60(9): 3689–3698. DOI:10.1109/TIE.2012.2206337 |
| [7] | Fu W Z, Zhang B, Qiu D Y. Study on frequency-tracking wireless power transfer system by resonant coupling[J]. World of Inverters, 2009: 2658–2663. |
| [8] | Fu M F, Yin H, Zhu X N, et al. Analysis and tracking of optimal load in wireless power transfer systems[J]. IEEE Transactions on Power Electronics, 2015, 30(7): 3952–3963. DOI:10.1109/TPEL.2014.2347071 |
| [9] |
张献, 杨庆新, 陈海燕, 等.
电磁耦合谐振式无线电能传输系统的建模、设计与实验验证[J]. 中国电机工程学报, 2012, 32(21): 153–158.
ZHANG Xian, YANG Qingxin, CHEN Haiyan, et al. Modeling and design and experimental verification of contactless power transmission systems via electromagnetic resonant coupling[J]. Proceedings of the CSEE, 2012, 32(21): 153–158. (in Chinese) |
| [10] |
李阳, 杨庆新, 闫卓, 等.
磁耦合谐振式无线电能传输系统的频率特性[J]. 电机与控制学报, 2012, 16(7): 7–11.
LI Yang, YANG Qingxin, YAN Zhuo, et al. Frequency characteristics of wireless power transfer system via coupled magnetic resonances[J]. Motor and Control Journal, 2012, 16(7): 7–11. (in Chinese) |
| [11] |
李阳, 杨庆新, 闫卓, 等.
磁耦合谐振式无线电能传输方向性分析与验证[J]. 电工技术学报, 2014, 29(2): 197–203.
LI Yang, YANG Qingxin, YAN Zhuo, et al. Analysis and validation on characteristic of orientation in wireless power transfer system via coupled magnetic resonances[J]. Transactions of China Electrotechnical Society, 2014, 29(2): 197–203. (in Chinese) |
| [12] |
傅文珍, 张波, 丘东元, 等.
自谐振线圈耦合式电能无线传输的最大效率分析与设计[J]. 中国电机工程学报, 2009, 29(18): 21–26.
FU Wenzhen, ZHANG Bo, QIU Dongyuan, et al. Analysis and design of the maximum efficiency of the coupling of the self resonant coil in the wireless transmission[J]. Proceedings of the CSEE, 2009, 29(18): 21–26. (in Chinese) |
| [13] |
孙跃, 夏晨阳, 戴欣, 等.
感应耦合电能传输系统互感耦合参数的分析与优化[J]. 中国电机工程学报, 2010, 30(33): 44–50.
SUN Yue, XIA Chenyang, DAI Xin, et al. Analysis and optimization of mutual inductance for inductively coupled power transfer system[J]. Proceedings of the CSEE, 2010, 30(33): 44–50. (in Chinese) |
| [14] |
刘修泉, 曾昭瑞, 黄平.
空心线圈电感的计算与实验分析[J]. 工程设计学报, 2008, 15(2): 149–153.
LIU Xiuquan, ZENG Zhaorui, HUANG Ping. Numerical and experimental analysis on performances of coreless coil inductance[J]. Journal of Engineering Design, 2008, 15(2): 149–153. (in Chinese) |
| [15] |
朱春波, 于春来, 毛银花, 等.
磁共振无线能量传输系统损耗分析[J]. 电工技术学报, 2012, 27(4): 13–17.
ZHU Chunbo, YU Chunlai, MAO Yinhua, et al. Analysis of the loss of magnetic resonant wireless power transfer[J]. Transactions of China Electrotechnical Society, 2012, 27(4): 13–17. (in Chinese) |
 2016, Vol. 39
2016, Vol. 39



