2. 天津工业大学 电工电能新技术天津市重点实验室, 天津 300387
2. Key Laboratory of Advanced Electrical Engineering and Energy Technology, Tianjin Polytechnic University, Tianjin 300387, P. R. China
电磁超声换能器(electromagnetic acoustic transducer,EMAT)与传统的压电超声换能器相比,因不需要耦合剂,从而避免了耦合剂带来的诸多不利影响。EMAT通过电磁耦合的方式直接在试件内产生超声波,大大提高了检测的精度与灵活性[1]。针对现代科技发展对无损检测技术的需求,电磁超声技术以其高效、灵活及不与被测物体接触等特点日益成为研究的热点[2]。
然而,电磁超声兰姆波在同一激发条件下存在多模式和频散现象,且信号较弱[3]。多模式现象会使接收到的回波信号复杂并且混乱,因而无法分辨各模式的波[4];随着兰姆波传播距离的增加,回波信号会因为频散现象而发生重叠,造成检测能力下降[5];试件中信号强度较弱使得电磁超声系统对缺陷的识别和检测能力降低,从而限制了电磁超声换能器的发展[6]。国内外学者针对电磁超声兰姆波信号较弱的问题展开了大量研究并取得了一些成果。Jian等[7]通过在EMAT的线圈和永磁铁之间增加一层铁氧体支撑板来增强试件中的涡流和洛仑兹力分布。Kim等[8]在被测试件上放置一个圆形镍带,提高了曲折线圈EAMT激发Lamb波的声场指向性。高松巍等[9]通过改变线圈间距、改变线圈提离距离和改变永磁铁的尺寸来提高EMAT的换能效率。王淑娟等[10]采用有限元仿真软件对兰姆波EMAT进行了建模分析,并通过正交试验方法优化了EMAT的参数,使优化后的EMAT换能效率较原来提高了25.2%。
在电磁超声技术已有发展的基础上,从兰姆波信号强度较弱方面着手,提出了一种使用超微晶带材优化EMAT磁路的方法,通过提高被测试件中涡流的强度和磁场的分布,进而增强回波信号强度,为电磁超声Lamb波换能器优化设计提供理论基础。
1 超微晶优化磁路增强回波信号机理电磁超声换能器由3部分组成,分别为线圈、磁铁、被测试件[11]。本文中试件为铝合金板材,其电磁超声换能机理以洛仑兹力为主[12]。在发射过程中,线圈中通入高频电流,高频电流会在空气和铝板中产生一个与发射电流频率相同的交变磁场,进而在导体集肤深度内感生出与线圈中的电流方向相反、频率相同的涡流[13-14]。当空间中存在一外加静态偏置磁场时,涡流和该静态磁场相互作用将会产生洛仑兹力,在洛仑兹力的作用下,铝板表面就会产生周期性的振动和弹性形变,当这种振动能量以波的形式沿试件传播时,就完成了电磁超声的发射[15]。同时,在发射过程中,提供静磁场的永磁铁表面也会感生出涡流,如图 1(a)所示。这一涡流将影响试件中的涡流,进而影响试件中洛仑兹力作用下引起被测试件表面的振动和弹性形变,从而影响EMAT的换能效率[16-17],而且磁铁中也会产生一定幅值的超声波,在一定条件下也会对接收回波产生干扰。超微晶带材具有初始磁导率高、高频性能突出、损耗低、矫顽力低、饱和磁感应强度高等优点。利用超微晶带材的这些优点,将超微晶带材做成若干一定尺寸的矩形叠片,沿z轴方向垂直于线圈排列,放置在永磁铁和线圈之间,从而削弱永磁铁表面涡流,以达到优化磁路增强信号强度的目的,如图 1(b)所示。通过优化EMAT的结构,改变静磁场分布并将永磁铁表面的涡流减小或消除,从而在一定程度上提高EMAT的换能效率。
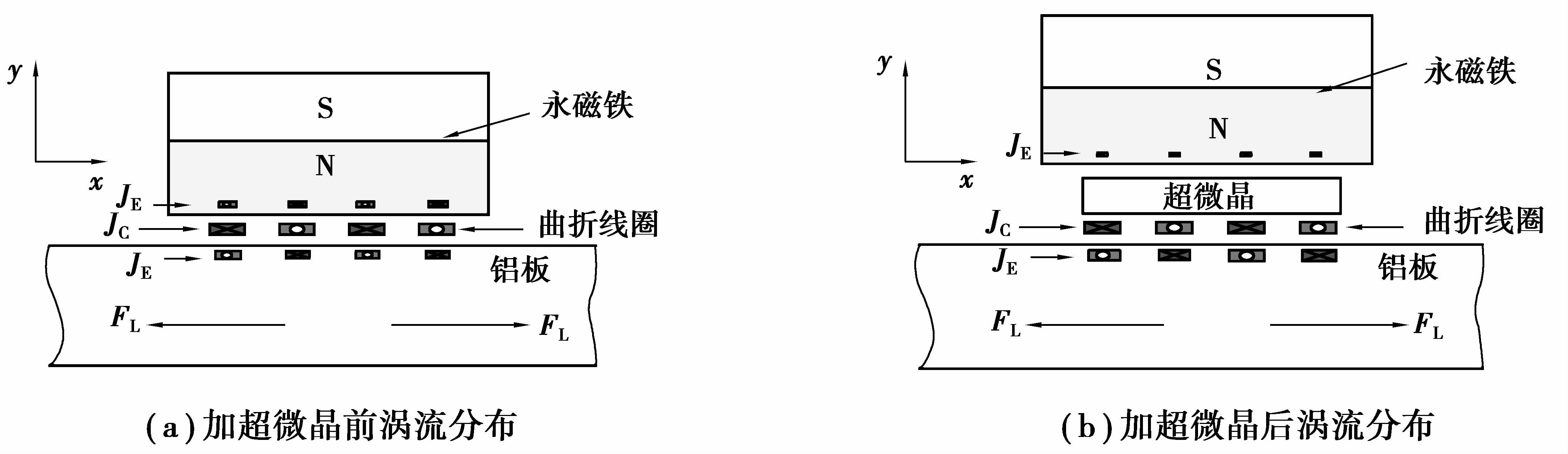
|
图 1 优化前后EMAT涡流分布示意图 Figure 1 The eddy current distribution before and after optimization of EMAT |
当线圈产生的交变磁场穿过磁铁时,会在其集肤层内感生出涡流,进而会对试件中的涡流产生一定的影响。笔者采用叠片式超微晶作为对永磁铁中磁场的磁屏蔽,以减小磁铁中的涡流,其结构如图 2所示。
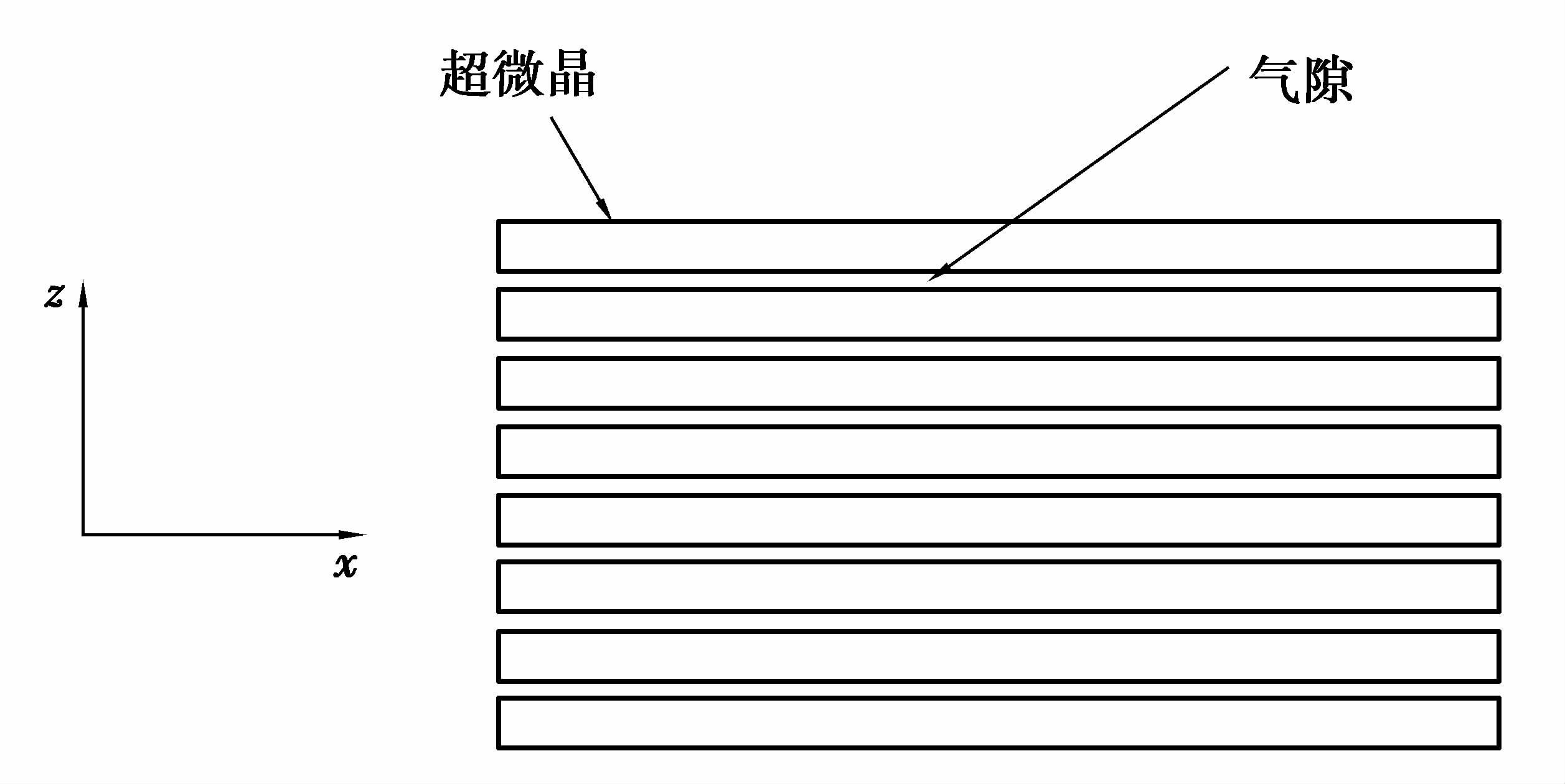
|
图 2 超微晶叠片示意图 Figure 2 The diagram of ultracrystalline lamination |
对叠片式超微晶电参数进行等效处理[18],其等效磁导率推导过程如下:
1) 超微晶磁屏蔽在叠积方向,即z轴方向,叠片与叠片间气隙的磁阻形成串联,如图 3所示。
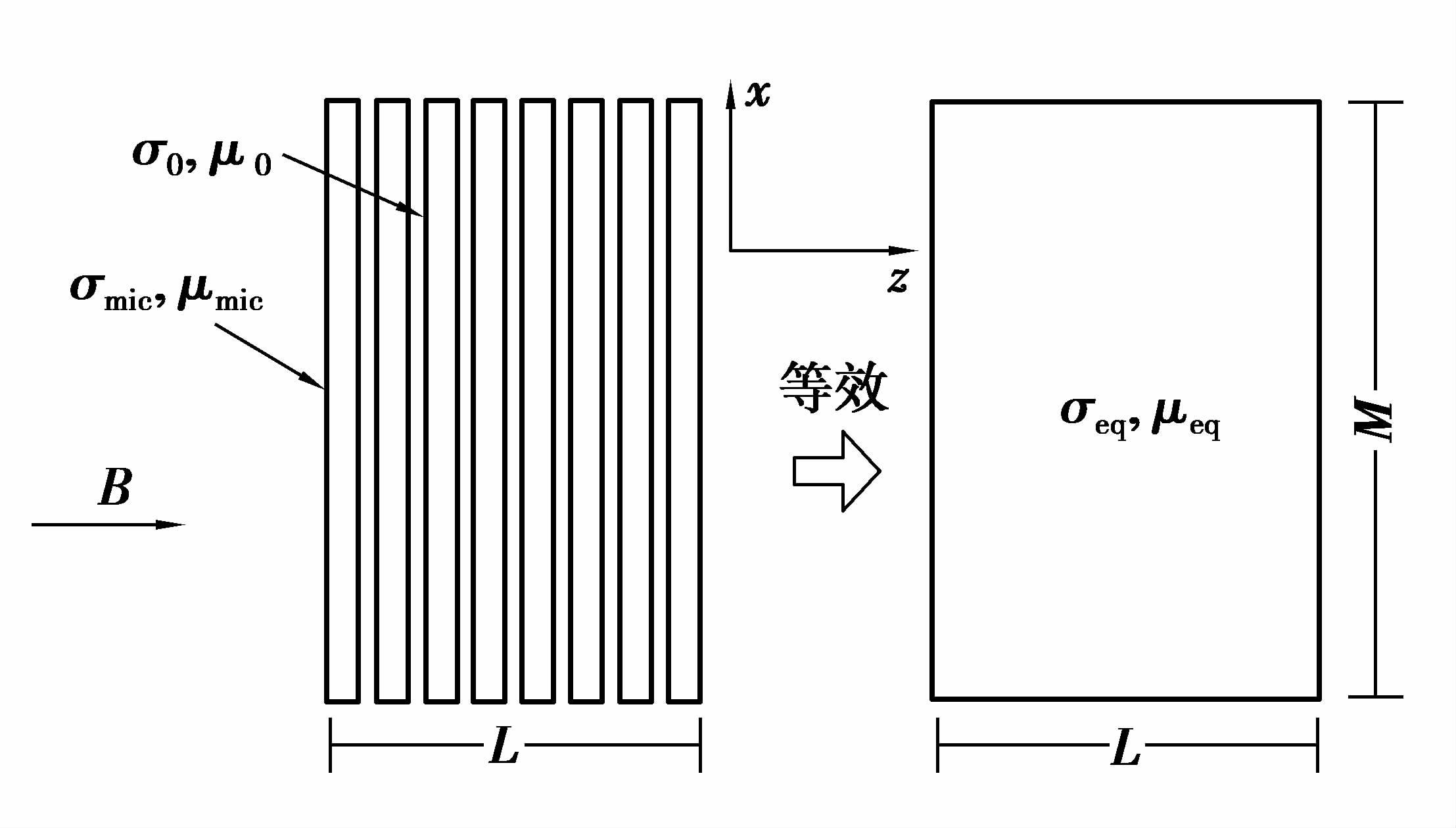
|
图 3 叠片方向电参数等效示意图 Figure 3 The electrical parameters of equivalent structure in laminated direction |
根据串联磁阻原理可得:
| Req=Rmic+Rair, | (1) |
其中:
式中:μeq为等效磁导率;μmic为超微晶的磁导率;μ0为真空中的磁导率;L为超微晶叠片组厚度;M为超微晶叠片组宽度;Cf为叠片系数,Cf<1。
又μmic=μrμ0,则等效相对磁导率为
| μr_eq=μeqμ0=μrCf+(1−Cf)μr, | (2) |
由于μr>>Cf,则上式可化简为
| μr_eq=1(1−Cf) | (3) |
2) 超微晶磁屏蔽在平行叠片方向,即x方向,叠片与叠片间的磁阻形成并联,如图 4所示。
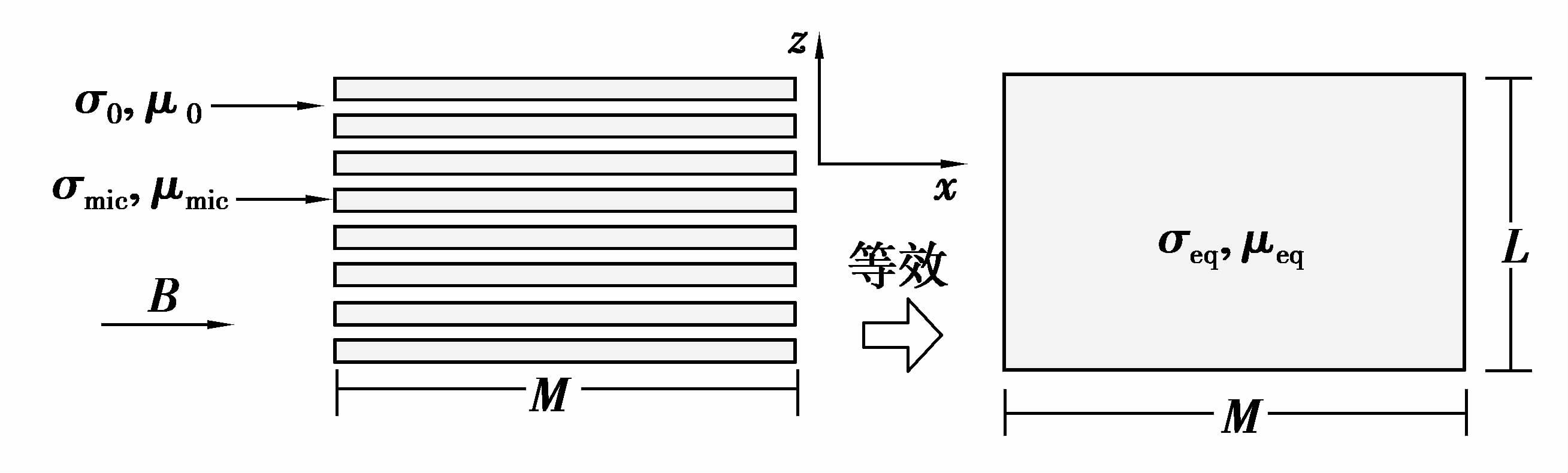
|
图 4 平行叠片方向电参数等效示意图 Figure 4 The electrical parameters of equivalent structure in parallel laminated direction |
根据并联磁阻原理可得:
| 1Req=1Rmic+1Rair, | (4) |
其中:
则等效相对磁导率为
| μr_eq=μrCf+(1−Cf), | (5) |
由于μr>>1-Cf,则上式可化简为
| μr_eq=μrCf。 | (6) |
因此,超微晶叠片磁屏蔽的等效磁导率各项异性,可写成:
| μ=(Cfμmicx000Cfμmicy000μ01−Cf)。 | (7) |
由于单片超微晶片厚度很小,再加上片与片之间的绝缘,在叠积方向(z轴方向)可认为电导率为零。因此,超微晶叠片磁屏蔽的等效电导率各项异性,可写成:
| σ=(Cfσmic000Cfσmic0000)。 | (8) |
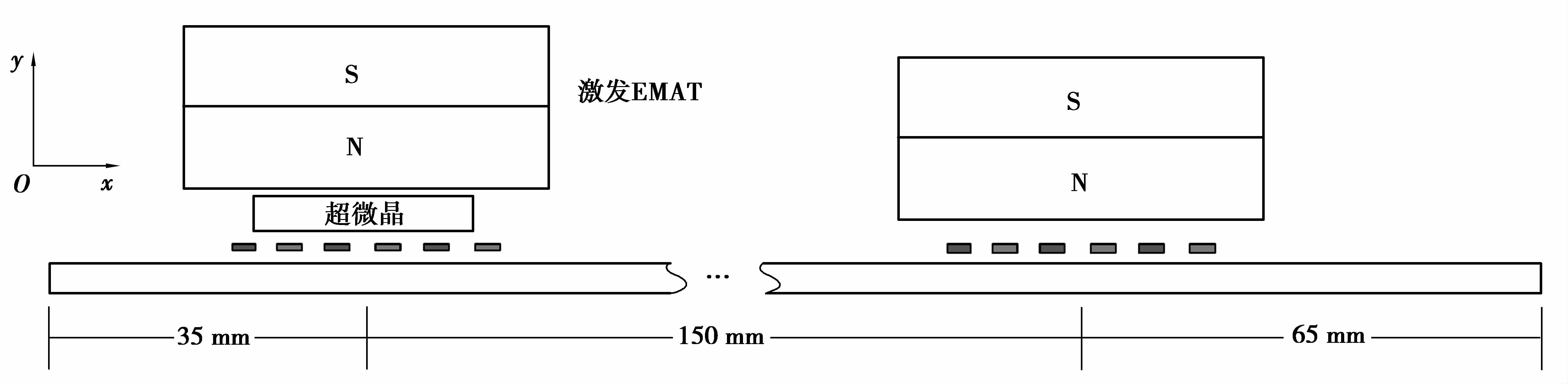
EMAT激发与接收二维有限元仿真模型如图 5所示,铝板的尺寸为250 mm×1 mm;永磁铁的尺寸为10 mm×10 mm,充磁方向为y轴方向,采用N35型钕铁硼材料,剩余磁通密度为1.2T;采用曲折线圈,导线匝数为1匝,宽度为0.2 mm,厚度为50 μm,线圈周期数为3;曲折线圈与铝板之间的提离距离为0.3 mm;磁铁和线圈之间的距离为0.4 mm;超微晶叠片高为1 mm,叠片宽度为3.5~6 mm不等;激发与接收EMAT之间的距离为150 mm。在1 MHz激励频率下,EMAT将在1 mm厚铝板中同时激发出A0和S0两种模式的Lamb波,其群速度分别是:3 160 m/s和5 170 m/s,导线间距按A0模式进行设计,即线间距为1.17 mm。
|
图 5 EMAT二维有限元模型示意图 Figure 5 Two-dimensional finite element model of EMAT |
加超微晶之前的EMAT二维有限元模型如图 1(a)所示,磁铁和试件间距为0.7 mm;加超微晶之后的EMAT二维有限元模型如图 1(b)所示,磁铁和试件间距为1.7 mm。
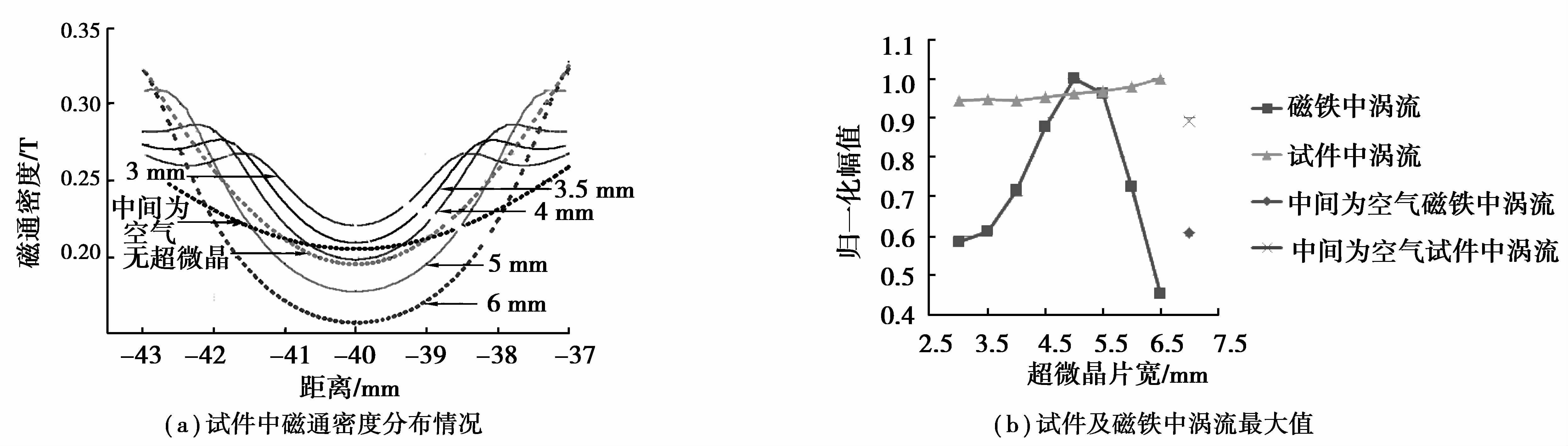
超微晶叠片的使用,一方面减小了涡流在超微晶和磁铁中的分布,另一方面也使磁铁和试件的提离距离增加,势必会对试件中的静磁场产生影响。但超微晶叠片的相对磁导率较高,数量级约为104,会对静磁场的分布产生影响。为此,笔者分析不同宽度的超微晶叠片对试件中静磁场、磁铁和试件中涡流及接收端电压的影响。选取试件表面下0.01 mm,横坐标在-43 mm至-37 mm处(线圈正下方)的磁通密度及试件和磁铁中涡流进行分析,结果如图 6所示。
|
图 6 不同超微晶片宽对磁通、涡流的影响 Figure 6 The effect of different ultracrystalline lamination width on magnetic flux and eddy current |
可以看出由于磁铁边缘效应的影响,磁铁下方磁通密度分布不均匀。由图 6(a)可知,当超微晶叠片宽度和线圈宽度一致时(6 mm),试件中磁通密度整体小于无超微晶时(磁铁与试件间距为0.7 mm)的磁通密度;随着超微晶宽度的减小,靠近中间部分的磁通密度逐渐增大,靠近边缘部分的磁通密度逐渐减小;在超微晶片宽小于4 mm时,试件中磁通密度很大一部分(靠近中间位置)大于无超微晶时的磁通密度,其原因是超微晶改变了静磁场的磁路。由图 6(b)可知,随着超微晶片宽的减小,磁铁中的涡流先增加后减小,在5 mm时磁铁中的涡流最大;随着超微晶片宽的减小,试件中的涡流逐渐减小;当中间为空气时,磁铁提离距离与加超微晶时的提离距离相同(1.7 mm),磁铁中的涡流相对较小,但试件中的涡流也最小。加超微晶之后,相当于在线圈上方添加了导磁背板,改变了线圈的阻抗,进而影响了涡流的分布。
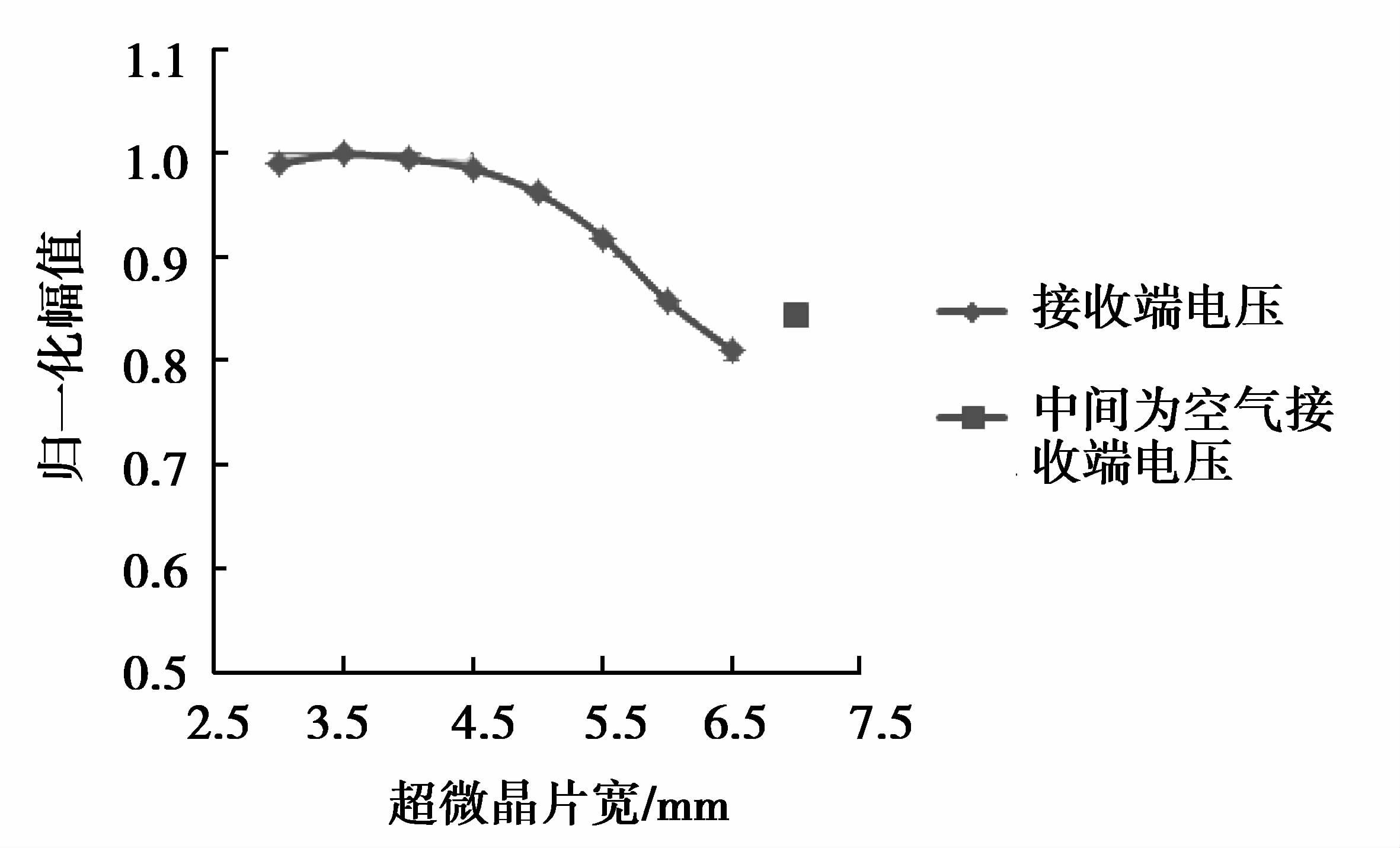
影响试件中超声波幅值的因素包括静态磁场及试件中的涡流,综合考虑这两方面因素,通过接收端电压来衡量这两个因素。Lamb波在传播过程中会出现多模态,选取Lamb波A0模式作为超微晶片宽的选择参考,不同超微晶片宽下电压仿真结果如图 7所示。
|
图 7 不同超微晶片宽下接收端电压 Figure 7 The simulation results of receiving voltage with different ultracrystalline lamination width |
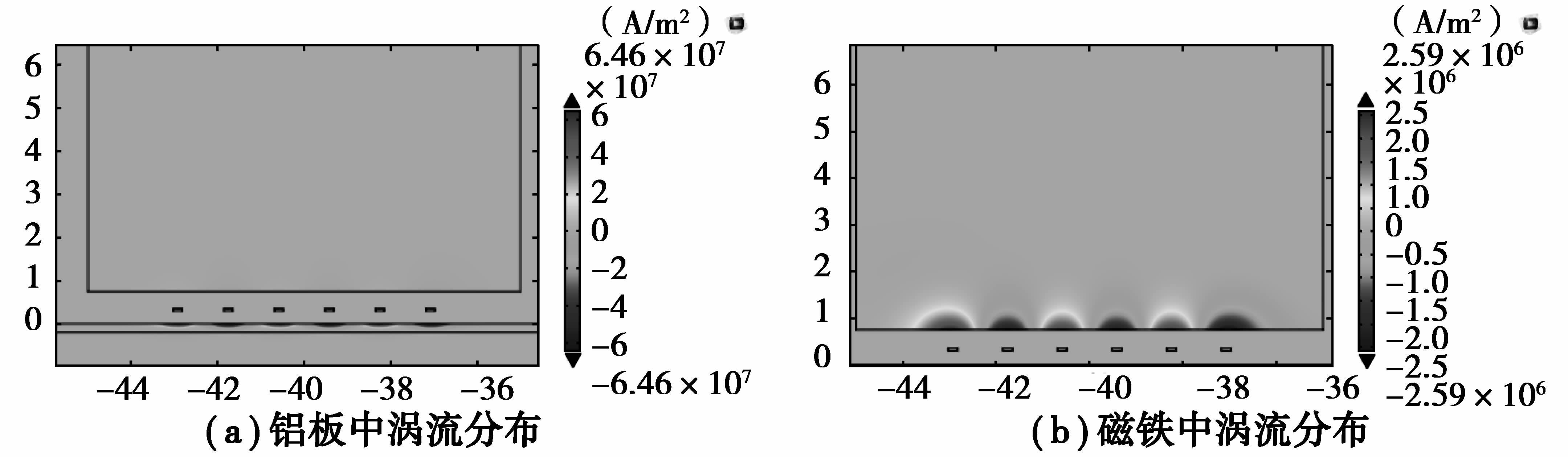
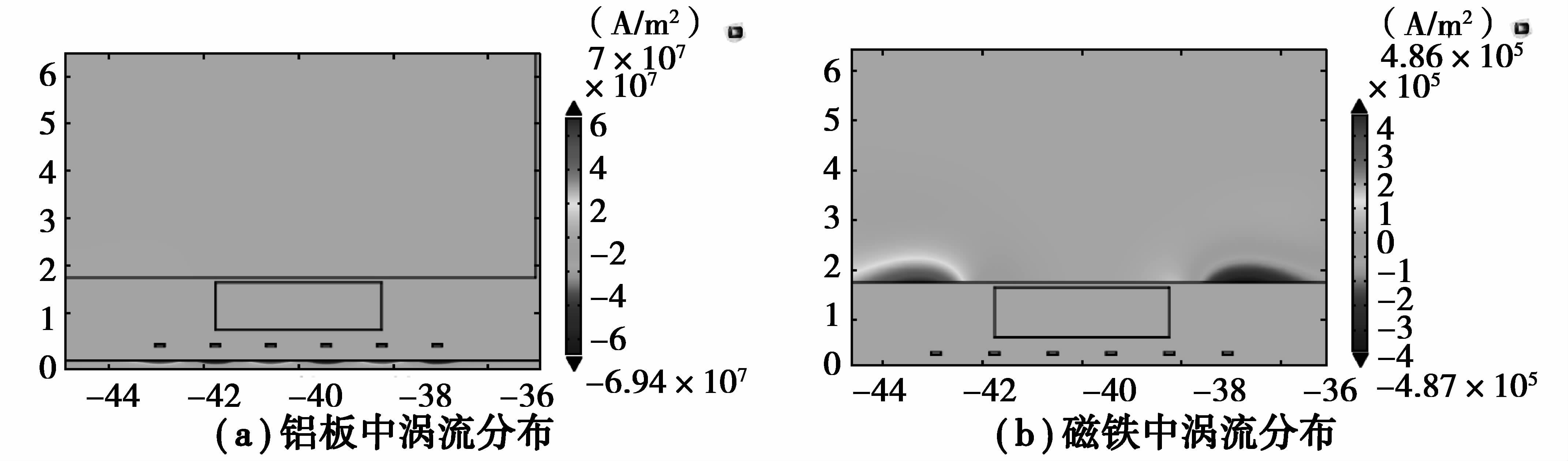
由图 7可知,当超微晶片宽为3.5 mm时,接收端电压最大。选取超微晶片宽为3.5 mm,通过有限元仿真计算对比有、无超微晶对涡流和接收端电压的影响。在t=2.4×10-6 s时铝板中的涡流最大,t=2.35×10-6 s时磁铁中的涡流最大,加微晶前后铝板中涡流分布如图 8(a)和图 9(a)所示,加微晶前后磁铁中涡流分布如图 8(b)和图 9(b)所示。可以看出放置超微晶后,导线下方铝板中的涡流最大值由6.46×107 A/m2增加到7×107 A/m2,而磁铁中的涡流则由2.59×106 A/m2减小到4.86×105 A/m2。
|
图 8 加超微晶前铝板及磁铁中涡流分布 Figure 8 The eddy current distribution in aluminum plate and magnet without ultracrystalline |
|
图 9 加超微晶后铝板及磁铁中涡流分布 Figure 9 The eddy current distribution in aluminum plate and magnet with ultracrystalline |
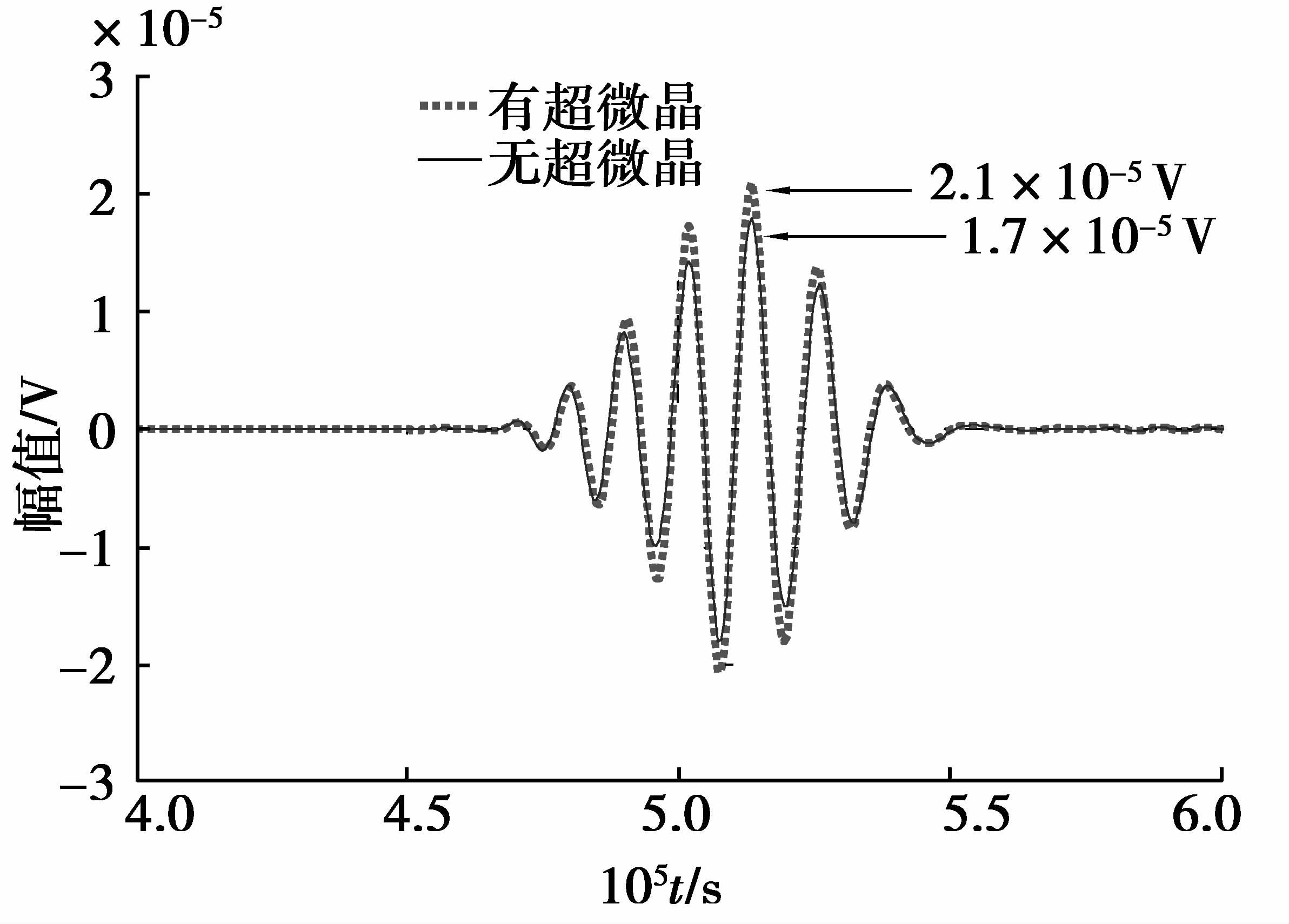
接收端电压仿真结果如图 10所示,实线表示没有加超微晶时接收端电压(磁铁提离距离为0.7 mm),其幅值为1.7×10-5 V;虚线表示加超微晶后接收端电压(磁铁提离距离为1.7 mm),其幅值为2.1×10-5 V。加入超微晶之后,虽然磁铁的提离距离增大,但由图 6可以看出超微晶叠片的使用,优化了磁路及改变了线圈的阻抗,使得永磁铁表面的涡流有所减小,铝板表面的涡流有所增大;而且增加了磁铁中间较弱区域的静磁场,使磁铁中间部分下方试件中的磁通密度有所增加,虽然磁铁边缘部分下方试件中磁通密度也有所减小,但其仅覆盖最外侧线圈,当涡流和磁通密度共同作用时,产生的洛仑兹力得到加强,从而增强了激发模态Lamb波的幅值。
|
图 10 加3.5 mm宽超微晶前后接收端电压比较 Figure 10 The comparison of receiving voltage with and without 3.5 mm ultracrystalline |
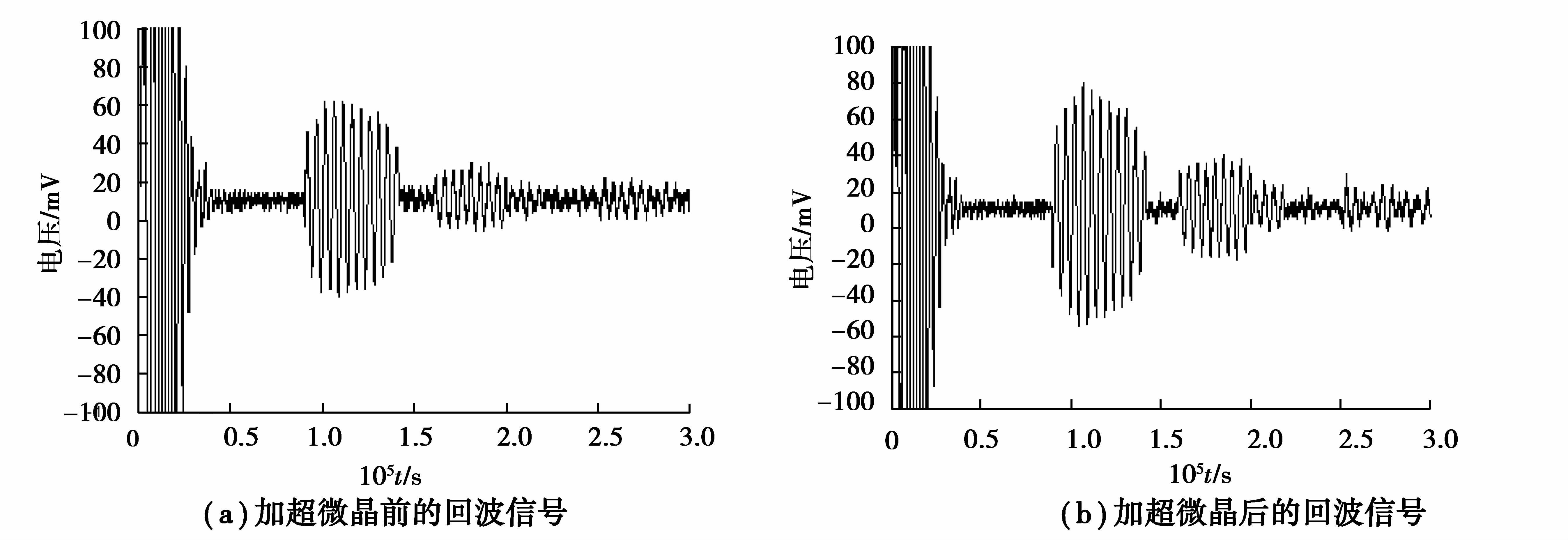
为了验证该方法的有效性,本文对优化前后电磁超声兰姆波换能器进行了实验对比,图 11为实验接线图。采用1K107型超微晶带材,将薄片叠放在一起,制成超微晶叠片,叠片置于永磁铁与铝板之间。铝板的尺寸为300 mm×1 mm,永磁铁的尺寸为14 mm×10 mm×40 mm,剩余磁通密度为1.2T。调整发射探头和接收探头之间的相对位置,同时观察接收到的电磁超声信号强度,选择信号强度最大的点来固定接收探头。在收发探头之间距离相同的情况下,分别得到加超微晶前后的电磁超声信号,如图 12所示。

|
图 11 实验接线图 Figure 11 Experimental connection diagram |
|
图 12 加超微晶前后的回波信号 Figure 12 The echo signal with and without ultracrystalline |
通过对比实验可以看出,加超微晶前,回波信号的幅值最大值为60 mV,加超微晶之后,回波信号的幅值最大值为80 mV,可以看出加入超微晶之后,电磁超声兰姆波信号强度得到一定的增强。
4 结 语笔者提出了一种用超微晶增强回波信号的方法。通过有限元仿真分析了优化前后铝板中涡流的分布及接收端电压幅值,仿真结果表明,加超微晶后铝板中涡流及接收端电压均增大;通过实验对比接收端电压验证了仿真结果的正确性。仿真及实验结果表明,该方法能够在一定程度上解决电磁超声兰姆波信号较弱的问题,为电磁超声Lamb换能器的优化设计提供参考。
| [1] |
刘素贞, 张闯, 金亮, 等.
电磁超声换能器的三维有限元分析[J]. 电工技术学报, 2013, 28(8): 7–12.
LIU Suzhen, ZHANG Chuang, JIN Liang, et al. 3D finite analysis of electromagnetic ultrasonic transducers[J]. Transactions of China Electrotechnical Society, 2013, 28(8): 7–12. (in Chinese) |
| [2] | Wilcox P D, Lowe M J, Cawley P, et al. The excitation and detection of Lamb waves with planar coil electromagnetic acoustic transducers[J]. IEEE Transactions on Ultrasonics Ferroelectrics & Frequency Control, 2005, 52(12): 2370–2383. |
| [3] | Zhai G F, Liu B, Deng C R, et al. An inspection device based on multiple Lamb wave electromagnetic acoustic transducers[C]//Nondestructive Evaluation/Testing (FENDT), 2014 IEEE Far East Forum on[S.l.]:IEEE, 2014:14-18. |
| [4] |
康磊.用于铝板检测的电磁超声导波换能器优化设计技术研究[D].哈尔滨:哈尔滨工业大学,2010. KANG Lei. Research on optimal design technique of guided wave emats for aluminum plate inspection[D]. Harbin:Harbin Institute of Technology,2010. (in Chinese) http://industry.wanfangdata.com.cn/dl/Detail/Thesis?id=Thesis_D264256 |
| [5] | Dhayalan R, Balasubramaniam K. A two-stage finite element model of a meander coil electromagnetic acoustic transducer transmitter[J]. Nondestructive Testing and Evaluation, 2011, 26(2): 101–118. DOI:10.1080/10589759.2010.511220 |
| [6] |
蒋涛, 康磊, 翟国富, 等.
一种优化激发电磁超声Lamb波的方法[J]. 无损检测, 2010, 32(12): 914–917.
JIANG Tao, KANG Lei, ZHAI Guofu, et al. An optimal excitation mode of electromagnetic ultrasonic Lamb wave[J]. Nondestructive Testing, 2010, 32(12): 914–917. (in Chinese) |
| [7] | Jian X, Dixon S. Enhancement of EMAT and eddy current using a ferrite back-plate[J]. Sensors and Actuators A Physical, 2007, 136(1): 132–136. DOI:10.1016/j.sna.2006.10.028 |
| [8] | Lee J S, Kim Y Y, Cho S H. Beam-focused shear-horizontal wave generation in a plate by a circular magnetostrictive patch transducer employing a planar solenoid array[J]. Smart Materials and Structures, 2009, 18(1): 9–15. |
| [9] |
高文凭,高松巍.金属板电磁超声导波机理研究与仿真分析[D].沈阳:沈阳工业大学,2012. GAO Wenpin, GAO Songwei. The mechanism research analysis on electromagnetic and simulation ultrasonic guided wave in metal plate[D]. Shenyang:Shenyang University of Technolog, 2012. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10142-1011085071.htm |
| [10] | Kang L, Dixon S, WANG K C, et al. Enhancement of signal amplitude of surface wave EMATs Based on 3-D simulation analysis and orthogonal test method[J]. Ndt & E International, 2013, 59: 11–17. |
| [11] |
李振才.
电磁超声(EMA)技术的发展与应用[J]. 无损探伤, 2006, 30(6): 4–13.
LI Zhencai. The development and application of electromagnetic acoustic technology[J]. Nondestructive Test, 2006, 30(6): 4–13. (in Chinese) |
| [12] |
罗斯. 固体中的超声波[M]. 北京: 科学出版社, 2004.
Rose Joseph L. Ultrasonic waves in solid media eng[M]. Beijing: Science Press Ltd, 2004. (in Chinese) |
| [13] |
周佳伟.电磁超声换能器的机理研究及其仿真分析[D].沈阳:沈阳工业大学,2010. ZHOU Jiawei. Simulation and analysis of electromagnetic acoustic transducer mechanism[D]. Shenyang:Shenyang University of Technolog, 2010. (in Chinese) http://xuewen.cnki.net/CMFD-1011085133.nh.html |
| [14] | Mirkhani K, Chaggares C, Masterson C, et al. Optimal design of EMAT transmitters[J]. Ndt & E International, 2004, 37(3): 181–193. |
| [15] | Ribichini R, Nagy P B, Ogi H. The impact of magnetostriction on the transduction of normal bias field EMATs[J]. Ndt & E International, 2012, 51(10): 8–15. |
| [16] | Petcher P A, Potter M D G, Dixon S. A new electromagnetic acoustic transducer (EMAT) design for operation on rail[J]. Ndt & E International, 2014, 65: 1–7. |
| [17] | Jafari-Shapoorabadi R, Konrad A, Sinclair A N. Improved finite element method for EMAT analysis and design[J]. IEEE Transactions on Magnetics, 2001, 37(4): 2821–2823. DOI:10.1109/20.951317 |
| [18] |
赵志刚, 赵新丽, 程志光, 等.
HVDC中电力变压器直流偏磁屏蔽效应研究[J]. 电工技术学报, 2014, 29(7): 45–52.
ZHAO Zhigang, ZHAO Xinli, CHENG Zhiguang, et al. Research on the shielding effects of power transformer under DC-biased condition in HVDC[J]. Transactions of China Electrotechnical Society, 2014, 29(7): 45–52. (in Chinese) |
 2016, Vol. 39
2016, Vol. 39


