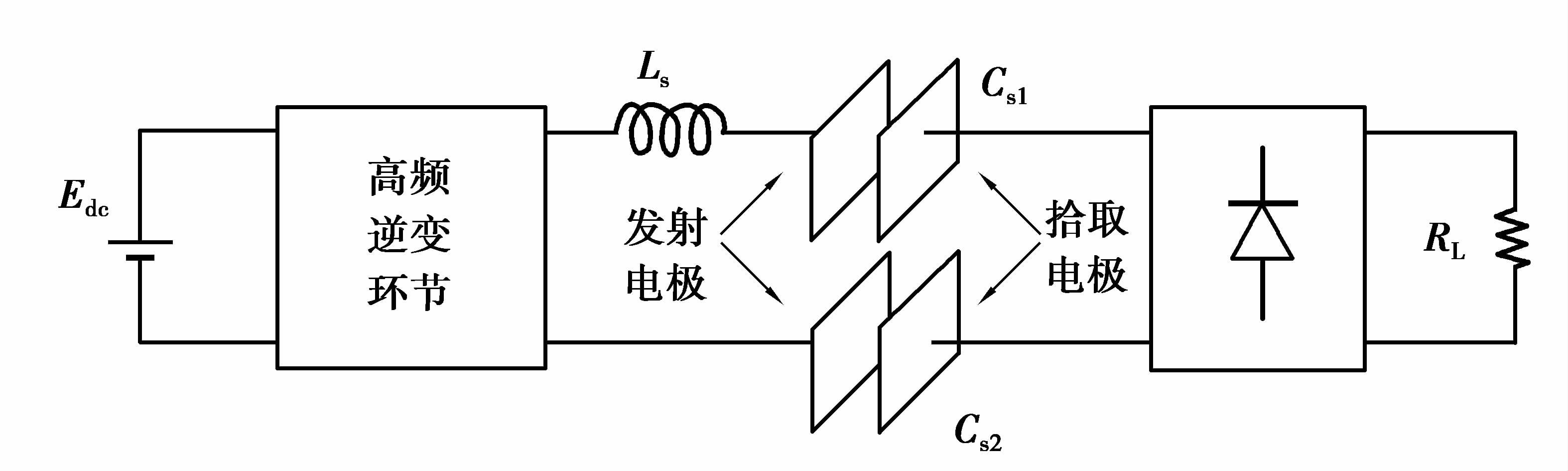
电场耦合无线电能传输系统是一种以金属极板作为耦合机构,高频电场为能量载体的无线电能传输技术。由于电场耦合无线电能(capacitive power transfer,CPT)系统耦合机构的轻便性、对周围导体没有涡流效应、电磁兼容性较好等诸多特点,因而受到了国内外专家学者的高度关注[1-2]。典型CPT系统的结构如图 1所示,直流电源Edc经过高频逆变环节后转变为交变电压,在其激励作用下发射电极激发出高频电场。当拾取电极放置在与发射电极相对的位置时,拾取电极上将会形成电势差,再经过整流滤波环节为负载RL提供能量。发射和拾取电极的相互耦合可用等效电容Cs1和Cs2来表示[3-4]。
|
图 1 CPT系统的原理框图 Figure 1 Block diagram of a typical CPT system |
目前,耦合机构的补偿方式主要分为有源补偿和无源补偿[5]。有源补偿方式较为复杂,故实际中应用较少[6]。无源补偿方式主要有一阶串联电感[7]、二阶并联LC网络[8]、三阶LCL网络[5]以及四阶LCLC网络[9]。前两种谐振网络的电路简单,成本较低,但是这两种网络会使得耦合机构的位移电流过大,从而引起电磁干扰问题[5];四阶LCLC谐振网络具有泵升电流的能力,可以在较小位移电流条件下,为负载输出较大的电流,从而规避了系统的EMI(electro magnetic interference)问题[9]。然而四阶谐振网络的拓扑结构较为复杂,在应用中发现这种网络的参数敏感性较高,系统的稳定性难以保证;三阶LCL谐振网络既具有四阶网络的电流泵升能力,同时参数敏感性又比四阶网络低,因此文中采用LCL谐振网络来补偿耦合机构。
文献[5]将LCL谐振网络引入CPT系统,在较小的补偿电流下即可传输所需的功率。该文献主要是分析了LCL谐振电路的特性,而系统的主要参数则通过一种以电感体积和重量为目标函数的智能优化算法来确定。该方法运算量较大,需要辅助其他软件来进行计算,在实际工程应用中受到了一定的限制,而且该文献所设计的系统不能工作在软切换状态,逆变器的开关损耗较大。另外,在实际应用中耦合机构的发射和拾取电极的间距可能会在一定范围内发生变化,同时负载也可能会改变。对于这类高阶系统,这种变化有可能会造成软切换频率发生跳变。目前尚未见相关文献对此类系统的软开关频率特性进行研究。
针对LCL型CPT系统参数设计较复杂且不能运行在软切换状态的问题,笔者基于阻抗变换原理提出了一种简易可行的参数设计方法,并采用频闪映射非线性建模方法和周期不动点理论分析了系统的零电流切换(zero current switching,ZCS)软开关频率的特性,进而优化了系统的工作频率,使得系统工作在完全谐振状态,在此基础上研究了耦合电容和负载变化对ZCS频率的影响。仿真和实验验证了所提出的参数设计方法和软开关频率的准确性,为LCL型CPT系统的应用推广提供了较为可行的参数设计和频率优化方法。
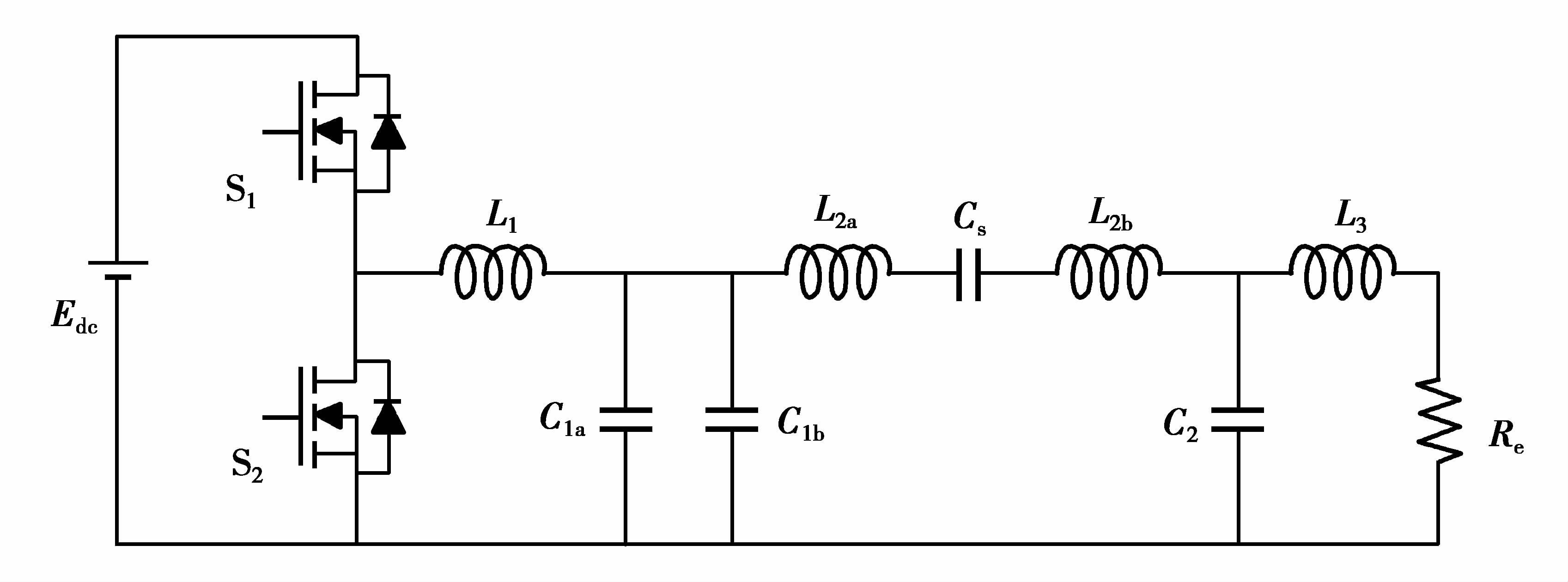
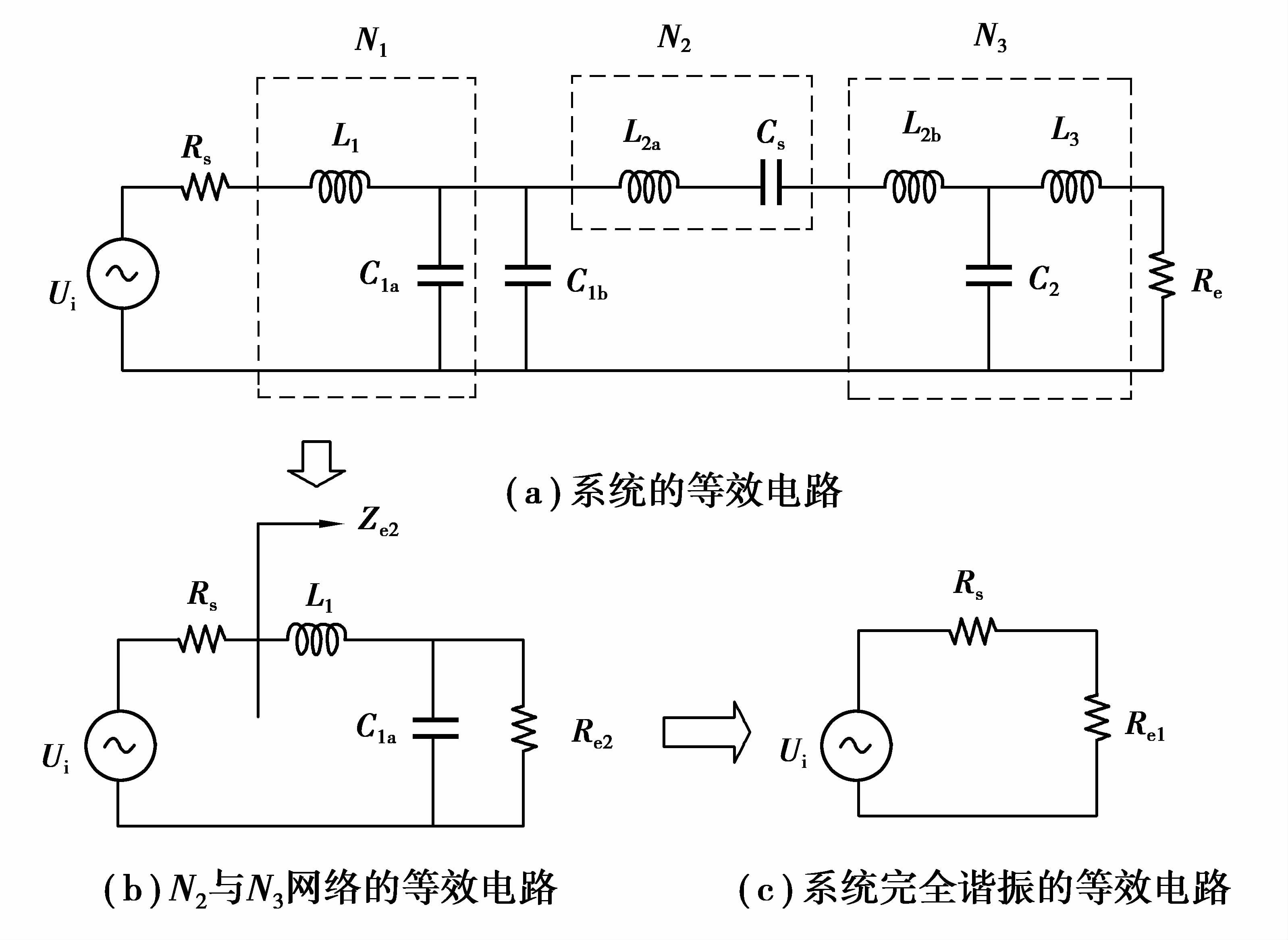
1 谐振网络的参数设计LCL型CPT系统的拓扑如图 2。为了便于分析,将整流滤波环节等效为阻性负载Re[13],并且假设所有开关管均为瞬时通断,则图 2可简化为图 3(a)。根据基波近似原理,逆变输出的电压可由其基波等效如图中Ui;Rs为逆变网络的等效内阻,由开关管的等效通态电阻和电源的等效串联电阻组成[13];N1网络由L1和C1a组成,用于逆变网络的内阻与N2、N3网络阻抗的匹配,电容C1b具有补偿N2与N3网络电抗的作用。N2网络的L2a用以补偿耦合机构等效电容Cs,Cs为Cs1与Cs2的等效串联电容。N3为L2b、L3和C2构成的LCL谐振网络,用来提高耦合机构的传输功率。由于在电感内阻中的损耗功率要远小于系统的输出功率,因而在有关无线电能传输系统参数设计的诸多文献中,均忽略了电感的内阻[1, 5, 7]。文中提出的参数设计方法同样也忽略了电感的内阻。
|
图 2 LCL型CPT系统主电路 Figure 2 Circuit of CPT system with LCL |
|
图 3 LCL型CPT系统等效电路图 Figure 3 Equivalent circuit of CPT system with LCL network |
系统的输出功率Po、等效负载Re、耦合机构等效电容Cs和直流输入Edc由实际应用中的具体需求来确定,而工作频率f和负载回路的品质因数Q由一般的工程经验来设置[13]。由于N2网络处于谐振状态,L2a满足
| ${{L}_{2a}}=\frac{1}{{{\omega }^{2}}{{C}_{s}}}DD$ | (1) |
为简化参数之间的表达式,设L2b,L3的比值为k,两者的等效并联电感为Lcom。当LCL网络的参数满足式(2),网络将具有泵升电流的作用。
| $\left\{ \begin{matrix} k=\frac{{{L}_{2b}}}{{{L}_{3}}}, \\ {{L}_{com}}=\frac{1}{1/{{L}_{2b}}+1/{{L}_{3}}}, \\ {{\omega }^{2}}{{C}_{2}}{{L}_{com}}=1, \\ \end{matrix} \right.$ | (2) |
其中k的取值根据实际中成本、体积和环境等因素进行选择[5]。由于L3满足式(3),所以结合式(2)即可得到LCL网络中元件L2b、L3和C2的取值。
| $Q=\frac{\omega {{L}_{3}}}{{{R}_{e}}},$ | (3) |
LCL网络的参数如下
| $\left\{ \begin{matrix} {{L}_{3}}=\frac{Q{{R}_{e}}}{\omega }, \\ {{L}_{2b}}=k{{L}_{3}}, \\ {{C}_{2}}=\frac{{{L}_{2b}}+{{L}_{3}}}{{{\omega }^{2}}{{L}_{2b}}{{L}_{3}}}, \\ \end{matrix} \right.$ | (4) |
从电容C1a向右侧看进去的等效阻抗为
| ${{Z}_{C1b-LCL}}=\frac{1}{j\omega {{C}_{1b}}+{{Z}_{LCL}}},$ | (5) |
式中,ZLCL为N3网络的阻抗,可表示为
| ${{Z}_{LCL}}=\frac{{{k}^{2}}{{Q}^{2}}{{R}_{L}}}{B}+j\frac{A({{Q}^{2}}+k+1)+B}{\omega B{{C}_{s}}},$ | (6) |
其中B=Q2+k2+2k+1,A=kωCsReQ。
当C1b的取值满足式(7),ΖC1b-LCL则可等效为纯阻性负载Re2,如式(8),由此系统可简化为图 3(b)
| ${{C}_{1b}}=\frac{1+k}{kA}{{C}_{s}},$ | (7) |
| ${{R}_{e2}}={{k}^{2}}{{R}_{e}}。$ | (8) |
N1用于匹配内阻Rs与N2、N3网络的等效阻值Re2,匹配后系统进一步简化为图 3(c)。图中Re1消耗的平均功率等于输出功率Po[13]。为了获得所需求的输出功率,同时系统又具有较大的传输效率。根据最大传输功率原理,Re1的设计应满足
| ${{R}_{e1}}=\frac{{{U}^{2}}_{i}/{{P}_{o}}-2{{R}_{s}}+{{U}_{i}}\sqrt{{{U}^{2}}_{i}/{{P}^{2}}_{o}-4{{R}_{s}}/{{P}_{o}}}}{2},$ | (9) |
其中Ui=$\frac{\sqrt{2}}{\pi }$。
为了将N2、N3网络的阻抗转换为Re1,并保证等效后输入电抗为零,网络N1的取值应满足
| $\left\{ \begin{matrix} {{L}_{1}}={{R}_{e1}}\frac{\sqrt{{{R}_{e2}}/{{R}_{e1}}-1}}{\omega }, \\ {{C}_{1a}}=\frac{\sqrt{{{R}_{e2}}/{{R}_{e1}}-1}}{\omega {{R}_{e2}}}。 \\ \end{matrix} \right.$ | (10) |
至此,由式(1)、(4)、(7)、(10)即可确定系统的主要参数。可见该方法的运算量较小,无需辅助工具即可完成。然而在实际应用中,受电感内阻、等效耦合电容的变化以及负载的变化的影响,这种方法所设计的系统并不能工作在软开关状态[2],逆变器将产生较大的损耗,为此在所设计的系统的基础上,基于频闪映射建模以及不动点理论来分析系统的软开关频率特性,得到系统的软开关频率范围,从而对系统的工作频率进行优化。
2 LCL型CPT系统建模LCL型CPT系统是一个高阶非线性系统,为求解包含电感内阻条件下系统的软开关频率,需要建立它的非线性模型。频闪映射建模方法及周期不动点理论是一种用来计算软开关工作点的方法[14]。用此方法可以建立非线性系统的分段线性的频闪映射模型,得出系统的软开关频率和各状态变量的稳态数值解。根据基尔霍夫定律,可建立图 2的包含了器件内阻的电路微分方程模型
| $\left\{ \begin{matrix} \frac{d{{i}_{L1}}}{dt}=\frac{1}{{{L}_{1}}}\left( -{{i}_{{{L}_{1}}}}\left( {{R}_{L1}}+{{R}_{s}} \right)-{{V}_{C1}}+{{u}_{i}} \right), \\ \frac{d{{V}_{C1}}}{dt}=\frac{1}{{{C}_{1}}}({{i}_{L1}}-{{i}_{L2}}), \\ \frac{d{{V}_{{{C}_{s}}}}}{dt}={{\frac{1}{C}}_{s}}{{i}_{L2}}, \\ \frac{d{{i}_{L2}}}{dt}=\frac{1}{{{L}_{2}}}(-{{i}_{L2}}{{R}_{L2}}+{{V}_{C1}}-{{V}_{Cs}}-{{V}_{C2}}), \\ \frac{d{{V}_{C2}}}{dt}=\frac{1}{{{C}_{2}}}({{i}_{L2}}-{{i}_{L3}}), \\ \frac{d{{i}_{L3}}}{dt}=\frac{1}{{{L}_{3}}}({{V}_{C2}}-({{R}_{e}}-{{R}_{L3}}){{i}_{L3}})。 \\ \end{matrix} \right.$ | (11) |
假设稳态时系统开关周期为T,则式(11)中的逆变器输出电压ui表示为
| ${{u}_{i}}=\left\{ \begin{matrix} {{E}_{dc}},t~mod~T\in \left[ 0 \right.,\left. \frac{T}{2} \right), \\ 0,t~mod~T\in \left[ \frac{T}{2} \right.,\left. T \right), \\ \end{matrix} \right.$ | (12) |
式中:iL2=iL2a=iL2b;VC2=VC2a=VC2b;RL1、RL2a、RL2b、RL3分别为L1、L2a、L2b、L3的内阻。取所有电容电压和电感电流为状态变量。令向量x=iL1,VC1,VCs,iL2,VC2,iL3T及直流输入电压u=Edc分别为系统的状态变量和输入变量。则由微分方程组(11)可得系统状态空间模型为
| $\dot{x}=Ax+Bu,$ | (13) |
式中:
| $\begin{align} & A=\left[ \begin{matrix} -\frac{{{R}_{L1}}+{{R}_{S}}}{{{L}_{1}}} & -\frac{1}{{{L}_{1}}} & 0 & 0 & 0 & 0 \\ \frac{1}{{{C}_{1}}} & 0 & 0 & -\frac{1}{{{C}_{1}}} & 0 & 0 \\ 0 & 0 & 0 & \frac{1}{{{C}_{S}}} & 0 & 0 \\ -\frac{{{R}_{1}}}{{{L}_{2}}} & \frac{1}{{{L}_{2}}} & -\frac{1}{{{L}_{2}}} & 0 & -\frac{1}{{{L}_{2}}} & 0 \\ 0 & 0 & 0 & \frac{1}{{{C}_{2}}} & 0 & -\frac{1}{{{C}_{2}}} \\ 0 & 0 & 0 & 0 & \frac{1}{{{L}_{3}}} & -\frac{{{R}_{e}}-{{R}_{3}}}{{{L}_{3}}}~ \\ \end{matrix} \right], \\ & B={{\left[ \begin{matrix} \frac{1}{{{L}_{1}}} & 0 & 0 & 0 & 0 & 0 \\ \end{matrix} \right]}^{T}}。 \\ \end{align}$ |
根据开关状态可以将系统线性化为两个线性模态,即开关管S1导通S2关断,S1关断S2导通,则根据频闪映射建模方法[14],可知各模态下的状态映射函数为
| $\left\{ \begin{matrix} {{f}_{1,\frac{T}{2}}}=\Phi \left( \frac{T}{2} \right)x+\left( \Phi \left( \frac{T}{2} \right)-I \right){{A}^{-1}}B{{E}_{dc}},{{S}_{1}}导通,{{S}_{2}}关断, \\ {{f}_{2,\frac{T}{2}}}=\Phi \left( \frac{T}{2} \right)x,{{S}_{1}}关断,{{S}_{2}}导通W。 \\ \end{matrix} \right.$ |
根据周期不动点理论的软开关频率确定方法,可知系统的稳态周期不动点x*为
| ${{x}^{*}}=I+{{\left( \Phi \left( \frac{T}{2} \right) \right)}^{-1}}\Phi \left( \frac{T}{2} \right){{A}^{-1}}B{{E}_{dc}},$ | (14) |
式中I为与A同阶的单位矩阵,Φ(t)=eAt。为取出不动点x*中的逆变桥的输出电流分量iL1,设定对应的状态选择矩阵为YiL1=[1, 0, 0, 0, 0, 0],则可得逆变器输出电流的周期不动点函数为
| ${{f}_{x*}}\left( t \right)={{Y}_{{{i}_{L1}}}}{{\left( I+\Phi \left. \left( \frac{t}{2} \right) \right) \right.}^{-1}}\Phi \left( \frac{t}{2} \right){{A}^{-1}}B{{E}_{dc}}DDD$ | (15) |
假设方程fx*(t)=0的所有非零解为Ti(i=1,2…n),那么以这些非零解作为系统的开关周期就可得出系统的n个ZCS频率
| ${{f}_{ZCS}}=\frac{1}{{{T}_{1}}}\left( i=1,2,\ldots n \right)。$ | (16) |
将对应的稳态周期不动点x*(Ti)作为系统稳态周期的初始状态,则由状态映射函数即可得出系统稳态周期内状态变量的分段解析函数式为
| $x\left( t \right)=\left( \begin{matrix} \Phi \left( t \right){{x}^{*}}\left( {{T}_{i}} \right)+\left( \Phi \left( t \right)-I \right){{A}^{-1}}B{{E}_{dc}},t\in \left[ 0,\frac{{{T}_{i}}}{2} \right], \\ \Phi t-\frac{{{T}_{i}}}{2}x\frac{{{T}_{i}}}{2},t\in \left( 0,\left. \frac{{{T}_{i}}}{2} \right] \right.。 \\ \end{matrix} \right.$ |
为获得不动点x*中的负载电流iL3,设定状态选择矩阵为YiL3=[0, 0, 0, 0, 0, 1],则系统的输出电压可表示为
| ${{V}_{o}}\left( t \right)={{Y}_{{{i}_{L3}}}}x\left( t \right){{R}_{e}}。$ | (17) |
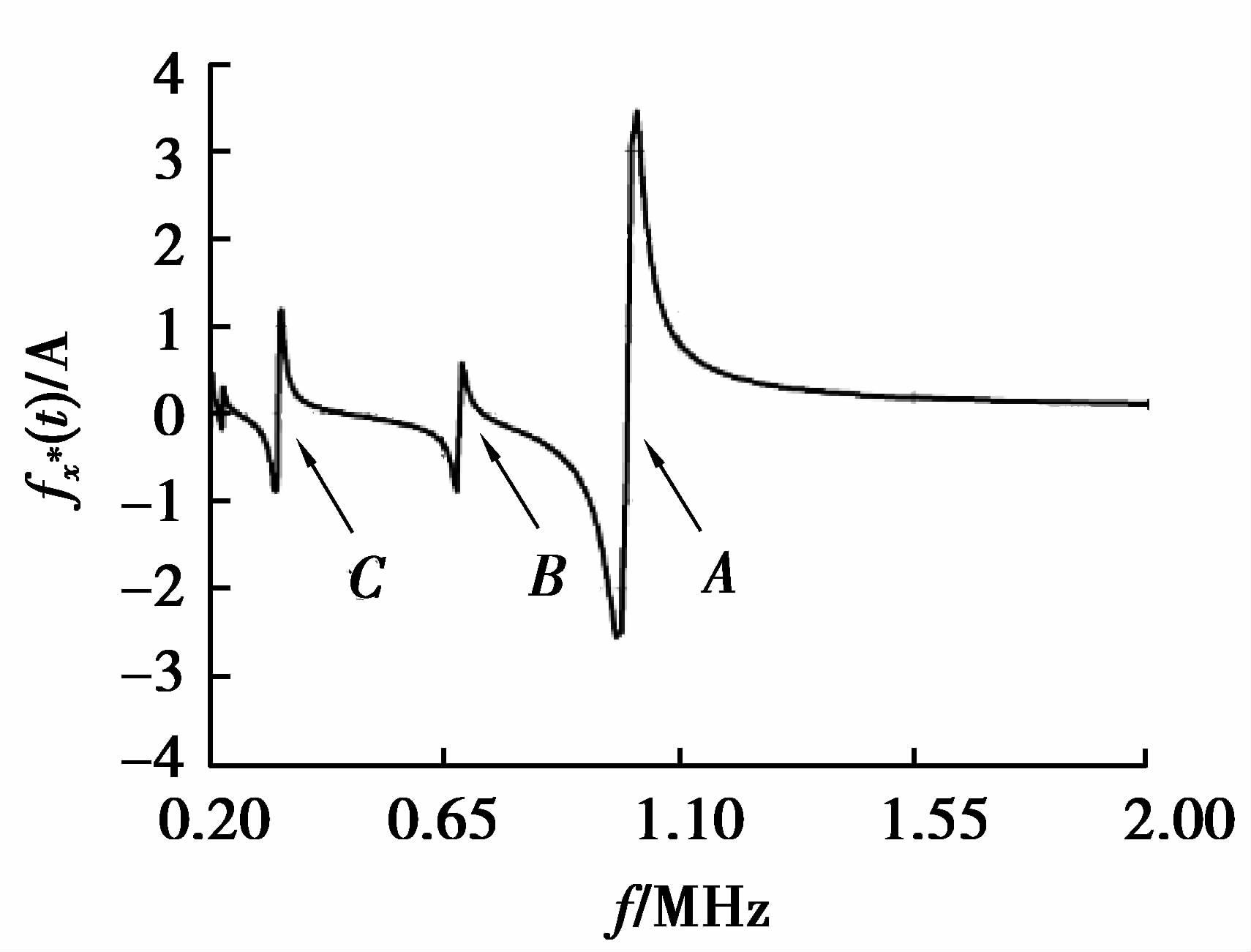
根据上一节建立的逆变器输出电流和负载电压的不动点函数,可对系统的ZCS频率特性进行分析。为此搭建了一个仿真模型,输入为Edc=24 V,预设定工作频率f=1 MHz,等效耦合电容Cs=500 pF,负载Re=10 Ω,品质因数Q=10,电感比值k=10,输出功率Po=25 W。由即可确定系统的主要参数,如表 1所示。采用MATLAB中的数值求解工具包,可得到逆变器输出电流的周期不动点函数的曲线如图 4所示。由图可知,所搭建CPT系统的不动点函数在(0.2~2 MHz)频段有9个过零点,其中A、B、C3点的幅值较高,且分别对应频率1.001 MHz、680.3 kHz、333.8 kHz。为了增大系统功率传输能力,确保系统工作于完全ZCS状态,而参数又无需改动,只要将工作频率微调至1.001 MHz即可。
| 表 1 系统的主要参数 Table 1 The key system parameters |
|
图 4 逆变器输出电流周期不动点函数曲线 Figure 4 Curve of the fixed points of the inverter output current |
对于这类高阶LCL型CPT系统,在应用中可能会存在参数敏感性问题,所以需要分析系统参数的变化对ZCS频率造成的影响。如图 5(a)为耦合等效电容Cs在(50 pF,1 000 pF)的范围变化时,系统的ZCS频率的变化曲线。可以看到,在所设定的等效耦合电容Cs=500 pF附近,Cs的变化不会引起ZCS频率的跳变。然而,当等效耦合电容Cs小于207 pF,即传输距离增加过大时,ZCS软开关频率将出现跳变。因此,当等效耦合电容降得过小时,需要增加相应的调谐控制电路,这将是笔者后续的研究内容,在此不予以详细介绍。总体而言,耦合机构等效电容在一定范围内的变化不造成ZCS频率的急剧变化。另外,由图 5(a)中的Vo曲线可见,在A工作点系统具有最大的输出电压,但由于对耦合机构移位过于敏感,在实际工作中不能满足要求。负载的变化对系统ZCS软开关频率的影响如图 5(b)。可以看到在所设定的等效负载Re=10 Ω附近,负载的变化不会引起ZCS频率的跳变,而且输出电流Io也不会随着输出负载的变化而大范围变化。因此,所设计的系统对耦合机构及负载的变化不敏感。
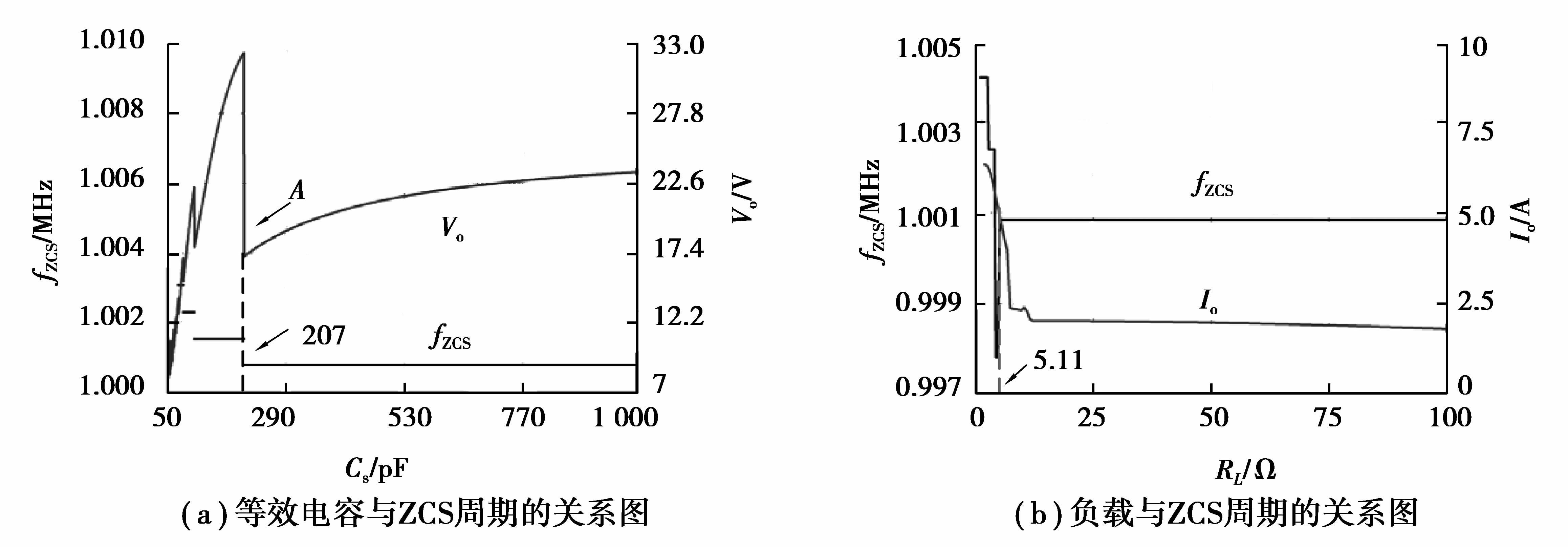
|
图 5 等效电容与负载对ZCS周期及输出的影响 Figure 5 Curves of ZCS periods and output against coupling capacitor and loads |
在MATLAB仿真平台上搭建系统的仿真模型,所采用的参数如表 1,系统工作频率设定为1.001 MHz。仿真波形如图 6(a),其中VS2是开关管S2的端电压,而Is2为管子的电流。可以看到,在开关由导通转变为关断的时刻,通过开关管的电流均接近为零,系统能达到ZCS软开关的工作状态。如图 6(b)中的IL3与IL2b分别为LCL谐振网络中流经电感L3和L2b的电流。由于流过L2b的电流与耦合电流相等,因此,耦合机构中仅需较小的电流即可在负载端获得较大的电流。
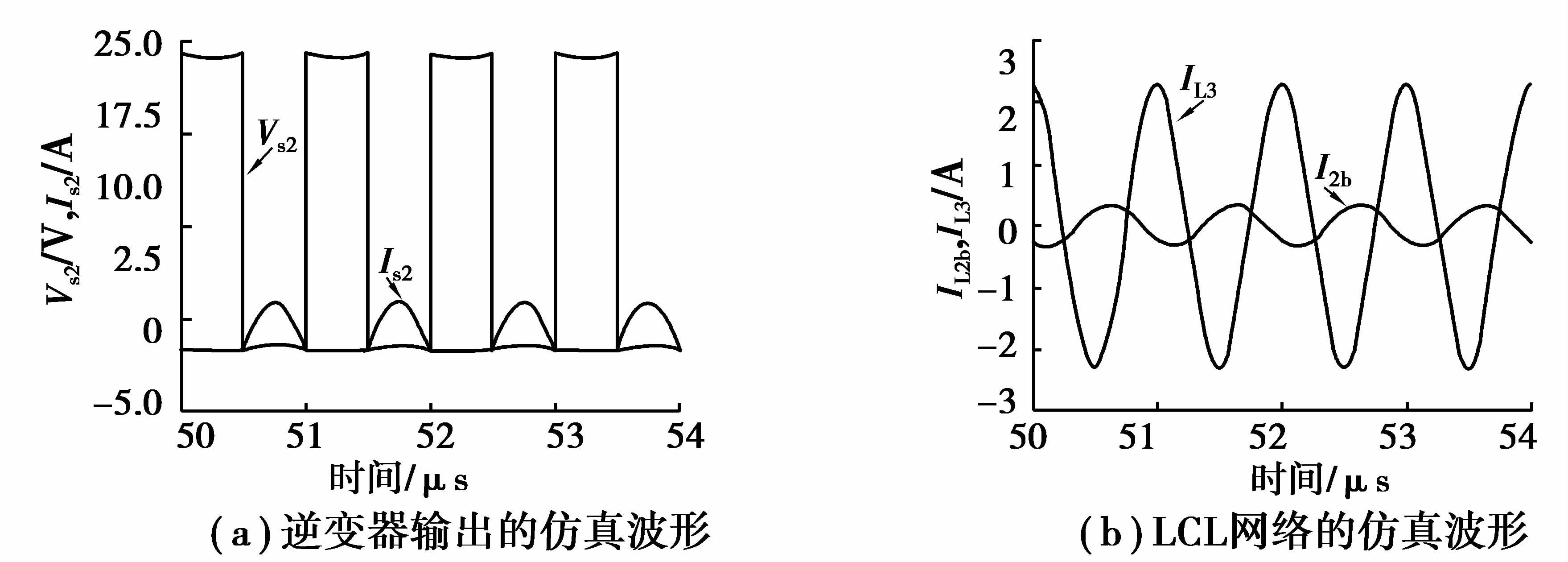
|
图 6 仿真波形 Figure 6 Simulation waveforms |
根据图 7搭建实验电路来验证所提出的参数设计方法及软开关频率优化的正确性。为了确保系统运行在软开关频率上,开关管S1和S2的驱动信号是根据逆变器输出电流的过零点来产生。具体的工作过程为:首先通过电流互感器检测得到逆变器的输出电流,再经由电流过零检测环节对逆变电流进行整形,继而通过超前校正环节后输入给控制器,当逆变电流的工作频率处于软开关频率点附近时,控制器给驱动电路使能信号。其中过零检测环节采用高速比较器LMV7219、超前校正环节采用RC超前校正电路、控制器由FPGA组成、驱动电路为IDXN404。耦合机构采用200 mm×200 mm的紫铜箔作为极板,在间距1 mm下,可获得1 nF的等效电容。为了确保系统具有较好的高频特性,所有的谐振电容采用银云母电容,C1=1.7 μF,C2=2.0 nF。逆变器的开关管型号为STP30NF20。
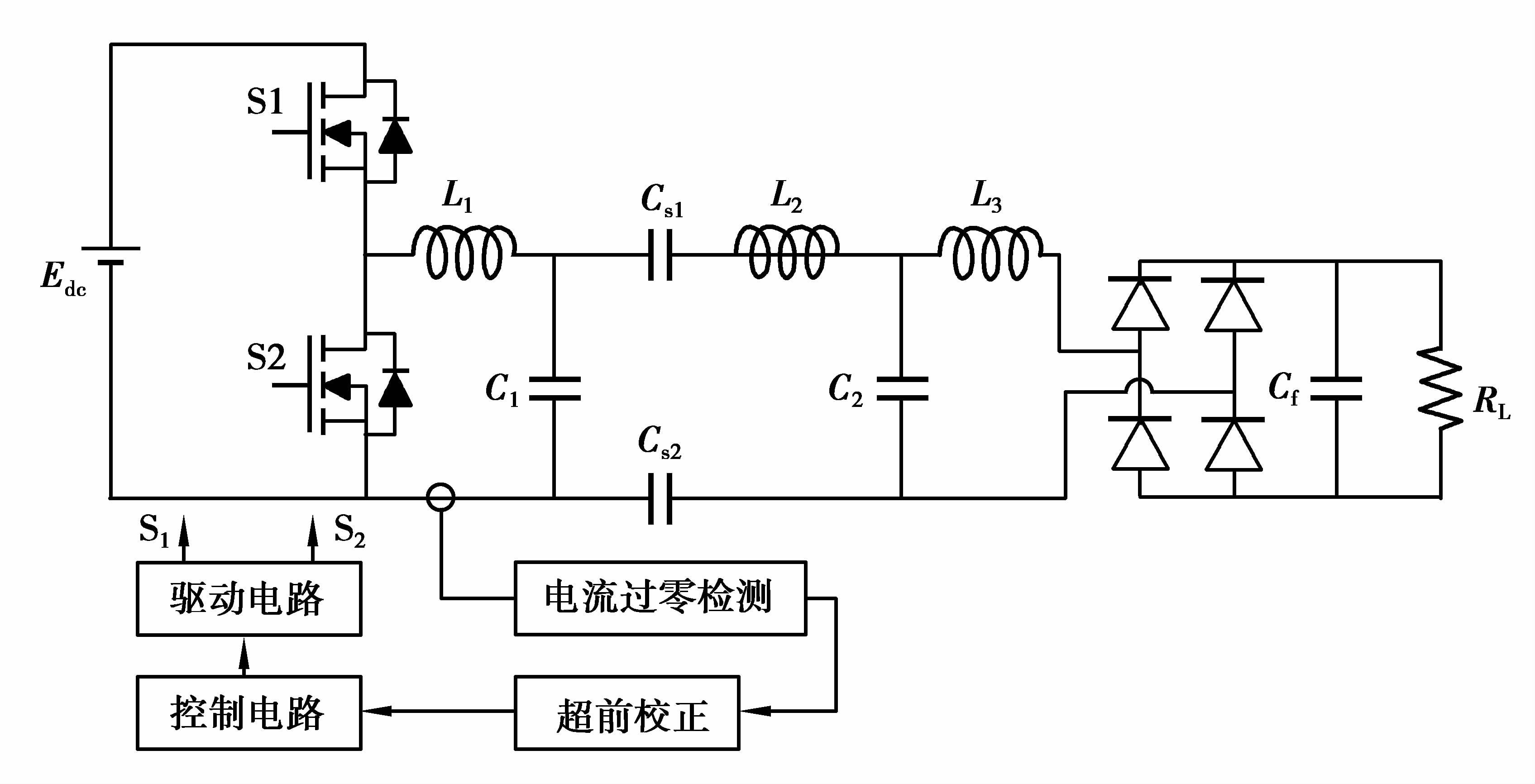
|
图 7 实验样机系统电路框图 Figure 7 block diagram of experimental prototype |
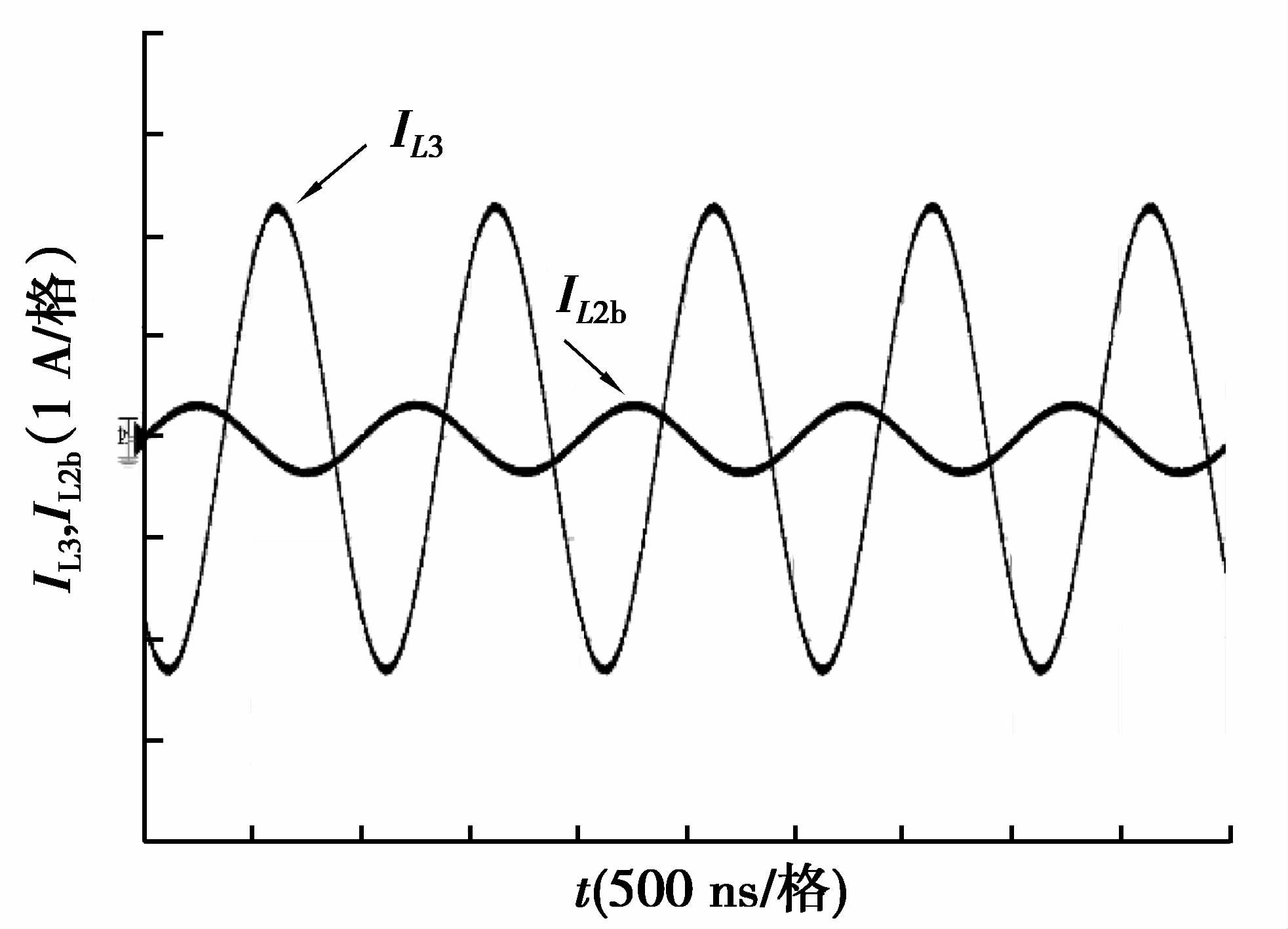
由于实验系统所采用的开关管的输入电容Ciss,以及驱动信号死区时间的存在,管子不能瞬时导通及关断,因此,在开关管切换时刻存在1.68 A的电流尖峰,如图 8中的虚框所示。此尖峰造成电压冲击对于所选开关管在可接受范围内,由此引起的管子温升在10 ℃左右。通过在开关管外围增加吸收电路可大大改善这种情况,总体上可认为系统达到软开关工作状态。消除开关管寄生参数所引起的电流尖峰,需要对逆变器的动力学行为进行分析,这将会在后续的研究继续进行。实验系统的负载可获得功率25.72 W,直流电源注入功率为29.30 W,系统传输效率约为87%。同时从图 9可以看到,LCL网络的输入电流IL2b与输出电流IL3的幅值比为6.9,耦合机构在178 V的端电压下可传输所需求的功率。相比于传统的串联补偿CPT系统,LCL网络的引入将大大降低补偿电感所流通的电流。
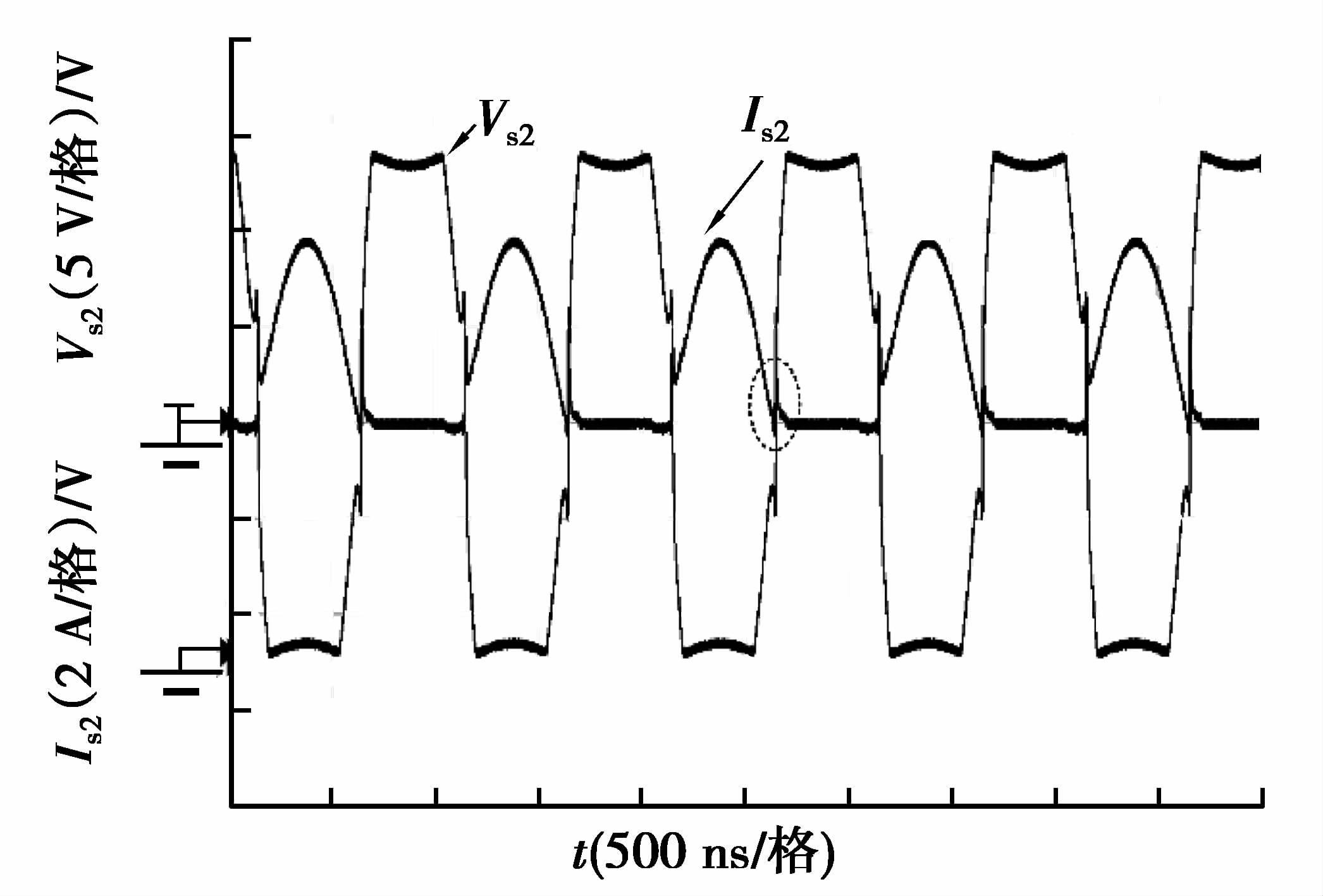
|
图 8 开关管S2端电压与电流 Figure 8 Voltage and current waveforms of MOSFET S2 |
|
图 9 LCL网络的输入电流与输出电流 Figure 9 Input current and output current of LCL network |
针对LCL型CPT系统现有参数设计计算复杂且不能运行在软开关状态的问题,笔者提出了一种基于阻抗变换原理的简易可行参数设计方法,并在频闪映射理论的基础上建立了系统的非线性电路模型,应用周期不动点理论精确求解了系统的ZCS软开关频率。同时,优化了系统的工作频率,使得系统可工作在完全软开关状态。仿真和实验结果表明,本文所设计的系统可工作于近似的ZCS软开关切换状态,系统的效率较高。本文所构建的模型与参数设计方法为LCL型CPT系统的分析及设计提供了理论指导。
| [1] | Liu C, Hu A P, Covic G A, et al. Comparative study of CCPT systems with two different inductor tuning positions[J]. IEEE Transactions on Power Electronics, 2012, 27(1): 294–306. DOI:10.1109/TPEL.2011.2158322 |
| [2] |
苏玉刚, 徐健, 谢诗云, 等.
电场耦合型无线电能传输系统调谐技术[J]. 电工技术学报, 2013, 28(11): 189–194.
Su Yugang, Xu Jian, Xie Shiyun, et al. A tuning technology of electrical-field coupled wireless power transfer system[J]. Transactions of China Electrotechnical Society, 2013, 28(11): 189–194. (in Chinese) |
| [3] | Ludois D C, Reed J K, Hanson K. Capacitive power transfer for rotor field current in synchronous machines[J]. IEEE Transactions on Power Electronics, 2012, 27(11): 4638–4645. DOI:10.1109/TPEL.2012.2191160 |
| [4] | Ludois D C, Erickson M J, Reed J K. Aerodynamic fluid bearings for translational and rotating capacitors in noncontact capacitive power transfer systems[J]. IEEE Transactions on Industry Applications, 2014, 50(2): 1025–1033. DOI:10.1109/TIA.2013.2273484 |
| [5] | Theodoridis M P. Effective capacitive power transfer[J]. IEEE Transactions on Power Electronics, 2012, 27(12): 4906–4913. DOI:10.1109/TPEL.2012.2192502 |
| [6] | Fnato H, Chiku Y. Wireless power distribution with capacitive coupling excited by switched mode active negative capacitor[C]//International Conference on Electrical Machines and System. IEEE, 2010:117-122. |
| [7] | Chao L, Hu A P, Wang B, et al. A capacitively coupled contactless matrix charging platform with soft switched transformer control[J]. IEEE Transactions on Industrial Electronics, 2013, 60(1): 249–260. DOI:10.1109/TIE.2011.2172174 |
| [8] | Sepahvand A, Kumar A, Afridi K, et al. High power transfer density and high efficiency 100 MHz capacitive wireless power transfer system[C]//Control and Modeling for Power Eletronics. IEEE, 2015. |
| [9] | Lu F, Zhang H, Hofmann H, et al. A double-sided lclc compensated capacitive power transfer system for electric vehicle charging[J]. IEEE Transactions on Power Electronics, 2015, 30(11): 6011–6014. DOI:10.1109/TPEL.2015.2446891 |
| [10] | Kline M, Izyumin I, Boser B, et al. Capacitive power transfer for contactless charging[C]//2011 Twenty-Sixth Annual Applied Power Electronics Conference and Exposition (APEC). IEEE, 2011:1398-1404. |
| [11] | Liu C, Hu A P. Effect of series tuning inductor position on power transfer capability of CCPT system[J]. Electronics Letters, 2011, 47(2): 136–137. DOI:10.1049/el.2010.2380 |
| [12] | Liu C, Hu A P, Nair N K C. Modelling and analysis of a capacitively coupled contactless power transfer system[J]. IET Power Electronics, 2011, 4(7): 808–815. DOI:10.1049/iet-pel.2010.0243 |
| [13] |
陈希有, 伍红霞, 牟宪民, 等.
电流型电场耦合无线电能传输技术[J]. 中国电机工程学报, 2015, 35(9): 2279–2286.
CHEN Xiyou, WU Hongxia, MU Xianmin, et al. The current-type capacitively coupled wireless power transfer technology[J]. Proceedings of the CSEE, 2015, 35(9): 2279–2286. (in Chinese) |
| [14] | Chun S T, Yue S, Yu G S, et al. Determining multiple steady-state zcs operating points of a switch-mode contactless power transfer system[J]. IEEE Transactions on Power Electronics, 2009, 24(2): 416–425. DOI:10.1109/TPEL.2008.2007642 |
 2016, Vol. 39
2016, Vol. 39


