随着科学技术的迅速发展,各种对周边电磁环境要求越来越高的电子产品和弱电系统大量涌现,特高压输电线路对周围环境的无源干扰问题越显突出[1-3]。
输电线路无源干扰的早期研究方法是采用缩比模型实验进行测量,通过观测空间电场强度的变化明确干扰水平,确定干扰极大值[4-6]。1996年IEEE(institute of electrical and electronics engineers)制定了输电线路无源干扰的相关标准,该标准基于天线理论,阐述了535~1 705 kHz的谐振机理,给出了输电线路对中波部分频段的无源干扰计算和谐振频率预测的公式[7]。IEEE标准认为输电线路无源干扰谐振分为2种情况:当铁塔和地线未绝缘时,地线将相邻的2座基铁塔连接起来,加上铁塔和地线对地镜像组成了“环形天线”,当“环形天线”长度等于整数倍波长的1.08倍时,会产生干扰谐振现象,1.08为通过计算及实验研究的方法所得出的经验系数[8];当铁塔与地线绝缘时,基于“半波天线”原理,结合文献[9]的研究结果,认为铁塔高度达到λ/4(λ为波长)时会产生干扰谐振,考虑到铁塔横担的影响,将铁塔电气高度比实际塔高增加了15%。但这种场强变化分析手段无法解释1.7 MHz以上频率仍存在的无源干扰谐振现象[10]。
西安电子科技大学的学者在研究阵列天线时,从电磁场能量的角度出发,提出了广义谐振理论[11-12],将多天线电磁开放系统的谐振行为转变为针对多端口网络谐振品质因数的研究,并较好地预测出多天线系统在近场区的谐振频率。因此,可考虑将广域空间下的输电线路视为同样的电磁开放系统,将广义谐振理论引入输电线路这类电大尺寸的无源干扰研究领域。
采用广义谐振理论,构建广域空间下特高压输电线路及N组天线所组成的电磁开放系统,从而基于复坡印廷定理,通过寻找电场能量和磁场能量平衡时的频点对谐振频率进行预测。这种方法由于从电磁场能量出发,以谐振品质因数反映谐振强度,从而避开了传统研究受制于铁塔等效为线天线的电尺寸极限问题,可以阐述超过1.7 MHz以上的谐振现象。
1 输电线路无源干扰广义谐振的求解 1.1 广义谐振理论西安电子科技大学基于对飞机、舰船等大型电磁散射体的研究,将电磁散射在某一频率突然增强的现象定义为广义谐振[11],并对广义谐振行为进行了较为深入的研究,从传输线理论、广义谐振腔理论等方面对其进行了分析,推导了广义Foster定理与广义谐振条件的计算公式[12-15]。
上述广义谐振研究虽然针对的是以线天线为对象的多天线系统在近场区的谐振现象,但其理论方法和相关结论可为处于开放空间的输电线路无源干扰谐振提供较好的借鉴。因此,可考虑从电磁场能量的角度,以广义谐振理论为基础,将输电线路无源干扰谐振传统研究中的电场分析转变为电磁场能量平衡的研究,即可以通过电磁开放系统电磁场能量平衡的频点来预测谐振频率。
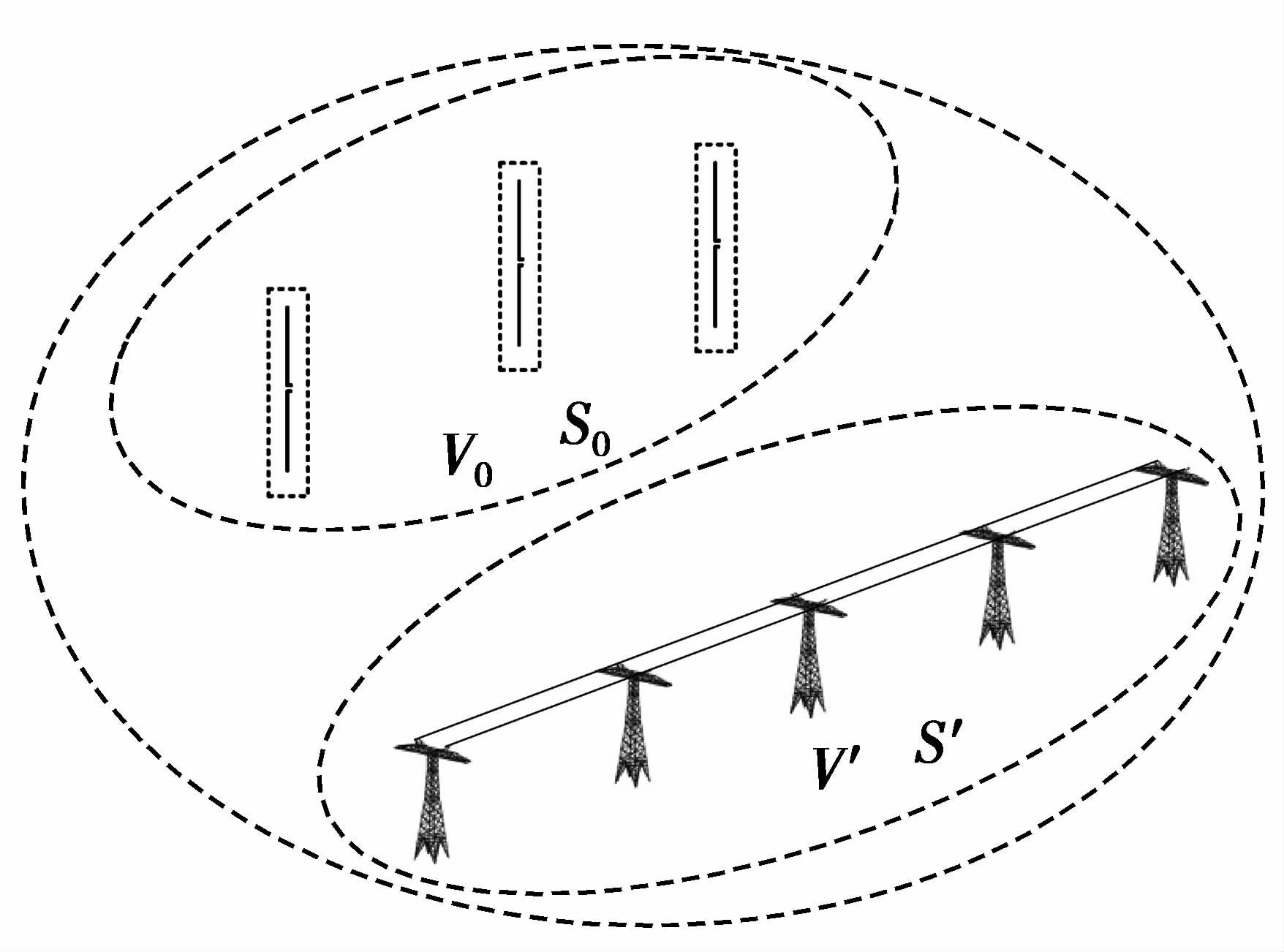
1.2 输电线路广义谐振模型输电线路和N组天线组成的电磁开放系统如图 1所示,封闭球面S包围的区域V中包含输电线路阵列铁塔和N组激励天线。天线阵列处于区域V0,每组天线分别处于区域vi,天线表面为Si,其中每组天线可等效为一个单端口网络,由于天线作为激励源,因此天线所在区域V0为有源区域。输电线路处于区域V′,为无源区域,S′为输电线路的表面。
|
图 1 输电线路及N组天线的广义电磁开放系统 Figure 1 Generalized electromagnetic open system of power transmission lines and N groups antenna |
广域空间下特高压输电线路阵列铁塔及激励天线组成的系统可以等效为一个电磁开放系统。现在假如将S面扩大到无穷远处,该电磁开放系统边界面上流过的复能量流密度为零,即该系统可以等效为广义电磁封闭系统,从而可以引入封闭系统的电磁场理论来研究电磁开放系统。在$V=\sum\limits_{i=1}^{N}{{{v}_{i}}}$区域中应用无源区域的复坡印廷定理,可将$S=\sum\limits_{i=1}^{N}{{{S}_{i}}}$所组成的广义电磁封闭系统中由空间场量表示的电磁场能量计算转化为导体电流计算。
1.3 基于复坡印廷定理的电磁能求解引入复频率s=α+jω(α与j分别代表实部和虚部,ω为频率),文献[11]给出了图 1中不包括输电线路V′区域的天线系统复坡印廷定理表达式:
| $-\underset{S}{\mathop{\oint }}\,\frac{1}{2}(\dot{E}\times {{\dot{H}}^{*}})\cdot dS=2\alpha ({{W}_{m}}+{{W}_{e}})+j2\omega ({{W}_{m}}-{{W}_{e}})+{{P}_{loss}},$ | (1) |
式中:${{P}_{loss}}={{\int }_{V}}\frac{1}{2}\sigma \dot{E}\cdot {{\dot{E}}^{*}}dv\ge 0$表示电磁封闭系统内部电磁场能量的损耗量;${{W}_{m}}={{\int }_{V}}\frac{1}{4}\mu \dot{H}\cdot {{\dot{H}}^{*}}dv\ge 0$和${{W}_{e}}={{\int }_{V}}\frac{1}{4}\varepsilon \dot{E}\cdot {{\dot{E}}^{*}}dv\ge 0$分别表示储存于电磁封闭系统内部的电场能和磁场能。参数ε、μ、σ分别为介电常数、磁导率和电导率;E和H分别为电场强度和磁场强度。
由于输电线路在整个电磁封闭系统内不主动发出电磁信号,这也即输电线路无源干扰的名称由来,因此,天线辐射场、输电线路散射场及空间任意场点的频率相同,从而可以同样采用如式(1)所示的复矢量形式表示$V-\sum\limits_{i=1}^{N}{{{v}_{i}}}$的无源区域麦克斯韦方程。假设天线是理想导体,在V′处σ≠0,因此,可得到$V-\sum\limits_{i=1}^{N}{{{v}_{i}}}$的复能量定理表达式:
| $\begin{align} & -{{\int }_{S}}\frac{1}{2}(\dot{E}\times {{{\dot{H}}}^{*}})\cdot dS+\sum\limits_{i=1}^{N}{{{\int }_{{{S}_{i}}}}}\frac{1}{2}(\dot{E}\times {{{\dot{H}}}^{*}})\cdot d{{S}_{i}}= \\ & 2\alpha ({{\int }_{V-\sum\limits_{i=1}^{N}{{{v}_{i}}}}}\frac{1}{4}\mu \dot{E}\times {{{\dot{H}}}^{*}}dv+{{\int }_{V-\sum\limits_{i=1}^{N}{{{v}_{i}}}}}\frac{1}{4}\varepsilon \dot{E}\times {{{\dot{E}}}^{*}}dv)+j2\omega \\ & ({{\int }_{V-\sum\limits_{i=1}^{N}{{{v}_{i}}}}}\frac{1}{4}\mu \dot{H}\times {{{\dot{H}}}^{*}}dv-{{\int }_{V-\sum\limits_{i=1}^{N}{{{v}_{i}}}}}\frac{1}{4}\varepsilon E\cdot \times E{{\cdot }^{*}}dv)+{{\int }_{V\prime }}12\sigma \dot{E}\times {{{\dot{E}}}^{*}}dv。 \\ \end{align}$ | (2) |
除天线端口位置外,在Si上其余点的切向电场为零,$(\dot{E}\times {{{\dot{H}}}^{*}})$·n=0,n为外法线方向。若天线i端口的等效电压为Ui,等效电流为Ii,可得
| $\sum\limits_{i=1}^{N}{{{\int }_{{{S}_{i}}}}}\frac{1}{2}(\dot{E}\times {{\dot{H}}^{*}})\cdot d{{S}_{i}}=\sum\limits_{i=1}^{N}{\frac{1}{2}}{{U}_{i}}{{I}^{*}}_{i}。$ | (3) |
同时,采用复函数表达,令
| ${{\int }_{S}}\frac{1}{2}(\dot{E}\times {{\dot{H}}^{*}})\cdot dS=Re{{\int }_{S}}\frac{1}{2}(\dot{E}\times {{\dot{H}}^{*}})\cdot dS+lm{{\int }_{S}}\frac{1}{2}(\dot{E}\times {{\dot{H}}^{*}})\cdot dS,$ | (4) |
将式(3)和(4)带入式(2),得
| $\begin{align} & \sum\limits_{i=1}^{N}{\frac{1}{2}{{U}_{i}}}{{I}^{*}}_{i}=Re{{\int }_{S}}\frac{1}{2}\left( \dot{E}\times {{{\dot{H}}}^{*}} \right)\cdot dS+ \\ & 2\alpha ({{\int }_{V-\sum\limits_{i=1}^{N}{{{v}_{i}}}}}\frac{1}{4}\mu \dot{H}\cdot {{{\dot{H}}}^{*}}dv+{{\int }_{V-\sum\limits_{i=1}^{N}{{{v}_{i}}}}}\frac{1}{4}\varepsilon \dot{E}\cdot {{{\dot{E}}}^{*}}dv)+ \\ & j\left[ \begin{matrix} 2\omega ({{\int }_{V-\sum\limits_{i=1}^{N}{{{v}_{i}}}}}\frac{1}{4}\mu \dot{H}\cdot {{{\dot{H}}}^{*}}dv-{{\int }_{V-\sum\limits_{i=1}^{N}{{{v}_{i}}}}}\frac{1}{4}\varepsilon \dot{E}\cdot {{{\dot{E}}}^{*}}dv)+ \\ lm{{\int }_{S}}\frac{1}{2}(\dot{E}\times {{{\dot{H}}}^{*}})\cdot dS+ \\ \end{matrix} \right] \\ & {{\int }_{V\prime }}\frac{1}{2}\sigma \dot{E}\cdot {{{\dot{E}}}^{*}}dv。 \\ \end{align}$ | (5) |
令${{P}_{rad}}=Re{{\int }_{S}}\frac{1}{2}(\dot{E}\times {{{\dot{H}}}^{*}})\cdot dS$表示天线向无穷远空间的辐射损耗功率,${{W}_{m}}={{\int }_{V-\sum\limits_{i=1}^{N}{{{v}_{i}}}}}\frac{1}{4}\mu \dot{H}\cdot {{{\dot{H}}}^{*}}dv、{{W}_{e}}={{\int }_{V-\sum\limits_{i=1}^{N}{{{v}_{i}}}}}\frac{1}{4}\varepsilon \dot{E}\cdot {{{\dot{E}}}^{*}}dv$分别表示$V-\sum\limits_{i=1}^{N}{{{v}_{i}}}$区域储存的磁场能和电场能,式(5)可表示为
| $\begin{align} & \sum\limits_{i=1}^{N}{\frac{1}{2}}{{U}_{i}}{{I}^{*}}_{i}={{P}_{rad}}+{{\int }_{V\prime }}\frac{1}{2}\sigma \dot{E}\cdot {{{\dot{E}}}^{*}}dv+2\alpha ({{W}_{m}}+{{W}_{e}})+ \\ & j[2\omega ({{W}_{m}}-{{W}_{e}})+lm{{\int }_{S}}12(\dot{E}\times {{{\dot{H}}}^{*}})\cdot dS]。 \\ \end{align}$ | (6) |
显然,式(6)为天线输电线路系统的复功率平衡关系。
将S面视为一个广义端口,引入正弦电路理论的复功率概念进行类比,复坡印廷矢量的虚部可表示为
| $lm{{\int }_{S}}\frac{1}{2}(\dot{E}\times {{{\dot{H}}}^{*}})\cdot dS=2\omega (W\prime m-W\prime e),$ | (7) |
式中,W′m、W′e分别表示天线系统$\sum\limits_{i=1}^{N}{{{v}_{i}}}$区域在S面内外交换的电场能和磁场能。
令${\tilde{W}}$m、${\tilde{W}}$e分别表示天线输电线路系统中总的磁场能和电场能,从而可以得到:
| ${{{\tilde{W}}}_{m}}={{W}_{m}}+W\prime m,{{{\tilde{W}}}_{e}}={{W}_{e}}+W\prime e。$ | (8) |
将式(7)和(8)带入式(6),可得
| $\sum\limits_{i=1}^{N}{\frac{1}{2}}{{U}_{i}}{{I}^{*}}_{i}={{P}_{rad}}+2\alpha ({{W}_{m}}+{{W}_{e}})+j2\omega (\tilde{W}m-\tilde{W}e)+{{\int }_{v\prime }}\frac{1}{2}\sigma \dot{E}\cdot {{{\dot{E}}}^{*}}dv。$ | (9) |
由式(9)可知,在电磁开放系统中,当V=V∞时,即r∞的球面所包围的体积,r∞表示天线系统的远场区,由于坡印廷矢量在远场区是一个实矢量,所以W′m=W′e=0。此时,天线辐射的电磁场能量中一部分以电场能和磁场能的形式储存于铁塔对地电容、线路电感等内部,另一部分被输电线路等有耗导体系统消耗。
1.4 特高压输电线路无源干扰的广义谐振因子从电磁场能量的角度,图 1所示的电磁开放系统可视为由S∞面和$\sum\limits_{i=1}^{N}{{{S}_{i}}}$面共同组成的一个广义的封闭系统,可将处于入射电磁波激励下的线路铁塔及其大地镜像构成的多基铁塔天线阵列系统等效为复杂多端口网络。
将级数$\sum\limits_{i=1}^{N}{\frac{1}{2}}$UiIi*采用矩阵形式进行表达,得
| $\sum\limits_{i=1}^{N}{\frac{1}{2}}{{U}_{i}}{{I}^{*}}_{i}=\frac{1}{2}{{I}^{+}}U,$ | (10) |
式中,[]+表示为共轭转置[*]+。
引入阻抗矩阵Z,有U=ZI,则式(9)可变为
| ${{I}^{+}}ZI={{P}_{rad}}+2\alpha ({{W}_{m}}+{{W}_{e}})+{{\int }_{v\prime }}\frac{1}{2}\sigma \dot{E}\cdot {{{\dot{E}}}^{*}}dv\text{ }+j2\omega (\tilde{W}m-\tilde{W}e)。$ | (11) |
广义电磁开放系统发生谐振的条件为系统储存的电场能量与储存的磁场能量平衡,即满足$\tilde{W}m=\tilde{W}e$,也即天线输电线路电磁开放系统发生广义谐振的条件为lm(I+ZI)=0。
定义广义谐振因子(GRF,generalized resonance factor)为
| ${{F}_{GRF}}=lm({{I}^{+}}ZI)。$ | (12) |
由此可以看出,通过计算广义谐振因子,可以准确预测电磁开放系统的广义谐振,广义谐振因子虚部等于0的点即为系统发生广义谐振的频点。显然,对于输电线路无源干扰的广义谐振,不仅与天线与输电线路系统之间所形成的系统有关,而且也与复杂的激励方式和输电线路本体负载情况有关。这也从理论上证明了在平面波和线天线激励下,输电线路无源干扰存在一定差异的原因。
同样可以采用等效导纳矩阵Y描述的形式为
| ${{F}_{GRF}}=lm({{U}^{+}}YU)。$ | (13) |
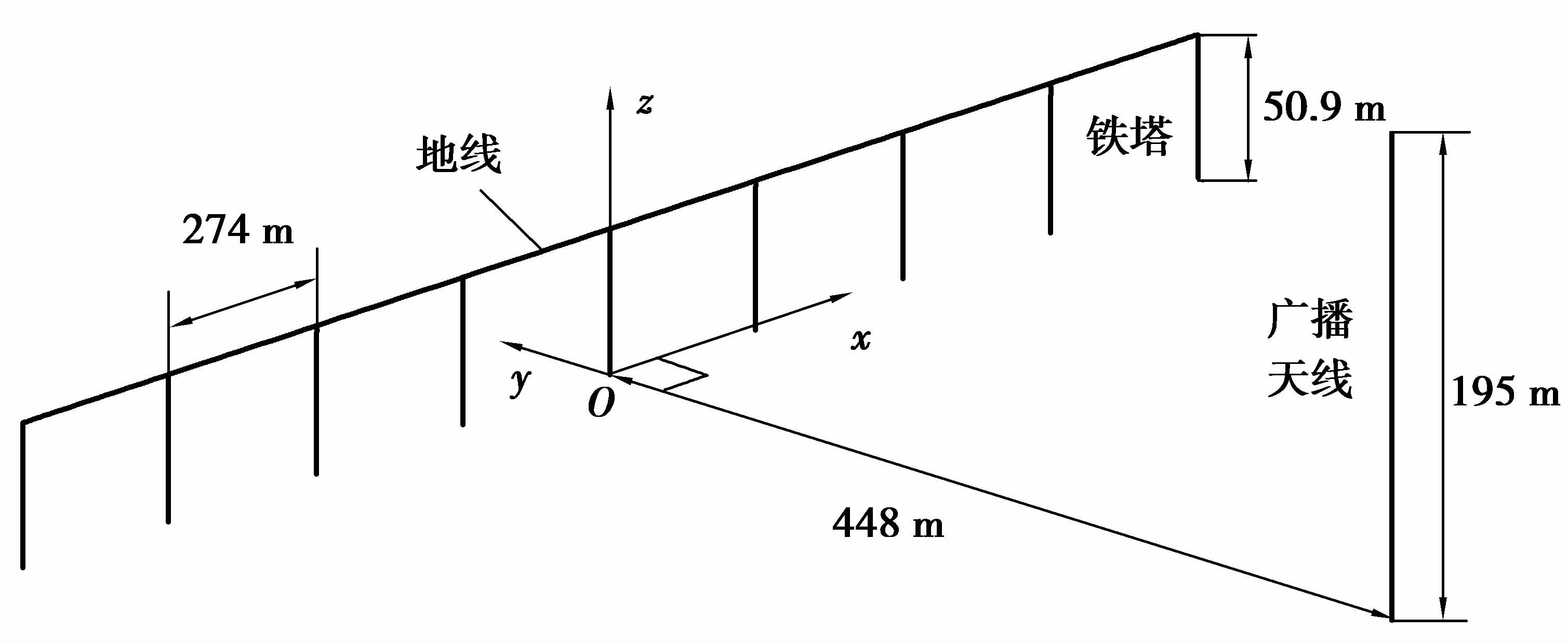
采用文献[16]提出算例进行研究,如图 2所示,9基铁塔作为研究对象,铁塔和地线均等效为直线模型,等效半径分别为3.51、0.71 m。激励源为高度195 m的线天线,与线路中心线相距448 m,馈电电压1 V,馈电段位于地面,研究远场区的无源干扰水平。
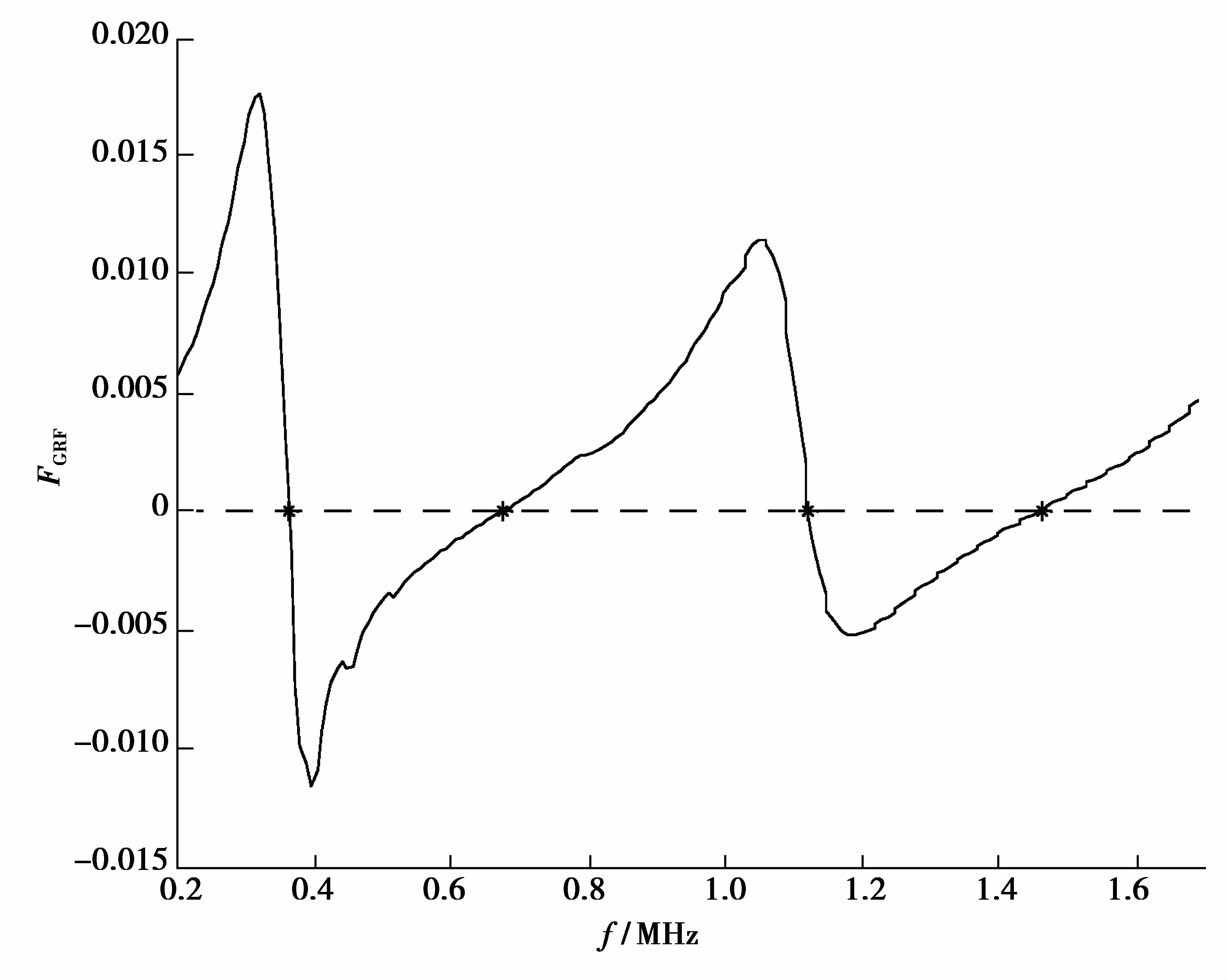
根据图 2所示的实际输电线路,文献[16]建立1:600尺寸比例缩比模型,通过实验得到中波广播频段内谐振频率测量值分别为0.434、0.850、1.280 MHz。图 2所示的“环形天线”长度为751.6 m,由IEEE标准给出的谐振频率预测公式求解的谐振频率为0.431、0.862、1.293、1.724 MHz。建立与文献[16]完全一致的模型,采用文中提出的算法,得到广义谐振因子预测曲线如图 3所示。图 3中,广义谐振因子等于0的点即为输电线路电磁开放系统谐振发生的频点。
|
图 3 铁塔和地线相连时的广义谐振因子 Figure 3 Generalized resonance factor when tower connected to ground |
IEEE标准、GRF谐振频率预测值与实验数据的对比,如表 1所示。由表 1可以看出,与缩比模型实测值相比,GRF谐振频率预测值最大误差为0.169 MHz。需要注意的是,文献[16]没有给出缩比模型的4倍波长谐振点测量值。
| 表 1 IEEE标准、GRF谐振频率预测值与实验数据的对比 Table 1 Resonance frequency comparison of the predicted values with the experimental data of IEEE Standard and GRF |
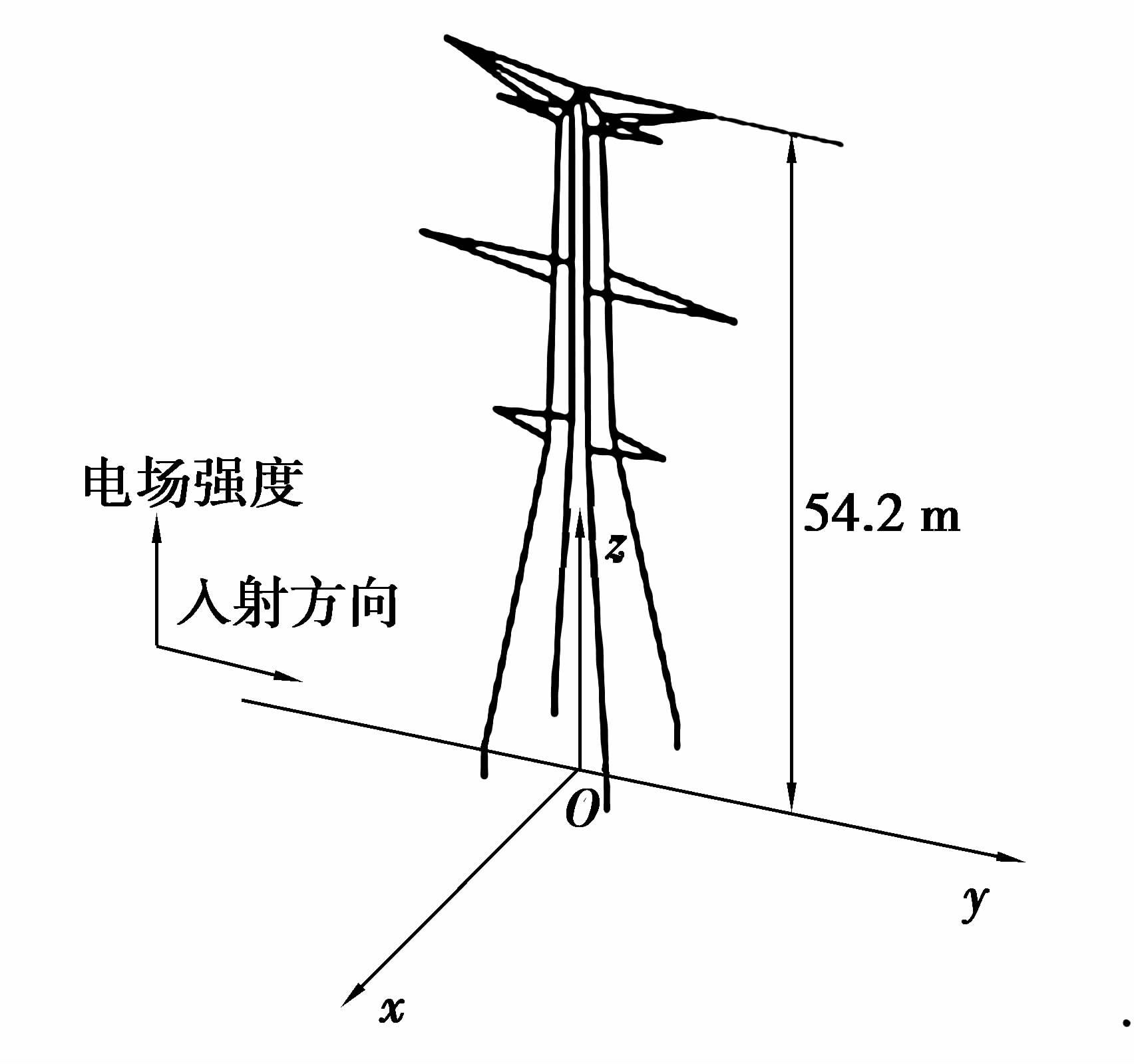
采用文献[17]提出的500 kV双回输电线路V1S型铁塔算例进行研究。如图 4所示,选择1基铁塔作为研究对象,铁塔的角钢等效为半径0.01 m圆柱,按照真实铁塔结构建模。激励源为频率范围0.6~2 MHz的垂直极化平面电磁波,电场强度为1 V/m,研究1 km处的无源干扰水平。
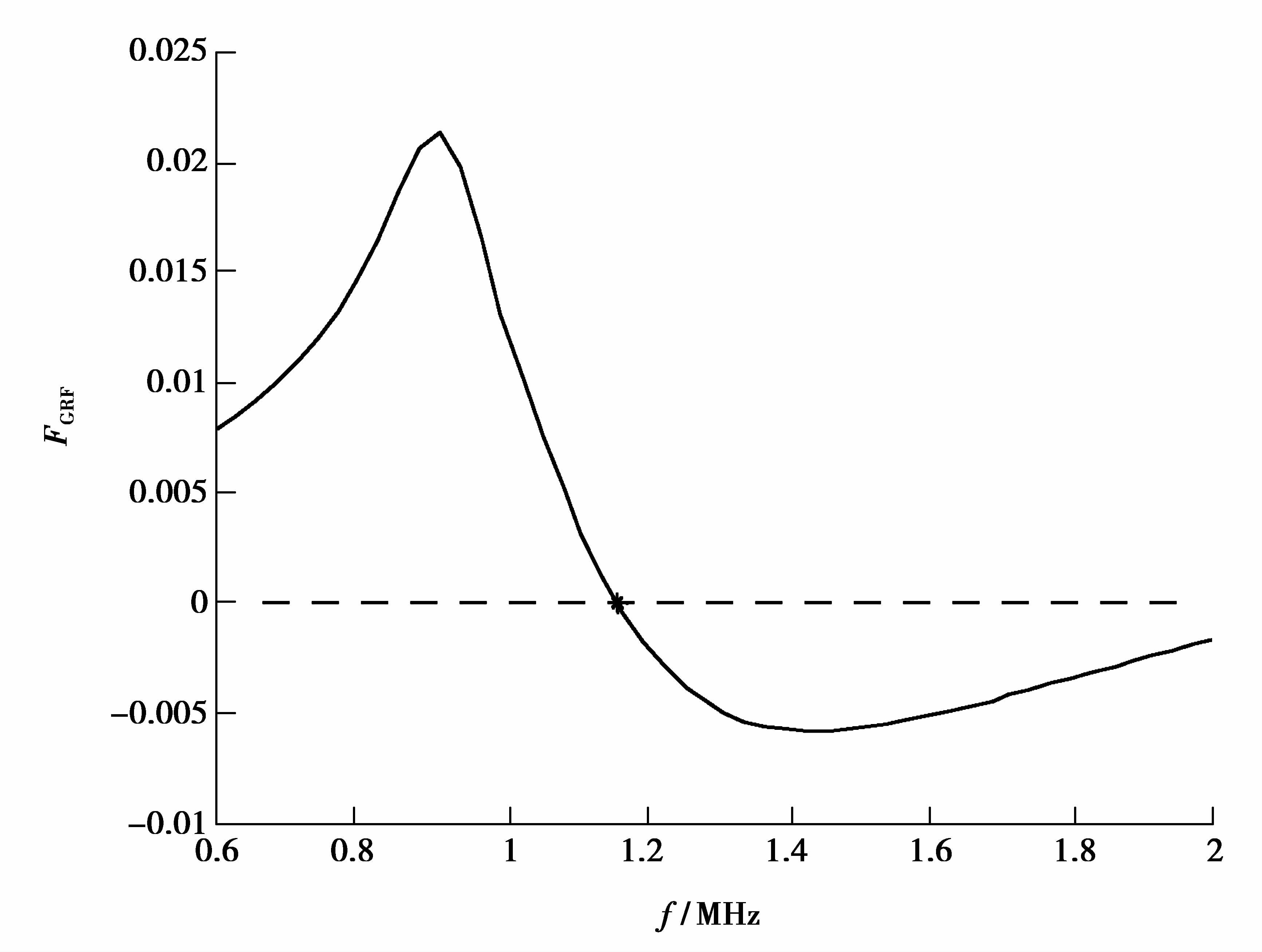
根据图 4对应的实际铁塔,文献[17]建立了1:200尺寸比例缩比模型。通过实验得到中波广播频段测量值为1.105 MHz。由IEEE标准给出的谐振频率预测公式求取的谐振频率为1.203 MHz。建立与文献[17]完全一致的模型,采用文中提出的算法,得到广义谐振因子预测曲线如图 5所示。
|
图 5 铁塔与地线绝缘时的广义谐振因子 Figure 5 Generalized resonance factor when tower and ground insulation |
IEEE标准、GRF谐振频率预测值与实验数据的对比,如表 2所示。可以看出,与缩比模型实测值相比,GRF谐振频率预测值最大误差为0.058 MHz。
| 表 2 IEEE标准、GRF谐振频率预测值与实验数据的对比 Table 2 Resonance frequency comparison of the predicted values with the experimental data of IEEE Standard and GRF |
实验采用较为简化的输电线路缩比模型,和实际线路有所区别,如没有考虑铁塔辅材及各种线路金具等。根据缩比模型实验理论,保证缩比模型能反映真实的场强,若缩比模型尺寸较实际线路缩小600倍,则电磁波频率和模型电导率必须同时增大600倍[18]。然而,实验中虽保证了频率的增大,但模型塔仍用钢进行制造,即电导率实际上没有变化。
2.3.2 仿真模型的误差仿真模型中的大地设为理想电导体,且铁塔与大地良好接地,这种理想化的处理使仿真模型无法完全模拟实际线路的感应电流分布及电磁波的传播特性。另外,仿真计算采用计算机完成,每个数据在计算机内都有一定的位数,在每一步计算中,都会存在舍入误差。
2.3.3 GRF计算引起的误差由公式(12)可以看出,电磁开放系统广义谐振与阻抗矩阵及激励方式有关。考虑到算例中,均严格按照IEEE的激励方式进行加载,这2个算例的激励方式对误差没有影响,误差主要来自系统的阻抗矩阵。
输电线路广义电磁开放系统的阻抗矩阵满足
| $\left[ \begin{matrix} 0 \\ {{U}_{l}} \\ \end{matrix} \right]=\left[ \begin{matrix} {{Z}_{tt}} & {{Z}_{tl}} \\ {{Z}_{lt}} & {{Z}_{ll}} \\ \end{matrix} \right]\left[ \begin{matrix} {{I}_{t}} \\ {{I}_{l}} \\ \end{matrix} \right],$ | (14) |
式中:t表示散射体铁塔的相关量;l表示激励源线天线的相关量;Ul表示线天线上的激励项;分块矩阵Ztt表示散射体铁塔感应电流对铁塔的自作用;分块矩阵Ztl表示线天线电流对铁塔的作用;分块矩阵Zlt表示铁塔感应电流对线天线的作用;分块矩阵Zll表示线天线电流对线天线的自作用,Zlt和Ztl互为转置矩阵;It表示铁塔表面的感应电流;Il表示线天线的电流。
电磁开放系统阻抗矩阵的取值直接影响谐振频点的预测,而铁塔的形状、高度是影响系统阻抗矩阵最主要的因素。下面对这些因子干扰谐振频点预测的影响情况进行探讨。
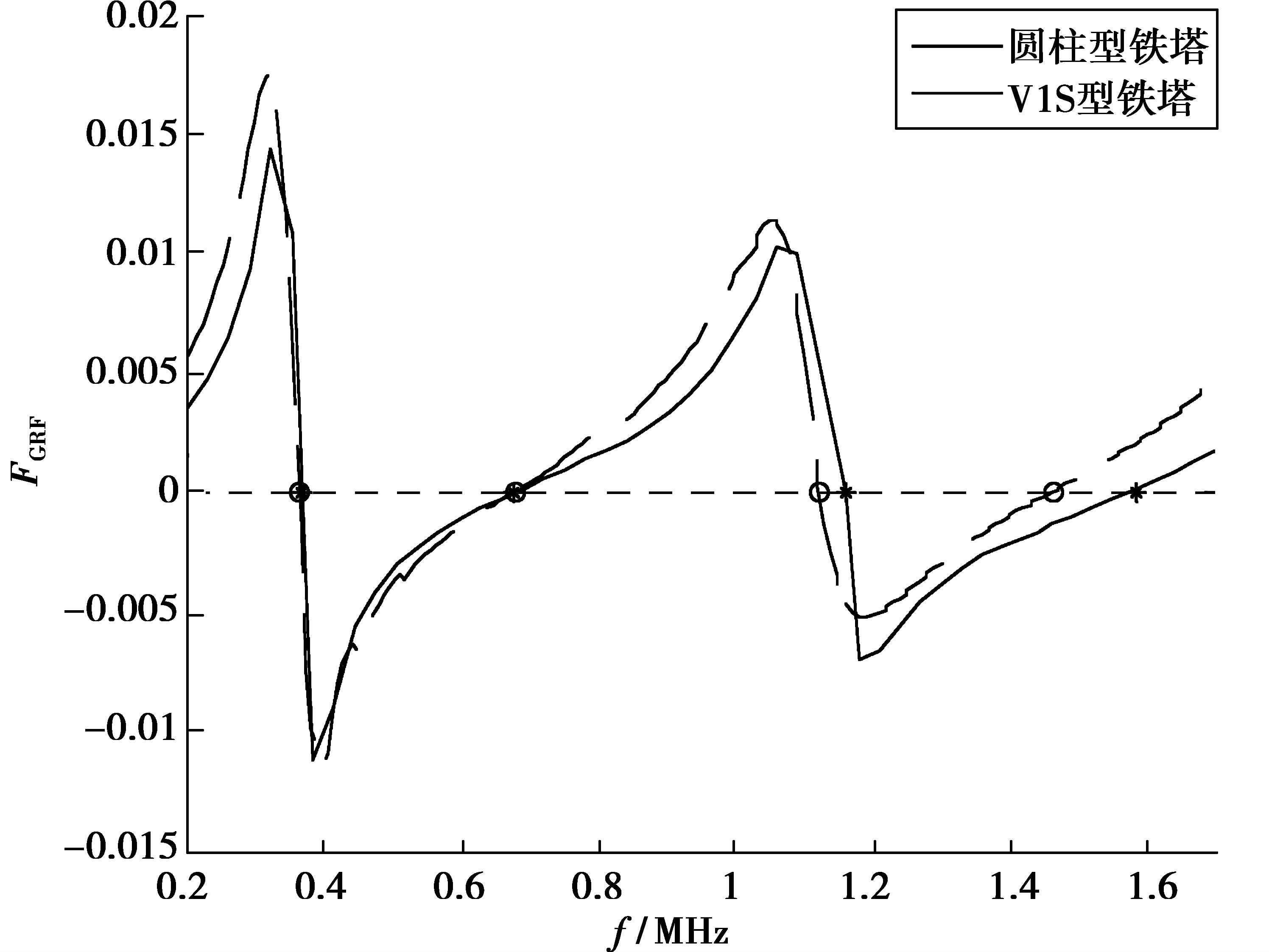
3 阻抗矩阵取值对谐振频率预测的影响 3.1 铁塔形状对回路波长谐振频率预测的影响上述算例中,铁塔所用模型为文献[16]提出的铁塔线模型,即将桁架式的铁塔等效为半径为3.51 m的圆柱体。现改变铁塔模型的形状,采用按V1S型铁塔桁架结构进行建模的复杂铁塔模型,其他参数保持不变,求得广义谐振因子预测曲线如图 6所示。
|
图 6 回路条件下铁塔形状变化的广义谐振因子 Figure 6 Generalized resonance factor of the tower shape changes under circuit conditions |
IEEE标准、GRF谐振频率预测值与实验数据的对比,如表 3所示。结合图 6与表 3可以看出,与缩比模型谐振频率的实测值相比,V1S型铁塔情况下,GRF谐振频率预测值最大误差不超过0.162 MHz。
| 表 3 IEEE标准、GRF谐振频率预测值与实验数据的对比 Table 3 Resonance frequency comparison of the predicted values with the experimental data of IEEE Standard and GRF |
从表 3可以看出,铁塔的形状影响整个电磁开放系统阻抗矩阵的取值,在考虑实际铁塔结构后,可以一定程度减小广义谐振频率预测误差。同时,随着频率的增大,即激励波长减小,2种塔型对谐振频率的预测准度有明显变化,这也从另一角度证明了文献[19]提出随频率增加,铁塔细节对无源干扰影响逐步突出的研究结论。
需要注意的是,结合表 1和表 3,即使考虑真实塔型,算例中1.28 MHz以下,采用广义谐振理论进行预测仍然较采用“环形天线”理论得到的“整数倍回路波长谐振频率”预测方法误差大。这说明1.7 MHz以下,输电线路回路中的感应电流对无源干扰占据决定性地位,其他细节因素对无源干扰的影响权重可以忽略。广义谐振理论虽也能预测无源干扰谐振频率,但受仿真模型及计算误差的影响,尚不能突破IEEE标准提出的“环形天线”理论预测精度。
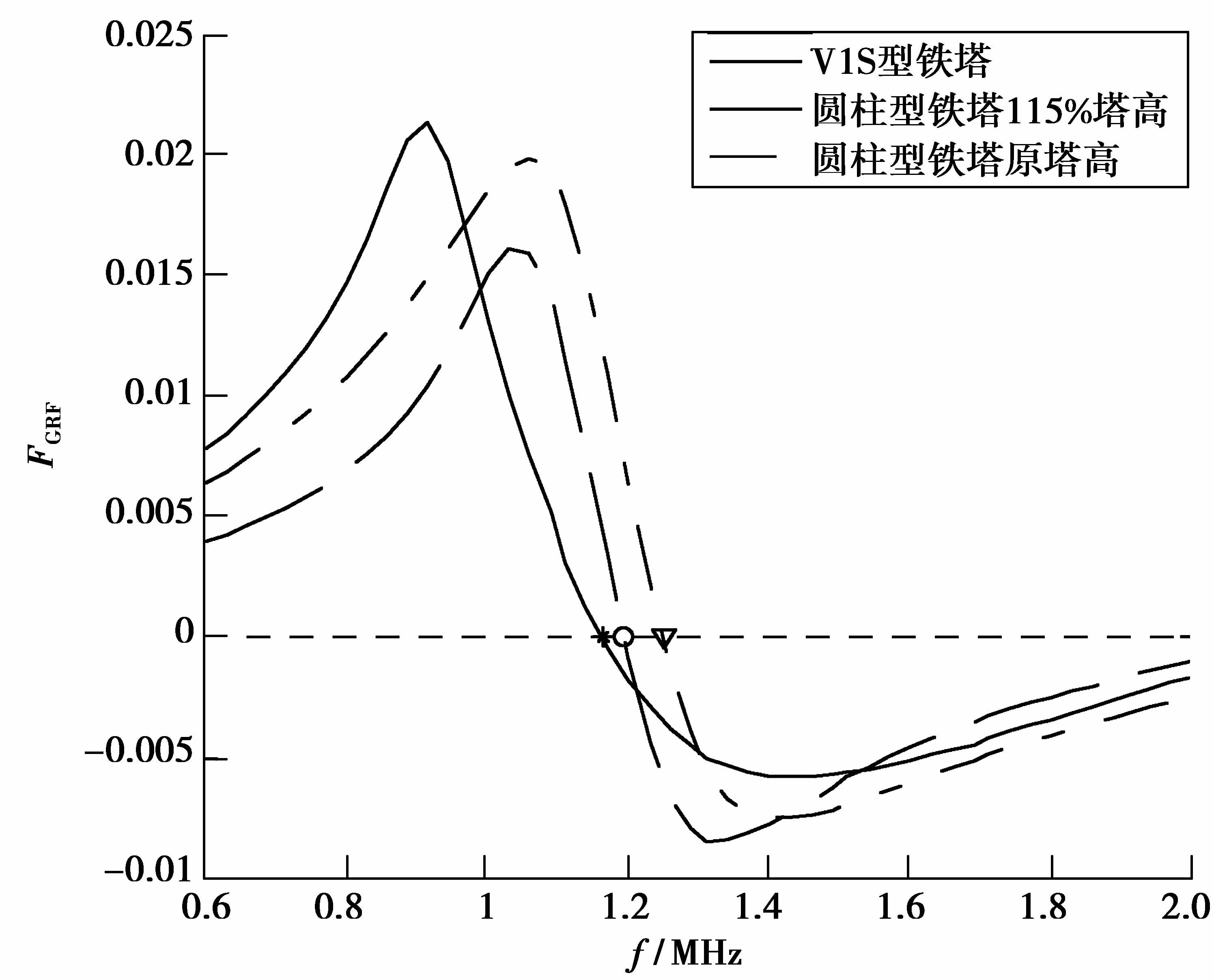
3.2 铁塔形状对单基铁塔谐振频率预测的影响算例中,按照真实塔型进行建模计算。此处,采用IEEE标准的建议,用半径为3.51 m的圆柱型模型等效替代V1S型铁塔,并按照IEEE标准的要求,圆柱型铁塔的高度增加15%,即模型高62.33 m。激励条件不变,求取的广义谐振因子预测曲线如图 7所示。同时,按原塔高建立圆柱铁塔模型,以供参考。
|
图 7 单基铁塔模型变化的广义谐振因子 Figure 7 Generalized resonance factor when single-base tower model changed |
IEEE标准、GRF谐振频率预测值与实验数据的对比,如表 4所示。结合图 7与表 4,也可以得出按真实塔型进行预测,结果更为准确的结论。
| 表 4 IEEE标准、GRF谐振频率预测值与实验数据的对比 Table 4 Resonance frequency comparison of the predicted values with the experimental data of IEEE Standard and GRF |
由于IEEE标准在处理铁塔与地线绝缘时,采用天线理论,即把整基铁塔视为激励天线从而进行谐振预测。显然,这种思想与铁塔被动散射电磁波的实情不符,结合表 2和表 4可以看出,此时广义谐振预测方法较IEEE标准的精度要高一些。
4 结 论1) 采用广义谐振理论,可以直接从电磁场能量的角度对特高压输电线路无源干扰进行研究,从而避开了传统研究受制于铁塔等效为线天线的电尺寸极限问题,实现更高频率的输电线路无源干扰谐振预测。从文中算例分析结果来看,这种方法较IEEE标准可以更为准确地预测中波频段干扰谐振频率。
2) 由于仅采用已有算例进行分析验证,研究频率尚未超出中波频段。下一步可考虑进行短波乃至更高频率的算例及实验验证,以对文中成果的应用频率范围进行拓展。
3) 当激励源固定后,影响谐振频率预测精度的因子是整个广义系统的阻抗矩阵,而阻抗矩阵受到特高压线路结构特性的影响。因此,可研究阻抗矩阵的决定性影响因子,在实际工程对线路进行针对性改造,从而大幅减小特高压线路无源干扰水平及其谐振特性。
| [1] |
刘振亚. 特高压电网[M]. 北京: 中国经济出版社, 2006: 2-8.
LIU Zhenya. Ultra-high voltage grid[M]. Beijing: China Economy Press, 2006: 2-8. (in Chinese) |
| [2] |
刘振亚. 智能电网技术[M]. 北京: 中国电力出版社, 2010: 1-4.
LIU Zhenya. Smart gird technology[M]. Beijing: China Electric Power Press, 2010: 1-4. (in Chinese) |
| [3] |
邬雄, 万保全. 输变电工程的电磁环境[M]. 北京: 中国电力出版社, 2009: 83-94.
WU Xiong, WAN Baoquan. Power transmission and transformation engineering of electromagntic environment[M]. Beijing: China Electric Power Press, 2009: 83-94. (in Chinese) |
| [4] | Kannus K, Lehtio A, Lakerv E. Radio and TV interference caused by public 24 kV distribution networks[J]. IEEE Transactions on Power Delivery, 1991, 6(4): 1856–1861. DOI:10.1109/61.97732 |
| [5] | Morris R M, Morse A R, Griffin J P, et al. The corona and radio interference performance of the nelson river HVDC transmission lines[J]. IEEE Transactions on Power Apparatus and Systems, 1979. |
| [6] |
唐波, 文远芳, 赵志斌, 等.
特高压角钢铁塔无源干扰计算的三维面模型[J]. 中国电机工程学报, 2011, 31(4): 104–111.
TANG Bo, WEN Yuanfang, ZHAO Zhibin, et al. Three-dimensional surface computation model of the reradiation interference from UHV angle-steel tower[J]. Proceedings of the CSEE, 2011, 31(4): 104–111. (in Chinese) |
| [7] | IEEE.IEEE Standard 1260-1996, IEEE guide on the prediction,measurement,and analysis of AM broadcast reradiation by power Lines[S].New York:IEEE, Inc.,1996. |
| [8] | Trueman C W, Kubina S J. Detuning power lines by isolating towers for the suppression of resonances[J]. IEEE Transactions on Broadcasting, 1986, 32(3): 44–55. |
| [9] | Trueman C W, Roobroeck T M, Kubina S J. Stub detuners for free-standing towers[J]. IEEE Transactions on Broadcasting, 1989, 35(4): 325–338. DOI:10.1109/11.40833 |
| [10] |
唐波, 张建功, 王惠丽, 等.
特高压输电线路无源干扰谐振特性及其影响因子研究[J]. 电工电能新技术, 2013, 33(6): 63–67.
TANG Bo, ZHANG Jiangong, WANG Huili, et al. Resonance characteristics and its impact factors of reradiation interference on radio station from UHV power Lines[J]. Advanced Technology of Electrical Engineering and Energy, 2013, 33(6): 63–67. (in Chinese) |
| [11] |
李龙, 梁昌洪, 史琰.
多天线系统的广义谐振研究[J]. 电子学报, 2003, 31(12): 2205–2209.
LI Long, LIANG Changhong, SHI Yan. Research on generalized resonance in multi-antenna system[J]. Acta Electronica Sinica, 2003, 31(12): 2205–2209. (in Chinese) |
| [12] |
李龙, 刘海霞, 史琰, 等.
电磁开放系统谐振行为的广义系统函数研究[J]. 中国科学, 2005, 35(10): 1096–1110.
LI Long, LIU Haixia, SHI Yan, et al. Generalized system function analysis of resonant behavior of electromagnetic open systems[J]. Science in China(Series F:Information Sciences), 2005, 35(10): 1096–1110. (in Chinese) |
| [13] |
金谋平, 梁昌洪, 史小卫.
多导体开放系统广义谐振传输线分析[J]. 电波科学学报, 2000, 15(1): 123–125.
JIN Mouping, LIANG Changhong, SHI Xiaowei. Transmission line analysis of generalized resonance in multiple conductors open system[J]. Chinese Journal of Radio Science, 2000, 15(1): 123–125. (in Chinese) |
| [14] |
褚庆昕, 梁昌洪.
广义Foster定理[J]. 西安电子科技大学学报, 1995, 22(4): 435–438.
CHU Qingxin, LIANG Changhong. Generalized Fosterd theorem[J]. Journal of Xi'an Electronic Science, 1995, 22(4): 435–438. (in Chinese) |
| [15] |
金谋平, 梁昌洪, 史小卫.
多导线散射中的广义谐振分析[J]. 电波科学学报, 2001, 16(3): 315–317.
JIN Mouping, LIANG Changhong, SHI Xiaowei. Analysis of generalized resonance in scattering by multiple wires[J]. Chinese Journal of Radio Science, 2001, 16(3): 315–317. (in Chinese) |
| [16] | Trueman C W, Kubina S J. Numerical computation of the reradiation from power lines at MF frequencies[J]. IEEE Transactions on Broadcasting, 1981, 27(2): 39–45. |
| [17] | Trueman C W, Kubina S J. Power line tower models above 1000 kHz in the standard broadcast band[J]. IEEE Transactions on Broadcasting, 1990, 36(3): 207–218. DOI:10.1109/11.59847 |
| [18] |
陈京平, 刘建平, 田军生.
特高压输电线路线塔对电磁波的衰减效应试验研究[J]. 现代电子技术, 2008(15): 146–148.
CHEN Jingping, LIU Jianping, TIAN Junsheng. Test study on the attenuation effects of electromagnetic wave caused by uhv overhead transmission lines and towers[J]. Modern Electronics Technique, 2008(15): 146–148. (in Chinese) |
| [19] |
唐波, 文远芳, 张小武, 等.
中短波段输电线路无源干扰防护间距求解的关键问题[J]. 中国电机工程学报, 2011, 31(19): 129–137.
TANG Bo, WEN Yuanfang, ZHANG Xiaowu, et al. Key problems of solving reradiation interference protecting distance between power transmission line and radio station at MF and SF[J]. Proceedings of the CSEE, 2011, 31(19): 129–137. (in Chinese) |
 2016, Vol. 39
2016, Vol. 39