2. 西北工业大学 机电学院, 西安 710072;
3. 陕西法士特齿轮有限责任公司, 西安 710009
2. School of Mechanical Engineering, Northwestern Polytechnical University, Xi'an 710072, P. R. China;
3. Shaanxi Fast Gear Co., Ltd., Xi'an 710009, P. R. China
星型齿轮传动广泛地应用于航空直升机的主减速器中,功率分流星型齿轮传动采用均载技术,但是在实际当中,由于不可避免的制造和安装误差,致使星型齿轮传动系统无法实现对载荷的完全平均分配,因此,解决星轮间载荷分配不均匀性问题,研究其均载特性,对于该系统充分发挥其优越性是非常重要的。
目前,国内外学者对星型齿轮传动系统的均载问题做了大量研究,文献[1]分析了两级星形4分支传动的均载特性,并通过均载试验进行了验证;文献[2]针对风电行星传动齿轮箱进行了均载特性的分析,认为制造误差是影响均载的主要因素;文献[3]对分扭传动系统的均载和轻量化进行了优化设计;文献[4]通过考虑齿轮位移协调,对2级星形传动多分流系统进行了均载特性研究;文献[5]以Ravigneaux式复合行星轮系为研究对象,通过计算传动系统的均载系数,获得各齿轮啮合误差与均载系数的关系曲线,分析了安装误差和偏心误差对系统均载特性的影响;文献[6]考虑到齿轮副齿侧间隙、系统综合误差和齿轮副模数与压力角的不相等,计算了系统的均载系数,分析了动态均载特性;文献[7]考虑了变形协调的应用,研究了2K-H行星齿轮传动系统的均载特性;文献[8]依据串联型行星轮系统均载机理,分析了齿轮制造误差和安装误差以及间隙浮动等因素对均载的影响;文献[9]针对多级行星齿轮传动的静力学均载特性进行了研究,分析了各种误差对均载的影响。还有一些学者对均载问题进行了研究[10-11]。
但以上研究中较少考虑星型齿轮功率流闭环的特性,不能从整体反应分流系统的力学特性。笔者建立两级星型五路功率分流传动的功率流闭环变形协调条件,结合力矩平衡条件,给出了一种计算均载系数的新方法,分析各构件的齿面制造误差、安装误差对均载特性的影响,研究太阳轮基于花键间隙浮动、内齿圈径向浮动对系统均载特性的影响,并通过实验来验证理论算法的正确性。
1 力学平衡及变形协调条件建立图 1所示是两级星型五路功率分流传动系统的传动形式示意图,其中,输入功率经太阳轮Zs分流给5个 Ⅰ 级星轮ZpⅠ,又经5个Ⅱ 级星轮ZpⅡ汇流到内齿轮Zr输出。
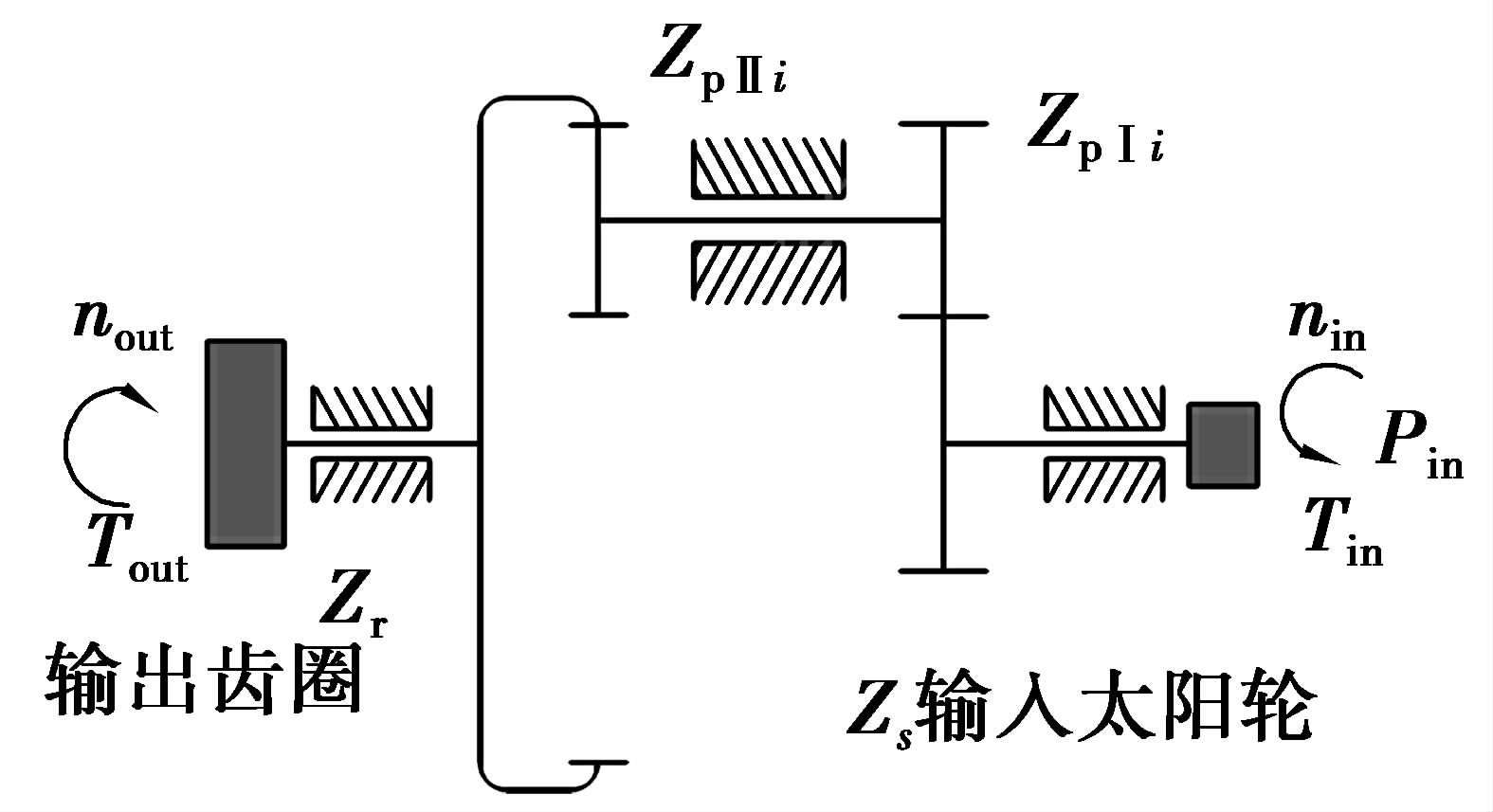
|
图 1 两级星型五路功率分流 Figure 1 Schematic diagram of the two stage star five way power split transmission system |
图 2为系统各构件之间的力学平衡关系示意图。
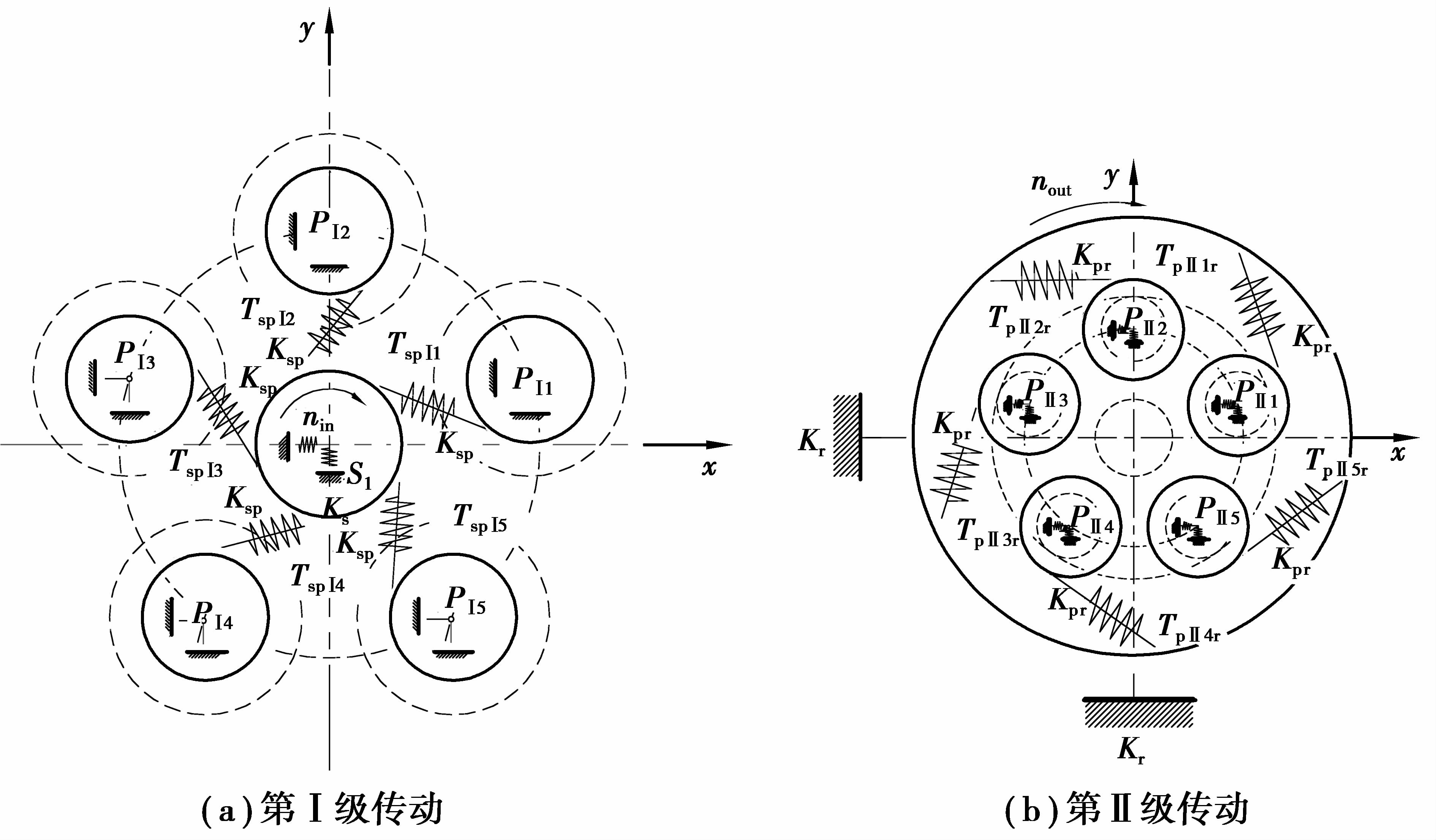
|
图 2 系统的力学平衡关系示意图 Figure 2 Diagram of the mechanical equilibrium diagram of the system |
图 2中,Ksp表示太阳轮和星轮之间的轮齿啮合刚度;Krp表示星轮和内齿圈之间的轮齿啮合刚度;Ks和Kr分别表示太阳轮和内齿轮支承处的等效弹性支撑刚度。PⅠi和PⅡi(i=1,2,…,5)分别表示第Ⅰ级和第Ⅱ级各星齿轮;FspⅠi和FpⅡir分别表示太阳轮和第Ⅰ级星轮之间的啮合作用力以及第Ⅱ级星轮和内齿圈之间的啮合作用力;T
根据图 2扭矩的关系,得到平衡条件:
| $\left\{ \begin{matrix} {{T}_{\text{in}}}+\sum\limits_{i=1}^{5}{{{T}_{\text{sp}i}}=0;} \\ -({{r}_{\text{bp}i}}/{{r}_{\text{bs}}}){{T}_{\text{sp}i}}+{{T}_{\text{p}i\text{r}}}=0. \\ \end{matrix} \right.$ | (1) |
其中rbpⅠi
图 3表示了系统两级各齿轮的扭转角关系,其中,ΔφPⅠi和ΔφPⅠi分别表示第Ⅰ级和第Ⅱ级星轮的扭转角;Δφs表示太阳轮的扭转角;Δφr表示内齿圈的扭转角,ΔφspⅠi表示太阳轮在扭矩作用下相对于第Ⅰ级星轮i的扭转角变形,ΔφspⅠi是TspⅠi的函数;ΔφpⅡir表示第Ⅱ级星轮i在扭矩作用下相对于内齿圈的扭转角变形,ΔφpⅡir是TpⅡir的函数。
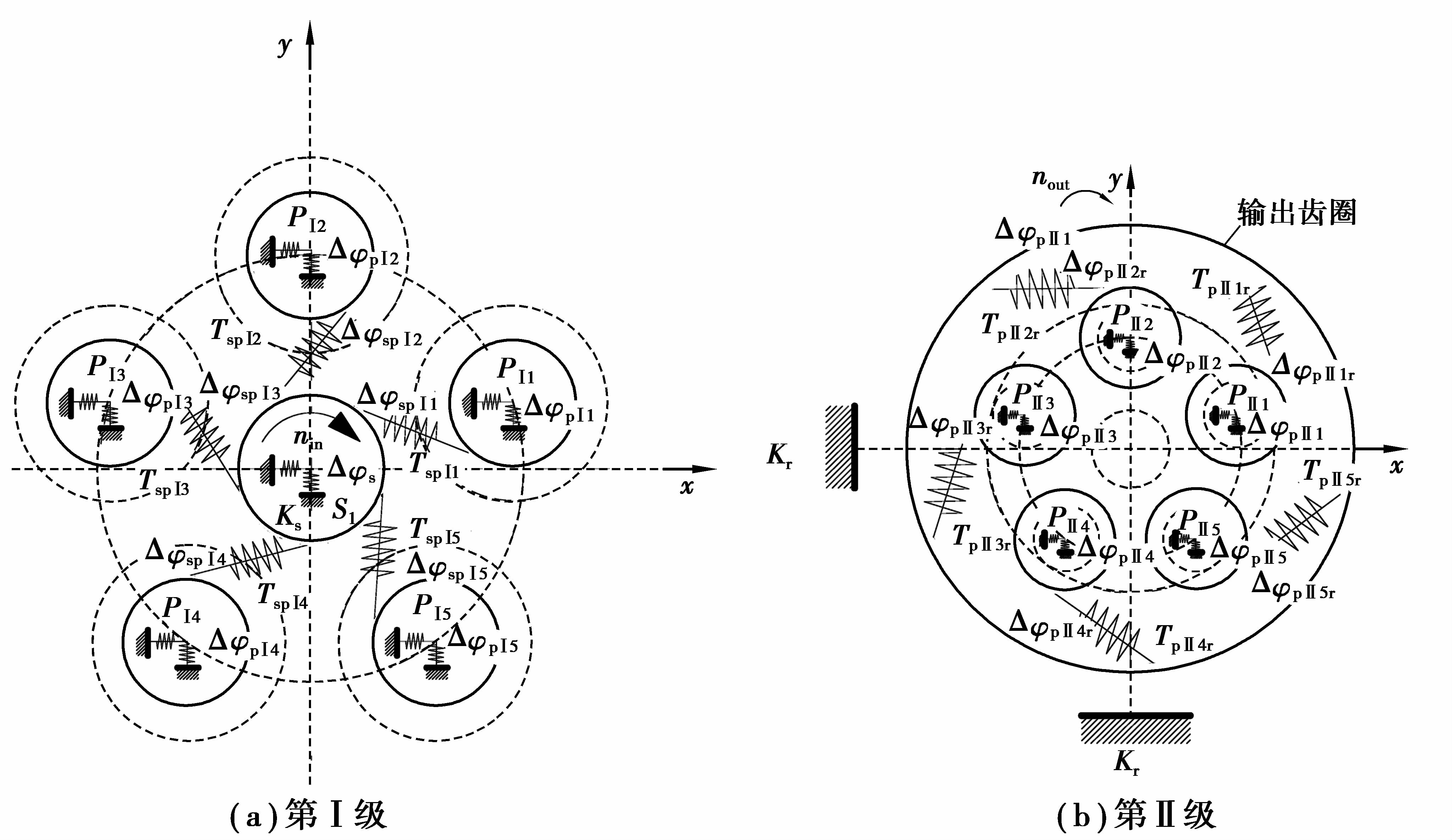
|
图 3 各齿轮扭转角关系示意图 Figure 3 Schematic diagram of the relationship between the torsion angle of the gear |
图 3中各齿轮的啮合扭转角满足如下关系:
| $\left\{ \begin{matrix} \Delta {{\varphi }_{\text{sp}i}}({{T}_{\text{sp}i}})=\Delta {{\varphi }_{s}}({{T}_{\text{sp}i}})-({{r}_{\text{bp}i}}/{{r}_{\text{bs}}})\Delta {{\varphi }_{\text{p}i}}({{T}_{\text{sp}i}}), \\ \Delta {{\varphi }_{\text{p}i\text{r}}}({{T}_{\text{p}i\text{r}}})=\Delta {{\varphi }_{\text{p}i}}({{T}_{\text{p}i\text{r}}})-({{r}_{\text{br}}}/{{r}_{\text{bp}i}})\Delta {{\varphi }_{\text{r}}}({{T}_{\text{p}i\text{r}}}). \\ \end{matrix} \right.$ | (2) |
由于ΔφijTij是Tij的函数,因此有:
| $\Delta {{\varphi }_{i}}=\Delta {{\varphi }_{\text{sp}i}}({{T}_{\text{sp}i}})+({{r}_{\text{bp}i}}/{{r}_{\text{bs}}})\Delta {{\varphi }_{\text{p}i\text{r}}}({{T}_{\text{sp}i}})=\Delta {{\varphi }_{s}}-({{r}_{\text{br}}}/{{r}_{\text{bp}i}})\Delta {{\varphi }_{\text{r}}}.$ | (3) |
由于Δφ1=Δφi,可以得到变形协调条件为
| $\left\{ \begin{matrix} \Delta {{\varphi }_{\text{sp}1}}({{T}_{\text{sp}1}})+({{r}_{\text{bp}1}}/{{r}_{\text{bs}}})\Delta {{\varphi }_{\text{p}1\text{r}}}({{T}_{\text{p}1\text{r}}})=\Delta {{\varphi }_{\text{sp}2}}({{T}_{\text{sp}2}})+({{r}_{\text{bp}1}}/{{r}_{\text{bs}}})\Delta {{\varphi }_{\text{p}2\text{r}}}({{T}_{\text{p}2\text{r}}}), \\ \Delta {{\varphi }_{\text{sp}1}}({{T}_{\text{sp}1}})+({{r}_{\text{bp}1}}/{{r}_{\text{bs}}})\Delta {{\varphi }_{\text{p}1\text{r}}}({{T}_{\text{p}1\text{r}}})=\Delta {{\varphi }_{\text{sp}3}}({{T}_{\text{sp}3}})+({{r}_{\text{bp}1}}/{{r}_{\text{bs}}})\Delta {{\varphi }_{\text{p}3\text{r}}}({{T}_{\text{p}3\text{r}}}), \\ \Delta {{\varphi }_{\text{sp}1}}({{T}_{\text{sp}1}})+({{r}_{\text{bp}1}}/{{r}_{\text{bs}}})\Delta {{\varphi }_{\text{p}1\text{r}}}({{T}_{\text{p}1\text{r}}})=\Delta {{\varphi }_{\text{sp}4}}({{T}_{\text{sp}4}})+({{r}_{\text{bp}1}}/{{r}_{\text{bs}}})\Delta {{\varphi }_{\text{p}4\text{r}}}({{T}_{\text{p}4\text{r}}}), \\ \Delta {{\varphi }_{\text{sp}1}}({{T}_{\text{sp}1}})+({{r}_{\text{bp}1}}/{{r}_{\text{bs}}})\Delta {{\varphi }_{\text{p}1\text{r}}}({{T}_{\text{p}1\text{r}}})=\Delta {{\varphi }_{\text{sp}5}}({{T}_{\text{sp}5}})+({{r}_{\text{bp}1}}/{{r}_{\text{bs}}})\Delta {{\varphi }_{\text{p}5\text{r}}}({{T}_{\text{p}5\text{r}}}). \\ \end{matrix} \right.$ | (4) |
将误差激励投影到啮合线方向上,得到位移激励ΔLij,如下所示:
| $\left\{ \begin{matrix} \Delta {{L}_{\text{sp}i}}=[({{x}_{\text{s}}}+\Delta {{A}_{x\text{s}}})-({{x}_{\text{p}i}}+\Delta {{A}_{x\text{p}i}})]\text{cos}{{\chi }_{\text{sp}i}}+[({{y}_{s}}+\Delta {{A}_{y\text{s}}})-({{y}_{\text{p}i}}+\Delta {{A}_{y\text{p}i}})]\text{sin}{{\chi }_{\text{sp}i}}, \\ \Delta {{L}_{\text{p}i\text{r}}}=[({{x}_{\text{p}i}}+\Delta {{A}_{x\text{p}i}})-({{x}_{\text{r}}}+\Delta {{A}_{x\text{r}}})]\text{cos}{{\chi }_{\text{p}i\text{r}}}+[({{y}_{\text{p}i}}+\Delta {{A}_{y\text{p}i}})-({{y}_{\text{r}}}+\Delta {{A}_{y\text{r}}})]\text{sin}{{\chi }_{\text{p}i\text{r}}}. \\ \end{matrix} \right.$ | (5) |
xs,ys,xpⅠi,ypⅠi,xpⅡi,ypⅡi,xr,yr分别为太阳轮、第Ⅰ级各星轮、第Ⅱ级各星轮、内齿圈沿x、y向的轴心变形量;ΔAxs,ΔAys,ΔAxpⅠi,ΔAypⅠi,ΔAxpⅡi,ΔAypⅡi,ΔAxr,ΔAyr分别为太阳轮、第Ⅰ级各星轮、第Ⅱ级各星轮、内齿圈沿x、y向的误差幅值;χspⅠi和χpⅡi
| $\left\{ \begin{matrix} {{T}_{\text{sp}i}}/{{r}_{\text{bs}}}={{K}_{\text{sp}}}({{r}_{\text{bs}}}\Delta {{\varphi }_{\text{s}}}-{{r}_{\text{bp}}}\Delta {{\varphi }_{\text{r}}}+\Delta {{L}_{\text{sp}i}}), \\ {{T}_{\text{p}i\text{r}}}/{{r}_{\text{bp}}}={{K}_{\text{pr}}}({{r}_{\text{bp}}}\Delta {{\varphi }_{\text{p}}}-{{r}_{\text{br}}}\Delta {{\varphi }_{\text{r}}}+\Delta {{L}_{\text{p}i\text{r}}}). \\ \end{matrix} \right.$ | (6) |
误差影响下的各齿轮副啮合转角为:
| $\left\{ \begin{matrix} \Delta {{\varphi }_{\text{sp}i}}({{T}_{\text{sp}i}})={{T}_{\text{sp}i}}/({{K}_{\text{sp}}}r_{\text{bs}}^{2})\Delta {{L}_{\text{sp}i}}/{{r}_{\text{bs}}}, \\ \Delta {{\varphi }_{\text{p}i\text{r}}}({{T}_{\text{p}i\text{r}}})={{T}_{\text{p}i\text{r}}}/({{K}_{\text{pr}}}r_{\text{bp}}^{2})\Delta {{L}_{\text{p}ir}}/{{r}_{\text{bp}}}. \\ \end{matrix} \right.$ | (7) |
偏心误差和装配误差的大小分别以E和A表示,各误差的方向角以β和γ表示。s,pⅠi,pⅡi,r,b为下标符号,分别对应太阳轮,第Ⅰ级第i个星轮,第Ⅱ级第i个星轮,内齿轮和轴承。第Ⅰ级传动中,由太阳轮偏心误差Es引起的角位移φEsi,太阳轮安装误差As引起的角位移φAsi,第i个星轮的偏心误差EpⅠi引起的角位移φEpⅠi和第i个星轮的安装误差ApⅠi引起的角位移φApⅠi分别如下:
| $\left\{ \begin{matrix} {{\varphi }_{}}_{{{E}_{}}_{si}}=-{{E}_{\text{s}}}\text{sin}({{\omega }_{\text{s}}}t+{{\beta }_{\text{s}}}+{{\alpha }_{w}}-{{\varphi }_{i}})/{{r}_{\text{bs}}}, \\ {{\varphi }_{}}_{{{A}_{}}_{si}}=-{{A}_{\text{s}}}\text{sin}({{\gamma }_{\text{s}}}+{{\alpha }_{w}}-{{\varphi }_{i}})/{{r}_{\text{bs}}}, \\ {{\varphi }_{}}_{{{E}_{}}_{\text{p}i}}=-{{E}_{\text{p}i}}\text{sin}(-{{\omega }_{\text{p}}}t+{{\beta }_{\text{p}i}}+{{\alpha }_{w}})/{{r}_{\text{bp}}}, \\ {{\varphi }_{}}_{{{A}_{}}_{\text{p}i}}=-{{A}_{\text{p}i}}\text{sin}({{\gamma }_{\text{p}i}}+{{\alpha }_{w}})/{{r}_{\text{bp}}}. \\ \end{matrix} \right.$ | (8) |
式中:第Ⅱ级传动中,第i个星轮偏心误差EpⅡi引起的角位移φEpⅡi,第i个星轮安装误差ApⅡi引起的角位移φApⅡi,内齿轮偏心误差Er引起的角位移φEr和内齿轮安装误差Ar引起的角位移φAr分别如下所示:
| $\left\{ \begin{matrix} {{\varphi }_{{{E}_{\text{p}i}}}}={{E}_{\text{p}i}}\sin (-{{\omega }_{\text{p}}}t+{{\beta }_{\text{p}2i}}-{{\alpha }_{\text{n}}})/{{r}_{\text{bp}}}, \\ {{\varphi }_{}}_{{{A}_{}}_{\text{p}}i}={{A}_{\text{p}i}}\sin ({{\gamma }_{\text{p}i}}-{{\alpha }_{\text{n}}})/{{r}_{\text{bp}}}, \\ {{\varphi }_{}}_{{{E}_{}}_{\text{r}}}={{E}_{\text{r}}}\sin (-{{\omega }_{\text{r}}}t+{{\beta }_{\text{r}}}-{{\alpha }_{\text{n}}}-{{\varphi }_{i}})/{{r}_{\text{br}}}, \\ {{\varphi }_{}}_{{{A}_{}}_{\text{r}}}={{A}_{\text{r}}}\sin ({{\gamma }_{\text{r}}}-{{\alpha }_{\text{n}}}-{{\varphi }_{i}})/{{r}_{\text{br}}}. \\ \end{matrix} \right.$ | (9) |
式中:太阳轮轴承偏心误差Ebs引起的角位移φEbs,第i个星轮联接轴轴承的偏心误差EbpⅠi引起的第Ⅰ级角位移φEbpⅠi,第i个星轮联接轴轴承的偏心误差EbpⅡi引起的第Ⅱ级角位移φEbp2i和内齿轮轴承偏心误差Ebr引起的角位移φEbr分别为:
| $\left\{ \begin{matrix} {{\varphi }_{{{E}_{}}_{\text{bs}}}}=-{{E}_{\text{bs}}}\text{sin}({{\omega }_{s}}t+{{\beta }_{\text{bs}}}+{{\alpha }_{w}}-{{\varphi }_{i}})/{{r}_{\text{bs}}}, \\ {{\varphi }_{{{E}_{}}_{\text{bp}i}}}={{E}_{\text{bp}i}}\text{sin}(-{{\omega }_{\text{p}}}t+{{\beta }_{\text{bp}i}}+{{\alpha }_{{}}}w)/{{r}_{bp}}, \\ {{\varphi }_{{{E}_{}}_{\text{bp}i}}}={{E}_{\text{bp}i}}\text{sin}(-{{\omega }_{\text{p}}}t+{{\beta }_{\text{bp}i}}-{{\alpha }_{\text{n}}})/{{r}_{\text{bp}}}, \\ {{\varphi }_{{{E}_{}}_{\text{br}}}}={{E}_{\text{br}}}\text{sin}(-{{\omega }_{r}}t+{{\beta }_{\text{br}}}-{{\alpha }_{\text{n}}}-{{\varphi }_{i}})/{{r}_{\text{br}}}. \\ \end{matrix} \right.$ | (10) |
式中:ωs、ωp和ωr分别为太阳轮、星轮和内齿轮的角速度;αw和αn分别为第Ⅰ和Ⅱ级传动的啮合角;φi为第i个星轮的位置角;rbpⅠ和rbpⅡ分别为第Ⅰ和Ⅱ级星轮的基圆半径。
将上述各项当量啮合误差叠加,由制造误差与安装误差在第一级和第二级啮合线上产生的累积角位移φEspi和φErpi分别为
| $\left\{ \begin{matrix} {{\varphi }_{{{E}_{}}_{\text{sp}i}}}={{\varphi }_{{{E}_{si}}}}_{}+{{\varphi }_{{{A}_{si}}}}_{}+{{\varphi }_{{{E}_{}}_{\text{p}i}}}+{{\varphi }_{{{A}_{}}_{\text{p}i}}}+{{\varphi }_{{{E}_{}}_{\text{bs}i}}}+{{\varphi }_{{{E}_{}}_{\text{bp}i}}}, \\ {{\varphi }_{{{E}_{}}_{\text{rp}i}}}={{\varphi }_{{{E}_{\text{r}i}}}}+{{\varphi }_{{{A}_{\text{r}i}}}}+{{\varphi }_{{{E}_{}}_{\text{p}i}}}+{{\varphi }_{{{A}_{}}_{\text{p}i}}}+{{\varphi }_{{{E}_{}}_{\text{br}i}}}+{{\varphi }_{{{E}_{}}_{\text{bp}r}}}. \\ \end{matrix} \right.$ | (11) |
设太阳轮、第Ⅰ级各星轮、第Ⅱ级各星轮、内齿圈沿x、y向的轴心浮动位移量分别为xs,ys,xpⅠi,ypⅠi,xpⅡi,ypⅡi,xr,yr,则浮动构件引起的侧隙改变量分别为:
| $\left\{ \begin{matrix} {{\Delta }_{\text{s}}}=-({{x}_{\text{s}}}\cos {{A}_{i}}+{{y}_{\text{s}}}\sin {{A}_{i}}), \\ {{\Delta }_{\text{r}}}=-({{x}_{\text{r}}}\cos {{B}_{i}}+{{y}_{\text{r}}}r\sin {{B}_{i}}), \\ {{\Delta }_{\text{p}i}}={{x}_{\text{p}i}}\cos {{A}_{i}}+{{y}_{\text{p}i}}\sin {{A}_{i}}, \\ {{\Delta }_{\text{p}i}}={{x}_{\text{p}i}}\cos {{B}_{i}}+{{y}_{\text{p}i}}\sin {{B}_{i}}. \\ \end{matrix} \right.$ | (12) |
式中:Ai为太阳轮与第Ⅰ级第i个星轮啮合线的方位角;Bi为第Ⅱ级第i个星轮与内齿轮啮合线的方位角。Ai和Bi分别可以表示为
| $\left\{ \begin{matrix} {{A}_{i}}=\pi /2-{{\alpha }_{\text{w}}}+{{\varphi }_{i}}, \\ {{B}_{i}}=\pi /2+{{\alpha }_{\text{n}}}+{{\varphi }_{i}}. \\ \end{matrix} \right.$ | (13) |
将上述两类啮合侧隙加起来,可以分别得到太阳齿轮与第Ⅰ级第i个星轮的综合啮合误差ΔspⅠi和第Ⅱ级第i个星轮与内齿轮的综合啮合误差ΔpⅡir为
| $\left\{ \begin{matrix} {{\Delta }_{\text{sp}i}}={{e}_{\text{sp}i}}+{{\Delta }_{\text{s}i}}, \\ {{\Delta }_{\text{p}i\text{r}}}={{e}_{\text{p}i\text{r}}}+{{\Delta }_{\text{r}i}}. \\ \end{matrix} \right.$ | (14) |
太阳轮通过花键间隙进行自由浮动,如果浮动件受力不平衡时,利用短花键及其联接的侧面间隙允许基本构件作径向及偏转位移,调整载荷的平均分配,实现均载,这种浮动结构的定心效果好,可以传递大扭矩。太阳轮基于花键间隙浮动形成的封闭力学关系,太阳轮的支撑刚度如图 4所示。
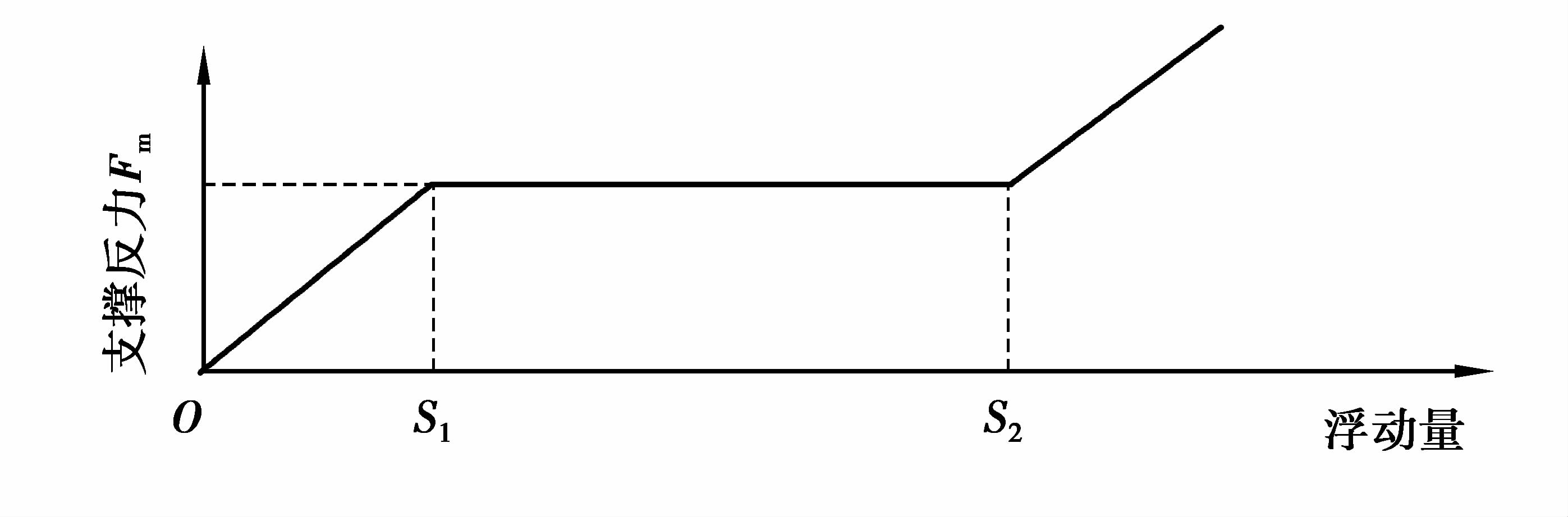
|
图 4 太阳轮浮动力学关系示意图 Figure 4 The diagram of the mechanical relationship of the floating of the sun gear |
太阳轮浮动过程中,受到5个与之相啮合的星轮的啮合力TspⅠi以及花键联接轴的支承反力Fm的共同作用。在花键传递扭矩的过程中,内外花键摩擦力Fm=τFN,FN表示内外花键之间的正压力,τ为摩擦系数,取τ=0.1。浮动太阳轮在一个啮合周期中,产生的浮动量${{R}_{\text{s}}}=\sqrt{\left( x_{\text{s}}^{\left( m \right)2}+y_{\text{s}}^{\left( m \right)2} \right)}\cdot x_{\text{s}}^{\left( m \right)}$和ys(m)分别表示在x和y方向的浮动量,m代表计算迭代次数。
图 4中的S1~S2为内外花键的径向间隙,浮动过程中,当支承反力小于摩擦力Fm时,内外花键之间不产生滑移,由输入轴的弯曲适应太阳轮位置变化,即0~S1段;当支承反力大于摩擦力Fm时,内外花键产生滑移,由滑移量适应浮动轮的位置变化,即S1~S2段;当滑移量超出S2时,即内外花键消除了径向间隙量,太阳轮位置变化重新由输入轴的弯曲变形决定,因此,太阳轮的支承反力在x、y向的分量ΔFxs(m)、ΔFys(m)分别为:
| $\begin{align} & \Delta F_{x\text{s}}^{\left( m \right)}=\left\{ \begin{matrix} -{{K}_{\text{w}}}\cdot {{R}_{\text{s}}}\cdot \cos (\xi _{\text{s}}^{\left( m \right)}), & 0\le {{R}_{s}}<{{S}_{1}}; \\ -{{F}_{\text{m}}}\cdot \text{cos}(\xi _{\text{s}}^{(m)}), & {{S}_{1}}\le {{R}_{\text{s}}}\le {{S}_{2}}; \\ -[{{F}_{\text{m}}}+{{K}_{\text{w}}}\cdot ({{R}_{s}}-{{S}_{2}})]\cdot \text{cos}(\xi _{\text{s}}^{(m)}), & \text{ }{{R}_{\text{s}}}>{{S}_{2}}. \\ \end{matrix} \right. \\ & \Delta F_{y\text{s}}^{(m)}=\left\{ \begin{matrix} -{{K}_{\text{w}}}\cdot {{R}_{\text{s}}}\cdot \text{sin}(\xi _{\text{s}}^{\left( m \right)}), & 0\le {{R}_{s}}<{{S}_{1}}; \\ -{{F}_{\text{m}}}\cdot \text{sin}(\xi _{\text{s}}^{\left( m \right)}), & {{S}_{1}}\le {{R}_{\text{s}}}\le {{S}_{2}}; \\ -[{{F}_{\text{m}}}+{{K}_{\text{w}}}\cdot ({{R}_{\text{s}}}-{{S}_{2}})]\cdot \text{sin}(\xi _{\text{s}}^{\left( m \right)}), & {{R}_{\text{s}}}>{{S}_{2}}. \\ \end{matrix} \right. \\ \end{align}$ | (15) |
式中:Kw表示弯曲刚度;ξ(m)表示向量(xs(m),ys(m))的方向角。
因此,得到太阳轮的浮动平衡条件为
| $\left\{ \begin{matrix} \sum\limits_{i=1}^{5}{{{T}_{\text{sp}i}}/{{r}_{\text{bs}}}\cdot \text{cos}{{\chi }_{\text{sp}i}}-\Delta {{F}_{x\text{s}}}=0,} \\ \sum\limits_{i=1}^{5}{{{T}_{\text{sp}i}}/{{r}_{\text{bs}}}\cdot \text{sin}{{\chi }_{\text{sp}i}}-\Delta {{F}_{y\text{s}}}=0.} \\ \end{matrix} \right.$ | (16) |
得到内齿圈浮动平衡条件为
| $\left\{ \begin{matrix} \sum\limits_{i=1}^{5}{{{T}_{\text{p}i\text{r}}}/{{r}_{\text{bp}}}\cdot \text{cos}{{\chi }_{\text{p}i\text{r}}}-{{K}_{\text{r}}}{{x}_{\text{r}}}=0,} \\ \sum\limits_{i=1}^{5}{{{T}_{\text{p}i\text{r}}}/{{r}_{\text{bp}}}\cdot \text{sin}{{\chi }_{\text{p}i\text{r}}}-{{K}_{\text{r}}}{{y}_{\text{r}}}=0.} \\ \end{matrix} \right.$ | (17) |
式中:Kr为太阳轮和内齿圈的支承刚度;xr、yr为内齿圈沿x、y向的轴心变形量。
3 均载系数求解及影响分析 3.1 均载系数求解以上各式联立求解,得到第Ⅰ级传动的均载系数JPⅠi和第Ⅱ级的均载系数JPⅡi为
| $\left\{ \begin{matrix} {{J}_{\text{p}i}}={{T}_{\text{sp}i}}/({{T}_{\text{in}}}/5), \\ {{J}_{\text{p}i}}=\frac{{{T}_{\text{p}i\text{r}}}}{({{r}_{\text{bp}i}}/{{r}_{\text{bp}i}})({{T}_{\text{in}}}/5)}. \\ \end{matrix} \right.$ | (18) |
则系统的均载系数J=max(JpⅠi,JpⅡi),均载系数的大小表征着系统的均载特性的好坏,均载系数越大,系统的均载特性越差。
3.2 误差对均载系数的影响两级星型五分支齿轮传动的各齿轮主要参数如表 1所示。
| 表 1 各齿轮的主要参数数据 Table 1 Main parameters of the gear data |
其中,系统的输入功率P=220 kW,输入转速为6 800 r/min,太阳轮与第Ⅰ级星轮的等效啮合刚度为Ksp=8.6×109 N/m,第Ⅱ级星轮与内齿圈的等效啮合刚度为Kpr=9.3×109 N/m,花键轴的弯曲刚度Kw=1.78×107 N/m,内齿圈的支承刚度为Kr=9.31×106 N/m。齿轮啮合刚度根据GB3480—83来计算,各长度误差值为6 μm,各构件的制造误差和安装误差的数值根据(GB1182—1184-80)的位置度误差而定。
太阳轮安装误差As,两级星轮安装误差ApⅠi和ApⅡi,内齿轮安装误差Ar单独作用时,得到各均载系数的计算结果如表 2所示。
| 表 2 安装误差单独作用时的均载系数 Table 2 Load sharing coefficient under the influence of the assembly error |
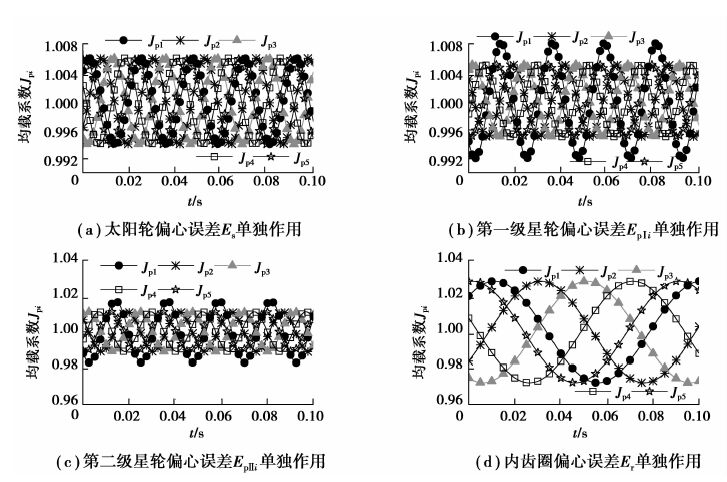
太阳轮偏心误差Es,两级星轮偏心误差EpⅠi和EpⅡi,内齿轮偏心误差Er单独作用时,均载系数随时间的曲线如图 5所示。
|
图 5 偏心误差分别单独作用时的均载系数 Figure 5 The load sharing coefficient of the effect of the eccentric error |
各偏心误差影响下的均载系数分别为1.006、1.010、1.017、1.028。对于制造和安装误差,在误差值相同的情况下,内齿轮的误差影响最大,第二级星轮误差次之,太阳轮的误差影响最小。
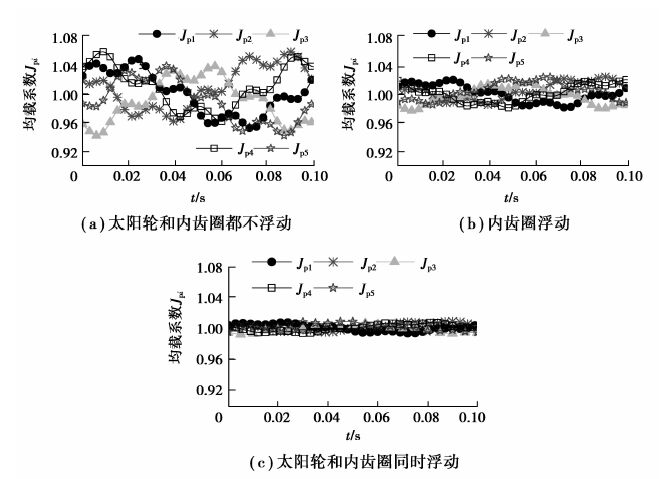
3.3 浮动对均载系数的影响构件浮动对均载的影响如图 6(a)(b)(c)所示。
|
图 6 太阳轮和内齿圈浮动对均载特性的影响 Figure 6 Effect of the floating of the sun gear and inner ring gear on the load sharing characteristics |
太阳轮和内齿圈都不浮动的情况下,均载系数为1.058,且波动较大;内齿圈浮动,太阳轮固定时,均载系数为1.023;同时浮动时,均载系数为1.008,具有良好的均载特性,可满足系统载荷的均匀分配。由于太阳轮基于花键间隙浮动,受到花键和相邻星轮的共同作用,因此花键间隙量不宜过大,过大的浮动间隙量会引起较大的冲击和振动。
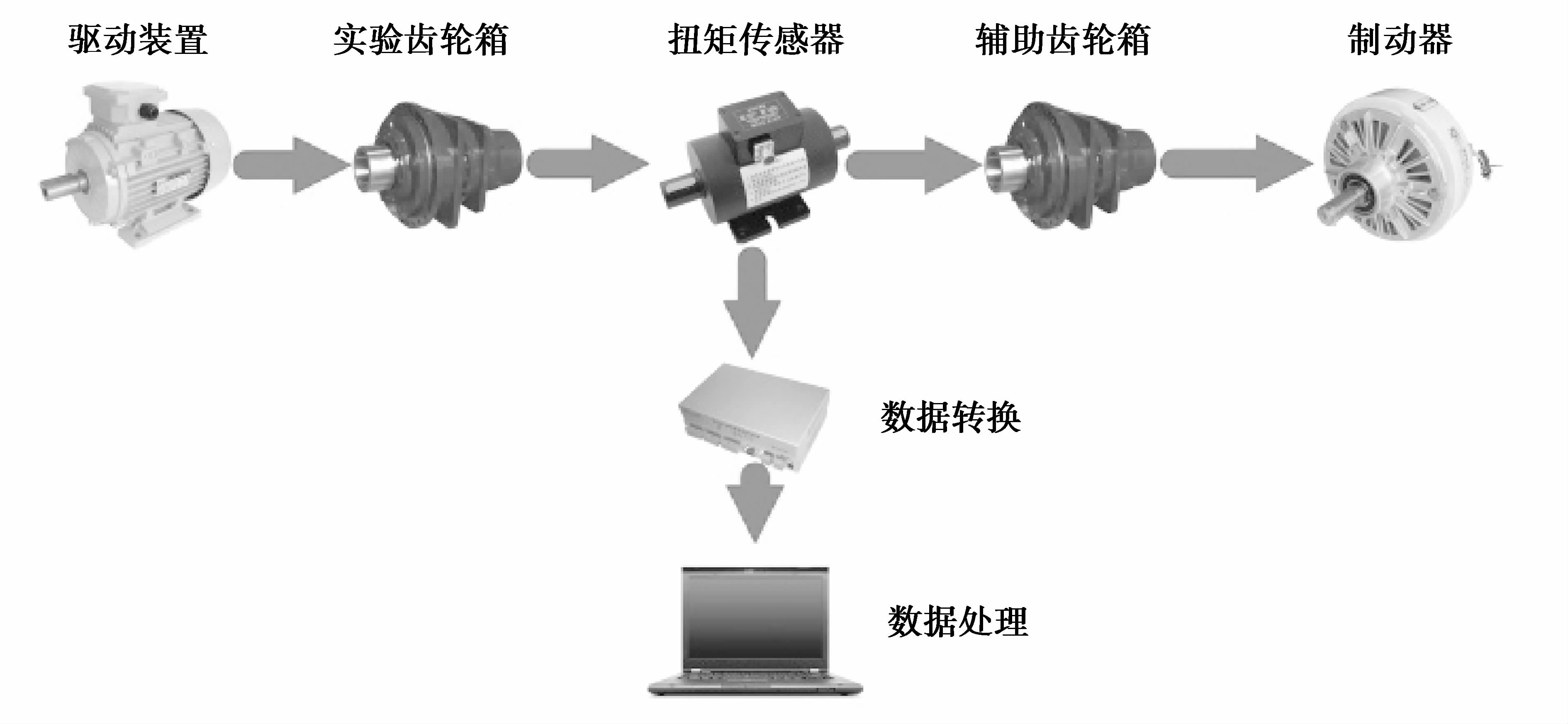
4 试验验证试验原理如图 7所示,整个试验台由5部分构成:动力源、主试齿轮箱、测量系统、陪试辅助齿轮箱以及负载。由电动机提供动力,通过变频器调节转速;主试齿轮箱为一个星型齿轮箱;测量系统包括两个扭矩传感器及其显示仪表;陪试齿轮箱为另一个星型齿轮箱;负载由磁粉制动器提供。将试验台安装完成并对系统的同轴度进行调试完成后,对系统的均载特性进行试验。五星轮轴通过扭力传感器分别测出5个斜齿星轮轴向力为P1、P2、P3、P4、P5,则星型齿轮系均载系数J=Pmax/(P1+P2+P3+P4+P5),式中Pmax为3个星轮轴向力最大值。在试验中,根据该星型减速器的实际状态分了5个载荷状态,对每个载荷状态进行了4次测量,取其平均值作为该载荷下的均载系数。
|
图 7 均载实验原理示意图 Figure 7 schematic diagram of the experimental principle |
测量得到的试验值与理论计算值对比,如表 3所示。
| 表 3 不同负载的理论和试验测量均载系数对比 Table 3 Comparison of theoretical and experimental measurements of different loads |
试验数据的变化趋势与理论计算值的变化趋势基本保持一致,试验数据较理论计算值偏大5%左右,基本在误差允许范围之内。理论分析中所建立的力学模型以及求解的方法是正确的。
5 结 论1) 变形协调条件更真实地反映了系统的整体力学特性,简化了两级星型五路功率分流传动的均载力学模型,该条件中构件的各类误差会相互叠加或者抵消,从本质上反映了由误差导致的均载问题,有利于系统的总体设计和分析,可以在具有功率分流闭环特性的其他齿轮传动系统中推广应用。
2) 载荷分配不均衡的主要原因是加工和装配时导致各齿轮间啮合状态发生改变,偏心和安装误差对系统的均载特性影响较大,误差的影响具有累加作用,尤其应注意第Ⅱ级构件的误差分布情况。
3) 两级星型五路分支传动系统较三路分支传动的承载能力得到很大提高,各分支的齿轮承受载荷变小,提高了疲劳寿命,太阳轮基于花键间隙的浮动支撑、内齿圈径向浮动支撑均载结构极大的改善了系统的均载性能。
| [1] | Mo S, Zhang Y D, Wu Q. Research on multiple-split load sharing of two-stage star gearing system in consideration of displacement compatibility[J]. Mechanism and Machine Theory, 2015, 88: 1–15. DOI:10.1016/j.mechmachtheory.2015.01.005 |
| [2] | Qiu X H, Han Q K, Chu F L. Load-sharing characteristics of planetary gear transmission in horizontal axis wind turbi-nes[J]. Mechanism and Machine Theory, 2015, 92: 391–406. DOI:10.1016/j.mechmachtheory.2015.06.004 |
| [3] |
付晨曦, 赵宁, 赵永志, 等.
基于FA-NSGA分扭传动系统的均载和轻量化优化设计[J]. 航空动力学报, 2014, 29(9): 2247–2255.
FU Chenxi, ZHAO Ning, ZHAO Yongzhi, et al. Load sharing and lightweight optimization design of torque-split transmission system based on FA-NSGA[J]. Journal of Aerospace Power, 2014, 29(9): 2247–2255. (in Chinese) |
| [4] |
莫帅, 张以都, 吴琼, 等.
考虑齿轮位移协调的2级星形传动多分流均载研究[J]. 四川大学学报(工程科学版), 2015, 47(4): 175–180.
MO Shuai, ZHANG Yidu, WU Qiong, et al. Research on lultiple-split load sharing of 2-stage star gearing system[J]. Journal of Sichuan University(Engineering Science Edition), 2015, 47(4): 175–180. (in Chinese) |
| [5] |
巫世晶, 彭则明, 王晓笋, 等.
啮合误差对复合行星轮系动态均载特性的影响[J]. 机械工程学报, 2015, 28(3): 29–36.
WU Shijing, PENG Zeming, WANG Xiaosun, et al. Impact of mesh errors on dynamic load sharing characteristics of compound planetary gear sets[J]. Journal of Mechanical Engineering, 2015, 28(3): 29–36. (in Chinese) |
| [6] |
叶福民, 朱如鹏, 靳广虎, 等.
考虑齿侧间隙的非等模数非等压力角行星齿轮系统的均载特性研究[J]. 振动与冲击, 2015, 34(11): 206–211.
YE Fumin, ZHU Rupeng, JIN Guanghu, et al. Study on load sharing characteristics of planetary gear train system with non-equivalent modulus and pressure angle considering backlashes[J]. Journal of Vibration and Shock, 2015, 34(11): 206–211. (in Chinese) |
| [7] |
杜进辅, 方宗德, 王宝宾, 等.
基于变形协调的行星轮系均载特性研究[J]. 航空动力学报, 2012, 27(5): 1166–1171.
DU Jinfu, FANG Zongde, WNAG Baobin, et al. Study on load sharing behavior of planetary gear train based on deformation compatibility[J]. Journal of Aerospace Power, 2012, 27(5): 1166–1171. (in Chinese) |
| [8] |
刘文彬, 刘更, 李阳.
串联型行星齿轮动系统均载特性分析[J]. 机械传动, 2012, 36(7): 92–95.
LIU Wenbin, LIU Geng, LI Yang. Research on static load sharing character of series planetary gear train[J]. Journal of Mechanical Transmission, 2012, 36(7): 92–95. (in Chinese) |
| [9] |
赵又红, 刘飞明, 谭援强, 等.
多级行星齿轮传动静力学均载研究[J]. 机械传动, 2012, 36(9): 19–22.
ZHAO Youhong, LIU Feiming, TAN Yuanqiang, et al. Statics analysis of uniform load in multistage planetary gear transmi-ssion[J]. Journal of Mechanical Transmission, 2012, 36(9): 19–22. (in Chinese) |
| [10] |
石万凯, 邱红友, 韩振华, 等.
风电齿轮箱人字行星传动的动态分析[J]. 重庆大学学报, 2015, 38(1): 95–102.
SHI Wankai, QIU Hongyou, HAN Zhenhua, et al. Dynamics research of wind turbine gearbox with herringbone planetary gear[J]. Journal of Chongqing University, 2015, 38(1): 95–102. (in Chinese) |
| [11] |
刘忠明.
提高风电齿轮箱功率密度的方法[J]. 重庆大学学报, 2015, 38(1): 133–139.
LIU Zhongming. Approaches to enhance power density of gearboxes for wind turbines[J]. Journal of Chongqing University, 2015, 38(1): 133–139. (in Chinese) |
 2016, Vol. 39
2016, Vol. 39

