关节臂式坐标测量机是三坐标测量机的一种类型,具有高精度和高效率的特点,是非常精密的测量仪器,现已广泛应用于各种领域,对保证产品质量起着重要的作用[1]。随着现代工业的快速发展,坐标测量领域在追求精度的同时也在追求更高的测量效率和更低的测量成本,这就对现有的坐标测量机提出了更高的要求,为此,国内外专家学者进行了大量的创新和研究。
Rugbani等[2]构建了一种新型的坐标测量机动力学模型,可基本消除阿贝误差,通过蒙特卡罗法对该模型测量结果进行评定,结果表明,此模型对测量精度有所提高。Ramu等[3]开发一种多传感器坐标测量机的参数模型,通过参数估计与误差校正策略进行实时测试,得到了较好的测量精度。高贯斌等[4]建立了坐标测量机的坐标系统和误差模型,通过仿真绘制关节空间误差分布图,得出关节长度等部件误差对测量结果的影响,提出对零件的加工精度要求及测量位置要求,进而提高测量精度。以上方法从坐标测量机内部机理出发,通过误差来源分析建模,不可避免出现各误差源相互影响的情况,导致动态测量误差精度受限。笔者采用虚拟建模法,通过测量软件测量检验,避免内部建模各个误差源相互影响,以期实现较精确的测量。
1 虚拟关节臂式坐标测量机构建 1.1 D-H矩阵建模虚拟关节臂式坐标测量机是依据关节臂的运动学规则构建的计量模型[5],以便对其测量过程进行模拟。D-H矩阵法将物理坐标系与测量机机械臂的各个关节坐标系相联系,通过前向动力学规则中相邻关节的坐标变换,进而在物理坐标系中确定关节臂末端执行器的位置和方向。
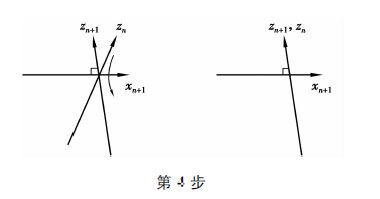
下面采用海克斯康公司的ROMER六轴关节臂式坐标测量机,以D-H矩阵法构建关节臂式测量机运动学模型[6-7]。D-H法坐标转换示意图如图 1所示,假设本地坐标系(xn,yn,zn),达到下一个坐标系(xn+1,yn+1,zn+1)步骤如下:
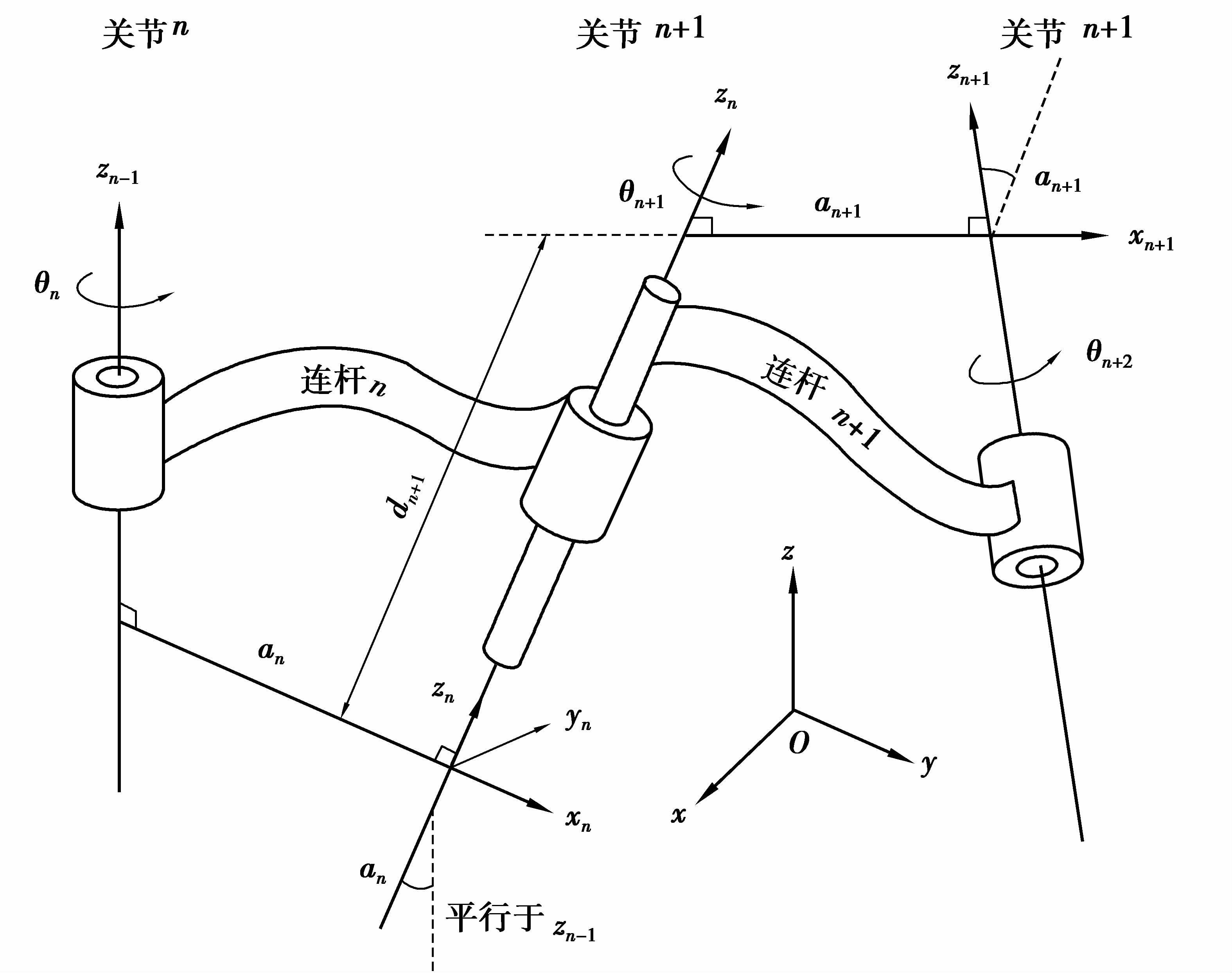
|
图 1 D-H法坐标转换示意图 Figure 1 Coordinate transformation of D-H method |
第1步,绕zn轴旋转θn+1,使得xn和xn+1互相平行,因为an和an+1都是垂直于zn轴的,因此,绕zn轴旋转θn+1使他们平行且共面。
第2步,沿zn轴平移dn+1距离,使得xn和xn+1共线,因为xn和xn+1已经平行且垂直于zn,沿着zn移动则可以使他们互相重叠在一起。
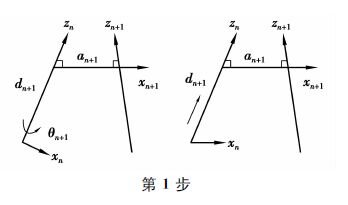
|
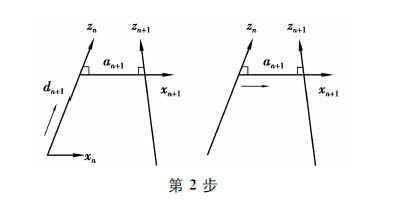
|
第3步,沿xn轴平移an+1的距离,使得xn和xn+1的原点重合。这时,2个参考坐标系的原点处在同一位置。
第4步,将zn轴绕着xn+1轴旋转αn+1,使得zn和zn+1轴对准。
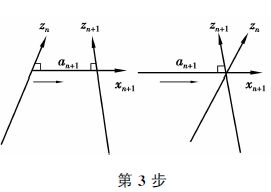
|
|
此时,坐标系(xn,yn,zn)和(xn+1,yn+1,zn+1)完全重合,实现了相邻坐标系变换。其中,θ为绕z轴的旋转角,d为在z轴上两条相邻公垂线之间的距离,a为关节偏移量,β为关节扭转。
综上所述,相连坐标变换分为4步:旋转、平移、平移、旋转。可以将物理坐标系转换到机械臂的基座,然后到第1个关节,第2个关节…直至末端执行器。右乘相连坐标变换矩阵得到矩阵Aii-1:
| $A_{i}^{i-1}=\text{Rot}(z,{{\theta }_{n+1}})\times \text{Tran}(0,0,{{d}_{i}})\times \text{Tran}({{a}_{n+1}},0,0)\times \text{Rot}(x,{{a}_{n+1}})$ | (1) |
式中:Aii-1为坐标变换矩阵;Rot为旋转;Tran为平移。
对ROMER六轴关节臂式坐标测量机进行建模,得到模型中相邻关节坐标的D-H变换矩阵:
| $A_{i}^{i-1}=\left[ \begin{matrix} \cos {{\theta }_{i}} & -\cos {{\beta }_{i}}\sin {{\theta }_{i}} & \sin {{\beta }_{i}}\sin {{\theta }_{i}} & {{a}_{i}}\cos {{\theta }_{i}} \\ \sin {{\theta }_{i}} & \cos {{\beta }_{i}}\cos {{\theta }_{i}} & -\sin {{\beta }_{i}}\cos {{\theta }_{i}} & {{a}_{i}}\sin {{\theta }_{i}} \\ 0 & \sin {{\beta }_{i}} & \cos {{\beta }_{i}} & {{d}_{i}} \\ 0 & 0 & 0 & 1 \\ \end{matrix} \right],$ | (2) |
式中:θi为绕z轴的旋转角;αi为关节扭转;di为在z轴上两条相邻公垂线之间的距离[8]。从公式(2)中可以得出D-H变换矩阵由4个部分构成:
| $A_{i}^{i-1}=\left[ \begin{matrix} {{s}_{x}} & {{o}_{x}} & {{r}_{x}} & {{p}_{x}} \\ {{s}_{y}} & {{o}_{y}} & {{r}_{y}} & {{p}_{y}} \\ {{s}_{z}} & {{o}_{z}} & {{r}_{z}} & {{p}_{z}} \\ 0 & 0 & 0 & 1 \\ \end{matrix} \right]=\left[ \begin{matrix} R & R \\ O & I \\ \end{matrix} \right].$ | (3) |
式中:s,o,r为相对坐标系(x,y,z)对于参考坐标系的方向余弦;P为位置向量;O为零矩阵;I为单位1。
1.2 前向动力学规划采用前向动力学规划将一个设备的结构位置转换到物理坐标系中。前向动力学规划[9]可表述为骨骼运动,一个典型的具有层次的骨骼运动如下:当举起手臂时,手肘会跟随运动,手腕跟随手肘运动,手指跟着手腕运动,即父骨骼运动时,所有的子骨骼也随之运动。
上述原理可用矩阵乘法表达:
| ${{T}_{n,i}}={{A}_{i+1}}{{A}_{i+2}}{{A}_{i+3}}\cdots {{A}_{n}},$ | (4) |
式中:n为自由度,即关节数量;i为某一关节;A为相邻关节坐标的变换矩阵,存储了关节间的位置和方向信息;Tn,i为从基座到末端执行器所有关节坐标的总变换矩阵。
2 测量机几何参数的精度测定关节臂式坐标测量机几何参数的精度测定是一个多级的任务,对各个关节坐标进行前行动力学适配,得到实际的关节臂式坐标测量机参数,且实际参数都必须在一定的测量不确定度范围以内。通过实测参数与制造商提供的数据进行对比,进而根据差异改良模型。
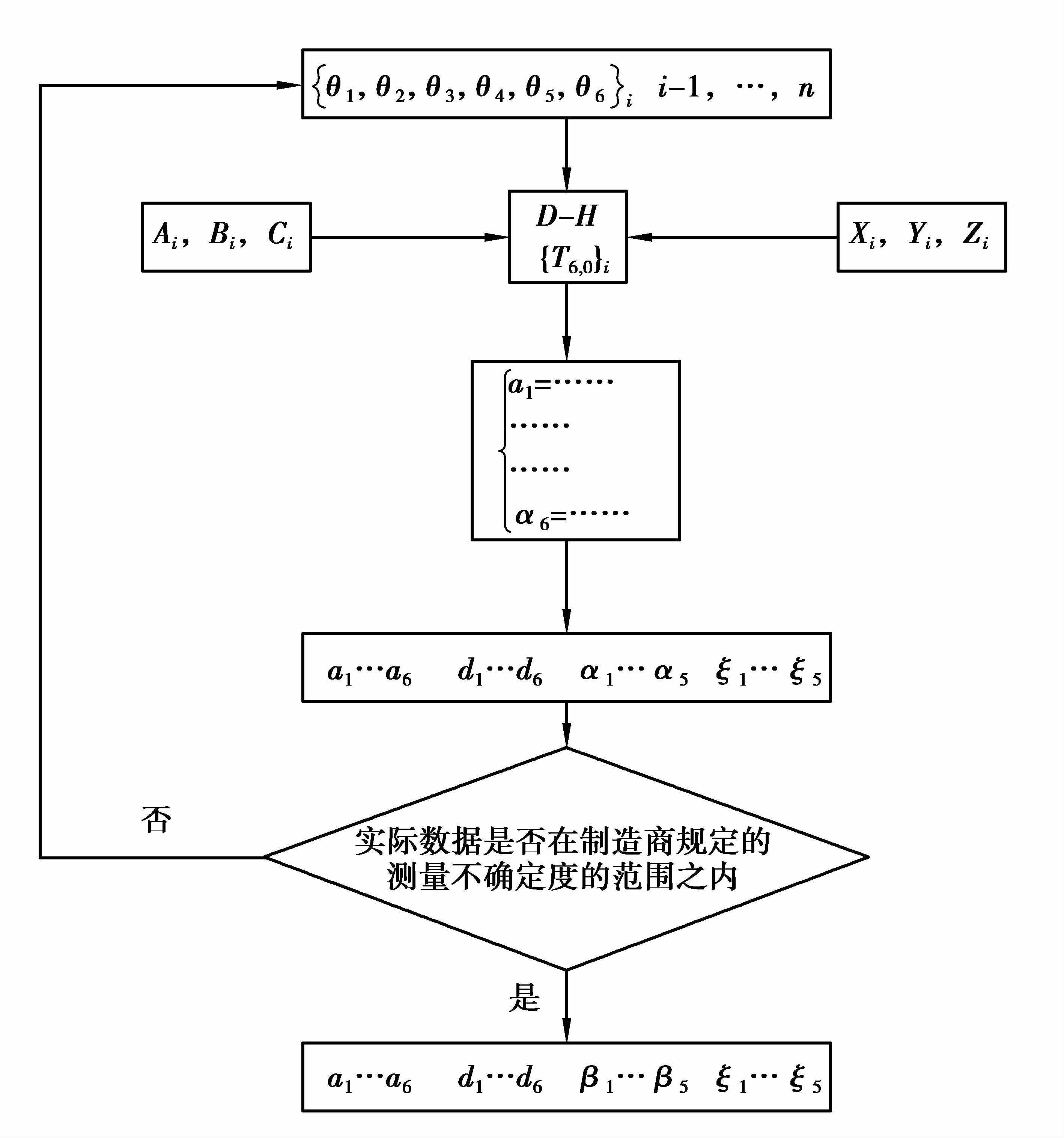
六轴关节臂式坐标测量机包括公垂线长度、相连Z轴的角度、相连公垂线距离和零点漂移共有22个参数[10-11]。为确定实际关节臂参数,需进行多次关节臂测量。测量时利用公式(4)建立22个方程组,进而求出22个参数的实际解,具体参数测量流程如图 2所示。
|
图 2 几何参数测量流程 Figure 2 Measurement process of geometric parameters |
为实现上述过程,每次测量需规定一个末端位置,将配置坐标θi(相邻两个关节坐标变换时绕z轴的旋转角称作配置坐标)、真实关节坐标(Xi,Yi,Zi)及末端触针的方向坐标(Ai,Bi,Ci)带入先前的方程组中求解,以得到准确的几何参数。
表 1为关节臂式坐标测量机给定参数与实测参数对比,由表中数据可以看出,计量模型已可以较准确地模拟物理坐标测量机测量。 其中,θi的读数来自编码器的角度测量系统;(Ai,Bi,Ci)为末端触针的方向坐标;(Xi,Yi,Zi)是从测量机配套软件中获得的坐标参数。
| 表 1 制造商给定参数与实测参数对比 Table 1 Comparison of the measured parameters and parameters given by manufacturter |
其中:βi为相邻z轴之间的角度;ai为公垂线的长度;di为z轴上两条相邻公垂线之间的距离;ξi为零点漂移。
3 模型的校验与测量分析模型检验是进行实际工件测量的基础,此处采用PC-DMIS测量软件对模型进行检验。PC-DMIS测量软件可以在一定范围内选择若干随机点,且点的分布符合高斯分布(x,σ),其中x表示高斯分布的平均值,σ表示高斯分布的标准差。在仿真出每个随机点的坐标之前,首先利用物理关节臂式坐标测量机测量出若干随机点的实际坐标数据,并将这些实际坐标数据的平均数作为平均值,将制造商给出的标准不确定度作为标准差。之后,利用此前实际测量时保存的编码器角度数据,测量触针的方向数据,建立编码器的数学模型。最终,对其余每个随机点的测量过程都由符合高斯分布的概率密度函数分配给编码器指令,并以此控制虚拟关节臂的动作,完成所有随机点的坐标测量和校验工作。
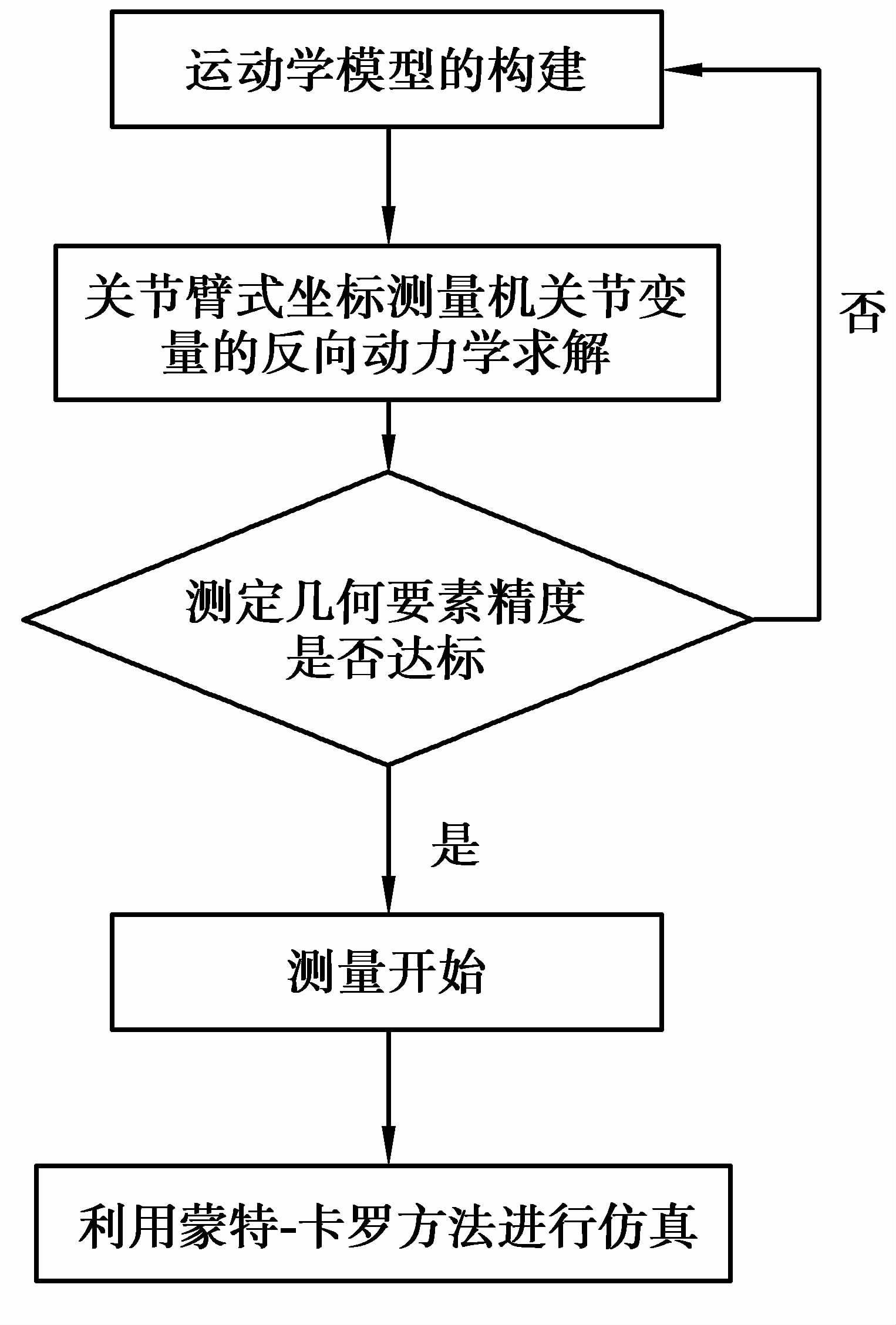
采用蒙特卡罗方法测量不确定度,其过程如图 3所示:第1步是公式化,首先定义输出量Y,即被测量,然后确定Y所依赖的输入量X=(X1,…,XN)T,建立关联Y
|
图 3 蒙特卡罗法测量步骤 Figure 3 Measurement process of Monte Carlo method |
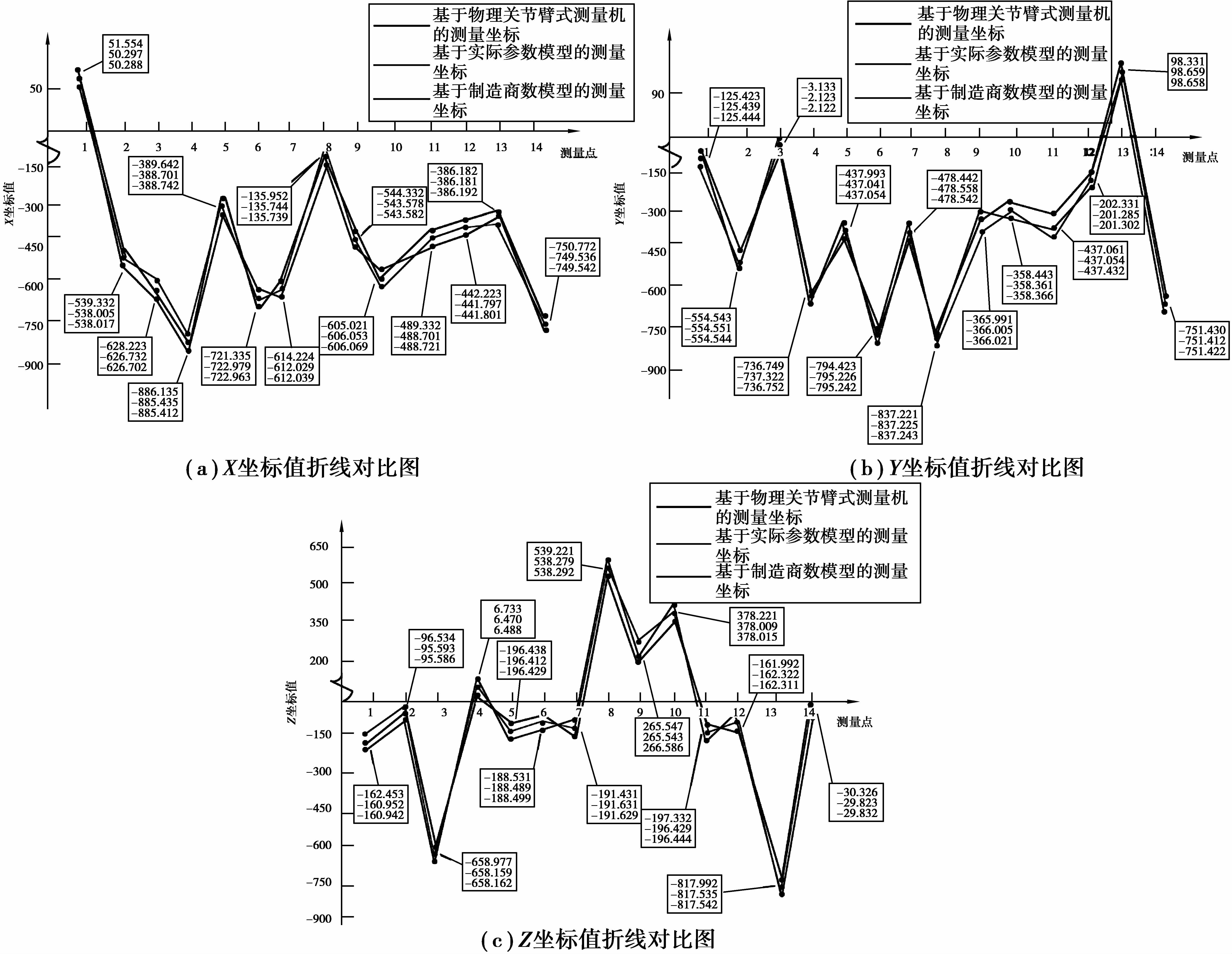
通过PC-DMIS软件随机选取14个坐标点,并利用物理关节臂式坐标测量机、实际参数构建的模型、制造商参数构建的模型分别测量这些点所得出坐标的对比折线图,如图 4所示。
|
图 4 坐标值折线对比图 Figure 4 Comparison line chart of Z axis coordinate value |
由图中线条的重合度以及数据差异大小可知虚拟关节臂式坐标测量机模型可大致模拟物理关节臂式坐标测量机进行实际工件的测量。
4 结 语采用D-H矩阵法构建虚拟六轴关节臂式坐标测量机。重点讨论4步法实现坐标变换和测量机前向动力学规划,对测量机几何参数的精度进行了必要的测定,之后通过模型检验的工作,证实了虚拟关节臂式坐标测量机也可以进行虚拟测量。虚拟关节臂式坐标测量机的使用可以使测量工作的操作性得到有效提升,此外,虚拟模型的使用,可大大提高后续测量结果和测量不确定度计算和估计过程的便捷性。虚拟关节臂式坐标测量机的这些优势可以用于辅助测量,精确估计以及仿真测量,具有一定的实际应用价值。
| [1] |
王文, 林铿, 高贯斌, 等.
关节臂式坐标测量机角度传感器偏心参数辨识[J]. 光学精密工程, 2010, 18(1): 135–141.
WANG Wen, LIN Qiang, GAO Guanbin, et al. Para-meter Identification of articulated arm coordinate measuring machine eccentric angle sensor[J]. Optics and Precision Engineering, 2010, 18(1): 135–141. (in Chinese) |
| [2] | Rugbani A, Schreve K. The kinematics and error modelling of a novel micro-CMM[J]. International Journal of Advanced Manufacturing Technology, 2014, 78(5-8): 961–969. |
| [3] | Ramu P, Yagüe J A, Hocken R J, et al. Development of a para-metric model and virtual machine to estimate task specific measurement uncertainty for a five-axis multisensor coordinate measuring machine[J]. Precision Engineering, 2011, 35(3): 431–439. DOI:10.1016/j.precisioneng.2011.01.003 |
| [4] |
高贯斌, 王文, 林铿, 等.
关节臂式坐标测量机误差仿真系统建模与分析[J]. 算机集成制造系统, 2009, 15(8): 1534–1540.
GAO Guanbin, WANG Wen, LIN Qiang, et al. Articulated arm CMM error simulation modeling and analysis[J]. Computer Integrated Manufacturing Systems, 2009, 15(8): 1534–1540. (in Chinese) |
| [5] |
林超, 曾庆龙, 聂玲, 等.
高阶椭圆锥齿误差的三坐标测量方法[J]. 重庆大学学报, 2013, 36(10): 1–7.
LIN Chao, ZENG Qinglong, NIE Ling, et al. Pitch error measurement of high-order oval bevel gear on three dimensional measuring machine[J]. Journal of Chongqing University, 2013, 36(10): 1–7. (in Chinese) |
| [6] | Li F, Longstaff A P, Fletcher S, et al. A practical coordinate unification method for integrated tactile-optical measuring system[J]. Optics and Lasers in Engineering, 2014, 55(7): 189–196. |
| [7] |
刘英卓.
拟人机器人的建模[J]. 重庆大学学报, 2006, 29(2): 1–5.
LIU Yingzhuo. Humanoid robot modeling[J]. Journal of Chongqing University, 2006, 29(2): 1–5. (in Chinese) |
| [8] | Linh B T H, Kung Y S. Digital hardware realization of forward and inverse kine-matics for a five-axis articulated robot arm[J]. Mathematical Problems in Engineering, 2015(2015): 1–10. |
| [9] | Ferreira F A M, Oliva J D V Y, Perez A M S. Evaluation of the performance of coordinate measuring machines in the industry, using calibrated artefacts[J]. Procedia Engineering, 2013(63): 659–668. |
| [10] | Kovač I, Frank A. Testing and calibration of coordinate measuring arms[J]. Precision Engineering, 2001, 25(2): 90–99. DOI:10.1016/S0141-6359(00)00057-X |
| [11] | Carlson S A, Red W E, Jensen C G. Development of a variational part model using in-process dimensional measurement error[J]. Computer-Aided Design and Applications, 2013, 3(1): 405–414. |
 2016, Vol. 39
2016, Vol. 39

