在计划经济时期,中国总供需是计划当局确定的一个外生变量,具有较大的波动性,潜在经济增长率的测定也就失去了理论基础和现实意义。改革开放以来,特别是1992年明确建立社会主义市场经济体制以来,中国市场化程度不断提高,经济自主性与内生性显著增强,社会总供给的形成和总需求的内在结构出现了许多新的特征,短缺经济现象基本消失,大量商品的供应出现过剩,长期存在的商品卖方市场被买方市场取代,经济增长已经由原来的资源约束型为主转变为需求约束型为主,有效需求相对不足这一市场经济的普遍现象成为中国当前经济的一种基本态势。保罗·萨缪尔森和威廉·诺德豪斯在《宏观经济学》(第17版)中对潜在经济增长的定义为:潜在经济增长率是一个国家可持续的最大的国民产出水平,以商品与生产要素的总供需平衡作为分析的逻辑起点。因此,在当前经济条件下,尤其是供给侧结构性改革的大背景下,从总供需基本平衡的角度去理解潜在经济增长率和产出缺口,可以说是一种积极而务实的做法。
由于潜在产出和产出缺口不可直接观测,国内外众多学者在潜在产出和产出缺口的定量估计方面进行了大量研究。早期,Chow[1]采用生产函数法估计中国的经济总量及农业、工业、建筑业、交通运输业、商贸业5部分产出,进而分析中国的资本形成和经济增长;美国、日本、国际货币基金组织(IMF)、经济合作和发展组织(OECD)等一些国家和组织均采用了假定技术进步为哈罗德中性的Cobb-Douglas生产函数法来估计潜在产出[2]等。近年来,对潜在产出和产出缺口的研究依旧不减,Hirose等[3]建立贝叶斯动态随机一般均衡模型估算产出缺口的结构;Paccagnini[4]建立了增强因子向量自回归动态随机一般均衡模型预测美国潜在产出,实证分析美国潜在经济增长;Iiboshi等[5]建立动态随机一般均衡模型预测日本潜在产出;Fernald[6]对美国大萧条时期以及大萧条前后经济发展和潜在产出进行研究;Kiley[7]对产出缺口的估算模型及参数进行分析讨论;Garratt等[8]建立VAR模型对产出缺口近期预报的不确定性问题进行研究;陈亮等[9]以日本、韩国以及金砖4国为对象,利用HP滤波法估计经济潜在增长率变动,分析中国及上述6国经济增长率的变动特征;王少平等[10]应用状态分解的方法将中国的GDP分解为确定性趋势、随机趋势与周期,研究随机冲击的持久效应;王子博[11]构建多参数动态系统模型进行Kalman滤波,估算中国1978—2009年潜在产出、产出缺口、潜在产出增长率及均衡增长率。各种研究方法及成果,对掌握一国的经济发展走势,探索经济发展规律发挥了重要的作用。
目前潜在产出的估算方法主要可归结为两大类:一类是利用统计技术直接对现实产出进行处理的消除趋势法,其基本思想是利用平滑工具将现实产出分解为趋势成分与周期成分,趋势成分认为是潜在产出,而周期成分则作为产出缺口;另一类是基于经济理论的生产函数法,其基本思想是先利用现实数据估算总量生产函数,并得到全要素生产率,进一步得到趋势全要素生产率,再估算潜在就业,最后将趋势全要素生产率和潜在就业带入总量生产函数得到潜在产出。消除趋势法虽然具有简便易用的明显优势,但也普遍存在一些问题,诸如:对样本数据长度非常敏感、因所选的平滑权数或初始值一般靠主观经验判断而对产出缺口和潜在产出构成的分布会产生很大影响等缺点。生产函数法具有其他方法无可替代的优点是,能够从供给角度反映潜在水平与实际产出的波动,且全面考虑了生产要素利用率和技术进步的影响,从而体现出潜在产出的供给面特征,因此是目前国际上使用最多的方法;但该方法具有估算过程较为复杂、对数据要求较高的不足。广义神经网络(general regression neural network,GRNN)[12]作为非参数估计的预测模型,通过学习过程实现具有隐含关系的最终目标,输入与输出变量之间分为若干层,相邻层间由含有非线性结构的神经元连结,具有非线性、适应性、容错性等特点,在数据挖掘上具有独特的优势。陈建功等[13]建立识别锚杆杆侧刚度系数的神经网络模型,为锚杆系统的锚固质量评价提供了一个有效的智能化手段;辜小花等[14]采用广义回归神经网络建立抽油机节能优化模型;Zhou等[15]构建GRNN模型估算中国国债收益率,分析货币政策调整对国债收益率曲线的影响;Kokkinos等[16]提出一种集成多个局部广义回归神经网络的渐进局部学习预测模型;Dash等[17]采用人工神经网络建立面向对象的软件系统可持续预测模型等,针对不同问题的各种神经网络模型层出不穷,且模型的估算效果均展现出稳定性强、精度高的优点。在估算潜在增速和产出缺口时,针对生产函数法中由于事先假设确定的函数形式、且选择不同函数形式结果不同的问题,选择具有明确概率意义的GRNN方法建立估算模型,既能克服一般径向基网(radial basis function net,RBFN)设计和训练上的困难,还能实现任意非线性函数的任意精度近似,在逼近能力和学习速度方面均优于BP神经网络(back-propagation network)。虽然一般均衡概念在神级网络方法中存在无法回避的缺陷,但将神经网络与生产函数法相结合,具有经济理论和统计技术消除趋势共有的优势,既保留了生产函数法的主要优点,也极大程度上简化了估算过程,且降低了对数据的要求。研究在构建GRNN潜在产出估算模型的基础上,对中国的产出缺口、潜在产出增速进行估算,并对“十三五”期间经济增长与潜在增长进行预测,比较分析中国产出缺口、潜在增长率和经济增长的关系。
1 潜在产出及其估算方法 1.1 潜在产出及产出缺口设Zt为实际产出,Zt*记为潜在产出,2个量分别取对数为Ln Zt和Ln Zt*,实际产出增速rt和潜在产出增速rt*分别为
| ${{r}_{t}}=\text{Ln}{{Z}_{t}}-\text{Ln}{{Z}_{t-1}}=\text{Ln}\left( 1+\frac{{{Z}_{t}}-{{Z}_{t-1}}}{{{Z}_{t-1}}} \right)\approx \frac{{{Z}_{t}}-{{Z}_{t-1}}}{{{Z}_{t-1}}},$ | (1) |
| $r_{t}^{*}=\text{Ln}~Z_{t}^{*}-\text{Ln}~Z_{t-1}^{*}=\text{Ln}\left( 1+\frac{Z_{t}^{*}-Z_{t-1}^{*}}{Z_{t-1}^{*}} \right)\approx \frac{Z_{t}^{*}-Z_{t-1}^{*}}{Z_{t-1}^{*}},$ | (2) |
产出缺口则为
| ${{R}_{t}}=\text{Ln}{{Z}_{t}}-\text{Ln}~Z_{t}^{*}=\text{Ln}\left( 1+\frac{{{Z}_{t}}-Z_{t}^{*}}{Z_{t}^{*}} \right)\approx \frac{{{Z}_{t}}-Z_{t}^{*}}{Z_{t}^{*}}.$ | (3) |
产出缺口近似表示成实际产出背离潜在产出的百分比。
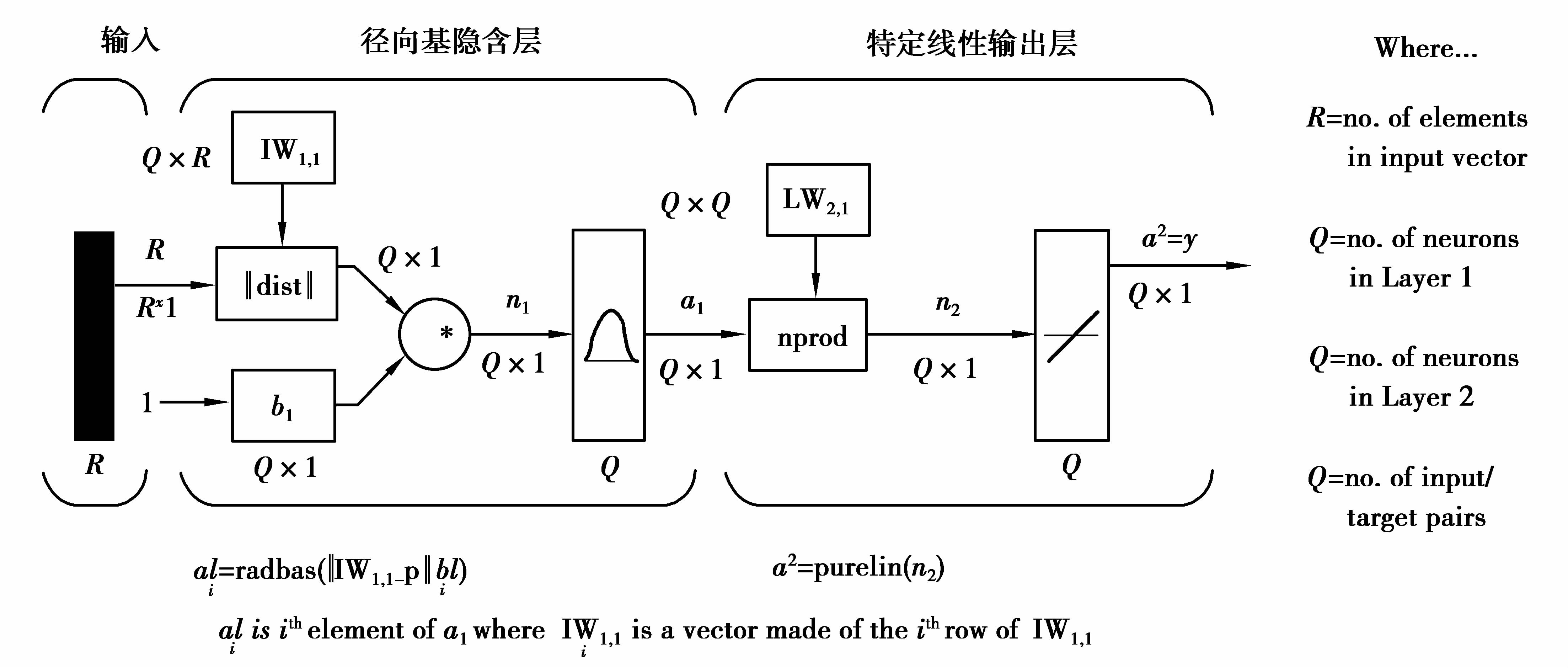
1.2 潜在产出和产出缺口估算方法选取广义回归神经网络(GRNN)建立模型,估算潜在产出和产出缺口,将确定性与随机性寻优操作相融合,构建和发现隐含结点更加准确快速,还可根据样本数据类型动态调整网络隐含层节点数,实现了高效全局优化。GRNN拓扑结构如图 1所示。
|
图 1 GRNN神经网络拓扑结构图 Figure 1 Neural network topology map of GRNN |
GRNN网络的输入为X(R维向量),训练样本对数为Q,网络输出为向量Y。GRNN包含2层:第1层为径向基隐含层,单元个数等于训练样本数Q,该层的权值函数为欧几里德距离度量函数(用${{\left\| \text{dist} \right\|}_{i}}$表示),其作用是计算网络输入与第1层的权值IW1,1之间的距离。
| ${{\left\| \text{dist} \right\|}_{i}}=\sqrt{\sum\limits_{j=1}^{R}{{{\left( {{x}_{j}}{{-}_{i,j}}T{{W}^{1,1}} \right)}^{2}}}}i=\left( 1,2,\cdots ,Q \right).$ | (4) |
图 1中,b1为隐含层阈值,可根据需要选取。网络积函数netprod将阈值与权输入相乘的结果形成净输入n1,传送到传递函数radbas。隐含层的传递函数为径向基函数(radial basis function,用radbas表示),用高斯函数作为网络的传递函数,则隐含层的输入可由下式得
| $\begin{align} & a{{1}_{i}}=\text{radbas}\left( \text{netprod}\left( {{\left\| \text{dist} \right\|}_{i}}b{{1}_{i}} \right) \right)=\exp \left\{ -\frac{{{\left( n{{1}_{i}} \right)}^{2}}}{2\sigma _{i}^{2}} \right\}= \\ & \exp \left\{ -\frac{{{\left( {{\left\| \text{dist} \right\|}_{i}}b{{1}_{i}} \right)}^{2}}}{2\sigma _{i}^{2}} \right\}, \\ \end{align}$ | (5) |
式中,σi决定第i个隐含层位置处基函数的形状,σi越大则基函数越平缓,故又被称为平滑因子。显然,高斯基函数为一种局部分布对中心径向对称衰减的非负非线性函数;隐含层节点中的基函数对输入信号将在局部产生响应。也就是说,当输入信号靠近基函数的中央范围时,隐含层节点将产生较大的输出,由此看出GRNN网络具有局部逼近能力,这也是其之所以学习速度更快的原因。
网络的第2层为特定线性输出层,其权函数nprod为归范化点积权函数,将前一层的输出与本层的权值的点积作为权输入,直接送入传递函数。传递函数purelin为线性函数。网络输出由下式计算
| $\begin{align} & n{{2}_{k~}}=\sum\limits_{i=1}^{Q}{_{k,i}}L{{W}^{2,1}}\centerdot a{{1}_{i}} \\ & k\text{ }=\text{ }\left( 1,2,\cdots ,Q \right), \\ \end{align}$ | (6) |
| ${{y}_{k}}=a{{2}_{k}}=\text{purelin}(n{{2}_{k}}).$ | (7) |
在GRNN模型中采用遗传算法进行网络结构优化,搜索过程从一组初始点集出发,具有隐含并行搜索特性,不受函数连续可微等限制,且对问题依赖性小。
2 潜在产出及产出缺口估算模型根据生产函数理论,一国产出主要由劳动、资本投入和技术进步所决定。经济增长理论也认为,劳动、资本投入增长和全要素生产率增长率是决定经济增长水平的根本原因。经济学上认为潜在产出具有随时间增长的趋势,实际产出围绕该潜在值上下波动,波动部分即是产出的周期性成分。有的研究认为对潜在产出的影响因素还有许多,例如,通货膨胀、金融发展等,但由于影响机制的稳定性和数据获取的不确定性等问题,为了简化模型过程,有效降低数据要求,提取最核心的影响因素,研究在建立广义回归神经网络(GRNN)模型时,引入资本存量K和劳动投入L作为输入变量,输出变量为实际产出Z,模型拟合输出值作为潜在产出,残差项作为产出缺口,即
| $Y=\left( K,L \right)=({{y}_{1}},{{y}_{2}}).$ | (8) |
则潜在产出的GRNN模型可表示为关系式
| $Z=H\left( Y \right).$ | (9) |
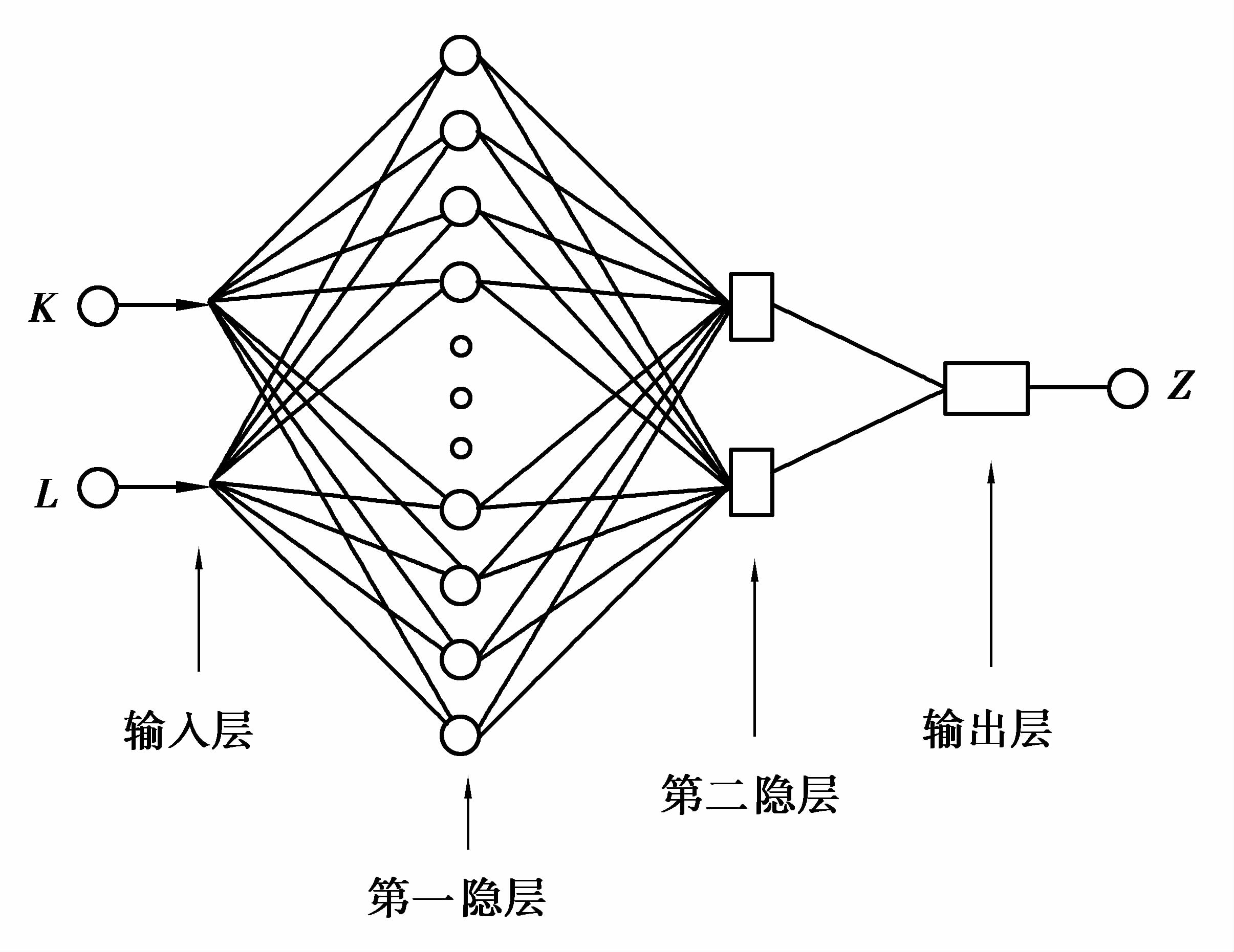
GRNN潜在产出模型结构如图 2所示,输入层为决定经济增长水平的主要因素构成的向量Y,输出为实际产出Z。模型网络包含2个隐层:第1隐层为径向基隐含层,节点个数等于训练样本数n,权值函数为度量函数D,用作计算输入层与第1隐层的权值IW1,1之间的距离。
|
图 2 GRNN潜在产出模型结构图 Figure 2 Structure diagram of GRNN potential output model |
| ${{D}_{i}}=\sqrt{\sum\limits_{j=1}^{2}{{{({{y}_{j}}{{-}_{i,j}}I{{W}^{1,1}})}^{2}},}}i=1,2,\cdots ,n.$ | (10) |
在每一个节点,Di流入一个非线性核,核函数是一个指数函数,通常为高斯函数
| $W({{D}_{i~}})\text{ }=~\exp \left( -\frac{D_{i}^{2}}{2\sigma _{i}^{2}} \right),$ | (11) |
式中,σi为平滑因子,决定基隐含层第i个节点位置处核函数的形状,σi越大则核函数越平缓,基隐含层节点中的核函数对输入信号将在局部产生响应。当输入信号靠近核函数的中央时,基隐含层节点将产生较大的输出,由此看出GRNN网络具有局部逼近能力,所以学习速度更快。
第2隐层为求和层,它仅由2个节点组成。输入到第1个节点的值P是第1隐层各节点输出值W(Di)的加权求和,权重为对应样本的实际产出Z的观测值${{{\hat{Z}}}_{i}}$。第2个节点的值Q为第1隐层各节点输出值之和。即
| $P=\sum\limits_{i=1}^{n}{{{{\hat{Z}}}_{i}}}\cdot W({{D}_{i}}),$ | (12) |
| $Q=\sum\limits_{i=1}^{n}{W({{D}_{i}})}.$ | (13) |
输出层为实际产出Z,由第2隐层中2节点值之比获得。即
| $Z=\frac{P}{Q}=\frac{\sum\limits_{i=1}^{n}{{{{\hat{Z}}}_{i}}}\cdot W({{D}_{i}})}{\sum\limits_{i=1}^{n}{W({{D}_{i}})}}.$ | (14) |
该模型将确定性与随机性寻优操作相融合,实现构建和发现隐含节点更加准确快速,而且可根据样本数据类型动态调整网络隐含层节点数,实现了高效全局优化,还能较好地支持小样本数据,更好地挖掘深度非线性隐含波动传导特性。
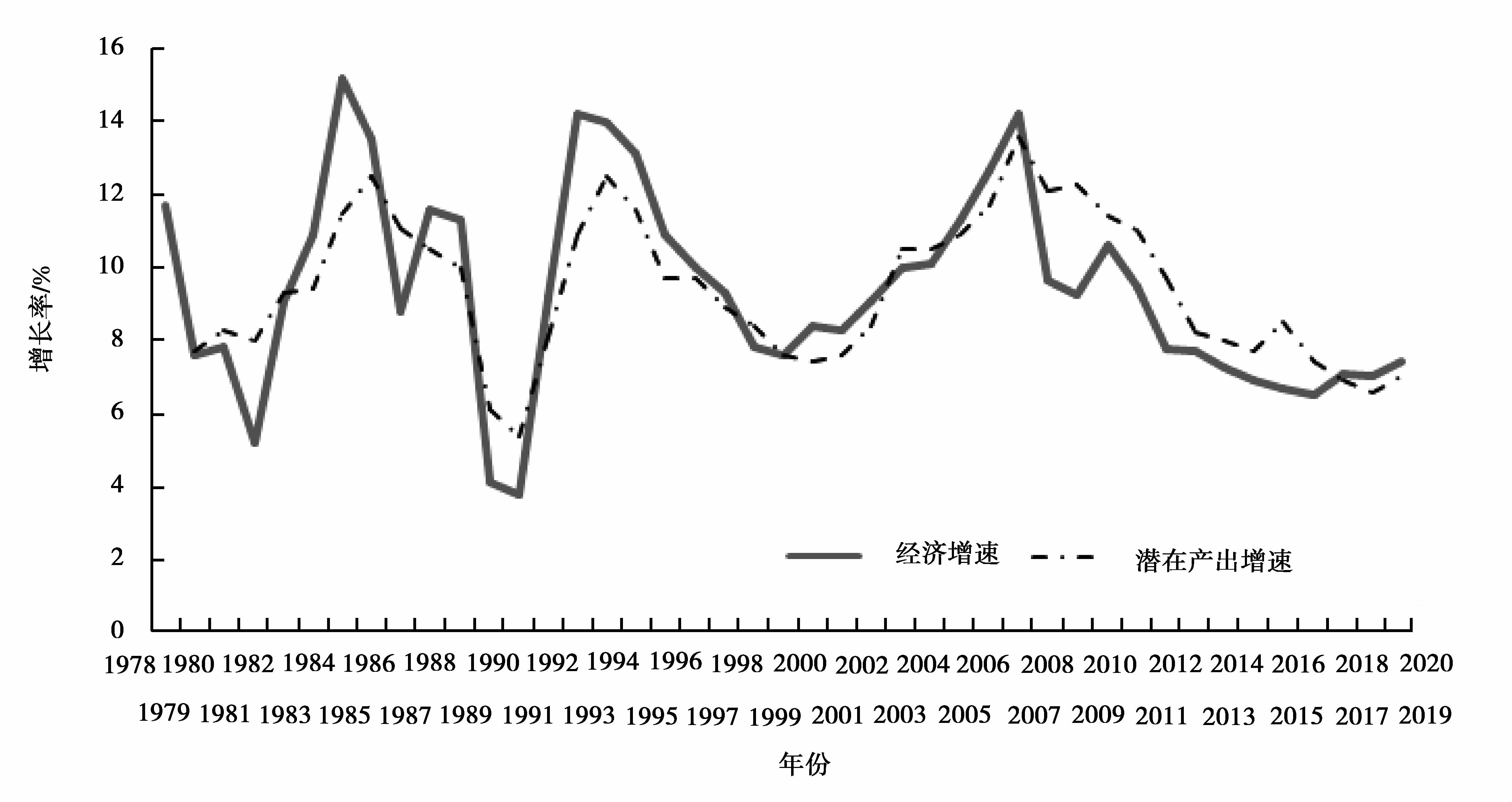
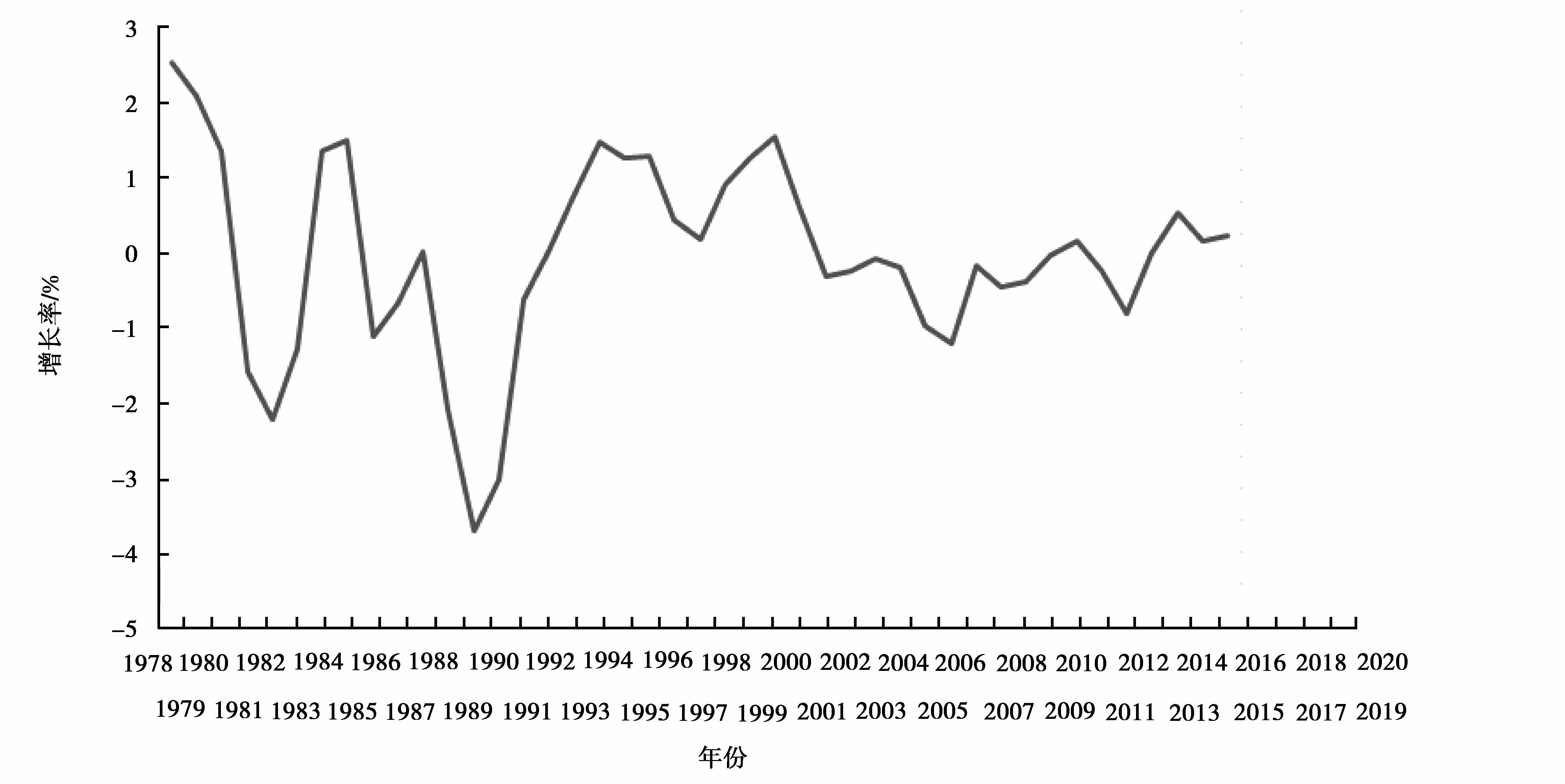
3 潜在产出及产出缺口估算模型实证分析 3.1 潜在产出及产出缺口估算与预测利用上述GRNN模型估算中国1978—2015年潜在产出与产出缺口,数据主要来源于《中国统计年鉴》,其中衡量国民经济整体产出的指标选用按1978年不变价格进行换算的实际GDP,资本存量则由固定资产净值数据采用王小鲁和樊纲[18]假定的固定资产5%的折旧率并利用郭庆旺[19]根据张军和章元所估算的全国固定资产投资价格指数折算序列中的1978—1990年数据推算得到。估算过程中,输入变量中资本K和劳动投入L对输出变量的方差贡献率分别为0.833和0.167,表明中国实际产出主要影响因素是资本,而非劳动力。模型拟合精度为R2=0.999 7,平均误差为0.012 2,潜在产出增速与实际产出增速的序列相关系数为0.887,表明模型具有较高的拟合度精度,并且估算结果与现实经济走势契合度较高。进一步在模型中,采用多步预测法对2016—2020年经济增速和潜在产出、产出缺口估算进行提前5步预测。估算和预测结果参见图 3和图 4(2图中2016—2020年数据均为预测值)。
|
图 3 潜在产出增速与经济增速走势图 Figure 3 Potential output growth rate and economic growth rate based on GRNN |
|
图 4 GRNN模型产出缺口测算结果 Figure 4 Results of output gap based on GRNN |
从计算结果看出,1978—2007年中国的产出缺口出现了波动水平正负交替的古典周期情形,1978—1988年和1989—1998年形成了2个较为完整的周期,从1997年开始,正的产出缺口处于缩小阶段,并于1999年接近于0,于2002年出现一些反转迹象。在1995以前,产出缺口的波动幅度比较剧烈且较为频繁,而1996年以后,虽然出现过各种外部冲击(例如亚洲金融危机和美国“9.11”事件,甚至2009年美国次贷危机引发的世界金融风暴),产出缺口的变化均较为平缓。究其原因,1995年以前正是中国经济体制和市场条件发生剧烈频繁变化的时期,而从1998年开始,中国政府积极应对外部环境的变化,采取了积极财政政策,对宏观经济的稳定起到了重要作用。从计算结果还可看出,在经济繁荣阶段,产出缺口都达到阶段性正的最大值(1988、1995和2002左右);在现实经济的相对低潮期(1982、1990、1999和2009年左右),产出缺口都达到阶段性负的最大值,这些观察都与中国宏观经济运行的实际情况比较吻合。
整个样本期内,1980—1983、1989—1992、1998—2002以及2009—2017年,中国一直处于实际需求小于潜在产出水平的状态,与此相伴的是经济增长持续走低和通货紧缩。自80年代中期开始,政府为刺激增长而采取了过于宽松的信贷货币政策,同时多数消费品价格被放开,引起了过高的通胀率。为了抑制通胀,政府从1988年第四季度开始大幅提高银行存款利率、削减基本建设投资。高利率和严格的信贷限额造成了乡镇企业大量倒闭以及国有企业严重亏损。同时出于政治稳定角度考虑,市场化改革的步伐也暂时停顿了。这些措施直接导致了持续期达3年的严重衰退。1997年开始的衰退期则可能源于为追求“软着陆”的紧缩政策、强力国有企业改革政策以及亚洲金融危机。从1997年到2001年,中国国有企业大量破产,大量的工人失业以及经济结构性矛盾(例如城乡收入差距加大)造成了国内需求不足,同时亚洲金融危机的冲击也抑制了出口需求。从1998年开始,为了治理通货紧缩,中国政府采取了积极财政政策,到2001年左右基本上遏止住了经济下滑趋势。1999年以后,产出缺口增加的幅度明显趋缓。2003年以来,国民经济则又开始进入负产出缺口为主的阶段。2004 年以来的中国经济实际增速与潜在增速偏差不大,存在平缓的周期波动和较强的结构变动。这在潜在产出及产出缺口的GRNN模型估算结果得到了很好体现。
从预测结果中看出,“十三五”期间中国经济增速将处于1978年以来最低的五年规划期,将维持在6.5~7.5%的增长速度,头三年会延续“十二五”末期调整的下行走势,随着供给侧结构性改革实施效果的初步显现,从2018年开始出现回升。相比较,这期间潜在增速也保持在较低的水平,2018年开始出现低于经济增速的情况,整个“十三五”潜在增长率以下行为主要表现,直到最后一年才出现抬头之势。从产出缺口看,5年间正负交错,2018年左右将出现由负转正的翻转。总体上,“十三五”期间,中国经济增长围绕潜在增速在较小的范围内波动;前三年延续“十二五”末期结构调整带来的较大冲击,“新常态”下经济发展向中低增速调整,“十三五”末期调整处于平稳阶段,经济将长期沿着中低速增长路径发展。
4 结 论经济潜在增长率是度量某一时期一国或地区经济潜在产出增长速度大小的指标。产出缺口则衡量实际产出偏离潜在产出的程度,测度的是经济周期性波动对产出的影响,反映了现有经济资源的利用程度。研究构建潜在产出和产出缺口的非参数估计广义回归神经网络(GRNN)模型,实证分析1978—2015年中国经济增长的周期性规律,模型估算结果与现实经济走势契合度较高,结合实证检验中较高的拟合精度和潜在产出增长率与实际产出增速的高相关性,体现出模型的可靠性。进一步采用多步预测法对2016—2020年中国经济增速、潜在产出增长率和产出缺口进行预测,表现出GRNN模型在估算与预测中较好的实用效果。在对模型测算和预测结果分析的基础上,结合对经济中供求关系理论的研究认为,潜在经济增长率是可持续的现实经济增长的稳定趋势,“十三五”期间,只要中国经济的增长速度大致维持在潜在产出增长率水平附近,通货膨胀率可以维持在一个可接受的水平上并实现供需总体平衡,结构调整的成效将初步显现。
| [1] | Chow G C. Capital formation and economic growth in China[J]. The Quarterly Journal of Economics, 1993, 108(3): 809–842. DOI:10.2307/2118409 |
| [2] | Elmeskov J. High and persistent unemployment:assessment of the problem and its causes[M]. Paris: OECD Economics Department Working, 1993. |
| [3] | Hirose Y, Naganuma S. Structural estimation of the output gap:a bayesian DSGE approach[J]. Economic Inquiry, 2010, 48(4): 864–879. DOI:10.1111/j.1465-7295.2009.00228.x |
| [4] | Paccagnini A. Estimating point and density forecasts for the US economy with a factor-augmented vector autoregressive DSGE model[J]. Studies in Nonlinear Dynamics & Econometrics, 2014, 19(2): 107–136. |
| [5] | Iiboshi H, Matsumae T, Namba R, et al. Estimating a DSGE model for Japan in a data-rich environment[J]. Journal of the Japanese & International Economies, 2015, 36: 25–55. |
| [6] | Fernald J G. Productivity and potential output before, during, and after the great recession[J]. Nber Macroeconomics Annual, 2014, 29(1): 1–51. |
| [7] | Kiley M T. Output gaps[J]. Journal of Macroeconomics, 2013, 37(27): 1–18. |
| [8] | Garratt A, Mitchell J, Vahey S P. Measuring output gap nowcast uncertainty[J]. International Journal of Forecasting, 2014, 30(2): 268–279. DOI:10.1016/j.ijforecast.2013.07.012 |
| [9] |
陈亮, 陈霞, 吴慧.
中国经济潜在增长率的变动分析:基于日韩及金砖四国等典型国家1961~2010年的经验比较[J]. 经济理论与经济管理, 2012(6): 44–55.
CHEN Liang, CHEN Xia, WU Hui. Research on the chinese potenial gdp growth rate:based on the comparison of Japan, Korea, and BRIC countries[J]. Economic Theory and Business Management, 2012(6): 44–55. (in Chinese) |
| [10] |
王少平, 胡进.
中国GDP的趋势周期分解与随机冲击的持久效应[J]. 经济研究, 2009(4): 65–76.
WANG Shaoping, HU Jin. Trend cycle decomposition and stochastic impact effect of Chinese GDP[J]. Economic Research Journal, 2009(4): 65–76. (in Chinese) |
| [11] |
王子博.
中国潜在产出估算模型的设计与应用:基于Kalman滤波的实证分析[J]. 统计与信息论坛, 2012, 27(1): 27–32.
WANG Zibo. Design and application of Chinese potential output estimation modelan empirical analysis:based on kalman filtering[J]. Statistics & Information Forum, 2012, 27(1): 27–32. (in Chinese) |
| [12] | Specht D F. A general regression neural network[J]. IEEE Transactions on Neural Networks, 1991, 2(6): 568–576. DOI:10.1109/72.97934 |
| [13] |
陈建功, 刘海源, 张永兴.
锚杆锚固质量的定量分析方法[J]. 重庆大学学报, 2009, 32(9): 1043–1048.
CHEN Jiangong, LIU Haiyuan, ZHANG Yongxing. Quantitative assessment method for the quality of anchors[J]. Journal of Chongqing University, 2009, 32(9): 1043–1048. (in Chinese) |
| [14] |
辜小花, 廖志强, 李太福, 等.
面向抽油机节能的GRNN过程建模及工艺参数优化[J]. 重庆大学学报, 2013, 36(6): 130–136.
GU Xiaohua, LIAO Zhiqiang, LI Taifu, et al. Beam pumping process modeling and parameters optimization based on generalized regression neural networks for energy conservation[J]. Journal of Chongqing University, 2013, 36(6): 130–136. (in Chinese) |
| [15] | Zhou Z K, Zhang Q J, Yang H. Analyzing effects of monetary policy change government bond yield curve in exchange by using GRNN[C]//2013 International Conference on Computing, Networking and Communications (ICNC). Tianjian:IEEE Computer Society Press, 2009:75-80. |
| [16] | Kokkinos Y, Margaritis K G. A fast progressive local learning regression ensemble of generalized regression neural networks[C]//ACM Proceedings of the Panhellenic Conference on Informatics. New York:ACM Press, 2015:109-114. |
| [17] | Dash Y, Dubey S K, Rana A. Maintainability prediction of object oriented software system by using artificial neural network approach[J]. International Journal of Soft Computing and Engineering, 2012, 2(2): 420–423. |
| [18] |
王小鲁, 樊刚.
中国收入差距的走势和影响因素分析[J]. 经济研究, 2005(10): 24–36.
WANG Xiaolu, FAN Gang. Income inequality in China and its influential factors[J]. Economic Research Journal, 2005(10): 24–36. (in Chinese) |
| [19] |
郭庆旺, 贾俊雪.
中国潜在产出与产出缺口的估算[J]. 经济研究, 2004(5): 31–39.
GUO Qingwang, JIA Junxue. Estimating potential output and the output gap in China[J]. Economic Research Journal, 2004(5): 31–39. (in Chinese) |
 2016, Vol. 39
2016, Vol. 39

