b. 重庆大学 汽车工程学院, 重庆 400044
b. College of Automotive Engineering, Chongqing University, Chongqing 400044, P. R. China
随着石化能源的严重短缺和法规要求的日益严格, 通过技术进步提高汽车发动机的燃油经济性, 减少汽车所消耗的石油资源, 已成为政府部门和生产厂商关注的焦点。曲轴主轴承作为发动机中的主要摩擦副, 其润滑特性的好坏直接影响发动机的摩擦损耗, 从而影响发动机的燃油经济性。Coy[1]的研究表明, 发动机主轴承的摩擦功率损失约占发动机机械功率损失的25%, 个别车用发动机甚至达到了40%。因此, 通过改善曲轴主轴承的润滑特性来减少摩擦损耗是提高发动机燃油经济性的有效途径之一。
曲轴主轴承的润滑特性与曲轴轴承座孔的变形有关[2], 两者之间存在强耦合关系。已有大量研究工作围绕曲轴主轴承润滑展开, 但通常将机体当作简单弹性支座[3-5]或刚性元件[6-10]来处理, 考虑整机体弹性变形的相对较少。尽管参考文献[11-12]建立了缸体的有限元模型, 但实际仅考虑了油膜压力作用下的轴承孔表面变形, 未考虑缸筒侧推力对轴承孔变形的影响。
为此, 笔者以某直列四冲程四缸汽油发动机为研究对象, 在考虑整机体和曲轴弹性的条件下, 建立发动机曲柄连杆机构多柔体动力学模型, 结合基于质量守恒边界条件的广义雷诺方程和Greenwood/Tripp接触模型, 分析机体弹性对曲轴主轴承润滑特性的影响。
1 弹性流体动力润滑模型 1.1 平均雷诺方程采用Patir等[13-14]提出的平均流量模型来计算主轴承的流体动压分布。平均Reynolds方程为
| ∂∂x(ˉθφxh312μ∂p∂x)+∂∂z(ˉθφxh312μ∂p∂x)=∂∂x(ˉθ(ˉh+σsφs)U2)+∂∂t(ˉθˉh), | (1) |
式中:θ为润滑油填充率; p为油膜压力, Pa; t为时间, s; μ为润滑油动力粘度, Pa·s; U为主轴颈的周向运动速度, m/s; h为油膜厚度, m; h为平均油膜厚度, m; φx和φz分别为x和z方向上的压力流量因子; φs为剪切流量因子; σs为综合表面峰值粗糙度均方根值, m, 即
| σs=√σ2sJ+σ2sS, | (2) |
式中, σsJ、σsS分别为轴颈、轴瓦表面粗糙度均方根值, m。
实际润滑油膜厚度h为
| h=h0+hj+hs, | (3) |
式中:名义油膜厚度h0=C+ecos (θ-θξ), 其中C为半径间隙, mm; e为偏心距, mm; θ为由轴承上方垂线计量的角度, (°), θ=x/R, R为轴承孔半径, mm; θξ为偏位角, (°); hj和hs分别为轴颈和轴瓦的弹性变形引起的油膜厚度变化量, mm。
求解所用油膜破裂边界条件和油膜再形成边界条件为
| ∂p∂n=0, | (4) |
| h212μ∂p∂n=V2(1−ˉθ), | (5) |
式中, V为油膜法向速度, m/s。
1.2 主轴承载荷主轴承载荷N包括油膜载荷NH和接触载荷NA, 即
| {NHx=−∫ApcosθdA,NHy=−∫ApsinθdA, | (6) |
设油膜载荷NH在x、y方向上的分量分别为NHx、NHy。
| {NHx=−∫ApcosθdA,NHy=−∫ApsinθdA, | (7) |
式中, A为轴承展开面积。
则油膜载荷为
| NH=√N2Hx+N2Hy. | (8) |
根据Greenwood等[5]提出的粗糙表面接触理论来确定固-固接触所产生的接触压力, 在弹性变形下轴颈与轴瓦间峰元接触压力
| pa=KE∗F5/2(Hs), | (9) |
式中:
| F5/2(Hs)={4.408610−5(4−Hs)6.804Hs<4,0Hs≥4;E∗=[1−v21E1+1−v22E2]−1; |
式中:ηs为粗糙表面峰元密度, 个/m2, β为峰元曲率半径, m; E1、E2分别为轴颈和轴瓦材料的杨氏模量, Pa; v1、v2分别为轴颈和轴瓦材料泊松比; Hs=h/σs为无量纲间隙参数; δs=δsJ+δsS, 为综合平均峰值高度, δsJ和δsS分别表示轴颈和轴瓦表面的平均峰值高度, mm。
设接触载荷在x、y向的分量分别为NAx、NAy, 则
| {NAx=−∫ApaccosθdA,NAy=−∫ApacsinθdA, | (10) |
接触载荷为
| NA=√N2Ax+N2Ay. | (11) |
在混合润滑状态下, 主轴颈的摩擦力FF由流体粘性剪切力FH和峰元摩擦力FA两部分组成, 即
| FF=FH+FA. | (12) |
流体剪应力[16]为
| τH=μUh(Φf+Φfs)+Φfph2⋅∂p∂x, | (13) |
式中:Φf、Φfs和Φfp为剪应力因子。
峰元剪应力为
| τA=μ0⋅pa⋅Aa, | (14) |
式中:μ0为边界摩擦系数; Aa为峰元接触面积。
摩擦力及摩擦功耗分别为
| FF=FH+FA=∫∫A(τH+τA)dxdz, | (15) |
| Pf=FFωR, | (16) |
式中:FF和Pf分别为主轴颈的摩擦力和摩擦功耗。
润滑端泄流量[17]为
| Qout=|∫2π0h312μ∂p∂z|z=B/2Rdθ|+|∫2π0h312μ∂p∂z|z=−B/2Rdθ|, | (17) |
式中, B为轴瓦宽度, mm。
1.4 曲轴和机体结构动力学方程基于有限单元法理论建立机体和曲轴的动力学方程。机体的动力学方程为
| Mb⋅¨xb+Cb⋅˙xb+Kb⋅xb=Fb, | (18) |
式中:上角标b表示缸体; M为质量矩阵; C为阻尼矩阵; K为刚度矩阵; F为载荷阵列, 包括机体外载荷、油膜力和微凸峰接触力;
曲轴的动力学方程[18]为
| [McθθMcθfsym.Mcff][¨θc¨efc]+[000Ccff][˙θc˙ecf]+[000Kcff]{θecf}=Qcv+Qce, | (19) |
式中:上角标c表示曲轴; 下角标θ、f分别代表缸体旋转运动和弹性变形; θ为曲轴旋转角, 即由轴承上方垂线计量的角度; ef为节点的弹性自由度; M、C、K分别代表质量矩阵、阻尼矩阵和刚度矩阵; Qv包括离心力和科氏力; Qe为曲轴广义外载荷矢量, 包括油膜力和微凸峰接触力。
2 动力学模型实际计算时, 为了缩减计算量、简化计算过程, 采用模态缩减技术压缩曲轴和机体自由度。曲轴和机体的模态缩减采用有限元分析软件MD.Nastran来完成。在对接触区域进行有限元网格划分时, 曲轴轴颈主自由度节点数为7×72, 轴承座主自由度节点数为7×48。机体和曲轴有限元模型如图 1所示。
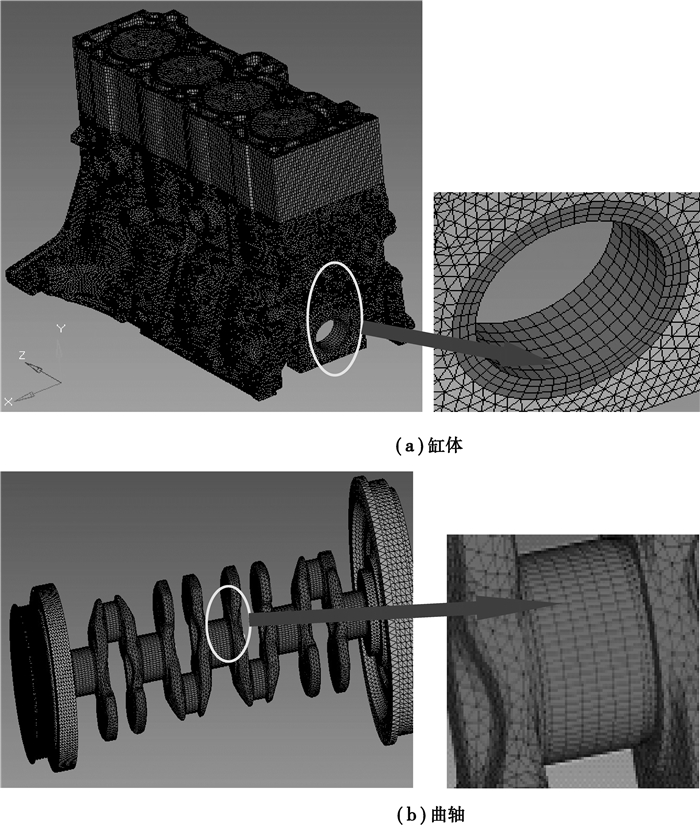
|
图 1 曲轴和缸体有限元模型 Figure 1 Finite element model of crankshaft and engine block |
计算过程中输入的主要参数如表 1所示, 图 2所示为发动机曲轴轴变多体动力学仿真模型, 图 3为作用在活塞顶部的气体压力曲线。
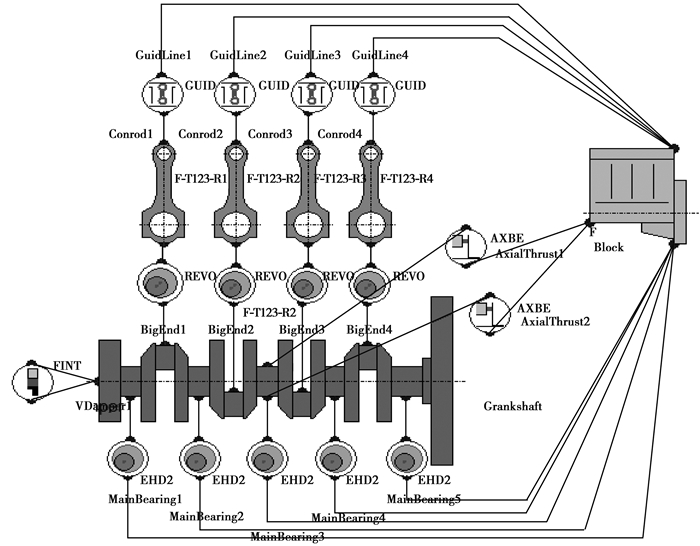
|
图 2 发动机曲轴轴变多体动力学仿真模型 Figure 2 Multi-body dynamics simulation model of crankshaft system |
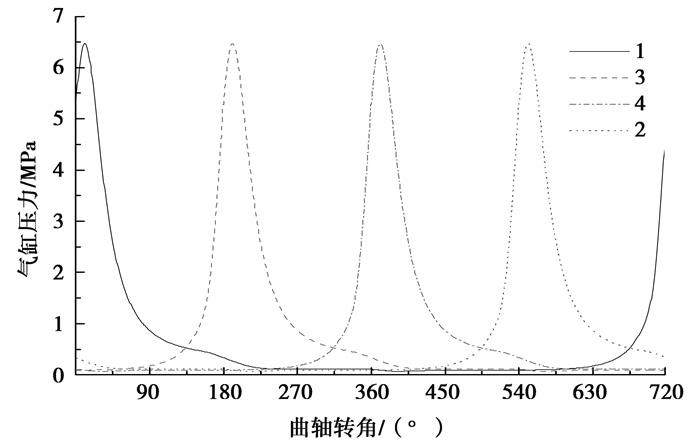
|
图 3 作用在活塞顶部的气体压力(点火顺序:1-3-4-2) Figure 3 Combustion gas force variation (Firing order:1-3-4-2) |
| 表 1 主要参数 Table 1 Primary input parameters |
表 2所示为计算所得的各个轴承的主要润滑性能参数。表中结果对比表明, 与刚性缸体相比, 考虑缸体弹性变形后, 主轴承的润滑油平均端泄量和平均总摩擦功耗变化较小, 最大粗糙接触压力降低, 最大油膜压力变化明显, 尤其是轴承2和轴承4, 其峰值降幅分别为21.2%和24.6%, 其余轴承峰值降幅为5.0%左右; 最小油膜厚度的最小值增加明显, 其中轴承2和轴承4增幅较大, 分别为8.1%和20.0%, 轴承1、3、5增幅相对较小, 分别为2.7%、2.7%、2.5%。
| 表 2 整周期内各主轴承润滑性能 Table 2 Lubrication performance of main bearings in one cycle |
鉴于轴承2和轴承4的润滑特性变化较大, 以下对其润滑特性进行详细分析。
3.1.1 最大油膜压力图 4~图 5所示分别为曲轴主轴承最大油膜压力随曲轴转角的变化情况和油膜压力在轴瓦上的分布情况。从图 4中可以看出, 考虑缸体弹性后, 最大油膜压力随曲轴转角的变化趋势与将缸体处理为刚性时基本一致, 但做功行程中值的大小变化明显, 最大油膜压力峰值降低, 轴承2和4的降幅分别为21.2%和24.7%。这是由于在考虑缸体弹性变形后, 下半轴承孔增大使轴承间隙变大, 因此液动油膜压力减小。从图 5可以看出, 考虑缸体弹性变形后, 油膜压力峰值出现位置及油膜压力在轴瓦上的分布几乎没有变化。

|
图 4 最大油膜压力随曲轴转角的变化 Figure 4 Variation of the peak oil film pressure with the crank angle |
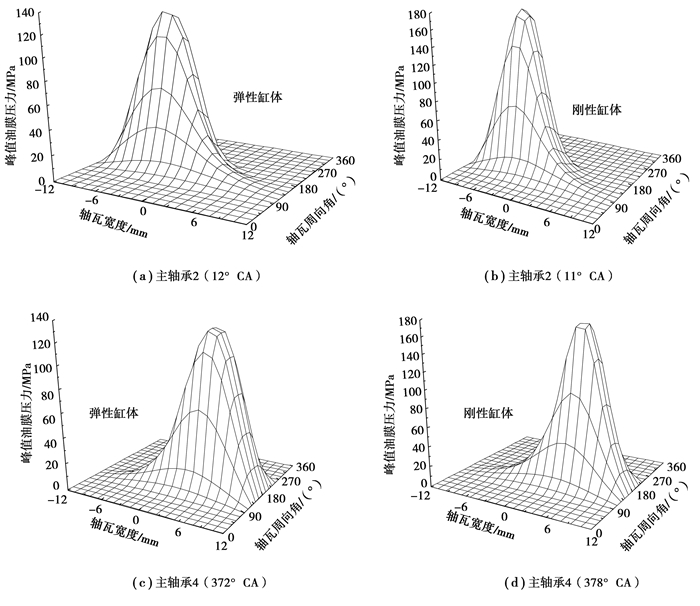
|
图 5 峰值油膜压力在轴瓦上的分布 Figure 5 The peak oil film pressure of its maximum distribution under the different crank angle |
图 6为曲轴主轴承最小油膜厚度随曲轴转角的变化情况。从图中可以看出, 考虑缸体弹性变形后, 最小油膜厚度随曲轴转角的变化趋势与将缸体处理为刚性时基本一致, 在做功行程最小油膜厚度稍有增大, 轴承2和轴承4的最小油膜厚度的最小值增幅分别为8.1%和20.0%。原因是在考虑缸体弹性后, 轴承孔间隙增加, 油膜压力降低, 因而最小油膜厚度增大。

|
图 6 最小油膜厚度 Figure 6 Minimum oil film thickness of bearings |
图 7为曲轴主轴承最大粗糙接触压力随曲轴转角变化情况, 从图中可以看出, 考虑缸体弹性变形后, 最大粗糙接触压力明显降低, 主轴承2和4的峰值降幅分别为56.8%和84.4%, 且主轴承2仅在第1缸的做功行程出现粗糙接触压力, 轴承4仅在第4缸的做功行程出现粗糙接触压力。图 8为曲轴主轴承总摩擦功耗随曲轴转角的变化情况, 从图中可以看出, 考虑缸体弹性变形后, 总摩擦功耗随曲轴转角的变化趋势与将缸体处理为刚性时基本一致, 仅在做功行程总摩擦功耗有一定减小。

|
图 7 最大粗糙接触压力 Figure 7 Peak asperity contact pressure of bearings |
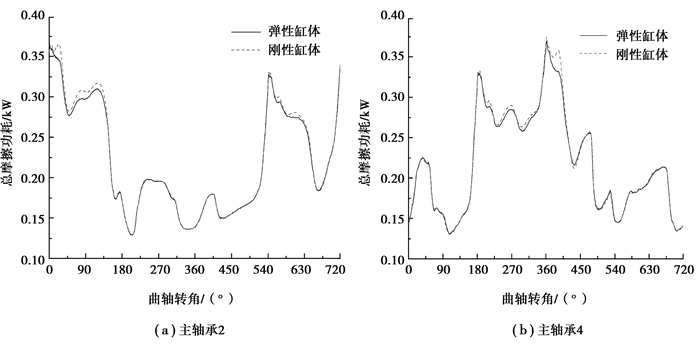
|
图 8 总摩擦功耗 Figure 8 Total friction power loss of bearings |
图 9为曲轴主轴承润滑油端泄量随曲轴转角的变化情况, 从图中可以看出, 考虑缸体弹性后, 润滑油端泄量随曲轴转角的变化趋势与将缸体处理为刚性时基本一致。
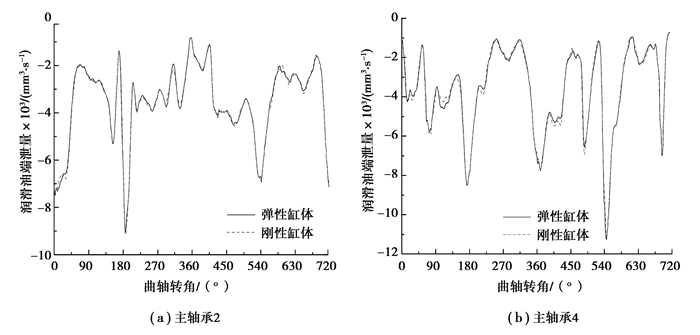
|
图 9 润滑油端泄量 Figure 9 Sum of lubricating oil outflow |
与刚性缸体相比, 考虑缸体弹性后, 主轴承的润滑特性随曲轴转角的变化趋势与将缸体处理为刚性时基本一致, 润滑油平均端泄量和总摩擦功耗在各个工作行程均变化较小, 而润滑油最小油膜厚度、最大油膜压力和轴承的最大粗糙接触压力在发动机一个工作循环内的某些时刻变化明显:
1)主轴承1、3和5不存在粗糙接触, 主轴承2和4分别在1缸和4缸的做功行程出现粗糙接触压力, 且最大粗糙接触压力明显降低, 峰值降幅分别为56.8%和84.4%;
2)最大油膜压力在做功行程下降明显, 尤其是轴承2和轴承4, 其峰值降幅分别为21.2%和24.7%, 其余轴承峰值降幅为5.0%左右;
3)油膜压力峰值出现位置及油膜压力在轴瓦上的分布变化较小; 最小油膜厚度最小值在做功行程增加明显, 其中轴承2和轴承4增幅较大, 分别为8.1%和20.0%, 轴承1、3、5增幅相对较小, 分别为2.7%、2.7%、2.5%。
| [1] | Coy R C. Practical applications of lubrication models in engines[J]. Tribology International, 1998, 31(10): 563–571. DOI:10.1016/S0301-679X(98)00077-2 |
| [2] |
宋现浩, 段京华, 孙军, 等.
内燃机曲轴轴承润滑影响因素的研究进展[J]. 机械设计, 2015(5): 1–5.
SONG Xianhao, DUAN Jinghua, SUN Jun, et al. Review on lubrication of crankshaft bearings in internal combustion engine[J]. Journal of Machine Design, 2015(5): 1–5. (in Chinese) |
| [3] | Priestner C, Allmaier H, Priebsch H H, et al. Refined simulation of friction power loss in crank shaft slider bearings considering wear in the mixed lubrication regime[J]. Tribology International, 2012, 46(1): 200–207. DOI:10.1016/j.triboint.2011.03.012 |
| [4] | Bukovnik S, Offner G, Čaika V, et al. Thermo-elasto-hydrodynamic lubrication model for journal bearing including shear rate-dependent viscosity[J]. Lubrication Science, 2007, 19(4): 231–245. DOI:10.1002/(ISSN)1557-6833 |
| [5] | Allmaier H, Priestner C, Six C, et al. Predicting friction reliably and accurately in journal bearings:a systematic validation of simulation results with experimental measurements[J]. Tribology International, 2011, 44(10): 1151–1160. DOI:10.1016/j.triboint.2011.05.010 |
| [6] | Khatri C B, Sharma S C. Influence of textured surface on the performance of non-recessed hybrid journal bearing operating with non-Newtonian lubricant[J]. Tribology International, 2015, 95: 221–235. |
| [7] |
赵小勇, 孙军, 刘利平, 等.
不同工况下内燃机曲轴轴承的润滑性能[J]. 内燃机学报, 2011, 29(4): 348–355.
ZHAO Xiaoyong, SUN Jun, LIU Liping, et al. Lubrication performance of crankshaft bearing for internal combustion engine at different working condition[J]. Transactions of CSICE, 2011, 29(4): 348–355. (in Chinese) |
| [8] | Hili M A, Bouaziz S, Maatar M, et al. Hydrodynamic and elastohydrodynamic studies of a cylindrical journal bearing[J]. Journal of Hydrodynamics, 2010, 22(2): 155–163. DOI:10.1016/S1001-6058(09)60041-X |
| [9] | Tala-Ighil N, Fillon M, Maspeyrot P. Effect of textured area on the performances of a hydrodynamic journal bearing[J]. Tribology International, 2011, 44(3): 211–219. DOI:10.1016/j.triboint.2010.10.003 |
| [10] |
戴旭东, 马雪芬, 赵三星, 等.
曲轴主轴承油膜动力润滑与系统动力学的耦合分析[J]. 内燃机学报, 2003, 21(1): 86–91.
DAI Xudong, MA Xuefen, ZHAO Sanxing, et al. Study on coupling of lubrication and dynamical behavior in internal combustion engine[J]. Transactions of CSICE, 2003, 21(1): 86–91. (in Chinese) |
| [11] |
赵波, 戴旭东, 吴仕昊.
柴油机曲轴主轴承润滑性能分析[J]. 润滑与密封, 2011, 36(11): 32–36.
Zhao Bo, Dai Xudong, Wu Shihao. The analysis of lubrication properties of crankshaft main bearing on diesel engine[J]. Lubrication Engineering, 2011, 36(11): 32–36. (in Chinese) |
| [12] |
赵秀栩, 黄安健, 胡志祥, 等.
大功率船用柴油机主轴承典型工况润滑性能分析[J]. 内燃机工程, 2015(5): 128–133.
ZHAO Xiuxu, HUANG Anjian, HU Zhixiang, et al. Analysis of main bearing lubrication performance of high-power marine diesel engine under typical operation conditions[J]. Chinese Internal Combustion Engine Engineering, 2015(5): 128–133. (in Chinese) |
| [13] | Patir N, Cheng H S. An average flow model for determining effects of three dimensional roughness on partial hydrodynamic lubrication[J]. Journal of Lubrication Technology, 1978, 100(1): 12–17. DOI:10.1115/1.3453103 |
| [14] | Patir N, Cheng H S. Application of average flow model to lubrication between rough sliding surfaces[J]. ASME Transactions Journal of Lubrication Technology, 1979, 101(2): 220–230. DOI:10.1115/1.3453329 |
| [15] | Greenwood J A, Tripp J H. The contact of two nominally flat rough surface[J]. Proceedings Institution of Mechanical Engineers, 1970, 185(48): 625–634. |
| [16] | Zhu D, Cheng H S, Arai T, et al. A numerical analysis for piston skirts in mixed lubrication-part Ⅰ:basic modeling[J]. Journal of Tribology, 1992, 114(3): 553–562. DOI:10.1115/1.2920917 |
| [17] | Paranjpe R S, Goenka P K. Analysis of crankshaft bearings using a mass conserving algorithm[J]. Tribology Transactions, 1990, 33(3): 333–344. DOI:10.1080/10402009008981963 |
| [18] | Hu K, Vlahopoulos N, Mourelatos Z P. A finite element formulation forcoupling rigid and flexible body dynamics of rotating beams[J]. Journal of Sound and Vibration, 2002, 253(3): 603–630. DOI:10.1006/jsvi.2001.4066 |
 2017, Vol. 40
2017, Vol. 40


