2. 长安汽车股份有限公司, 重庆 400023
2. Chongqing Chang'an Automobile Ltd. CO., Chongqing 400023, P. R. China
V型橡胶带式无极变速器(continuously variable transmission, CVT)因其具有灵活的变速特性, 常被运用在汽车和摩托车的变速机构[1]中, 汽车CVT结构常常在发动机曲轴与CVT之间设置一个离合器或者液力变矩器。现因非道路车辆的特殊结构和成本限制, 要求其结构尽量小巧, 不允许离合器或者液力耦合器的存在, 提出四缸柴油发动机中采用CVT刚性联接曲轴轴系结构。然而将CVT与四缸柴油发动机曲轴刚性联接, 必将影响曲轴乃至发动机的整体性能。而曲轴轴系的扭振频率较低, 易在工作转速范围内发生强烈共振[2]。同时曲轴作为发动机转子系统的重要组成部分, 需要对该新型轴系结构进行扭振分析。
国内外对曲轴轴系扭转振动的研究已经成熟。发动机曲轴系扭振测试和测试方法依然是研究的基础和重点, 测量精度得到进一步提高, 能满足工程应用[3-5]; 其次, 学者利用数值解法和编写分析软件来计算曲轴扭振[6-10]。随着计算机技术的迅速发展, 各种有限元软件和多体动力学软件的不断出现, 用有限元法和多体动力学法在曲轴动力学分析中得到了广泛的应用[11-14]。如Su[15]配合实验, 采用多体动力学对柴油发动机曲轴进行结构优化, 模拟曲轴实际动力学状态, 求解精度较高。
笔者结合实验, 采用多体动力学法, 建立四缸柴油刚性联接发动机曲轴EXCITE-DESIGN计算模型, 综合分析得出非道路车辆低速四缸柴油发动机可以采纳CVT刚性联接曲轴轴系结构。
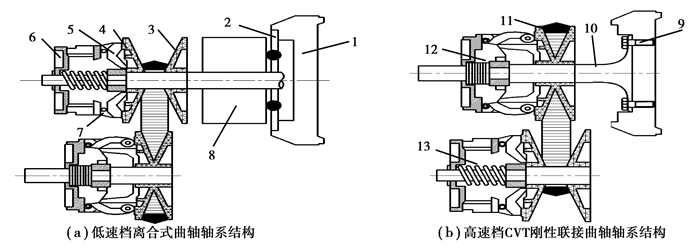
1 CVT刚性联接曲轴轴系结构及原理新型CVT刚性联接四缸柴油发动机曲轴轴系结构及原理, 如图 1(b)所示, 新型结构采用螺栓9将联接盘和飞轮刚性联接, 通过轴10将动力传递给CVT结构。而目前普遍的离合式曲轴轴系结构, 如图 1(a)所示, 在CVT结构与发动机曲轴之间设置一个离合器, 摩擦式离合器通过从动盘摩擦片与飞轮结合。研究涉及的V型橡胶带式无级自动变速器主要由3个功能部件组成:主动带轮、V型橡胶带及从动带轮等, 通过适当调整这三部分的相互作用, 使无级变速传动系统完成无级变速传动机构的基本功能。主动带轮安装在曲轴上, 由固定轮盘、移动轮盘、调速蹄块、回位弹簧、三角架、压盘和滚子等组成, 其工作原理是调速蹄块随曲轴旋转产生的离心力, 通过滚子转换为作用于移动轮盘上的轴向力实现对整个传动系统速比的调节。
|
图 1 CVT刚性联接曲轴轴系结构及原理 Figure 1 Structure and principle of the crankshaft with rigidly coupling CVT 注:1.飞轮; 2.摩擦片; 3.CVT固定盘; 4.CVT移动盘; 5.调速蹄块; 6.压盘; 7.滚子; 8.离合器; 9.螺栓; 10.CVT刚性联接轴; 11.V型橡胶皮带; 12.主动带轮; 13.从动带轮 |
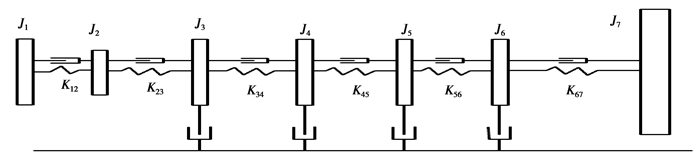
研究采用集总参数模型和霍尔茨求解法, 对几何结构模型当量化。如图 2所示, 为四缸发动机曲轴简化后的质量-弹簧-阻尼系统, 其中J1, J2, …, J7是各集中质量的转动惯量, K12, K23, …, K67分别为相邻两集中质量间的扭转刚度。气缸转动惯量主要包括活塞、连杆、曲拐等运动部件的转动惯量, 其质量的集中点在气缸中心线上; 飞轮、扭振减振器的质量集中点在各自的中心位置。发动机的气缸阻尼和扭转阻尼分配在集中质量处作为质量阻尼; 金属材料的阻尼分配在各自中心位置。
|
图 2 质量-弹簧-阻尼系统 Figure 2 Mass-spring-damper system |
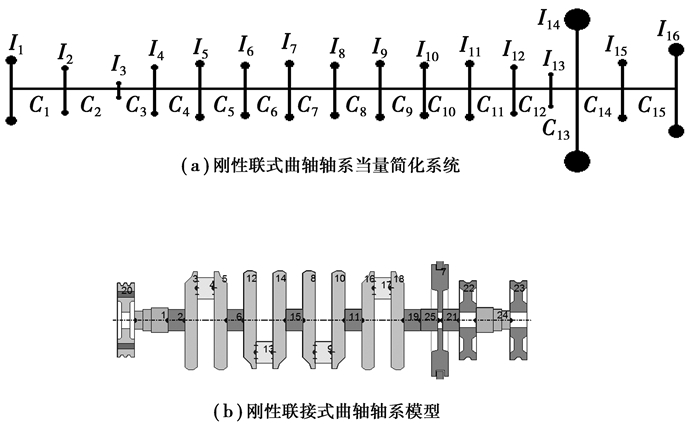
将上述质量-弹簧-阻尼系统的集中质量加以细化, 细化后的集中质量成为节点, 连接的弹簧成为单元, 得到节点-单元模型。简化后的曲轴节点-单元模型由14个节点和13个单元组成, 如图 3所示, 其中, I1, I2, …, I14是各集中质量的转动惯量, C1, C2, …, C13分别为相邻两集中质量间的扭转刚度。

|
图 3 节点-单元模型 Figure 3 Node-element model |
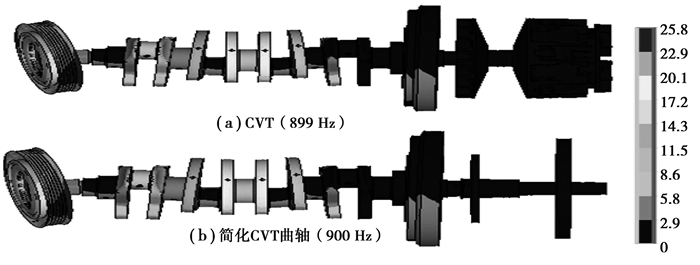
CVT结构复杂, 不易分析计算, 需要进行结构当量简化。将CVT主动带轮结构简化为2个盘转结构, 其中, 固定盘转动惯量为4.07×10-2 kg·m2; 移动盘转动惯量为1.70×10-2 kg·m2。对CVT结构当量简化进行有限元模态验证, 振型(见图 4)和自由振动频率(见表 1)基本一致, 验证了CVT结构当量简化的合理性。得出CVT结构的具体转动惯量参数, 其余结构转动惯量参数通过常规方法和三维软件可确定。
|
图 4 曲轴第三阶扭转振型 Figure 4 Torsional vibration shape of the third-order to crankshaft |
| 表 1 曲轴自由振动频率 Table 1 Free vibration natural frequency of crankshaft |
由于有限元法对复杂零件的扭转刚度计算的准确性较高, 文中采用有限元法计算部件的扭转刚度。以半拐为例, 通过施加一扭矩M, 来计算得出曲柄销相对于主轴颈中心的变形角度θ, 从而计算出半拐的扭转刚度
| $ {C_{{\rm{half}}}} = M/\theta , $ | (1) |
另外, 对于本研究的橡胶型阻尼减振器的扭转刚度为
| $ f = 1/2{\rm{\pi *}}\sqrt {C/{I_{{\rm{ring}}}}} . $ | (2) |
式中, Chalf的单位为N·m/rad, Iring为惯性环的转动惯量, f为减振器的固有频率。
2.4 CVT曲轴简化与EXCITE建模结合以上建模方法、CVT结构当量简化以及参数确定, 以某四缸柴油发动机为基础, 建立CVT刚性联接式曲轴轴系当量简化系统(见图 5(a))与EXCITE模型(见图 5(b)), 包括1个扭振减振器、阶梯轴、5个主轴颈、5个曲柄销、8个曲柄臂及平衡重和1个飞轮, 以及CVT结构当量简化后的2个盘转结构。表 2和表 3分别为具体的当量简化转动惯量参数和当量简化扭转刚度参数。
|
图 5 CVT曲轴轴系当量简化系统与EXCITE建模 Figure 5 Simplified system and EXCITE model of the crankshaft with rigidly coupling CVT 注:1.扭振减振器(外轮); 2.扭振减振器(内轮); 3.阶梯轴①; 4.主轴承①; 5.曲柄销①及左右曲柄; 6.主轴承②; 7.曲柄销②及左右曲柄; 8.主轴承③; 9.曲柄销③及左右曲柄; 10.主轴承④; 11.曲柄销④及左右曲柄; 12.主轴承⑤; 13.阶梯轴②; 14.飞轮; 15.CVT固定盘; 16.CVT可移动盘 |
| 表 2 当量简化转动惯量参数 Table 2 Equivalent simplified rotational inertia |
| 表 3 当量简化扭转刚度参数 Table 3 Equivalent simplified torsional stiffness |
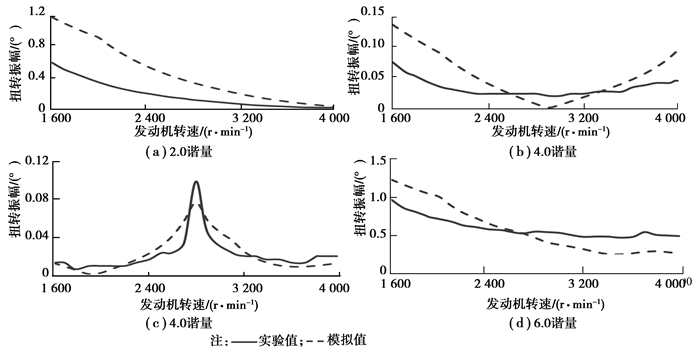
实验测试原理:曲轴前端的扭转振动可以看作曲轴的匀速转动加上扭转波动, 这类似于信号间传输中的调频波。曲轴的匀速转动相当于调频波中的载波, 扭转波相当于调频波中的信号波。调频波通过鉴频器解调, 从而检出信号波。类似于鉴频器的原理和步骤, 也可以从曲轴的转动中检出扭转波动, 从而达到检测扭转目的。对于四冲程发动机, 由于曲轴每两圈点火一次, 即每转点火0.5次, 因此四缸发动机的最低主谐次为2.0, 即四冲程四缸发动机的主谐量依次为2.0、4.0、6.0…。同时, 随着激励阶次的升高, 其激振力矩迅速减小, 所引起的振动可忽略不计, 因此只考虑发动机低阶主谐量所引起的共振, 故本研究只考虑2.0、4.0、6.0三个谐量的振动曲线。
四缸柴油发动机离合式曲轴轴系实验与模拟结果如图 6所示。二者的主要表现在6.0谐量图 6(c), 振动曲线在2 800 r/min处有一个波峰, 即此处曲轴系产生了共振, 其振动幅值低于0.2°, 且十分接近; 二者4.0谐量的振动曲线表现均不明显; 而对于2.0谐量图 6(a)的振动曲线在2 800 r/min之前很大, 但其振动曲线变化趋势并不符合一般共振产生的机理(没有凸点), 因此考虑二阶振动主要成分为滚振, 滚振轴段不产生扭转应力, 且计算值包含的滚振成分比实验测试值要大, 也使得合成谐量图 6(d)中模拟和实验值有些差异。总体来看, 在各阶次激励作用下曲轴前端扭转振动角位移的实验值与模拟值基本一致, 尤其是第6阶次激励作用下的振幅峰值和峰值频率吻合较好, 证明了所建模型和模型参数确定方法的正确性。
|
图 6 离合式曲轴轴系实验与模拟对比 Figure 6 Sxperimental data and simulation results of the crankshaft |
刚性联接式CVT曲轴自由振型如图 7(b)所示, 自由振动频率主要有258.3、292.6、570.6、1 394.2 Hz (与模态验证频率有一定差别, 二者模型有异)。离合式CVT曲轴振型如图 7(a)所示, 自由振动频率主要有286.3、570.4、1 395.2 Hz。离合式CVT的主要表现为第一节点(减振器)的相对振幅较大, 其余节点的振幅表现不明显, 说明扭振减振器起到了很好的减振作用。对比之下, 刚性联接式CVT曲轴的自由振动频率一阶(258.3 Hz)要低些, 刚性联接式CVT曲轴的一阶和二阶振型的第一节点(减振器)和CVT端相对振幅较大, 一方面说明扭振减振器也对刚性联接式CVT曲轴起到了很好的减振作用, 另一方面也说明CVT端存在着一定振动。

|
图 7 曲轴自由振型 Figure 7 Free vibration of crankshaft |
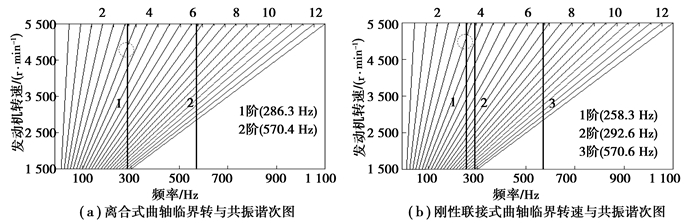
临界转速反映出自由振动频率与各激励谐量的相互关系, 如图 8(a)所示, 竖直的两根线为曲轴的第一阶、第二阶自由振动频率, 斜线表示激励的各个简谐分量, 两者的交点代表其在某个激励简谐分量的作用下引起曲轴强迫振动点, 横坐标表示对应的转速, 即临界转速。与离合式曲轴临界转速与共振谐次图 8(a)相比, 刚性联接式CVT曲轴图 8(b)仅仅是多了一阶自由振动频率, 其中较低的第一阶自由振动频率与激励简谐分量的第一个交点是与3.0谐量斜线相交的, 对应的曲轴转速为5 100 r/min。图 8(a)离合式CVT曲轴第一阶自由振动频率与激励简谐分量的第一个交点是与3.5谐量斜线相交, 对应的曲轴转速为4 900 r/min。
|
图 8 曲轴临界转速与共振谐次图 Figure 8 Critical speed and resonant harmonic figure of crankshaft |
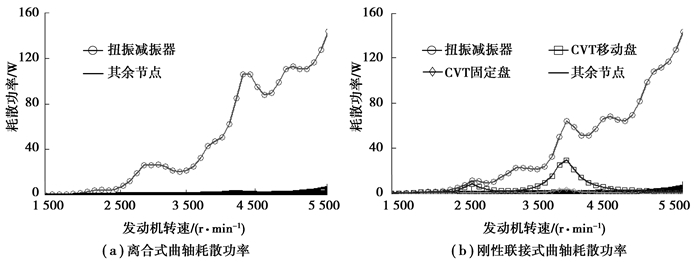
耗散功率图反映出曲轴各个节点的能量耗散情况, 间接可以看出曲轴各个节点的扭振状况, 同时也可以看出扭振减振器是否与发动机匹配, 且扭振减振器的耗散功要求小于200 W。图 9(b)刚性联接式CVT曲轴耗散功图, 除了扭转减振器有明显的耗散功功能外, CVT轴也有较为明显的耗散功作用, 表现在转速为2 600 r/min和3 900 r/min处, CVT移动盘的耗散功曲线出现波峰, 该两点的最大耗散功分别为9 W和30 W, 明显大于其余节点的耗散功的能力, 而离合式CVT曲轴图 9(a)则没有该现象。说明CVT轴起到了一定的耗散振动能量的功能, CVT端将会有一定的扭振振动。不过最大耗散功也小于200 W, 说明刚性联接式CVT曲轴耗散了一定的振动能量, 但影响较小。
|
图 9 曲轴耗散功率 Figure 9 Power dissipation of crankshaft |
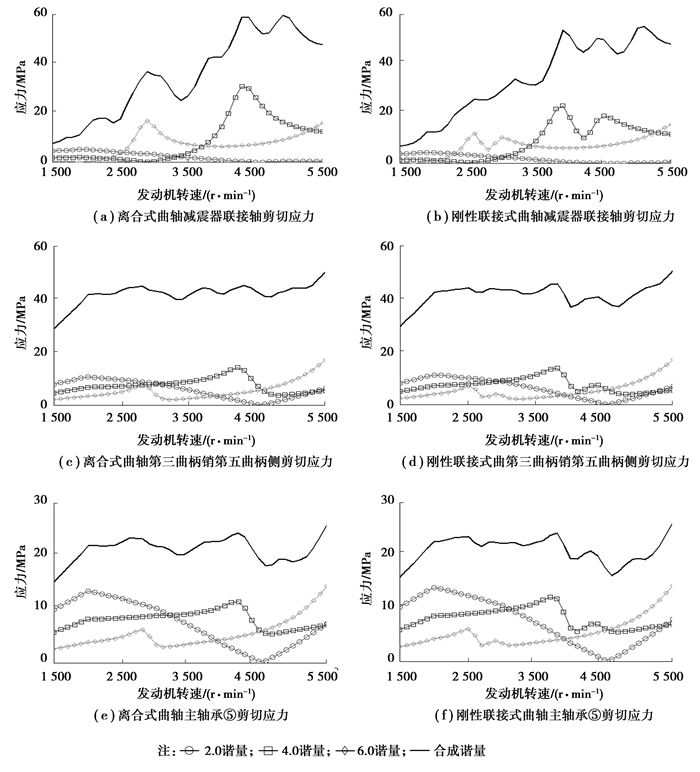
曲轴强度反映曲轴在运转过程中, 各危险节点剪切应力变化情况(如图 10所示)。
|
图 10 曲轴曲柄销剪切应力 Figure 10 Shear stress of crankshaft main journal |
图 10(a)为离合式曲轴减震器联接轴剪切应力, 其中6.0谐量和4.0谐量的最大剪切应力分别为17 MPa和30 MPa, 合成的剪切应力为58 MPa。图 10(b)为刚性联接式曲轴减震器联接轴剪切应力, 其中第2.0谐量和4.0谐量的最大剪切应力分别为12 MPa和23 MPa, 而合成的剪切应力低于55 MPa, 处于低应力工作环境。同时, 不难判断出曲轴上曲柄销所承受的扭矩是较大的地方, 故此处选取曲柄销剪切应力最大处, 曲轴第三曲柄销第五曲柄侧, 如图 10(c)和图 10(d)所示, 离合式与刚性联接式曲轴系的各曲柄销剪切应力均在50 MPa以下, 处于较低水平。另外, 选取曲轴主轴承剪切应力较大处, 主轴承⑤, 如图 10(e)和图 10(f)所示, 二者的合成剪切应力均在30 MPa以下, 处于低应力工作环境。说明刚性联接式曲轴对曲轴各拐剪切应力幅度的影响不大, 但有高转速工况降低而中低转速剪切应力幅值增加的普遍趋势。
4.5 扭振减振器振幅对比分析扭振减振器的皮带轮是发动机配气机构动力的来源, 故减振器的扭振振动对发动机配气机构影响非常大, 要求其各谐量的最大扭振振幅小于0.4°。离合式CVT曲轴扭振减振器(见图 11(a))扭转振动在2 900 r/min处和4 300 r/min处有2个波峰, 其振动幅值分别为0.2°和0.39°, 符合减振器使用要求。刚性联接式CVT曲轴扭振减振器的振幅(见图 11(b))主要表现为第4.0谐量和6.0谐量, 其最大振幅幅值分别为0.18°和0.35°, 对应的曲轴转速分别在2 600 r/min和3 900 r/min, 低于减振器所允许的0.4°范围; 同时, 第2.0谐量的振动表现为滚振。与离合式CVT曲轴扭振器的振幅相比, 其振幅变化不大, 仅仅是对应的转速发生了变化。故CVT结构对曲轴扭振减振器的影响较小。
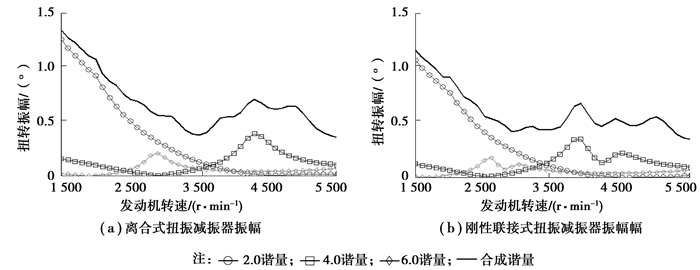
|
图 11 曲轴轴系扭振减振器振幅 Figure 11 Damper amplitude of crankshaft |
由前文分析得出, 刚性联接式CVT曲轴结构存在扭转振动, 使得连接CVT与飞轮之间的刚性联接轴和CVT轴的剪切应力增大。图 12(a)中, CVT刚性联接轴剪切应力曲线有两个波峰, 分别在2 600 r/min和3 900 r/min, 后者的剪切应力较大, 其剪切应力值为32 MPa; 其余转速点的应力值均较小。可以看出, 在CVT刚性联接轴端的剪切应力波动较大, 即验证了前面扭振计算的结果。总的来说剪切应力还是较小, 处于低应力工作环境。图 12(b)为CVT轴剪切应力, 有2个较大的应力波峰值, 一个是在低转速点2 600 r/min时, 剪切应力值为85 MPa主要由第6谐量的振动引起; 另一个是在高转速点3 900 r/min, 最大剪切应力值达到了129 MPa, 主要由第4谐量的振动引起。此处说明了CVT轴的扭振振动有2个波动点, 且波动均较大。同时, 对于整个曲轴系, 该处的剪切应力为最大, 不过仍没有达到曲轴的极限应力强度, 而且出现在高转速点, 对于低速四缸柴油刚性联接发动机的影响不大。
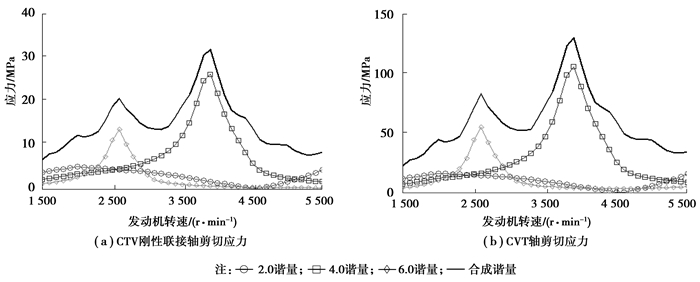
|
图 12 CVT刚性联接式曲轴轴系强度分析 Figure 12 Structure strength analysis of the crankshaft with rigidly coupling CVT |
笔者提出四缸柴油发动机中采用CVT刚性联接曲轴轴系结构, 阐述该新型结构的特征和工作原理。建立四缸柴油发动机刚性联接式曲轴轴系当量简化系统和EXCITE模型, 通过曲轴前端实验验证了所建模型和模型参数确定方法的正确性。并对所有的模型进行求解计算, 得出具体的扭振特性和参数。结果表明CVT刚性联接使得曲轴一阶自由振动频率降低, 轴系振动波动加大, 减振器耗散能增加, 影响均在合理规定范围之内。对曲轴各拐剪切应力幅度的影响较小, 但有高转速工况降低而中低转速剪切应力幅值增加的普遍趋势。CVT轴总剪切应力较大, 不过仍然没有达到曲轴的极限应力强度, 而且出现在高转速点。综合分析得出非道路车辆低速四缸柴油发动机可以采纳CVT刚性联接曲轴轴系结构。
| [1] | Carbone G, Mangialardi L, Bonsen B, et al. CVT dynamics:theory and experiments[J]. Mechanism and Machine Theory, 2007, 42(4): 409–428. DOI:10.1016/j.mechmachtheory.2006.04.012 |
| [2] |
陈翔, 崔志琴.
发动机曲轴轴系扭振技术研究的方法分析[J]. 机械工程与自动化, 2013(6): 216–217.
CHEN Xiang, CUI Zhiqin. Current situation and prospect of engine crankshaft torsional vibration technology research[J]. Mechanical Engineering & Automation, 2013(6): 216–217. (in Chinese) |
| [3] | Subbu R, Samy B A, Sharma P M, et al. Measurement and validation of two wheeled vehicle single cylinder engine unbalance force calculation on the crankshaft[C/OL]//SAE/JSAE 2014 Small Engine Technology Conference & Exhibition.[S.l.]:SAE, 2014[2016-02-19].http://papers.sae.org/2014-32-0061/. |
| [4] |
李玉梅, 华春蓉, 闫兵.
内燃机轴系扭振测试方法研究[J]. 车用发动机, 2010(1): 77–80.
LI Yumei, HUA Chunrong, YAN Bing. Study on testing method of crankshaft torsional vibration[J]. Vehicle Engine, 2010(1): 77–80. (in Chinese) |
| [5] | Shangguan W B. Experimental and calculation analysis of rotational vibration for an engine front end accessory drive system[J]. SAE International Journal of Passenger Cars Mechanical Systems, 2011, 4(2): 1000–1017. DOI:10.4271/2011-01-1534 |
| [6] |
徐科达, 俞水良.
柴油机曲轴扭振计算分析软件的开发与应用[J]. 机电工程技术, 2011, 40(2): 71–74.
XU Keda, YU Shuiliang. Computational and analytic software development for the torsional vibration of dieselengine crankshaft[J]. Mechanical & Electrical Engineering Technology, 2011, 40(2): 71–74. (in Chinese) |
| [7] | Villalva S G, Bittencourt M L, Zampieri P R. Methodology for automotive crankshaft design using analytical and flexible models[C/OL]//22nd SAE Brasil International Congress and Display.[S.l.]:SAE, 2013[2016-02-19].http://papers.sae.org/2013-36-0590/. |
| [8] | Nerubenko G. Tuned torsional vibration damper[C/OL]//SAE 2013 Noise and Vibration Conference and Exhibition.[S.l.]:SAE, 2013[2016-02-19].http://papers.sae.org/2013-01-1897/. |
| [9] |
蒋爱香, 李为.
某柴油机的曲轴系扭振计算研究[J]. 柴油机, 2014, 36(6): 35–38.
JIANG Aixiang, LI Wei. Torsional vibration calculation for a certain diesel engine[J]. Diesel Engine, 2014, 36(6): 35–38. (in Chinese) |
| [10] | Rodrigues A, Silva R L E, Cruz R, et al. Experimental and numerical modal analysis of 6 cylinders diesel crankshaft[C/OL]//SAE Brasil 2011 Congress and Exhibition.[S.l.]:SAE, 2011[2016-02-19].http://papers.sae.org/2011-36-0358/. |
| [11] | Kandreegula S K, Paroche S, Mukherjee S, et al. Static and dynamic study of 4-cylinder diesel engine crankshaft using FEM and analytical approaches[C/OL]//International Mobility Conference, [S.l.]:SAE, 2016[2016-02-19]. http://papers.sae.org/2016-28-0108/. |
| [12] |
宋武强.
基于EXCITE-Designer的车用汽油机曲轴扭转振动分析和不同减振器性能对比[J]. 内燃机与动力装置, 2010(1): 21–24.
SONG Wuqiang. Analysis of torsion vibration of crankshaft and performance comparison with different dampers on EXCITE-designer software[J]. Internal Combustion Engine & PowerPlant, 2010(1): 21–24. (in Chinese) |
| [13] | Mendes A S, Kanpolat E, Rauschen R. Crankcase and crankshaft coupled structural analysis based on hybrid dynamic simulation[J]. SAE International Journal of Engines, 2013, 6(4): 2044–2053. DOI:10.4271/2013-01-9047 |
| [14] | Ukhande M, Mane R, Shegavi G. Optimization of crankshaft torsional rigidity for fatigue strength improvement using CAE[C/OL]//SAE 2012 World Congress & Exhibition.[S.l.]:SAE, 2012[2016-02-19]. http://papers.sae.org/2012-01-0404/. |
| [15] | Su W T. Structural optimization of a diesel engine crankshaft[C/OL]//22nd SAE Brasil International Congress and Display.[S.l.]:SAE, 2013[2016-02-19]. http://papers.sae.org/2013-36-0595/. |
 2017, Vol. 40
2017, Vol. 40

