2. 重庆大学 机械传动国家重点实验室, 重庆 400044
2. The State Key Laboratory of Mechanical Transmission, Chongqing University, Chongqing 400044, P. R. China
对于斜齿轮传动,虽然在啮合过程中齿对的交替不是突变的,但是啮合过程中轮齿的啮合刚度和轮齿的载荷也是周期性变化的,同样会引起啮合过程的动态刚度激励。实践证明对渐开线斜齿轮进行适当的修形后,可以有效地改善其啮合性能,降低噪音和延长齿轮的使用寿命[1]。
关于齿廓修形对齿轮时变啮合刚度、静态传递误差以及轮齿接触应力和齿根弯曲应力的影响国内外许多的学者做了大量的研究工作。He[2]在其学位论文中利用有限元与接触力学法(FE/CM)的程序代码建立了精确的齿轮副计算模型,获得了齿顶修形后的综合啮合刚度曲线。Tesfahunegn等[3]利用非线性有限元方法详细地研究了不同齿廓修形形状对传递误差、齿根应力及接触压力的影响。Ohno等[4]建立了齿轮三维有限元模型,分析了齿轮接触应力和修形量的关系,确定了斜齿轮的最佳修形量。Chen等[5-6]考虑齿顶修形和齿根裂纹等轮齿误差的影响建立了通用的齿轮副啮合刚度和传递误差计算模型。
在上述文献的基础上,Özgüven等[7]建立了6个自由度的非线性半定直齿轮模型,考虑时变啮合刚度、齿轮误差以及齿廓修形等因素,建立了非线性直齿轮转子模型,通过静态传递误差方法计算内部激励引起的响应。Liu等[8]建立了考虑动载荷分布、时变啮合刚度、齿廓修形以及接触损耗等因素的非线性分析模型,研究了齿廓修形对多啮合齿轮组振动的影响。陈思雨等[9]利用有限单元方法得到不同修形齿轮的啮合刚度和静态传递误差,提出以齿轮副的振动幅值及动态因子来衡量齿轮修形的优劣方法。马辉等[10]以直齿轮为例,获得了不同齿顶修缘量后的时变啮合刚度和静态传递误差曲线,并分析了其对齿轮转子系统振动响应的影响。
从以上文献中可以看出,考虑齿廓修形对齿轮啮合刚度、静态传递误差和系统振动响应影响的研究中,多见于是对直齿轮副的分析,而对于考虑齿廓修形对斜齿轮系统啮合刚度和传递误差的影响,分析修形后斜齿轮系统振动响应的研究还不多见。因此,笔者基于ANSYS-APDL参数化建模,建立可以考虑不同齿顶修缘量的斜齿轮啮合模型,通过轮齿承载接触分析得到斜齿轮不同齿顶修缘量的静态传递误差和啮合刚度,并将其引入斜齿轮耦合转子系统有限元模型中,分析不同齿顶修缘量对斜齿轮振动响应的影响规律。
1 修缘对斜齿轮啮合刚度的影响 1.1 考虑齿廓修形斜齿轮有限元精确模型的建立为了得到较为精确的齿轮分析模型,文中利用ANSYS-APDL对含有齿顶修缘的渐开线斜齿轮进行参数化建模,建立斜齿轮三维啮合模型,提高了建立斜齿轮的效率和建模精度。现以某高铁牵引齿轮传动系统大小齿轮为例进行建模进行有限元分析。齿轮参数如表 1所示。
| 表 1 齿轮参数 Table 1 Gear parameters |
合理的齿廓修形能够有效地避免轮齿啮入啮出时的尖角接触,降低齿轮传动系统的振动噪声水平。因为齿根部齿廓修形和与之啮合的轮齿齿顶修形影响效果相同[12],故本节仅研究齿顶修形对啮合参数的影响,并进一步假设齿轮副轮齿修形量相同。
笔者采用参考文献[14]中介绍的修缘方法对轮齿进行齿顶修缘,齿顶修缘示意图如图 1所示,图中FH段表示修缘渐开线齿廓,BF段表示原渐开线齿廓,Ca为齿顶修缘量,rb为原齿廓渐开线基圆半径,rb′为修缘齿廓渐开线基圆半径。

|
图 1 齿顶修缘 Figure 1 Schematic of tip relief |
以表 1中的斜齿轮参数为例,利用ANSYS参数化建模,建立未修形和含不同修形量的斜齿轮三维啮合模型,并进行轮齿承载接触分析。为了减少计算时间和资源的占用,文中只建立斜齿轮局部啮合模型,如图 2所示。

|
图 2 齿轮啮合模型 Figure 2 Mesh model of the gear pair |
通过有限元对局部斜齿轮啮合模型进行承载接触分析,不考虑齿廓误差的对接触分析的影响,即承载时静态传递误差等于轮齿的变形。
齿轮的啮合刚度可表示为齿轮所受载荷与轮齿啮合变形的比值。齿轮的啮合刚度Kn可以表示为
| Kn=Fnδn, | (1) |
式中:Fn为齿面的法向载荷;δn为齿面法向综合弹性变形,其包括局部赫兹接触产生的接触弹性变形、轮齿受载弯曲产生的接触位置的变形以及轮毂变形产生的接触位置的位移。
对于斜齿轮接触,由于轮齿接触线的长度是变化的,这使得直接求解齿面接触的法向载荷和接触位置啮合线方向的变形值变得困难。因此,文中采取文献[15]提出的基于转矩和齿轮啮合点转角变形,推导到计算齿轮啮合线位移的方法来求解齿轮啮合刚度的方法,使利用有限元法求解齿轮啮合刚度问题变得简单易行。
取未修形齿轮从轮齿开始啮入点到下一齿开始啮入的过程为一个啮合周期,在一个周期内,主动轮转过的角度为10.285 7°,将此转角等分成10份,得到11个离散的转角位置,对每个转角位置进行加载求解,提取每一个位置处的主动轮转角变形量,进而求出每一个位置处的啮合刚度。
齿轮扭转啮合刚度KT为齿轮所受转矩Tm和齿轮啮合点转角变形量Δθ的比值,其表达式为
| KT=TmΔθ. | (2) |
将
| Kn=KT⋅4cosβ(mnz2)2cosαn. | (3) |
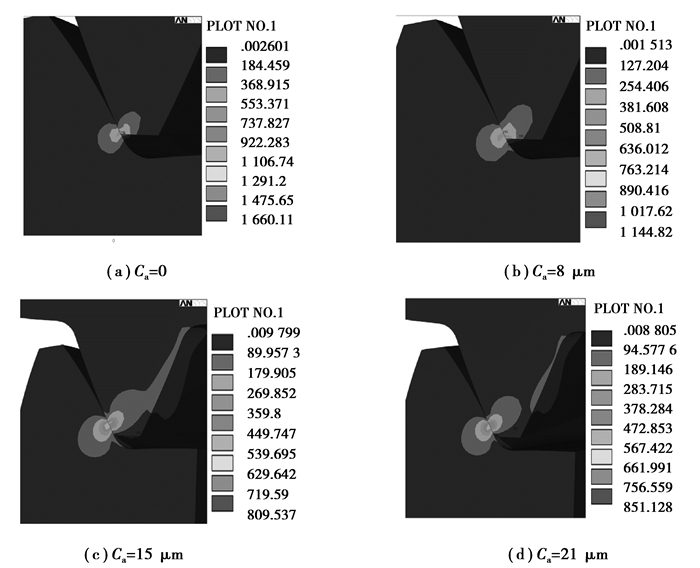
文中取修形长度为定量,主要分析不同齿顶修缘量对斜齿轮静态传递误差和啮合刚度的影响。设齿廓修形量分别为0、8、15、21 μm,对这4种工况加载求解,斜齿轮啮入位置的等效应力云图如图 3所示,斜齿轮不同修形量的静态传递误差和时变啮合刚度曲线如图 4、图 5所示。
|
图 3 齿轮啮入点的等效应力云图 Figure 3 Meshes into point equivalent stress nephograms |
|
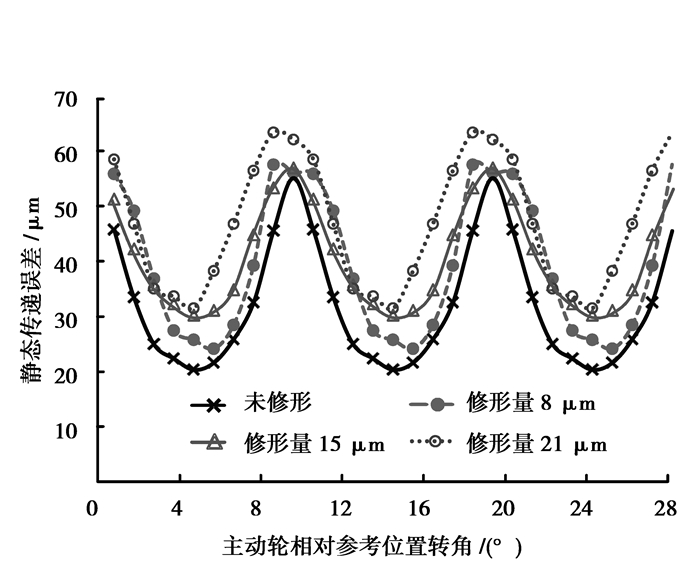
图 4 不同修缘量下静态传递误差 Figure 4 Helical gear static transmissions error curve under different amounts of tip relief |
|
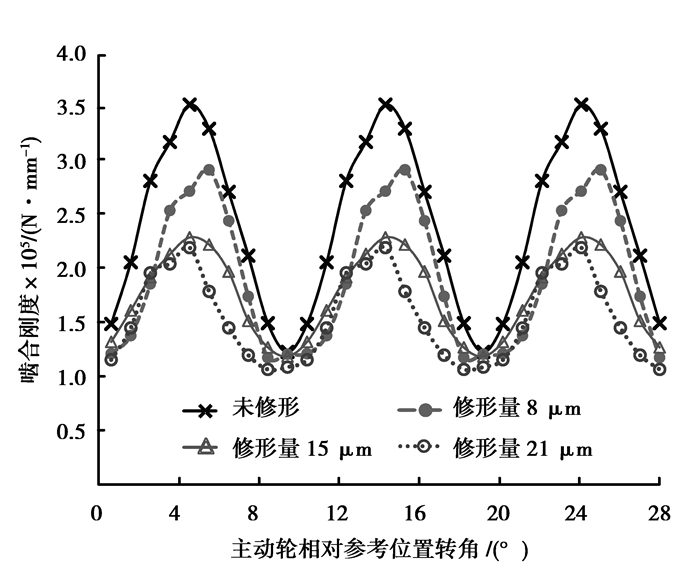
图 5 不同修缘量下综合啮合刚度曲线 Figure 5 Helical gear mesh stiffness curve under different amounts of tip relief |
从图 4、图 5中可以看出,与未修形的齿轮相比,修形后斜齿轮的静态传递误差和啮合刚度波动幅值减小。随着修形量的增大,静态传递误差和啮合刚度波动幅值逐渐减小,当修形量为21 μm时,与15 μm相比,静态传递误差和啮合刚度波动幅值略有增大,且啮合刚度明显减小。
2 斜齿轮系统动力学模型 2.1 斜齿轮轴段单元模型文中以某高铁牵引齿轮箱平行轴系两斜齿轮系统为研究对象,建立平行轴系斜齿轮转子系统数学模型,如图 6所示,2个齿轮也简化为轴系,将轴系单元划分为多个弹性轴段,假设轴段的两个节点分别承受弯矩、扭矩和轴向力的作用,各轴段的受力状态借助于Timoshenko梁单元理论进行分析。

|
图 6 齿轮-转子轴系单元模型 Figure 6 Simple shafting element model |
如图 7所示,轴段每个节点有6个自由度,则第K个梁单元两节点在局部坐标系下的位移为
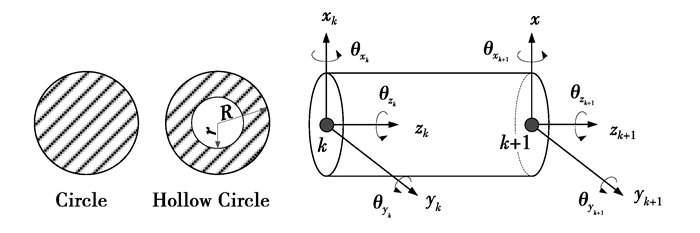
|
图 7 Timoshenko梁单元 Figure 7 Timoshenko beam element |
| XK={xk,yk,zk,θxk,θyk,θzk,xk+1,yk+1,zk+1,θxk+1,θyk+1,θzk+1}T, | (4) |
式中:x、y为横向自由度;z为轴向自由度;θx、θy为摆动自由度;θz为扭转自由度。
单元的自由振动方程可表示为
| MK¨XK+˙CK˙XK+KKXK=0 | (5) |
式中:MK为轴段质量矩阵,CK为轴段阻尼矩阵,KK为轴段刚度矩阵。
轴段质量矩阵
| MK=diag{mk,mk,mk,Ixk,Iyk,Izk,mk+1,mk+1,mk+1,Ixk+1,Iyk+1,Izk+1} | (6) |
式中:
利用弹性力学相关理论,可得Timoshenko梁单元12×12阶的刚度矩阵
| KK=[AEL0ax00ay000GJLSym.00−cy0ey0cx000ex−AEL00000AEL0−ax000−cx0ax00−ay0cy000ay000GJL00000GJL00−cy0fy000cy0ey0cx000fx0−cx000ex]. | (7) |
| {ax=ay=12EIL3(1+φ),cx=cy=6EIL2(1+φ),ex=ey=(4+φ)EIL(1+φ),fx=fy=(2−φ)EIL(1+φ), | (8) |
式中:E为材料弹性模量;μ为泊松比;A为单元横截面面积;L为单元长度;G为剪切模量;J为扭转惯性矩;I为直径惯性矩;φ为剪切影响因子,
| K=6(1+μ)/(7+6μ); | (9) |
当梁单元为空心时
| K=6(1+μ)(1+m2)2(7+6μ)(1+m2)2+(20+12μ)m2,(m=r/R). | (10) |
式(5)中,材料阻尼CK假定为经典阻尼,为
| CK=αMK+βKK, | (11) |
式中,α、β为质量矩阵和刚度矩阵比例系数。
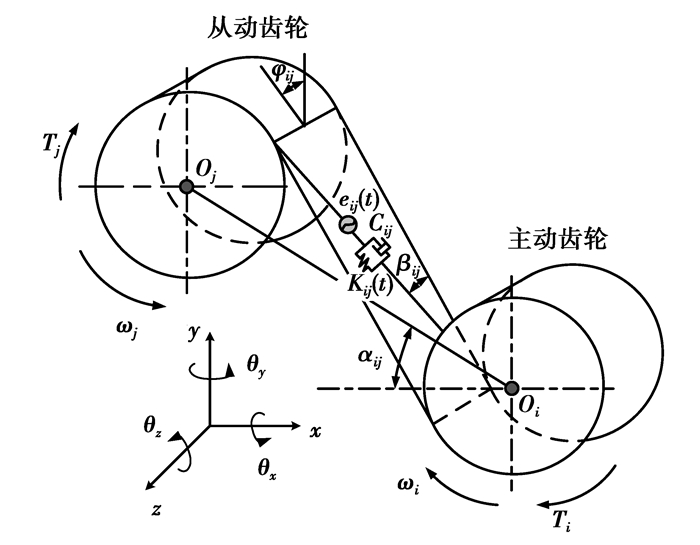
2.2 斜齿轮副啮合模型建立斜齿轮副12自由度啮合动力学模型,如图 8所示,齿轮i为主动轮,齿轮j为从动轮,在啮合面上ωi、ωj分别为主从动齿轮的转动角速度,取顺时针为正,逆时针为负;Ti、Ti分别为主从动轮上的转矩。
|
图 8 斜齿轮副啮合动力学模型 Figure 8 Meshing dynamic model of helical gear pair |
Cij为沿啮合线方向的啮合阻尼,与式(11)取值相同。kij(t)为沿啮合线方向的啮合刚度,由1.3节得到的斜齿轮综合啮合刚度进行曲线拟合,并将其引入到动力学方程中。
eij(t)为齿轮静态传递误差,可表示为
| eij(t)=eijsin(ωiz1t), | (12) |
式中, eij为齿轮静态传递误差的幅值。
将图 8中个啮合副各方向位移向啮合线方向投影,可得转化的投影
| V=[cosβijsinφij,±cosβijcosφij,sinβij,risinβijsinφij,−risinβijcosφij,±ricosβij,−cosβijsinφij,∓cosβijcosφij,−sinβij,rjsinβijsinφij,−rjsinβijcosφij,±rjcosβij], | (13) |
式中:ri、rj分别为主、从轮的基圆半径;βij为基圆螺旋角;φij为端面啮合线与y轴正向的夹角。
由于啮合面的方向随着主动轮的转向变化而改变,所以会导致各元素前的正负号产生变化,其中上半部分对应于主动轮逆时针旋转时,下半部分对应于主动轮顺时针旋转时。主动轮转向变化同时会影响夹角φij为
| φij={φij−αij,逆时针方向,−(φij+αij),顺时针方向, | (14) |
式中:φij为齿轮副的端面压力角;αij是齿轮中心线与x轴向的夹角。
斜齿轮副运动耦合方程可表示为
| Mij¨Xij+(Cij+Gij)˙Xij+KijXij=Fij, | (15) |
式中:Mij为斜齿轮副质量矩阵,Cij为啮合阻尼矩阵,Gij为陀螺矩阵,Kij为啮合刚度矩阵,Fij为外部载荷。
| Mij=diag{mi,mi,mi,Ixi,Iyi,Izi,mj,mj,mj,Ixj,Iyj,Izj}, | (16) |
| Xij={xi,yi,zi,θxi,θyi,θzixi,yj,zj,θxj,θyj,θzj}T | (17) |
| Cij=CijVTV, | (18) |
| Kij=kij(t)⋅VTV. | (19) |
根据以上单元理论组合后建立斜齿轮转子系统的动力学模型为
| M¨X+C˙X+KX=F, | (20) |
式中:M为质量矩阵,包括转子质量和齿轮质量;C为阻尼矩阵,包括转子轴承阻尼和陀螺力矩;K为刚度矩阵,包括转子刚度、啮合刚度和轴承刚度;F为外载荷向量。
3 系统振动响应分析如图 6所示,研究斜齿轮系统的振动响应,该系统由齿轮、轴和轴承组成。齿轮参数如表 1所示,轴和轴承简化为弹簧单元参数如表 2所示。
| 表 2 轴承刚度参数 Table 2 Parameters of stiffness |
取斜齿轮未修形时的平均啮合刚度分析斜齿轮系统的固有频率,不考虑阻尼的影响。前10阶固有频率结果如表 3所示。
| 表 3 斜齿轮系统固有频率 Table 3 Natural frequencies of helical gear system |
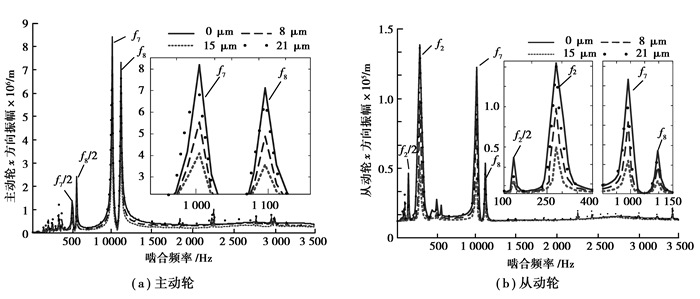
文中对未修形和齿廓修形量分别为0、8、15、21 μm这4种工况下的斜齿轮系统进行振动响应分析,结果如图 9所示。
|
图 9 不同修缘量下齿轮处径向振动响应曲线 Figure 9 Radial vibration responses of the gear under different amounts of tip relief |
从图 9(a)中可以看出,无论主动齿轮修形前还是修形后,当齿轮的啮合频率分别与固有频率f7/2、f8/2、f7、f8相同时系统的径向振动幅值较大(当啮合频率等于其他固有频率时,系统的径向振动幅值也有一定的波动,由于振动的幅值较小,此处暂不进行分析)。修形后系统的径向振动幅值减小,且随着修缘量的增加,系统的径向振动幅值先减小后增大。修缘量为21 μm时,相对于修缘量为8 μm和15 μm时,f7、f8处振动幅值增加,修缘量为15 μm时,系统的径向振动幅值最小。
从图 9(b)中可以看出,从动轮的径向振动响应曲线的趋势与主动轮略有不同,从动轮在啮合频率为f2/2、f2、f7、f8处系统的径向振动幅值较大。与主动轮振动趋势相同的是,随着齿轮修缘量的增加,系统的径向振动幅值也是先减小后增大。在修缘量为21 μm时,系统的径向振动幅值相对于修缘量为8 μm和15 μm时增加,修缘量为15 μm时,系统的径向振动幅值最小。
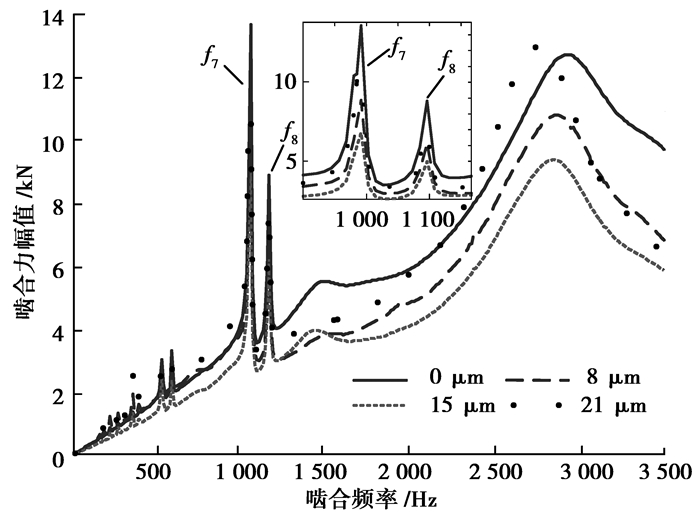
图 10是斜齿轮不同修缘量啮合力的变化曲线,从图中可以看出,与未修形相比,当齿轮的修缘量为8 μm和15 μm时,齿轮的啮合力明显减小,并且在修缘量为15 μm时,啮合力的幅值最小。当啮合频率等于f7、f8时,啮合力的波动幅值较大,且随着齿轮修缘量的增加,啮合力也是先减小后增大。
|
图 10 不同修缘量下斜齿轮啮合力变化曲线 Figure 10 The curves of meshing force under different amounts of tip relief |
综合图 9和图 10可知,啮合频率在0~3 500 Hz范围内,当齿轮的修缘量为8 μm和15 μm时,主从动齿轮的径向振动和啮合力幅值均小于未修形时,在啮合频率等于固有频率处,幅值也明显减小,且在修缘量为15 μm时,齿轮的径向振动和啮合力幅值最小。当修缘量为21 μm时,相对于修缘量为8 μm和15 μm,主从动齿轮的径向振动和啮合力幅值均略有增加,当啮合频率在0~1 100 Hz和2 200~2 800 Hz范围内,修缘量为21 μm时,主从动齿轮的径向振动和啮合力幅值均略大于未修形时。在图 9、图 10中第7阶和第8阶固有频率及其谐波项对系统影响较大,齿顶修缘可以减小啮合频率等于第7、8阶固有频率时的振动幅值,但不能使其降低在合理的范围内。
4 结论建立了考虑齿顶修缘的渐开线斜齿轮啮合模型,基于轮齿承载接触分析给出不同修缘量的斜齿轮静态传递误差和啮合刚度的计算结果,并将其引入所建立的平行轴系斜齿轮转子系统动力学模型中进行系统动态特性分析,研究结论如下:
1)与未修形的斜齿轮相比,齿顶修缘后斜齿轮的静态传递误差和啮合刚度波动幅值减小。在一定的范围内随着修缘量的增大,静态传递误差和啮合刚度波动幅值逐渐减小,但当修缘量达到一定值后,静态传递误差和啮合刚度波动幅反而增大。
2)分析不同修缘量对斜齿轮系统振动响应的影响,从分析结果中可知,在一定范围内,随着修缘量的增加,齿轮的径向振动和啮合力幅值明显降低,但不是修缘量越大越好。
3)在齿轮转速较低时,系统中出现某些固有频率的共振响应幅值较大;在转速较高时,系统的共振响应的幅值较平缓。
| [1] |
李润方, 王建军. 齿轮系统动力学:振动冲击与噪声[M]. 北京: 科学出版社, 1997.
LI Runfang, WANG Jianjun. Gearsystem dynamics vibration and noise[M]. Beijing: Science Press, 1997. (in Chinese) |
| [2] | He S. Effect of sliding friction on spur and helical gear dynamics and vibro-acoustics[D]. Columbus:The Ohio State University, 2008. https://etd.ohiolink.edu/rws_etd/document/get/osu1200371418/inline |
| [3] | Tesfahunegn Y A, Rosa F, Gorla C, et al. The effects of the shape of tooth profile modification on the transmission error, bending and contact stress of spur gears[J]. Proceedings of the Institution of Mechanical Engineers Part C Journal of Mechanical Engineering Science, 2010, 224(8): 1749–1758. DOI:10.1243/09544062JMES1844 |
| [4] | Ohno K, Tanaka N. Contact stress analysis for helical gear with 3-dimensional finite element method.The profile correction amount to reduce the PV factor of helical gear teeth[J]. Transactions of the Japan Society of Mechanical Engineers Part C, 1998, 64(628): 4821–4826. DOI:10.1299/kikaic.64.4821 |
| [5] | Chen Z, Shao Y. Mesh stiffness calculation of a spur gear pair with tooth profile modification and tooth root crack[J]. Mechanism and Machine Theory, 2013, 62(4): 63–74. |
| [6] | Chen Z, Shao Y. Dynamic simulation of spur gear with tooth root crack propagating along tooth width and crack depth[J]. Engineering Failure Analysis, 2011, 18(8): 2149–2164. DOI:10.1016/j.engfailanal.2011.07.006 |
| [7] | Özgüven H N. A non-linear mathematical model for dynamic analysis of spur gears including shaft and bearing dynamics[J]. Journal of Sound and Vibration, 1991, 145(2): 239–260. DOI:10.1016/0022-460X(91)90590-G |
| [8] | Liu G, Pareker R G. Dynamic modeling and analysis of tooth profile modification for multi-mesh gear vibration[J]. Journal of Mechanical Design, 2008, 130(2): 1–13. |
| [9] |
陈思雨, 唐进元, 王志伟, 等.
修形对齿轮系统动力学特性的影响规律[J]. 机械工程学报, 2014, 50(13): 59–65.
CHEN Siyu, TANG Jinyuan, WANG Zhiwei, et al. Effect of modification on dynamic characteristics of gear transmissions system[J]. Journal of echanical Engineering, 2014, 50(13): 59–65. (in Chinese) |
| [10] |
马辉, 逄旭, 宋溶泽, 等.
考虑齿顶修缘的齿轮-转子系统振动响应分析[J]. 机械工程学报, 2014, 50(7): 39–45.
MA hui, PANG Xu, SONG Rongze, et al. Vibration response analysis of a geared rotor system considering the tip relief[J]. Journal of Mechanical Engineering, 2014, 50(7): 39–45. DOI:10.3901/JME.2014.07.039 (in Chinese) |
| [11] | Zhang Y M, Wang Q B, Ma H, et al. Dynamic analysis of three-dimensional helical geared rotor system with geometric eccentricity[J]. Journal of Mechanical Science and Technology, 2013, 27(11): 3231–3242. DOI:10.1007/s12206-013-0846-8 |
| [12] | Lin H H, Townsend D P, Oswald F B. Profile modification to minimize spur gear dynamic loading[C/OL]//Design Engineering Technical Conference, September 24-28, 1988, Orlando, Florida.1988[2016-11-16].https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19870019485.pdf. |
| [13] | Kubur M, Kahraman A, Zini D M, et al. Dynamic analysis of a multi-shaft helical gear transmission by finite elements:model and experiment[J]. Journal of Vibration & Acoustics, 2004, 126(3): 398–406. |
| [14] |
张希康.
渐开线齿轮齿顶修缘的计算与加工[J]. 机械传动, 1985, 9(6): 22–25.
ZHANG Xikang. Calculation and process of involute gear considering the tip relief[J]. Mechanical Transmission, 1985, 9(6): 22–25. (in Chinese) |
| [15] | Sirichai S, Howard I, Morgan L, et al. Finite element analysis of gears in mesh[C/OL]//Fifth International Congress on Sound and Viberation, December 15-18, 1997, Adelaide, South Australia. 1997:869-876[2016-11-16]. http://www.acoustics.asn.au/conference_proceedings/ICSVS-1997/pdf/scan/sv970264.pdf. |
| [16] |
王峰, 方宗德, 李声晋.
斜齿轮动力学建模中啮合刚度处理与对比验证[J]. 振动与冲击, 2014, 33(6): 13–17.
WANG Feng, FANG Zongde, LI Shengjin. Treatment and contrast verification of meshing stiffness in dynamic model of helical gear[J]. Journal of vibration and shock, 2014, 33(6): 13–17. (in Chinese) |
| [17] | Liu G, Parker R G. Dynamic modeling and analysis of tooth profile modification for multi-mesh gear vibration[J]. Journal of Mechanical Design, 2008, 130(12): 1–13. |
| [18] | Wang J, Howard I. Finite element analysis of high contact ratio spur gears in mesh[J]. Journal of Tribology, 2005, 127(3): 469–483. DOI:10.1115/1.1843154 |
 2017, Vol. 40
2017, Vol. 40



