2. 重庆大学 土木工程学院, 重庆 400045
2. College of Civil Engineering, Chongqing University, Chongqing 400045, P. R. China
近年来, 超限、超载车辆逐渐增多,桥梁维修养护措施不到位,造成危桥数增速较快。我国“十一五”期间,投入危桥改造资金189.5亿元,改造危桥16 875座[1]。目前,桥梁加固方法最常用的是纤维增强塑料(fiber reinforced polymer,FRP)。究其原因主要是FRP具有强度高、重量轻、耐腐蚀、抗疲劳等特点,是结构加固的理想材料,特别是在钢筋混凝土梁的抗弯加固中应用非常普遍[2-4]。现有加固规范[5]FRP材料直接粘贴在被加固构件的受拉面,因FRP易发生剥离、二次受力应变滞后等原因不能很好发挥其强度[6-8]。为了解决以上问题,FRP片材的预应力加固技术应运而生,国内外对此开展了较多的研究[9-12]。笔者正是为了实现快速加固危旧桥梁而研制出了一套利用波形齿对碳纤维进行横向张拉的多点锚固的预应力碳纤维加固施工技术[13]。
目前,多点锚固CFRP带预应力加固实验数量有限的主要原因是试验费用较高、试验数据采集部位有一定的局限性等。随着计算机技术和有限元理论的发展,非线性有限元分析已经成为土木工程领域研究的一种有效的手段[14]。笔者利用非线性有限元ABAQUS对4根加固梁进行模拟,模拟结果与试验进行对比验证,再利用验证后的模型展开改变锚固点数及中段加固量对加固效果的影响进行研究。
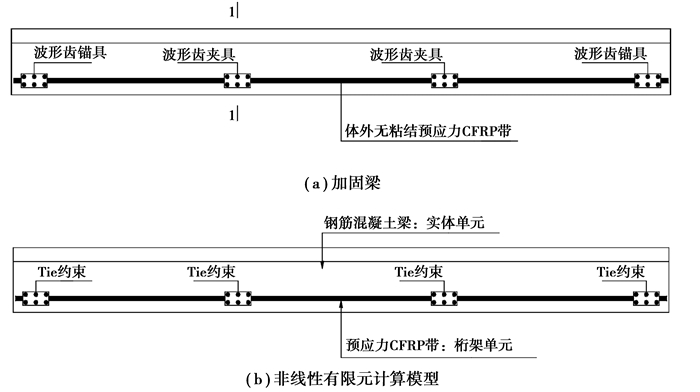
1 建立有限元模型利用非线性有限元ABAQUS程序对预应力碳纤维带无粘结加固钢筋混凝土梁进行大变形非线性分析。波形齿夹具横向张拉CFRP带进行施加预应力,之后波形齿锚固CFRP带,该方法是张拉并实现多点锚固,因而CFRP带与混凝土梁只在锚固点处变形协调。这也是有限元分析模型难以按有粘结预应力梁的常规建模方法建立的主要原因。下面主要介绍非线性有限元ABAQUS程序对预应力CFRP带体外无粘结加固钢筋混凝土梁的建模。
1.1 非线性有限元的计算模型预应力碳纤维带体外无粘结梁侧对称加固钢筋混凝土简支梁及其有限元计算模型如图 1所示。预应力碳纤维带体外无粘结梁底加固钢筋混凝土简支梁及其有限元计算模型与梁侧对称加固相似。该有限元计算模型的主要单元分别如下:梁内非预应力纵向钢筋为桁架单元、梁底或梁侧的无粘结体外预应力碳纤维带为桁架单元、混凝土为实体单元。在波形齿夹具或锚具处碳纤维带的桁架单元与实体梁单元用非线性有限元ABAQUS中的Tie约束连接,该约束使桁架单元和实体单元的节点具有相同的曲率和位移,用此模拟锚具或夹具处混凝土和无粘结体外预应力碳纤维带之间变形协调。
|
图 1 非线性有限元计算模型简图 Figure 1 simplified diagram of the finite element model |
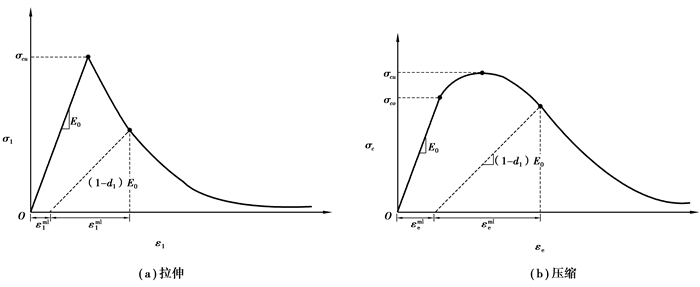
损伤塑性模型(concrete damaged plasticity)和弥散裂缝模型(concrete smeared cracking)是非线性有限元ABAQUS为混凝土类材料提供的2个较好的本构模型。弥散裂缝模型利用各向等压塑性的概念和定向损伤弹性来描述混凝土的非线性特征;损伤塑性模型描述混凝土的非线性特征是利用等压塑性和各向等拉以及等向损伤弹性的概念,文中的混凝土是采用损伤塑性模型以及C3D8R实体单元。模型中混凝土σ-ε曲线参照《混凝土结构设计规范》(GB50010-2010)附录C中的单轴混凝土受压、拉的σ-ε曲线公式,其损伤因子取值文献[15],弹性模量E0取混凝土受拉开裂时的割线模量作为混凝土的初始弹性模量,双轴受压与单轴受压极限强度比取1.12,流动势偏移量参数取0.1,剪胀角参数取25,不变量应力比为0.666 7,如图 2所示。
|
图 2 混凝土单轴下的σ-ε曲线 Figure 2 Stress-strain of concrete under uniaxial loading |
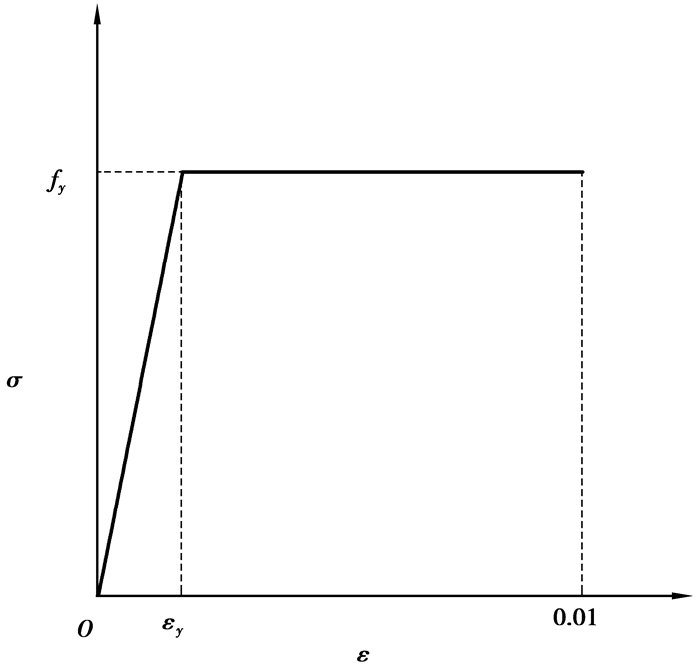
混凝土结构中的加强筋将通过埋入单元(embed element)将钢筋的桁架单元埋入实体单元中。T3D2桁架单元为普通加强钢筋。有粘结钢筋的材料参数利用ABAQUS的弹塑性材料模型来定义。钢筋采用理想弹塑性σ-ε曲线。钢筋的屈服强度及应变由钢材的试验值确定即:fy=365.33 MPa,εy=2 100(με);钢筋的极限拉应变为0.01, 如图 3所示。
|
图 3 钢筋应力应变曲线 Figure 3 Stress-strain curve of steel bar |
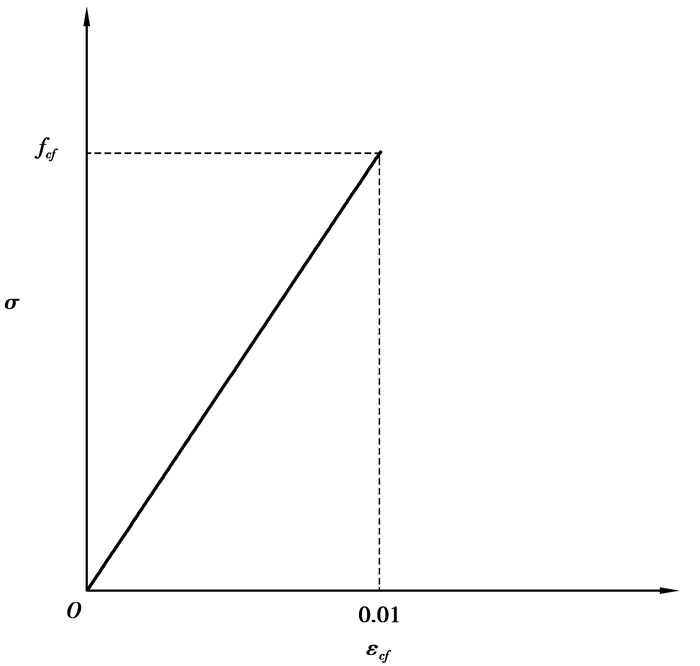
CFRP片材或带的σ-ε曲线为线弹性,当CFRP材料的应变到达0.01时,即达到了其极限抗拉强度fcf,如图 4所示。CFRP材料模型的参数按试验测试所获得的值来确定。
|
图 4 CFRP带应力应变曲线 Figure 4 Stress-strain curve of CFRP belt |
有限元模型中用空间桁架T3D2来模拟预应力碳纤维带体外无粘结加固钢筋混凝土简支梁中的碳纤维带,是因为其只承受轴向拉力。对于体外无粘结加固中的预应力CFRP带中的预应力值的定义方法有降或升温法、加初应力法等。用Edit keywords通过*initial condtions来定义一次加载构件中的CFRP带的预应力值,通过升温方法来施加试验梁TL4预应力CFRP带上的预应力值以考虑二次加载并持荷影响。
2 实例分析 2.1 四点锚固加固T梁分析试验梁的计算结果、试验值及对比值如表 1所示。
| 表 1 试验梁的计算结果与试验值比较 Table 1 Results comparison between analytical simulation and experimental test for the specimens |
图 5是计算模型的跨中弯矩位移曲线模拟的计算结果。该计算模型采用上述建模方法建立三维实体模型。计算结果是计算模型在单调荷载作用下获取的。钢筋混凝土T截面梁加固后的TL2-TL5的试验数据来自文献[13]。表 1是各加固梁的数值模拟和试验中各数值的对比。
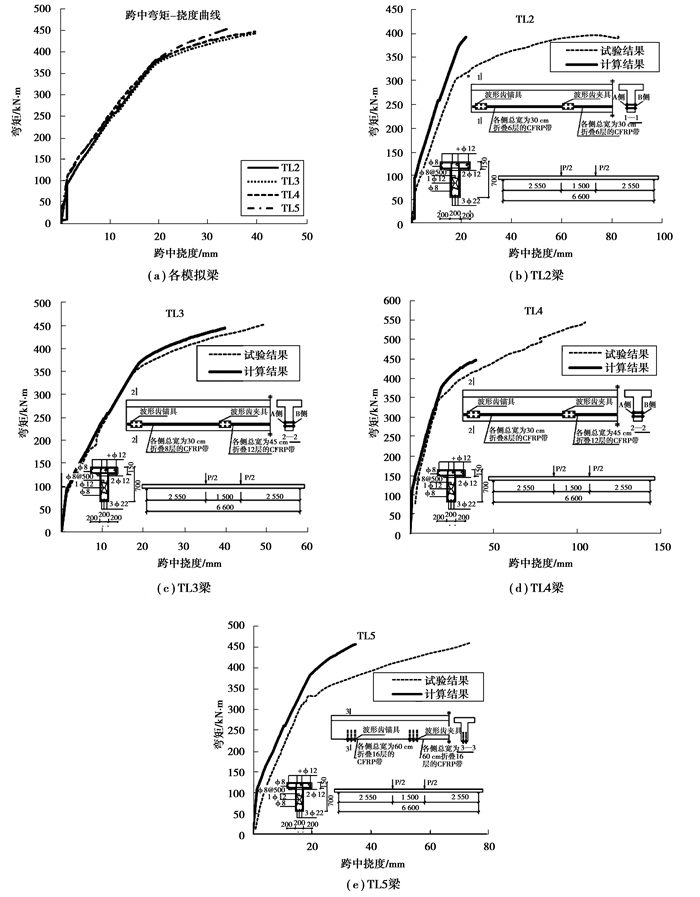
|
图 5 跨中弯矩挠度的结果比较 Figure 5 Comparison of the mid-span moment-deflection under monotonic loading for different specimens |
从图 5可以看出,TL2~TL5所模拟分析的跨中弯矩挠度曲线计算值与试验值较接近,特别是TL3、TL4两根试验梁试验值与有限元分析的计算值较吻合。但荷载较大的加载后期弯矩挠度曲线计算值与试验值吻合程度均不够理想。从图 5(a)中可以看出,在加载的前期,无论是梁侧或梁底加固,一次加载或二次加载均没有明显的区别,在后期一次加载与二次加载仍区别不大,梁底加固则表现出加固后的梁刚度改善较明显。
从表 1中试验梁的极限荷载、挠度(分别为Pu、Δu)与屈服荷载、挠度(分别为Py、Δy)有限元计算值与试验结果进行对比,各试验梁的极限挠度的计算值与试验值吻合较差。
2.2 锚固点数对比分析除CFRP的用量及预应力值不同外,其它参数“四点锚固”的分析模型与TL3构件的模型是相同的。CFRP的用量及预应力值的区别在于“四点锚固”的分析模型中梁两侧三段的CFRP带各段的预应力值和加固量均采用TL3中段的预应力值和加固量。除两侧CFRP带与构件之间的锚固点数不同外,“两点锚固”的分析模型与“四点锚固”均相同。“两点锚固”与“四点锚固”的分析模型中的钢筋、混凝土参数直接采用TL3中的参数。表 2为各分析模型的CFRP带预拉应力值及加固量。
| 表 2 分析模型的加固参数 Table 2 Parameters of CFRP strengthening for different analytical models |
各分析模型的极限状态、钢筋屈服的挠度及弯矩对比见表 3。从表 3可以看出,“四点锚固”与“两点锚固”的极限弯矩以及屈服弯矩比分别增加了2%和4%,“四点锚固”与“两点锚固”的承载力增加不多,而“四点锚固”与“两点锚固”的极限挠度相比减少了8%,由此可见,“四点锚固”加固方式在改善变形能力方面稍好。“四点锚固”与TL3相比屈服弯矩、挠度基本相同,而极限弯矩、挠度均有增加,可以看出,基于构件弯矩的变化而改变CFRP材料的加固量在满足加固要求的同时还能降低加固造价。
| 表 3 参数不同的计算模型计算结果比较 Table 3 Comparison of results for different analytical models of different parameter |
把“四点锚固”与“两点锚固”加固方式进行对比,可以看出CFRP带两端各段的拉力值有所减小,因此,“四点锚固”两端部的波形齿锚具处混凝土所承受的压力会降低, 如表 4所示。
| 表 4 参数不同的计算模型的CFRP带应力结果 Table 4 Stress of CFRP belts in different analytical models of different parameter |
图 6可以看出,在加载前期锚固点数对加固构件承载力的提高和变形能力的改善没有区别,在加载后期“两点锚固”与“四点锚固”相比承载力提高和变形能力的改善有所下降。而“四点锚固”与TL3无论是承载力提高或是变形能力的改善没有任何区别,故根据加固构件的弯矩设置多锚固点数及各段加固量的方法既能保证加固效果的不降低,又能节约CFRP材料。

|
图 6 各计算模型梁跨中弯矩跨中挠度的曲线 Figure 6 Mid-span moment-deflection curve for the beam using different models |
在试验和理论研究的基础上,对多点波形齿锚固预应力CFRP带体外无粘结加固钢筋混凝土T形截面梁建立了三维实体模型,进行了计算值与试验值的对比分析,主要结论如下。
1) 通过模型的弯矩挠度曲线与试验的对比分析,可知ABAQUS数值分析中,混凝土采用损伤塑性模型,钢筋和CFRP带采用桁架单元,钢筋通过embed将其进入混凝土实体单元,CFRP带上的预应力一次加载情况通过edit keywords中通过*initial condtions来定义,二次加载通过升温的方法来施加等进行建立的分析模型能较好的模拟加固梁的抗弯性能。
2) 无论是梁侧或梁底加固,或一、二次加载用ABAQUS程序进行模拟的数据与试验值相比,加载前期承载力和变形吻合程度较好,后期差异较大,故有必要对分析模型进一步研究。
3) 多点波形齿锚的预应力CFRP带梁侧或梁底加固加载前期承载力提高或变形能力的改善区别不明显。无论是一、二次加载前后期均未表现出明显的区别。
4) 通过对锚固点数及加固量改变的对比分析可知,依据加固构件的弯矩改变各段加固量及布置锚固点数的方法既可以保证加固效果不降低,又可以节约CFRP材料。
| [1] |
高崇明, 杨明松.
桥梁养护的新视角[J]. 中国公路, 2013(14): 36–39.
GAO Chongming, YANG Mingsong. A new perspective of bridge maintenance[J]. China Highway and Transport, 2013(14): 36–39. (in Chinese) |
| [2] |
郭晓媛.加固后桥梁技术状况的评估方法研究[D].南宁:广西大学, 2013. GUO Xiaoyuan.An method for research of technical condition state evaluation of bridge reinforced[D].Nanning:Guangxi University, 2013.(in Chinese) http://www.cnki.com.cn/Article/CJFDTotal-KJZF201424091.htm |
| [3] | Cerullo D, Sennah K, Azimi H, et al. Experimental study on full-scale pretensioned bridge girder damaged by vehicle impact and repaired with fiber-reinforced polymer technology[J]. Journal of Composites for Construction, 2013, 17(5): 662–672. DOI:10.1061/(ASCE)CC.1943-5614.0000383 |
| [4] | Ali O, Bigaud D, Ferrier E. Comparative durability analysis of CFRP-strengthened RC highway bridges[J]. Construction & Building Materials, 2012, 30(5): 629–642. |
| [5] |
中华人民共和国建设部.纤维增强复合材料建设工程应用技术规范:GB50608-2010[S].北京:中国计划出版社, 2011. Ministry of Construction of the People's Republic of China. Technical code for infrastructure application of FRP composites:GB50608-2010[S]. Beijing:China Planning Press, 2011.(in Chinese) |
| [6] |
飞渭, 江世永, 彭飞飞, 等.
预应力碳纤维布加固混凝土受弯构件试验研究[J]. 四川建筑科学研究, 2003, 29(2): 56–60.
FEI Wei, JIANG Shiyong, PENG Feifei, et al. Experimental study on flexural strength of RC beams strengthened with prestressed CFRP sheets[J]. Building Science Research of Sichuan, 2003, 29(2): 56–60. (in Chinese) |
| [7] |
尚守平, 彭晖, 童桦, 等.
预应力碳纤维布材加固混凝土受弯构件的抗弯性能研究[J]. 建筑结构学报, 2003, 24(5): 24–30.
SHANG Shouping, PENG Hui, TONG Hua, et al. Study of strengthening reinforced concrete beam using prestressed carbon fiber sheet[J]. Journal of Building Structures, 2003, 24(5): 24–30. (in Chinese) |
| [8] |
彭晖.预应力碳纤维布加固混凝土受弯构件的试验研究[D].长沙:湖南大学, 2002. PENG Hui.Study of strengthening reinforced concrete beam using prestressed carbon fiber sheet[D].Changsha:Hunan University, 2002.(in Chinese) http://www.cqvip.com/QK/94745X/2003005/8508269.html |
| [9] |
吴善能, 韩仁宽.
预应力碳纤维板锚具试验研究[J]. 结构工程师, 2013, 29(1): 143–148.
WU Shanneng, HAN Renkuan. Experimental study of anchorages for prestressed CFRP plate[J]. Structural Engineers, 2013, 29(1): 143–148. (in Chinese) |
| [10] |
周朝阳, 贺学军, 王兴国, 等.
连续纤维加固结构技术及其发展中的若干问题[J]. 施工技术, 2003, 32(6): 4–6.
ZHOU Chaoyang, HE Xuejun, WANG Xingguo, et al. Some problems of structural strengthening technology with FRP and it's development[J]. Construction Technology, 2003, 32(6): 4–6. (in Chinese) |
| [11] |
沙吾列提·拜开依, 叶列平, 杨勇新, 等.
预应力CFRP布加固钢筋混凝土梁的施工技术[J]. 施工技术, 2004, 33(6): 23–24.
SHAWULIETI Baikaiyi, YE Lieping, YANG Yongxin, et al. Construction technology of prestress CFRP sheet strengthening reinforcement concrete beams[J]. Construction Technology, 2004, 33(6): 23–24. (in Chinese) |
| [12] |
吴志平, 赵海东, 张田田, 等.
预应力碳纤维板加固混凝土受弯构件应用设计[J]. 结构工程师, 2013, 29(4): 172–178.
WU Zhiping, ZHAO Haidong, ZHANG Tiantian, et al. Design of prestressed CFRP plates in strengthening reinforced concrete flexural members[J]. Structural Engineers, 2013, 29(4): 172–178. (in Chinese) |
| [13] |
陈小英, 李唐宁, 黄音, 等.
CFRP体外预应力加固钢筋混凝土T型梁试验[J]. 中国公路学报, 2010, 23(2): 56–63.
CHEN Xiaoying, LI Tangning, HUANG Yin, et al. Experimental research on reinforced concrete T-beams strengthened with external prestressed CFRP Sheets[J]. China Journal of Highway and Transport, 2010, 23(2): 56–63. (in Chinese) |
| [14] |
张智梅, 考书姣, 白世烨, 等.
CFRP布加固钢筋混凝土梁的抗弯性能研究[J]. 结构工程师, 2012, 28(4): 139–143.
ZHANG Zhimei, KAO Shujiao, BAI Shiye, et al. Study on flexural behaviour of RC beams strengthened by CFRP sheets[J]. Structural Engineers, 2012, 28(4): 139–143. (in Chinese) |
| [15] |
张劲, 王庆扬, 胡守营, 等.
ABAQUS混凝土损伤塑性模型参数验证[J]. 建筑结构, 2008, 38(8): 127–130.
ZHANG Jin, WANG Qingyang, HU Shouying, et al. Parameters verification of concrete damaged plastic model of ABAQUS[J]. Structural Engineers, 2008, 38(8): 127–130. (in Chinese) |
 2017, Vol. 40
2017, Vol. 40


