2. 中国地震局工程力学研究所, 哈尔滨 150080;
3. 中国兵器工业北方勘察设计研究院有限公司, 石家庄 050011
2. Institute of Engineering Mechanics, China Earthquake Administration, Harbin 150080, P. R. China;
3. China North Industries Norengeo Ltd., Shijiazhuang 050011, P. R. China
边坡稳定性是岩土工程研究的热点问题,滑动面的形状可简化为平面、圆弧面和对数螺旋面等[1-3]。砂土边坡破裂面具有平面剪切破坏的特点,工程应用广泛,因此研究这种坡体在渗流和地震两种外因作用下的失稳具有重要的意义[2-3]。
边坡在渗流或者地震作用下的稳定性研究较多,而两种作用对边坡的失稳评价目前并不多见。以往的研究多侧重于工程分析,如龚文俊等[4]分析了降雨和地震耦合作用对甘肃西和Ⅲ号滑坡的影响,得出耦合作用会极大削弱边坡的整体稳定性。张永兴等[5]对岸边水下边坡的稳定性进行了数值分析,模拟了地下水流动对边坡的动力影响,讨论了水库边坡的抗震问题。宋波等[6]采用数值模拟和模型试验分析了地震和地下水耦合下的砂土边坡稳定性,确定了剪出口以及水位对稳定性的影响趋势。赖杰等[7]对自重、渗流以及地震耦合作用下的人工岛进行了动力稳定性分析,同时也模拟了人工岛的液化问题。研究结果在讨论渗流和地震对稳定性的影响时起到了一定作用,研究手段也多以数值模拟和模型试验为主,但缺乏必要的失稳力学模型和理论分析。Choudhury等[8]虽采用拟静力法和拟动力法结合的方式分析了印度某水坝的动力特性,但却没有相关的渗流分析;Basha等[9]在分析挡墙背后土体失稳时,同样也忽略了渗流的作用。由此可知,得到渗流和地震作用下稳定性系数的解析解对研究砂土边坡的失稳力学机理具有重要的参考价值[10-11]。
笔者提出了一种渗流和地震2种工况存在时的边坡稳定性计算方法。该方法基于极限平衡理论,以渗流和拟静力法、拟动力法相结合的形式得到砂土边坡安全系数的解析解。通过与相关算例对比,验证了解析式的合理性,并从安全系数的分布特点分析了水力梯度、地震加速度系数以及水位对稳定性的影响。文中的计算方法和结果可为进一步深入研究边坡在渗流地震耦合作用下的破坏机理提供参考。
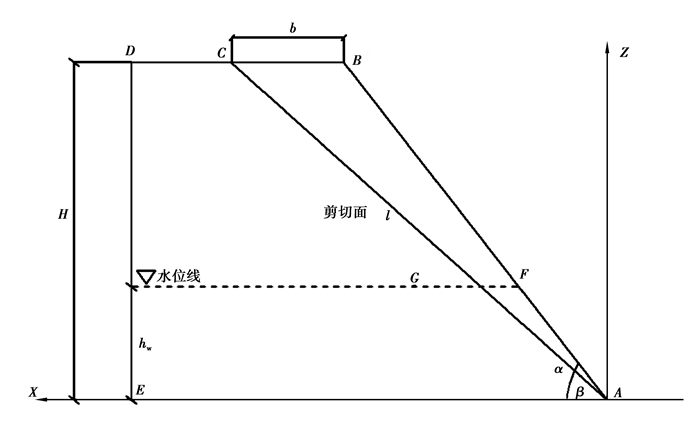
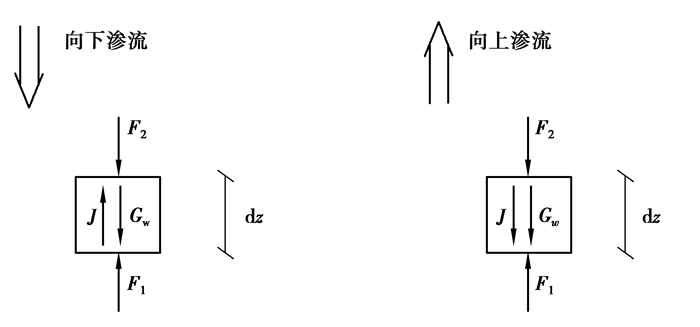
1 渗流地震耦合的稳定性计算方法 1.1 渗流作用下的孔隙水压力计算实际工程中的渗流是非常复杂的,以水平水位替代真实水位可以简化渗流孔压的计算,在稳定渗流中的计算模型如图 1所示。边坡高度为H,坡角为α,滑面倾角为β,土体的自然重度为γ,饱和重度为γsat,水的重度为γw。坡体内水位线距边坡底部的高度为hw,坡面可以近似看作不透水表面且水位高度始终保持一致。坡体在自然状态下发生稳定竖向渗流,渗流方向分为向上或向下两种情况,如图 2所示。
|
图 1 渗流计算模型 Figure 1 Seepage calculation model |
|
图 2 水体计算模型 Figure 2 Water calculation model |
将水的渗流方向分为2种工况,假设向下渗流为工况1,向上渗流为工况2,根据“水土分离”模式[12],水的计算模型如图 2所示。在距离底部任意高度位置z处取出土单元体,土单元体包含土骨架和水2部分,对其中含水的部分进行受力分析,并假设单元体的表面面积为dA,F1、F2分别为单元体下、上表面的水头压力,Gw为水体的自重,水体中渗透力方向与土骨架中渗透力方向恰好相反,用J表示。
由伯努利定理可知[12],任意位置水体受到的各部分力的大小可以表示为
| $ \left. \begin{gathered} {F_1} = \left[{h\left( z \right)-z} \right]{\gamma _{\text{w}}}\eta {\text{d}}A \hfill \\ {F_2} = \left[{h\left( {z + {\text{d}}z} \right)-z-{\text{d}}z} \right]{\gamma _{\text{w}}}\eta {\text{d}}A \hfill \\ J = i{\gamma _{\text{w}}}\eta {\text{d}}A{\text{d}}z \hfill \\ {G_{\text{w}}} = {\gamma _{\text{w}}}\eta {\text{d}}A{\text{d}}z \hfill \\ \end{gathered} \right\}, $ | (1) |
式中:h(z)为总水头;γw为水的重度;η为孔隙率;i为水力梯度,根据水体受力的竖向平衡方程可知,不同工况的受力平衡可表示为
| $ 工况1:\;{F_1} + J = {G_{\text{w}}} + {F_2}。 $ | (i) |
| $ 工况2:\;{F_1} = {G_{\text{w}}} + {F_2} + J。 $ | (3) |
将式(1)带入式(2)、式(3),再根据总水头h(0)=0和h(hw)=hw的边界条件可以得到2种工况下的任意一点z处的孔隙水压力p表示为
| $ 工况1:\;p = {\gamma _{\text{w}}}\left( {{h_{\text{w}}}-z} \right)\left( {1-i} \right)。 $ | (4) |
| $ 工况2:\;p = {\gamma _{\text{w}}}\left( {{h_{\text{w}}}-z} \right)\left( {1 + i} \right)。 $ | (5) |
地震作用时因惯性力的产生会引起土体中超孔隙水压力的出现,超孔隙水压Δp和地震影响系数之间的关系可以用式(6)表示,其中,μ为土的泊松比,α和β均为孔隙水压力系数,kh和kv分别为水平和竖向地震加速度系数[13]。对于饱和固结土,取值为β=1,α=0.5~1.0,可得
| $ \Delta p = {\gamma _{{\text{sat}}}}\left[\begin{gathered} \beta \left( {{k_{\text{h}}} + {k_{\text{v}}}} \right)\left( {1 + \mu } \right)/3 + \hfill \\ \sqrt 2 \alpha \sqrt {{{\left( {{k_{\text{h}}} + {k_{\text{v}}}} \right)}^2}\left( {{\mu ^2}-\mu + 1} \right)-3{k_{\text{h}}}{k_{\text{v}}}} \hfill \\ \end{gathered} \right]。 $ | (6) |
取出滑体如图 3所示,多边形AFBCGA为平面滑体。在渗流和地震的作用下,令W为滑体总重量,水平地震惯性力为Eh,竖向地震惯性力为Ev,渗流引起的水压力为U1,地震惯性力引起的动水压力为U2,N和S分别是滑床对滑体的法向力和切向力。将滑体划分为2部分进行受力分析,即楔体AFGA和BFGCB,总的力可等效于此2部分受力之和。

|
图 3 滑体受力计算简图 Figure 3 Slide mass calculated model |
如图 3所示的计算坐标系,水下楔体AFGA的重力为
| $ {{\text{W}}_{{\text{AFGA}}}} = \int_0^{{h_{\text{w}}}} {{\gamma _{{\text{sat}}}}\left( {\cot \beta-\cot \alpha } \right)z{\text{d}}z = \frac{1}{2}{\gamma _{{\text{sat}}}}h_{\text{w}}^2} \left( {\cot \beta-\cot \alpha } \right)。 $ | (7) |
水上楔体BFGCB的重力为
| $ {{\text{W}}_{{\text{BFGCB}}}} = \int_{{h_{\text{w}}}}^H {\gamma \left( {\cot \beta-\cot \alpha } \right)z{\text{d}}z = \frac{1}{2}\gamma \left( {{H^2}-h_{\text{w}}^2} \right)} \left( {\cot \beta-\cot \alpha } \right)。 $ | (8) |
因此,滑体总的重力就等效为AFGA和BFGCB 2部分之和,即
| $ W = {{\text{W}}_{{\text{AFGA}}}} + {{\text{W}}_{{\text{BFGCB}}}} = \frac{1}{2}\left[{{\gamma _{{\text{sat}}}}h_{\text{w}}^2 + \gamma \left( {{H^2}-h_{\text{w}}^2} \right)} \right]\left( {\cot \beta -\cot \alpha } \right)。 $ | (9) |
1)基于拟静力法的惯性力计算
拟静力法是计算地震惯性力的一种简单方法,同时也是抗震规范计算安全系数所采用的方法,文中滑体惯性力采用拟静力法进行计算,即惯性力可用滑体自重与地震加速度系数之积来表示,因此滑体总的惯性力可以表示为
| $ 水平惯性力:\;\;\;\;\;\;{E_{\text{h}}} = {k_{\text{h}}}W。 $ | (10) |
| $ 竖向惯性力:\;\;\;\;\;\;{E_{\text{v}}} = {k_{\text{v}}}W。 $ | (11) |
2)基于拟动力法的惯性力计算
为了考虑地震持时和相位对边坡稳定性的影响,引入拟动力法计算地震惯性力来分析边坡稳定性随时间变化的规律,并与传统的拟静力法相比分析2种计算方法的差异。拟动力法最早由Steedman提出,主要用于挡土墙背后的土压力计算,该方法的可靠性已在实验中得到验证[14]。为简化惯性力的计算,在忽略岩体放大系数的条件下,拟动力法输入的振动波可以表示为
| $ \left. \begin{gathered} {a_{\text{h}}}\left( {z, t} \right) = {k_{\text{h}}}g\sin \left[{\omega \left( {t-\frac{z}{{{v_{\text{s}}}}}} \right)} \right] \hfill \\ {a_{\text{v}}}\left( {z, t} \right) = {k_{\text{v}}}g\sin \left[{\omega \left( {t-\frac{z}{{{v_{\text{p}}}}}} \right)} \right] \hfill \\ \end{gathered} \right\}, $ | (12) |
式中:t为振动时间;z为自坡底向上的深度;ah和av分别为水平和竖直地震加速度;g为重力加速度;w为角速度;vs和vp为剪切波速和纵波波速。土的剪切模量是G,由土动力学可知地震波剪切波速和纵波波速与岩土材料参数之间的关系可以表示为
| $ \left. \begin{gathered} {v_{\text{s}}} = \sqrt {\frac{G}{\rho }} \hfill \\ {v_{\text{p}}} = \sqrt {\frac{{G\left( {2-\mu } \right)}}{{\rho \left( {1-2\mu } \right)}}} \hfill \\ \end{gathered} \right\}, $ | (13) |
式中:ρ为计算土的密度;μ为泊松比。
以滑体为研究对象,分别计算水平和竖向的惯性力,即水下楔体AFGA的水平惯性力为
| $ \begin{gathered} {E_{{\text{h- AFGA}}}} = \int_0^{{h_{\text{w}}}} {{\gamma _{{\text{sat}}}}{k_{\text{h}}}} \left( {\cot \beta- \cot \alpha } \right)\sin \left[{\omega \left( {t-\frac{z}{{{v_{\text{s}}}}}} \right)} \right]z{\text{d}}z = \hfill \\ {\gamma _{{\text{sat}}}}{k_{\text{h}}}\left( {\cot \beta -\cot \alpha } \right)\left( {{m_1} + {m_2}} \right) \hfill \\ \end{gathered} 。 $ | (14) |
其中,
| $ \left\{ \begin{gathered} {m_1} = {h_{\text{w}}}\frac{{{v_{\text{s}}}}}{\omega }\cos \left[{\omega \left( {t-\frac{{{h_{\text{w}}}}}{\omega }} \right)} \right]; \hfill \\ {m_2} = \frac{{v_{\text{s}}^2}}{{{\omega ^2}}}\left\{ {\sin \left[{\omega \left( {t-\frac{{{h_{\text{w}}}}}{\omega }} \right)} \right] -\sin \;\omega t} \right\} \hfill \\ \end{gathered} \right.。 $ |
同理,AFGA的竖向惯性力为
| $ \begin{gathered} {E_{{\text{v- AFGA}}}} = \int_0^{{h_{\text{w}}}} {{\gamma _{{\text{sat}}}}{k_{\text{v}}}} \left( {\cot \beta- \cot \alpha } \right)\sin \left[{\omega \left( {t-\frac{{{h_{\text{w}}}}}{{{v_{\text{p}}}}}} \right)} \right]z{\text{d}}z = \hfill \\ {\gamma _{{\text{sat}}}}{k_{\text{v}}}\left( {\cot \beta -\cot \alpha } \right)\left( {{m_3} + {m_4}} \right) \hfill \\ \end{gathered}, $ | (15) |
其中,
| $ \left\{ \begin{gathered} {m_3} = {h_{\text{w}}}\frac{{{v_{\text{p}}}}}{\omega }\cos \left[{\omega \left( {t-\frac{{{h_{\text{w}}}}}{\omega }} \right)} \right]; \hfill \\ {m_4} = \frac{{v_{\text{p}}^2}}{{{\omega ^2}}}\left\{ {\sin \left[{\omega \left( {t-\frac{{{h_{\text{w}}}}}{\omega }} \right)} \right] -\sin \;\omega t} \right\} \hfill \\ \end{gathered} \right.。 $ |
水上楔体BFGCB的水平惯性力为
| $ \begin{gathered} {E_{{\text{h- BFGCB}}}} = \int_{{h_{\text{w}}}}^H {\gamma {k_{\text{h}}}} \left( {\cot \beta- \cot \alpha } \right)\sin \left[{\omega \left( {t-\frac{z}{{{v_{\text{s}}}}}} \right)} \right]z{\text{d}}z = \hfill \\ \gamma {k_{\text{h}}}\left( {\cot \beta -\cot \alpha } \right)\left( {{m_5} + {m_6}} \right) \hfill \\ \end{gathered}, $ | (16) |
其中,
| $ \left\{ \begin{gathered} {m_5} = \frac{{{v_{\text{s}}}}}{\omega }\left\{ {H\cos \left[{\omega \left( {t-\frac{H}{\omega }} \right)} \right] - {h_{\text{w}}}\cos \left[{\omega \left( {t-\frac{{{h_{\text{w}}}}}{\omega }} \right)} \right]} \right\}; \hfill \\ {m_6} = \frac{{v_{\text{s}}^2}}{{{\omega ^2}}}\left\{ {\sin \left[{\omega \left( {t-\frac{H}{\omega }} \right)} \right] - \sin \;\left[{\omega \left( {t-\frac{{{h_{\text{w}}}}}{\omega }} \right)} \right]} \right\} \hfill \\ \end{gathered} \right.。 $ |
水上楔体BFGCB的竖向惯性力为
| $ \begin{gathered} {E_{{\text{v- BFGCB}}}} = \int_{{h_{\text{w}}}}^H {\gamma {k_{\text{v}}}} \left( {\cot \beta- \cot \alpha } \right)\sin \left[{\omega \left( {t-\frac{z}{{{v_{\text{p}}}}}} \right)} \right]z{\text{d}}z = \hfill \\ \gamma {k_{\text{v}}}\left( {\cot \beta -\cot \alpha } \right)\left( {{m_5} + {m_6}} \right), \hfill \\ \end{gathered}, $ | (17) |
其中,
| $ \left\{ \begin{gathered} {m_7} = \frac{{{v_p}}}{\omega }\left\{ {H\cos \left[{\omega \left( {t-\frac{H}{\omega }} \right)} \right] - {h_w}\cos \left[{\omega \left( {t-\frac{{{h_w}}}{\omega }} \right)} \right]} \right\} \hfill \\ {m_8} = \frac{{v_p^2}}{{{\omega ^2}}}\left\{ {\sin \left[{\omega \left( {t-\frac{H}{\omega }} \right)} \right] - \sin \left[{\omega \left( {t-\frac{{{h_w}}}{\omega }} \right)} \right]} \right\} \hfill \\ \end{gathered} \right.。 $ |
滑动面上总的水压力是渗流和地震各自引起的水压之和,渗流引起的水压力可等效成集中力分布在滑动面上。因此,渗流水压大小可以将孔隙水压沿着滑面高度进行积分求和,表示为
工况1:
| $ {U_1} = \int_0^{{h_{\text{w}}}} {\frac{{{\gamma _{\text{w}}}\left( {{h_{\text{w}}}-z} \right)\left( {1-i} \right)}}{{\sin \beta }}} {\text{d}}z = \frac{{{\gamma _{\text{w}}}h_{\text{w}}^2\left( {1-i} \right)}}{{2\sin \beta }}。 $ | (18) |
工况2:
| $ {{\text{U}}_1} = \int_0^{{h_{\text{w}}}} {\frac{{{\gamma _{\text{w}}}\left( {{h_{\text{w}}}-z} \right)\left( {1 + i} \right)}}{{\sin \beta }}} {\text{d}}z = \frac{{{\gamma _{\text{w}}}h_{\text{w}}^2\left( {1 + i} \right)}}{{2\sin \beta }}。 $ | (19) |
地震引起的动水压力同样按照等效集中力的方式将孔压沿着滑面高度进行积分求和,则
| $ \begin{gathered} {U_2} = \int_0^{h{\text{w}}/\sin \beta } {{\gamma _{{\text{sat}}}}} \left[\begin{gathered} \frac{{\beta \left( {{k_{\text{h}}} + {k_{\text{v}}}} \right)\left( {1 + \mu } \right)}}{3} + \hfill \\ \sqrt 2 \alpha \sqrt {{{\left( {{k_{\text{h}}} + {k_{\text{v}}}} \right)}^2}\left( {{\mu ^2}-\mu + 1} \right)-3{k_{\text{h}}}{k_{\text{v}}}} \hfill \\ \end{gathered} \right] \hfill \\ {\text{d}}z = \frac{{{\gamma _{{\text{sat}}}}{h_{\text{w}}}}}{{\sin \beta }}\left[\begin{gathered} \frac{{\beta \left( {{k_{\text{h}}} + {k_{\text{v}}}} \right)\left( {1 + \mu } \right)}}{3} + \hfill \\ \sqrt 2 \alpha \sqrt {{{\left( {{k_{\text{h}}} + {k_{\text{v}}}} \right)}^2}\left( {{\mu ^2}-\mu + 1} \right)-3{k_{\text{h}}}{k_{\text{v}}}} \hfill \\ \end{gathered} \right] \hfill \\ \end{gathered} 。 $ | (20) |
根据极限平衡原理,滑体在上述力作用下的安全系数可以用滑动面上的抗力与下滑力之比表示,将所有力分解在滑动面的法线和切线方向,列出平衡方程,即
由滑动面法线
| $ N + {U_1} + {U_2} + {E_{\text{h}}}\sin \beta-\left( {W-{E_{\text{v}}}} \right)\cos \beta = 0。 $ | (21) |
由滑动面切向
| $ {E_{\text{h}}}\cos \beta + \left( {W-{E_{\text{v}}}} \right)\sin \beta-S = 0。 $ | (22) |
实际砂土的黏聚力并非为零,只是很小,为保证计算精度,在公式中预先保留该项,视实际黏聚力的大小进行取舍,根据摩尔库伦屈服准则可知砂土的安全系数表示为
| $ F = \frac{{cl + \left[{\left( {W-{E_{\text{v}}}} \right)\cos \beta-{E_{\text{h}}}\sin \beta-{U_1} - {U_2}} \right]\tan \varphi }}{{{E_{\text{h}}}\cos \beta + \left( {W -{E_{\text{v}}}} \right)\sin \beta }}。 $ | (23) |
对于拟静力法而言,不存在输入振动特性的影响,因此通过式(23)可知边坡的安全系数是关于滑面倾角β的三角函数,利用函数求极值的方法,即dF/dβ=0就可得到关于倾角β的参数方程
| $ \left\{ {\begin{array}{*{20}{l}} {{{\sin }^2}\beta {{\cos }^2}\beta \times - {f_1}{k_{\rm{h}}}{m^2}\left[ {3\left( {1 - {k_{\rm{v}}}} \right){f_2} + \left( {1 - {k_{\rm{v}}}} \right) + 2{f_2}} \right] + {f_1}{m^2}{f_2}k_{\rm{h}}^2 + }\\ {{f_1}{m^2}f_3^2\left[ {{{\left( {1 - {k_{\rm{v}}}} \right)}^2} - 2k_{\rm{h}}^2} \right] + {f_3}{m^2}\left[ {\left( {1 - {k_{\rm{v}}}} \right)\left( {2{k_{\rm{v}}} - 1} \right) + 3k_{\rm{h}}^2} \right] + }\\ {\sin \beta \cos \beta \times A{f_1}{f_2}m\left[ {{k_{\rm{h}}} - 2\left( {1 - {k_{\rm{v}}}} \right)} \right] - A{f_1}m\left[ {\left( {1 - {k_{\rm{v}}}} \right) + 2{k_{\rm{h}}}} \right] \\+ 2{f_3}m\left( {{k_{\rm{h}}} + {f_2}} \right) + }\\ {{{\sin }^3}\beta \cos \beta \times - 2{f_1}{f_2}{m^2}{k_{\rm{h}}}\left( {1 - {k_{\rm{v}}}} \right) + {f_1}{m^2}\left[ {\left( {2 + {f_2}} \right){{\left( {1 - {k_{\rm{v}}}} \right)}^2} + {f_2}k_{\rm{h}}^2} \right] + }\\ {\sin \beta {{\cos }^3}\beta \times {f_1}{f_2}m\left[ {2\left( {1 - {k_{\rm{v}}}} \right) + 2k_{\rm{h}}^2 - {{\left( {1 - {k_{\rm{v}}}} \right)}^2}} \right] + }\\ {{{\sin }^2}\beta \times A{f_1}{f_2}m\left[ {\left( {1 - {k_{\rm{v}}}} \right) + {k_{\rm{h}}}} \right] + m\left( {1 - {k_{\rm{v}}}} \right)\left( {{f_3} - A{f_1}} \right) + }\\ {{{\cos }^2}\beta \times - A{f_1}m\left( {{f_2}{k_{\rm{h}}} + {k_{\rm{v}}}} \right) - {f_3}\left[ {{f_2}{k_{\rm{h}}} + m\left( {1 - {k_{\rm{v}}}} \right)} \right] + }\\ {{{\sin }^2}\beta \cos \beta \times - {f_1}{U_2}m\left[ {{f_2}\left( {1 - {k_v}} \right) + 2m{k_{\rm{h}}}} \right] + {{\cos }^3}\beta \times \left( { - {f_1}m{U_2}} \right){\rm{ + }}}\\ {\sin \beta {{\cos }^2}\beta \times \left[ {2{f_1}m{U_2}\left( {1 - {k_{\rm{v}}}} \right)} \right] + {{\sin }^4}\beta \times - {f_1}f_2^2{m^2}\left[ {{{\left( {1 - {k_{\rm{v}}}} \right)}^2} + k_{\rm{h}}^2} \right] + }\\ {{{\cos }^4}\beta \times - {f_1}{m^2}\left[ {k_{\rm{h}}^2 + {{\left( {1 - {k_{\rm{v}}}} \right)}^2}} \right] + {{\sin }^3}\beta \times - {f_1}m{U_2}\left[ {{f_2}{k_{\rm{h}}} + m\left( {1 - {k_{\rm{v}}}} \right)} \right] = 0} \end{array}} \right., $ | (24) |
式(24)中的各系数分别为
| $ \left\{ \begin{gathered} {U_2} = {h_{\text{w}}}{\gamma _{{\text{sat}}}}\left[\begin{gathered} \frac{{\beta \left( {{k_{\text{h}}} + {k_{\text{v}}}} \right)\left( {1 + \mu } \right)}}{3} + \hfill \\ \sqrt 2 \alpha \sqrt {{{\left( {{k_{\text{h}}} + {k_{\text{v}}}} \right)}^2}\left( {{\mu ^2}-\mu + 1} \right)-3{k_{\text{h}}}{k_{\text{v}}}} \hfill \\ \end{gathered} \right]; \hfill \\ A = \frac{{{\gamma _{\text{w}}}h_{\text{w}}^2\left( {1 -i} \right)}}{2}\;\;AA\;\;A = \frac{{{\gamma _{\text{w}}}h_{\text{w}}^2\left( {1 + i} \right)}}{2}; \hfill \\ m = {\gamma _{{\text{sat}}}}h_{\text{w}}^2/2 + \gamma \left( {{H^2} -h_{\text{w}}^2} \right)/2; \hfill \\ {f_1} = \tan \varphi ; \hfill \\ {f_2} = \cot \alpha ; \hfill \\ {f_3} = cH \hfill \\ \end{gathered} \right.。 $ |
式(24)可通过数据编程实现滑动面倾角极值的求解,然后再联合式(23)便可解出边坡的整体安全系数。
对于拟动力法而言,整体安全系数会随时间而发生变化,在拟静力法得到滑面倾角极值的基础上,可以得到拟动力法下的整体安全系数变化规律,结果可与动力时程法对比。
2 算例分析 2.1 解析式合理性讨论及影响因素分析以文献[6]的砂土边坡为研究对象,坡高H=10 m,边坡坡度比为1:1.5,砂土容重γ=20.5 kN/m3,黏聚力c=3 kPa,内摩擦角φ=40°,泊松比为μ=0.3,饱和重度取γsat=22 kN/m3。边坡所在地区基本烈度为7度,水平地震峰值加速度为0.1 g, 且不考虑竖向地震动的影响。坡体内地下水位高度分别取2、6、10 m。经计算得到坡体的剪切波速vs=97.53 m/s,纵波波速vp=201.06 m/s,则角频率w可由Kramer[15-16]提供的关系式进行计算,有T=2π/w=4H/vs,w=15.32 rad/s,周期T=0.41 s,而水平加速度系数kh=0.1, 孔隙水压系数α=0.75,β=1.0。把土体参数带入相关解析计算式,得到整体安全系数,并与文献[6]中其他方法结果对比如表 1所示。
| 表 1 不同方法计算的安全系数 Table 1 Safety factor calculated by different methods |
从表 1可以看出文中采用的渗流拟静力法和渗流拟动力法得到的边坡安全系数与文献[6]的结果和规范法的结果基本一致。在高水位时,文中的拟静力法只给出了计算失稳的临界值,即安全系数识别到小于1即可,也就是安全系数小于1即终止计算,因此与规范法和文献[6]中取值标准为最小系数是不一样的,故计算结果略有差别。而文中拟动力法的最小安全系数与文献[6]的动力时程法更为接近。这是因为拟动力法考虑了输入波的振动特性,与真实的波动更具有相似性。
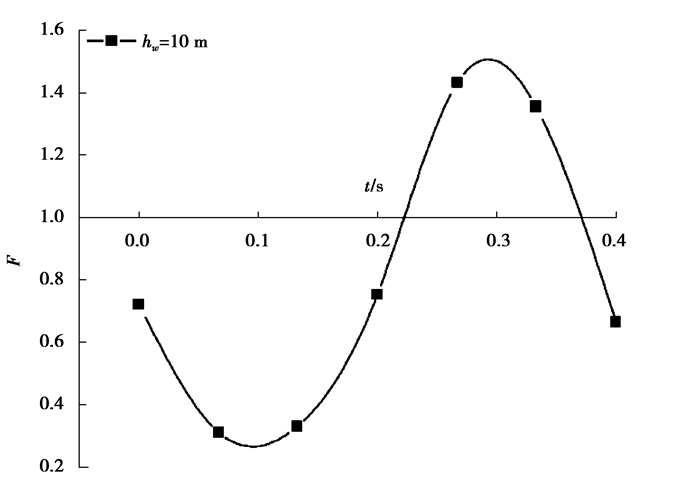
在水位为10 m时,以文中拟动力法的结果为例,给出一个振动周期的安全系数随时间的变化规律如图 4所示,可以发现整个时域内最小安全系数与动力时程法结果是最为接近的。
|
图 4 拟动力法计算的安全系数 Figure 4 Safety factor by Pseudo-Dynamic method |
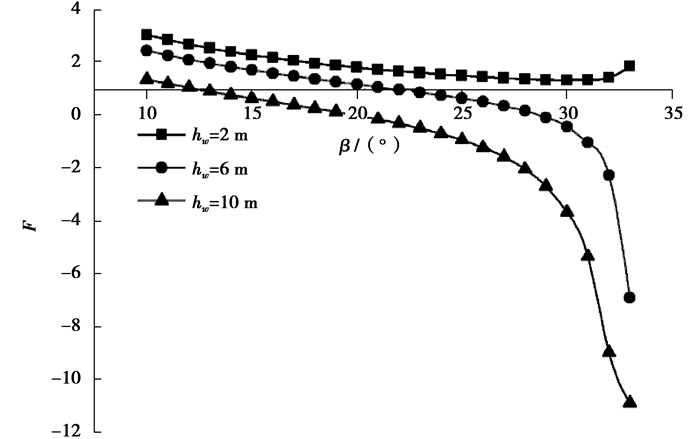
拟静力法中不同水位和安全系数的对应关系如图 5所示,可知水位为2 m时,边坡是稳定的,最小安全系数为1.33,与文献[6]的结果一致,与规范法结果相差为14.5%。图 5反映出拟静力法计算的安全系数与滑面倾角并非线性关系,近似为半抛物线状。当水位在6 m和10 m时,边坡会发生失稳,相应失稳的临界滑面倾角分别为21°和13°。从图 5还可以看出,水位越高,失稳时的滑面倾角越小,安全系数变化越明显,边坡越容易失稳。
|
图 5 拟静力法中安全系数与倾角关系 Figure 5 Relationship of sliding incline angle and safety factor in Pseudo-Static method |
图 6中拟动力法中基本烈度为7度,不同水位与安全系数的关系,提取整个周期内每个水位下的最小安全系数值如表 1所示。从图 6可知,水位越高,安全系数的损失越明显,安全系数随时间发生动态变化,最终的稳定性评价应以整个时域内的最小系数为准。可以得出,水位为2 m的边坡是稳定的,而水位在6 m和10 m时,边坡已失稳。
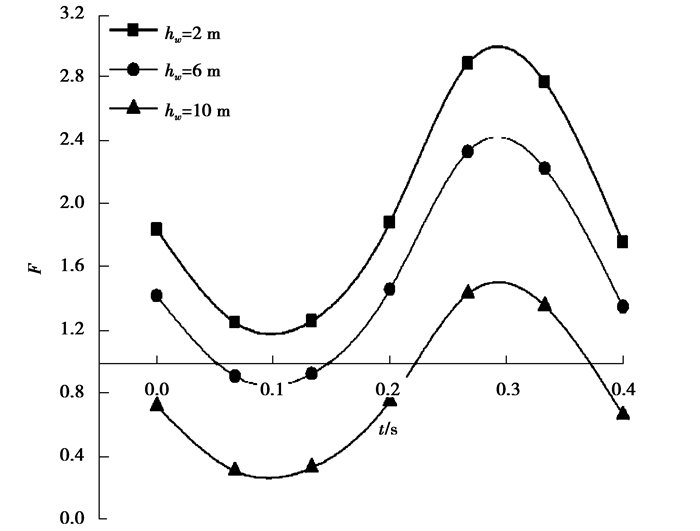
|
图 6 拟动力法中安全系数与不同水位的关系 Figure 6 Relationship of water level and safety factor in Pseudo-Dynamic method |
图 7所示是安全系数与水力梯度i的关系,渗流作用主要体现在地下水位越高越容易失稳,而水力梯度的作用则表现在其大小和符号上,同一水位下水力梯度与安全系数基本成线性关系。渗流方向向下时,安全系数随水力梯度增加而增大,渗流方向向上时,变化规律相反。
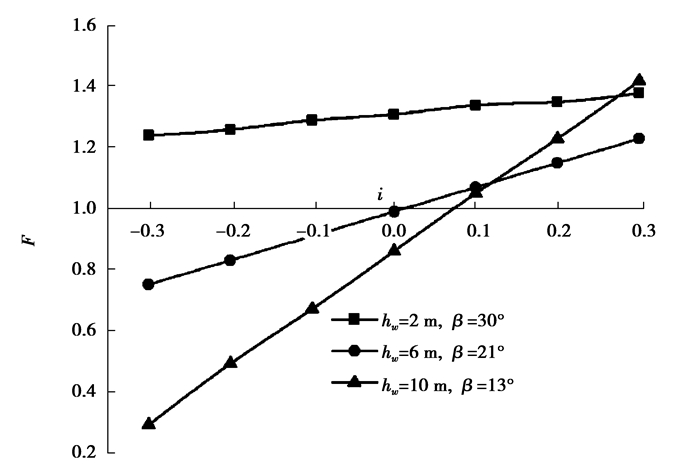
|
图 7 安全系数与水力梯度关系 Figure 7 Relationship of hydraulic gradient and safety factor |
图 8所示是拟静力法中地震加速度系数与安全系数之间的关系,由图 8可知安全系数受水平地震加速度系数的影响显著,这也是抗震规范中重点强调水平地震危害的重要原因,而竖向地震加速度系数影响较小,简化计算中可不考虑竖向地震动的作用。通过计算模型中的惯性力方向也可以得出,背离边坡的水平地震惯性力会显著削弱其稳定性。
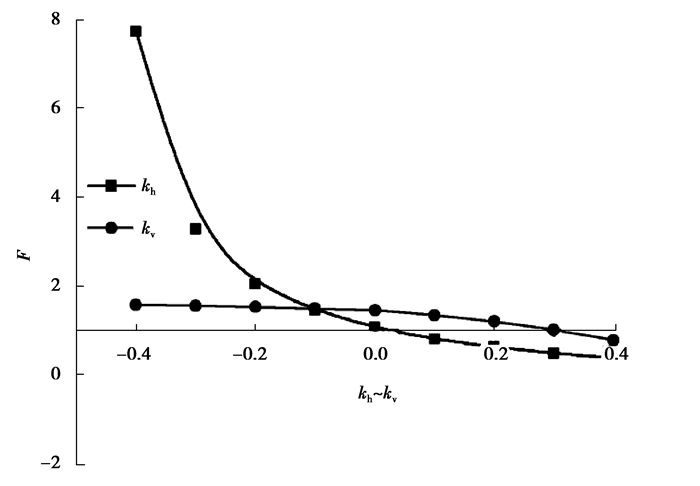
|
图 8 拟静力法中kh~kv与安全系数的关系 Figure 8 Relationship of seismic acceleration factor (kh~kv) an safety factor in Pseudo-Static method |
图 9所示是拟动力法计算的水平地震加速度系数与安全系数的关系,可以发现同一水位下,随烈度的增加边坡失稳的可能性在加剧。当kh=0.4 g时,边坡已是失稳状态,而当kh=0.2 g时,边坡己接近欠稳定状态。结合图 5、图 6和图 9可知,拟动力法与拟静力法相比能够反映安全系数随时间的动态变化关系,能够确定最小安全系数以及发生的时刻。拟动力法与动力时程法的思路是一致的,但计算量要小于动力时程法。
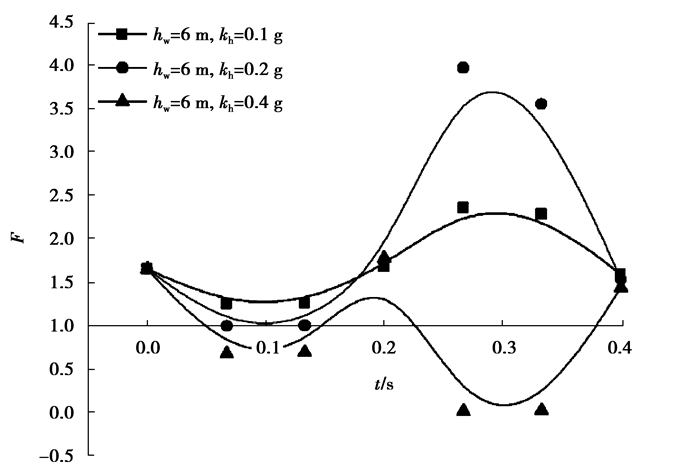
|
图 9 拟动力法中kh与安全系数的关系 Figure 9 Relationship of seismic acceleration factor (kh) and safety factor in Pseudo-Dynamic method |
从算例对比的结果和影响因素的分析可以得出,渗流拟静力法和渗流拟动力法都是分析多因素条件下边坡稳定性的有效工具,但两者存在差别。拟静力法计算简单,只能给出单一的安全系数结果,评价单调。而拟动力法可以给出安全系数随时间的变化规律,以及最小系数发生的时刻,比拟静力法的结论更加具体。工程中应根据边坡的复杂程度及评价要求适当选用两种方法。
3 结论1) 通过拟静力法、拟动力法和地下水渗流耦合的模式构建了砂土边坡的计算力学模型,基于数学函数极值法确定了拟静力法中边坡安全系数和滑面倾角。通过拟动力法确定了不同水位、不同烈度下的安全系数随时间的变化规律。与算例对比可以得出两种方法的解析式是合理的。
2) 地下水位、水力梯度和地震加速度系数是影响边坡在耦合条件下稳定性的重要因素,然而各因素对稳定性的敏感度各不相同。基于简化的渗流计算方法,可以得出地下水位越高,竖直向上的水力梯度越大边坡越容易失稳,而背离边坡的水平惯性力对稳定性影响最明显,竖向的地震加速系数影响较小,计算中可近似忽略。
3) 拟静力法解析式的计算思路简单,结果实用,在几何条件和计算参数明确的前提下可得到安全系数的显示解。而拟动力法充分发挥了输入波的振动特性,能够描述安全系数在耦合作用下的动态变化规律,有利于全面认识动力作用下的坡体稳定性。文中两种方法都可以作为边坡评价的依据,是现有边坡稳定性评价方法的有益补充,当拟静力法评价边坡为失稳时,应考虑采用拟动力法或时程法来分析边坡的稳定性。
| [1] | Duncan J M. State of the art:limit equilibrium and finite-element analysis of slopes[J]. Journal of Geotechnical Engineering, 1996, 122(7): 577–596. DOI:10.1061/(ASCE)0733-9410(1996)122:7(577) |
| [2] |
卢玉林, 薄景山, 陈晓冉, 等.
渗流边坡地震拟静力法稳定性的简化计算[J]. 水力发电, 2016, 42(1): 29–33.
LU Yulin, BO Jingshan, CHEN Xiaoran, et al. Simplified calculation of slope stability under seepage condition and pseudo-static method[J]. Water Power, 2016, 42(1): 29–33. (in Chinese) |
| [3] |
卢玉林, 薄景山, 陈晓冉, 等.
渗流耦合作用的基坑两级边坡应力场分析[J]. 地下空间与工程学报, 2016, 12(4): 946–951.
LU Yulin, BO Jingshan, CHEN Xiaoran, et al. Stress field analysis of a stepped-slope pit based on the seepage coupling method[J]. Chinese Journal of Underground Space and Engineering, 2016, 12(4): 946–951. (in Chinese) |
| [4] |
龚文俊, 李明永, 吴志坚.
降雨和地震耦合作用对滑坡稳定性的影响:以甘肃西和Ⅲ号滑坡为例[J]. 西北地震学报, 2012, 34(2): 161–166.
GONG Wenjun, LI Mingyong, WU Zhijian. Stability analysis of landslide under coupling action of earthquake and rainfall:taking the No.Ⅲ landslide of Xihe country, Gansu province as an example[J]. North western Seismological Journal, 2012, 34(2): 161–166. (in Chinese) |
| [5] |
张永兴, 陈林, 陈建功.
地震作用下边坡稳定性分析的坐标转换法[J]. 山地学报, 2010, 28(2): 129–134.
ZHANG Yongxing, CHEN Lin, CHEN Jiangong. A coordinate transformation method for evaluation stability of slope under seismic conditions[J]. Journal of Mountain Science, 2010, 28(2): 129–134. (in Chinese) |
| [6] |
宋波, 黄帅, 蔡德钩, 等.
地震和地下水耦合作用下砂土边坡稳定性研究[J]. 岩土工程学报, 2013, 35(Sup2): 862–868.
SONG Bo, HUANG Shuai, CAI Degou, et al. Stability of sandy soil slope under the coupling of earthquake and groundwater[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(Sup2): 862–868. (in Chinese) |
| [7] |
赖杰, 郑颖人, 李秀地, 等.
自重、渗流及地震耦合作用下人工岛动力稳定性分析[J]. 振动与冲击, 2016, 35(5): 175–180.
LAI Jie, ZHENG Yinren, LI Xiudi, et al. Dynamic stability of an artificial island triggered by self weight, seepage and earthquake[J]. Journal of Vibration and Shock, 2016, 35(5): 175–180. (in Chinese) |
| [8] | Choudhury D, Nimbalkar S S. Pseudo-dynamic approach of seismic active earth pressure behind retaining wall[J]. Geotechnical & Geological Engineering, 2006, 24(5): 1103–1113. |
| [9] | Basha B M, Babu G L S. Reliability assessment of internal stability of reinforced soil structures:a pseudo-dynamic appr-oach[J]. Soil Dynamics and Earthquake Engineering, 2010, 30(5): 336–353. DOI:10.1016/j.soildyn.2009.12.007 |
| [10] | Pantelidis L, Griffiths D V. Stability of earth slopes. Part I:two-dimensional analysis in closed-form[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2013, 37(13): 1969–1986. DOI:10.1002/nag.v37.13 |
| [11] | Pantelidis L, Griffiths D V. Stability of earth slopes. Part Ⅱ:three dimensional analysis in closed-form[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2013, 37(13): 1987–2004. DOI:10.1002/nag.v37.13 |
| [12] |
黄睿, 夏唐代, 房凯, 等.
竖向稳定渗流条件下的地震主动土压力分析[J]. 岩土力学, 2014, 35(9): 2522–2528.
HUANG Rui, XIA Tangdai, FANG Kai, et al. Analysis of seismic active earth pressure under vertical steady seep-age[J]. Rock and Soil Mechanics, 2014, 35(9): 2522–2528. (in Chinese) |
| [13] | Wang J J, Zhang H P, Chai H J, et al. Seismic passive resistance with vertical seepage and surcharge[J]. Soil Dynamics & Earthquake Engineering, 2008, 28(9): 728–737. |
| [14] | Steedman R S, Zeng X. The influence of phase on the calculation of pseudo-static earth pressure on a retaining wall[J]. Géotechnique, 1990, 40(1): 103–112. DOI:10.1680/geot.1990.40.1.103 |
| [15] | Kramer S L. Geotechnical earthquake engineering[J]. Mcgraw Hill Handbooks, 2001, 11(6): 302–313. |
| [16] | Das B M, Ramana G V. Principles of soil dynamics[M]. Stamford: Cengage Learning, 2010. |
 2017, Vol. 40
2017, Vol. 40

