2. 杭州前进齿轮箱集团股份有限公司, 杭州 311203
2. Hangzhou Advance Gearbox Group Co., Ltd., Hangzhou 311203, P. R. China
电动汽车被认为是未来新能源汽车发展的重要方向[1-2]。随着消费者对舒适性的要求越来越高,电动车的振动噪音问题成为制约电动汽车技术发展的关键问题,其中齿轮传动系统是产生振动噪声的主要贡献部件[3]。因此对电动车齿轮传动系统动态特性开展优化研究具有重要意义。
国内外学者对如何减小齿轮系统的结构噪声进行了一系列研究。Hedlund等[4]建立了参数化有限元模型,分析了由啮合刚度变化产生的激励。Liu等[5]通过建立齿轮副的有限元模型计算啮合刚度和接触线长度,观察宏观参数变化前后啮合刚度和接触线长度的变化情况。朱才朝等[6]对某兆瓦级齿轮箱各级齿轮进行修形,并在台架上对修形前后齿轮箱动态特性进行试验研究。郭栋等[7]对某5速变速器啸叫问题进行分析,并对主减齿轮进行齿向修形,降低了啸叫声。陆波等[8]分析在内、外部激励下系统结构预估噪声。王奇斌等[9]建立齿轮副啮合刚度模型,发现齿向修形降低了齿轮副啮合刚度。杜雪松等[10]以齿轮的振动加速度和质量为目标函数,对船用齿轮传动进行多目标动态优化,有效降低了船用齿轮的振动水平。林腾蛟等[11]通过有限元的直接积分法获取齿轮箱动力学性能,并通过零阶与一阶优化算法对箱体结构参数进行优化。众多文献也认为通过对齿形和齿向的修形,能够明显降低齿轮副在啮合过程中的振动[12-13]。Kang等[14]以传递误差作为优化目标,提供了一种斜齿轮螺旋角的优化方法。Kim等[15]利用Taguchi方法对某激光打印机的高速齿轮传动进行了降噪优化。Bruyère等[16]以齿轮副的传递误差和动态性能为目标,提供了最佳修形量的计算公式。
综上所述,现有研究主要基于实验手段以及微观修形对齿轮传动系统进行动态特性优化。笔者以某电动车的轮边减速器为研究对象,以与螺旋角和中心距直接关联的重合度为优化变量,以齿轮副的传递误差峰峰值等动态性能为优化目标,基于MASTA对齿轮副动态特性进行优化,研究结果对指导电动车高速轮边齿轮传动宏观几何参数的选取与设计具有重要工程应用价值。
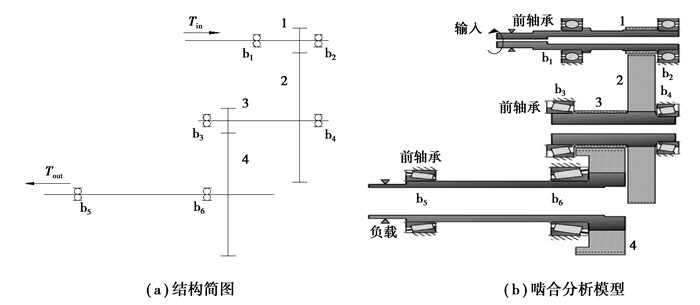
1 电动车高速轮边减速器啮合模型电动车减速器的传动系统采用两级斜齿轮传动,其结构简图如图 1(a)所示,扭矩从高速轴输入,经过中间级传递到低速级,从低速轴输出。各级齿轮副的基本参数如表 1所示,根据减速器传动结构及齿轮副参数在MASTA中建立如图 1(b)所示的减速器啮合分析模型。
|
图 1 轮边减速器传动原理 Figure 1 Transmission system of the wheel gear 1.输入级主动轮;2.输入级从动轮;3.输出级主动轮;4.输出级从动轮;bi(i=1~6):滚动轴承;Tin:输入扭矩;Tout:输出扭矩 |
| 表 1 减速器齿轮副参数 Table 1 Structural parameters of the wheel gear |
选择最高转速、额定转速和最大转矩3种最典型的工况进行分析,各工况参数如表 2所示。
| 表 2 各工况参数 Table 2 Parameters of the load cases |
传动误差为沿啮合线方向度量被动轮上的齿廓在实际啮合时所处位置同理想条件下应处位置之间的偏差,是判断齿轮副运转平稳性的重要指标之一。
| $ \delta ({\varphi _1}) = ({\varphi _2}-\varphi _{_2}^{^{(0)}})-{z_1}/{z_2}({\varphi _1}-\varphi _{_1}^{^{(0)}}) $ | (1) |
式中:φ为齿轮的啮合转角;z为齿数;φ(0)为齿轮在参考点啮合时的初始转角。
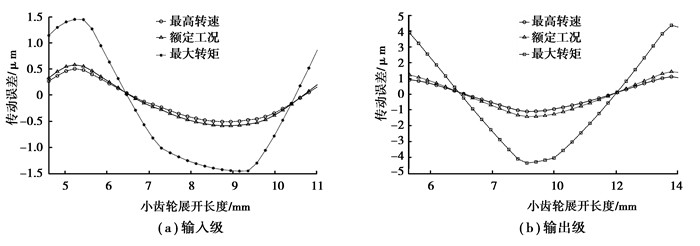
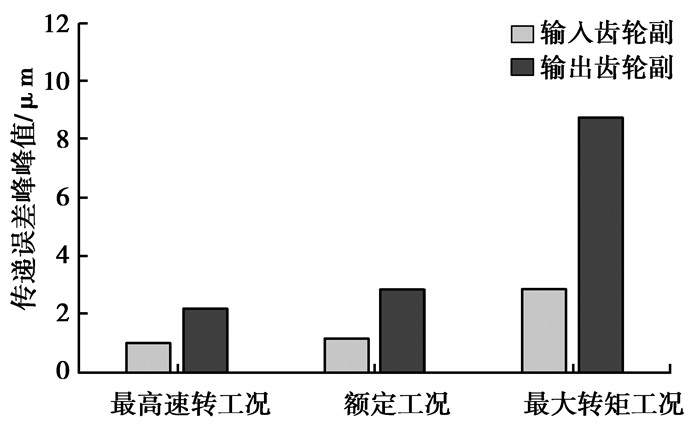
对各工况下齿轮传动系统动态性能进行分析,图 2为各工况下输入级与输出级一个啮合周期内的传动误差,图 3为其传动误差峰峰值的对比。理论上,齿轮副传动误差峰峰值小于2 μm则具有较好振动噪声性能。可以看出,该减速器输出齿轮副各工况的传动误差峰峰值均大于2 μm,特别是最大转矩工况达到8.742 1 μm,最大转矩工况的输入级齿轮副传动误差峰峰值超过2 μm。
|
图 2 各齿轮副传动误差 Figure 2 Transmission error of gear pairs |
|
图 3 各工况齿轮副传动误差峰峰值 Figure 3 The peak-to-peak transmission errors of gear pairs |
啮合刚度是齿轮啮合时轮齿抵抗变形的能力。齿轮副啮合过程中变形越大,造成的冲击越剧烈,直接影响到系统的振动噪音。在一个啮合周期里,啮合刚度变化过大,对系统带来的影响将更大,定义啮合刚度变化率为
| $ {\eta _{{c_\gamma }}} = \frac{{\Delta {c_\gamma }}}{{{c_{\gamma {\rm{m}}}}}} \times 100\%, $ | (2) |
式中:cγm为平均啮合刚度;Δcγ为啮合刚度最大值和最小值之差。
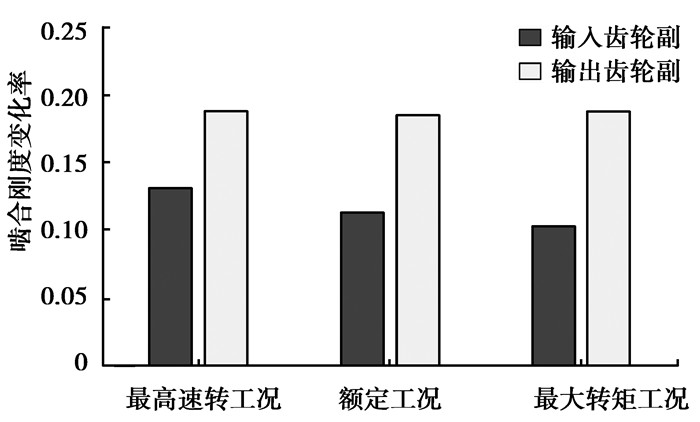
计算得到cγm与Δcγ,再由式(2) 得到齿轮副在各工况下的啮合刚度变化率,如图 4所示,可以看出输出级齿轮副的啮合刚度变化率大于输入级,各齿轮副在不同工况的啮合刚度变化率改变很小。同时计算减速器各轴承处的结构噪声,发现转速在3 000~9 000 r/min时结构噪声偏大,是进行优化的重点参考区间。
|
图 4 各工况齿轮副啮合刚度变化率 Figure 4 The fluctuation value of mesh stiffness of gear pairs |
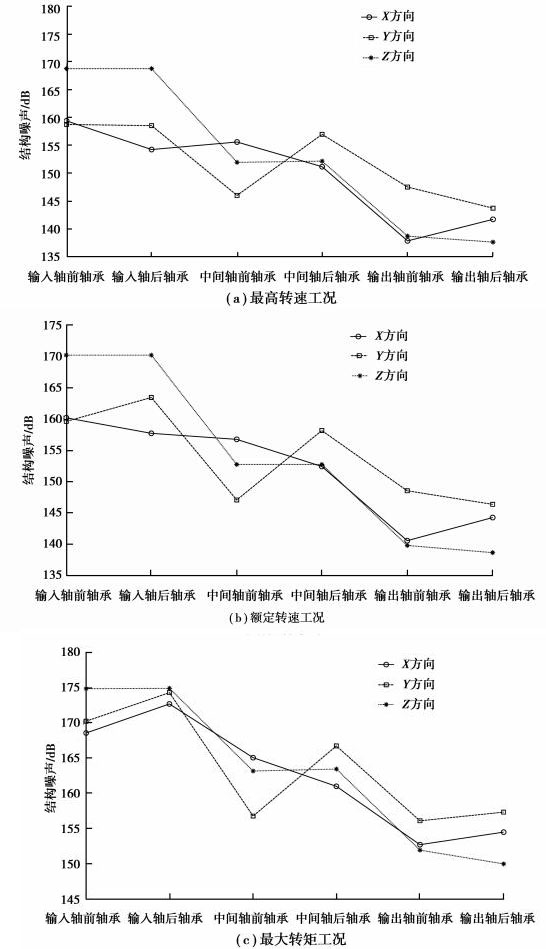
图 5是各工况下轴承在各方向结构噪声对比。可以看出最大结构噪声值在各工况下的分布趋势大致相同,输入轴上轴承的结构噪声相对较大,而输出轴上轴承的结构噪声较小。
|
图 5 各工况轴承的最大结构噪声 Figure 5 The peak structural-born noise of bearings |
为了改善该型轮边减速器的动态性能,以与螺旋角和中心距直接关联的重合度为优化变量,以齿轮副的传递误差峰峰值、啮合刚度变化率以及系统结构噪声为优化目标,基于MASTA研究不同参数齿轮副在啮合过程中其动态特性的变化规律。对于渐开线斜齿圆柱齿轮,其重合度为端面重合度εα和轴向重合度εβ之和,用εγ来表示,即
| $ {\varepsilon _\gamma } = {\varepsilon _\alpha } + {\varepsilon _{\rm{ \mathit{ β} }} }, $ | (3) |
其计算公式为
| $ {\varepsilon _\alpha } = \frac{{{z_1} \times \left( {\tan {\alpha _{{\rm{at}}1}}-{\mathop{\rm tan}\nolimits} {{'}_{{\alpha _t}}}} \right) + {z_2} \times \left( {\tan {\alpha _{{\rm{at2}}}}-{\mathop{\rm tan}\nolimits} {{'}_{{\alpha _{\rm{t}}}}}} \right)}}{{2\pi }} $ | (4) |
| $ {\varepsilon _{\rm{ \mathit{ β} }}} = \frac{{B\sin \beta }}{{\pi {m_{\rm{n}}}}}, $ | (5) |
式中:αat为端面齿顶压力角;α′t为端面啮合角;B为齿宽;β为螺旋角;mn为端面模数。
从公式(5) 可以看出斜齿轮轴向重合度的大小与螺旋角、模数和齿宽有关。保持齿轮副的模数、压力角等基本参数不变改变螺旋角和中心距来获得具有不同重合度的齿轮副,如表 3所示。随着螺旋角的增加,端面重合度越来越小,而轴向重合度则与之相反。
| 表 3 齿轮副宏观参数优化方案 Table 3 The optimized macro parameters of the gear pairs |
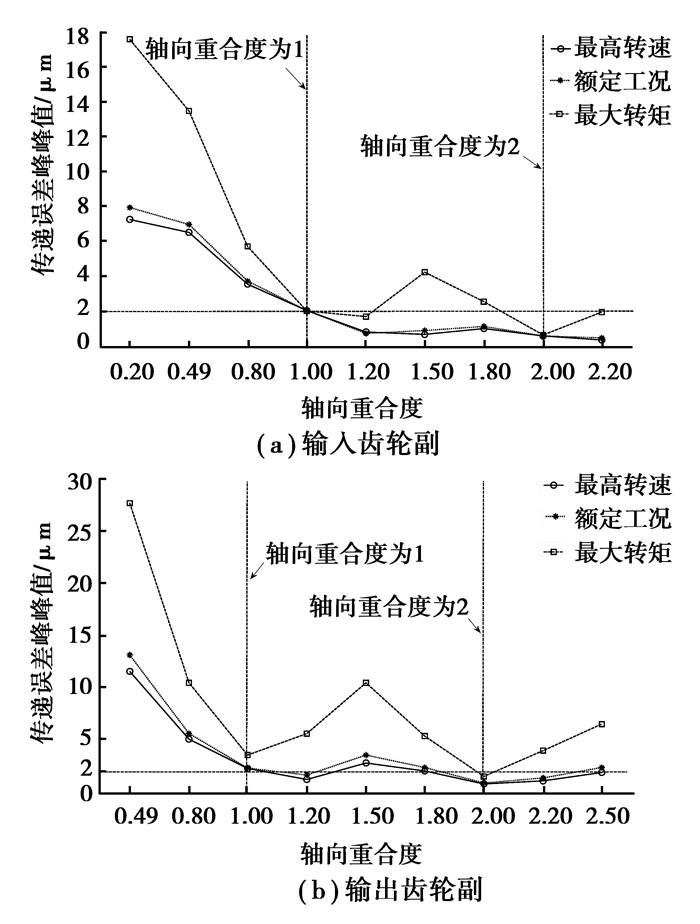
图 6是齿轮副在各工况下的传动误差峰峰值,可以看出输入齿轮副有3组设计工况的传动误差峰峰值小于2 μm,但输出齿轮副中只有轴向重合度为2.002 7时才符合要求。
|
图 6 不同轴向重合度对传动误差峰峰值的影响 Figure 6 The effect of different axial contact ratio to the peak-to-peak transmission errors |
在轴向重合度接近整数时,传动误差峰峰值通常优于附近重合度所对应的传动误差峰峰值,尤其在最大转矩工况规律较为明显。
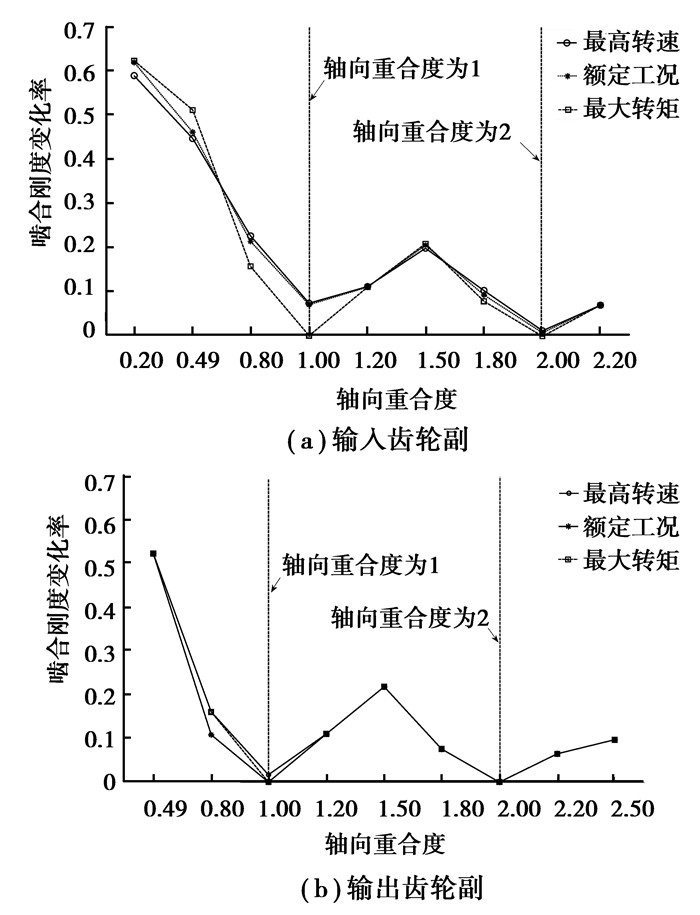
3.2 啮合刚度变化率图 7是各工况下齿轮副在不同轴向重合度的啮合刚度变化率,可以看出啮合刚度变化率的变化趋势为波浪式递减,波谷均发生在轴向重合度接近整数的部位,并且随着轴向重合度的增大,啮合刚度变化率的整体趋势是逐渐减小。
|
图 7 不同轴向重合度对啮合刚度变化率的影响 Figure 7 The effect of different axial contact ratio to the fluctuation value of mesh stiffness |
接触线全长变动程度表示了齿轮在啮合过程中接触载荷分布情况及大小的变动程度,也直接影响啮合过程中齿轮副啮合性能。为了观察整个啮合过程中接触线长度的变化情况,定义接触线长度变化率为
| $ {\eta _{\rm{L}}} = \frac{{{L_{{\rm{max}}}}-{L_{{\rm{min}}}}}}{{{L_{\rm{m}}}}} \times 100\%, $ | (6) |
式中:Lmax为接触线长度最大值;Lmin为接触线长度最小值;Lm为平均接触线长度。代入Lmax、Lmin和Lm的计算公式,得到以下ηL的计算公式:
eα+eβ≤1时,
| $ {\eta _{\rm{L}}} = \frac{{{e_1}}}{{{\varepsilon _\alpha }{\varepsilon _{\mathtt{β }}}}}, $ | (7) |
eα+eβ>1时,
| $ {\eta _{\rm{L}}} = \frac{{1 - {e_2}}}{{{\varepsilon _\alpha }{\varepsilon _{\mathtt{β }}}}}, $ | (8) |
式中:e1=min(eα, eβ);e2=max(eα, eβ),eα和eβ为εα和εβ的小数部分。
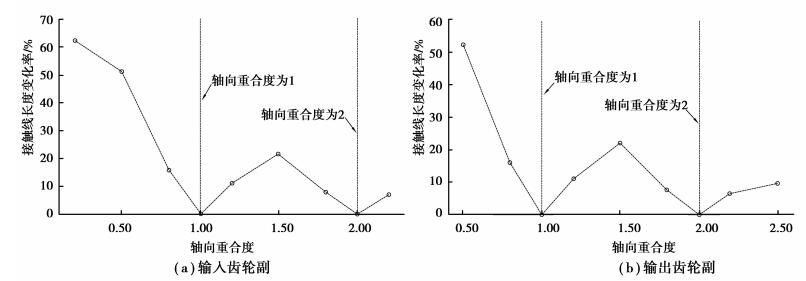
通过该公式计算得到各齿轮副在不同重合度下的接触线长度变化率,从图 8可以看出其变化规律与啮合刚度变化规律相似。同时从公式(7)(8) 可知接触线长度变化率与工况无关,仅受重合度的影响,验证了各工况下传动误差峰峰值和啮合刚度变化率随轴向重合度的增加,均呈波浪式递减趋势的规律。
|
图 8 不同重合度齿轮副的接触线长度变化率 Figure 8 The effect of different axial contact ratio to the changing ratio of the total length of contact lines |
通过上述计算分析,提出该款轮边减速器传动系统的优化方案:输入齿轮副,轴向重合度选择2.001 5,即30.2°螺旋角;输出齿轮副,轴向重合度选择2.002 7,即24.8°螺旋角。
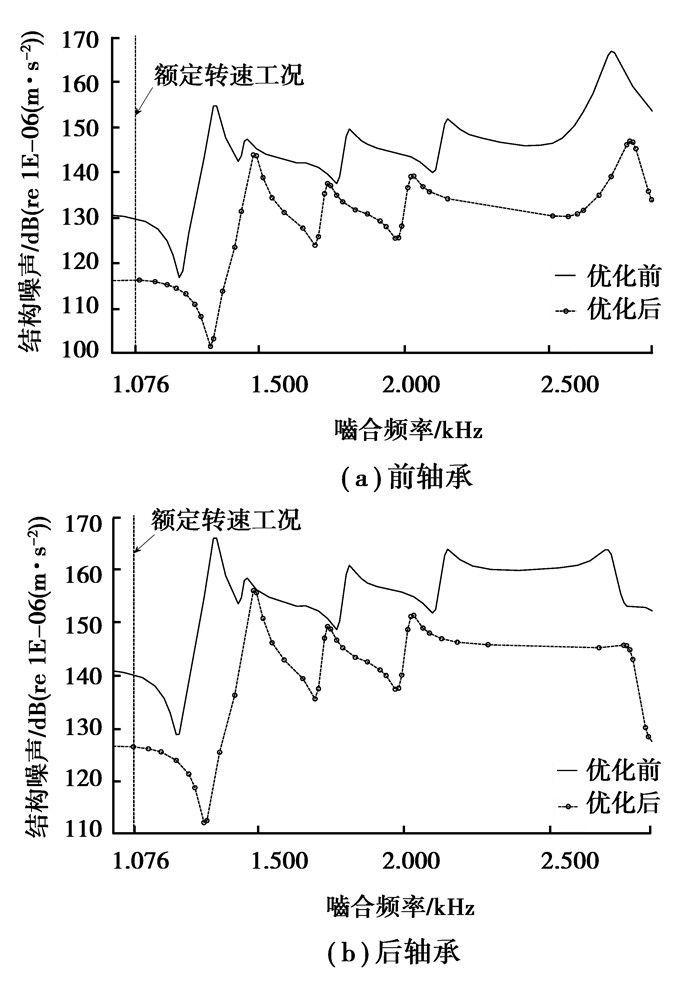
表 4是优化前后齿轮副传动误差峰峰值和啮合刚度变化率的变化情况。可以明显看出,优化后各齿轮副传动误差峰峰值和啮合刚度变化率得到明显降低。系统最大结构噪声位于输入齿轮副轴承部位,在最大转矩工况振动噪声较为严重,当转速处于3 000~9 000 r/min时,即输入齿轮副处于啮合频率950~2 850 kHz,噪声较为明显。对比优化前后输入轴轴承在最大转矩工况下,转速处于3 000~9 000 r/min范围内的结构噪声变化情况(如图 9所示),可以看出,竖直线对应的额定转速工况下,结构噪声值得到有效的降低,在其余转速工况下也均有所减小,达到了优化的目的。
| 表 4 优化前后改变情况 Table 4 The comparison of results before and after optimization |
|
图 9 输入轴各轴承结构噪声图 Figure 9 The structural-born noise of bearings on the input shaft |
同时各轴承在典型工况下,最大结构噪声在优化前后的变化情况如表 5所示,可以看出,优化后轴承在各工况下的结构噪声最大值均有所减小。
| 表 5 优化前后各轴承最大结构噪声对比 Table 5 The comparison of the peak structural-born noise of bearings before and after optimization |
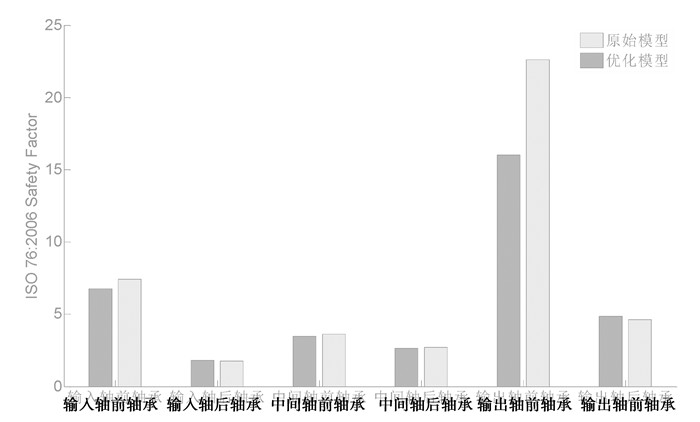
齿轮副动态性能得到优化的同时,还必须考虑螺旋角变化对系统安全性的影响,图 10为各轴承在最大转矩工况下安全系数(ISO 76:2006) 的变化情况,可以看出优化后,轴承的安全系数(ISO 76:2006) 稍有降低,但都在允许的范围内。
|
图 10 优化前后轴承最大转矩工况的安全系数 Figure 10 The safety factor of bearings at the peak load case |
笔者以某电动车高速轮边减速器为研究对象,建立减速器齿轮传动系统的动态啮合分析模型,以轴向重合度为优化变量对系统动态特性进行优化研究,得到主要结论如下:
1) 轮边减速器输出级齿轮副在各工况的传动误差峰峰值均大于2 μm,系统主要结构噪声位于高速级输入轴轴承处。
2) 与轴向重合度为非整数设计工况相比,当齿轮副的轴向重合度接近整数时,齿轮副的传动误差峰峰值、啮合刚度变化率得到明显的改善,轴承处的结构噪声均得到降低。
3) 提出轮边减速器传动系统的优化方案(输入齿轮副轴向重合度选择2.001 5,输出齿轮副轴向重合度选择2.002 7),优化前后各齿轮副在各工况下的传动误差峰峰值平均减少3.273 2 μm,啮合刚度变化率平均降低96.74%。
| [1] |
方源, 章桐, 于蓬, 等.
集中驱动式电动车噪声特性分析与试验研究[J]. 振动与冲击, 2015, 13(34): 89–94.
FANG Yuan, ZHANG Tong, YU Peng, et al. Acoustic characteristic analysis and tests for a centralized driving electric vehicle[J]. Journal of Vibration and Shock, 2015, 13(34): 89–94. (in Chinese) |
| [2] |
曹秉刚.
中国电动汽车技术新进展[J]. 西安交通大学学报, 2007, 41(1): 114–118.
Cao Binggang. Current progress of electric vehicle development in China[J]. Journal of Xi'an Jiaotong University, 2007, 41(1): 114–118. DOI:10.7652/xjtuxb200701026 (in Chinese) |
| [3] | Li Z X, Sui N, Wang G. Experimental study on vibration and noise of pure electric vehicle (PEV) drive system[C]//International Conference on Electric Information and Control Engineering. IEEE, 2011:5914-5917. |
| [4] | Hedlund J, Lehtovaara A. A parameterized numerical model for the evaluation of gear mesh stiffness variation of a helical gear pair[J]. Drive System Technique, 2008, 222(7): 1321–1327. |
| [5] | Liu L, Ding Y F, Wu L Y, et al. Effects of contact ratios on mesh stiffness of helical gears for lower noise design[C]//International Gear Conference 2014:26th-28th August 2014, Lyon. 2014:320-329. |
| [6] |
朱才朝, 陈爽, 马飞, 等.
轮齿修形对兆瓦级风电齿轮箱动态特性影响[J]. 振动与冲击, 2013, 32(7): 123–128.
ZHU Caichao, CHEN Shuang, MA Fei, et al. Effect of gear teeth modification on dynamic characteristics of a megawatt level wind turbine gearbox[J]. Journal of Vibration and Shock, 2013, 32(7): 123–128. (in Chinese) |
| [7] |
郭栋, 邓斌, 石晓辉, 等.
国产轿车变速器啸叫噪声源的识别与控制[J]. 中国机械工程, 2011, 22(18): 2264–2267.
GUO Dong, DENG Bin, SHI Xiaohui, et al. Transmission ccoupled nonlinear dynamic characteristics analysis and noise pre-estimation of a large burden marine gearbox[J]. China Mechanical Engineering, 2011, 22(18): 2264–2267. (in Chinese) |
| [8] |
陆波, 朱才朝, 宋朝省, 等.
大功率船用齿轮箱耦合非线性动态特性分析及噪声预估[J]. 振动与冲击, 2009, 28(4): 76–80.
LU Bo, ZHU Caichao, SONG Chaosheng, et al. Identification and reduction of gear whine noise of domestic[J]. Journal of Vibration and Shock, 2009, 28(4): 76–80. (in Chinese) |
| [9] |
王奇斌, 张义民.
齿向修形直齿轮系统动力学特性分析[J]. 振动工程学报, 2016, 29(1): 61–68.
WANG Qibin, ZHANG Yimin. Dynamic characteristics analysis of a spur gear system with the lead crown relief[J]. Journal of Vibration Engineering, 2016, 29(1): 61–68. (in Chinese) |
| [10] |
杜雪松, 朱才朝, 宁杰.
船用齿轮传动的动态优化设计[J]. 重庆大学学报, 2011, 34(5): 14–18.
DU Xuesong, ZHU Caichao, NING Jie. Dynamic optimization design of marine gear transmission system[J]. Journal of Chongqing University, 2011, 34(5): 14–18. DOI:10.11835/j.issn.1000-582X.2011.05.003 (in Chinese) |
| [11] |
林腾蛟, 宋建军, 孟令宽, 等.
风电增速齿轮箱动力学性能优化方法[J]. 重庆大学学报, 2016, 39(4): 16–23.
LIN Tengjiao, SONG Jianjun, MENG Lingkuan, et al. A dynamic behavior optimization method of wind power speed-increase gearbox[J]. Journal of Chongqing University, 2016, 39(4): 16–23. DOI:10.11835/j.issn.1000-582X.2016.04.003 (in Chinese) |
| [12] | Fernández A, Iglesias M, De-Juan A, et al. Gear transmission dynamic:effects of tooth profile deviations and support flexibility[J]. Applied Acoustics, 2014, 77(3): 138–149. |
| [13] | Velex P, Chapron M, Fakhfakh H, et al. On transmission errors and profile modifications minimising dynamic tooth loads in multi-mesh gears[J]. Journal of Sound and Vibration, 2016, 379: 28–52. DOI:10.1016/j.jsv.2016.05.044 |
| [14] | Kang J S, Choi Y S. Optimization of helix angle for helical gear system[J]. Journal of Mechanical Science & Technology, 2008, 22(12): 2393–2402. |
| [15] | Kim H K, Jeon J Y, Park J Y, et al. Noise reduction of a high-speed printing system using optimized gears based on Taguchi's method[J]. Journal of Mechanical Science and Technology, 2010, 24(12): 2383–2393. DOI:10.1007/s12206-010-0911-5 |
| [16] | Bruyère J, Gu X, Velex P. On the analytical definition of profile modifications minimising transmission error variations in narrow-faced spur helical gears[J]. Mechanism and Machine Theory, 2015, 92: 257–272. DOI:10.1016/j.mechmachtheory.2015.06.001 |
 2017, Vol. 40
2017, Vol. 40


