2. 中国北方车辆研究所 车辆传动重点实验室, 北京 100072;
3. 重庆长安汽车股份有限公司动力研究院, 重庆 400023
2. Science and Technology on Vehicle Transmission Laboratory, China North Vehicle Research Institute, Beijing 100072, P. R. China;
3. Powertrain Research Institute of Chongqing Changan Automobile Co., Ltd., Chongqing 400023, P. R. China
深沟球轴承广泛应用于航天、高铁和矿山机械等装备中。在大载荷作用下,该类轴承会处于贫油状态,甚至会出现滚动体与滚道直接接触,进一步影响轴承的使用寿命。因此研究该类轴承的接触性能具有重要的工程意义。
长期以来,人们对包含深沟球轴承在内的滚动轴承接触性能进行了大量研究,其研究成果大致可归为两类。首先是基于Hertz接触理论的轴承接触性能解析分析。Harris等[1]基于Hertz接触理论对包括深沟球轴承在内的系列滚动轴承进行了动力学性能分析。之后,刘旺玉等[2]提出了深沟球轴承动态弹性变形量的计算方法,发现轴承滚动体与滚道间接触区随径向载荷的增大而增大。
随着有限单元法(FEM, finite element method)的推广和计算机技术的不断提升,诸多学者采用FEM求解深沟球轴承接触问题。刘显军等[3]提出了计算多支撑轴承系统中深沟球轴承受力和变形的有限元迭代法,并通过试验验证了该方法的正确性。谢伟等[4]和黄志高[5]运用ANSYS软件对径向力作用下深沟球轴承的载荷分布进行了仿真,结果表明轴承最大接触压力位于径向力作用线正下方滚动体与内、外滚道的接触区上。白桂彩等[6]和仲丛华[7]借助LS_DYNA研究了深沟球轴承中滚动体接触压力的动态变化情况,研究发现滚动体接触压力以波峰波谷形式交替变化,且当滚动体与内、外滚道接触时接触压力达到最大。
尽管一些学者对深沟球轴承的接触性能进行了有益的探索,但以往研究大多在假设轴承表面为光滑的条件下进行。另外传统的解析法难以分析重载轴承的塑形行为;现有商用有限元软件虽然能分析轴承的塑形性能,但由于无法按照真实表面粗糙度建立几何模型且没有在物理数学模型中引入粗糙度效应,因而亦难以分析表面粗糙度对轴承接触性能的影响。由于深沟球轴承滚动体和滚道表面因机械加工存在一定的粗糙度,它势必影响轴承的接触性能。因此,对表面粗糙的深沟球轴承弹塑性接触性能进行研究显得十分必要。
在计入轴承表面粗糙度下,运用半解析法(SAM, semi-analytical method)[8-9]研究深沟球轴承的接触性能。首先采用共轭梯度法(CGM, conjugate gradient method)[10-11]求解滚动体与内滚道间的接触压力,采用快速傅里叶变换(FFT, fast fourier transform)方法[12]计算轴承中滚动体与内滚道的综合弹性变形,运用相关塑形理论求解内滚道的塑形变形和残余应力,并重点考察表面粗糙度对该类轴承中滚动体与内滚道之间弹塑性接触性能的影响,以期为该类轴承的接触性能研究提供参考。
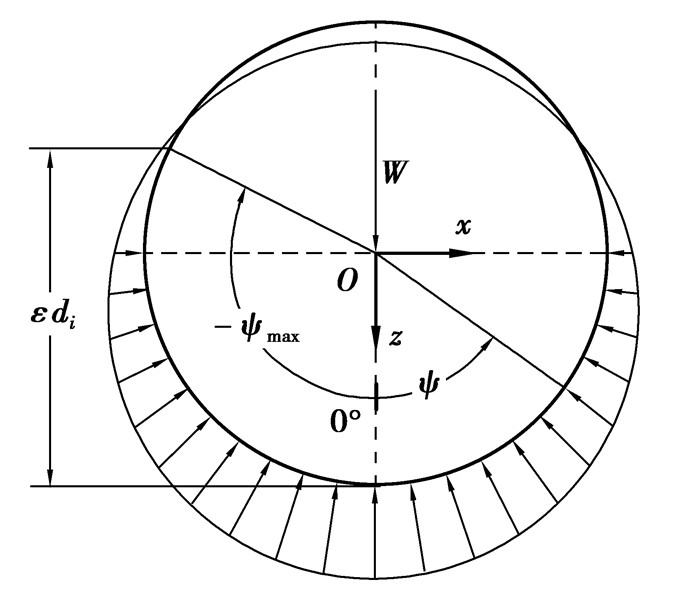
1 控制方程为研究表面粗糙的深沟球轴承弹塑性接触性能,以滚动体与内滚道间的接触为例进行分析。对于承受单一径向载荷且游隙为负的深沟球轴承,其滚动体载荷分布[1]如图 1所示。
|
图 1 深沟球轴承滚动体载荷分布 Figure 1 Load distribution of rolling elements for deep groove ball bearing |
图 1中W表示轴承受到的外载荷,ε为载荷分布系数,di为轴承公称内径,ψ表示以z轴正方向为始边的滚动体位置角。根据文献[1], 承载最大滚动体位于轴承最下方,其承载量F为
| $ F = \frac{W}{{Z{J_{\rm{r}}}\left( \varepsilon \right)}}, $ | (1) |
式中Z为滚动体数目,径向载荷积分表达式[1]为
| $ {J_{\rm{r}}}\left( \varepsilon \right) = \frac{1}{{2\pi }}\int_{-{\psi _{\max }}}^{{\psi _{\max }}} {{{\left( {1-\frac{1}{{2\varepsilon }}\left( {1-\cos \psi } \right)} \right)}^{3/2}}\cos \psi {{\rm{d}}}\psi, } $ | (2) |
式(2) 中ψmax和-ψmax分别表示以z轴正方向为始边,沿逆时针方向和顺时针方向的滚动体最大位置角,载荷分布系数ε=1/2-Pd/(4δr),其中Pd为径向游隙,δr为ψ=0°处轴承内圈的径向移动量。
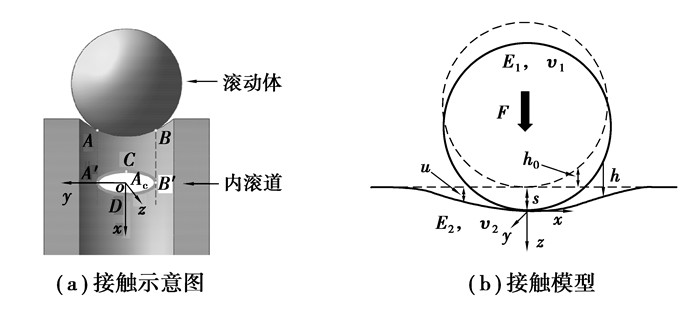
滚动体与内滚道间的接触示意图如图 2(a)所示,图中A′,B′两点分别与实际接触点A,B对应,接触区Ac由A′B′CD表示,其中点A′和B′为椭圆接触区沿宽度方向的两端点,点C和D为椭圆接触区沿滚动方向的两端点。x,y和z坐标方向分别表示轴承的圆周方向、宽度方向和径向。相对滚动体半径,内滚道沿轴承圆周方向的曲率半径较大,因此可将滚动体与内滚道间的接触等效转换为球与半空间的接触,进而建立如图 2(b)所示的滚动体内滚道弹塑性接触物理模型。
|
图 2 滚动体与内滚道接触模型 Figure 2 Contact model between rolling element and inner raceway |
在图 2(b)中h0和h分别表示半径为r滚动体与滚道之间的初始间隙和受载时实际接触间隙,h0=(x2+y2)/2r+(δ1+δ2),δ1和δ2分别为轴承中滚动体和滚道的表面粗糙度。s为滚动体的径向刚体位移,u为滚道的径向变形,E1,E2与ν1,ν2分别为滚动体与滚道的弹性模量和泊松比。在最大外载荷F作用下,滚动体和滚道会发生接触。根据载荷平衡条件有
| $ F=\iint\limits_{{{A}_{\rm{c}}}}{{{p}_{\left( x, y \right)}}{\rm{d}}x{\rm{d}}y}, $ | (3) |
式中p(x, y)为滚道上点(x, y)处的径向压力。基于最小余能原理,上述接触问题可转换为二次型函数的条件极值问题[13],得
| $ \mathit{\boldsymbol{G}}\left( \mathit{\boldsymbol{p}} \right)=\mathit{\boldsymbol{h}}_{\rm{c}}^{\rm{T}}\cdot \mathit{\boldsymbol{p}}+\frac{1}{2}{{\mathit{\boldsymbol{p}}}^{\rm{T}}}\cdot {{\mathit{\boldsymbol{I}}}_{\rm{c}}}\cdot \mathit{\boldsymbol{p, }} $ | (4) |
式中:G(p)为目标函数;hc为接触间隙矩阵;p为压力矩阵;Ic表示影响系数矩阵,式(4) 采用CGM进行求解,且满足式(3) 所示载荷平衡条件。在接触区域Ac内的约束条件为
| $ {{p}_{(x, y)}}>0, {{h}_{(x, y)}}=0, \left( x, y \right)\in {{A}_{\rm{c}}}, $ | (5) |
对于非接触区域,需满足
| $ {{p}_{(x, y)}}=0, {{h}_{(x, y)}}>0, \left( x, y \right)\notin {{A}_{\rm{c}}}, $ | (6) |
此外,间隙和位移参数之间的关系可表示为
| $ {{h}_{(x, y)}}={{h}_{0(x, y)}}+{{u}_{(x, y)}}-s, $ | (7) |
| $ {{u}_{(x, y)}}=u_{_{(x, y)}}^{^{e}}+u_{_{(x, y)}}^{^{p}}, $ | (8) |
式(8) 中u(x, y)e为由接触压力产生的表面弹性变形,u(x, y)p为塑性应变引起的表面残余变形。
滚动体和内滚道表面的综合弹性变形u(x, y)e可通过Boussinesq积分求得
| $ u_{_{(x, y)}}^{^{e}}=\frac{1}{\pi {{E}^{*}}}\iint\limits_{{{A}_{\rm{c}}}}{\frac{p\left( \alpha, \beta \right)}{\sqrt{{{\left( x-\alpha \right)}^{2}}+{{\left( y-\beta \right)}^{2}}}}{\rm{d}}\alpha {\rm{d}}\beta }, $ | (9) |
式中p(α, β)为已知点(α, β)处的接触压力,E*为综合弹性模量,且1/E*=(1-ν12)/E1+(1-ν22)/E2。将式(9) 采用影响系数法(ICM, influence coefficient method)[14]进行离散得
| $ u_{_{(x, y)}}^{^{e}}=\sum\limits_{\beta =1}^{N}{\sum\limits_{\alpha =1}^{M}{A_{_{\left( x-\alpha \right)(y-\beta )}}^{^{e}}{{p}_{(\alpha, \beta )}}}}, $ | (10) |
式(10) 中A(x-α)(y-β)e表示由接触压力p(α, β)产生的弹性变形影响系数,该影响系数可通过解析的方法求得,M和N分别表示计算区域内沿x和y方向的网格节点数。
根据von Mises准则,应力偏张量的第二不变量J2达到临界值σs2/3时,内滚道开始发生塑性变形,其表面残余变形u(x, y)p离散表达式[15]为
| $ u_{_{(x, y)}}^{P}=\sum\limits_{\beta =1}^{N}{\sum\limits_{\alpha =1}^{M}{B_{_{ij{ }(x-\alpha, y-\beta, \gamma )}}^{^{p}}\varepsilon _{_{ij{ }(\alpha, \beta, \gamma )}}^{^{p}}}}, $ | (11) |
式中Bij(x-α, y-β, γ)p为轴承内滚道塑性应变对残余变形的影响系数,εij(α, β, γ)p为点(α, β, γ)处的塑性应变。
根据应力关系有
| $ {{\sigma }_{ij}}=\sigma _{_{ij}}^{^{e}}+\sigma _{_{ij}}^{^{p}}, $ | (12) |
式中:σij为总应力张量;σije为弹性应力张量;σijp为塑性应力张量。同理,采用ICM进行离散后,σije和σijp的计算表达式[15]分别为
| $ \sigma _{_{ij{ }(x, y, z)}}^{^{e}}=\sum\limits_{\beta =1}^{N}{\sum\limits_{\alpha =1}^{M}{C_{_{ij{ }(x-\alpha, y-\beta, z)}}^{^{e}}{{p}_{(\alpha, \beta )}}}}, $ | (13) |
| $ \sigma _{_{ij{ }(x, y, z)}}^{^{p}}=\sum\limits_{\gamma =1}^{L}{\sum\limits_{\beta =1}^{N}{\sum\limits_{\alpha =1}^{M}{D_{_{ij{ }(x-\alpha, y-\beta, z-\gamma )}}^{^{p}}\varepsilon _{_{ij{ }(\alpha, \beta, \gamma )}}^{^{p}}}}}, $ | (14) |
式中:Cij(x-α, y-β, z)e为接触压力p(α, β)对弹性应力的影响系数;Dij(x-α, y-β, z-γ)p为塑性应变εij(α, β, γ)p对塑性应力的影响系数。为加速计算,式(10)(11)(13) 和(14) 可采用FFT方法计算得到。
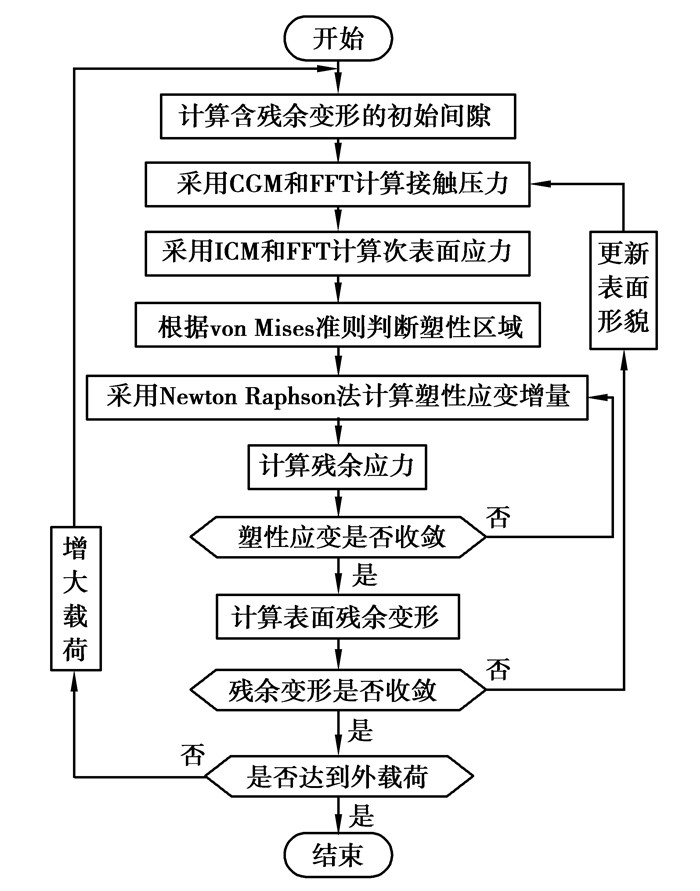
2 求解流程基于半解析法的轴承弹塑性接触性能求解流程见图 3。图 3中,整个求解流程包含三重迭代循环。最外层循环中,对于每一载荷步,首先采用CGM并结合FFT对轴承滚动体和内滚道间的接触压力、接触变形进行计算,并采用ICM和FFT计算出次表面应力;然后根据von Mises准则确定塑性区域,并采用Newton Raphson法迭代计算塑性应变增量,进而可求得轴承残余变形。求解过程中,若塑性应变不收敛,进行塑性应变增量循环计算。若表面残余变形不收敛,则将当前残余变形叠加到轴承表面形貌,进行表面形貌循环计算。计算中当累加载荷达到已指定的外载荷,塑性应变和残余变形均满足收敛精度时,输出最终计算结果,终止计算。
|
图 3 轴承弹塑性接触算法流程图 Figure 3 Flowchart of bearing's elastoplastic contact algorithm |
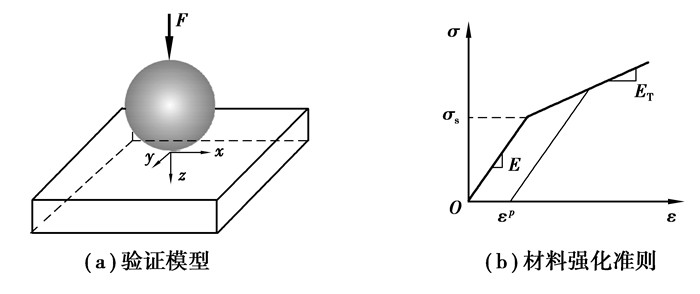
采取与FEM计算结果对比的方法进行轴承弹塑性接触算法验证。由于滚动体半径远小于滚道沿圆周方向的曲率半径,可选取刚性球体与弹塑性平板之间的接触模型作为验证模型,其受力示意图如图 4所示。
|
图 4 弹塑性接触算法验证 Figure 4 Verification of elastoplastic contact algorithm |
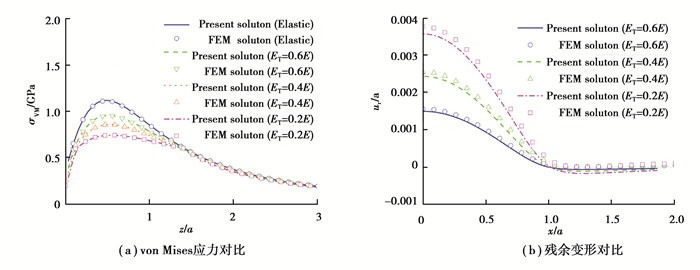
验证时所取参数为:球体半径R=20 mm,平板弹性模量E=100 GPa,平板泊松比ν=0.3,屈服极限σs=600 MPa。同时,考虑3种双线性等向强化准则(塑性模量ET=0.2E,ET=0.4E和ET=0.6E)模拟材料的塑性特性。球固定且不考虑摩擦作用,在球上施加的法向载荷F为1 000 N。计算结果中的变形和压力分别采用弹性Hertz接触半径a(0.514 885 8 mm)和最大Hertz接触压力pH(1 801.024 MPa)进行无量纲化。
不同线性强化准则下的von Mises应力分布对比如图 5(a)所示,可以看出本方法计算得到的结果与FEM解比较吻合。图 5(b)显示了沿x轴的残余变形分布对比。由该图可知,最大残余变形随着材料塑性的增加(塑性模量ET减小)而增大,本方法计算结果与FEM计算结果基本一致。此外,表 1给出了本方法与FEM计算得到的无量纲残余变形最大值对比,可以看出在塑性本构为ET=0.6E情况下出现最大误差,其值仅为-5.053%。这是由于FEM通过节点位移插值得到单元内各点的位移,而本方法采用的有限差分法则直接计算得到各网格节点的位移。总体而言,本方法计算结果与FEM计算结果基本吻合,因而本弹塑性接触算法可用于后续考虑粗糙度因素的深沟球轴承弹塑性接触性能研究。
|
图 5 本方法与FEM计算得到的结果比较 Figure 5 Comparison between results obtained by present method and FEM |
| 表 1 本方法与FEM计算得到的无量纲残余变形最大值对比 Table 1 Comparison between maximum values of dimensionless residual deformations obtained by present method and FEM |
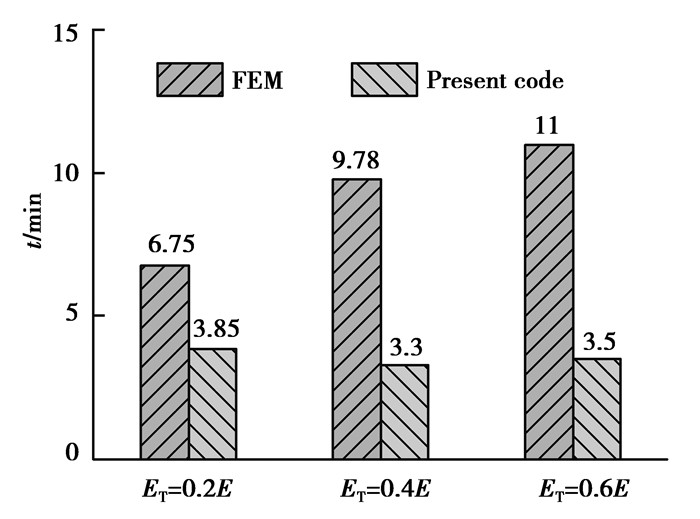
此外,将本弹塑性接触算法与FEM的计算效率进行对比。针对上述3种双线性等向强化准则下的算例,相同计算机配置、相同载荷步、相同收敛精度(塑性应变和残余变形的收敛精度分别为10-4和10-3)下轴承弹塑性接触算法与FEM计算所需时间对比如图 6所示。由图可知,在保证精度条件下,基于SAM的轴承弹塑性接触算法的求解效率高于FEM。
|
图 6 计算时间对比 Figure 6 Comparison between calculation times |
以航天、车辆和风电等领域[16]广泛使用的61830型深沟球轴承为研究对象,该轴承中滚动体和内滚道的尺寸参数和材料属性[17]如表 2所示。
| 表 2 滚动体和内滚道参数 Table 2 Parameters of rolling element and inner raceway |
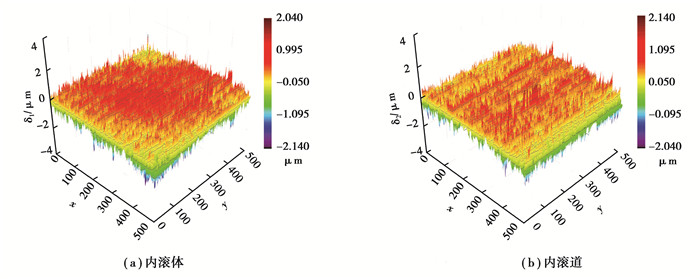
借助多功能摩擦试验机MFT-5000上集成的白光干涉仪,对滚动体和内滚道进行表面形貌测试。测试结果如图 7所示,被测滚动体和内滚道的表面轮廓算术平均偏差Ra值分别为0.309和0.249 μm,它们的表面轮廓均方根偏差Rq值分别为0.397 μm和0.325 μm。求解轴承接触性能时,计算区域取-2.56≤x≤2.56,-5.12≤y≤5.12和0≤z≤2.56(单位为mm),网格节点数取128×256×128,塑性应变和残余变形的收敛精度分别为10-4和10-3。
|
图 7 滚动体和内滚道表面形貌 Figure 7 Surface topographies of rolling element and inner raceway |
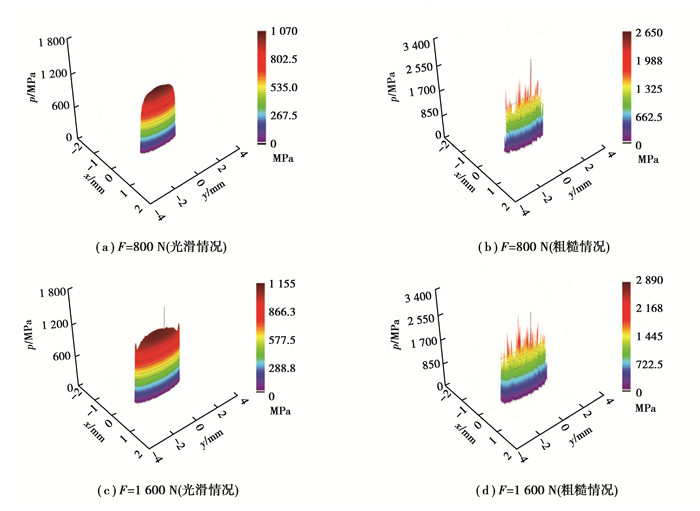
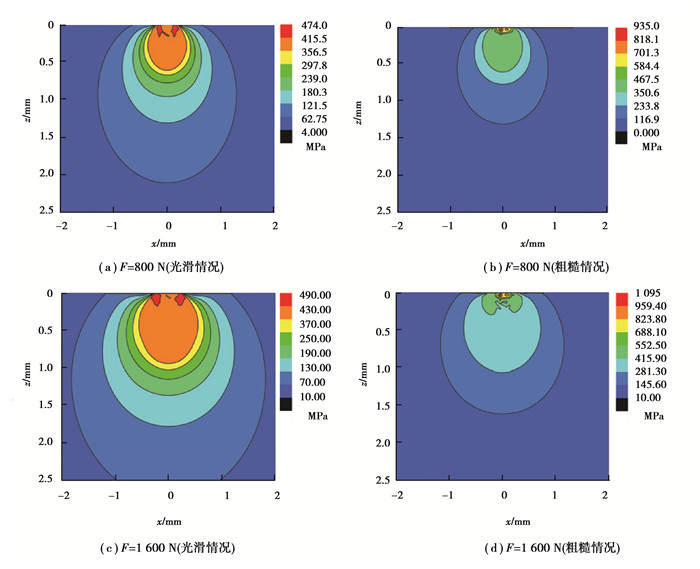
运用本弹塑性接触算法对不同载荷下滚动体与内滚道之间的弹塑性接触性能进行求解。接触压力计算结果如图 8所示。图 8(a)(b)以及图 8(c)(d)对应的外载荷F分别为800 N和1 600 N,且图 8(a)(c)中滚动体与内滚道表面光滑,图 8(b)(d)中滚动体与内滚道表面粗糙(表面形貌见图 7)。
|
图 8 不同载荷下接触压力 Figure 8 Contact pressures under different loads |
由图 8可知,无论是否考虑表面粗糙度,接触区域和最大接触压力均随着外载荷F的增大而增大。比较图 8(a)与(c)可知,光滑情况下,当载荷达到1 600 N时,椭圆接触区沿宽度方向两端点(图 2(a)所示点A,B两点)处出现局部压力峰,这是由于滚动体与滚道接触时,椭圆接触区沿宽度方向两端点优先与内滚道接触,与文献[18]所得结论一致,但文献[18]未考虑轴承塑性变形的影响。另外,对比图 8(c)和(d)可看出,轴承表面粗糙时,由于粗糙峰优先接触,椭圆接触区沿内滚道宽度方向两端点(图 2(a)所示A,B两点)处的压力峰值相对于光滑情况下减小。
此外,在图 8中,在相同载荷下,轴承表面粗糙时最大接触压力远大于表面光滑情况下的接触压力。而且由图 8(b)和(d)可以看出,粗糙情况下接触压力出现了局部波动,其峰值随载荷的增大而增大,这是由于滚动体和滚道表面上的粗糙峰引起。波动的接触压力易导致滚道发生点蚀、裂纹等失效,最终影响轴承的使用寿命。
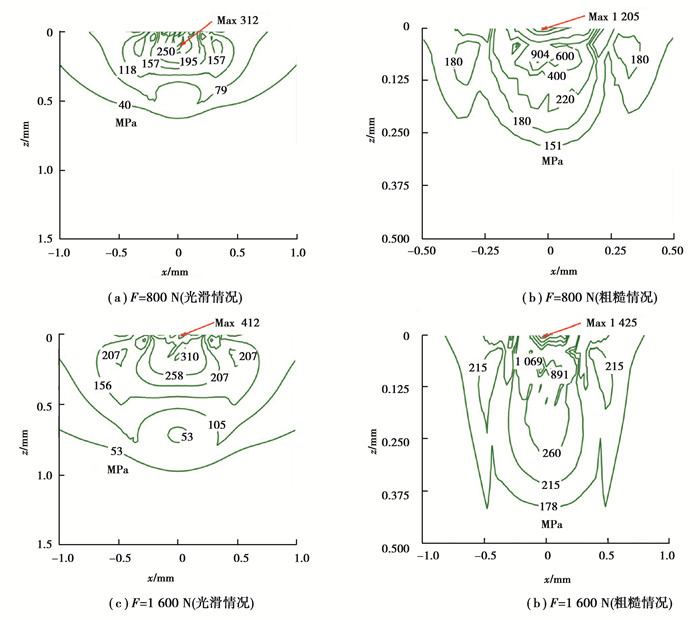
内滚道宽度方向中截面(y=0) 上von Mises应力分布如图 9所示。计算表明,无论轴承表面光滑还是粗糙,最大应力发生在次表面,与文献[19]所得结论一致。随着外载荷的增大,应力的分布区域和最大应力值均逐渐增大。对比图 9(a)(c),以及图 9(b)(d)可知,相同载荷下,粗糙情况下最大应力约是光滑时的两倍,且粗糙内滚道表面更易出现应力集中,这是由表面粗糙峰引起。
|
图 9 不同载荷下内滚道总von Mises应力(y=0) Figure 9 Total von Mises stresses of inner raceway under different loads(y=0) |
图 10给出了轴承宽度方向中截面(y=0) 上不同载荷下内滚道的残余应力分布情况。由图 10可知,轴承表面光滑和粗糙情况下对应的最大残余应力和残余应力分布区域均随载荷增大而明显增大。由图 10(a)和(c)可以看出,当滚动体和内滚道均光滑、载荷从800 N增加到1 600 N时,最大残余应力逐渐由内滚道基体向接触表面靠近。当载荷增大到超过内滚道屈服极限时,塑性应变和表面残余变形开始产生,且随载荷增大而不断增加,这点由式(14) 也可以看出。
|
图 10 不同载荷下内滚道残余应力(y=0) Figure 10 Residual stresses of inner raceway under different loads |
此外,对比图 10(b)和(a),以及图 10(d)和(c)可看出,相同载荷下,与光滑情况相比,轴承表面粗糙时的最大残余应力更大,且更容易发生残余应力集中以及不连续。且上述应力分布的不连续性随载荷增大而更加明显,因此,表面粗糙度对轴承接触性能的影响不容忽视。
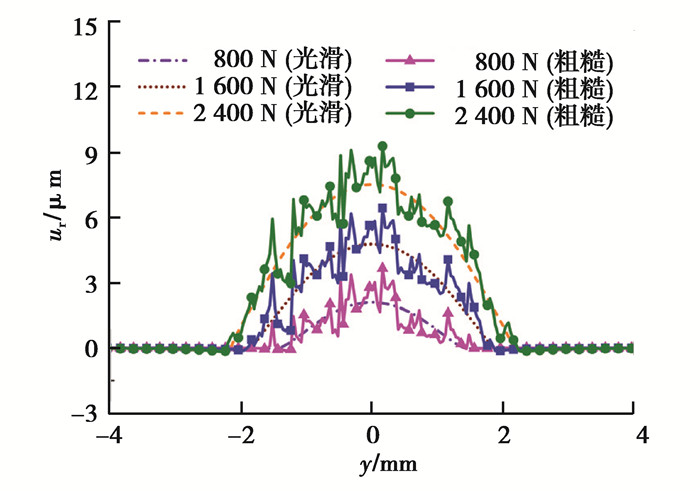
图 11给出了不同载荷下内滚道残余变形。由图可知,残余变形随载荷增大而增大,且最大残余变形发生在接触中心位置。虽然粗糙情况下的残余变形变化曲线的趋势与表面光滑情况大体一致,但前者的残余变形表现得不规则,而且变形幅值远大于后者。因此,轴承游隙设计时应考虑粗糙度的影响。
|
图 11 不同载荷下内滚道宽度方向残余变形 Figure 11 Residual deformations along inner raceway's width direction under different loads |
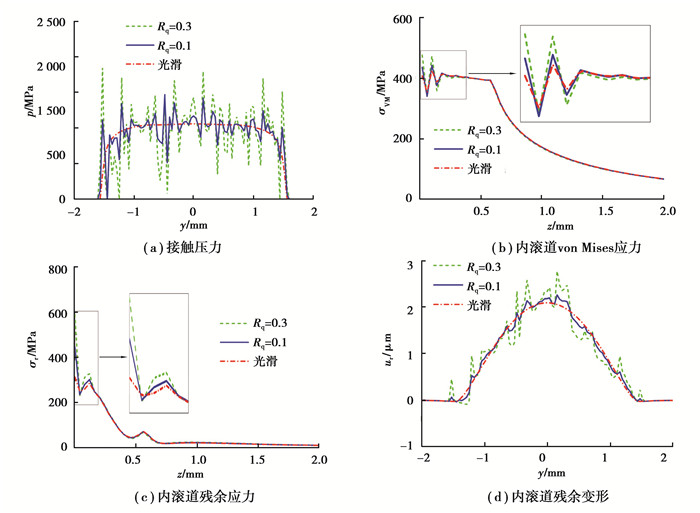
滚动体和内滚道的表面轮廓均方根偏差Rq值对轴承接触性能的影响如图 12所示,计算过程中滚动体和内滚道的表面轮廓均方根偏差取相同的值。图 12(a)为滚动体与内滚道之间沿宽度方向的接触压力,可以发现表面粗糙度导致轴承接触压力波动,且随着Rq值的增大,压力峰值增大。同时,还可看出Rq变化时,接触压力的变化趋势基本一致。由图 12(b)~(d)可以看出,与光滑情况相比,表面粗糙度也导致内滚道von Mises应力、残余应力和残余变形波动性增加。这是因为Rq值越大,滚动体和内滚道的表面轮廓线偏离轮廓中位线越严重。
|
图 12 不同均方根偏差对轴承接触性能的影响 Figure 12 Effect of different root mean square deviations on bearing's contact performances |
1) 运用半解析法求解重载粗糙轴承的弹塑性接触性能,该方法计算得到的结果与FEM计算结果吻合,且具有更高的计算效率。
2) 表面粗糙度会导致深沟球轴承中滚动体与滚道之间椭圆接触区域沿内滚道宽度方向两端点处的压力峰值减小。
3) 相同载荷作用时,粗糙情况下内滚道接触压力、von Mises应力、残余应力和残余变形均分别大于光滑情况下的值,且表面粗糙度会引起von Mises应力范围减小和残余应力范围增大。
4) 表面粗糙度导致内滚道接触压力波动,同时会导致内滚道von Mises应力和残余应力集中,以及残余应力的不连续,进而影响轴承使用寿命。
5) 研究的算例虽然有限,但所得结论仍可为深沟球轴承弹塑性接触性能研究提供有益的参考。笔者将在后续的研究中考虑滚动体与内滚道之间摩擦力作用、轴承材料热特性等因素的影响。
| [1] | Harris T A, Crecelius W J. Rolling bearing analysis (fifth edition)[M]. London: John Wiley and Sons, 2009. |
| [2] |
刘旺玉, 李静.
基于Hertz理论的深沟球轴承动态接触分析[J]. 机械设计与制造, 2011(8): 224–227.
LIU Wangyu, LI Jing. Dynamic contact analysis of deep groove ball bearing based on the theory of hertz[J]. Machinery Design and Manufacture, 2011(8): 224–227. (in Chinese) |
| [3] |
刘显军, 洪军, 朱永生, 等.
多支承轴系轴承受力与刚度的有限元迭代计算方法[J]. 西安交通大学学报, 2010, 44(11): 41–45.
LIU Xianjun, HONG Jun, ZHU Yongsheng, et al. Iterative method to solve bearing's force and stiffness for a multi-support spindle system based on finite element analysis[J]. Journal of Xi'an Jiaotong University, 2010, 44(11): 41–45. DOI:10.7652/xjtuxb201011009 (in Chinese) |
| [4] |
谢伟, 姚廷强.
深沟球轴承接触力学特性分析[J]. 机械传动, 2012(10): 78–81.
XIE Wei, YAO Tingqiang. Analysis of contact mechanics characteristic of deep groove ball bearing[J]. Mechanical Transmission, 2012(10): 78–81. (in Chinese) |
| [5] |
黄志高.
深沟球轴承接触力学特性分析[J]. 机械工程师, 2016(6): 119–120.
HUANG Zhigao. Analysis on contact mechanics characteristic of deep groove ball bearing[J]. Mechanical Engineer, 2016(6): 119–120. (in Chinese) |
| [6] |
白桂彩, 申屠留芳.
深沟球轴承动态接触特性有限元仿真分析[J]. 机械传动, 2015(2): 137–141.
BAI Guicai, SHENTU Liufang. Finite element simulation analysis of dynamic contact characteristic of deep groove ball bearing[J]. Mechanical Transmission, 2015(2): 137–141. (in Chinese) |
| [7] |
仲丛华.
曲率半径对深沟球轴承接触特性的影响[J]. 机械传动, 2016(5): 134–138.
ZHONG Conghua. Influence of the curvature radius on contact characteristic of deep groove ball bearing[J]. Mechanical Transmission, 2016(5): 134–138. (in Chinese) |
| [8] | Zhang L, Zhao X, Yan X, et al. A semi-analytical method of stress-strain analysis of buried steel pipelines under submarine landslides[J]. Applied Ocean Research, 2016, 59: 38–52. DOI:10.1016/j.apor.2016.05.007 |
| [9] | Yu C J, Wang Z J, Sun F, et al. A deterministic semi-analytical model for the contact of a wafer and a rough bi-layer pad in CMP[J]. Journal of Solid State Science and Technology, 2013, 2(9): 368–374. DOI:10.1149/2.017309jss |
| [10] | Meng F M, Zhou R, Davis T, et al. Study on effect of dimples on friction of parallel surfaces under different sliding conditions[J]. Applied Surface Science, 2010, 256(9): 2863–2875. DOI:10.1016/j.apsusc.2009.11.041 |
| [11] | Meng F M. On influence of cavitation in lubricant upon tribological performances of textured surfaces[J]. Optics and Laser Technology, 2013, 48: 422–431. DOI:10.1016/j.optlastec.2012.10.020 |
| [12] | Wang L, Wang W Z, Wang Z J, et al. Numerical study of contacts between a flat-ended punch and a half-space embedded with inhomogeneities[J]. Science China Physics Mechanics & Astronomy, 2014, 57(4): 684–697. |
| [13] | Zhou Q H, Jin X Q, Wang Z J, et al. A mesh differential refinement scheme for solving elastic fields of half-space inclusion problems[J]. Tribology International, 2016, 93: 124–136. DOI:10.1016/j.triboint.2015.09.009 |
| [14] | Wang Y L, Wang W Z, Zhao Z Q. Effect of race conformities in angular contact ball bearing[J]. Tribology International, 2016, 104: 109–120. DOI:10.1016/j.triboint.2016.08.034 |
| [15] | HuangY Y, Wang Z J, Zhou Q H. Numerical studies on the surface effects caused by inhomogeneities on torsional fretting[J]. Tribology International, 2016, 96: 202–216. DOI:10.1016/j.triboint.2015.12.028 |
| [16] |
俞黎萍, 石亦平, 刘瑞峰.
风电机组主轴承选型与设计分析[J]. 重庆大学学报, 2015, 38(1): 80–86.
YU Liping, SHI Yiping, LIU Ruifeng. Arrangement and design of main bearing for wind turbine[J]. Journal of Chongqing University, 2015, 38(1): 80–86. DOI:10.11835/j.issn.1000-582X.2015.01.011 (in Chinese) |
| [17] |
朱诚意, 吴炳新, 张志成, 等.
高品质GCr15轴承钢二次精炼过程中夹杂物的演变规律[J]. 重庆大学学报, 2015, 38(5): 89–97.
ZHU Chengyi, WU Bingxin, ZHANG Zhicheng, et al. The evolution of inclusions high quality GCr15 bearing steels during secondary refining process[J]. Journal of Chongqing University, 2015, 38(5): 89–97. DOI:10.11835/j.issn.1000-582X.2015.05.014 (in Chinese) |
| [18] |
钱璐, 王文中, 赵自强, 等.
考虑滚道表面油层分布的滚动轴承润滑分析[J]. 摩擦学学报, 2014, 34(2): 165–172.
QIAN Lu, WANG Wenzhong, ZHAO Zhiqiang, et al. Lubrication analysis for rolling bearing considering lubrication layers distribution on raceway surface[J]. Tribology, 2014, 34(2): 165–172. (in Chinese) |
| [19] | Meng F M. Effect of the cut-off frequency on rough-point and flat-surface contacts[J]. Journal of Mechanical Science and Technology, 2012, 26(9): 2889–2901. DOI:10.1007/s12206-012-0712-0 |
 2017, Vol. 40
2017, Vol. 40


