现代工业生产中,高效率、高精密零部件加工市场的需求量日益增加。在数控机床所有误差源中,热误差的比例高达40%~ 70%[1-2],成为影响机床加工精度的主要因素。因此,有效检测及补偿机床热误差是提高数控机床加工精度的重要手段。
近年来,国内外专家在机床热误差的降低和补偿上做了大量研究,并提出诸多改善机床热误差的方法,这些方法主要是从两个方向出发:1) 通过改善机床机构设计、零部件制造工艺、机身工作热量的散除,整体上降低机床加工时各部件温度变化及温度升降不均等情况;2) 通过对机床热误差的检测与分析,运用一定的数学计算方法建立热误差的产生模型,对实际加工中所产生的热误差进行预测并补偿,以满足机床的高精度要求[3]。Abdulshahed等[4]提出了自适应神经模糊推理系统(ANFIS)来计算机床各部分温度变化与机床热误差大小间的模糊逻辑关系,以此建立机床热误差预测模型;Lee[5]等将神经网络技术运用在机床热误差模型的建立上,该方法通过对一段时间内的机床热误差序列来预测下一时刻机床热误差的大小。文献[6]对机床主轴系统进行有限元热分析,根据机床温度场瞬态变化情况来预测机床热误差大小。此外,常用在机床热误差建模上的数学理论有:基于传统灰色系统的改进GM(1, 1) 模型[7],最小二乘法[8],多元线性回归[9]及时序分析等[7]。基于这些理论的建模在实际生产中已取得一定的成果,但仍然存在一些预测结果波动大、稳定性差,预测方式跟机床实际运行状况关联性差[5]等问题。
灰色系统模型在处理热误差建模普遍存在的不确定性和随机现象具有非常重要的的指导意义。灰色系统理论以微分方程为工具,能够反映事物发展的本质,不需要对预测系统有明确的了解,其研究数据可以随机产生,因此相对传统统计研究方法具有能够研究小样本、贫信息、任意分布数据的优点[7]。机床加工热误差的影响因素多而杂,具有明显的灰色性,利用灰色系统的基本理论,可以根据现场检测的热误差数据,建立灰色系统模型,并检测所建模型的预测精度,最终对机床热误差实行补偿,以满足机床加工高精度的要求。笔者采用灰色系统GM(1, 4) 建立机床的热误差补偿模型,在避免以上算法不足的同时保证机床热误差预测精度。
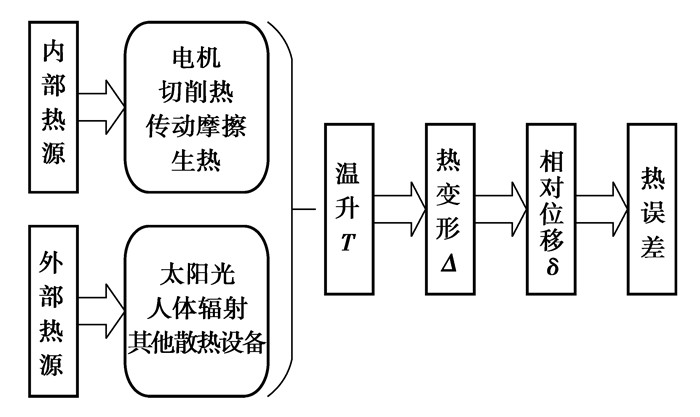
1 机床热误差分析 1.1 机床热误差产生机理数控机床在工作过程中,电主轴中电动机的耗散发热和轴承的摩擦发热是不可避免的[10],各零部件因为受不同热源影响,散热条件不一,产生相对温度差异,相应零部件会产生热变形,由此而产生机床热误差。数控机床的热源主要分为两大类:外部热源和内部热源[11]。外部热源是指机床所在环境中温度条件,主要包括日照辐射、人类活动及车间其他散热装置;内部热源则是指机床在工作过程中自身产生的热量,主要包括电机功率损耗、切削热与运动副摩擦产生的热量。机床加工过程中,内、外热源共同作用,机床各部件通过热传导、热对流和热辐射3种方式进行热交换。由于机床结构中各零部件形状各异、约束条件不同,引起了胀、弯曲和收缩等热变形现象,并最终导致为刀具与被加工零件间的相对运动关系发生改变,机床加工精度下降。数控机床热误差产生机理如图 1所示。
|
图 1 机床热误差产生机理 Figure 1 Mechanism of thermal error of machine tool |
灰色GM(1, 4) 模型,以选定测点温度值为自变量,通过模型方程来预测对应条件下的热误差大小,因此合理地布置温度传感器对模型的预测精度、效率和鲁棒性至关重要。从辨识效率上考虑,传感器数目越多,布置的引线就越多,会给实验的测量带来极大不便,所耗费的采集时间与数据处理时间也会相应增加,不利于模型的补偿效率。从模型预测的精度上考虑,温度传感器太少,不能准确及时获取关键点的温度数据;传感器过多,会带来更多的测量过程中的干扰误差,从经济上考虑,传感器过多也会造成经济上的浪费。因此在建立模型方程之前,需要根据实际加工过程中机床各测温点的温度变化与机床热误差的变化情况,对测温点的数目和位置进行优化。
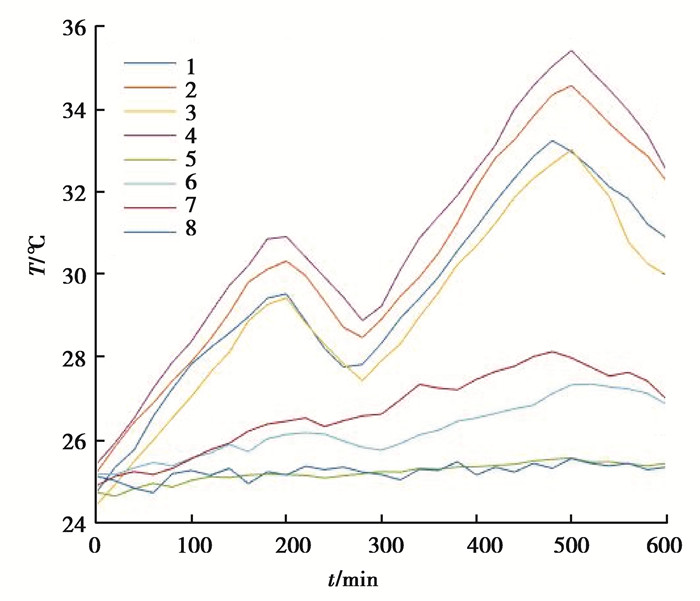
实验以精密卧式加工中心THM6380为研究对象,要从事先选择的8个温度测量点中(分别为:机床立柱、主轴、底座、主轴箱、冷却液、机床床身、导轨和环境温度),确定数个与热误差相关性较大的测量点。实验过程中,让机床处于空切状态,环境温度为25℃,数据采集周期设定为20 min,机床主轴转速设置为1 500 r/min,整个实验时间为10 h,机床的工作过程为空切3.5 h,停机1.5 h,再空切3.5 h,最后停机1.5 h。整个实验过程共检测了30组温度数据,并根据所测数据绘得折线图如图 2所示。
|
图 2 各温度测量点温度随时间变化折现图 Figure 2 The temperature of each temperature measurement point with time line chart 1.机床立柱温度; 2.主轴温度; 3.底座温度; 4.主轴箱温度; 5.冷却液温度; 6.机床床身温度; 7.导轨温度; 8.环境温度 |
笔者利用灰色理论建立灰色关联模型,分析温度变化曲线,找出各测量点中温度变化与热变形之间相关系数较大的点,去掉相关系数较小的温度点,得到最终热误差模型的温度测量点。各温度测量点的关联度计算如下[12]。
1) 根据灰色关联度计算理论,由8个温度传感器采集得来的数据序列与一组标准序列组成评价指标体系,形成的聚成为
| $ ({{\mathit{\boldsymbol{X}}}_{0}}, {{\mathit{\boldsymbol{X}}}_{1}}, \cdots, {{\mathit{\boldsymbol{X}}}_{8}})=\left[\begin{matrix} {{x}_{0}}\left( 1 \right)~ & {{x}_{1}}\left( 1 \right) & \cdots & {{x}_{8}}\left( 1 \right) \\ {{x}_{0}}\left( 2 \right) & {{x}_{1}}\left( 2 \right) & \cdots & {{x}_{8}}\left( 2 \right) \\ \vdots & \vdots & {} & \vdots \\ {{x}_{0}}\left( n \right) & {{x}_{1}}\left( n \right) & \cdots & {{x}_{8}}\left( n \right) \\ \end{matrix} \right], $ | (1) |
式中n为个数据序列的数据个数。其中
X0=(x0(1), x0(2), …,x0(n))T为标准数据序列,此处X0数据列为机床Z轴方向的热误差值;Xi=(xi(1), xi(2), …,xi(n))T,(i=1, 2, …, 8) 为相应8个温度传感器所采集的温度序列值。该矩阵最终计算得到的关联系数即为各温度测量点的温度变化情况与Z轴方向误差变化情况的关联度大小。
2) 用均值化法对所有数据进行无量纲化,并凸显各数据序列的变化趋势,令
| $ {{{{x}'}}_{i}}\left( k \right)=\frac{{{x}_{i}}\left( k \right)}{\frac{1}{n}\sum\limits_{k=1}^{n}{{{x}_{i}}\left( k \right)}}\left( k=1, 2, \cdots, n \right)。$ | (2) |
将式(2) 所述运算方法运用于式(1) 中每个数据列,可得如下矩阵:
| $ (\mathit{\boldsymbol{x}}{{^{\prime} }_{0}}, \mathit{\boldsymbol{x}}{{^{\prime} }_{1}}, \cdots, \mathit{\boldsymbol{x}}{{^{\prime} }_{8}})=\left[\begin{matrix} x{{^{\prime} }_{0}}\left( 1 \right) & x{{^{\prime} }_{0}}\left( 1 \right) & \cdots & x{{^{\prime} }_{8}}\left( 1 \right) \\ x{{^{\prime} }_{0}}\left( 2 \right) & x{{^{\prime} }_{1}}\left( 2 \right) & \cdots & x{{^{\prime} }_{8}}\left( 2 \right) \\ \vdots & \vdots & {} & \vdots \\ x{{^{\prime} }_{0}}\left( n \right) & x{{^{\prime} }_{1}}\left( n \right) & \cdots & x{{^{\prime} }_{8}}\left( n \right) \\ \end{matrix} \right]。$ | (3) |
3) 分别计算每一温度测量点的温度序列与标准数据列中对应元素的绝对差值,令
| $ \begin{align} & {{\Delta }_{i}}\left( k \right)=\left| x{{^{\prime} }_{0}}\left( k \right)-x{{^{\prime} }_{i}}\left( k \right) \right|, \\ & m=\underset{i=1}{\overset{n}{\mathop{\rm{min}}}}\, \underset{k=1}{\overset{8}{\mathop{\rm{min}}}}\, \left| x{{^{\prime} }_{0}}\left( k \right)-x{{^{\prime} }_{i}}\left( k \right) \right|, \\ & M=\underset{i=1}{\overset{n}{\mathop{\rm{max}}}}\, \underset{k=1}{\overset{8}{\mathop{\rm{max}}}}\, \left| x{{^{\prime} }_{0}}\left( k \right)-x{{^{\prime} }_{i}}\left( k \right) \right|。\\ \end{align} $ |
4) 逐个计算各比较序列与标准序列对应元素的关联系数:
| $ r(x{{^{\prime} }_{0}}\left( k \right), x{{^{\prime} }_{i}}\left( k \right))=\frac{m+\xi \cdot M}{{{\Delta }_{i}}\left( k \right)+\xi \cdot M}, $ | (4) |
式中ξ为分辨系数,ξ在此取值为0.5。ξ越小,关联系数间的差异越大,区分能力越强。根据式(4) 计算各温度测量点的序列与标准参考序列的关联度为
| $ r({{\mathit{\boldsymbol{X}}}_{0}}, {{\mathit{\boldsymbol{X}}}_{i}})=\frac{1}{n}\sum\limits_{k=1}^{n}{{{r}_{0i}}}\left( k \right)。$ |
5) 代入数值计算各温度测量点温度序列值与标准参考序列的关联度,计算结果为
R=[0.672 0.676 0.671 0.678 0.637 0.645 0.646 0.635]。
选择其中关联系数大于0.650的测量点,即可选定4个关联度较大的温度测量点,它们是T1 (机床立柱温度),T2(机床主轴温度),T3(机床底座温度),T4(主轴箱温度)。
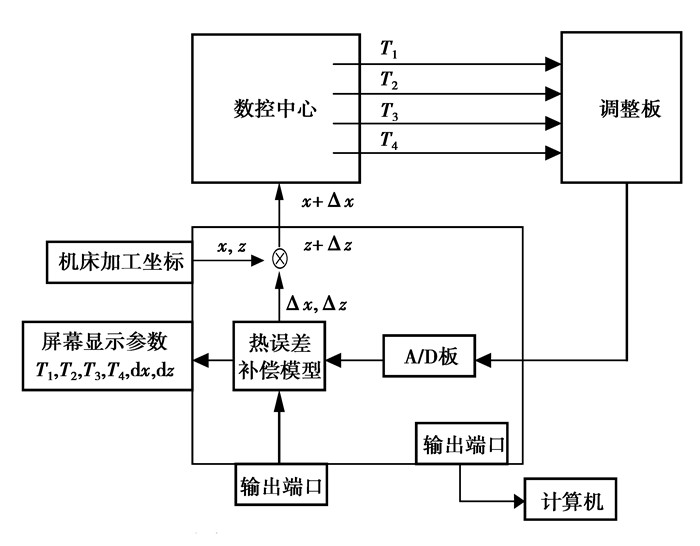
1.3 机床热误差补偿系统根据上一节温度检测点的优化可知,补偿系统需设置4个温度传感器在机床4个关键温度点上。温度传感器以固定频率采集温度信号,经过调整板放大后,再经过A/D转换板进入数控系统[13]。数控系统中预先植入灰色GM(1, 4) 模型,可以根据传入温度拟合得出机床X、Z方向的补偿值,并通过机床控制器对切削加工进行实时修正热变形造成的误差。对于试验机床THM6380,Z方向热误差较X方向热误差更加显著,故仅取机床Z方向误差作为模型补偿对象。机床热误差补偿系统工作过程如图 3所示。
|
图 3 机床热误差补偿系统 Figure 3 Thermal error compensation system for machine tool |
灰色GM(1, 1) 模型及其改进模型近年来在热误差预测与补偿方面运用较为广泛。该模型是通过机床某一方向(X方向或Z方向)热误差元素自身时序数据来建立模型,而忽略考量机床关键升温点与热误差大小的关系。笔者采用灰色GM(1, 4) 模型,综合分析4个关键点温度测量点与热误差元素之间的内在数学关系,建立机床各部位温度变化与机床热误差的映射关系,更加准确地预测机床热误差值的大小。
灰色系统模型的建立需要对原始数据序列进行一定的运算处理,以减弱其随机性并凸显数据列的变化趋势,这里首先对各种运算形式进行定义[14-15]。
设X(0)=(x(0)(1), x(0)(2), …, x(0)(n))为原始序列,则其一阶累加生成(1—AGO)序列定义为X(1)=(x(1)(1), x(1)(2), …, x(1)(n)),其中
序列X(1)的紧邻均值生成序列Z(1),定义为Z(1)=(z(1)(2), z(1)(3), …z(1)(n)),其中z(1)(n)=(x(1)(n)+x(1)(n-1))/2,x(1)(n)为原始序列X(0)的相应一阶累加生成值。
根据以上定义,设x1(0)为机床Z方向各个温度情况下对应热误差序列值,xj(0)(j=2, 3, 4, 5) 为所选4个关键温度测量点的温度序列值。建立GM(1,4) 方程为:
| $ x_{_{1}}^{^{(0)}}\left( k \right)+az_{_{1}}^{^{(1)}}\left( n \right)=\sum\limits_{j=2}^{5}{{{b}_{j}}}x_{_{j}}^{^{(1)}}。$ | (5) |
该模型方程即建立了4个关键温度测量点的温度值与机床Z方向热误差值的函数关系,式(5) 中,a和bj构成系数矢a=[a b2 b3 b4 b5]T,根据最小二乘法可得模型系数矢量方程a=(BTB)-1BTY,其中:
| $ \mathit{\boldsymbol{B=}}\left[\begin{matrix} -z_{_{1}}^{^{(1)}}\left( 2 \right) & x_{_{2}}^{^{(1)}}\left( 2 \right) & \cdots & x_{_{5}}^{^{(1)}}\left( 2 \right) \\ -z_{_{1}}^{^{(1)}}\left( 3 \right) & x_{_{2}}^{^{(1)}}\left( 3 \right) & \cdots & x_{_{5}}^{^{(1)}}\left( 3 \right) \\ \vdots & \vdots & {} & \vdots \\ -z_{_{1}}^{^{(1)}}\left( n \right) & x_{_{2}}^{^{(1)}}\left( n \right) & \cdots & x_{_{5}}^{^{(1)}}\left( n \right) \\ \end{matrix} \right], \mathit{\boldsymbol{Y=}}\left[\begin{matrix} x_{_{1}}^{^{(0)}}\left( 2 \right) \\ x_{_{1}}^{^{(0)}}\left( 3 \right) \\ \vdots \\ x_{_{1}}^{^{(0)}}\left( n \right) \\ \end{matrix} \right]。$ |
该其近似时间响应为:
| $ \hat{x}_{1}^{^{(1)}}(n+1)=\left[x_{1}^{(0)}(1)-\frac{1}{a}\sum\limits_{j=2}^{5}{bj}x_{j}^{(1)}(n+1) \right]{{e}^{-an}}+\frac{1}{a}\sum\limits_{j=2}^{5}{bj}x_{j}^{(1)}(n+1)。$ | (6) |
将GM(1, 4) 模型的系数矢量代入式(6) 计算可得
| $ \hat{x}_{1}^{^{(0)}}(n+1)=\hat{x}_{1}^{^{(1)}}(n+1)-\hat{x}_{1}^{^{(1)}}(n)。$ | (7) |
该模型为包含倒数运算的动态模型,可以根据机床选定温度测量点的温度值来预测机床热误差的大小。
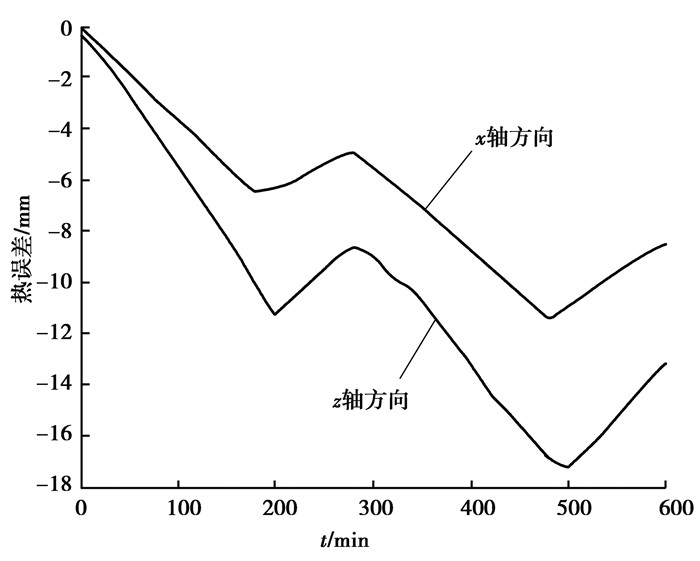
3 机床实验及模型验证 3.1 机床实验实验采用四川普什宁江机床厂生产的THM6380精密卧式加工中心。根据第1节中温度测量点的灰色关联度计算,在机床上已选定的4个温度测量点处安装温度传感器。设定机床处于空切状态,环境温度为25 ℃,数据采集周期设定为20 min,机床转速设置为1 500 r/min,整个实验时间为10 h,机床的工作过程为空切3.5 h,停机1.5 h,再空切3.5 h,最后停机1.5 h。实验过程中,让机床间断性启动与停机,是为了更好地检测与验证机床各测温点温度裱花情况与机床热误差大小之间的关系。根据本文第1节温度测量点位置优化可知,冷却液的温度变化对机床热误差值得影响较小,基本可以忽略,即实切过程产生的热对加工过程中刀具与工件的相对位置几乎没有影响,因此实验仅让机床处于空切状态。整个实验过程中,共检测了30组机床热误差数据,并根据所测数据绘得折线图如图 4所示。
|
图 4 机床热误差变化折线图 Figure 4 Machine tool thermal error change line chart |
根据实验所得数据,将其代入第2节中GM(1, 4) 模型的运算方程,计算可得:
| $ \mathit{\boldsymbol{\hat{a}=}}{{\left[-0.1471\ -0.8238\ -1.5313\ \ 1.122\ \ 1.2222 \right]}^{\rm{T}}}。$ | (7) |
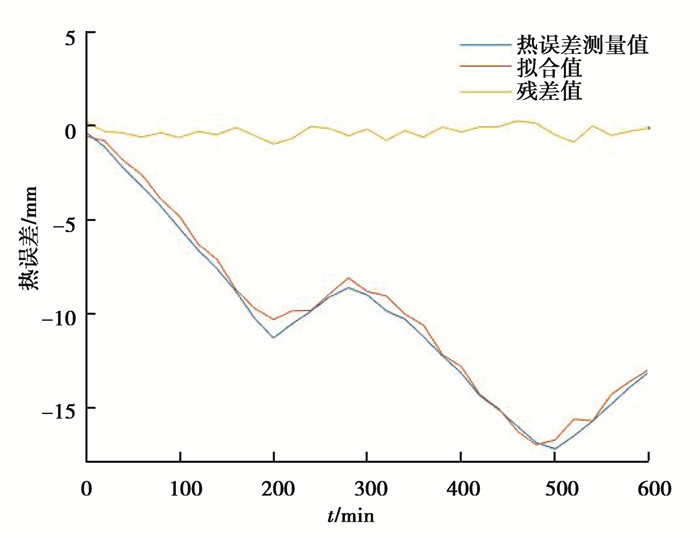
将各系数值代入式(7) 可得到灰色系统机床热误差拟合模型。对比热误差拟合值与实际热误差值,并计算两者之间的残差值,得到图 5所示对比效果。由图可知:该模型对于机床热误差的拟合残差基本围绕零轴分布,残差的大小在±1 μm以内,拟合效果较为理想[16-17]。
|
图 5 机床热误差模型拟合效果对比图 Figure 5 Comparison of Fitting Results of Machine Thermal Error Model |
将本文所用的GM(1, 4) 预测模型预测结果,与文献[18]中运用到的BP神经网络预测模型及文献[19]中运用到的改进GM(1, 1) 预测模型进行对比,可得各模型残差统计数据如表 1所示。可知,由于GM(1, 4) 预测模型为动态模型,基于机床实际生产运作情况来预测机床实际的热误差,预测结果更加精确。
| 表 1 不同补偿方法的补偿结果对比 Table 1 Comparison of compensation results of different compensation methods |
笔者通过灰色GM(1, 4) 预测模型,建立了机床热误差与各关键测温点的映射关系。该模型能够动态实时预测机床的热误差值, 相对于仅考虑热误差本身随时间变化的时间序列内部关系的预测方法(如GM(1, 1)、BP神经网络),具有更好的预测效果。灰色模型预测可根据不同实验对象的物理结构、加工精度选择不同数目的温度测量点,以建立与之相应的灰色补偿模型。因时间和资源等方面的限制,仅考虑了机床温度变化对加工精度的影响,后续研究可将加工应力、机床振动等因素加入到该补偿模型中,以更大程度地提高机床加工精度。
| [1] |
王海同, 李铁民, 王立平, 等.
机床热误差建模研究综述[J]. 机械工程学报, 2015, 51(9): 119–128.
WANG Haitong, Li Tiemin, Wang Liping, et al. Review on thermal error modeling of machine tools[J]. Journal of Mechanical Engineering, 2015, 51(9): 119–128. (in Chinese) |
| [2] |
张根保, 刘杰, 高琦樑, 等.
多台数控机床不完全维修的可靠性评估[J]. 重庆大学学报, 2014, 37(2): 1–6.
Zhang Genbao, Liu Jie, Gao Qiliang, et al. Reliability assessment of mulity NC machine Tools with imperfect repair[J]. Journal of Chongqing University, 2014, 37(2): 1–6. DOI:10.11835/j.issn.1008-5831.2014.02.001 (in Chinese) |
| [3] | Ramesh R, Mannan M A, Poo A N. Error compensation in machine tools-a review:Part Ⅱ:thermal errors[J]. International Journal of Machine Tools and Manufacture, 2000, 40(9): 1257–1284. DOI:10.1016/S0890-6955(00)00010-9 |
| [4] | Abdulshahed A, Longstaff A P, Fletcher S, et al. The application of ANFIS prediction models for thermal error compensation on CNC machine tools[J]. Applied Soft Computing, 2015, 27: 158–168. DOI:10.1016/j.asoc.2014.11.012 |
| [5] | Lee J, Kramer B M. Analysis of machine degradation using a neural network based pattern discrimination model[J]. Journal of Manufacturing Systems, 1993, 12(5): 379–387. DOI:10.1016/0278-6125(93)90306-E |
| [6] | Han J, Wang L, Wang H, et al. A new thermal error modeling method for CNC machine tools[J]. International Journal of Advanced Manufacturing Technology, 2012, 62(1/2/3/4): 205–212. |
| [7] | Abdulshahed A, Longstaff A P, Fletcher S, et al. Application of GNNMCI(1, N) to environmental thermal error modelling of CNC machine tools[C]//The the 3rd International Conference on Advanced Manufacturing Engineering and Technologies, Stockholm, 2013:253-262. |
| [8] | Zhang T, Ye W H, Liang R J, et al. Temperature variable optimization for precision machine tool thermal error compensation on optimal threshold[J]. Chinese Journal of Mechanical Engineering, 2013, 26(1): 158–165. DOI:10.3901/CJME.2013.01.158 |
| [9] |
姜辉. 五轴数控机床几何与热误差实时补偿关键技术及其试验研究[D]. 上海: 上海交通大学, 2014. JIANG Hui. Key technologies and experimental research of real-time compensation for geometrical and thermal errors of five-axis CNC machine tool[D]. Shanghai:Shanghai Jiao Tong University, 2014. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10248-1015807782.htm |
| [10] |
刘飞, 徐宗俊.
机床主传动系统能量传输数学模型[J]. 重庆大学学报(自然科学版), 1990, 13(2): 13–19.
LIU Fei, Xu Zongjun. Energy transmission mathematical models of main driving system of machine tools[J]. Journal of Chongqing University (Natural Science Edition), 1990, 13(2): 13–19. (in Chinese) |
| [11] | Tan B, Mao X, Liu H, et al. A thermal error model for large machine tools that considers environmental thermal hysteresis effects[J]. International Journal of Machine Tools and Manufacture, 2014, 82/83(7): 11–20. |
| [12] | Velmurugan T. Performance based analysis between k-Means and Fuzzy C-Means clustering algorithms for connection oriented telecommunication data[J]. Applied Soft Computing, 2014, 19(6): 134–146. |
| [13] | Rizal M, Ghani J A, Nuawi M Z, et al. Online tool wear prediction system in the turning process using an adaptive neuro-fuzzy inference system[J]. Applied Soft Computing, 2013, 13(4): 1960–1968. DOI:10.1016/j.asoc.2012.11.043 |
| [14] |
张成新, 高峰, 李艳.
基于实时反馈的机床热误差在线补偿模型[J]. 中国机械工程, 2015, 26(3): 361–365.
ZHANG Chengxin, GAO Feng, LI Yan. On-ling compensation model based on real-time feedback thermal errors of machine tools[J]. China Mechanical Engineering, 2015, 26(3): 361–365. (in Chinese) |
| [15] |
王乾俸, 张松, 陈舟, 等.
基于指数函数的机床主轴热误差补偿模型[J]. 计算机集成制造系统, 2015, 21(6): 1553–1558.
WANG Qiangfeng, ZHANG Song, CHEN Zhou, et al. Thermal error compensation model of machine spindle based on exponential function[J]. Computer integrated manufacturing system, 2015, 21(6): 1553–1558. (in Chinese) |
| [16] |
苗恩铭, 龚亚运, 徐祗尚, 等.
数控机床热误差补偿模型稳健性比较分析[J]. 机械工程学报, 2015(7): 130–135.
MIAO Enming, GONG Yayun, XU Zhishang, et al. Comparative analysis of thermal error compensation model robustness of CNC machine tools[J]. Journal of Mechanical Engineering, 2015(7): 130–135. (in Chinese) |
| [17] |
曹华军, 杜彦斌, 刘飞.
机床再制造综合测试与评价支持系统的开发及应用[J]. 重庆大学学报:自然科学版, 2009, 32(11): 1262–1267.
CAO Huajun, DU Yanbin, LIU Fei. Development and evaluation system for machine tool remanufactruing[J]. Journal of Chongqing University, 2009, 32(11): 1262–1267. (in Chinese) |
| [18] |
张毅, 杨建国.
基于灰色神经网络的机床热误差建模[J]. 上海交通大学学报, 2011, 45(11): 1581–1586.
ZHANG Yi, YANG Jianguo. Grey neural network modeling for machine tool thermal error[J]. Journal of Shanghai Jiao Tong University, 2011, 45(11): 1581–1586. (in Chinese) |
| [19] |
李永祥, 杨建国.
灰色系统模型在机床热误差建模中的应用[J]. 中国机械工程, 2006, 17(23): 2439–2442.
LI Yongxiang, YANG Jiangguo. Application of grey system model to thermal error modeling on machine tools[J]. China Mechanical Engineering, 2006, 17(23): 2439–2442. DOI:10.3321/j.issn:1004-132X.2006.23.005 (in Chinese) |
 2017, Vol. 40
2017, Vol. 40


