近年来,随着电商行业的迅猛发展,快递业务量也迎来高速增长期,2015年快递业完成业务量206.6亿件,同比增长48%。中国的物流总费用占GDP的比重为18%左右,比世界平均水平高出约6.5个百分点。城市配送是电商供应链中成本最高、效率最低的一环,成为制约电商发展的瓶颈[1]。究其原因,一方面,网购客户分布不集中,需求量小、频次高等特点增加了城市物流配送的复杂性;另一方面,快递独立进行城市配送导致资源的浪费,高频次、小批量的配送难以产生规模效益。因此,快件的城市集约化配送已成为学者和业界关注的热点问题,共同配送和同时取送货成为实现商品集约化配送的有效途径。
为了降低共同配送成本,需要解决联盟配送车辆的路径(VRP)优化问题,路径问题最早是由Dantzig和Ramser进行研究,可以按照车型、配送中心数量、任务、时间约束等进行分类[2]。Aghezzaf等[3]研究了单车型的路径优化问题,Kovacs等[4]研究了考虑车辆容量限制的多目标车辆路径优化问题,Xiao等[5]研究了多目标绿色车辆路径优化问题,Spliet等[6]研究了基于离散时间窗的路径优化问题,王勇等[7]研究了基于道路交通条件、车辆承载能力等条件下的车辆调度问题,王征等[8]研究了带二维装箱约束的物流配送车辆路径问题。分析发现,以上研究都没有考虑到车辆的同时取送货任务,并且把车辆在不同节点之间的单位运输成本设置为定值不符合实际应用需求。
VRP问题是多目标、多约束的组合优化问题,属于NP难题,该问题求解方法可分为精确式算法和启发式算法[9]。常用的精确式算法有分支定界法[10]、动态规划[11]、拉格朗日松弛法[12]等。越来越多的学者采用启发式算法求解VRP问题:张景玲等[13]提出了混合2-OPT量子进化算法求解多车型开放式动态需求的车辆路径问题,唐金环等[14]采用改进的多目标粒子群优化算法求解时变网络下考虑碳排放的车辆路径优化问题。
笔者打破传统独立配送的模式,假设多家快递企业组成城市共同配送联盟,同时考虑客户的取货和送货需求,把不同运输节点之间单位运输成本看作动态变化的过程,建立配送节点之间的单位配送成本与车辆载货量之间的函数关系,构建考虑同时取送货的城市共同配送路径优化模型,并针对模型的特点设计了改进的遗传算法,最后通过算例对模型及算法的有效性进行验证。
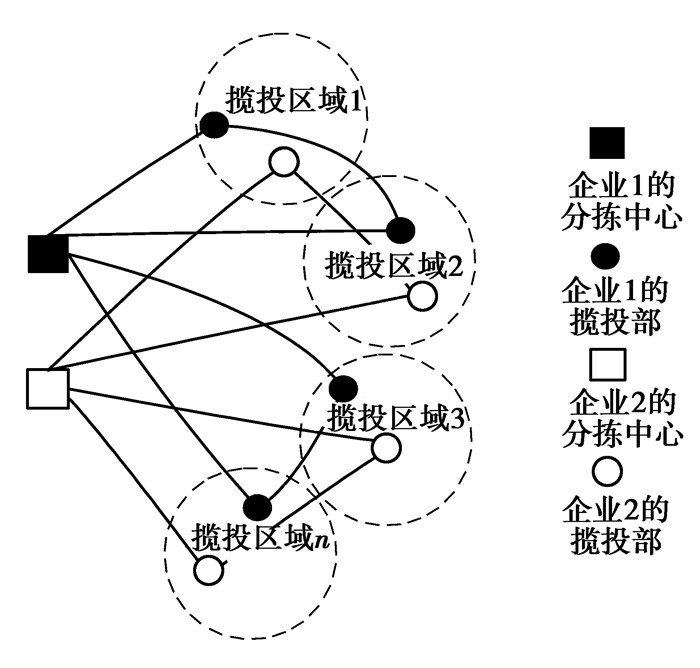
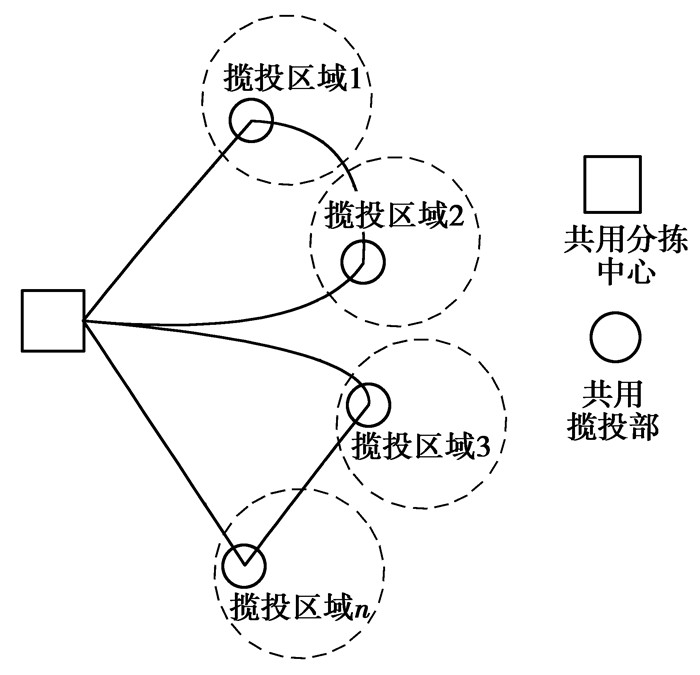
1 问题描述假设有m家快递企业n个区域进行揽投部布局,在独立配送网络中(如图 1),各家快递企业都有独立的分拣中心,在各个区域都有独立的揽投部,每个企业的配送车辆从其分拣中心出发,依次完成各个揽投区域的配送任务后再返回其分拣中心。从城市快递的整体配送网络来看,在同一个区域存在多个揽投部,这就造成了网点的重复建设,使整体的配送效率降低,而且各个企业独立配送会使车辆空载严重,投入的车辆数量也会增加。如果快递企业组成城市共同配送联盟,共用一个分拣中心,并且把各个区域内的揽投部进行集并进行共同配送(如图 2),车辆从分拣中心出发到各个揽投区域同时进行配送和揽收任务,根据各个区域的总配送量、揽收量优化车辆的路径,降低各家快递企业的配送成本。
|
图 1 独立配送示意图 Figure 1 Independent distribution |
|
图 2 共同配送示意图 Figure 2 Joint distribution |
考虑同时取送货的城市快递共同配送路径优化可定义如下:配送联盟的共用分拣中心位置已知,各家快递企业的揽投部位置已知,每个揽投部的日均配送、揽收货物量已知,不同快递企业的配送物品可以混装,车辆从共同分拣中心出发,依次到各个共用揽投部同时完成取送货任务后返回该分拣中心。模型首先要对各个区域内配送联盟各家快递企业的揽投部进行集并,然后再对车辆的配送路径进行优化。
为突出主要问题又不失一般性,构建模型需做如下假设:1) 共用分拣中心的容量可以满足揽投部的需求;2) 车辆所配送的客户的总需求量不能超过车辆的最大装载量;3) 车辆的配送距离不能超过其最大行驶距离。
2 模型构建 2.1 揽投部的集并设第i个区域内第j家快递企业的坐标为(xij, yij),送货量为dij,取货量为pij,则在第i个区域内总的配送需求为:
| $ {{x}_{i}}=\frac{\sum\limits_{j=1}^{m}{{{x}_{ij}}\left( {{d}_{ij}}+{{p}_{ij}} \right)}}{{{d}_{i}}+{{p}_{i}}}, {{y}_{i}}=\frac{\sum\limits_{j=1}^{m}{{{y}_{ij}}\left( {{d}_{ij}}+{{p}_{ij}} \right)}}{{{d}_{i}}+{{p}_{i}}}。$ | (1) |
在实际配送过程中,配送车辆的油耗主要取决于配送车辆的行程和装载量,车辆的装载率与装载量是正相关的,因此可以用车辆的装载率和车辆行程与油耗成本之间的函数关系计算油耗成本。记eik为车辆k在第i段运输距离中实载率,qijk为任意车辆k访问完区域i的共用揽投部后在访问区域j的共用揽投部之前的装载量,则
| $ {{c}_{ik}}={{e}_{{\rm{o}}k}}+{{e}_{ik}}({{e}_{1k}}-{{e}_{{\rm{o}}k}}), $ | (2) |
式中:eok为车辆k空载时单位距离油耗;e1k为车辆k满载时单位距离油耗。车辆k在第i段运输中的行程为sij,则车辆k在第i段的总油耗成本为:
| $ {{c}_{\rm{T}}}={{s}_{ij}}[{{e}_{{\rm{o}}k}}+{{e}_{ik}}({{e}_{1k}}-{{e}_{{\rm{o}}k}})], $ | (3) |
现有的有关VRP的文献很少考虑逆向物流,这里在共同配送的背景下,建立模型时不仅考虑到车辆的送货任务,同时也考虑了车辆的揽货任务。该模型目标为系统总成本最小,模型如下:
| $ Min\ F=\sum\limits_{j\in {{N}_{\rm{D}}}}{\sum\limits_{k\in K}{{{F}_{\rm{k}}}{{x}_{{\rm{o}}jk}}}}+\sum\limits_{i\in N}{\sum\limits_{j\in N}{\sum\limits_{k\in K}{{{s}_{ij}}}}}\left[{{e}_{0k}}+\frac{{{q}_{ijk}}}{{{C}_{k}}}({{e}_{1k}}-{{e}_{0k}}) \right]{ }{{x}_{ijk}}, $ | (4) |
| $ \text{st}:\sum\limits_{k\in K}{\sum\limits_{i\in N}{{{x}_{ijk}}}=1}, \forall j\in {{N}_\text{D}}, $ | (5) |
| $ \sum\limits_{i\in N}{{{x}_{ijk}}}-\sum\limits_{i\in N}{{{x}_{jik}}}=0, \forall j\in {{N}_{\rm{D}}}, k\in K, $ | (6) |
| $ \sum\limits_{j\in N}{{{x}_{ijk}}}={{h}_{ik}}, \forall i\in {{N}_{\rm{D}}}, k\in K, $ | (7) |
| $ \sum\limits_{i\in N}{{{x}_{ijk}}}={{h}_{jk}}, \forall j\in {{N}_{\rm{D}}}, k\in K, $ | (8) |
| $ \sum\limits_{i\in {{N}_{\rm{D}}}}{{{x}_{{\rm{o}}ik}}}+\sum\limits_{i\in {{N}_{\rm{D}}}, i\ne j}{{{x}_{ijk}}}\le 2, \forall j\in {{N}_{\rm{D}}}, \forall k\in K, $ | (9) |
| $ \sum\limits_{j\in {{N}_{\rm{D}}}}{{{x}_{{\rm{o}}jk}}}\le 1, \forall k\in K, $ | (10) |
| $ \sum\limits_{j\in {{N}_{\rm{D}}}}{{{x}_{j{\rm{o}}k}}}\le 1, \forall k\in K, $ | (11) |
| $ {{q}_{oik}}=\sum\limits_{j\in {{N}_{\rm{D}}}}{{{d}_{j}}{{h}_{jk}}}, \forall k\in K, i\in {{N}_{\rm{D}}}, $ | (12) |
| $ {{q}_{iok}}=\sum\limits_{j\in N}{{{p}_{j}}{{h}_{jk}}}, \forall k\in K, i\in {{N}_{\rm{D}}}, $ | (13) |
| $ \sum\limits_{i\in N}{{{q}_{ijk}}}-{{d}_{j}}=\sum\limits_{i\in N}{{{q}_{jik}}}-{{p}_{j}}, \forall k\in K, j\in {{N}_{\rm{D}}}, $ | (14) |
| $ {{q}_{ijk}}\le {{C}_{k}}, \forall i, j\in N, k\in K, $ | (15) |
| $ \sum\limits_{i\in N}{\sum\limits_{j\in N}{{{s}_{ij}}{{x}_{ijk}}}}\le {{D}_{K}}, \forall k\in K, $ | (16) |
| $ {{x}_{ojk}}\in \{0, 1\}, \forall j\in {{N}_{\rm{D}}}, k\in K, $ | (17) |
| $ {{x}_{jOk}}\in \{0, 1\}, \forall j\in {{N}_{\rm{D}}}, k\in K, $ | (18) |
| $ {{x}_{ijk}}\in \{0, 1\}, \forall i, j\in N, k\in K, $ | (19) |
| $ {{h}_{ik}}\in \{0, 1\}, \forall i\in {{N}_{\rm{D}}}, k\in K, $ | (20) |
式中:N=NO∪ND为配送网络中所有节点的集合, NO代表分拣中心;ND为共用揽投部的集合;sij为节点i和节点j之间的距离;车辆的集合为k;Fk为任意k∈K的车辆k的固定费用;Ck为其最大载质量;Dk为其最大行驶距离;di为区域i内共用揽投部的日平均送货量;pi为区域i内共用揽投部的日平均取货量;qijk为任意车辆k访问完i区域共用揽投部后在访问j区域共用揽投部之前的装载量;xojk为0~1变量,当其为1时表示车辆k从分拣中心出发,否则,其值为0;xjok为0~1变量,当其为1时表示车辆k返回分拣中心,否则,其值0;xijk为0~1变量,当其为1时表示车辆k从节点i到节点j,否则,其值为0;hik为0~1变量,当其值为1时,表示公用揽投部i由车辆k服务,否则其值为0。
式(4) 为优化目标,包括车辆的固定成本和油耗成本;式(5) 表示任何一个区域内的共用揽投部都有车辆经过;式(6) 表示网络中节点的流入流出平衡;式(7)(8) 表示每个共用揽投部仅由1辆车服务;式(9) 表示分拣中心服务的共用揽投部是从该分拣中心出发的车辆途径的共用揽投部;式(10)(11) 表示1辆车只配送1次;式(12)(13) 表示车辆从分拣中心出发和返回分拣中心时的载货量分别等于该车辆所服务公用揽投部的送货需求量和取货需求量;式(14) 表示车辆经过共用揽投部j的前后路段上的载货量的变化等式;式(15) 表示车辆在任意路段上的载货量不能超过车辆的最大载货量;式(16) 表示任意车辆k的配送距离不能超过其最大行驶距离;式(17)(18)(19)(20) 分别表示xojk、xjok、xijk、hik为0~1决策变量。
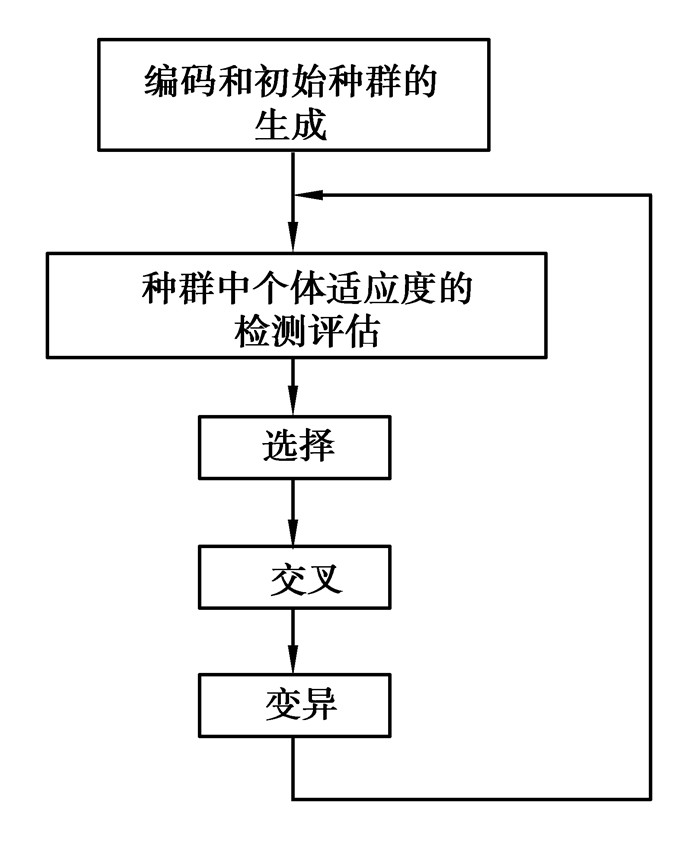
3 算法设计 3.1 遗传算法VRPSPD问题是NP难问题的集成问题,传统的精确算法在求解小规模问题中的优势明显,但很难求解大规模问题,而对于NP问题的求解,启发式算法具有普遍的适用性。遗传算法(GA)是美国Michigan大学的Holland教授及其学生受到生物模拟技术的启发创造出的一种基于生物遗传和进化机制的适合于复杂系统优化的自适应概率优化技术,自提出以来,已经被广泛运用于多种优化组合问题中,其完整的运算流程为:编码、初始种群的生成、适应度值的评价检测、选择、交叉、变异及终止条件判断,其基本流程如图 3[15]。但实践证明,标准遗传算法容易出现未成熟先收敛的现象。后来很多学者针对各自的研究问题,提出了很多改进的遗传算法。
|
图 3 遗传算法的基本流程 Figure 3 The basic process of genetic algorithm |
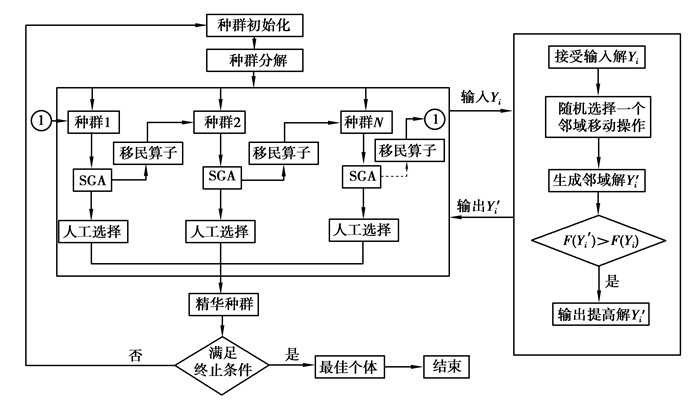
为解决标准遗传算法未成熟先收敛的问题,笔者设计多种群邻域搜索遗传算法(MPLSGA, multi population labor search genetic algorithm),该算法的创新性和优点主要体现在:1) 突破SGA仅靠单个种群进行遗传进化,通过引入多个种群同时进行搜索,不同的种群赋以不同的控制参数,加快收敛的速度;2) 通过引入3种邻域结构构造邻域解,增强算法的寻优能力;3) 种群之间通过移民算子实现协同进化;4) 通过人工选择算子保存各种群每个进化代中的最优个体,并作为算法收敛的依据。其算法流程图如图 4。
|
图 4 改进遗传算法的流程 Figure 4 The process of improved genetic algorithm |
具体的步骤为:
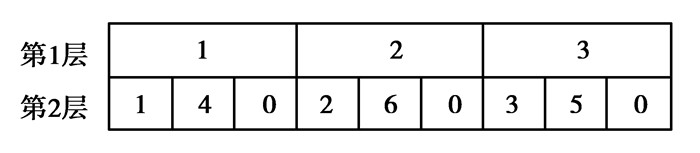
1) 编码。基于问题采用双向量映射实数编码方式,染色体由两部分组成,分别对应车型和路径,使遗传算法更接近问题空间。共用揽投部的编码规则为{1, 2…, n},0代表分拣中心。例如,6个公用揽投部的编码如图 5,代表车型为1、2、3的车辆的路径分别为0—1—4—0、0—2—6—0、0—3—5—0。
|
图 5 染色体编码方案 Figure 5 An example of solution representation |
2) 种群初始化。采用“先初始第2层车辆路径再第1层车型”的两阶段启发式算法生成初始解。具体而言:染色体长度为n+k,n为共用揽投部的数量,k为路径的数量。先生成n个揽投部的全排列,然后在排列末尾添加0,最后把k-1个0插入到全排列中,必须保证排列首位非0,并且不允许2个0相邻;染色体第1层以第2层的0为界限随机分配车型。随机生成N个个体作为初始种群x(0),规定种群数量为MP。
3) 适应度值评定。为了防止初始种群中出现适应度值超常的个体,同时为了避免由于种群中个体适应度值比较接近,导致继续优化选择较为困难,在最优解附近左右摇摆。首先,变形目标函数值的计算公式为:
| $ {{F}_{E}}=F+\alpha \sum\limits_{i\in Z}{\sum\limits_{j\in Z}{\max \left\{ 0, {{s}_{ij}}{{x}_{ijk}}-{{D}_{K}} \right\}}}+\beta \sum\limits_{i\in Z}{\sum\limits_{j\in Z}{\max \left\{ 0, {{q}_{ijk}}-{{C}_{k}} \right\}}}, $ |
式中:F为原目标函数值;α、β为惩罚系数。然后标定适应度值为:
| $ {f}'=\frac{1}{f+{{f}_{\min }}+\delta }\left( {{f}_{\min }}+{{f}_{\max }} \right)。$ |
式中:f′为标定后的适应度值;f为原适应度值,由新的目标函数值计算;fmin为适应度函数值的一个下界,若未知,可用目前为止种群中的最小适应度值代替;fmax为适应度函数值的一个上界,若未知,可用目前为止种群中的最大适应度值代替;δ为开区间(0, 1) 内的一个正实数,增加遗传算法的随机性。标定后的效果为:若fmin和fmax的差距越大,则标定后的适应度值差距越小,防止超常个体统治种群,避免算法在最优解附近摆动现象发生。
4) 选择算子。选择目标是为了得到优良个体,为了体现“适者生存”的思想,这里采用适应度比例选择法。假设种群规模为n, 个体i的适应度值为f′(i),则该个体被选中的概率为
| $ {{p}_{i}}=\frac{{f}'\left( i \right)}{\sum\limits_{i=1}^{n}{{f}'\left( i \right)}}。$ |
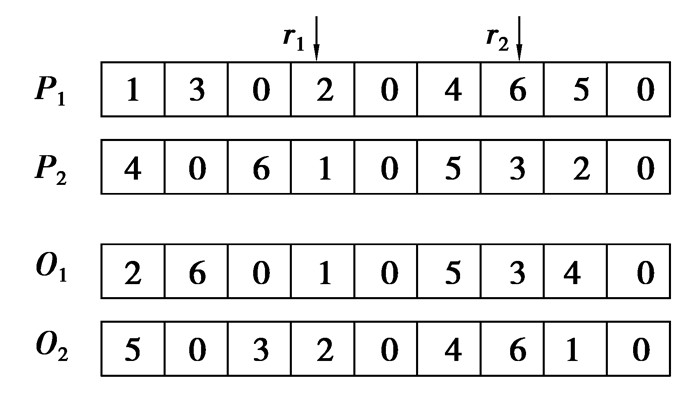
5) 交叉算子。第1层车型较少,交叉之后子代等概率分配一个车型排列即可;第2层采用两点交叉:随机从[1, n+k]中选择两个交叉基因位r1和r2, 互换两个基因位之间的基因,交叉后,同一个个体中重复的共用揽投部编号采用部分映射的方法消除冲突,具体如图 6所示。
|
图 6 两点交叉 Figure 6 PX operation |
6) 变异算子。从子代染色体中随机选择两个非分拣中心的位置,交换两个位置的基因。
7) 移民算子。移民算子的作用是找出第i种群中的最优个体和目标种群中的最劣个体,然后用第i种群中的最优个体代替目标种群中最劣个体。
8) 邻域搜索结构。这里采用3种随机移动操作的邻域结构来构造邻域解。
插入移动:针对任意环路车辆路径,随机选择除始末基因位的基因位i并随机插入到另一随机选择的基因位j之前。
互换移动:针对任意环路车辆路径,随机选择除始末基因位的两基因位i和j,互换二者位置。
2-opt移动:针对任意环路车辆路径,随机选择除始末基因位的两基因位i和j,逆序二者之间的基因序列。
4 算例分析 4.1 算例简介在重庆主城范围内选择3家快递企业进行研究,假设3家企业形成共同配送联盟。由于重庆快件的进口量大于出口量,因此不用考虑车辆在揽投部的装载量大于卸载量的问题,即车辆的容量允许车辆在一条可行的路径上同时完成取送货任务。在20 km×20 km范围内,分拣中心的位置为(8.0, 11.0),各家快递企业在各个区域的揽投部位置坐标和日均配送、揽收需求量如表 1所示,车辆的相关参数如表 2所示。
| 表 1 揽投部的位置及需求量 Table 1 Location and demand of the satellites |
| 表 2 车辆的相关费用参数 Table 2 Vehicle related cost parameters |
1) 揽投部集并。根据公式(1) 求出3家企业在各个区域的共用揽投部,结果如表 3所示。
| 表 3 共用揽投部的选址及需求量 Table 3 The location and demand of the shared satellites |
2) 考虑同时取送货的城市快递共同配送路径优化。根据共用揽投部的位置坐标和分拣中心的位置坐标,求出各节点之间的直线距离,然后再根据各道路状况,乘以相对应的系数,得出各节点之间的实际距离,结果如表 4所示。
| 表 4 各节点之间的实际距离 Table 4 Actual distance between nodes |
算法的参数设置:个体数目Nind=30,种群个数MP=20,在[0.7, 0.9]区间内随机产生交叉概率pc=0.7+(0.9-0.7) * rand(MP, 1),在[0.001, 0.05]区间内随机产生变异概率pm=0.001+(0.05-0.001) * rand(MP, 1),最优个体最少保持代数为10。算法在MATLAB R20111b平台上编译,在主频为2.3 GHz、双核、4.0 G内存、操作系统为Windows7的计算机上运行。
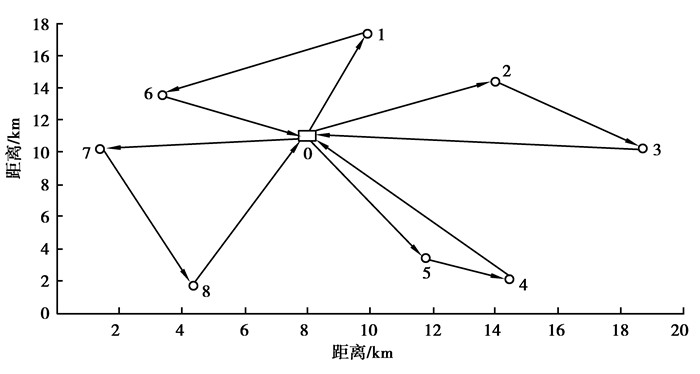
3) 结果分析。算法运行结果求出的车辆的配送路径如图 7,具体结果如表 5,在单条路径上车辆综合装载率计算公式为:
|
图 7 最优配送路径图 Figure 7 Optimal distribution route |
| 表 5 车辆最优路径结果 Table 5 The results of vehicle optimal path |
分析车辆的路径优化结果可知:从路径角度分析,车辆2的配送路径为1—4—9—1,分拣中心与共用揽投部4的距离(10.7 km)大于其与共用揽投部9的距离(8.4 km),因此,在实际配送中先配送距离分拣中心最近的需求点并不总是最优的,如果某个需求点的需求量较大,先配送该需求点才是最优的;从车辆装载率角度分析,车辆去程装载率(平均84.1%)远大于回程装载率(平均44%),导致综合装载率较低(平均67.7%),因此增加回程装载率是提高车辆利用率的关键。
为了验证模型的有效性,在相同的实验参数设置下对比共同配送同时取送(方案1)、共同配送不同时取送(方案2) 和独立配送同时取送(方案3)3种情况的最优方案,结果如表 6。
| 表 6 3种方案最优解结果 Table 6 Results of the three schemes' optimal solution |
比较方案1和方案2的结果可以发现:车辆配送过程同时取送货能够减少车辆的配送路程,提高车辆的装载率,降低油耗成本和车辆固定成本;比较方案1和方案3可以发现:在独立配送的情况下,由于单个企业的业务量有限,为了保证车辆的装载率,企业就要选择容量小的车型,增加单条路径的长度和单条路径配送揽投部的数量,这会使配送的时效性较差,并且配送路径总长、油耗成本和车辆固定成本都有所增加。
为了验证本文算法(MPLSGA)的有效性,在相同求解模型的基础上,在20 km×20 km的范围内随机生成不同规模的算例对算法的性能进行测试,并与标准遗传算法(SGA)和多种群遗传算法(multi group genetic algorithm,MGAG)进行对比,如表 7所示。
| 表 7 两种算法的求解结果对比 Table 7 The results' comparison of of two algorithms |
通过比较3种算法在不同规模下的求解结果可以发现:本文算法的最优解的质量和运算效率都比较优越,相对SGA,解的质量平均提高8.7%,求解的效率平均提高86%,说明本文算法更容易收敛到最优解,而且解的质量更高,尤其问题规模较大时,本文算法的优越性表现得更加明显。
5 结论笔者基于多家快递企业进行共同配送,考虑通过车辆在揽投部同时送货和取货的手段来增加车辆的装载率,建立装载率与车辆油耗成本的函数关系,构建了考虑同时取送货的城市快递共同配送路径优化模型,设计改进的遗传算法对模型进行求解,解决了配送揽投部的集并和车辆配送路径的优化问题。最后通过案例比较共同配送同时取送、共同配送不同时取送和独立配送同时取送3种情况的优化结果以及比较本文算法与标准遗传算法和多种群遗传算法的优化结果证明模型及算法的有效性。下一步的研究方向可以考虑建立共同配送的双层配送优化模型。
| [1] | Hayel Y, Quadri D, Jiménez T, et al. Decentralized optimization of last-mile delivery services with non-cooperative bounded rational customers[J]. Annals of Operations Research, 2016, 239(2): 451–469. DOI:10.1007/s10479-014-1647-x |
| [2] |
史春燕, 黄辉.
车辆路径问题:研究综述及展望[J]. 物流科技, 2014, 37(12): 75–77.
SHI Chunyan, HUANG Hui. Vehicle routing problem:research status and prospect[J]. logistics sci-tech, 2014, 37(12): 75–77. DOI:10.3969/j.issn.1002-3100.2014.12.024 (in Chinese) |
| [3] | Aghezzaf E H, Zhong Y, Raa B, et al. Analysis of the single-vehicle cyclic inventory routing problem[J]. International Journal of Systems Science, 2012, 43(11): 2040–2049. DOI:10.1080/00207721.2011.564321 |
| [4] | Kovacs A A, Parragh S N, Hartl R F. The multi-objective generalized consistent vehicle routing problem[J]. European Journal of Operational Research, 2015, 247(2): 441–458. DOI:10.1016/j.ejor.2015.06.030 |
| [5] | Xiao Y, Konak A A. Simulating annealing algorithm to solve the green vehicle routing and scheduling problem with hierarchical objectives and weighted tardiness[J]. Applied Soft Computing, 2015, 34: 372–388. DOI:10.1016/j.asoc.2015.04.054 |
| [6] | Spliet R, Desaulniers G. The discrete time window assignment vehicle routing problem[J]. European Journal of Operational Research, 2015, 244(2): 379–391. DOI:10.1016/j.ejor.2015.01.020 |
| [7] |
王勇, 吴志勇, 廖明, 等.
物流配送车辆调度决策支持系统[J]. 重庆大学学报(自然科学版), 2006, 29(9): 162–166.
WANG Yong, WU Zhiyong, LIAO Ming, et al. Logistics distribution vehicle scheduling decision support system[J]. Journal of Chongqing University (Natural Science Edition), 2006, 29(9): 162–166. (in Chinese) |
| [8] |
王征, 胡祥培, 王旭坪.
带二维装箱约束的物流配送车辆路径问题[J]. 系统工程理论与实践, 2011, 31(12): 2328–2341.
WANG Zheng, HU Xiangpei, WANG Xuping. Vehicle routing problem in distribution with two-dimensional loading constraint[J]. Systems Engineering Theory and Practice, 2011, 31(12): 2328–2341. DOI:10.12011/1000-6788(2011)12-2328 (in Chinese) |
| [9] |
谷炜, 张群, 卫李蓉.
基于GIS的物流配送中心末端大规模车辆路径优化问题研究[J]. 中国管理科学, 2013, Sup1(s1): 379–389.
GU Wei, ZHANG Qun, WEI Lirong. Method of large-scale vehicle routing problem based on GIS[J]. Chinese Journal of Management Science, 2013, Sup1(s1): 379–389. (in Chinese) |
| [10] | Archetti C, Bianchessi N, Speranza M G. A branch-price-and-cut algorithm for the commodity constrained split delivery vehicle routing problem[J]. Computers and Operations Research, 2015, 64: 1–10. DOI:10.1016/j.cor.2015.04.023 |
| [11] | Mahmoudi M, Zhou X. Finding optimal solutions for vehicle routing problem with pickup and delivery services with time windows:A dynamic programming approach based on state-space-time network representations[J]. Transportation Research Part B:Methodological, 2016, 89: 19–42. DOI:10.1016/j.trb.2016.03.009 |
| [12] | Shen Q, Chu F, Chen H. A Lagrangian relaxation approach for a multi-mode inventory routing problem with transshipment in crude oil transportation[J]. Computers and Chemical Engineering, 2011, 35(10): 2113–2123. DOI:10.1016/j.compchemeng.2011.01.005 |
| [13] |
张景玲, 赵燕伟, 王海燕, 等.
多车型动态需求车辆路径问题建模及优化[J]. 计算机集成制造系统, 2010, 16(3): 543–550.
ZHANG Jingling, ZHAO Yanwei, WANG Haiyan, et al. Modeling and algorithms for a dynamic multi-vehicle routing problem with Customers' dynamic requests[J]. Computer Integrated Manufacturing Systems, 2010, 16(3): 543–550. (in Chinese) |
| [14] |
唐金环, 戢守峰, 沈贵财.
时变网络下考虑碳排放的车辆路径优化[J]. 系统工程, 2015(9): 37–44.
TANG Jinhuan, JI Shoufeng, SHEN Guicai. Vehicle routing optimization with carbon emissions considered under time-varying network[J]. Systems Engineering, 2015(9): 37–44. (in Chinese) |
 2017, Vol. 40
2017, Vol. 40

