2. 重庆工程职业技术学院 机械工程学院, 重庆 402260
2. College of Mechanical Engineering, Chongqing Vocational Institute of Engineering, Chongqing 402260, P. R. China
转向节是汽车转向系统中的重要零件之一,直接影响汽车的操控性及安全性,优化转向节使其满足各项动力学要求具有理论和实用意义[1]。目前使用广泛的结构优化方法有形状优化和尺寸优化设计[2-3],还有一种能使材料在边界条件和载荷约束下重新分布的优化方法——拓扑优化[4]。拓扑优化能最大限度地优化载荷传递路径,使结构在满足轻量化的同时趋于合理,是目前很有效率的优化方法。拓扑优化在各个领域都有应用,文献[5]将拓扑优化方法拓展到航空领域,验证了该方法能有效地进行自适应机翼的优化设计。拓扑优化还可应用于热环境中动柔度以及共振声频率的优化设计[6-7]。
现阶段结构的优化以单目标拓扑优化为主,但随着实际工程中结构用途的多样化以及优化效率的不断提高,单目标拓扑优化在实际应用中因其很难满足实际需要而逐渐被多目标拓扑优化所取代。静态条件下的刚度以及动态条件下的固有频率多目标拓扑优化是典型的多目标拓扑优化问题[8]。范文杰等[9-10]利用折衷规划法对车架结构进行了多目标拓扑优化,使得车架的刚度和固有频率都得到了提高,优化了车架的性能。占金青等[11]以静态多工况下刚度和动态特征值为目标,实现了连续体结构的静动态多目标拓扑优化。张云清等[12]基于人工密度指数法,结合序列分层优化方法和折衷规划法,提出并建立了一种求解复杂工况下连续体结构多刚度拓扑优化设计问题的多目标混合优化策略。多目标拓扑优化不仅仅局限于刚度或者特征值作为优化目标,比如,2012年,刘嘉敏等[13]基于移动渐近线法对简单膨胀腔消声器内部结构进行了拓扑优化,提高了传递损失。孙伟等[14]针对风电增速器的动态性能优化问题,以传动系统体积最小和构件扭转振动加速度振动幅值最小为优化目标,以可靠性和强度等为约束条件对大功率风电增速器进行了多目标动态优化设计。此外,多目标拓扑优化还可以与尺寸优化结合,以达到更好的优化效果[15]。文献[16]介绍了多种建立多目标拓扑优化数学模型的方法;文献[17]分析并比较了多种不同的多目标优化进化算法,结果显示,基于人口增量学习的PBIL(population-based incremental learning)进化算法的优化效果最佳。Sleesongsom等[18]运用PBIL进化算法对齿轮齿条转向连杆机构进行了多目标拓扑优化设计。
笔者基于带惩罚因子的变密度插值方法[19-20](SIMP, solid isotropic material with punishment),以及带权重的折衷规划法对某太阳能赛车转向节进行了多目标拓扑优化设计,优化后的结构同时满足刚度和一阶振动频率要求,使转向节的质量减轻,在提高转向节性能的同时还节省了材料。
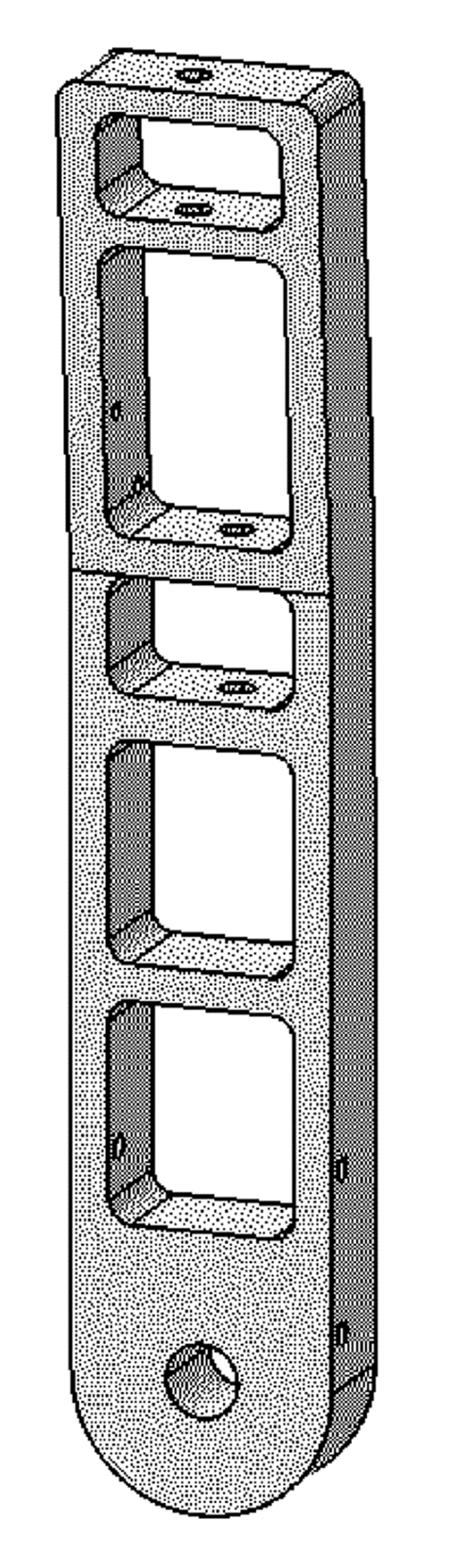
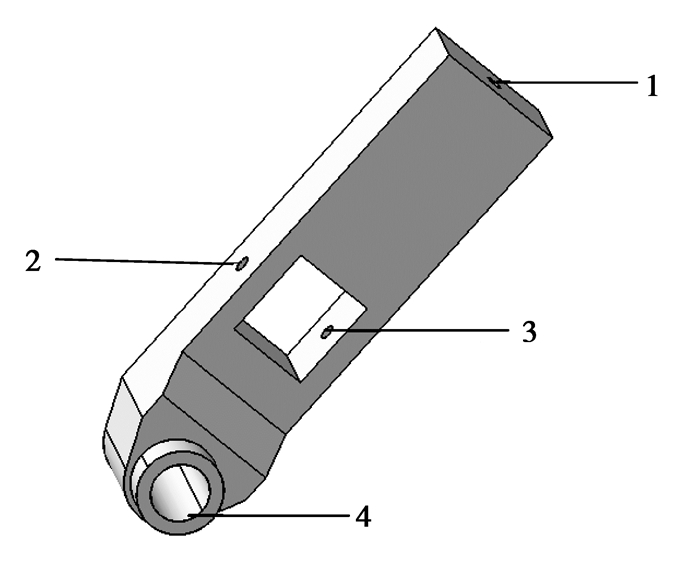
1 转向节的优化目标转向节需要保证具有较高的刚度、较高的低阶频率以及较低的质量。柔度为衡量结构刚度的一个标准,与刚度成反比。图 1为某太阳能汽车上正在投入使用的转向节,质量偏重,需要对其进行优化改进。为便于生成最佳载荷传递路径,将优化前转向节初始模型设计成如图 2所示的除预留出安装位置外其余部分均为实体的结构。图中1、2、3均为螺栓孔,上控制臂与安装在1处正上方的球绞联接,球绞通过螺栓固定于螺栓孔1处;下控制臂安装在2、3螺栓孔之间,与固定于螺栓上的球绞联接。车轮轴安装于轴承座4处。
|
图 1 某太阳能汽车转向节原有结构 Figure 1 The original steering knuckle on a racing car |
|
图 2 转向节初始模型 Figure 2 Initial knuckle model before optimization |
优化前转向节原有结构的柔度达到182.851,刚度较小。为提高转向节刚度,期望优化后的柔度降低80%;原始转向节一阶固有频率为1 046.255 Hz,为提高一阶固有频率,优化后的转向节一阶固有频率期望值比原始值提高60%;优化前转向节质量过大,为同时达到轻量化的目的,转向节质量分数上线约束值为优化前的40%。
2 转向节的多目标拓扑优化 2.1 转向节优化理论多目标拓扑优化所采用的软件是Altair HyperWorks,在Optistruct模块中可以方便地定义材料密度差值模型[21]。
综合目标函数同时考虑了静态下的刚度和动态固有频率,以质量和最大变形量作为约束,综合目标函数的值最小为目标进行优化。综合目标函数中包含静态刚度和动态频率两部分,其中频率由平均频率法定义并加权,通过权系数将两者统一于一个函数[8, 22]。
| $ {\rm{min}}\mathit{F}\left( \mathit{\rho } \right){\rm{ = }}{\left\{ {{\mathit{\omega }^{\rm{2}}}{{\left[{\sum\limits_{\mathit{k}{\rm{ = 1}}}^\mathit{m} {{\mathit{\omega }_\mathit{k}}} \frac{{{\mathit{C}_\mathit{k}}\left( \mathit{\rho } \right){\rm{-}}\mathit{C}_\mathit{k}^{{\rm{min}}}}}{{\mathit{C}_\mathit{k}^{{\rm{max}}}{\rm{-}}\mathit{C}_\mathit{k}^{{\rm{min}}}}}} \right]}^{\rm{2}}}{\rm{ + (1 - }}\mathit{\omega }{{\rm{)}}^{\rm{2}}}{{\left( {\frac{{{\mathit{\Lambda }_{{\rm{max}}}}{\rm{ - }}\mathit{\Lambda }\left( \mathit{\rho } \right)}}{{{\mathit{\Lambda }_{{\rm{max}}}}{\rm{ - }}{\mathit{\Lambda }_{{\rm{min}}}}}}} \right)}^{\rm{2}}}} \right\}^{\frac{1}{2}}}, $ |
式中: F(ρ)为综合目标函数;Λmax和Λmin分别为一阶固有频率的最大值和最小值;ω为柔度目标函数的权值; Ckmax和Ckmin分别为第k个工况下柔度的最大值和最小值;Ck(ρ)为第k个工况的柔度值;ωk为第k个工况下柔度的权值。
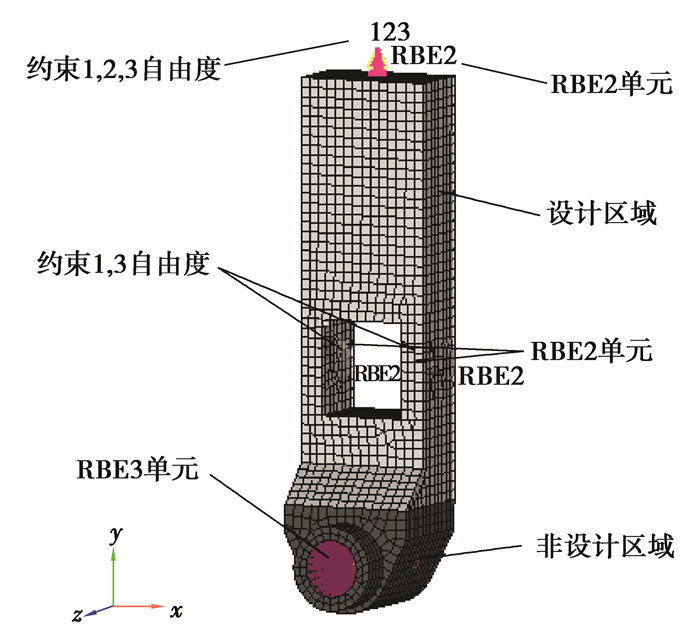
2.2 转向节有限元模型的建立在拓扑优化之前不能预知优化之后的材料分布,建立如图 3所示的转向节模型,作为拓扑优化的基础模型。与控制臂连接处建立3个RBE2单元模拟螺栓与转向节实体刚性连接。与轮毂连接区域为非设计区域,以上部分均为设计区域,材料内部均为实体。材料选择铝合金,屈服强度为330 MPa,弹性模量为74 000 MPa,泊松比为0.3,密度为2.7 g/cm3,质量分数约束为0.4。
|
图 3 转向节有限元模型 Figure 3 Finite element model of the knuckle |
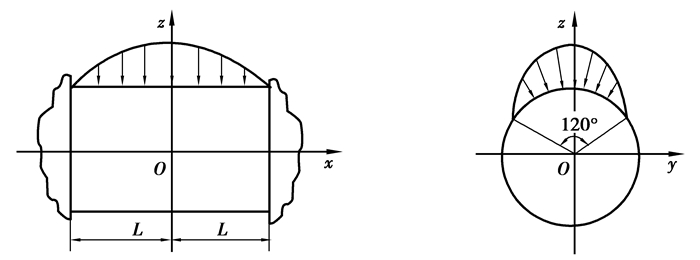
转向节与上控制臂连接处约束x, y, z 3个方向的移动自由度,与下控制臂连接处约束x和z 2个方向的移动自由度,由于模拟球绞连接,故释放3个转动自由度。根据太阳能赛车在静态工况下实际测得的轮毂对于转向节的作用力,并以此作为静态条件下的边界条件载荷, 载荷工况如表 1所示。为尽量模仿轮毂对转向节的作用力,根据接触面位置油膜压力的分布规律,假设压力沿轮毂轴线方向按二次抛物线规律分布,沿轮毂圆周方向对称地在120°范围内依照余弦规律分布。通过集中力的大小推算出作用在接触面各个位置处的压力,将压力分散在各个节点上,如图 4所示。
| 表 1 静态工况下载荷加载情况 Table 1 Loading conditions under static working conditions |
|
图 4 转向节轴承座与轮毂接触面受力分布 Figure 4 Pressure distribution on the contact surface between the hub and the knuckle |
弯矩作用在通过RBE3单元与轮毂接触面联接的节点上,通过RBE3单元传递给转向节。
在进行拓扑优化时,由于多个目标同时优化,目标函数不能通过直接定义来设置,而是利用Optistruct模块自定义函数的功能将柔度目标函数以及频率目标函数联合起来建立综合目标函数,并将其作为优化目标进行实现。在此综合目标函数中,将柔度与低阶频率视为同等重要,所以柔度目标函数和频率目标函数的权重均取0.5,惩罚因子q=2。
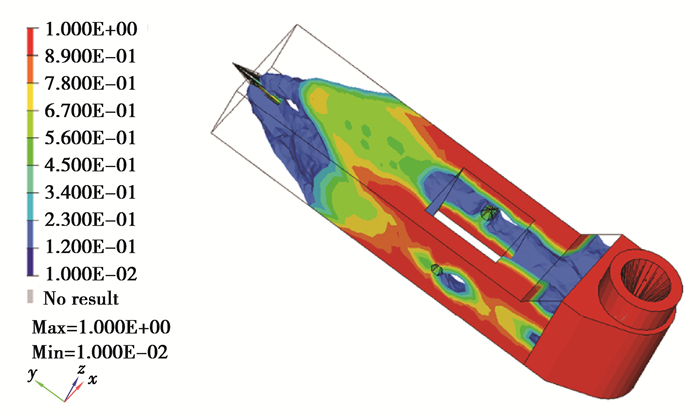
2.4 优化结果图 5为经过30次拓扑优化迭代后得到的转向节最终拓扑结构。由图可以看出材料在载荷以及边界条件的作用下进行了重新分布,载荷传递路径更加趋于合理。
|
图 5 优化结果材料分布图 Figure 5 Material distribution of the optimized topology structure |
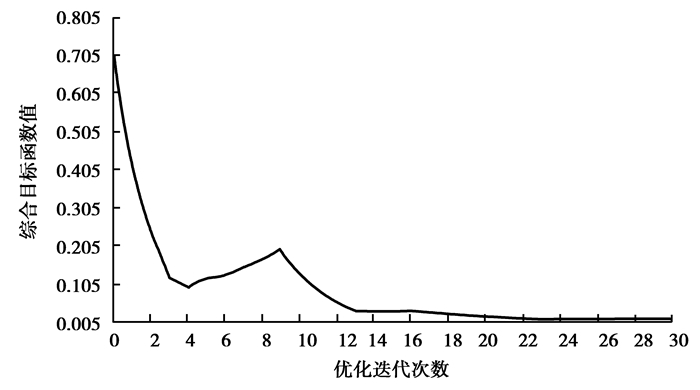
图 6至图 8显示的依次为综合目标函数、一阶频率目标函数和柔度目标函数值随优化过程的变化曲线。图 7和图 8显示的结果表明,转向节的一阶频率显著提高,柔度值下降也很明显。说明经过多目标拓扑优化后,转向节刚度得到提高的同时一阶振动频率也得到了提高,达到了多目标拓扑优化的目的。
|
图 6 综合目标函数值的变化曲线 Figure 6 Variation curve of the integrative objective function value |

|
图 7 一阶频率值的变化曲线 Figure 7 Variation curve of the first-order frequency objective function value |

|
图 8 柔度值的变化曲线 Figure 8 Variation curve of the compliance objective function value |
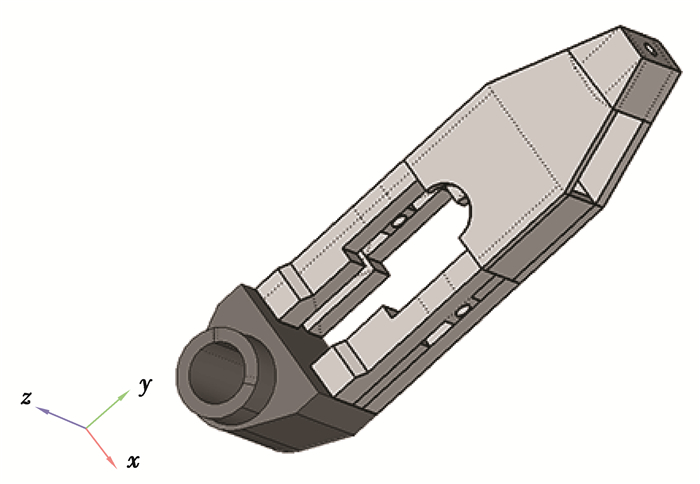
图 9为拓扑优化结果经光滑处理之后建立的几何模型。
|
图 9 光滑处理之后的几何模型 Figure 9 Geometrical model after being smoothed |
将经过光滑处理后重新建立的模型进行分析,得到优化前后转向节各项参数指标的比较,表 2显示了拓扑优化后的优化比例,并且显示了在刚度与一阶频率得到提高的同时,还满足了结构轻量化的要求。
| 表 2 优化前后转向节各性能参数比较及优化比例 Table 2 Comparison of parameters between the original non-optimized knuckle and the knuckle after being smoothed |
以某太阳能赛车转向节轻量化为目的,利用带惩罚因子的变密度插值方法以及折衷规划法,联合柔度目标函数和一阶频率目标函数建立了基于妥协解的联合优化目标函数,对转向节进行了多目标优化设计,不仅使转向节结构轻量化,而且其结构刚度和一阶振动频率均提高。
| [1] |
兰凤崇, 张浩锴, 王家豪, 等.
汽车转向节拓扑优化方法研究及应用[J]. 汽车工程, 2014, 36(4): 464–468.
LAN Fengchong, ZHANG Haokai, WANG Jiahao, et al. Study and application of topology optimization technique for vehicle steering knuckle[J]. Automotive Engineering, 2014, 36(4): 464–468. (in Chinese) |
| [2] |
方子帆, 杨磊, 杜道佳, 等.
支撑结构多目标拓扑优化设计研究[J]. 中国机械工程, 2010, 21(15): 1836–1839.
FANG Zifan, YANG Lei, DU Daojia, et al. Research on topology optimization design for support structure[J]. China Mechanical Engineering, 2010, 21(15): 1836–1839. (in Chinese) |
| [3] | Viktor S. Shape optimization of rigid inclusions for elastic plates with cracks[J]. Zeitschrift Für Angewandte Mathematik und Physik, 2016, 67(3): 71–83. DOI:10.1007/s00033-016-0666-7 |
| [4] | Yoon Y K, Tae S K. Topology optimization of beam cross sections[J]. International Journal of Solids and Structures, 2000, 37(3): 477–493. DOI:10.1016/S0020-7683(99)00015-3 |
| [5] | Tong X X, Ge W J, Sun C, et al. Topology optimization of compliant adaptive wing leading edge with composite materials[J]. Chinese Journal of Aeronautics, 2014, 27(6): 1488–1494. DOI:10.1016/j.cja.2014.10.015 |
| [6] | Yang X W, Li Y M. Topology optimization to minimize the dynamic compliance of a bi-material plate in a thermal environment[J]. Structural and Multidisciplinary Optimization, 2013(3): 399–408. |
| [7] | Yang X W, Li Y M. Structural topology optimization on sound radiation at resonance frequencies in thermal environments[J]. Science China(Physics, Mechanics & Astronomy), 2015, 58(3): 1–12. |
| [8] | Chen T Y, Wu S C. Multi-Objective Optimal Topology Design of Strctures[J]. Computational Mechanics, 1998, 21(6): 483–492. DOI:10.1007/s004660050327 |
| [9] |
范文杰, 范子杰, 桂良进, 等.
多工况下客车车架结构多刚度拓扑优化设计研究[J]. 汽车工程, 2008, 30(6): 531–533.
FAN Wenjie, FAN Zijie, GUI Liangjin, et al. Multi-stiffness topology optimization of bus frame with multiple loading conditions[J]. Automotive Engineering, 2008, 30(6): 531–533. (in Chinese) |
| [10] |
范文杰, 范子杰, 苏瑞意.
汽车车架结构多目标拓扑优化方法研究[J]. 中国机械工程, 2008, 19(12): 1505–1508.
FAN Wenjie, FAN Zijie, SU Ruiyi. Research on multi-objective topology optimization on bus chassis frame[J]. China Mechanical Engineering, 2008, 19(12): 1505–1508. DOI:10.3321/j.issn:1004-132X.2008.12.026 (in Chinese) |
| [11] |
占金青, 张宪民.
连续体结构的静动态多目标拓扑优化方法研究[J]. 机械强度, 2010, 32(6): 933–937.
ZHAN Jinqing, ZHANG Xianming. Research on static and dynamic multi-objective topology optimization of continuum structures[J]. Journal of Mechanical Strength, 2010, 32(6): 933–937. (in Chinese) |
| [12] |
张云清, 罗震, 陈立平, 等.
基于移动渐近线方法的结构多刚度拓扑优化设计[J]. 航空学报, 2006, 27(6): 1209–1216.
ZHANG Yunqing, LUO Zhen, CHEN Liping, et al. Topology optimization design for multiple stiffness structures using method of moving asymptotes[J]. Acta Aeronauticaet Astronautica Sinica, 2006, 27(6): 1209–1216. (in Chinese) |
| [13] |
刘嘉敏, 黄虹溥, 孙小园.
简单膨胀腔消声器声学特性的内部结构拓扑优化[J]. 重庆大学学报, 2012, 35(1): 34–38.
LIU Jiamin, HUANG Hongpu, SUN Xiaoyuan. Topology optimization of simple expansion chamber muffler internal configuration for acoustical performance[J]. Journal of Chongqing University, 2012, 35(1): 34–38. DOI:10.11835/j.issn.1000-582X.2012.01.008 (in Chinese) |
| [14] |
孙伟, 李想, 魏静, 等.
大功率风电增速器的多目标优化设计[J]. 重庆大学学报, 2015, 38(1): 110–119.
SUN Wei, LI Xiang, WEI Jing, et al. Multi-objective dynamic optimization design of high-power wind turbine gearbox[J]. Journal of Chongqing University, 2015, 38(1): 110–119. (in Chinese) |
| [15] | Zhong W, Su R Y, Gui L J, et al. Multi-objective topology and sizing optimization of bus body frame[J]. Struct Multidisc Optim, 2016, 54(3): 701–714. DOI:10.1007/s00158-016-1431-4 |
| [16] |
孙晓辉, 丁晓红.
结构多目标拓扑优化设计[J]. 机械设计与研究, 2012, 28(4): 1–9.
SUN Xiaohui, DING Xiaohong. Research on multi-objective topology optimization design methods for structure[J]. Machine Design and Research, 2012, 28(4): 1–9. (in Chinese) |
| [17] | Tawatchai K, Sujin B. Multi-objective topology optimization using evolutionary algorithms[J]. Engineering Optimization, 2011, 43(5): 541–557. DOI:10.1080/0305215X.2010.502935 |
| [18] | Sleesongsom S, cBureeratc S. Multiobjective optimization of a steering linkage[J]. Journal of Mechanical Science and Technology, 2016, 30(8): 3681–3691. DOI:10.1007/s12206-016-0730-4 |
| [19] |
谢伦杰, 张维刚, 常伟波, 等.
基于SIPM理论的电动汽车车身多目标拓扑优化[J]. 汽车工程, 2013, 35(7): 583–587.
XIE Lunjie, ZHANG Weigang, CHANG Weibo, et al. Multi-objective topology optimization for electric car body based on SIMP theory[J]. Automotive Engineering, 2013, 35(7): 583–587. (in Chinese) |
| [20] | Marck G, Nemer M, Harion J L, et al. Topology optimization using the simp method for multiobjective conductive problems[J]. Numerical Heat Transfer. Part B:Fundamentals, 2012, 61(6): 439–470. DOI:10.1080/10407790.2012.687979 |
| [21] |
祝小元, 方宗德, 申闪闪, 等.
汽车悬架控制臂的多目标拓扑优化[J]. 汽车工程, 2011, 33(2): 138–141.
ZHU Xiaoyuan, FANG Zongde, SHEN Shanshan, et al. Multi-objective optimization for the control arm of vehicle suspension[J]. Automotive Engineering, 2011, 33(2): 138–141. (in Chinese) |
| [22] | Marler R T, Arora J S. Survey of multi-objective optimization methods for engineering[J]. Struct Multidisc Optiom, 2004, 26(6): 369–395. DOI:10.1007/s00158-003-0368-6 |
 2017, Vol. 40
2017, Vol. 40

