传动实验平台用于测试减速器的传动效率、传动精度等性能参数,是减速器在研发制造过程中不可或缺的配套设备。精密传动实验平台主要用于rotor vector(RV)减速器、谐波减速器等精密减速器测试,因此必须保证测试结果的精度和可靠性。实验平台的动态特性对精密减速器测试结果的精度和可靠性具有直接影响,这就要求精密传动实验平台除了具有足够的强度、刚度以外,还必须具有良好的动态性能。传统搭建式的传动实验平台安装精度不稳定,位置调整不方便,不能满足精密减速器高精度、高可靠性、高效率的测试要求,因此开发新型的精密传动实验平台并对其动态特性进行分析具有重要意义。
国内外学者对多轴精密定位平台及其动态特性分析等方面进行了大量的研究。多轴精密定位平台主要应用于数控机床的进给定位系统,通过调整加工刀具或者工件的位置进行对刀,这为实验平台的设计提供了思路[1]。多轴定位系统中最常见的组合形式是双轴联动的十字滑台,Ulu等[2-3]将多轴精密定位系统的控制方法应用到十字滑台上,提高了平台的控制精度。多轴定位系统也被应用到数控实验台的开发中,彭玉海等[4]研究开发了一种基于可编程多轴运动控制器(PMAC)的五轴数控实验台。对于动态特性分析,平台结合部刚度特性是关键影响因素。蒋书运等[5-6]验证了结合部处理方法对机床整机动态特性具有明显影响;朱坚民等[7]和Vicente等[8-9]进一步分析了各参数对进给系统动态特性的影响大小;Zhang等[10]分析了结合部间隙所引起的摩擦对隔振平台动态特性的影响。对于交叉滚子导轨的建模方法,Liu等[11-12]将交叉滚子导轨简化为5自由度的动力学系统并通过模态实验测定系统的刚度和阻尼;李要芳等[13]针对滚珠丝杆十字滑台计算了结合部刚度并进行了模态分析。在动力学性能优化方面,林腾蛟等[14-15]提出了一种动力学性能优化方法,以齿轮箱表面振动加速度的均方根值作为目标函数,利用零阶与一阶优化算法求得最优设计变量。但以上研究没有提出交叉滚子导轨结合部刚度的理论计算方法,在不同工况下动力学的建模方法不够完善,导致应用情况受限。
笔者设计开发一种多轴精密传动实验平台,根据平台在极限工况下的结构特点建立动力学模型,并通过理论模态分析得到系统固有频率,最后通过样机测试验证实验平台的动态特性。
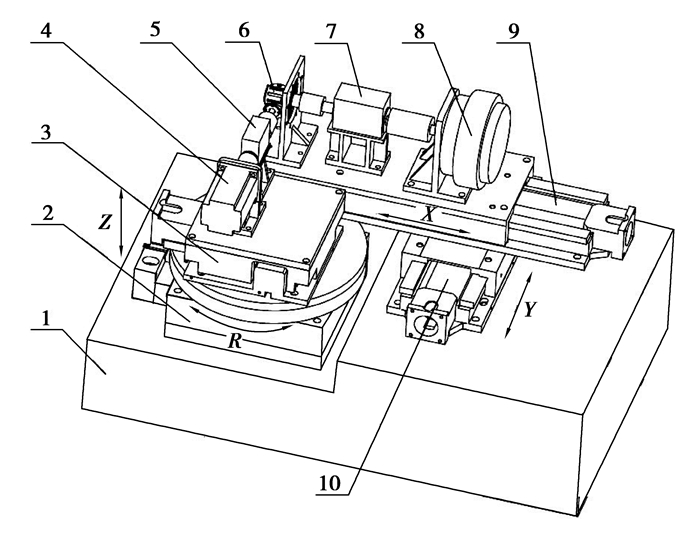
1 试验平台结构方案实验平台的结构方案如图 1所示。
|
图 1 实验平台结构方案 Figure 1 Structure scheme of test platform 1.支撑底座;2.R轴旋转平台;3.Z轴升降平台;4.驱动电机;5.输入端传感器; 6.被测减速器;7.输出端传感器;8.加载器;9.X轴直线平台; 10.Y轴直线平台 |
实验平台采用开放功率流的结构形式,通过被测减速器输入端和输出端的位置关系调整,实现多种类型减速器的测试。实验平台共有4个调节自由度,输入端通过旋转平台和升降平台实现绕Z轴旋转和沿Z轴升降2个自由度;输出端通过十字滑台实现沿X轴移动和沿Y轴移动2个自由度。实验平台可以测试同轴、平行轴、相交轴及交错轴等类型的减速器,典型产品包括谐波减速器、螺旋伞齿减速器及蜗轮蜗杆减速器等,应用范围广泛。
R轴旋转平台采用极低侧隙的蜗轮蜗杆驱动;Z轴升降平台采用精密滚珠丝杆和楔形斜面的结构驱动;X、Y十字滑台均采用精密滚珠丝杆驱动,同时滑台和底座之间采用交叉滚子直线导轨导向,保证高的定位精度和承载能力。
2 实验平台模态分析减速器输出端和输入端相比传递扭矩更大, 测试设备质量大,X、Y十字滑台受力面积较小,容易承受偏载,尤其是当测试相交轴和交错轴减速器时,滑台均工作在接近行程极限的位置,相当于悬臂梁支撑,直线导轨受载的滚子个数大幅度减少,支撑刚度达到最小,所以这里只对十字滑台在极限位置下进行模态分析,验证实验平台的动态特性。
2.1 结合部刚度计算 2.1.1 滚珠丝杆刚度计算滚珠丝杆在进给传动时只承受轴向载荷,结合部只存在轴向刚度[16]。滚珠丝杆系统主要由丝杆、螺母、滚动体以及两端的支承轴承等组成,因此滚珠丝杆的轴向刚度由丝杆的轴向刚度、滚珠丝杆副的结合部刚度以及支承轴承的轴向刚度共同决定,且等于他们的串联总和[17]。滚珠丝杆轴向刚度为
| $ \frac{1}{{{\mathit{k}_{\rm{a}}}}}{\rm{ = }}\frac{1}{{{\mathit{k}_{\rm{S}}}}}{\rm{ + }}\frac{1}{{{\mathit{k}_{\rm{N}}}}}{\rm{ + }}\frac{1}{{{\mathit{k}_{\rm{B}}}}}{\rm{, }} $ | (1) |
式中:ka为滚珠丝杆轴向刚度;kS为丝杆轴向刚度;kN为滚珠丝杆副结合部刚度;kB为支承轴承轴向刚度。实验平台采用KURODA品牌GR1505DS型号的滚珠丝杆,配套的支撑轴承型号为BUM-12,根据产品样本资料最终计算得到滚珠丝杆副轴向刚度为5.24×107 N/m。
2.1.2 交叉滚子直线导轨刚度计算十字滑台采用非循环的交叉滚子直线导轨,直线导轨主要由固定导轨、圆柱滚子、保持架和移动导轨组成,滚子呈45°接触角交叉间隔排列在导轨的V形滚道中。在实际产品中,为了防止端面摩擦,滚子的直径尺寸略大于长度尺寸,保证滚子只有圆柱面参与工作而端面不参与工作。
1) 垂直刚度计算。
直线导轨结合部垂直刚度是滚柱与滚道在垂直方向产生单位的相对弹性位移量所需垂直方向的外加负荷,即
| $ {\mathit{k}_{\rm{v}}}{\rm{ = }}\frac{{\partial {\mathit{F}_{\rm{v}}}}}{{\partial {\mathit{\delta }_{\rm{v}}}}}, $ | (2) |
式中:kv为直线导轨垂直刚度;Fv为直线导轨垂直方向所受载荷;δv为滚柱与滚道之间垂直方向相对弹性位移量。
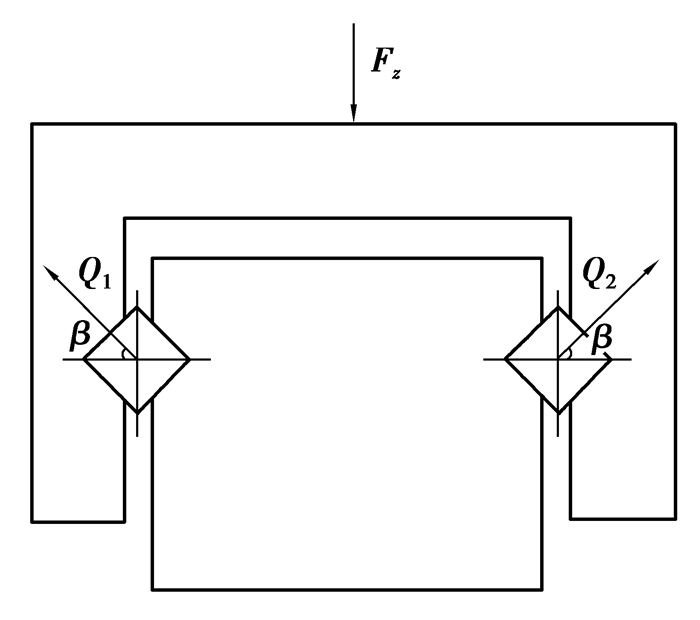
当移动平台受到垂直向下的载荷Fv时,不考虑制造误差所产生的影响,载荷在同一排滚子之间均布,由于只有圆柱面接触,所以左右两排滚子各只有一半滚子承受载荷,受力分析如图 2所示。
|
图 2 直线导轨承受垂直载荷时的受力分析 Figure 2 Force analysis of linear guide way under vertical load |
根据受力平衡条件可得
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{Z}{2}{Q_{\rm{1}}}{\rm{cos}}\beta {\rm{ - }}\frac{Z}{2}{Q_{\rm{2}}}{\rm{cos}}\beta {\rm{ = 0}},}\\ {\frac{Z}{2}{Q_{\rm{1}}}{\rm{sin}}\beta {\rm{ + }}\frac{Z}{2}{Q_{\rm{2}}}{\rm{sin}}\beta {\rm{ - }}{F_{\rm{v}}}{\rm{ = 0。}}} \end{array}} \right. $ | (3) |
式中:Z为单排滚子个数;Q1为左导轨滚子承受的法向力;Q2为右导轨滚子承受的法向力;β为滚子接触角。
在对动力学建模精度要求不高的情况下,可认为滚子与丝杆和螺母滚道的接触满足Hertz接触理论的4个假设条件,因此导轨结合部的变形量完全由滚子与滚道面的弹性接触变形所引起,可利用赫兹弹性接触理论来进行计算。
根据Palmgren对于带有凸度的圆柱滚子变形公式为[18]
| $ \mathit{\delta }{\rm{ = 3}}{\rm{.84 \times 1}}{{\rm{0}}^{{\rm{ - 5}}}}\frac{{{\mathit{Q}^{{\rm{0}}{\rm{.9}}}}}}{{{\mathit{l}^{{\rm{0}}{\rm{.8}}}}}}, $ | (4) |
式中:δ为滚子和滚道的相对位移趋近量;Q为滚子法向载荷;l为有效接触长度。
滚子和滚道总的接触变形为滚子和固定导轨之间、滚子和移动导轨之间的变形总和,且他们的变形量相等,根据滚子和滚道变形协调有:
| $ \mathit{\delta }{\rm{ = }}\frac{1}{2}{\mathit{\delta }_{\rm{v}}}{\rm{sin}}\;\mathit{\beta, } $ | (5) |
联立式(2)~(5)得到直线导轨垂直刚度为
| $ {\mathit{k}_{\rm{v}}}{\rm{ = 4}}{\rm{.15 \times 1}}{{\rm{0}}^{\rm{4}}}\mathit{Z} \cdot {\rm{si}}{{\rm{n}}^{{\rm{19/9}}}}\mathit{\beta }{\rm{\cdot}}{\mathit{l}^{{\rm{8/9}}}}{\rm{\cdot}}\mathit{\delta }_{^{\rm{v}}}^{{\rm{1/9}}}。$ | (6) |
对于存在水平预压力的直线导轨,根据式(4)有
| $ {\mathit{\delta }_{\rm{0}}}{\rm{ = 3}}{\rm{.84 \times 1}}{{\rm{0}}^{{\rm{ - 5}}}}\left( {\frac{{{\mathit{F}_{\rm{0}}}}}{{\mathit{Z}{\rm{cos}}\;\mathit{\beta }}}} \right){{\rm{}}^{{\rm{0}}{\rm{.9}}}}。$ | (7) |
联立式(5)(7)计算得到
| $ {\mathit{\delta }_{\rm{v}}}{\rm{ = }}\frac{{{\rm{7}}{\rm{.68 \times 1}}{{\rm{0}}^{{\rm{ - 5}}}}\mathit{F}_0^{0.9}}}{{{\mathit{Z}^{{\rm{0}}{\rm{.9}}}}{\mathit{l}^{{\rm{0}}{\rm{.8}}}}{\rm{co}}{{\rm{s}}^{{\rm{0}}{\rm{.9}}}}\mathit{\beta }{\rm{sin}}\;\mathit{\beta }}}。$ | (8) |
2) 横向刚度计算。
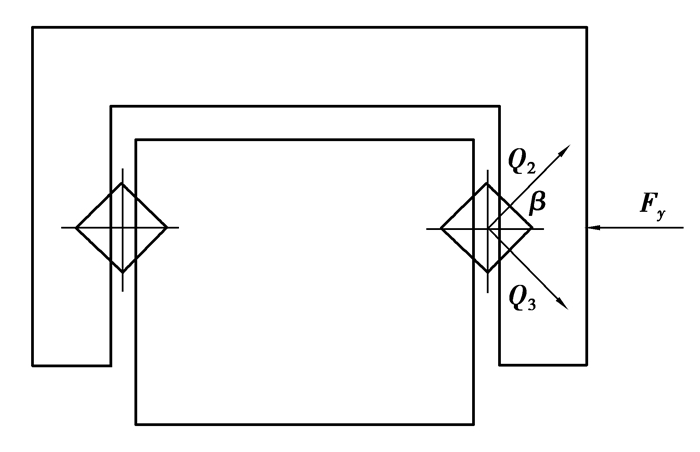
当直线导轨受到水平方向的载荷Fh时,如图 3所示,受载侧直线导轨有一半的滚子受到的法向力沿Q2方向,另一半的滚子受到的法向力沿Q3方向,且载荷在滚子之间均布。
|
图 3 直线导轨承受水平载荷时的受力分析 Figure 3 Force analysis of linear guide way under horizontal load |
根据受力平衡条件有
| $ \left\{ \begin{array}{l} \frac{\mathit{Z}}{2}{\mathit{Q}_{\rm{2}}}{\rm{sin}}\;\mathit{\beta }{\rm{ - }}\frac{\mathit{Z}}{2}{\mathit{Q}_{\rm{3}}}{\rm{sin}}\;\mathit{\beta }{\rm{ = 0}}, \\ \frac{\mathit{Z}}{2}{\mathit{Q}_{\rm{2}}}{\rm{cos}}\;\mathit{\beta }{\rm{ + }}\frac{\mathit{Z}}{2}{\mathit{Q}_{\rm{3}}}{\rm{cos}}\;\mathit{\beta }{\rm{ - }}{\mathit{F}_{\rm{h}}}{\rm{ = 0。}} \end{array} \right. $ | (9) |
与垂直刚度的计算类似,最终可得直线导轨横向刚度为
| $ {\mathit{k}_\mathit{y}}{\rm{ = 4}}{\rm{.15 \times 1}}{{\rm{0}}^{\rm{4}}}\mathit{Z} \cdot {\rm{co}}{{\rm{s}}^{{\rm{19/9}}}}\mathit{\beta }{\rm{\cdot}}{\mathit{l}^{{\rm{8/9}}}}{\rm{\cdot}}\mathit{\delta }_{_\mathit{y}}^{{\rm{1/9}}}, $ | (10) |
其中
| $ {\mathit{\delta }_\mathit{y}}{\rm{ = }}\frac{{{\rm{7}}{\rm{.68 \times 1}}{{\rm{0}}^{{\rm{ - 5}}}}\mathit{F}_0^{0.9}}}{{{\mathit{Z}^{{\rm{0}}{\rm{.9}}}}{\mathit{l}^{{\rm{0}}{\rm{.8}}}}{\rm{co}}{{\rm{s}}^{{\rm{19/10}}}}\;\mathit{\beta }}}。$ |
直线平台选用IKO交叉滚子直线导轨,X轴型号为CRW 4-400,根据产品样本资料计算出单条导轨垂直刚度和横向刚度分别为3.96×108 N/m和7.93×108 N/m;Y轴型号为CRW 4-240,计算出垂直刚度和横向刚度分别为2.44×108 N/m和4.88×108 N/m。
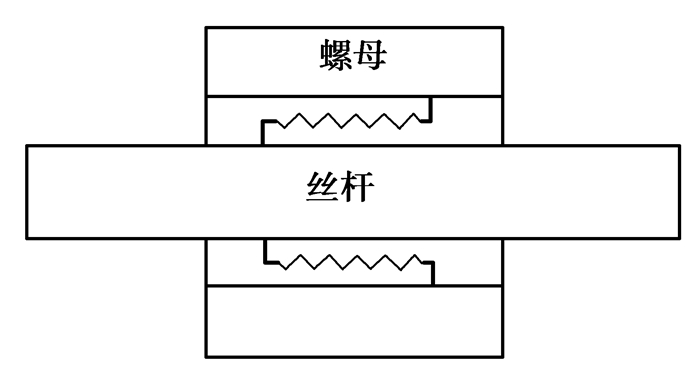
2.2 平台极限位置下动力学建模 2.2.1 滚珠丝杆结合部动力学建模滚珠丝杆结合部在运动传递方向只存在轴向刚度,因此采用沿圆周方向均布的4个弹簧单元连接丝杆和螺母组件,等效替代滚珠丝杆副实际结构,建模方法如图 4所示。每个弹簧单元的刚度为滚珠丝杆副轴向刚度的1/4。
|
图 4 滚珠丝杆结合部动力学模型 Figure 4 Dynamic model of ball screw joint part |
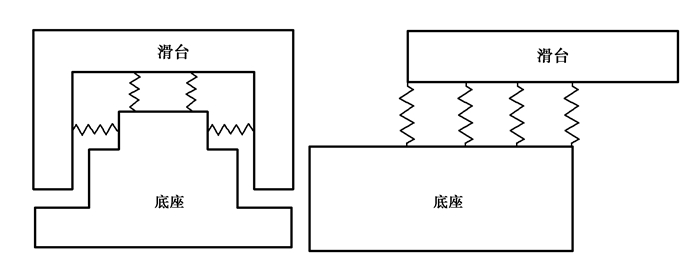
直线导轨结合部存在垂直刚度和横向刚度,十字滑台在极限位置时只有部分导轨承受载荷,因此建模方法如图 5所示。在导轨实际承载长度范围内均布多组垂直方向和横向的弹簧单元连接底座和滑台,等效替代交叉滚子直线导轨的实际结构,每个弹簧单元的刚度为
| $ \left\{ \begin{array}{l} {{\mathit{k'}}_{{\rm{v}}}}{\rm{ = }}\frac{{\mathit{Z'}}}{{\mathit{ZN}}}{\mathit{k}_{\rm{v}}}{\rm{, }}\\ {{\mathit{k'}}_{{\rm{h}}}}{\rm{ = }}\frac{{\mathit{Z'}}}{{\mathit{ZN}}}{\mathit{k}_{\rm{h}}}, \end{array} \right. $ | (11) |
|
图 5 直线导轨结合部动力学模型 Figure 5 Dynamic model of linear guide way joint part |
式中:k′v为单个弹簧单元垂直刚度;Z′为单排导轨是实际承载的滚子个数;N为单排弹簧单元个数;k′h为单个弹簧单元横向刚度。
2.3 平台极限位置下模态分析采用ANSYS Workbench软件对平台进行模态分析,滚珠丝杆结合部和直线导轨结合部采用2.2.2节建立的动力学模型,边界条件根据实际情况在Y轴平台底面施加固定约束,最终获得十字滑台前4阶固有频率和模态振型如表 1和图 6所示。
| 表 1 交错轴工况下十字滑台固有频率 Table 1 Natural frequency of cross platform at limit position |

|
图 6 前4阶模态振型 Figure 6 The first four steps of modal shapes |
分析得到的平台各阶固有频率和模态振型是系统在外部激振力作用下进行动态响应分析的重要参数,也为后续平台的振动测试提供了理论依据。
3.1 测试过程为了验证实验平台的动态特性,拟通过减速器样机测试对实验平台在实际工况下的振动特性进行评估。为了测试平台在极限位置下的振动特性,实验采用交错轴形式的蜗轮蜗杆减速器样机。为了得到实验平台振动的最大幅值,将加速度传感器的测点设置在离悬臂支撑的最远端,测试现场安装图如图 7所示。振动测试的设备采用BK 4535B型三向加速度传感器,通过BK 3050-A-060型号的数据采集器和PULSE软件进行数据采集和分析。

|
图 7 样机测试现场安装 Figure 7 Installation of sample test spot |
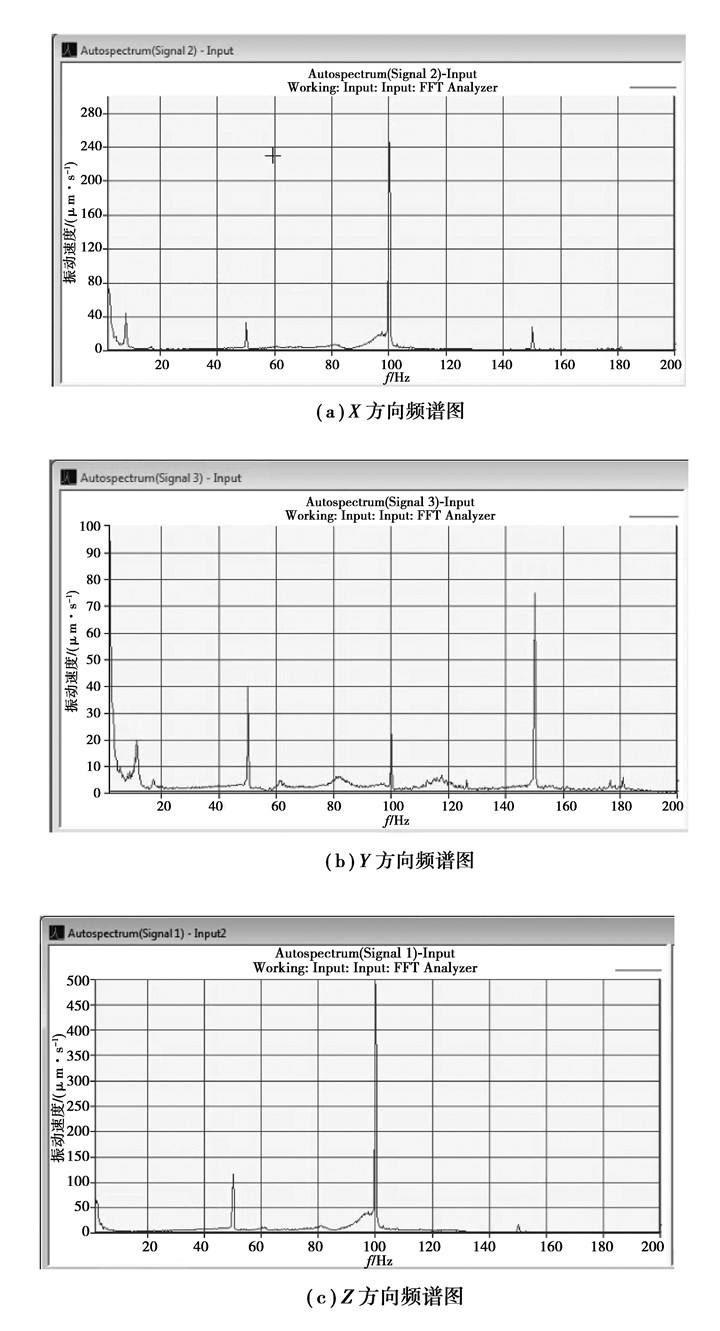
实验过程设置驱动电机转速为3 000 r/min,输出端扭矩为5 N·m,即电机轴转频为50 Hz,减速器样机为双头蜗杆传动,因此啮合频率为100 Hz,最终测试结果如图 8所示。
|
图 8 平台振动速度频谱 Figure 8 spectrum of vibration velocity of platform |
结果表明,X、Y、Z3个方向振动速度的主要频率成分为50、100、150 Hz,X和Z方向的振动速度总值明显大于Y方向,且这两个方向幅值最大的频率均为100 Hz,与啮合频率一致。实验平台沿Z方向的振动速度总值最大,是因为悬臂支持导致垂直刚度减小。
实验平台最大振动速度总值为0.487 mm/s。根据GB/T 6075.1—2012的机器振动评价标准,按照15 kW以下的小型设备的评价标准,实验平台具有良好的动态性能。如果按照GB 50463—2008隔振设计规范的评价标准,实验平台的振动性能与表面粗糙度为0.8~1.6 μm的精密车床和磨床等设备相当,因此实验平台满足精密设备的振动标准,可以满足高精度、高可靠性的测试要求。
4 结论笔者针对多轴精密传动实验平台的结构特点,建立平台在极限位置下的动力学模型并在此基础上进行了模态分析,获得了平台的固有频率和模态振型;同时在实际工况下对平台进行了振动测试,验证了平台具有良好的动态特性。但是由于平台结构比较复杂,在建模过程中进行了较大的简化,使得分析结果不够精确。后续将进一步考虑结合部的刚度阻尼特性以及结构的内部激振源,进行试验模态测试和动态响应分析研究,从而为平台的动态性能优化奠定基础。
| [1] | Matthew J B, Richard M S, Jeremy J K, et al. An uncertainty analysis of tool setting methods for a precision lathe with a B-axis rotary table[J]. Precision Engineering, 2010, 34(2): 242–252. DOI:10.1016/j.precisioneng.2009.06.003 |
| [2] | Ulu N G, Ulu E, Cakmakci M. Design and analysis of a modular learning based cross-coupled control algorithm for multi-axis precision positioning systems[J]. International Journal of Control, Automation and Systems, 2016, 14(1): 272–281. DOI:10.1007/s12555-014-0125-1 |
| [3] | Ulu N G, Ulu E, Cakmakci M. Learning based cross-coupled control for multi-axis high precision positioning systems[C]//Dynamic Systems and Control Conference Joint with the Jsme 2012, Motion and Vibration Conference., Fort Lauderdale, Florida, USA, October 17-19. 2012:535-541. |
| [4] |
彭玉海, 白海清, 何宁.
基于PMAC的数控试验台研究与开发[J]. 陕西理工学院学报, 2008, 24(2): 34–36.
PENG Yuhai, BAI Haiqing, HE Ning. Study and development of NC test platform based on PMAC[J]. Journal of Shanxi University of Technology, 2008, 24(2): 34–36. (in Chinese) |
| [5] |
蒋书运, 祝书龙.
带滚珠丝杠副的直线导轨结合部动态刚度特性[J]. 机械工程学报, 2010, 46(1): 92–99.
JIANG Shuyun, ZHU Shulong. Dynamic characteristic parameters of linear guideway joint with ball screw[J]. Chinese Journal of Mechanical Engineering, 2010, 46(1): 92–99. (in Chinese) |
| [6] | Wu J S S, Chang J C, Hung J P. The effect of contact interface on dynamic characteristics of composite structures[J]. Mathematics and Computers in Simulation, 2007, 74(6): 454–467. DOI:10.1016/j.matcom.2006.07.003 |
| [7] |
朱坚民, 张统超, 李孝茹.
带滚珠丝杠副的直线导轨结合部动态刚度特性[J]. 机械工程学报, 2015, 51(17): 72–82.
ZHU Jianmin, ZHANG Tongchao, LI Xiaoru. Dynamic characteristic analysis of ball screw feed system based on stiffness characteristic of mechanical joints[J]. Chinese Journal of Mechanical Engineering, 2015, 51(17): 72–82. (in Chinese) |
| [8] | Vicente D A, Hecker R L, Villegasv F J, et al. Modeling and vibration mode analysis of a ball screw drive[J]. The International Journal of Advanced Manufacturing Technology, 2012, 58(1/2/3/4): 257–265. |
| [9] | Hazimeh R, Challita G, Khalil K, et al. Finite element analysis of adhesively bonded composite joints subjected to impact loadings[J]. International Journal of Adhesion & Adhesives, 2014, 56: 24–31. |
| [10] | Zhang Jingrui, Guo Zixi, Zhang Yao. Dynamic characteristics of vibration isolation platforms considering the joints of the struts[J]. Acta Astronautica, 2016, 126: 120–137. DOI:10.1016/j.actaastro.2016.04.001 |
| [11] | LIU Yanjie, SONG Lei, LIU Niuniu. Modeling and parameters identification of the cross roller guide way[C]//International Conference on Mechatronics and Automation, 5-8 Aug, 2012, Chengdu, China[S.l.]:IEEE, 2012:692-696. |
| [12] |
宋磊. 超高加速精密运动平台的动态设计与优化[D]. 哈尔滨: 哈尔滨工业大学, 2012. SONG Lei. Dynamic design and Optimization of high Acceleration and high precision motion platform[D]. Harbin:Harbin Institute of Technology, 2012. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10213-1013038784.htm |
| [13] |
李要芳, 李锻能, 刘智, 等.
采用静压导轨的硬切削车床十字滑台刀架动刚度分析[J]. 机械设计与制造, 2013(5): 143–145.
LI Yaofang, LI Duanneng, LIU Zhi, et al. Dynamic stiffness analysis of cross platform on using hydrostatic guide-way hard turning machine tool[J]. Machine Design & Manufacture, 2013(5): 143–145. (in Chinese) |
| [14] |
林腾蛟, 宋建军, 孟令宽, 等.
风电增速齿轮箱动力学性能优化方法[J]. 重庆大学学报, 2016, 39(4): 16–23.
LIN Tengjiao, SONG Jianjun, MENG Lingkuan, et al. A dynamic behavior optimization method of wind power speed-increase gearbox[J]. Journal of Chongqing University, 2016, 39(4): 16–23. DOI:10.11835/j.issn.1000-582X.2016.04.003 (in Chinese) |
| [15] |
林腾蛟, 郭进, 刘波, 等.
风电增速箱结合部刚度分析及振动噪声预估[J]. 重庆大学学报, 2015, 38(1): 87–94.
LIN Tengjiao, GUO Jin, LIU Bo, et al. Junction stiffness analysis and vibration noise prediction of wind power speed-increase box[J]. Journal of Chongqing University, 2015, 38(1): 87–94. DOI:10.11835/j.issn.1000-582X.2015.01.012 (in Chinese) |
| [16] |
刘衍, 汪劲松, 赵彤, 等.
滚珠丝杠传动系统的刚度模型[J]. 清华大学学报(自然科学版), 2011, 51(5): 601–606.
LIU Yan, WANG Jingsong, ZHAO Tong, et al. Stiffness model for a ball screw drive system[J]. Journal of Tsinghua University(Science and Technology), 2011, 51(5): 601–606. (in Chinese) |
| [17] |
廖伯瑜, 周新民, 尹志宏. 现代机械动力学及其工程应用[M]. 北京: 机械工业出版社, 2003: 245-248.
LIAO Boyu, ZHOU Xinmin, YIN Zhihong. Modern mechanical dynamics and its engineering applications[M]. Beijing: China Machine Press, 2003: 245-248. (in Chinese) |
| [18] | Harris T A, Kotzalas M N. Rolling Bearing Analysis[M]. Suite: CRC Press, 2010: 124-132. |
 2017, Vol. 40
2017, Vol. 40


