轮毂电机驱动电动汽车是指采用轮毂电机直接驱动车轮的清洁能源汽车,具有系统布置灵活,结构简洁紧凑,力矩响应精确迅速,能效高等优点。在以节能、环保和安全作为当今汽车发展三大主题的潮流下,该驱动形式以其独特的优势,成为了电动汽车发展的主要方向[1-2]。
横摆稳定性能的优劣直接影响到汽车的安全性和操稳性。近年来,大量的研究表明,直接横摆力矩控制(DYC, direct yaw moment control)是提升汽车操纵稳定性最有效的技术途径。通过精确和智能的控制汽车横摆力矩可以有效识别和避免汽车的危险状况和不良操作[3-4]。而传统汽车只能通过车辆现有的防抱死制动系统和驱动防滑控制系统,利用差动制动的方式实现DYC,但是制动系统的介入往往会影响汽车的加速性能和正常的驾驶感受[5-6]。与传统汽车相比,轮毂电机驱动电动汽车以其各个车轮的驱动/制动力矩可以更快速、更精确地进行独立控制,因此更加有利于实现车辆的直接横摆力矩控制[7-8]。目前针对轮毂电机驱动电动汽车横摆力矩控制常用的计算控制方法有PID控制、模型跟踪控制、基于前馈与反馈的线性二次型最优控制、滑模变结构控制(SMC, sliding mode control)、模糊控制(FLC, fuzzy logic control)等[9-12]。其中对系统数学模型精度要求小的滑模控制和完全不依赖系统模型的模糊控制具有结构简单、控制鲁棒性好的特点受到了广泛的关注和研究。然而文献[13]指出这两种控制方法都有控制原理上的不足,比如SMC的抖振问题以及FLC在完全脱离系统模型后,其控制参数的确定只能凭借经验反复试凑,缺乏系统的理论指导。
为了充分利用SMC和FLC控制上的优势,弥补其性能缺陷,笔者建立了基于模糊滑模控制(FSMC, fuzzy sliding mode control)横摆力矩控制器。针对现有设备难以精确测量车辆质心侧偏角等参数的问题,建立了结构简单,计算快速的非线性滑模观测器。最后为了验证FSMC控制器的有效性,建立了充分考虑地面附着、电机输出等实际约束情况的等比例转矩分配控制器,并结合MATLAB/Simulink与Carsim联合仿真平台进行了仿真分析。
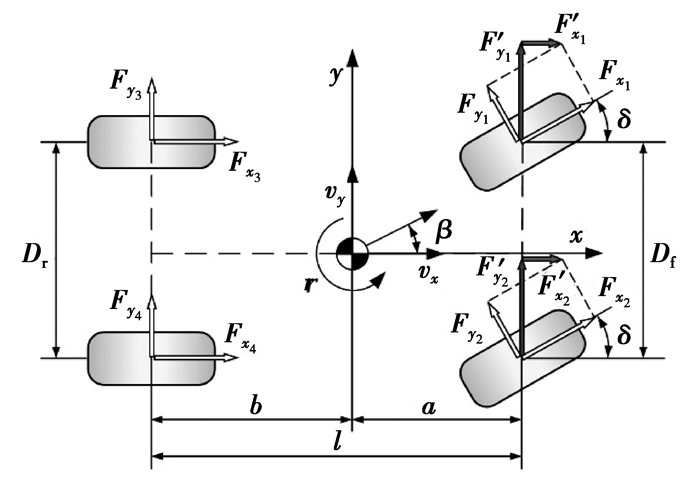
1 车辆动力学建模 1.1 7自由度整车模型由于横摆运动和侧向运动是决定车辆稳定性的主要运动特征[14],所以建立了一个具有横摆、侧向、纵向以及4个车轮回转运动的7自由度整车模型,如图 1所示。
|
图 1 七自由度整车模型 Figure 1 7-DOF whole vehicle model |
车辆运动方程为:
纵向运动
| $ m{a_x} = m\left( {\dot vx - {v_y}r} \right) = \left( {{{F'}_{{x_1}}} + {{F'}_{{x_2}}} + {F_{{x_3}}} + {F_{{x_4}}}} \right), $ | (1) |
侧向运动
| $ m{a_y} = m\left( {\dot vv - {v_x}r} \right) = \left( {{{F'}_{{y_1}}} + {{F'}_{{y_2}}} + {F_{{y_3}}} + {F_{{y_4}}}} \right), $ | (2) |
横摆运动
| $ {I_z}\dot r = a\left( {{{F'}_{{y_1}}} + {{F'}_{{y_2}}}} \right) - b\left( {{F_{{y_3}}} + {F_{{y_4}}}} \right) + {D_{\rm{f}}}\left( {{{F'}_{{x_2}}} - {{F'}_{{x_1}}}} \right)/2 + {D_{\rm{r}}}\left( {{F_{{x_4}}} - {F_{{x_3}}}} \right)/2, $ | (3) |
其中
| $ \left[ {\begin{array}{*{20}{c}} {{{F'}_{{x_i}}}}\\ {{{F'}_{{y_i}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\cos \delta }&{ - \sin \delta }\\ {\sin \delta }&{\cos \delta } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{F_{{x_i}}}}\\ {{F_{{y_i}}}} \end{array}} \right],i = 1,2。$ | (4) |
4轮回转运动
| $ {I_{wi}}{{\dot \omega }_i} = {T_i} - {F_{{x_i}}}R, $ | (5) |
式中:ax和ay分别为整车的纵向、侧向加速度;vx和vy分别为整车纵向、侧向速度;a和b分别为质心到前后轴的距离;Df和Dr分别为前后轮距;r为横摆角速度;δ为前轮转角;Iz为整车绕z轴的转动惯量;R为车轮滚动半径;Iwi为各车轮绕回转轴的转动惯量;ωi为各个车轮角速度;Fxi和Fyi分别为各个轮胎的纵向力和横向力;Ti为各个车轮所受到的总转矩,且驱动为正, 制动为负,i=1, 2, 3, 4为4个车轮代号。
1.2 轮胎模型笔者采用拟合精度高、使用简便的魔术轮胎模型,同时为了更好地描述路面附着系数对轮胎附着力的影响,在传统的魔术公式中加入路面附着系数μ,形成改进的魔术公式轮胎模型[15]。其统一表达式为
| $ {F_{\rm{t}}} = {D^ * }\sin \left\{ {{C^ * }\arctan \left( {{B^ * }\sigma - E\left( {{B^ * }\sigma - \arctan \left( {{B^ * }\sigma } \right)} \right]} \right.} \right\} + {S_v}, $ | (6) |
其中
| $ \left\{ \begin{array}{l} {B^ * } = \left( {2 - \mu } \right)B,\\ {C^ * } = \left( {5/4 - \mu /4} \right)C,\\ {D^ * } = \mu D。\end{array} \right. $ |
式中:Ft为输出的纵向力或侧向力;σ为轮胎侧偏角或纵向滑移率;B,C,D,E为与轮胎垂向载荷相关的多项式,其具体表达式见参考文献[16]。
公式(6)为车轮纯滑移或纯侧偏工况下的轮胎力计算模型,在对汽车操稳性控制过程中,轮胎实际工作在联合工况下,即同时存在滑移和侧偏工况。其联合工况下的力学响应可以根据文献[17]中所提出的广义位移进行计算。
| $ \sigma _x^ * = \frac{{{\sigma _x}}}{{1 + {\sigma _x}}},\sigma _y^ * = \frac{{\tan \left( {{\sigma _y}} \right)}}{{1 + {\sigma _x}}}。$ | (7) |
则等效联合广义位移为
| $ {\sigma ^ * } = \sqrt {\sigma _x^{ * 2} + \sigma _y^{ * 2}} 。$ | (8) |
联合工况下轮胎纵向力和侧向力的响应为
| $ {F_x} = \frac{{\sigma _x^ * }}{{{\sigma ^ * }}}{F_{\rm{t}}}\left( {{\sigma ^ * }} \right),{F_y} = \frac{{\sigma _y^ * }}{{{\sigma ^ * }}}{F_{\rm{t}}}\left( {{\sigma ^ * }} \right)。$ | (9) |
由于现代电机制造和控制技术都比较成熟,其瞬时响应速度比车轮的瞬时响应要快几十倍,所以可以将其简化为一个二阶响应系统[18]。其传递函数为
| $ G\left( s \right) = \frac{{{T_{{\rm{m}}i}}}}{{T_{{\rm{m}}i}^ * }} = \frac{1}{{2{\xi ^2}{s^2} + 2\xi s + 1}}, $ | (10) |
式中:Tmi为给各个电动轮实际输入的驱动/制动电磁转矩;Tmi*为各电动轮期望的驱动/制动电磁转矩输入;ξ为与驱动电机参数相关的阻尼比,笔者根据永磁同步电机响应特性,将其取值为0.001。
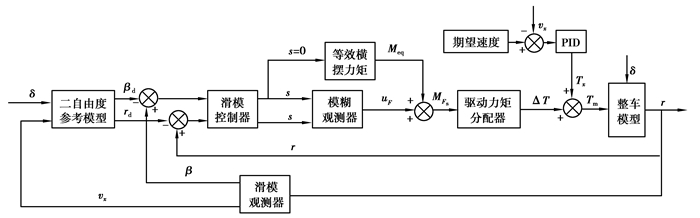
2 电动汽车稳定性控制器笔者所设计的控制器整体采用上下层结构,上层为模糊滑模控制器,用以计算使车辆状态跟踪期望横摆角速度和质心侧偏角所需要的横摆力;下层控制为驱动力矩分配器,用以根据上层输入的期望横摆力矩和其他约束条件,计算各个车轮所需的驱动力矩。控制器的具体结构如图 2所示。
|
图 2 横摆稳定性控制器结构原理图 Figure 2 The structure of yaw stability controller |
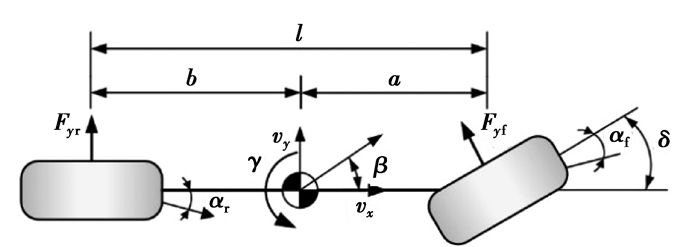
由于线性2自由度模型表达简单,却包含了车身质量、前后轴侧偏刚度、轴距等反映汽车侧向运动最为关键的几个量,所以国内外许多学者将线性2自由度车辆模型作为车辆动力学稳定性控制的参考模型。其受力分析如图 3所示。
|
图 3 线性二自由度车辆模型 Figure 3 Linear reference model of 2-DOF vehicle |
以汽车的质心侧偏角β和横摆角速度r为2自由度系统的状态变量,以前轮转角δ作为输入,则汽车转向时的运动特性可以表示为如下状态方程:
| $ \left[ {\begin{array}{*{20}{c}} {\dot \beta }\\ {\dot r} \end{array}} \right] = A\left[ {\begin{array}{*{20}{c}} \beta \\ r \end{array}} \right] + B\delta , $ | (11) |
| $ A = \left[ {\begin{array}{*{20}{c}} {\frac{{{C_{\rm{f}}} + {C_{\rm{r}}}}}{{m{v_x}}}}&{\frac{{a{C_{\rm{f}}} - b{C_{\rm{r}}}}}{{mv_x^2}} - 1}\\ {\frac{{a{C_{\rm{f}}} - b{C_{\rm{r}}}}}{{{I_z}}}}&{\frac{{{a^2}{C_{\rm{f}}} + {b^2}{C_{\rm{r}}}}}{{{I_z}{v_x}}}} \end{array}} \right],B = \left[ {\begin{array}{*{20}{c}} { - \frac{{{C_{\rm{f}}}}}{{m{v_x}}}}\\ { - \frac{{a{C_{\rm{f}}}}}{{{I_z}}}} \end{array}} \right], $ | (12) |
式中Cf和Cr为前后轴的等效侧偏刚度。
由此可以计算出汽车理想的质心侧偏角βd和理想的横摆角速度rd[19]:
| $ {\beta _{\rm{d}}} = \frac{{al{C_{\rm{f}}}{C_{\rm{r}}} + mv_x^2a{C_{\rm{f}}}}}{{b{l^2}{C_{\rm{f}}}{C_{\rm{r}}} + mv_x^2\left( {a{C_{\rm{f}}} - b{C_{\rm{r}}}} \right)}}\delta , $ | (13) |
| $ {r_{\rm{d}}} = \frac{{l{C_{\rm{f}}}{C_{\rm{r}}}{v_x}}}{{b{l^2}{C_{\rm{f}}}{C_{\rm{r}}} + mv_x^2\left( {a{C_{\rm{f}}} - b{C_{\rm{r}}}} \right)}}\delta 。$ | (14) |
为了更好地限制车辆侧滑,保持行驶方向的一致性,将理想质心侧偏角定义为
| $ {\beta _{\rm{d}}} = 0。$ | (15) |
此外由于路面附着条件的限制,理想横摆角速度还需要满足关系式
| $ \left| {{r_{\rm{d}}}} \right| \le \left| {0.85\frac{{\mu g}}{{{v_x}}}} \right|, $ | (16) |
式中g为重力加速度。考虑路面附着系数的限制,理想横摆角速度的取值为
| $ {r_{\rm{d}}} = \min \left\{ {\left| {{r_{\rm{d}}}} \right|,\left| {0.85\frac{{\mu g}}{{{v_x}}}} \right|} \right\}{\rm{sgn}}\;\delta 。$ | (17) |
图 4反映了理想横摆角速度与车速的关系,实线为等前轮转角线,虚线为等路面附着系数的限制界限,图中直观地表明了理想横摆角速度受到路面所能提供最大支持力的限制。

|
图 4 理想横摆角速度与车速的关系 Figure 4 The relationship between rd and vx |
根据公式(1)~(5),可以将轮毂电机驱动电动汽车7自由度车辆模型表示为如下非线性系统
| $ \mathit{\boldsymbol{ \boldsymbol{\dot \varGamma} }} = {f_7}\left( {\mathit{\Gamma ,u}} \right), $ | (18) |
| $ \mathit{\boldsymbol{ \boldsymbol{\varPsi} }} = CT, $ | (19) |
其中车辆系统的状态向量为
| $ \mathit{\boldsymbol{ \boldsymbol{\varGamma} }} = {\left[ {\begin{array}{*{20}{c}} {{v_x}}&{{v_y}}&{{\omega _1}}&{{\omega _2}}&{{\omega _3}}&{{\omega _4}} \end{array}} \right]^{\rm{T}}}。$ | (20) |
车辆系统的输入量则是方向盘转角和4个车轮的驱动力矩,故输入向量为
| $ \mathit{\boldsymbol{u}} = {\left[ {\begin{array}{*{20}{c}} \delta &{{T_1}}&{{T_2}}&{{T_3}}&{{T_4}} \end{array}} \right]^{\rm{T}}}。$ | (21) |
根据目前常规的车辆传感器可以容易获得车辆的横摆角速度以及车轮角速度,所以将输出向量定义为
| $ \mathit{\boldsymbol{ \boldsymbol{\varPsi} }} = {\left[ {\begin{array}{*{20}{c}} \gamma &{{\omega_1}}&{{\omega_2}}&{{\omega_3}}&{{\omega_4}} \end{array}} \right]^{\rm{T}}}, $ | (22) |
由此输出矩阵C可以由式(19)(20)和(22)得出。
由于车轮转速可以方便获得,故不需要进行估计。而且轮胎的纵向力和横向力也可由测得的车轮转速和公式(6)计算得出。为了降低观测器的规模,简化其结构,可以将车辆系统简化为
| $ \mathit{\boldsymbol{\dot X}} = {f_7}\left( {X,u} \right), $ | (23) |
| $ Y = r, $ | (24) |
其中状态向量为
| $ \mathit{\boldsymbol{X}} = {\left[ {\begin{array}{*{20}{c}} {{v_x}}&{{v_y}}&r \end{array}} \right]^{\rm{T}}}, $ | (25) |
输出值即为横摆角速度。
滑模观测器是基于滑动模态理论,利用易测量状态量的测量值与其估计值的误差,对观测器的估计值进行修整,使得观测器可以消除干扰的影响,具有良好的鲁棒性。根据这一原理可以将车辆系统降维滑模观测器设计为[20]
| $ \mathit{\boldsymbol{\dot X}} = {f_3}\left( {\hat X,u} \right) - \mathit{\boldsymbol{\eta }}\left( {\hat r - r} \right) - \mathit{\boldsymbol{\kappa }}{\mathop{\rm sgn}} \left( {\hat r - r} \right), $ | (26) |
| $ \mathit{\boldsymbol{\hat X}} = {\left[ {\begin{array}{*{20}{c}} {{{\hat v}_x}}&{{{\hat v}_y}}&{\hat r} \end{array}} \right]^{\rm{T}}}, $ | (27) |
其中η和κ分别为滑模观测器的阻尼系数矩阵和鲁棒控制项系数矩阵,根据需要将其值分别定为
| $ \mathit{\boldsymbol{\eta }} = {\left[ {\begin{array}{*{20}{c}} 0&{12} \end{array}} \right]^{\rm{T}}},\mathit{\boldsymbol{\kappa }} = {\left[ {\begin{array}{*{20}{c}} 0&8&{16} \end{array}} \right]^{\rm{T}}}。$ |
车辆质心侧偏角的估计值可以表示为
| $ \hat \beta = {\rm{arctan}}\left( {{{\hat v}_y}/{{\hat v}_x}} \right)。$ | (28) |
滑模控制器的主要任务是计算出使车辆按照理想状态行驶所需要的附加横摆力矩。笔者以横摆角速度和质心侧偏角为控制变量,定义滑模控制的切换函数为
| $ s = r - {r_{\rm{d}}} + \lambda \left( {\beta - {\beta _{\rm{d}}}} \right), $ | (29) |
对s求导得
| $ \dot s = \dot r - {{\dot r}_{\rm{d}}} + \lambda \left( {\dot \beta - {{\dot \beta }_{\rm{d}}}} \right), $ | (30) |
式中λ为滑模面控制参数。根据公式(3)和(4)可得
| $ {I_z}\dot r = a\left( {{F_{{y_1}}} + {F_{{y_2}}}} \right)\cos \delta + a\left( {{F_{{x_1}}} + {F_{{x_2}}}} \right)\sin \delta - b\left( {{F_{{y_3}}} + {F_{{y_4}}}} \right) - {D_{\rm{f}}}\left( {{F_{{y_2}}} -\\ {F_{{y_1}}}} \right)\sin \delta /2 + {\mathit{\boldsymbol{M}}_{{\rm{zc}}}}, $ | (31) |
式中Mzc为控制器所施加的横摆力矩,其表达式为
| $ {M_{{\rm{zc}}}} = {D_{\rm{f}}}\left( {{F_{{x_2}}} + {F_{{x_1}}}} \right)\cos \delta /2 + {D_{\rm{r}}}\left( {{F_{{x_4}}} + {F_{{x_3}}}} \right)/2。$ | (32) |
根据
| $ {M_{{\rm{eq}}}} = {I_z}\left[ {{{\dot r}_{\rm{d}}} - \lambda \left( {r - {r_{\rm{d}}}} \right)} \right] - a\left( {{F_{{y_1}}} + {F_{{y_2}}}} \right)\cos \delta + b\left( {{F_{{y_3}}} + {F_{{y_4}}}} \right) +\\ {D_{\rm{f}}}\left( {{F_{{y_2}}} - {F_{{y_1}}}} \right)\sin \delta /2。$ | (33) |
为了保证控制系统在受到外界干扰后能在有限的时间内稳定到滑模控制面,还需要给等效横摆力矩添加一个滑模变结构控制律
| $ {u_{\rm{s}}} = - {\kappa _{\rm{s}}}{\mathop{\rm sgn}}\; s, $ | (34) |
式中κs为滑模控制系数,通常为了减小控制律中符号函数引起的抖振问题,利用饱和函数sat(s/Δ)代替,饱和函数的定义为
| $ {\rm{sat}}\left( {s/{\mathit{\Delta}} } \right) = \left\{ \begin{array}{l} s/{\mathit{\Delta}} ,\left| {s/{\mathit{\Delta}} } \right| \le 1;\\ {\mathop{\rm sgn}} \left( {s/{\mathit{\Delta}} } \right),\left| {s/{\mathit{\Delta}} } \right|1。\end{array} \right. $ | (35) |
则滑模控制的最终输出为
| $ {M_{\rm{s}}} = {M_{{\rm{eq}}}} + {u_{\rm{s}}} = {M_{{\rm{eq}}}} - {\kappa _{\rm{s}}}{\rm{sat}}\left( {s/{\mathit{\Delta}} } \right)。$ | (36) |
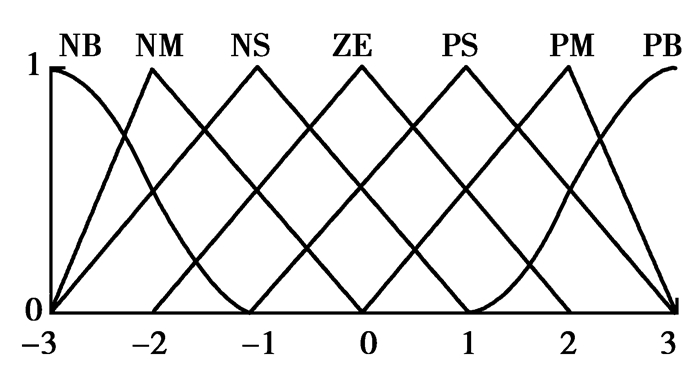
为了更加有效地减小由滑模控制律引起的系统抖振问题,笔者利用模糊控制理论进行控制律的计算。该模糊控制器以滑模切换函数s及其导数
| $ s = \left\{ {{\rm{NB}},{\rm{NM}},{\rm{NS}},{\rm{ZE}},{\rm{PS}},{\rm{PM}},{\rm{PB}}} \right\}, $ |
| $ \dot s = \left\{ {{\rm{NB}},{\rm{NM}},{\rm{NS}},{\rm{ZE}},{\rm{PS}},{\rm{PM}},{\rm{PB}}} \right\}, $ |
| $ {u_{\rm{F}}} = \left\{ {{\rm{NL}},{\rm{NB,NM}},{\rm{NS}},{\rm{ZE}},{\rm{PS}},{\rm{PM}},{\rm{PB}},{\rm{PL}}} \right\}。$ |
其论域为
| $ s = \left\{ { - 3, - 2, - 1,0, + 1, + 2, + 3} \right\}, $ |
| $ \dot s = \left\{ { - 3, - 2, - 1,0, + 1, + 2, + 3} \right\}, $ |
| $ {u_{\rm{F}}} = \left\{ { - 4, - 3, - 2, - 1,0, + 1, + 2, + 3, + 4} \right\}。$ |
|
图 5 s与 |
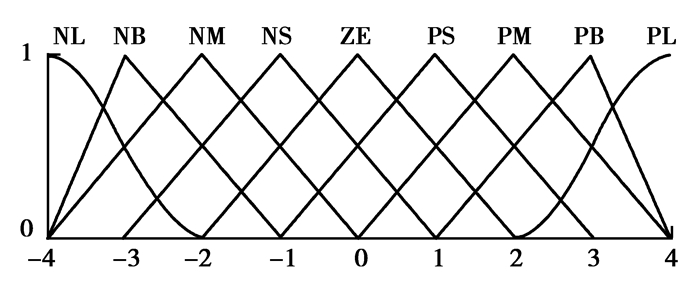
|
图 6 uF隶属度函数 Figure 6 The membership function of uF |
模糊控制规则作为模糊控制器的核心,一般的模糊控制器由于脱离了系统模型,只能根据经验反复试凑才能确定。
在FSMC中,模糊控制的输入为滑模切换函数s及其导数
| 表 1 模糊控制规则 Table 1 Fuzzy control rules |
图 7直观描述了滑模控制器的工作流程。
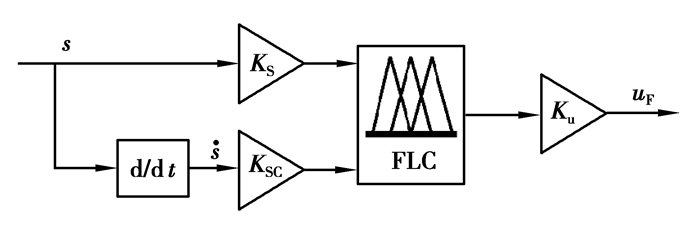
|
图 7 模糊控制结构图 Figure 7 The structure of fuzzy controller |
图中KS与KSC为输入的量化因子,是将输入从实际值域映射到其模糊论域中;Ku为输出比例因子,是将模糊输出转换为实际的控制输出。则模糊滑模控制的最终控制规律为
| $ {M_{{F_{\rm{s}}}}} = {M_{{\rm{eq}}}} + {u_{\rm{F}}}。$ | (37) |
为了使模糊滑模控制与单独的滑模控制输出结果具有可比性,这里将滑模控制系数κs取为300,模糊控制比例因子Ku取为300/4,使得us与uF的输出范围都为(-300, 300)。
2.4 驱动力矩分配通过上层控制计算得到的附加横摆力矩MFs,需要换算成各个车轮的转矩输入,才能最终实现对汽车的直接横摆力矩控制。
当不考虑轮胎的滚动阻力时,车轮的旋转动力学方程为
| $ {T_i} = {F_{{x_i}}}R, $ | (38) |
其中电机所能输出的转矩大小受到电动机最大电磁转矩的限制,参照文献[21]取电机的最大扭矩Tdmax=350 N·m, 则有
| $ - {T_{{\rm{dmax}} }} \le {T_i} \le {T_{{\rm{dmax}} }}。$ | (39) |
而轮胎的纵向力同样受到路面附着系数和轮胎垂向载荷的约束,即
| $ - \mu {F_{{z_i}}} \le {F_{{x_i}}} \le \mu {F_{{z_i}}}。$ | (40) |
根据式(38)与(40)可以得到为了使轮胎工作在附着极限内,而不至因为转矩输入过大使轮胎产生强烈滑转,严重恶化轮胎的受力情况,电机的转矩输出需满足以下约束
| $ - \mu {F_{{z_i}}}R \le {T_i} \le \mu {F_{{z_i}}}R。$ | (41) |
为了每个车轮因直接横摆力矩控制所承担的附加纵向力均较小,以提高车轮的稳定裕度,且控制系统能快速响应,采用等比例转矩分配的形式,即每个车轮所受到的转矩修正相等,即
| $ \left| {{T_i}} \right| = \left| {\frac{{{M_{{F_{\rm{s}}}}}R}}{{2D}}} \right|, $ | (42) |
这里假设汽车的前后轮距都相等,即:Df=Dr=D。
下层控制器除了确定每个车轮所分配的转矩大小外,还需要确定转矩方向,即确定各个车轮应该驱动还是制动。这就需要分析当前汽车所处的转向状态,也就是驾驶员的操作意图。利用前轮转角δ和横摆角速度偏差e=r -rd来判断汽车是不足转向还是过多转向,由此确定各个转矩的方向。
另外为了防止汽车对状态偏差e过于灵敏,防止控制器的频繁启停,设置了横摆角速度偏差的门限值erth≥0,使得汽车实际横摆角速度与理想横摆角速度偏差达到所设置的门限值时,控制器才起作用(进行横摆力矩控制)。详细决策如表 2所示。
| 表 2 车轮转矩分配规则 Table 2 Torque distribution rule |
由于实验条件的限制,笔者采用与文献[22]相同的车辆参数(表 3)、方向盘转角输入(图 8(a))和相同的车速80 km/h,进行仿真验证,仿真结果与其试验数据的对比如图 8(b)~8(d)所示。
| 表 3 车辆参数 Table 3 Main parameters of vehicle |
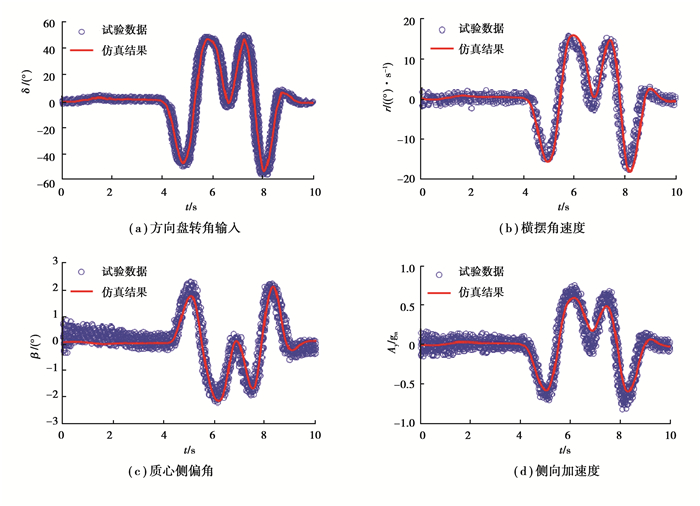
|
图 8 车辆仿真模型试验验证 Figure 8 Vehicle simulation model test verification |
由图 8可以得出,在相同的转角输入和运行工况下,车辆运行状态的仿真结果与试验数据基本保持一致,验证了车辆仿真模型的精确性,因此将该仿真模型视为参考车辆对本文所建立的稳定性控制器进行有效性验证。
3.2 算法验证为了验证所建立的控制器在车辆极限工况下的控制性能,在车辆仿真初始速度为100 km/h,路面附着系数为0.5的状况下,对车辆前轮进行正弦转角输入。仿真结果如图 9所示。
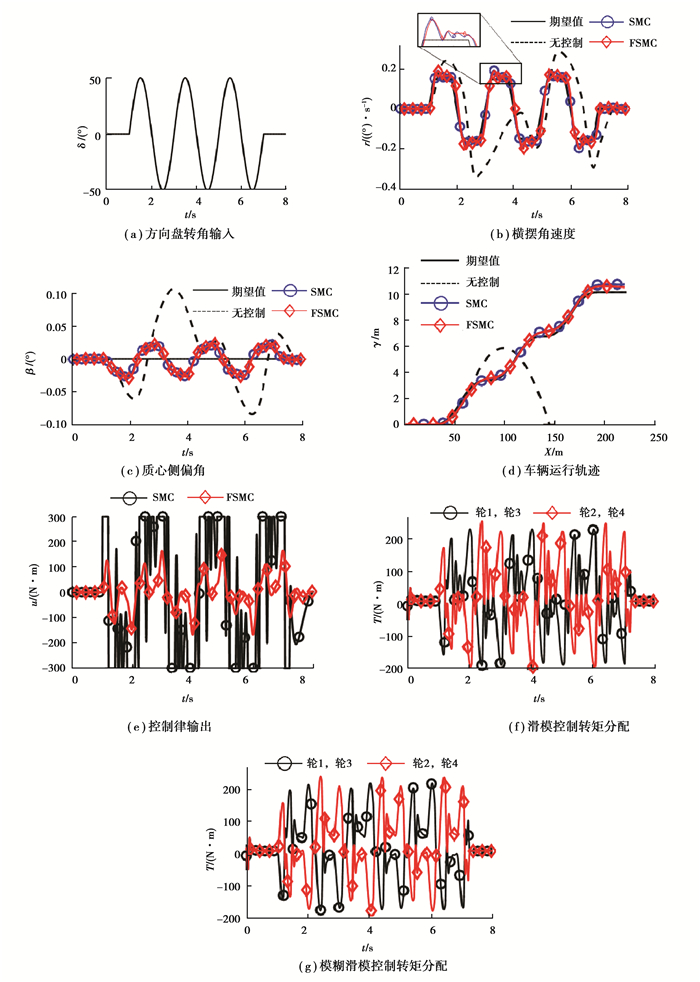
|
图 9 正弦输入仿真结果 Figure 9 The simulation results of sine input |
根据图 9(b)~(d)可知,车辆在没有控制的情况下,偏离期望值较大,而SMC与FSMC都取得了较好的控制效果。但是在后者的控制下车辆的横摆角速度变化更加平滑。图 9(e)~(g)更加表明由于在FSMC控制下的控制律变化波动较小,使得电机转矩的幅值和频率都得到了较大改善。这对驱动系统的疲劳寿命有很大的益处。
4 结论1) 由于整车系统具有高度的非线性,在紧急工况下,不施加任何控制,其横摆角速度不能快速响应,且与理想值之间有很大的误差,容易出现失稳现象。针对上述问题,笔者基于模糊滑模控制建立的稳定性控制器有效提高了轮边驱动电动汽车的行驶稳定性。
2) 将模糊控制与滑模控制相结合,既能有效改善滑模控制的抖振问题,也使模糊控制规则的制定具有理论依据。在保持控制系统良好控制效果的同时,使控制输出更加平顺,有效提高了控制系统的品质。
| [1] | Hori Y. Future vehicle driven by electricity and control-research on four wheel motored UOT Electric March Ⅱ[J]. IEEE Transactions on Industrial Electronics, 2002, 51(5): 1–14. |
| [2] | Murata S. Innovation by in-wheel-motor drive unit[J]. Vehicle System Dynamics, 2012, 50(6): 807–830. DOI:10.1080/00423114.2012.666354 |
| [3] | Goodarzi A, Diba F, Esmailzadeh E. Innovative active vehicle safety using integrated stabilizer pendulum and direct yaw moment control[J]. Journal of Dynamic Systems Measurement & Control, 2014, 136(5): 562–576. |
| [4] |
张为, 王伟达, 丁能根, 等.
汽车ESC系统主环伺服环分层结构控制策略[J]. 重庆大学学报, 2012, 35(7): 19–24.
ZHANG Wei, WANG Weida, DING Nenggen, et al. The main-loop and servo-loop structure control strategy of ESC[J]. Journal of Chongqing University, 2012, 35(7): 19–24. DOI:10.11835/j.issn.1000-582X.2012.07.004 (in Chinese) |
| [5] |
杨鹏飞, 熊璐, 余卓平.
四轮轮毂电机驱动电动汽车电机/液压系统联合控制策略[J]. 汽车工程, 2013(10): 921–926.
YANG Pengfei, XIONG Lu, YU Zhuoping. Motor/hydraulic systems combined stability control strategy for distributed electric drive vehicle[J]. Automotive Engineering, 2013(10): 921–926. DOI:10.3969/j.issn.1000-680X.2013.10.013 (in Chinese) |
| [6] | Jacobsen B. Potential of electric wheel motors as new chassis actuators for vehicle manoeuvring[J]. Proceedings of the Institution of Mechanical Engineers, Part D:Journal of Automobile Engineering, 2002, 216(8): 631–640. DOI:10.1177/095440700221600801 |
| [7] | Hori Y. Future vehicle driven by electricity and control-research on four-wheel-motored "UOT electric march Ⅱ"[J]. IEEE Transactions on Industrial Electronics, 2004, 51(5): 954–962. DOI:10.1109/TIE.2004.834944 |
| [8] | Kim D, Hwang S, Kim H. Vehicle stability enhancement of four-wheel-drive hybrid electric vehicle using rear motor control[J]. IEEE Transactions on Vehicular Technology, 2008, 57(2): 727–735. DOI:10.1109/TVT.2007.907016 |
| [9] | Song C, Li S, Song S, et al. Study of direct yaw moment control for IEV to improve handling and stability control[C]//Sixth International Conference on Intelligent Control and Information Processing, Beijing:2015:230-236. |
| [10] | Shino M, Nagai M. Yaw-moment control of electric vehicle for improving handling and stability[J]. Jsae Review, 2001, 22(4): 473–480. DOI:10.1016/S0389-4304(01)00130-8 |
| [11] | Zhao Y, Zhang Y. Fuzzy control for the handling stability of motor drive electric vehicle[C]//International Conference on Computer and Information Application, Tianjin:IEEE, 2010:361-365. |
| [12] |
李静, 余春贤, 朱冰, 等.
基于主动横摆力矩优化分配的车辆底盘集成控制[J]. 吉林大学学报(工学版), 2011(S1): 36–40.
LI Jing, YU Chunxian, ZHU Bing, et al. Integrated chassis control base on optimal distributing active yaw moment[J]. Journal of Jilin University (Engineering and Technology Edition), 2011(S1): 36–40. (in Chinese) |
| [13] |
傅春, 谢剑英.
模糊滑模控制研究综述[J]. 信息与控制, 2001, 30(5): 434–439.
FU Chun, XIE Jianying. A survey of research on fuzzy sliding mode control[J]. Information & Control, 2001, 30(5): 434–439. (in Chinese) |
| [14] |
马春卉, 吴志林, 王良模, 等.
汽车ESP系统的建模和控制方法[J]. 南京理工大学学报, 2010, 34(1): 108–112.
MA Chunhui, WU Zhilin, WANG Liangmo, et al. Modeling and controlling method for vehicle ESP System[J]. Journal of Nanjing University of Science and Technology, 2010, 34(1): 108–112. (in Chinese) |
| [15] | Jagt P, Parsons A W. Road surface correction of tire test data[J]. Vehicle System Dynamics, 1996, 25(2): 147–165. DOI:10.1080/00423119608968962 |
| [16] | Bakker E, Nyborg L, Pacejka H B. Tyre modeling for use in vehicle dynamics studies[C/OL]. Society of Automotive Engineers International Congress and Expo, Detroit, MI, USA, 23 Feb, 1987. Society of Automotive Engineers, Warrendale, PA, 1987. |
| [17] | Pacejka H. Tire and vehicle dynamics[M]. Amsterdam: Elsevier, 2005. |
| [18] | Tahami F, Kazemi R, Farhanghi S. A novel driver assist stability system for all-wheel-drive electric vehicles[J]. IEEE Transactions on Vehicular Technology, 2003, 52(3): 683–692. DOI:10.1109/TVT.2003.811087 |
| [19] | Rajamani R. Vehicle dynamics and control[M]. Massachusetts: Springer Science & Business Media, 2011: 146-148. |
| [20] | Chen Y, Ji Y, Guo K. A reduced-order nonlinear sliding mode observer for vehicle slip angle and tyre forces[J]. Vehicle System Dynamics, 2014, 52(12): 1716–1728. DOI:10.1080/00423114.2014.960430 |
| [21] | Xiong L, Yu Z, Wang Y, et al. Vehicle dynamics control of four in-wheel motor drive electric vehicle using gain scheduling based on tyre cornering stiffness estimation[J]. Vehicle System Dynamics, 2012, 50(6): 1–16. |
| [22] |
陈禹行. 布式驱动电动汽车直接横摆力矩控制研究[D]. 吉林大学, 2013. CHEN Yuxing. Study of direct yaw moment control for in-wheel motor electric vehicles[D]. Jilin University, 2013. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10183-1013193247.htm |
 2017, Vol. 40
2017, Vol. 40

