b. 重庆大学 山地城镇建设与新技术教育部重点实验室, 重庆 400045
b. Key Laboratory of New Technology for Construction of Cities in Mountain Area, Ministry of Education, Chongqing University, Chongqing 400045, P. R. China
结构内力分析需满足平衡、协调和本构三大基本方程以及边界条件。传统的矩阵位移法和矩阵力法[1]通常是将这3个方程和边界条件统一在一套结构刚度方程或柔度方程中,通过求解节点位移或多余未知力达到求解结构内力的目的。这种思路,对于求解材料非线性问题的位移法而言,存在“牵一动万”的不足,即结构局部进入屈服后,需要修正结构的整体刚度方程,重新计算整个结构,将大量的计算消耗在远离屈服区域、内力变形变化不大的单元上;此外,由于自动选取基本体系较难实现,矩阵力法虽然具有求解精度高、未知数少的特点,却一直未能在计算机上发挥优势[2-3]。
特大增量算法[4](large increment method,LIM) 是一种基于广义逆矩阵理论[5]、以力法为基础的迭代算法(始称广义逆算法[6])。该算法有如下主要特点:1)毋需像传统力法一样选取静定结构作为基本体系,而是直接利用当前带结构约束的体系作基本体系,从选取基本未知量到方程迭代求解都完全适合于电算[7-8];2)LIM天然具有很强的可并行性,无需进行子结构划分就可以直接以单元为最小单位并行求解本构方程,且对于材料非线性问题,无需像传统的逐步增量法递进求解,极大地提高了力法在大型数值分析中效率[8-9]。
研究表明,LIM的收敛性有理论保证,且算法通用性强,计算精度与FEM相比有较大优势。但目前的研究主要集中在材料非线性问题的实体单元的建立与扩展上[10],对于LIM在杆系结构中应用研究尚不充分。美国学者Aref教授等研究了LIM在受集中力的简单梁式结构弹塑性问题中的分析方法,与ABAQUS相比,在塑性铰开始出现以后,LIM拥有远超过前者的计算效率[11]。但该方法仍有诸多不足,笔者将针对其中平面框架结构的常见复杂约束条件以及组合节点的处理方法进行探讨,更加严密地推导出LIM在平面杆系结构中的基本方程,为LIM在复杂框架结构弹塑性分析中的应用打下基础。文中仅限于小变形及静力问题的讨论。
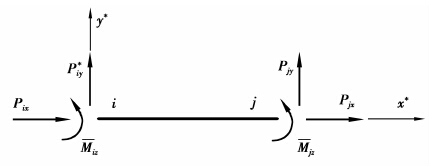
1 单元平衡矩阵与柔度矩阵 1.1 局部分析以平面框架结构为例,阐述平面杆件单元平衡矩阵与柔度矩阵的建立及其特性。图 1所示为局部坐标系下的单元杆端外力。
|
图 1 局部坐标下单元杆端外力 Figure 1 Element nodal forces in local coordinates |
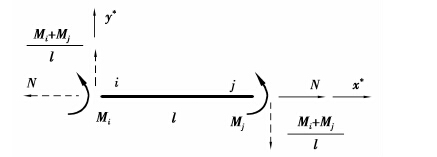
如图 2所示,受单元平衡条件约束,杆端内力向量只有3个独立分量,选取3个线性无关的单元内力分量作为单元广义内力向量[12],如:杆元轴力Nx、杆端弯矩Miz和Miz,记作Fe,即
| ${\mathit{\boldsymbol{F}}^e} = {\{ {N_x}{M_{iz}}{M_{jz}}\} ^T}$ | (1) |
|
图 2 局部坐标下单元广义内力 Figure 2 Element generalized inner forces in local coordinates |
杆件的弯矩和轴力分布为
| $M\left( x \right) = {{l - x} \over l}{M_i} - {x \over l}{M_j};{\rm{ }}N\left( x \right) = - N$ | (2) |
由单元平衡条件可知:
| $\left[ \matrix{ {P^*}_{ix} \hfill \cr {P^*}_{iy} \hfill \cr {\overline M _{iz}} \hfill \cr {P^*}_{jx} \hfill \cr {P^*}_{jy} \hfill \cr {\overline M _{jz}} \hfill \cr} \right] = \left[ {\matrix{ { - 1} & 0 & 0 \cr 0 & {{1 \over l}} & {{1 \over l}} \cr 0 & 1 & 0 \cr 1 & 0 & 0 \cr 0 & { - {1 \over l}} & { - {1 \over l}} \cr 0 & 0 & 1 \cr } } \right]\left[ \matrix{ {N_x} \hfill \cr {M_{iz}} \hfill \cr {M_{jz}} \hfill \cr} \right]$ | (3) |
即
| ${{\bf{P}}^*} = \left[ \matrix{ {{\bf{P}}^*}_i \hfill \cr {{\bf{P}}^*}_j \hfill \cr} \right] = \left[ \matrix{ {{\bf{H}}_i} \hfill \cr {{\bf{H}}_j} \hfill \cr} \right]{{\bf{F}}^e} = {{\bf{H}}^*}{F^e}$ | (4) |
|
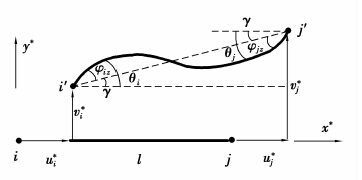
图 3 局部坐标下单元杆端位移与广义变形 Figure 3 Element nodal displacements and generalized deformations in local coordinates |
上式为局部坐标下的单元平衡方程,H*称为局部坐标下单元平衡矩阵。
如图 3所示,单元杆端位移向量为
| ${\mathit{\boldsymbol{D}}^*} = {\left\{ {{u_i}^*{\rm{ }}{v_i}^*{\rm{ }}{\theta _i}{\rm{ }}{u_j}^*{\rm{ }}{v_j}^*{\rm{ }}{\theta _j}} \right\}^T}$ | (5) |
选取与单元广义内力向量Fe共轭的变形向量δe,称为单元广义变形向量,具体如下:
| ${\delta ^e} = {\left\{ {{\Delta _x}{\rm{ }}{\varphi _{iz}}{\rm{ }}{\varphi _{jz}}} \right\}^T},$ | (6) |
其中:
Δx=u*i-u*j,单元轴向变形;
φiz=θi-γ,杆端i相对新轴线i′j′的转角 ;φjz=θj-γ,杆端j相对新轴线i′j′的转角;
γ为轴线ij与i′j′之间的夹角,即杆件的刚体转角,在小变形条件下,有γ=(v*i-v*j)/l。
则单元广义变形向量与杆端位移向量之间存在如下关系:
| $\left[ \matrix{ {\Delta _x} \hfill \cr {\varphi _{iz}} \hfill \cr {\varphi _{jz}} \hfill \cr} \right] = \left[ {\matrix{ { - 1} & 0 & 0 & 1 & 0 & 0 \cr 0 & {{1 \over l}} & 1 & 0 & { - {1 \over l}} & 0 \cr 0 & {{1 \over l}} & 0 & 0 & { - {1 \over l}} & 1 \cr } } \right]\left[ \matrix{ {u_i}^* \hfill \cr {v_i}^* \hfill \cr {\theta _i} \hfill \cr {u_j}^* \hfill \cr {v_j}^* \hfill \cr {\theta _j} \hfill \cr} \right],$ | (7) |
即
| ${\mathit{\boldsymbol{\delta }}^e} = {\left[ \matrix{ {\mathit{\boldsymbol{H}}_i} \hfill \cr {\mathit{\boldsymbol{H}}_j} \hfill \cr} \right]^T}\left[ \matrix{ {\mathit{\boldsymbol{D}}_i}^* \hfill \cr {\mathit{\boldsymbol{D}}_j}^* \hfill \cr} \right] = {\mathit{\boldsymbol{G}}^*}{\mathit{\boldsymbol{D}}^*}$ | (8) |
上式即单元协调方程,称为单元协调矩阵或单元几何矩阵。比较式(4)和式(8)可知,
| ${\mathit{\boldsymbol{G}}^*} = {({\mathit{\boldsymbol{H}}^*})^T}$ | (9) |
即,在局部坐标系下单元平衡矩阵与单元协调矩阵互为转置。显然,当单元广义内力与单元广义位移满足共轭条件时,单元平衡方程及其协调方程在形式上具有对偶性,即:
| $\left\{ \matrix{ {\mathit{\boldsymbol{P}}^*} = {\mathit{\boldsymbol{H}}^*}{\mathit{\boldsymbol{F}}^e} \hfill \cr {\mathit{\boldsymbol{\delta }}^e} = {({\mathit{\boldsymbol{H}}^*})^T}{\mathit{\boldsymbol{D}}^*} \hfill \cr} \right.$ | (10) |
从能量原理计算单元柔度矩阵[13],杆件应变能U为
| $U = \int \matrix{ l \hfill \cr 0 \hfill \cr} {{M{{\left( x \right)}^2}} \over {2E{I_z}}}dx + \int \matrix{ l \hfill \cr 0 \hfill \cr} {{N{{\left( x \right)}^2}} \over {2EA}}dx{\rm{ }}$ | (11) |
由卡氏第二定理可得单元柔度矩阵:
| ${\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^e} = \left[ {\matrix{ {{l \over {EA}}} & 0 & 0 \cr 0 & {{l \over {3E{I_z}}}} & { - {l \over {6E{I_z}}}} \cr 0 & { - {l \over {6E{I_z}}}} & {{l \over {3E{I_z}}}} \cr } } \right]$ | (12) |
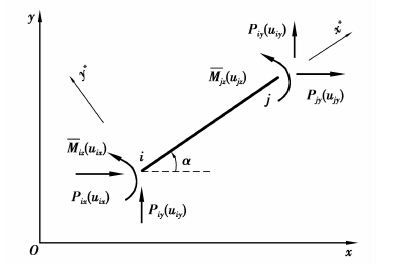
如图 4所示,在全局坐标系下分别定义单元等效结点荷载向量Pe和结点位移向量De 为[10]:
| ${\mathit{\boldsymbol{P}}^e} = {\{ {P_{ix}}{\rm{ }}{P_{iy}}{\rm{ }}{\overline M _{iz}}{\rm{ }}{P_{jx}}{\rm{ }}{P_{jy}}{\rm{ }}{\overline M _{jz}}\} ^T}$ | (13) |
| ${\mathit{\boldsymbol{D}}^e} = {\{ {u_{ix}}{\rm{ }}{v_{iy}}{\rm{ }}{\theta _i}{\rm{ }}{u_{jx}}{\rm{ }}{v_{jy}}{\rm{ }}{\theta _j}\} ^T}$ | (14) |
|
图 4 全局坐标系下单元杆端外力和杆端位移 Figure 4 Element nodal forces and displacements in global coordinates |
则局部坐标系与整体坐标系下,单元杆端力向量具有如下转换关系:
| ${\mathit{\boldsymbol{P}}^e} = \mathit{\boldsymbol{R}}{\mathit{\boldsymbol{P}}^*}$ | (15) |
R为坐标转换矩阵,且是正交矩阵:
| $\mathit{\boldsymbol{R}} = \left[ {\matrix{ {{\rm{cos}}\alpha } & { - {\rm{sin}}\alpha } & 0 \cr {{\rm{sin}}\alpha } & {{\rm{cos}}\alpha } & 0 \cr 0 & 0 & 1 \cr } } \right],$ | (16) |
则全局坐标下单元平衡方程为
| ${\mathit{\boldsymbol{P}}^e} = \left[ {{{{\mathit{\boldsymbol{P}}_i}} \over {{\mathit{\boldsymbol{P}}_j}}}} \right] = \left[ {{{\mathit{\boldsymbol{R}}{\mathit{\boldsymbol{P}}_i}^*} \over {\mathit{\boldsymbol{R}}{\mathit{\boldsymbol{P}}_j}^*}}} \right] = \left[ {{{\mathit{\boldsymbol{R}}{\mathit{\boldsymbol{H}}_i}{\mathit{\boldsymbol{F}}^e}} \over {\mathit{\boldsymbol{R}}{\mathit{\boldsymbol{H}}_j}{\mathit{\boldsymbol{F}}^e}}}} \right] = \left[ {{{\mathit{\boldsymbol{R}}{\mathit{\boldsymbol{H}}_i}} \over {\mathit{\boldsymbol{R}}{\mathit{\boldsymbol{H}}_j}}}} \right]{\mathit{\boldsymbol{F}}^e} = {\mathit{\boldsymbol{C}}^e}{\mathit{\boldsymbol{F}}^e}$ | (17) |
式中,Ce为整体坐标下的单元平衡矩阵。单元节点位移向量的转换关系与此类似。则整体坐标下的单元协调方程为
| $\mathit{\boldsymbol{\delta }^e} = \left[ {\mathit{\boldsymbol{H}^T}_i\mathit{\boldsymbol{R}^{ - 1}}|\mathit{\boldsymbol{H}^T}_j\mathit{\boldsymbol{R}^{ - 1}}} \right]\mathit{\boldsymbol{D}^e} = \mathit{\boldsymbol{G}^e}\mathit{\boldsymbol{D}^e}$ | (18) |
Ge为整体坐标下的单元协调矩阵。可知:
| $\left[ {{{\mathit{\boldsymbol{R}}{\mathit{\boldsymbol{H}}_i}} \over {\mathit{\boldsymbol{R}}{\mathit{\boldsymbol{H}}_j}}}} \right] = {\left[ {{\mathit{\boldsymbol{H}}_i}^T{\mathit{\boldsymbol{R}}^{ - 1}}|{\mathit{\boldsymbol{H}}_j}^T{\mathit{\boldsymbol{R}}^{ - 1}}} \right]^T}$ | (19) |
即
| $\mathit{\boldsymbol{G}^e} = {(\mathit{\boldsymbol{C}^e})^T}$ | (20) |
可见,在整体坐标下单元平衡矩阵与单元协调矩阵的转置关系依然成立,单元平衡条件和协调条件在形式上同样存在对偶性。即在小变形前提下,若:1)杆端力向量与杆件广义内力向量满足平衡条件;2)杆端位移向量与杆件广义变形向量满足协调条件;3)杆端力向量与杆端位移向量共轭;4)杆件广义内力向量与杆件广义变形向量共轭。则单元的平衡关系与协调关系具有式(17)和(18)所示的对偶性。该对偶性可采用虚功原理加以证明,详见文献[14]。
根据结点平衡条件,采用“对号入座”法装配结构整体平衡矩阵,以结点编号为行码、单元编号为列码,将各单元平衡矩阵填入相应位置,毋需叠加计算,这是有别于位移有限元集成系统刚度矩阵之处。
以结点k为例,平衡子矩阵Cke的确定规则如下:
| ${C_{ke}} = \left\{ \matrix{ \mathit{\boldsymbol{R}}{\mathit{\boldsymbol{H}}_i}{\rm{ 结点k与杆元e负关联;}} \hfill \cr \mathit{\boldsymbol{R}}{\mathit{\boldsymbol{H}}_j}{\rm{ 结点k与杆元e正关联;}} \hfill \cr 0{\rm{ 结点k与杆元犲不关联}} \hfill \cr} \right.$ | (21) |
设系统可离散为b个单元,每个单元广义内力向量有l个独立分量,B=bl,相应地,设系统有n个结点,每个结点有q个位移分量,N=nq。
系统整体平衡方程为
| $\mathit{\boldsymbol{CF}} = \mathit{\boldsymbol{P}},$ | (22) |
式中,C是N×B的平衡矩阵(N≤B)。对于静定结构,N=B,可以直接解出F(P为已知量)。
系统整体协调方程为
| $\mathit{\boldsymbol{\delta }} = \mathit{\boldsymbol{GD}} = {\mathit{\boldsymbol{C}}^T}\mathit{\boldsymbol{D}}$ | (23) |
单元本构关系可以表示为
| ${\mathit{\boldsymbol{\delta }}^e} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^e}{\mathit{\boldsymbol{F}}^e}{\rm{or }}{\mathit{\boldsymbol{F}}^e} = {\mathit{\boldsymbol{K}}^e}{\mathit{\boldsymbol{\delta }}^e},$ | (24) |
其中:Ke为单元刚度矩阵;Φe为单元柔度矩阵。对于整个系统可以写为
| $\mathit{\boldsymbol{\delta }} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( \mathit{\boldsymbol{F}} \right)$ | (25) |
其中,$\mathit{\boldsymbol{ \boldsymbol{\varPhi} }} = \left\lceil {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{^1}{\rm{ }}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{^2}{\rm{ }} \cdots {\rm{ }}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{^b}} \right\rceil $为对角阵。
引入边界约束条件即可求解结构的内力和位移。
以上平衡方程和协调方程对线性和非线性问题是通用的,本构方程在非线性问题中有很大不同,与材料本构特性有关,文中不作讨论。
2 基于广义逆理论的LIM 2.1 广义逆和系统控制方程对于超静定结构,由于N<B,C-1不再存在,系统平衡方程(22)将有无数多组解。引入广义逆矩阵理论可以得到满足式(22)的通解:
| $\mathit{\boldsymbol{F}} = {\mathit{\boldsymbol{C}}^ + }\mathit{\boldsymbol{P}} + \mathit{\boldsymbol{\beta X}},{\rm{ }}\forall \mathit{\boldsymbol{X}} \in {\mathit{\boldsymbol{R}}^B}$ | (26) |
| ${\mathit{\boldsymbol{C}}^ + } = {\mathit{\boldsymbol{C}}^T}{(\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{C}}^T})^{ - 1}}$ | (27) |
式中,C+为C阵的广义右逆。则C+P为满足平衡而不满足协调的内力矢;βX为满足协调的平衡力矢,两者之和即为同时满足平衡和协调的系统内力向量F。
令
| $\mathit{\boldsymbol{\alpha = }}{\mathit{\boldsymbol{C}}^\mathit{\boldsymbol{ + }}}\mathit{\boldsymbol{C,\beta = I}}{\mathit{\boldsymbol{C}}^\mathit{\boldsymbol{ + }}}\mathit{\boldsymbol{C}}$ | (28) |
由广义逆理论知:
| ${\rm{rank}}\left( \mathit{\boldsymbol{\alpha }} \right) = N;{\rm{rank}}\left( \mathit{\boldsymbol{\beta }} \right) = BN$ | (29) |
| $\mathit{\boldsymbol{C\alpha = C;C\beta }} = 0$ | (30) |
| ${\mathit{\boldsymbol{\alpha }}^\mathit{\boldsymbol{2}}}\mathit{\boldsymbol{ = \alpha ;}}{\mathit{\boldsymbol{\beta }}^\mathit{\boldsymbol{2}}}\mathit{\boldsymbol{ = \beta ;\alpha \beta = 0}}$ | (31) |
依据矩阵α和β的定义,易得
| $\mathit{\boldsymbol{\alpha \delta }} = \mathit{\boldsymbol{\delta }};{\rm{ }}\mathit{\boldsymbol{\beta \delta }} = 0$ | (32) |
| $\mathit{\boldsymbol{D}} = {(\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{C}}^T})^{ - 1}}\mathit{\boldsymbol{C\delta }}$ | (33) |
至此原问题转化为寻找满足如下控制方程的F和δ的解。
| $\mathit{\boldsymbol{CF}} = \mathit{\boldsymbol{P}};\mathit{\boldsymbol{\beta \delta }} = 0;\mathit{\boldsymbol{\delta }} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( \mathit{\boldsymbol{F}} \right)$ | (34) |
对式(34)所示问题可采用迭代的方法求解[4],基本思想是先寻找满足平衡方程(22)的初始解,而后通过协调方程(32)修正该初始解,最终得到同时满足平衡与协调条件的原问题的解。即将原问题转化为如下优化问题:
| $\mathit{\boldsymbol{CF = P}};\mathit{\boldsymbol{\delta = \boldsymbol{\varPhi} }}\left( \mathit{\boldsymbol{F}} \right);min\left\| {\mathit{\boldsymbol{\beta \delta }}} \right\|$ | (35) |
具体步骤如下:
第1步:首先由广义逆矩阵理论,求得平衡方程的一个特解,作为迭代初值:
| ${\mathit{\boldsymbol{F}}_0} = {\mathit{\boldsymbol{C}}^ + }\mathit{\boldsymbol{P}}$ | (36) |
第2步:由Fn迭代求解Fn+1。
1) 求解Fn对应的广义变形:
| ${{\mathit{\boldsymbol{\hat \delta }}}_n} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}({\mathit{\boldsymbol{F}}_n})$ | (37) |
2) 检验$\mathit{\boldsymbol{\hat \delta }}$n是否满足协调收敛标准:
| $\varepsilon ({{\mathit{\boldsymbol{\hat \delta }}}_n}) = {{\left\| {\beta {{\mathit{\boldsymbol{\hat \delta }}}_n}} \right\|} \over {\left\| {{{\mathit{\boldsymbol{\hat \delta }}}_n}} \right\|}} \le e{\rm{ }}$ | (38) |
式中e为给定协调收敛标准。若上式满足,迭代终止,Fn为内力最终解,跳转至第3步。否则,继续;
3) 确定搜索方向:
| $\left\{ \matrix{ {\mathit{\boldsymbol{S}}_n} = \mathit{\boldsymbol{\beta K\beta }}{{\mathit{\boldsymbol{\hat \delta }}}^n}; \hfill \cr {k_f} = {{{{\left( {{{\mathit{\boldsymbol{\hat \delta }}}_n} - {{\mathit{\boldsymbol{\hat \delta }}}_n}} \right)}^T}\mathit{\boldsymbol{S}}{'_n}} \over {\mathit{\boldsymbol{\hat \delta }}_{n - 1}^T\mathit{\boldsymbol{S}}{'_{n - 1}}}}; \hfill \cr {\mathit{\boldsymbol{S}}_n} = {k_f}{\mathit{\boldsymbol{S}}_{n - 1}} - S{'_n} \hfill \cr} \right.$ | (39) |
4) 确定搜索步长hn:
由$\mathit{\boldsymbol{\hat \delta }}$n+1Sn=0可得:
| $h = - {{\mathit{\boldsymbol{\hat \delta }}_n^T{\mathit{\boldsymbol{S}}_n}} \over {\mathit{\boldsymbol{S}}_n^T\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\mathit{\boldsymbol{S}}_n}}}$ | (40) |
5) 求Fn+1:
| ${\mathit{\boldsymbol{F}}_{n + 1}} = {\mathit{\boldsymbol{F}}_n} + {h_n}{\mathit{\boldsymbol{S}}_n};n = n + 1$ | (41) |
转至1)进行下一步迭代。
第3步:计算F、δ和D最终解:
| $\mathit{\boldsymbol{F}} = {\mathit{\boldsymbol{F}}_n}{\mathit{\boldsymbol{\delta }}_n}{\rm{ = }}\alpha {{\mathit{\boldsymbol{\hat \delta }}}_n}\mathit{\boldsymbol{D}} = {\left( {\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{C}}^T}} \right)^{ - 1}}\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{\delta }}_n}$ | (42) |
控制方程式(22)和式(23)中,F、P、D、δ可视为有限维矢量空间中的矢量,它们之间的相互关系可视为在有限维矢量空间中,像与像原的变换。即F、δ∈RM,P、D∈RL,RMRN,则存在与RM正交的子空间RL,使RN=RM+RL。
平衡方程(22)意味着在向量子空间RM中,内力矢量F经过矩阵C的作用后,成为与荷载矢量P同模反向的矢量,从而构成平衡力系。
因此,LIM的求解思想可阐释为:
1) 结构首先在荷载作用下产生内力,该内力可由广义逆矩阵理论求得,是1组满足平衡条件的特解Fp,Fp在C阵的列矢张成的像空间RM中;
2) Fp使杆件发生变形δ,该变形可由单元本构方程确定,因而产生结点位移D,通常D不满足协调条件;
进一步调整杆件变形,使其产生新的内力Fg,Fg是1组满足平衡条件CF=0的特解,存在于正交子空间RL中,它不会影响结构的平衡,但可以调整结构的协调性。则结构的内力矢为F=Fp+Fg。其中,Fg是正交子空间中的自由矢,但对于确定的结构,Fg是唯一的,应使F⊥RL,否则将导致新的不平衡力。
显然,满足F⊥RL的矢量,必是一切F中模最小者,所对应的δ的模也最小。可以证明,这符合最小势能原理。
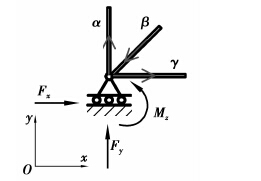
3 不同支座约束条件的处理事实上,式(22)、式(23)、式(25)尚需加入边界条件[15],才能唯一确定结构的内力与变形。常见平面杆系结构的支座,按其约束性质可分为:刚性支座、弹性支座和给定位移支座。以平面框架结构为例,设结构的 第s个支座的结点编号为nk,与结点相连的杆元记做α、β和γ。以下分别讨论三类支座约束以及组合节点的处理方法。
|
图 5 刚性支座示意图 Figure 5 Rigid support |
刚性支座指受力后不发生变形的支座,如图 5所示。由图 5可知,除y方向线位移被支座约束(称约束位移)外,其余方向位移均自由(称为自由位移)。
为加入边界条件,对式(22)做如下修正:
1) 在F中第b+s的位置上增加一个反力矢Fb+s,包含结点处全部反力分量,即:
| ${\mathit{\boldsymbol{F}}_{b + s}} = {\left\{ {{F_x}{\rm{ }}{F_y}{\rm{ }}{M_z}} \right\}^T}$ | (43) |
所对应的变形矢量δb+s为
| ${\mathit{\boldsymbol{\delta }}_{b + s}} = {\left\{ {{\Delta _x}{\rm{ }}{\Delta _y}{\rm{ }}{\varphi _z}} \right\}^T}$ | (44) |
2) 在平衡矩阵C中,对应第b+s杆元(即支座)处,增加3×3阶元阵列,该元阵列仅在第nk个节点处有一非零对角阵:
| $\mathit{\boldsymbol{\overline I}} {\rm{ = }}\left\lceil {{a_{1}}{\rm{ }}{a_{2}}{\rm{ }}{a_{3}}} \right\rceil $ | (45) |
式中,自由位移,ai=0;约束位移,ai=1 ,其余元阵均为0阵。
经过以上处理后的结构整体平衡方程变为:
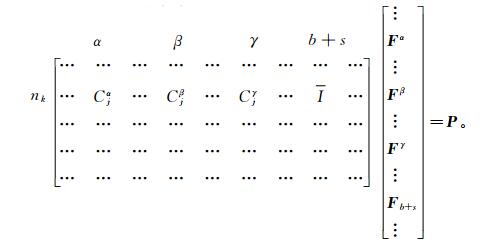
|
(46) |
这时反力已被当作内力包括在内力矢中。
在式(25)中与子块Fb+s相对应的位置上,给Φ加上如下“相当柔度矩阵”:
| $\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{n_k} = \left\lceil {{b_1}{\rm{ }}{b_2}{\rm{ }}{b_3}} \right\rceil $ | (47) |
|
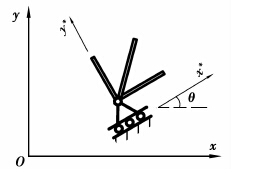
图 6 倾斜支座示意图 Figure 6 Tilting support |
式中,对于约束位移,bi=0;对自由位移,bi=1×1020(因该方向反力为0,无实际意义)。相当于在δ中的第b+s位置处增加了一个广义变形矢量δb+s,则式(25)成为
| $\eqalign{ & {\left[ {{\mathit{\boldsymbol{\delta }}^1}L{\rm{ }}{\mathit{\boldsymbol{\delta }}^\alpha }L{\rm{ }}{\mathit{\boldsymbol{\delta }}^\beta }L{\rm{ }}{\mathit{\boldsymbol{\delta }}^\gamma }L{\rm{ }}{\mathit{\boldsymbol{\delta }}_{b{\rm{ }} + {\rm{ }}s}}L} \right]^T} = \cr & \left\lceil {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{^1}L{\rm{ }}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{^\alpha }L{\rm{ }}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{^\beta }L{\rm{ }}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{^\gamma }L{\rm{ }}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{_{{n_k}}}L} \right\rceil \mathit{\boldsymbol{F}} \cr} $ | (48) |
式(23)中的CT及δ必须具备与式(46)和式(48)相同的符号含义。这样,最后求得的反力与真实反力反号。
当支座如图 6所示有倾斜角时,需要引入局部坐标系和转换矩阵进行修正,则
| $\overline I {\rm{ }} = \mathit{\boldsymbol{R}}\left\lceil {{a_{1}}{\rm{ }}{a_{2}}{\rm{ }}{a_{3}}} \right\rceil $ | (49) |
式中ai取值规则与式(45)相同。式(45)则为式(49)倾斜角为0的特殊情况,α为x轴到x*轴的夹角,逆时针为正。式(47)依然适用。
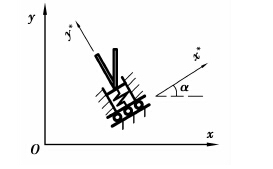
3.2 弹性支座弹性支座指受力后会发生弹性变形的支座,如图 7所示。
|
图 7 弹性支座示意图 Figure 7 Spring support |
此时,式(49)和式(47)依然适用,但弹性位移方向ai=1,bi=1/k(k为支座刚度系数)。
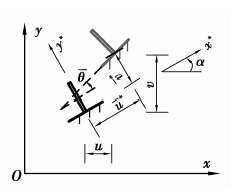
3.3 给定位移支座给定位移支座指在某些方向会发生给定位移值的支座,如图 8所示。
|
图 8 给定支座位移示意图 Figure 8 Given displacements of the support |
假定支座在局部坐标下,存在给定位移{u* v* θ}T,则全局坐标下的支座位移与之有如下约束条件:
| $u{\rm{ }}cos\alpha v{\rm{ }}sin\alpha = {\overline u ^*}$ | (50) |
| $ - u{\rm{ }}sin\alpha + v{\rm{ }}cos\alpha = {\overline v ^*}$ | (51) |
| $\theta = \overline \theta $ | (52) |
即
| $\mathit{\boldsymbol{R}^{1}}{\left\{ {u{\rm{ }}v{\rm{ }}\theta } \right\}^T} = \left\{ {{{\overline u }^{\rm{*}}}{\rm{ }}{{\overline v }^{\rm{*}}}{\rm{ }}{{\overline \theta }^T}} \right\}$ | (53) |
此时式(49)和式(47)依然适用,但给定位移方向ai=0,bi=1.0×1020(无实际意义),且给定位移只能在约束位移自由度方向发生。
通过向CT中添加新行和向广义变形矢量δ添加分量u*(或v*、或θ),将关系式(50)(或(51)、或(52))与添加过边界条件的几何方程(23)合并。
以图 6所示结点编号为nk的支座为例阐明合并方法,假设该支座在y*方向发生给定支座位移v*:
1) 向CT中添加的新行,该行仅在nk处有一非零向量Ri-1(为R-1的第i行,i=1,2,3,分别对应给定位移u*,v*,θ);
2) 向δ中添加一个新的分量δi(i=1,2,3,分别取值u*,v*,θ)。
则经合并后的几何方程为
| $\matrix{ {\matrix{ {} \cr \alpha \cr {} \cr {b + s} \cr {} \cr {} \cr } } & {\left[ {\matrix{ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \cr \cdots & \cdots & {C_i^\alpha } & \cdots & \cdots & \cdots \cr \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \cr \cdots & \cdots & {\bar I} & \cdots & \cdots & \cdots \cr \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \cr \cdots & \cdots & {R_i^{ - 1}} & \cdots & \cdots & \cdots \cr } } \right]} \cr } \left[ {\matrix{ \vdots \cr \vdots \cr {{D_{nk}}} \cr \vdots \cr \vdots \cr \vdots \cr } } \right] = \left[ {\matrix{ \vdots \cr {{\mathit{\boldsymbol{\delta }}^\alpha }} \cr \vdots \cr {{\mathit{\boldsymbol{\delta }}_{b + s}}} \cr \vdots \cr {{\mathit{\boldsymbol{\delta }}_i}} \cr } } \right] \circ $ | (54) |
实际计算中,直接向平衡方程的C中添加新列,与向CT中添加新行等价。
同时需要在式(46)中给F加上一个广义内力分量,此分量即为给定位移自由度方向的支反力。此时也需要给Φ加上一个柔度系数‘0’:
| $\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\rm{ = }}\ulcorner{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^1}\; \cdots \;{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^\alpha }\; \cdots \;{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^\beta }\; \cdots \;{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^\gamma }\; \cdots \;{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{nk}}\; \cdots \;0\lrcorner$ | (55) |
由于对应的广义变形分量δi为已知定值,给Φ加上一个‘0’柔度系数,是为了保证最优化计算过程中矩阵维度一致。
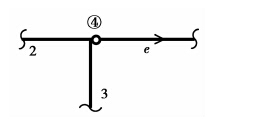
3.4 组合节点框架结构通常存在组合节点,如图 9所示,杆元一端或两端的连接方式为铰接时,此时需对单元平衡方程进行修正。图 9中杆元e的负端为铰接,则有
|
图 9 杆端铰接示意图 Figure 9 Member-end hinged |
| ${M^e}_i = 0{\rm{ }}$ | (56) |
通过向C中添加新行和向P添加一个0分量将式(56)与式(46)合并,以强制杆元e负端弯矩为0。此时计算出④结点位移角转角不能代表杆元e铰接端转角,需通过式(6)求出,并叠加外荷载在铰接端引起的转角。
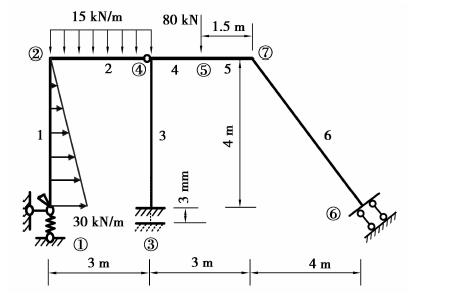
4 算 例采用前述特大增量步算法编程计算,如图 10所示。平面框架各结点的位移和各梁端内力及支座反力,并与商业有限元软件ANSYS计算结果对比。已知:结点⑥支座倾斜角45°,结点③支座沉降3 mm,弹簧刚度k=2.0×104 kN/m;EI=4.2×107 Pa·m2,EA=2.1×109 Pa·m2。
|
图 10 受复杂支座约束的平面框架 Figure 10 2D frame in control of complex support |
采用LIM经6次迭代计算得到的解与ANSYS解对比数据如表 1~3所示,LIM计算用时0.05 s,ANSYS计算用时0.03 s。
| 表 1 杆端内力 Table 1 Member-end Inner Force |
| 表 2 支座反力 Table 2 Supporting Force |
| 表 3 结点位移 Table 3 Nodal Displacement |
对比ANSYS的计算结果,可以验证文中所建立的方法是有效的,且两者具有相同的计算精度,计算效率相当。
5 结 论1) 该算法在复杂平面框架中的应用显示,与位移法集成总刚阵相比,LIM平衡矩阵的集成更加简洁直观。
2) 与文献[17]相比,文中阐述的边界条件处理方法适用的约束类型更广,计算更加简洁通用,为LIM在复杂平面框架弹塑性中的应用奠定了基础。新的约束处理方法不用对平衡矩阵进行局部冲零处理,不用另开辟内存储存被冲零元素,可一次性计算出内力和支反力,节约了内存和计算时间。
3) LIM以广义内力作为基本未知量,并将三大控制方程分离,理论上当有比位移有限元更高的计算精度,但在线弹性问题中未能发挥这样的优势,也没有表现出文献[11-12]论述的效率优势。笔者将在后续弹塑性问题研究中就效率和精度继续探讨。
| [1] | Bathe K J. Finite element procedures[M]. Upper Saddle River: Prentice Hall, 2014. |
| [2] | Giambanco F, Palizzolo L, Panzeca T. The indirect force method[J]. Computers & Structures, 1990, 37(5): 759–768. |
| [3] | Kaneko I, Lawo M, Thierauf G. On computational procedures for the force method[J]. International Journal for Numerical Methods in Engineering, 1982, 18(10): 1469–1495. DOI:10.1002/(ISSN)1097-0207 |
| [4] | 刘西拉,张春俊.基于广义逆矩阵的特大增量步算法[C/OL]//第三届全国结构工程学术会议. 北京:工程力学杂志社, 1994[2016-04-03]. http://cpfd.cnki.com.cn/Article/CPFDTOTAL-LXFY199406001006.htm. LIU Xila, ZHANG Chunjun. Generalized-inverse-based large increment method[C/OL]. Proceedings of the third National Conference on structural engineering. Beijing:Engineering Mechanics Presss, 1994[2016-04-03]. http://cpfd.cnki.com.cn/Article/CPFDTOTAL-LXFY199406001006.htm. (in Chinese) |
| [5] | Ben I A, Greville T. Generalized inverse:theory and application[M]. New York: Wiley, 1974. |
| [6] |
周其刚.
桁架结构分析的广义逆矩阵力法[J]. 西南交通大学学报, 1988(1): 60–66.
ZHOU Qigang. The force method using generalized inverse of matrices[J]. Journal of Southwest Jiaotong University, 1988(1): 60–66. (in Chinese) |
| [7] |
刘西拉, 王开健, 张春俊.
桁架结构材料非线性弹性问题的广义逆力法[J]. 工程力学, 2005, 22(S1): 7–15.
LIU Xila, WANG Kaijian, ZHANG Chunjun. The large increment method for nonlinear elastic problems of truss systems[J]. Engineering Mechanics, 2005, 22(S1): 7–15. (in Chinese) |
| [8] |
郭早阳.特大增量步方法和并行程序设计[D].北京:清华大学,1999. GUO Zaoyang. The large increment method and the parallelprograming[D]. Beijing:Tsinghua University, 1999. (in Chinese) |
| [9] |
王开健. 基于特大增量步算法的网络并行计算[D].北京:清华大学,2005. WANG Kaijian. Network parallel computation based on the large increment method[D]. Beijing:Tsinghua University, 2005. (in Chinese) |
| [10] |
龙丹冰.基于并行的特大增量步算法在计算固体力学中的应用[D].上海:上海交通大学,2012. LONG Danbing. The extended application of parallel computing-based large increment method in computational solid mechanics[D]. Shanghai:Shanghai Jiao Tong University, 2012. (in Chinese) |
| [11] | Barham WS, Aref A J, Dargush G F. Flexibility-based large increment method for analysis of elastic-perfectly plastic beam structures[J]. Computers & Structures, 2005, 83(28-29-30): 2453–2462. |
| [12] | Przemieniecki J S. Theory of matrix structural analysis[M]. New York: Mcgraw-hill, 1968. |
| [13] |
贾红学, 龙丹冰, 刘西拉.
特大增量步算法分析变截面梁问题[J]. 工业建筑, 2013(S1): 189–191.
JIA Hongxue, LONG Dandbing, LIU Xila. The analysis of the varying cross-section beam problem using large increment method[J]. Industrial Construction, 2013(S1): 189–191. (in Chinese) |
| [14] | Kassimal A. Matrix analysis of structures[M]. New York: Harper & Row, 1983. |
| [15] |
龙驭球.
结构矩阵分析中的平衡-几何互伴定理[J]. 工程力学, 2012, 29(5): 1–7.
LONG Yuqiu. An adjoint theorem between equilibrium matrix and geometric matrix in structural analysis[J]. Engineering Mechanics, 2012, 29(5): 1–7. (in Chinese) |
| [16] |
谢用九, 李伟.
用QR分解进行矩阵力法计[J]. 西南交通大学学报, 1981(3): 93–100.
XIE Yongjiu, LI Wei. The matrix force method based on QR decomposition[J]. Journal of Southwest Jiaotong University, 1981(3): 93–100. (in Chinese) |
 2017, Vol. 40
2017, Vol. 40

