装配精度是机床性能的重要评价指标,误差源及装配误差传递是分析机床精度的基本要素,也是装配精度研究的关键点[1-3]。不同的误差源对最终装配精度会产生不同的影响,文献[4-5]对影响装配精度的误差源进行分类并建立统一模型,为实现精度预测和装配精度设计提供了有效工具,但对误差分类并不全面,尚未对运动部件的位移误差深入研究。文献[6-8]对精密机床装配误差传递过程构建了状态空间模型,预测最终产品装配精度;文献[9-10]运用多体理论建立了“刀具—工件”链式误差传递路径,提出了机床通用误差模型;刘伟东等[11]建立了装配偏差有向图模型进行偏差分析和装配精度预测:这些研究工作提出的建模方法以机床基础大件或零件间误差传递与积累为对象,能够较好地解决静态、简单零件装配精度预测问题。对于数控机床这样一类复杂的机电产品,现有研究成果对误差传递与积累规律的分析不充分、不准确,由于运动部件的振动等因素的影响,部件之间的相互干涉耦合作用变得尤其重要,加工条件下机床结构动态特性已成为加工精度损失的重要原因之一[12]。
文献[13-15]以可靠性控制为目的,对数控机床整机进行功能—运动—动作 (function-movement-action, FMA) 结构化分解后得最小动作单元—元动作,该方法以动态观点看待机床,分析机床工作状态下的质量特性,但目前仅对元动作装配单元 (meta-action assembly unit, MAU) 内零件间的静态误差传递过程构建了模型,未对动态特性影响下的误差源及误差传递路径做深入分析。本文试图引入误差链接模型对元动作装配单元的误差传递过程进行描述与表达,并提出基于链接模型的误差传递路径求解方法,以期为装配过程控制提供依据。
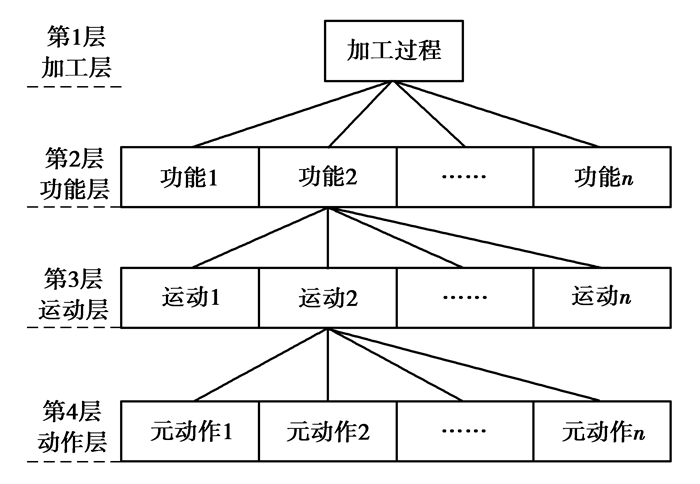
1 元动作装配单元 1.1 FMA功能分解方法数控机床是典型的复杂机电系统,为方便讨论其装配质量特性,首先需要对数控机床进行分解,将其简化为易建模的基本单元,然后分析基本单元装配质量,再综合讨论整机的装配质量。FMA结构化分解方法是将数控机床的加工过程按照“功能—运动—动作”的方式进行自上而下逐层分解的方法,其核心思想就是将机床加工功能这个复杂的综合运动拆分成一系列基本的动作单元,将机床的加工功能看作是一系列相互关联的动作,如图 1所示为FMA结构化分解方法。数控机床经过FMA结构化分解至不能再分解的动作层后,可得最小动作单元——元动作。元动作是结构相对独立能够实现目标动作,可控可分析并且不能再细分的动作单元,如蜗杆转动元动作。虽然数控机床的加工过程很复杂,通过FMA结构化分解得到的元动作一般是机械结构的两种基本动作形式:直线移动和转动,有利于简化装配质量的分析过程。
|
图 1 FMA结构化分解 Figure 1 'FMA' structure decomposition |
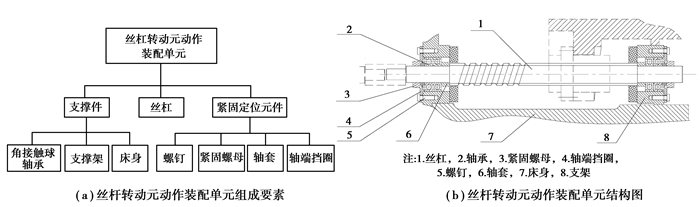
元动作装配单元是指在装配过程中,由一个实现元动作的基准件为装配基础,可以独立组装,达到规定的尺寸链与元动作技术要求,并能够实现该元动作规定功能的一组零件组成的独立组件[5]。典型的元动作结构单元由以下要素组成:支撑件、动力源、执行件和传动紧固件,如图 2为所示丝杠转动元动作装配单元。数控机床可视为由一系列MAU组装而成的产品,有关MAU误差源及误差传递模型的研究是整机装配精度预测的基础,元动作之间的配合方式对整机装配精度亦产生较大影响。MAU之间有两种配合方式:固定结合面配合和运动部件配合,如蜗轮转动MAU与蜗杆转动MAU之间既以箱体结合面配合,又以运动中的蜗杆蜗轮进行配合。
|
图 2 丝杠转动元动作装配单元 Figure 2 Lead screw rotate Meta-action assembly unit |
FMA结构化分解方法以动态观点对机床进行分解,赋予MAU以动态特性,因此它的误差区别于一般零部件的误差。元动作装配单元由零件装配而成,最终装配精度不仅体现在形位误差,还体现在运动部件的动态特性中,下面就MAU误差源进行概述。
1) 形状误差。几何形状误差是指实际被测要素的形状对其理想要素的变动量,包括平面度、直线度、圆度等[12]。在装配过程中以误差几何为基准或接触配合表面时,被配合的零件发生位姿变动,位姿变动逐渐累积影响最终MAU装配精度。
2) 位置误差。几何位置误差是指关联被测要素对其基准要素的变动量,可分为定向误差、定位误差和跳动误差3类[15]。当以误差几何为基准或接触配合面时,被装配零件会产生位姿变动,参与误差传递积累过程,影响MAU装配精度。
3) 装配位置误差。装配位置误差包括装夹定位误差引入的零件位置误差和间隙配合时位置不确定性引入的误差,包括定位和定向误差。装配位置误差在装配过程中会和形位误差产生耦合,共同影响最终的MAU装配精度。
4) 运动误差。产生相对运动的两零件间实际位移与理论位移之差称为运动误差,包括传动位移和回程位移,是零部件形位误差、装配位置误差和原理误差的综合反映。
对影响MAU装配精度的几点说明:
MAU的最终装配精度还受测量误差的影响。对于精密机床的装配过程,测量误差会产生放大效应,为提高精度预测准确度,测量误差不能被忽略;
对于长轴、薄板类零件,刚体假设不再适用,由装配力引起的零件变形误差不可忽略,可通过ANASYS有限元分析软件进行仿真求解,零件变形误差可看作是几何位置误差,参与误差传递积累过程。
2.2 基于链接的误差传递模型文献[16-17]引入链接的概念作为质量特性关联关系的基本封装单元,为质量问题发生机理的分析提供了新思路,文中试图引用链接概念构建误差关联关系模型,为误差传递路径的求解提供新的方法。
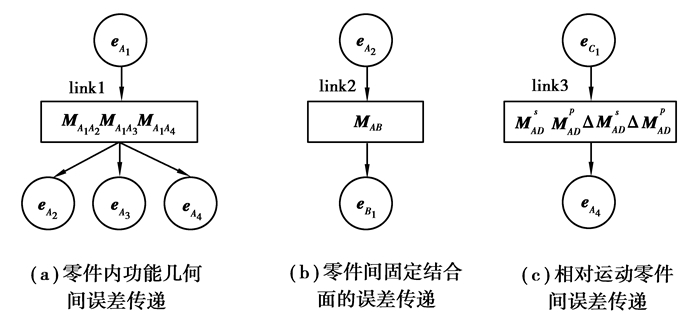
2.2.1 误差链接模型 (error linkage model, ELM)MAU误差链接模型是MAU误差关联关系的基本封装单元。构建链接就是误差关联关系结构化建模过程,用圆圈表示MAU各零件或装配结合面误差项,用矩形框表示误差传递关系准则,一般为误差转换矩阵,它们之间的连接用箭头表示,且箭头方向表示误差传递的方向 (图 3)。
|
图 3 误差链接模型 Figure 3 Error linkage model |
根据几何特征类型和误差传递性质,将链接分为以下3类:
1) a类误差传递:零件内几何特征间误差传递。
如图 3(a)所示link1,输入输出均为零件A的几何特征误差,输入误差项一般为零件的加工基准几何特征误差。误差传递关系准则为零件内两理想几何特征位姿变换矩阵,是基于齐次坐标变换得到的4×4阶矩阵。
| ${\boldsymbol{M}_{{A_1}{A_2}}} = \\ \left[{\begin{array}{*{20}{c}} {{\rm{c}}{\beta _{{A_1}{A_2}}}{\rm{c}}{\gamma _{{A_1}{A_2}}}}&{-{\rm{c}}{\beta _{{A_1}{A_2}}}{\rm{s}}{\gamma _{{A_1}{A_2}}}}&{{\rm{s}}{\gamma _{{A_1}{A_2}}}}&{{\mu _{{A_1}{A_2}}}}\\ {{\rm{c}}{\beta _{{A_1}{A_2}}}{\rm{s}}{\gamma _{{A_1}{A_2}}} + {\rm{s}}{\alpha _{{A_1}{A_2}}}{\rm{s}}{\beta _{{A_1}{A_2}}}{\rm{c}}{\gamma _{{A_1}{A_2}}}}&{{\rm{c}}{\alpha _{{A_1}{A_2}}}{\rm{c}}{\gamma _{{A_1}{A_2}}}-{\rm{s}}{\alpha _{{A_1}{A_2}}}{\rm{s}}{\beta _{{A_1}{A_2}}}{\rm{s}}{\gamma _{{A_1}{A_2}}}}&{-{\rm{s}}{\alpha _{{A_1}{A_2}}}{\rm{s}}{\beta _{{A_1}{A_2}}}}&{{\nu _{{A_1}{A_2}}}}\\ { - {\rm{s}}{\beta _{{A_1}{A_2}}}{\rm{s}}{\gamma _{{A_1}{A_2}}} - {\rm{c}}{\alpha _{{A_1}{A_2}}}{\rm{s}}{\beta _{{A_1}{A_2}}}{\rm{c}}{\gamma _{{A_1}{A_2}}}}&{ - {\rm{s}}{\alpha _{{A_1}{A_2}}}{\rm{c}}{\gamma _{{A_1}{A_2}}} + {\rm{c}}{\alpha _{{A_1}{A_2}}}{\rm{s}}{\beta _{{A_1}{A_2}}}{\rm{s}}{\gamma _{{A_1}{A_2}}}}&{{\rm{c}}{\alpha _{{A_1}{A_2}}}{\rm{c}}{\beta _{{A_1}{A_2}}}}&{{\omega _{{A_1}{A_2}}}}\\ 0&0&0&1 \end{array}} \right](1)$ |
式中:c=cos, s=sin; α、β、γ为两几何特征坐标系X、Y、Z轴之间的夹角,μ、ν、ω为两坐标系在X、Y、Z方向的相对位置,下标表示相对位姿变动的二维平面,圆柱形表面和螺纹形表面等几何特征。
2) b类误差传递:零件间固定结合面的误差传递。
如图 3(b)所示link2,输入输出为接触配合几何特征面误差,误差转换关系为
| ${\boldsymbol{e}_{{B_1}}} = {\boldsymbol{M}_{AB}}{\boldsymbol{e}_{{A_2}}}.$ |
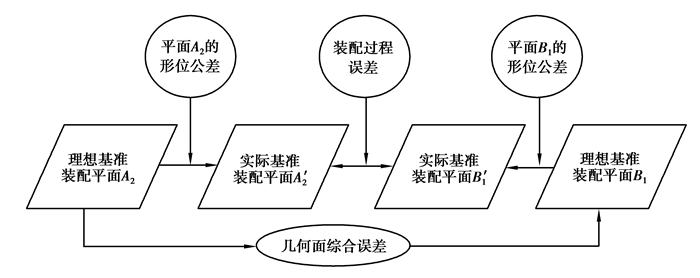
由于MAU的零件形位误差和装配过程误差的存在,两理想平面的实际装配位姿发生偏离,可通过描述理想装配平面B1相对于理想基准装配平面A2的位姿变动建立结合面误差关系矩阵 (假定A2、B1为两零件配合起主导作用的结合面)[18]。理想基准装配平面A2到理想装配平面B1的传递关系可描述为A2→A′2→B′1→B1, 结合面综合误差行成机理如图 4所示。
|
图 4 结合面综合误差行成机理图 Figure 4 Joint surface error formation mechanism |
忽略高阶小误差项后,装配结合面综合误差变动矩阵MAB(当零件A、B仅有一个结合面时,MA2B1可简化为MAB) 为
| ${\boldsymbol{M}_{AB}} = {\boldsymbol{M}_{AA'}}{\boldsymbol{M}_{A'B'}}{\boldsymbol{M}_{B'B}} = \left[{\begin{array}{*{20}{c}} 1&{-{\gamma _{AB}}}&{{\beta _{AB}}}&{{\mu _{AB}}}\\ {{\gamma _{AB}}}&1&{-{\alpha _{AB}}}&{{\nu _{AB}}}\\ {-{\beta _{AB}}}&{{\alpha _{AB}}}&1&{{\omega _{AB}}}\\ 0&0&0&1 \end{array}} \right], $ | (3) |
式中:αAB=αAA′+αBB′sin θ-αBB′cos θ,
βAB=βAA′+βBB′cos θ-βBB′sin θ,
γAB=γAA′+γA′B′+γB′B,
μAB=μAA′+μA′B′-μBB′cos θ+νBB′sin θ,
νAB=νAA′+νA′B′+μBB′cos θ+υBB′sin θ,
ωAB=ωAA′+ωBB′。
3) c类误差传递:相对运动零件间的误差传递。
加工过程中执行件处于运动状态,紧固件、支撑件等处于静止状态,MAU内必然存在相对运动的零部件,相对运动零件间的误差传递成为MAU误差传递重要组成部分。如图 3(c)所示link3,输入输出为相对运动几何特征面误差,误差转换关系为
| ${\boldsymbol{e}_{{A_4}}} = {\boldsymbol{M}_{AC}}{\boldsymbol{e}_{{C_1}}} = \boldsymbol{M}_{AC}^s\Delta \boldsymbol{M}_{AC}^s\boldsymbol{M}_{AC}^s\Delta \boldsymbol{M}_{AC}^p{\boldsymbol{e}_{{C_1}}}。$ | (4) |
相对运动两零件存在位姿误差和运动误差,因此综合误差变动矩阵MAC由位姿变换矩阵和运动变换矩阵构成,式中MACp为理想状态下两零件位姿变动矩阵,ΔMACp为位姿误差矩阵,MACs为理想状态下两零件运动变动矩阵,ΔMACs为运动误差矩阵,MACpΔMACpMACsΔMACs矩阵形式同式 (1)。
2.2.2 误差链接网络 (error linkage based network, ELN)误差链接是对零件间误差关联关系的图形化表达,而链接和链接间往往也存在着关联关系,本文用链接耦合和链接嵌套来表达误差链接之间的关联关系。如图 5(a)所示,eA4由link1和link3共同决定,称link1和link3为链接耦合。在振动,温升等因素的影响下,eA4并不是link1和link3的叠加结果,尤其是高频振动下呈现出明显的非线性关系,链接耦合能够形象地表示零件间的约束干涉关系。如图 5(b)所示,eA3是link1的输出,同时又是link2的输入,称link1和link2为链接嵌套。MAU误差链接网络是基于误差链接对复杂的误差关联关系进行综合描述的网络图形,是由链接耦合和链接嵌套形成的复杂关系网络。如图 5(c)所示,误差链接网络既展示了误差在零件间的传递与积累过程,又刻画了零件误差的耦合作用,是描述MAU误差关系强有力的工具。
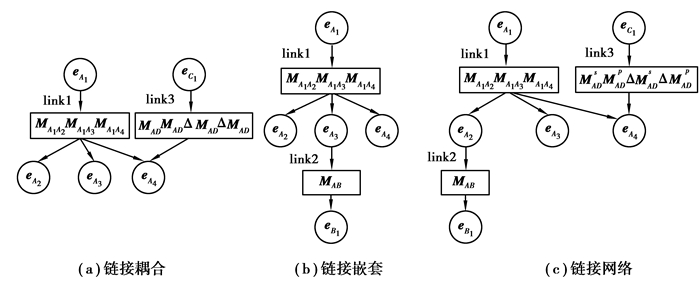
|
图 5 误差链接网络图 Figure 5 Error linkage based network |
链接网络是基于链接对MAU零件间误差传递机理或规律形象化表述与刻画,是定性的表达,若要定量表达误差间的关联关系,需将其转化为链接矩阵 (见表 1)。链接矩阵是以结构化的方法对链接网络中误差关联关系的定量描述,能够准确识别误差之间关联关系。链接矩阵主要包括链接、误差和误差传递关系三类要素,采用两级复合矩阵架构,其中行元素为链接,一级列元素为零件,二级列元素为几何特征误差项,矩阵要素有两类:误差传递基准B和误差变换矩阵M,其中基准通常为零件加工基准 (a类误差传递) 或装配基准 (b,c类误差传递)。
| 表 1 结构化的误差关联模型:误差链接矩阵 Table 1 Structural error association model: error linkage based matrix |
数控机床的任务由多个元动作配合完成,产品的最终装配误差不是MAU几何特征误差简单地叠加,误差及其影响因素关联关系复杂,误差传递因嵌套、耦合作用呈现出非线性、复杂性的基本特征,以关联强度rij标度MAU间关联关系强弱程度,构造MAU关联矩阵,rij反映MAU间关联强度,可进行MAU粒度的误差分析与控制,还可用于元动作的聚类划分。
| $\begin{array}{l} \boldsymbol{R} = {\left[{{r_{ij}}} \right]_{n \times n}} = \left[{\begin{array}{*{20}{c}} 1&{{r_{12}}}& \cdots &{{r_{1n}}}\\ {{r_{21}}}&1& \cdots &{{r_{2n}}}\\ \vdots&\vdots &{}& \vdots \\ {{r_{n1}}}&{{r_{n2}}}& \cdots &1 \end{array}} \right], \\ {r_{ij}} = \left\{ \begin{array}{l} \sum\limits_{k = 1}^p {{\lambda _{ijk}}\;\;\;i \ne j, } \\ 1\;\;\;\;\;i = j, \end{array} \right. \end{array}$ | (5) |
式中:n表示存在关联MAU数目;λijk表示MAU i和j共同参与链接的波动灵敏度,波动灵敏度表示输入误差项对输出误差项的影响程度,取值范围介于[0, 1]之间,可选用专家打分法,充分利用专家知识对误差的影响程度作出合理评价;p表示MAU i和j共同参与链接的数量。
3 基于误差链接模型 (ELM) 的误差传递路径求解方法基于误差链接模型求解误差传递路径可按照以下步骤进行。
3.1 建立误差链接网络将参与装配的零件及其几何特征编号,分别作为误差链接矩阵的一级列元素和二级列元素,根据前文所述方法及零件装配关系确定链接模型、链接网络和链接矩阵,链接矩阵的元素值用基准和误差变换矩阵标识。
3.2 搜索误差传递路径根据装配精度要求确定产品装配基准件及精度输出件,即确定误差传递路径的起点和终点,基于链接模型的误差传递路径搜索算法如下:
1) 计算误差邻接矩阵ML,并将其转化为标准布尔矩阵,通过集合运算符计算ML(i),i=1, 2, …, n。
2) 计算MR=ML+ML(1)+…+ ML(n-1),表示任意两误差之间存在简单路径的条数。
老鼠迷宫算法的基本思想为从入口出发,沿着某一方向进行试探,若行得通,则继续前进;否则沿原路返回,换一个方向搜索通往出口的路径,如此重复,直到所有可能的路径都被试探过。为方便移动,进入新位置前,需将入口到当前位置的所有路径保存在堆栈中。
3) 按照老鼠迷宫算法的基本思路从起点误差项出发,按照随机生成的方向序列进行试探,当前方向不通时,原路退回选择下一个方向进行试探,直至达到终点误差项,形成一条路径,可行前进方向需满足两个条件:当前和下一个误差项之间存在链接;当前路径 (包括下一个误差项) 为简单路径。
4) 多次调用老鼠迷宫算法,直至寻找到的路径数与矩阵MR中的数值相等时,停止搜索。
图 6所示起点终点分别为eA1、eB1的装配误差传递路径搜索图。
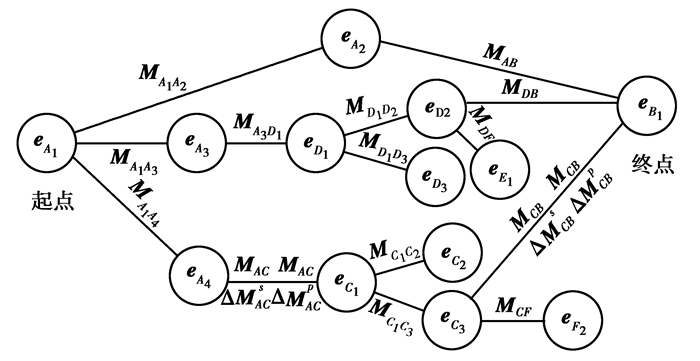
|
图 6 装配误差传递路径搜索 Figure 6 Assembly error transfer path search |
由图 6可得由eA1到eB1的误差传递路径如下:
路径1:eA1→eA2→eB1(MA1A2→MAB),
路径2:eA1→eB1→eA2(M A1A3→MA3D1→MD1D2→MDB),
路径3:eA1→eC1→eD3→eA2(M A1A””4→MACsMACpMACsMACp→MC1C3→MCBsMCBpMCBsMCBp)。
以上3条路径构成eA1到eB1的并联误差传递路径,其中路径1通过固定结合面配合传递误差;路径2通过中间零件D完成几何特征A1到B1的误差传递;路径3中零件C相对零件A、B相对运动,同时传递位姿误差和运动误差。
3.3 误差传递路径求解仅当某误差分量通过所有误差传递路径得到的值相等,装配才能成功,否则精度输出件的位姿无法确定。链接网络为误差实际传递路径提供了多种选择 (并联路径),不同的误差传递路径有不同的误差变化范围,准确识别对装配精度起主导作用的传递路径对于装配序列的划分,零件的选取等具有重要指导意义。装配定位优先级是指结合面在装配过程中根据功能要求,通过工艺手段使定位精度得到保证的先后顺序,当存在多条并联误差传递路径时,通常高定位优先等级意味着具有较高装配精度,对应的路径也就成为决定误差传递的主导因素,即误差传递有效路径[19]。
| $p\left( \varphi \right) = \left( {\min } \right.\left( {E{{\left( \varphi \right)}_{pa1}}, \left( {E{{\left( \varphi \right)}_{ps2}}, \cdots, \left( {E{{\left( \varphi \right)}_{pam}}} \right)} \right)} \right.$ | (6) |
式中,φ=α, β, γ, μ, ν, ω为输出误差分量,E(φ)pa1为误差分量φ第m条传递路径的误差值;m为φ的传递路径数量,p(φ) 表示误差分量的有效传递路径。
4 实例分析以某蜗杆转动MAU为例,分析蜗杆轴线平行度误差的有效传递路径。图 7所示蜗杆转动MAU装配图的零件及几何特征构成如表 2所示。
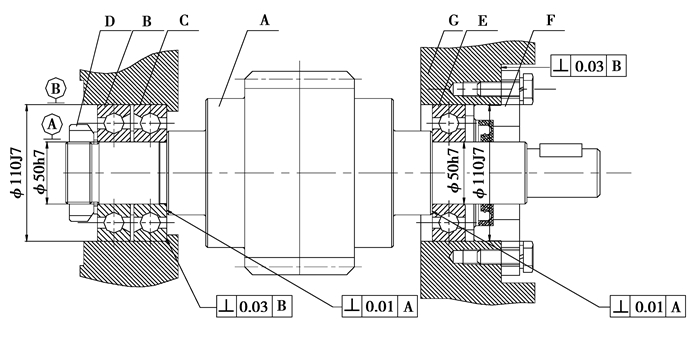
|
图 7 蜗杆转动MAU装配图 Figure 7 Worm drive MAU assembly drawing |
| 表 2 蜗杆转动MAU零件及几何特征构成 Table 2 Part of worm drive MAU and its geometrical characteristic |
由装配精度要求可知, 需求从eG0到eA0的误差分量β、γ、ν和ω的有效误差传递路径,步骤如下:
1) 建立误差链接网络及链接矩阵,由于篇幅限制仅列出部分链接矩阵,如表 3所示。
| 表 3 蜗杆转动MAU误差链接矩阵 Table 3 Worm drive MAU error linkage based matrix |
图中MA, MB, MC, MD, ME, MF表征零件内所有几何特征误差转换矩阵,阴影标注误差为链接模型基准误差,将轴承与箱体视为固定结合面配合,则轴承与蜗杆产生相对运动,link9, link10, link11, link12为相对运动零件间的误差链接模型。
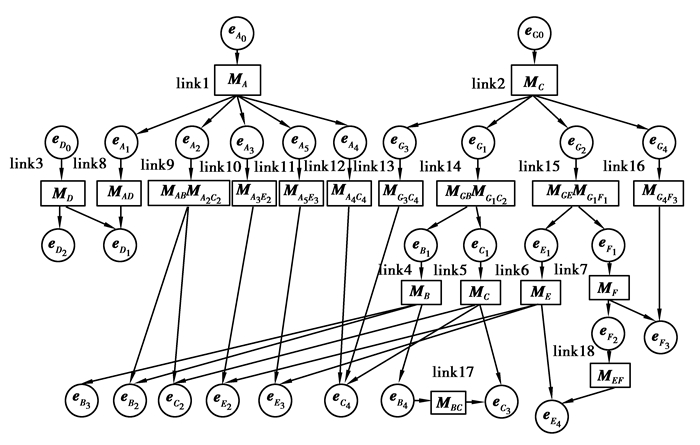
|
图 8 蜗杆转动MAU误差链接网络 Figure 8 Worm drive MAU error linkage based network |
2) 搜索误差传递路径,如图 9所示为误差路径搜索图。
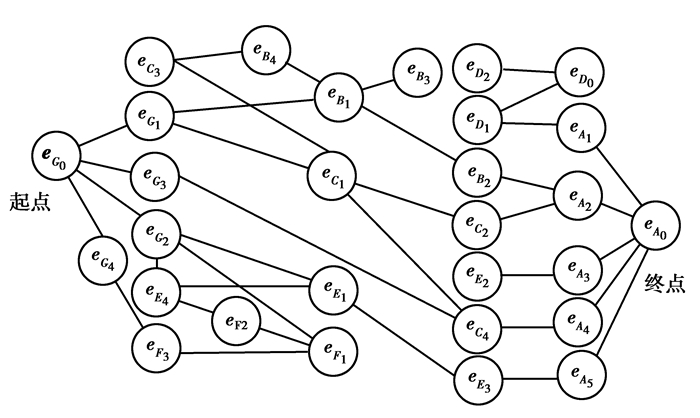
|
图 9 蜗杆转动MAU装配误差路径搜索 Figure 9 Worm drive MAU assembly error transfer path search |
对全部22条误差传递路径进行合并汇总得如下8条路径:
路径1 eG0→eG1→eC1→eC2→eA2→eA0,
路径2 eG0→eG1→eB1→eB2→eA2→eA0,
路径3 eG0→eG1→eC1→eC4→eA4→eA0,
路径4 eG0→eG3→eC4→eA4→eA0,
路径5 eG0→eG2→eE1→eE2→eA3→eA0,
路径6 eG0→eG2→eE1→eE3→eA5→eA0,
路径7 eG0→eG4→eF3→eF1→eF2→eE4→eE1→eE2→eA3→eA0,
路径8 eG0→eG4→eF3→eF1→eF2→eE4→eE1→eE3→eA5→eA0。
3) 误差传递路径求解。
第i条误差传递路径的积累装配误差求解过程为
| $\mathrm{e}_{A0}^{i}=\prod{{{\mathrm{M}}_{pi}}{{\mathrm{e}}_{G0}}, i=1, 2, \cdots, 8, }$ | (7) |
式中,
| 表 4 蜗杆转动MAU各路径误差分量变动区间宽度 Table 4 Worm drive MAU error component range of each path |
由表 4知:β、γ精度最高的路径为路径1和路径2,ν、ω精度最高的路径为路径7,故路径1或路径2为β、γ的有效传递路径,路径7为ν、ω的有效传递路径。
5 结论文章将复杂的数控机床结构化分解至元动作,全面分析了影响元动作装配单元装配精度的误差源;引入链接模型对MAU内不同类型的误差传递过程进行描述,并建立链接网络和链接矩阵,形象描述了误差间的关联关系。提出的基于链接的误差传递路径求解方法,通过老鼠迷宫算法可快速高效获得所有误差传递路径,最终装配精度的路径即为有效传递路径。结合某加工中心蜗杆转动MAU的精度分析实例,建立了MAU链接网络和链接矩阵,并验证了该误差路径求解方法的可行性。
| [1] | Qiu H, Li Y, Li Y. A new method and device for motion accuracy measurement of NC machine tools. Part 1: principle and equipment[J]. International Journal of Machine Tools & Manufacture, 2001, 41(4): 521–534. |
| [2] | Ding Y, Lin J, Ceglarek D, et al. Process-oriented tolerancing for multi-station assembly system[J]. IIE Transaction, 2005, 37(6): 493–508. DOI:10.1080/07408170490507774 |
| [3] | Ameta G, Serge S, Giordano M. Comparison of spatial math models for tolerance analysis: Tolerance-maps deviation domain, and TTRS[J]. Journal of Computing and Information Science in Engineering, 2011, 11(2): 255–267. |
| [4] |
刘伟东, 宁汝新, 刘检华, 等.
机械装配偏差源及其偏差传递机理分析[J]. 机械工程学报, 2012, 48(1): 156–168.
LIU Weidong, NING Ruxin, LIU Jianhua, et al. Mechanism analysis of deviation souring and propagation for mechanical assembly[J]. Journal of Mechanical Engineering, 2012, 48(1): 156–168. DOI:10.3901/JME.2012.01.156 (in Chinese) |
| [5] |
李东英, 李梦奇, 张根保, 等.
元动作装配单元误差源及误差传递模型研究[J]. 机械工程学报, 2015, 51(17): 146–155.
LI Dongying, LI Mengqi, ZHANG Genbao, et al. Mechanism analysis of deviation sourcing and propagation formeta-action assembly unit[J]. Journal of Mechanical Engineering, 2015, 51(17): 146–155. DOI:10.3901/JME.2015.17.146 (in Chinese) |
| [6] |
洪军, 郭俊康, 刘志刚, 等.
基于状态空间模型的精密机床装配精度预测与调整工艺[J]. 机械工程学报, 2013, 46(6): 114–121.
HONG Jun, GUO Junkang, LIU Zhigang, et al. Assembly accuracy prediction and adjustment process modeling of precision machine tool based on state space model[J]. Journal of Mechanical Engineering, 2013, 46(6): 114–121. (in Chinese) |
| [7] |
何博侠, 张志胜, 戴敏, 等.
机械装配过程的偏差传递建模理论[J]. 机械工程学报, 2008, 44(12): 62–68.
HE Boxia, ZHANG Zhisheng, DAI Min, et al. Theory of modeling variation propagation of mechanical assembly processes[J]. Chinese Journal of Mechanical Engineering, 2008, 44(12): 62–68. DOI:10.3901/JME.2008.12.062 (in Chinese) |
| [8] | Ceglarek D, Huang W, Zhou S. Time-based competition in multistage manufacturing Stream-of-variation analysis (SOVA) methodology-review[J]. International Journal of Flexible Manufacturing Systems, 2004, 16: 11–44. DOI:10.1023/B:FLEX.0000039171.25141.a4 |
| [9] |
黄强, 李青峰.
机床通用误差模型的建立及应用[J]. 中国机械工程, 2013, 24(12): 1626–1630.
HUANG Qiang, LI Qingfeng. Building and application of general model for machine tool errors[J]. China Mechanical Engineering, 2013, 24(12): 1626–1630. (in Chinese) |
| [10] | Huston R L, Passerello C E, Harlow M W. Dynamic Multirigid-body System[J]. Journal of Applied Mechanics, 1978, 45(4): 889–894. DOI:10.1115/1.3424437 |
| [11] |
刘伟东, 宁汝新, 刘检华, 等.
基于偏差有向图和D-H方法的产品装配精度预测技术[J]. 机械工程学报, 2012, 48(7): 125–140.
LIU Weidong, NING Ruxin, LIU Jianhua, et al. Precision predicting based on directed deviation graph modeling and D-H methodology[J]. Journal of Mechanical Engineering, 2012, 48(7): 125–140. DOI:10.3901/JME.2012.07.125 (in Chinese) |
| [12] |
叶佩青, 王仁彻, 赵彤, 等.
机床整机动态特性研究进展[J]. 清华大学学报, 2012, 52(2): 1758–1763.
YE Peiqing, WANG Renche, ZHAO Tong, et al. Recent research advances of whole machine tool dynamics[J]. Journal of Tsinghua University, 2012, 52(2): 1758–1763. (in Chinese) |
| [13] | Ran Y, Zhang G B, Li D Y. Functional decomposition and reliability modeling technology study of CNC machine[C]. IIE Annual Conference, Amazon, Arena, Boeing, et al.: Institute of Industrial Engineers 2014: 2191-2199. |
| [14] | Ran Y, Zhang G B, Zhang L. Quality characteristic association analysis of computer numerical control machine tool based on meta-action assembly unit[J]. Advances in Mechanical Engineering, 2016, 8(1): 1–10. |
| [15] |
张根保, 杨兴勇, 李东英, 等.
元动作装配单元的故障维修决策[J]. 机械科学与技术, 2016, 35(5): 722–728.
ZHANG Genbao, YANG Xingyong, LI Dongying, et al. Failure maintenance decision of meta-action assembly unit[J]. Mechanical Science and Technology for Aerospace Engineering, 2016, 35(5): 722–728. (in Chinese) |
| [16] |
王洋, 段桂江.
面向质量特性波动传播分析的产品特性关联建模技术[J]. 计算机集成制造系统, 2014, 20(3): 652–660.
WANG Yang, DUAN Guijiang. Product characteristic relationship modeling oriented to quality characteristic variation propagation analysis[J]. Computer Integrated Manufacturing Systems, 2014, 20(3): 652–660. (in Chinese) |
| [17] | Yang F, Duan G J. Developing a parameter linkage-based method for searching change propagation paths[J]. Research in Engineering Design, 2012, 23(4): 353–372. DOI:10.1007/s00163-011-0124-7 |
| [18] |
吕程, 刘子建, 艾彦迪, 等.
多公差耦合装配结合面误差建模与公差优化设计[J]. 机械工程学报, 2015, 51(18): 108–118.
LYV Cheng, LIU Zijian, AI Yandi, et al. Assembly joint surface modeling and tolerance optimization in the case of couple tolerance[J]. Journal of Mechanical Engineering, 2015, 51(18): 108–118. DOI:10.3901/JME.2015.18.108 (in Chinese) |
| [19] |
吕程, 刘子建, 秦欢, 等.
基于JJS矩阵的装配误差传递路径求解方法[J]. 机械工程学报, 2015, 51(20): 178–184.
LYV Cheng, LIU Zijian, QIN Huan, et al. Method of calculating the assembly error transfer path based on JSS matrix[J]. Journal of Mechanical Engineering, 2015, 51(20): 178–184. (in Chinese) |
 2017, Vol. 40
2017, Vol. 40

