2. 西南交通大学 信息科学与技术学院, 四川 成都 610031;
3. 江西师范大学 软件学院, 江西 南昌 330031
2. School of Information Science and Technology, Southwest Jiaotong University, Chengdu 610031, P. R. China;
3. School of Software, Jangxi Normal University, Nanchang 330022, P. R. China
随着经济社会发展及人民生活质量提升,物流与人民日常生活间的联系也越发紧密。在传统物资运输过程中,车辆路径优化问题 (vehicle routing problem, VRP),通常假定物资运输过程是单级方向配送,即从仓库中心到客户站点的直接物资配送方式[1]。但是因为物流长途运输所使用的车辆较大,如果路线规划不佳,极易造成城市交通堵塞、产生较严重的噪音及尾气排放污染,出于考虑城市舒适性居住环境角度,大部分城市都对货运大型车辆实行限行或禁行管制:远距离物资配送一般是由运输能力较大的车辆配送至郊区转运点,然后再利用小型配送车辆将物资发送至城区内不同的需求点,上述配送过程便构成两级配送车辆路径优化问题 (Two-echelon vehicle routing problem,2E-VRP)。
2E-VRP与VRP相比,在求解方式和难度上不同,前者是一级与二级配送模式的耦合,应用传统优化模型和算法存在精度差且运算时间长的问题。学者对2E-VRP方向的研究,主要分精确方式和启发优化方式2种,如文献[2]提出两级车辆路径优化问题的商品流模型,利用分支切割方法进行求解,精度高但运行时间稍长;文献[3]对上述分支切割算法进行改进,进一步提高算法性能;文献[4]使用不等式方法强化分支切割法中两级车辆路径优化问题的连续性和松弛性;文献[5]提出开放式车辆路径问题的启发式方法,并利用聚类最小生成树方式实现2E-VRP的启发式求解文献[6]提出改进禁忌搜索算法,对2E-VRP优化问题进行求解, 此算法包含2E-VRP问题下界文献[7]提出另一2E-VRP问题求解的禁忌搜索方法,取得理想优化结果;文献[8]设计混合蚁群算法实现2E-VRP优化问题求解,该算法利用禁忌搜索进行局部优化,实现后优化过程改进。精确算法精度高,但运行时间长,不适于大型配送网络。对此,启发式算法应运而生,如文献[9]提出分类规划并行启发式方法,将两级车辆路径优化问题拆解为2个子车辆配送问题,采用规划算法对2个子问题分别求解,虽加快了搜索速度,但因耦合及优化算法性能所限,求解精度仍然不佳。当前,国内对于2E-VRP问题的研究成果相对较少。
研究借鉴文献[9]的拆解方式,一级采用精确的最优割算法,以此作为二级优化的基础,二级采用改进的QDEMA算法进行全局寻优,来处理两级算法的耦合问题,并降低算法运行时间。
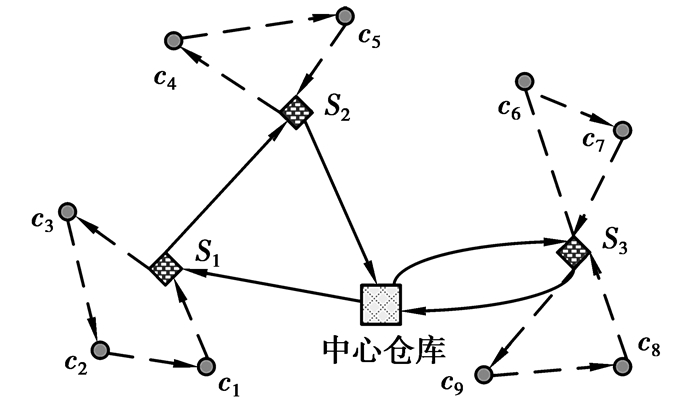
1 两级车辆路径问题2E-VRP问题如图 1所示,S1~S3为一级中转站,c1~c9为二级用户点,两级车辆路径采用不同线型区分 (一级实线,二级虚线)。
|
图 1 2E-VRP问题 Figure 1 Problem of 2E-VRP |
2E-VRP数学模型等价于最小配送路径问题,即最后一辆车完成配送所需总路径最小[10]
| $ f=\min \left( {{C}_{\text{max}}} \right), $ | (1) |
式中,Cmax表示总的配送路径。式 (2) 主要确保每个订单只被处理一次
| $ \sum\limits_{k=1}^{n}{{{Y}_{ik}}=1, i=1, 2, \cdots, n, } $ | (2) |
式中,Yik表示每个订单处理次数。式 (3) 则确保当
| $ \sum\nolimits_{i=1}^{n}{{{Y}_{i, k+1}}\le H}\sum\nolimits_{i=1}^{n}{{{Y}_{ik}}}, $ | (3) |
式 (4) 用来确保当
| $ {{y}_{k}}\le \sum\nolimits_{i=1}^{n}{{{Y}_{ik}}}, k=1, \cdots, n, $ | (4) |
式 (5) 用来确保当
| $ \sum\nolimits_{i=1}^{n}{{{Y}_{ik}}}\le H\times {{y}_{k}}, k=1, \cdots, n, $ | (5) |
式 (4)、(5) 含义是,当订单Bk为有效时,yk=1;而当订单Bk无效时,yk=0。式 (6)~(8) 给出交货车辆批次限制:
| $ \sum\limits_{g = 1}^G {{V_{kg}}} \leqslant 1,k = 1, \cdots ,n, $ | (6) |
| $ \sum\limits_{g=1}^{G}{{{V}_{kg}}}\le H\times {{y}_{k}}, k=1, \cdots, n, $ | (7) |
| $ \sum\limits_{k=1}^{n}{\sum\limits_{g=1}^{G}{{{V}_{kg}}}=}\sum\limits_{k=1}^{n}{{{y}_{k}}, } $ | (8) |
式中,Vkg表示单个车辆运行批次。式 (6) 限制每个订单只能由一辆货车交付,式 (7) 表示若该客户暂无订单,则不进行配送,车辆配送批次为0。
式 (9) 给出车辆容量限制
| $ \sum\limits_{i=1}^{n}{{{e}_{i}}}{{Y}_{ik}}\le {{z}_{g}}+H\left( 1-{{V}_{kg}} \right), k=1, \cdots, n, g=1, \cdots, G, $ | (9) |
式中,ei表示车辆i运输容量。式 (10) 和 (11) 给出批次Bk准备时间
| $ {{r}_{k}}\ge \sum\limits_{k'=1}^{k}{\sum\limits_{i=1}^{n}{{{p}_{i}}{{Y}_{ik'}}}-H\left( 1-{{y}_{k}} \right)}, k=1, \cdots, n, $ | (10) |
| $ {{r}_{k}}\le \sum\limits_{k'=1}^{k}{\sum\limits_{i=1}^{n}{{{p}_{i}}{{Y}_{ik'}}}-H\left( 1-{{y}_{k}} \right)}, k=1, \cdots, n, $ | (11) |
式中,pi表示车辆i准备时间。式 (12)~(14) 给出出发时间uk的限制
| $ {{u}_{k}}\le H\times {{y}_{k}}, k=1, \cdots, n, $ | (12) |
| $ \left\{ \begin{align} &{{u}_{1}}={{r}_{1}} \\ &{{u}_{k}}\ge {{r}_{k}}, \\ \end{align} \right.k=2, \cdots, n, $ | (13) |
| $ \left\{ \begin{align} &{{u}_{k}}'+t_{01}^{g}+t_{10}^{g}-H\left( 2-{{V}_{kg}}-{{V}_{k'g}} \right)\le {{u}_{k}}\le \\ &\ \ \ \ \ \ {{u}_{k}}'+t_{01}^{g}+t_{10}^{g}-H\left( 2-{{V}_{kg}}-{{V}_{k'g}} \right), \\ &k=2, \cdots, n;k'=1, \cdots, k-1;g=1, \cdots, G, \\ \end{align} \right. $ | (14) |
式中,uk表示车辆k准备时间。式 (15) 给出订单配送时间Tk的限制
| $ \left\{ \begin{align} &{{T}_{k}}\le H\times {{y}_{k}}, k=1, \cdots, n, \\ &{{u}_{k}}+t_{01}^{g}+t_{10}^{g}-H\left( 1-{{V}_{kg}} \right)\le {{u}_{k}}\le {{u}_{k}}+t_{01}^{g}+t_{10}^{g}-H\left( 1-{{V}_{kg}} \right), \\ &k=2, \cdots, n;g=1, \cdots, G。\\ \end{align} \right. $ | (15) |
差分进化算法 (differential evolution algorithm, DE),特点是结构简单、收敛快和精度佳,得到广泛使用。假设DE算法有NP个种群个体,则第G代种群为[11]
| $ {{P}_{G}}=\left\{ {{X}_{1}}\left( G \right), {{X}_{2}}\left( G \right), \cdots, {{X}_{NP}}\left( G \right) \right\}, $ | (16) |
式中,Xi(G), i∈1, …, NP代表种群个体,PG为当前种群。DE算法流程可通过下列操作实现[12]。
步骤1:(初始化) 对G=0代种群,个体Xi(0) 可在范围[Xmin, Xmax]中均匀随机初始化
| $ \left\{ \begin{align} &{{X}_{\min }}=\left\{ {{x}_{\min-1}}, \cdots, {{x}_{\min-D}} \right\}, \\ &{{X}_{\max }}=\left\{ {{x}_{\max-1}}, \cdots, {{x}_{\max -D}} \right\}, \\ \end{align} \right. $ | (17) |
式中,D为DE种群维度。那么,在G=0代个体i的第j个元素可由下式初始化
| $ {{x}_{ij}}\left( 0 \right)={{x}_{\min-j}}+\text{ran}{{\text{d}}_{ij}}\left( 0, 1 \right)\times \left( {{x}_{\max-j}}-{{x}_{\min-j}} \right), $ | (18) |
式中,randij(0, 1) 为[0,1]区间的均匀分布函数,并在[0,1]区间内随机初始化交叉概率因子Cr。
步骤2:(变异) 标准DE变异是随机选取2个种群个体 (Xrand-1(G),Xrand-2(G)),通过与目标个体Xi(G) 进行向量叠加产生新个体Vi(G)
| $ \begin{align} &{{V}_{i}}\left( G \right)={{X}_{i}}\left( G \right)+{{F}_{1}}\left( {{X}_{\text{best}}}\left( G \right)-{{X}_{i}}\left( G \right) \right)+ \\ &\ \ \ \ \ \ \ \ \ \ \ \ {{F}_{2}}\left( {{X}_{\text{rand-1}}}\left( G \right)-{{X}_{\text{rand-2}}}\left( G \right) \right), \\ \end{align} $ | (19) |
式中,F为比例因子,F∈[0,2]。选取相对简单的变异方式如式 (4)。
步骤3:(交叉) 通常有2种类型的交叉方式,分别为二项式和指数形式
二项式交叉:通过供体向量Vi(G) 和目标向量Xi(G) 进行交叉产生新个体Ui(G)
| $ {{u}_{ij}}\left( G \right)=\left\{ \begin{align} &{{v}_{ij}}\left( G \right), \text{if}\ \text{ran}{{\text{d}}_{ij}}\le Cr\ \text{or}\ j={{j}_{\text{rand}}}, \\ &{{x}_{ij}}\left( G \right), \text{otherwise, } \\ \end{align} \right. $ | (20) |
式中,randij和jrand表示随机数。
指数交叉:在区间[1, D]中随机选取整数n作为目标向量Xi(G) 的起点,表示其与供体向量Vi(G) 进行元素交换的开始。同样在区间[1, D]中随机选取另一个整数L,作为供体向量贡献给新个体向量的元素个数,则指数交叉形式如下
| $ {{u}_{ij}}\left( G \right)=\left\{ \begin{align} &{{v}_{ij}}\left( G \right), \text{for}\ j={{\left\langle n \right\rangle }_{D}}, \cdots, {{\left\langle n+L-1 \right\rangle }_{D}}, \\ &{{x}_{ij}}\left( G \right), \text{otherwise, } \\ \end{align} \right. $ | (21) |
式中,〈·〉D表示模量为D的模函数。
步骤4:(选择) 对于给定目标函数f(x) 的最小化问题,DE算法精英选择方式可表述如下
| $ \boldsymbol{{{X}}_{i}}\left( G+1 \right)=\left\{ \begin{align} &{{U}_{i}}\left( G \right), \text{if}\ f\left( {{U}_{i}}\left( G \right) \right)\le f\left( \boldsymbol{{{X}}_{i}}\left( G \right) \right), \\ &\boldsymbol{{{X}}_{i}}\left( G \right), \text{if}\ f\left( {{U}_{i}}\left( G \right) \right)>f\left( \boldsymbol{{{X}}_{i}}\left( G \right) \right)。 \\ \end{align} \right. $ | (22) |
Q学习是一种强化学习方法[13],通过一定操作引起环境状态变化,并赋予该操作相应奖励 (或惩罚),从而使操作向着明确的方向进行。在实际中,在状态s对未来状态s′的奖励进行预测是很难的。Q学习则仅考虑未来状态s′的最佳动作奖励回报。
令S={s1, …, sn}为给定环境下智能体状态集合;A={a1, …, an}为智能体在状态si∈S可供选择的动作集合;r(si, aj) 表示智能体在状态si选择动作aj的立即奖励回报;δ(si, aj) 为智能体在状态si选择动作aj的下一状态sk的过渡函数;γ为惩罚未来奖励延迟的贴现因子,γ∈[0,1];Q(si, aj) 为智能体在状态si选择动作aj的总奖励回报。则Q(s, a) 可表述为[14]
| $ Q\left( s, a \right)=r\left( s, a \right)+\gamma \overset{*}{\mathop{V}}\, Q\left( \delta \left( s, a \right) \right)=r\left( s, a \right)+\gamma {{\max }_{a}}'Q\left( \delta \left( s, a \right), a' \right), $ | (23) |
式中,
| $ Q\left( s, a \right)\leftarrow \left( 1-\alpha \right)Q\left( s, a \right)+\alpha \times \left( r\left( s, a \right)+\gamma \ {{\max }_{a}}'Q\left( \delta \left( s, a \right), a' \right) \right)。 $ | (24) |
上式主要是使Q(s, a) 在动作a指向δ(s, a) 时,Q-value递增,确保下步动作奖励r(s, a) 要大于Q(s, a),保证进化向更优方向进行。当α=0时停止学习,当α=1时表示智能体只考虑最新信息。贴现因子γ决定未来信息重要性,γ=0表示算法只注重当前奖励,而γ=1时表示算法注重长期高额回报。
3 基于QDEMA算法的2E-VRP问题优化 3.1 一级SVRP最优割算法如前所述,这里采用最优切割方式进行初始种群构建,然后利用QDEMA算法进行2E-VRP问题精细优化。
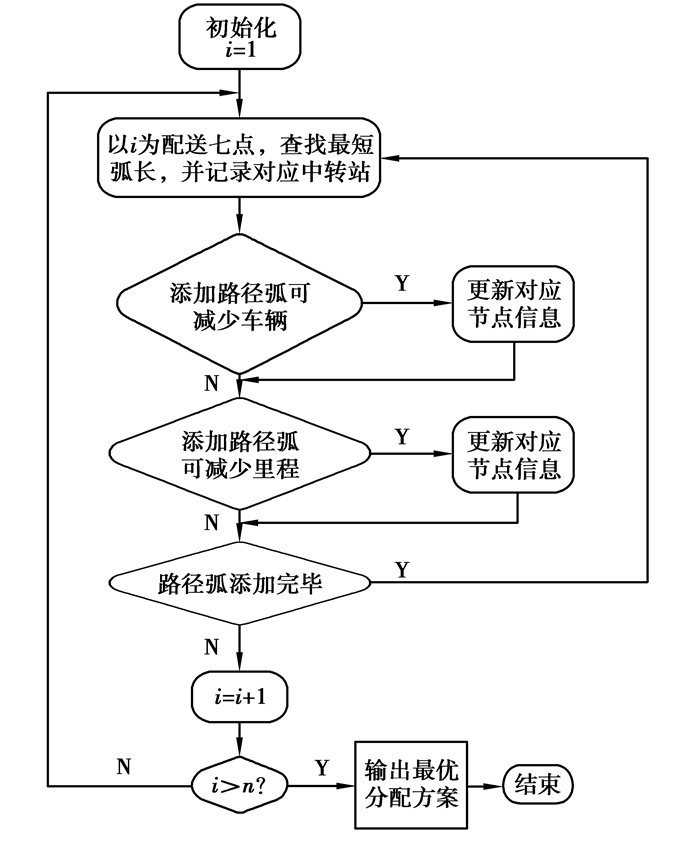
2E-VRP可看作一级SDVRP和二级MDVRP耦合问题,可从二级到一级顺序解耦。首先采用最优切割法得到一级SDVRP问题较合理配送计划,以此确定中转站数量,并作为QDEMA算法初始解。然后求解二级MDVRP配送方案得到总里程及总车辆数。而QDEMA只优化二级客户配送方案,此做法有助于提高算法效率。最优切割法流程如图 2[15]。
|
图 2 最优切割算法 Figure 2 Algorithm of optimal catting |
QDEMA算法利用差分进化算法实现全局寻优,利用差分Q学习 (differential Q learning, DQL) 算法实现局部深度探索。QDEMA算法伪代码见表 1,步骤如下:
| 表 1 QDEMA算法伪代码 Table 1 QDEMA algorithm pseudo-code |
步骤1:(初始化) 在初始搜索范围中初始化大小NP,维数D的种群。选取方式同式 (3),Q-table初始化为较小数值,如果Q-value能够达到最大100,则赋予相应的Q-table值为1;
步骤2:(参数自适应) Q-table奖励、惩罚措施主要用来选取算法合适的比例因子F,选择F=Fj的概率可由下式计算
| $ P\left( {{F}_{j}} \right)=\frac{Q\left( {{s}_{i}}, 10{{F}_{j}} \right)}{\sum\limits_{l=1}^{10}{Q\left( {{s}_{i}}, 10{{F}_{l}} \right)}}。 $ | (25) |
为保持每一行Q-value的自适应性,在区间[0,1]中随机产生数值r,然后选取Fj,满足
| $ \begin{align} &\ \ \ \ \ \ \sum\limits_{m=1}^{j-1}{P\left( F={{F}_{m}} \right) < r\le }\sum\limits_{m=1}^{j}{P\left( F={{F}_{m}} \right)} \\ &\Rightarrow \frac{\sum\nolimits_{m=1}^{j-1}{Q\left( {{s}_{i}}, 10{{F}_{m}} \right)}}{\sum\nolimits_{l=1}^{10}{Q\left( {{s}_{i}}, 10{{F}_{l}} \right)}} < 1\le \frac{\sum\nolimits_{m=1}^{j}{Q\left( {{s}_{i}}, 10{{F}_{m}} \right)}}{\sum\nolimits_{l=1}^{10}{Q\left( {{s}_{i}}, 10{{F}_{l}} \right)}}。\\ \end{align} $ | (26) |
步骤3:(DE操作) 利用DE算法进行个体排序和状态分配,令fi为个体i最新目标值,对fi归一化
步骤4:(Q-table更新) 若状态为si的个体在执行操作Fj后状态变为sk,其目标适应值增加,那么利用正奖励公式更新Q(si, 10Fj),形如
| $ \begin{align} &Q\left( {{s}_{i}}, 10{{F}_{j}} \right)=\left( 1-\alpha \right)Q\left( {{s}_{i}}, 10{{F}_{j}} \right)+ \\ &\alpha \left( \text{reward}\left( {{s}_{i}}, 10{{F}_{j}} \right)+\gamma {{\max }_{F}}'\left( {{s}_{k}}, 10F' \right) \right), \\ \end{align} $ | (27) |
否则,Q (si, 10Fj) 利用负奖励回报-K更新,reward (si, 10Fj) 表示奖励反馈值。
步骤5:(判断收敛) 重复步骤2~4,直到满足条件:达到迭代终止代数或满足收敛精度。
4 仿真实验与分析 4.1 QDEMA算法实验测试函数:f1为Dejong, f2为Griewank。f1~f2函数全局最优值为0。函数形式如下:
| $ \begin{align} &{{f}_{1}}=\frac{1}{4\ 000}\sum\limits_{i=1}^{n}{x_{i}^{2}}-\prod\limits_{i=1}^{n}{\cos \left( {{x}_{i}}/\sqrt{i} \right)+1, \left[-60, 60 \right], } \\ &{{f}_{2}}=\frac{{{\sin }^{2}}\left( \sqrt{x_{1}^{2}+x_{2}^{2}} \right)-0.5}{{{\left( 1+0.001\left( x_{1}^{2}+x_{2}^{2} \right) \right)}^{2}}}-0.5, \left[-100, 100 \right]。 \\ \end{align} $ |
对比算法选用改进自适应变空间差分进化算法 (SACPMDE)[16]、自适应交叉概率因子的差分进化算法 (ACPFDE)[18]、2种经典的数值改进算法DERL和DELR[19]。算法参数设置方式选取D=30, 种群大小NP=200, 迭代终止数8 000。
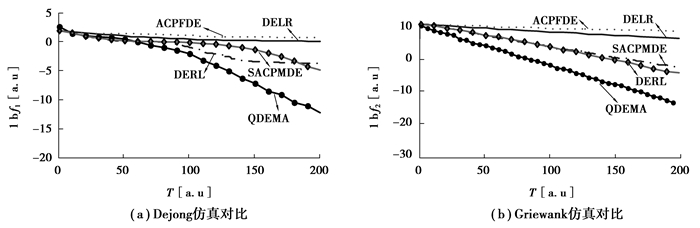
ACPFDE算法的交叉概率因子取值范围设为CR∈[0.3, 0.9],SACPMDE算法和ASMDE算法的参数设置同文献[16]相关设置,DERL和DELR算法参数设置同文献[17]相关设置,上述4种算法的交叉概率因子选取CR=0.9, 仿真精度选取VTR=10-6。对比算法的仿真对比结果如图 3(a)~3(b)所示。
|
图 3 测试函数仿真对比 Figure 3 Test function of simulation comparison |
图 3(a)~图 3(b)分别给出对比算法在Dejong和Griewank测试函数上的仿真对比结果。图 3(a)显示出几种算法呈2种不同收敛态势,一是QDEMA和SACPMDE算法未出现早熟收敛,但SACPMDE算法要明显比QDEMA算法收敛速度慢。二是其余几种算法均出现不同程度的早熟收敛现象。图 3(b)显示出几种算法均未出现早熟收敛现象,但QDEMA算法的收敛速度要明显快于对比算法。通过在测试函数上的仿真一定程度上验证了算法有效性。
4.2 算例实验这里借鉴相关文献做法,选取标准VRP算例:En33-k4、En22-k4、En51-k4,并以这3种算例为基础,通过设定对应的车辆配送约束,演化获得本文实验算例,该算例基于应用背景特点进行设计,具有一定应用研究价值。
实验设置:Intel (R) XeonX55502.60 GHz处理器,4 GB内存,Win7系统,仿真软件采用matlab2012b。参数设置:设置差分进化种群规模NP=50,交叉概率因子Pc=0.8,终止迭代次数Tmax=1 000,算法最大运行时间tmax=60 s。
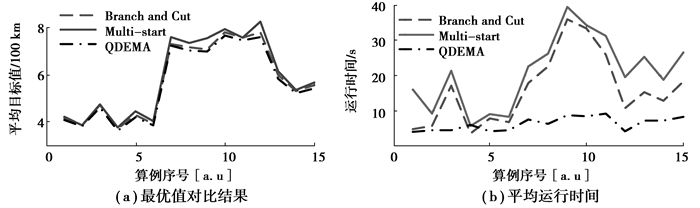
仿真对比指标:算法运行10次获得最佳配送路径值 (best),平均算法运行时间 (time)。对比算法采用Branch and Cut[20]算法和Multi-start[21]算法。仿真结果如表 2及图 4所示。
| 表 2 仿真对比结果 Table 2 Simulation results |
|
图 4 算法对比结果 Figure 4 Results of alogorithm comparison |
表 2给出3种对比算法在不同算例上的仿真数据,表中Best量单位是kM,Time量单位是s。图 4(a)~图 4(b)分别给出3种算法的平均配送路径值和运行时间对比图。图 4(a)可看出在最优配送路径值方面,虽相差不大,但QDEMA算法要优于Branch and Cut和Multi-start 2个对比算法,而Multi-start算法要始终优于Branch and Cut算法。在图 4(b)所示运行时间上,Multi-start算法所用时间最长,Branch and Cut算法的运行所需时间其次,用时最短的为QDEMA算法。说明Branch and Cut和Multi-start 2个算法相比,Multi-start是在牺牲计算时间的同时提高了算法收敛精度,而QDEMA算法不但收敛精度要高于2种算法,且在运行时间上也要优于对比算法,且算法的平均运行时间较平稳。极个别情况,如算例4,由于该算例较简单,Branch and Cut和Multi-start 2个算法的运行时间不高,甚至接近或比QDEMA算法运行时间短,主要是算例过于简单,而QDEMA算法仍采用种群寻优方式,耗时较长。综上所述,QDEMA算法适合大规模2E-VRP问题,而实际中2E-VRP问题规模都是非常大的。
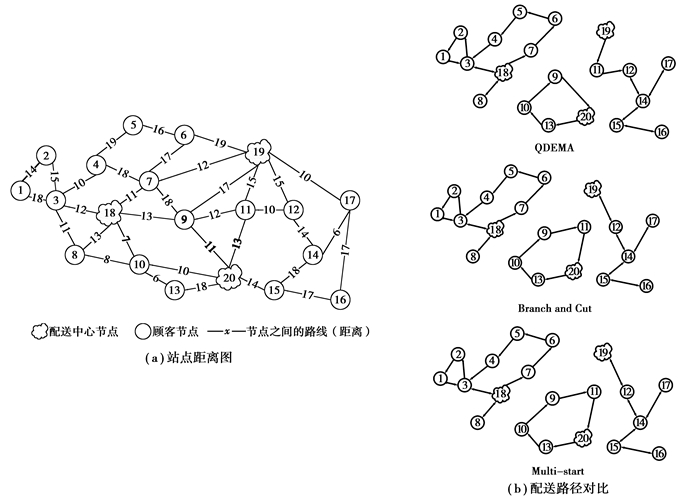
下面以E-n22-k4-s9-20算例为例,给出QDEMA、Branch and Cut和Multi-start算法的配送路径图,如图 5(a)~图 5(b)所示。其中,图 5(a)为原始的节点距离图,图中给出站点间的配送距离,单位kM。图 5(b)分别给出上述3种对比算法的配送路径图。从表 2仿真对比结果看,QDEMA算法的最佳配送路径总距离为458 kM,而Branch and Cut算法配送距离为481 kM,Multi-start算法为472 kM,QDEMA算法在配送距离上要优于对比算法。在算法运行时间上,QDEMA算法要优于Branch and Cut和Multi-start算法。图 5(b)给出不同算法的配送方案,图中可看出QDEMA算法略区别于对比算法。
|
图 5 配送方案路线图 Figure 5 Roadmao of distribution scheme |
根据两级车辆路径优化问题特性,将该问题分解为使用最优分割法算法精确分配的一级中转站优化,以及利用Q学习理论和差分进化算法设计了新的Memetic算法进行车辆路径优化的二级客户端优化。实现了两级车辆路径优化问题的有效解耦,仿真结果显示,所提算法相对于对比算法能够更有效解决两级车辆路径优化问题。
| [1] | Xia Y M, Cheng B. A vehicle routing problem based on intelligent batteries transfer management for the EV net-work[J]. China Communications, 2014, 11(5): 160–170. DOI:10.1109/CC.2014.6880471 |
| [2] | Crainic T G, Mancini S, Perboli G. Multi-start heuristics for the two-echelon vehicle routing problem[J]. Lecture Notes in Computer Science, 2011, 32(5): 179–190. |
| [3] | Perboli G, Tadei R, Vigo D. The two-echelon capacitated vehicle routing problem: Models and math-based heuri-stics[J]. Transportation Science, 2011, 45(3): 364–380. DOI:10.1287/trsc.1110.0368 |
| [4] | Jepsen M, Spoorendonk S, Ropke S. A branch-and-cut algorithm for the symmetric two-echelon capacitated vehicle routing problem[J]. Transportation Science, 2013, 47(1): 23–37. DOI:10.1287/trsc.1110.0399 |
| [5] | Saeiklis D, Powell S. A heuristic method for the open vehicle routing problem[J]. Journal of the Operational Research Society, 2000, 51(5): 564–573. DOI:10.1057/palgrave.jors.2600924 |
| [6] | Brandao J. A tabu search heuristic algorithm for open vehicle prohlem routing problem[J]. European JournaloI Operational Research, 2004, 157(3): 552–564. DOI:10.1016/S0377-2217(03)00238-8 |
| [7] |
符草.
带装载能力约束的开放式车辆路径问题及其禁忌搜索算法研究[J]. 系统工程理论与实践, 2004, 24(3): 123–128.
FU Cao. The capacitated open vehide routing problem and its tabu search algorithm[J]. Systems Engineering-theory & Practice, 2004, 24(3): 123–128. (in Chinese) |
| [8] |
李湘勇, 田澎.
开放式车辆路径问题的蚁群优化算法[J]. 系统工程理论与实践, 2008, 28(6): 81–93.
LI Xiangyong, TIAN Peng. Research on ant colong optimization algorithm for the open vehicle routing problem[J]. System Engineering-theory & Practice, 2008, 28(6): 81–93. (in Chinese) |
| [9] | Perboli G, Tadei R. New families of valid inequalities for the two-echelon vehicle routing problem[J]. Electronic Notes in Discrete Mathematics, 2010, 36(6): 639–646. |
| [10] | Crainic T G, Perboli G, Mancini S, et al. Two-echelon vehicle routing problem: a satellite location analysis[J]. Procedia Social and Behavioral Science, 2010, 2(3): 5944–5955. DOI:10.1016/j.sbspro.2010.04.009 |
| [11] |
吴亮红, 王耀南, 袁小芳.
基于快速自适应差分进化算法的电力系统经济负荷分配[J]. 控制与决策, 2013, 28(4): 557–562.
WU Lianghong, WANG Yaonan, YUAN Xiaofang. Fast self-adaptire differtial evolution algorithir for power economic load dispatch[J]. Control and Decision, 2013, 28(4): 557–562. (in Chinese) |
| [12] | Gao Z Q, Pan Z B, Gao J H. A new highly efficient differential evolution scheme and its application to waveform inver-sion[J]. IEEE Geoscience and Remote Sensing Letters, 2014, 11(10): 1702–1706. DOI:10.1109/LGRS.2014.2306263 |
| [13] | Konar A, Chakraborty I G, Singh S J. A deterministic improved q-Learning for path planning of amobile robot[J]. IEEE Transactions on Systems Man and Cybernetics Systems, 2013, 43(5): 1141–1153. DOI:10.1109/TSMCA.2012.2227719 |
| [14] |
于俊, 刘全, 傅启明.
基于优先级扫描Dyna结构的贝叶斯Q学习方法[J]. 通信学报, 2013, 34(11): 129–138.
YU Jun, LIU Quan, FU Qiming. Bayesian Q learning method with dyna architecture and prioritized sweeping[J]. Jounrnd on Communications, 2013, 34(11): 129–138. (in Chinese) |
| [15] | Prins C. A simple and effective evolutionary algorithm for the vehicle routing problem[J]. Computers & Operations Research, 2004, 31(12): 1985–2002. |
| [16] |
姚峰, 杨卫东, 张明.
改进自适应变空间差分进化算法[J]. 控制理论与应用, 2010, 27(1): 32–38.
YAO Feng, YANG Weidong, ZHANG Ming. Improved spale-adaptive-based differential evolution algorith[J]. Control Theory & Applictions, 2010, 27(1): 32–38. (in Chinese) |
| [17] | Hager T, Bruderl G, Lermer T. Current dependence of electro-optical parameters in green and blue (AlIn) GaN laser diodes[J]. Applied Physics Letters, 2012, 101(17): 1109–1116. |
| [18] |
杨卫东, 姚峰, 张明.
基于自适应交叉概率因子的差分进化算法及其应用[J]. 信息与控制, 2010, 39(2): 187–193.
YANG Weidong, YAO Feng, ZHANG Ming. Differential evolution algorithm based on adopitive crossover probaility factor and its application[J]. Information and Control, 2010, 39(2): 187–193. (in Chinese) |
| [19] | Kaelo P, Ali M M. A numerical study of some modified differential evolution algorithms[J]. European Journal of Operational Research, 2005, 169(3): 1176–1184. |
| [20] | Avella P, Boccia M, Vasilyev I. A branch-and-cut algorithm for the multilevel generalized assignment problem[J]. IEEE Access, 2013, 25(1): 475–479. |
| [21] | Oliveira H, Vasconcelos G C, Alvarenga G B. A multi-start simulated annealing algorithm for the vehicle routing problem with time windows[J]. Symposium on Neural Networks, 2012, 21(3): 137–142. |
 2017, Vol. 40
2017, Vol. 40

