b. 重庆大学 汽车工程学院, 重庆 400044
b. College of Automotive Engineering, Chongqing University, Chongqing 400044, P. R. China
根据世界卫生组织的调查,2013年有124万人死于道路交通,其中22%是行人,行人腿部是最容易受到伤害的部位[1]。为了降低行人腿部受到的伤害,国内外学者进行了相关的研究,文献[2]通过全因子试验,构造响应面,用序列二次规划求得最优的汽车前端结构参数组合;文献[3]运用刚度分析方法,通过分析算例,找出了影响行人保护最显著的结构因子;文献[4]建立汽车前端结构位置参数的正交表,找出了最优的因子水平组合。文献[5]通过正交试验构造响应面,运用序列二次规划法得出最优的结构参数组合。
但是,上述研究中,设计试验选取点并不具有全局代表性,优化方法也不能体现全局优化特性。笔者通过引入拉丁超立方抽样,抽取具有全局代表性的试验点,并运用具有全局优化特性的多目标遗传算法,得出了更全面的优化结果。
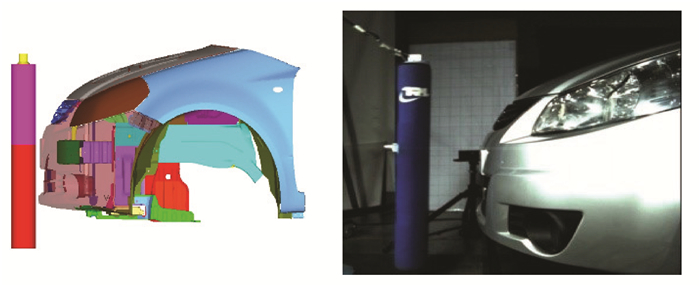
1 有限元模型仿真与试验汽车与行人碰撞事故中,行人腿部伤害主要来源于汽车的保险杠结构。为了提高计算效率,只建立某车型前端结构的有限元模型,如图 1所示,主要包括发动机罩、翼子板、保险杠蒙皮、前保险杠、格栅和冷凝器等。有限元模型采用BT薄壳单元,网格尺寸为6 mm,包含348 729个节点,337 344个单元。简化模型约束了车架末端、发动机罩后端、翼子板上端及悬架的6个自由度。碰撞模型中,使用标准的TRL腿部模型[6],腿部模型下端离地高度为150 mm,以11.1 m/s的速度正面撞向汽车前端的中心。采用LS-DYNA软件计算求解,并用hypergraph软件提取出胫骨加速度Pa、膝关节弯曲角度Pb及剪切位移Ps3条伤害指标曲线[7]。
|
图 1 碰撞有限元与试验模型 Figure 1 FE model and test |
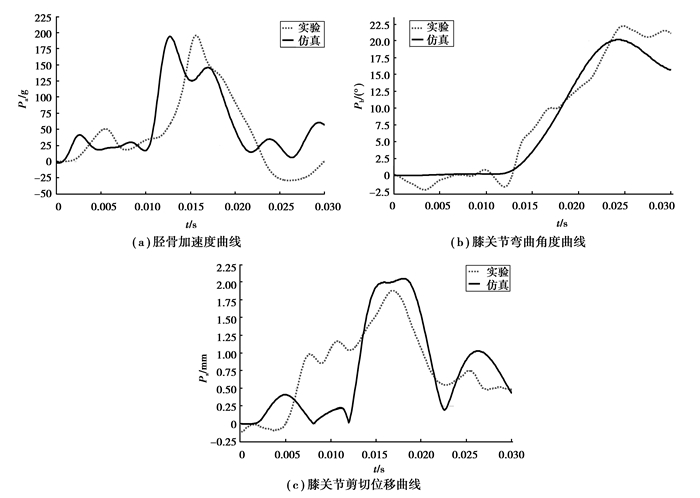
按照Euro-NCAP法规要求[8],在碰撞试验中,将质量为13.4 kg的下肢模块以11.1 m/s的速度正面撞向静止的汽车,撞击位置为保险杠横梁中心,通过传感器测量胫骨加速度Pa、膝关节弯曲角度Pb及剪切位移Ps,3个损伤指标限值分别为150 g,15°和6 mm。实验结果与仿真结果对比如图 2所示。
|
图 2 实验与仿真伤害曲线对比 Figure 2 Comparison between test and analysis results |
从3个损伤指标的对比结果可以看出,试验与仿真计算的各指标的趋势保持了较好的一致性。且从具体的实验值、仿真值与法规限值[7]对比表 1也可以得到,仿真结果与实验误差都在10%以内,说明了本次建立的有限元碰撞模型是可靠的,可以在该仿真模型基础上进行后续的分析。同时,试验和仿真计算的结果都反映出,该车在碰撞到行人下肢时造成的胫骨加速度与膝关节弯曲角度严重超过了法规的限值,需要对汽车前端结构进行优化来降低腿部受到的伤害。
| 表 1 实验值、仿真值与法规限值对比 Table 1 Comparison between the peak values of test and simulation, and regulations limit |
汽车前端结构作为汽车行人保护的主要部分,其吸能和缓冲性能,将决定该车在发生碰撞时对行人的损伤程度。
文献[9-14]研究发现吸能泡沫厚度,副保险杠刚度,主副保险杠垂向距离,是影响行人保护的3个重要的参数,因此选取这3个参数为设计变量。
原汽车前端模型没有吸能泡沫及副保险杠,改进方案中添加吸能泡沫及副保险杠。由于前端结构比较复杂,副保险杠位置及吸能泡沫的厚度范围受到保险杠蒙皮的限制,初步设定吸能泡沫采用30EEP材料,厚度为60 mm;副保险杠采用钢制薄壁圆管,厚度为1.5 mm,改进方案的有限元模型如图 3所示,各结构参数的选取如表 2所示。

|
图 3 改进后的有限元模型 Figure 3 Improved FE model |
| 表 2 有限元模型结构参数 Table 2 Structural parameters of FE model |
拉丁超立方抽样是一种生成均匀样本点的特殊多维分层抽样方法,能够以较少的样本点反映整个设计空间的特性,是一种有效的样本缩减技术。拉丁超立方具有效率高,均衡性能好的优点[15]。
优化的拉丁超立方抽样能使抽样点的空间分布更加均匀,并且能够快速地达到收敛。笔者采用优化的拉丁超立方抽样试验分析3个参数在其变化范围内对行人损伤指标的影响。采样数据及设计试验结果如表 3所示。
| 表 3 仿真分析结果 Table 3 Simulation analysis results |
响应面法是一种曲线拟合方法,拟合精度由响应面决定系数R2和调整的决定系数Radj2评价,其代表了拟合多项式与原模型的接近程度,其值越趋近1表明拟合精度越高。笔者所用的二阶响应面表达式如下[16]:
| $ \eta \left( x \right)={{a}_{0}}+\sum\limits_{i=1}^{n}{{{a}_{1i}}{{x}_{i}}}+\sum\limits_{i\le j}^{n}{{{a}_{2i}}{{x}_{j}}}{{x}_{i}}, $ | (1) |
式中:a0为常系数,a1i,a2i分别为一阶和二阶调整参数。对上述15个样本进行拟合,获得如表 4所示的响应面调整参数。
| 表 4 响应面调整参数 Table 4 RSM adjustment paramenters |
表 5为响应面模型决定系数和调整的决定系数,从表中可以看出,3个响应面的决定系数和调整的决定系数都在98%以上,说明了构造的响应面与实际模型高度拟合。
| 表 5 响应面模型决定系数和调整的决定系数 Table 5 RSM determination and adjusted determination coefficients |
工程优化领域大多数问题都是多目标优化,这些优化目标之间可能是相互冲突的,一般的解决方法是将这些目标通过加权系数归一化为单个目标,但这种方法主观随意性很大,会导致某些信息的缺失。
多目标遗传优化能够很好地避免这种缺失,可以为用户提供一组非劣解,非常适合用来处理有约束的多目标优化问题[17]。笔者也将通过引入多目标遗传优化的方法对建立的响应面模型进行优化。
3.2 优化分析最优的模型应使Pa,Pb,Ps3个指标最小,故需要对前文选取的结构参数a,b,c进行优化。
优化模型可以简化为:
目标函数:Minimize{Pa,Pb,Ps}
约束条件:205≤a≤235,0.5≤b≤3,40≤c≤80,
Pa≤150,Pb≤15,Ps≤6。
设计变量:a,b,c
将前面建立的响应面模型用多目标遗传算法进行优化。经过优化计算后,得出了一系列帕雷托解 (Pareto-optimal solutions),如表 6所示。
| 表 6 帕雷托解集 Table 6 Pareto solution |
考虑到生产成本,材料的节约及材料的加工,选用优化后主副保险杠垂向距离,副保险杠壁厚和吸能泡沫厚度分别为214.91,3.00和40.06 mm这一组。归整化为215,3和40 mm,并以有限元模型进行仿真验证。对比结果如表 7所示。
| 表 7 优化前后模型值对比 Table 7 Damage value comparison between test and optimization results |
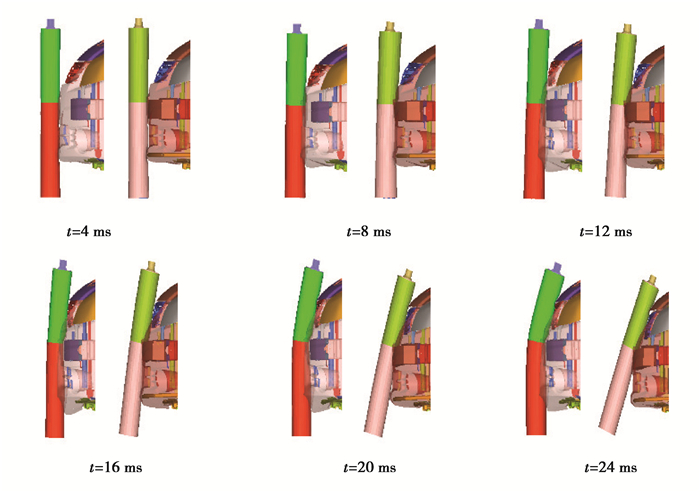
原模型与优化模型碰撞过程对比如图 4所示。从碰撞过程可以看出,改进后的模型由于吸能泡沫及副保险杠的加入,腿部模型的运动从平动改变为转动。平动时,腿部正向完全撞击保险杠,胫骨处产生极大的加速度,并且腿部上端绕膝关节转动产生很大的弯曲角度;而转动时,整个腿部模型一起绕发动机罩下沿转动,腿部模型没有完全正面撞向保险杠,同时膝关节处不会产生很大的弯曲角度。
|
图 4 原模型 (左) 与优化模型 (右) 碰撞过程对比 Figure 4 The original model (left) and optimization model (right) collision comparison |
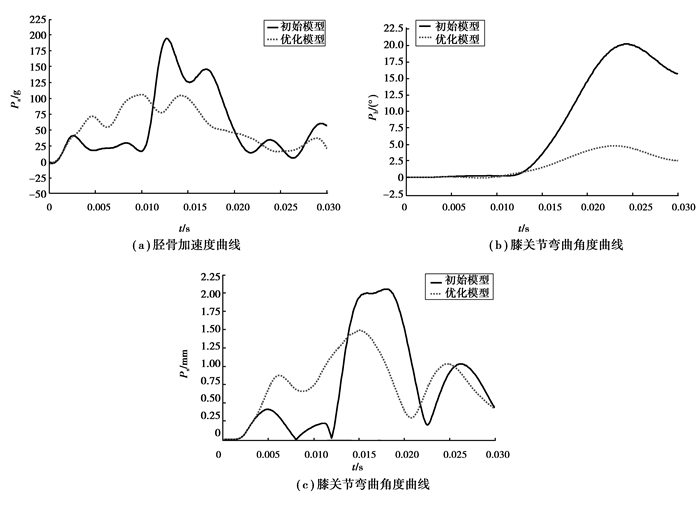
图 5为原模型与优化模型伤害曲线对比。原模型胫骨加速度在小腿刚碰撞到保险杠横梁时达到峰值;优化后胫骨加速度在5 ms达到峰值,此时小腿与吸能泡沫及副保险杠接触,峰值从193.8 g下降到106.09 g。由于副保险杠的加入,膝关节弯曲角度峰值出现的时间从24.2 ms提前到了20 ms左右,弯曲角度有了极大的改善,峰值从20.2°下降到4.79°,膝关节剪切位移的改善也较明显,峰值从2.05 mm降低到1.48 mm。
|
图 5 原模型与优化模型伤害曲线对比 Figure 5 Comparison between test and optimization results |
表 7为模型改进优化前后三项操作值的对比结果,从中可知,相较于原模型,改进优化后模型的胫骨加速度和膝关节弯曲角度峰值都得到明显改善,且都达到了法规的要求[7]。
4 结论为提高某车型的行人腿部保护性能,在原始车型中添加吸能泡沫及副保险杠,运用具有全局优化特性的多目标遗传算法对汽车前端结构参数进行综合优化。优化后车型的行人腿部保护性能有了显著的提高,该优化方法对汽车前端结构的优化设计以及行人腿部保护具有指导意义。后续还将从泡沫的材料及截面形状方面来改善行人保护性能。
| [1] |
许伟, 李凡, 刘琦.
车辆行人碰撞事故中小腿骨折伤害的研究[J]. 汽车工程, 2011, 33(4): 321–324.
XU Wei, LI Fan, LIU Qi. A study on tibia fracture injuries in car-pedestrian impact accidents[J]. Automotive Engineering, 2011, 33(4): 321–324. (in Chinese) |
| [2] | Zheng G J, Men Y X, Hu P, et al. A study on energy absorption panel of bumper based on impact of pedestrian's lower leg[C]//International Conference on Consumer Electronics, Communications and Networks. [S.l.]: IEEE, 2011: 3867-3871. |
| [3] | Huang J, Xia Y, Zhou Q. Stiffness-based method for improving pedestrian leg protection performance of vehicle front-end[C]//International Conference on Electric Information and Control Engineering. [S.l.]: IEEE, 2011:5335-5339. |
| [4] | Shin M K, Yi S I, Kwon O T, et al. Structural optimization of the automobile frontal structure for pedestrian protection and the low-speed impact test[J]. Proceedings of the Institution of Mechanical Engineers Part D Journal of Automobile Engineering, 2008, 222(12): 2373–2387. DOI:10.1243/09544070JAUTO788 |
| [5] |
曾宪中, 章桐.
序列二次规划法在行人小腿保护的保险杠系统优化中的应用[J]. 汽车工程, 2011, 33(2): 122–126.
ZENG Xianzhong, ZHANG Tong. The application of sequential quadratic programming to the optimization of bumper system for pedestrian lower leg protection[J]. Automotive Engineering, 2011, 33(2): 122–126. (in Chinese) |
| [6] | European New Car Assessment Programme. Pedestrian Testing Protocol Version 5.3[S/OL]. [2015-06-30]. http://www.docin.com/p-435427965.html. |
| [7] | Committee V S. Improvedtest methods to evaluate pedestrian protection afforded by passenger cars[J]. Eevc Working Group Report, 1998. |
| [8] | Official Journal of the European Union. Regulation (EC) NO 78/2009[S]. 2009. |
| [9] | Teng T L, Ngo V L, Nguyen T H. Design of pedestrian friendly vehicle bumper[J]. Journal of Mechanical Science and Technology, 2010, 24(10): 2067–2073. DOI:10.1007/s12206-010-0612-0 |
| [10] | Salem A Z. Using glass mat thermoplastic as automotive bumper's material to enhance pedestrian safety[J]. Advanced Materials Research, 2014, 875/876/877: 455–461. |
| [11] |
贺岩松, 杨海威, 徐中明, 等.
基于行人腿部保护的保险杠吸能结构设计[J]. 振动与冲击, 2014, 33(12): 171–175.
HE Yansong, YANG Haiwei, XU Zhongming, et al. Bumper energy absorption structure design based on pedestrian leg protection[J]. Journal of Vibration and Shock, 2014, 33(12): 171–175. (in Chinese) |
| [12] | Jiang K T, Yang J K. Optimization of bumper system for pedestrian lower leg impact protection[C]//Third International Conference on Digital Manufacturing and Automation. [S.l.]: IEEE, 2012: 578-581. |
| [13] | Mu W H, Yang J K. Optimization design of frontal bumper system for both pedestrian lower leg protection and low speed impact requirement[C]. The 10th Int.Forum of Automotive Traffic Safety (INFAST), Hongkong, China. [S.l.]: IEEE, 2013: 770-773. |
| [14] | Park D K, Jang C D. Optimum SUV bumper system design considering pedestrian performance[J]. International Journal of Automotive Technology, 2010, 11(6): 819–824. DOI:10.1007/s12239-010-0097-y |
| [15] | Jin R, Chen W, Sudjianto A. An efficient algorithm for constructing optimal design of computer experiments[J]. Journal of Statistical Planning and Inference, 2003, 134(1): 268–287. |
| [16] |
张勇, 陆勇.
基于近似模型技术的圆管耐撞性优化设计[J]. 华中科技大学学报 (自然科学版), 2010(9): 129–132.
ZHANG Yong, LU Yong. Optimizing design of tube crash worthiness using a pproximate model technique[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2010(9): 129–132. (in Chinese) |
| [17] | Yang H Z, Wang A J, Li H J. Multi-objective optimization for deepwater dynamic umbilical installation analysis[J]. Science China Physics, Mechanics and Astronomy, 2012, 55(8): 1445–1453. DOI:10.1007/s11433-012-4817-3 |
 2017, Vol. 40
2017, Vol. 40

