焊接结构在实际工作中往往同时承受多轴载荷作用,表现为主应力大小和方向的不断改变[1]。当前的诸多焊接接头设计标准提供了各种焊接接头的疲劳寿命评估曲线,但均是基于单轴加载试验推导而来。这些疲劳寿命曲线对于非比例非同相的多轴加载情况并不适用[2],因此解决多轴载荷作用下焊接结构疲劳寿命预测的问题具有重要意义。
由于焊接结构的多轴疲劳破坏机理和试验分析过程非常复杂,因此目前开展的相关研究和发布的疲劳数据比较有限。文献[3-6]针对各式管接头和十字接头分别进行了弯曲扭转和双向拉伸的多轴疲劳试验,这些数据数据分散性较大,难以在工程实践者中得到有效应用。而在疲劳评估中,缺口应力法的特点正好是将焊趾和焊根等缺口区域应力作为变量,不同疲劳等级的焊接接头只需一条共用的疲劳寿命曲线,这种焊接结构疲劳分析的新方法以其较高的准确性和实用性而应用越发广泛[7]。因此本文旨在结合缺口应力法和多轴疲劳准则,将多种类型的焊接接头多轴疲劳试验数据统一在同一缺口应力坐标系统下,获得适用于不同焊接接头多轴加载的疲劳寿命曲线。
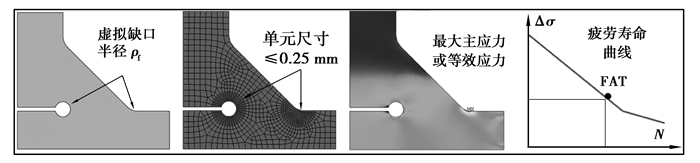
1 缺口应力法由于焊接接头存在的缺口点 (焊趾和焊根) 是疲劳裂纹产生的主要位置,因此缺口应力法采用焊趾焊根的最大应力作为疲劳评估参量。直接采用数值方法进行缺口点应力分析并不可行,原因在于:缺口点具有奇异性,并且忽视了由于缺口根部材料各向异性引起的微观结构约束效应。因此在缺口点构造虚拟缺口圆,既避免了缺口点的奇异性,同时计入了微观结构约束效应的影响。目前应用最为广泛的是Radaj等[8]基于Neuber应力平均概念提出的ρf=1 mm虚拟缺口半径法,考虑焊趾焊根缺口根部真实缺口半径ρ为0,采用1 mm的虚拟缺口圆进行替换。图 1给出了缺口应力法在焊接接头疲劳分析中的具体应用原理。
|
图 1 采用缺口应力法进行疲劳分析的原理 Figure 1 Principles of fatigue assessment using the notch stress approach |
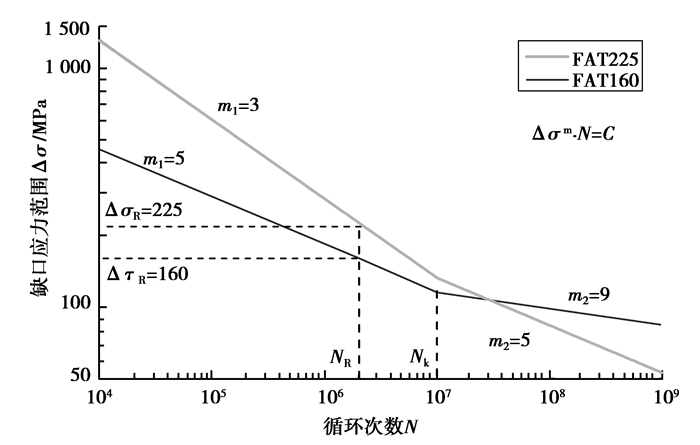
在不考虑残余应力,焊接缺陷等因素的情况下,假定应力集中是引起焊接接头疲劳破坏的唯一原因,那么所有的焊接接头在理论上均能统一在同一条缺口应力S-N曲线之下。单轴载荷下的缺口疲劳评估曲线采用了IIW (International Institute of Welding) 所推荐的标准形式 (图 2),以Nk=107次作为曲线拐点分为上下两段,以NR=2×106处的应力范围作为曲线疲劳等级值FAT (fatigue assesment class)。在拉伸应力作用下,上段曲线斜度m1=3,FAT值ΔσR=225 MPa;在剪切应力作用下,上段曲线斜度m1=5,FAT值ΔτR=160 MPa。考虑到小载荷对疲劳强度的影响,拐点以后的下段曲线斜度设置为m2=2m1-1,这些曲线均具有97.7%的存活率[2]。
|
图 2 单轴加载下的缺口疲劳寿命曲线 Figure 2 The notch fatigue lifecurves with uniaxial loading |
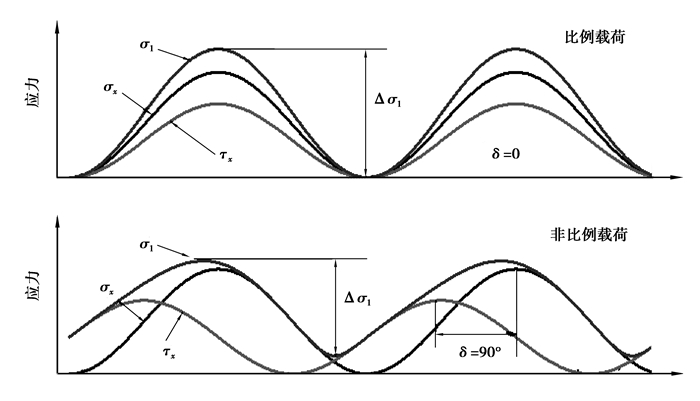
在多轴疲劳领域内,涉及到非同相非比列加载,主应力的大小和方向均不断变化。如图 3所示,若采用传统的单轴准则进行疲劳分析,同相加载产生的应力范围大于非同相加载下的应力范围,意味着后者具有更高的疲劳强度,但这与多轴加载导致结构疲劳寿命降低的事实显然不符。因此应采用更为合理的多轴疲劳准则。
|
图 3 比例加载和非比例加载示意图 Figure 3 Proportional loading and non-proportional loading |
早期的多轴疲劳规范一般直接采用Von Mises应力或主应力作为评价参量;之后则开始通过相关方程联合正应力和剪应力对多轴疲劳进行评估;另外则是基于临界平面假设提出了各种多轴等效应力准则[9]。因此文中选取了3种不同类型的多轴准则 (Von Mises、IIW、EESH) 分别进行焊接接头疲劳分析和比较。
2.1 Von Mises等效应力Von Mises等效应力准则适用于比例载荷和剪应力较为明显的情况。等效应力范围计算如式 (1) 所示。该准则的缺点是没有包括应力方向的信息,因此在进行疲劳评估时需要对裂纹萌生路径进行假设。文献[10]的研究表明该准则对于非比例载荷亦偏于危险。
| $ \Delta {{\sigma }_{\text{VM}}}=\sqrt{\Delta \sigma _{x}^{2}+\Delta \sigma _{y}^{2}-\Delta {{\sigma }_{x}}\Delta {{\sigma }_{y}}+3\Delta \tau _{xy}^{2}}。 $ | (1) |
IIW焊接结构疲劳设计标准中的多轴评定采用了Gough-Pollard方程
| $ {{\left( \frac{\Delta {{\sigma }_{x}}}{\Delta {{\sigma }_{\text{R}}}} \right)}^{2}}+{{\left( \frac{\Delta {{\tau }_{xy}}}{\Delta {{\tau }_{\text{R}}}} \right)}^{2}}\le \text{CV,} $ | (2) |
其中ΔσR和ΔτR分别为单轴载荷下的正应力和剪应力强度范围值 (图 2);CV是与载荷相关的比较值,比例载荷下取1,非比例载荷下取0.5[11]。该准则的原理是通过不同应力的联合方程进行评估,为了方便实际应用,也可以将之写为等效应力范围形式
| $ \Delta {{\sigma }_{\text{ⅡW}}}=\frac{1}{\sqrt{\text{CV}}}\sqrt{\Delta \sigma _{x}^{2}+{{\left( \frac{\Delta {{\sigma }_{\text{R}}}}{\Delta {{\tau }_{\text{R}}}} \right)}^{2}}\cdot \Delta \tau _{xy}^{2}}。 $ | (3) |
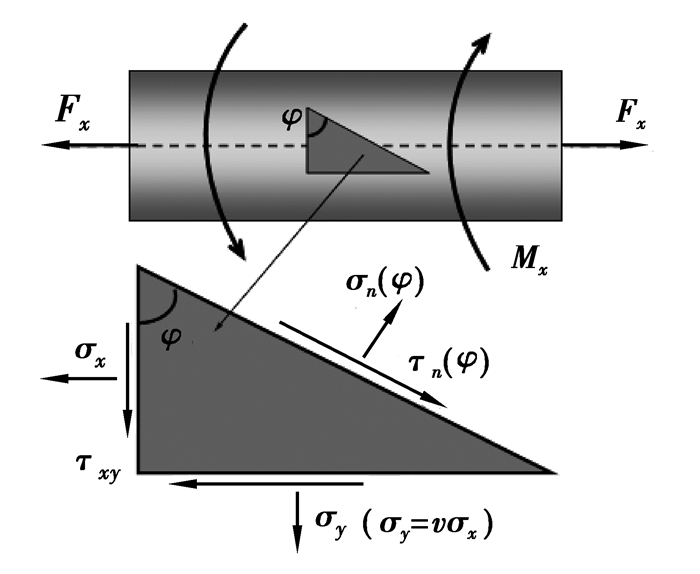
Sonsino基于临界平面定积分假设提出了等效平衡应力准则 (equivalent effective stress hypothesis, EESH)[5],适用于焊接钢结构等延展性材料。该方法假定非比例载荷下剪应力对所有平面均有损伤 (图 4),因此损伤参数F定义为所有剪应力平面 (φ=0~π) 的损伤总和 (式 (4)),积分后的F应当是与加载相位差δ相关的函数。多轴等效应力范围ΔσEESH可以表述为式 (5),其中包含了损伤函数F、焊接接头缺口应力集中系数Kt以及单轴载荷下的正应力和剪应力强度范围值。该准则在焊接接头多轴疲劳评估中的正确性通过Sonsino一系列的试验和分析得到了验证;但其计算过程较为复杂,所须参数也较多。
| $ F\left( \delta \right)=\frac{1}{\text{ }\!\!\pi\!\!\text{ }}\int_{0}^{\text{ }\!\!\pi\!\!\text{ }}{{{\tau }_{n}}\left( \varphi \right)\text{d}\varphi ,} $ | (4) |
|
图 4 临界平面及其应力示意 Figure 4 The stresses on the critical plane |
式中,τn(φ)=τxysin (ωt+δ)[cos2φ-sin2φ]-(σx-σy) sin φcos φ,其中,δ为正应力σx与剪应力τxy的相位差,ω为加载角频率,t为加载时间。
| $ \Delta {{\sigma }_{\text{EESH}}}=\Delta {{\sigma }_{\text{EESH}}}(0\text{ }\!\!{}^\circ\!\!\text{ })\frac{F\left( \delta \right)}{F(0\text{ }\!\!{}^\circ\!\!\text{ })}\sqrt{{{G}^{z}}}, $ | (5) |
式中:
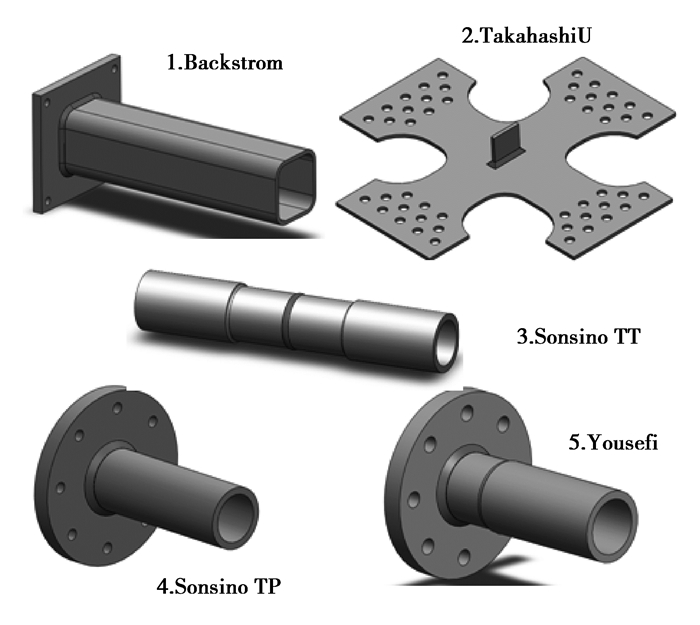
相对于单轴疲劳问题,焊接结构的多轴疲劳研究远远滞后。目前能获得的多轴疲劳试验数据非常有限。笔者收集了试样条件清楚和试验结果可靠的多轴疲劳数据,将之有效应用于缺口疲劳分析中。图 5列举了采用的焊接接头试样模型及其来源,其中包括进行弯曲和扭转试验的方管板接头[3], 圆管管接头[5], 圆管板接头[5-6]; 另外则是进行两轴拉伸的非承载式十字角接头[4]。文献中明确给出了试样的具体结构尺寸、加载方式、平均应力和焊缝质量等情况 (表 1)。这些典型的焊接接头的缺口疲劳等级 (焊接接头由于结构和工艺等原因会造成局部缺口应力集中,缺口等级则是将不同缺口应力集中的焊接接头进行的大小分级) 各不相同,因此其多轴缺口疲劳分析的综合结果在一定程度上具有较好的通用性。
|
图 5 多轴疲劳试验的焊接接头类型 Figure 5 Welded joint specimens with multi-axial fatigue test |
| 表 1 焊接接头几何参数及试验条件 Table 1 The geometry parameters and test condition of welded joints |
在焊接接头的多轴疲劳试验中,通常采用力加载或位移加载,然后根据截面参数或材料参数换算为应力结果,最终以名义应力范围和循环次数的形式给出疲劳数据。
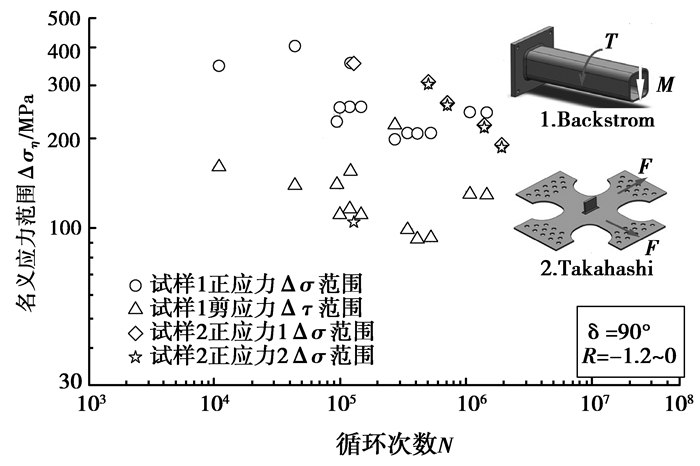
如图 6所示,分别给出了焊接接头试样1和2(方管-板接头和十字接头) 的应力数据。试验应力范围在90~400 MPa,应力比范围-1.2~0,第一轴与第二轴采用不定比例加载,试验寿命次数在1×104~2×106之间,两轴加载的相位差为90°。试样1的结果表明弯曲正应力对于接头疲劳破坏的贡献大于扭转剪切应力;试样2由于结构对称,因此其失效位置在两轴方向上的应力及寿命结果基本相同,略微的差别则源自纵向附板边缘失效点与两轴加载点距离不同所致。
|
图 6 接头试样1和2的疲劳寿命数据 Figure 6 Fatigue test data of specimen 1 and 2 |
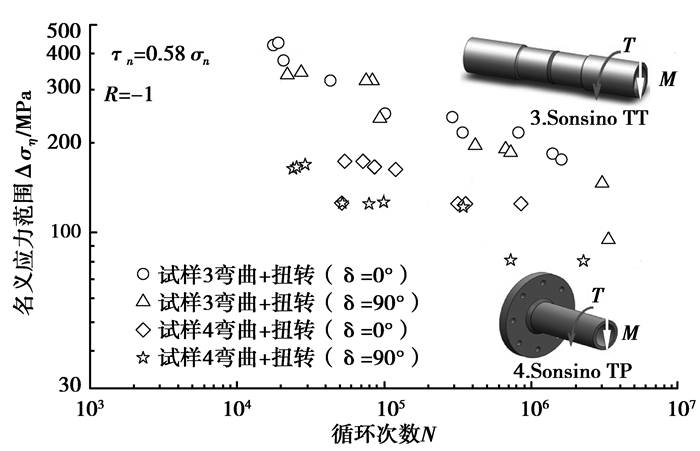
Sonsino在进行管管接头和管板接头 (试样3和4) 的多轴试验时,采用了比例同相加载和比例非同相加载,加载扭转剪应力和弯曲正应力之比为定值0.58,相位差有0°和90°两种情况, 试验应力范围在120~430 MPa之间,试验寿命范围在1×104~2×106次内。从图 7的数据可以看出,试样3的疲劳强度明显更高,因为其具有较低的缺口等级。同相加载下的疲劳应力值较非同相加载更大,表明多轴加载时的相位差对焊接接头的寿命具有影响。
|
图 7 接头试样3和4的疲劳寿命数据 Figure 7 Fatigue test data of specimen 3 and 4 |
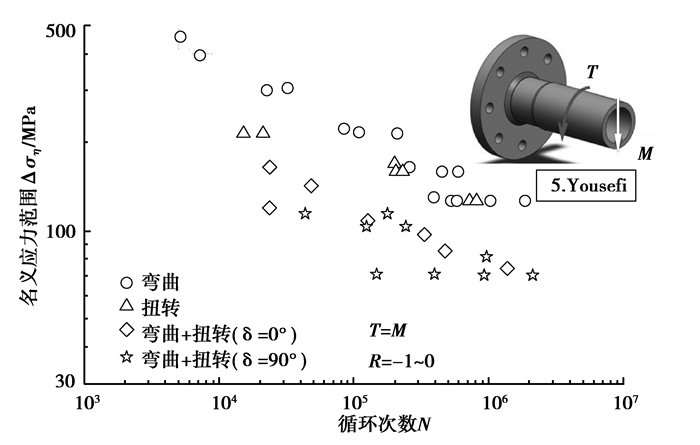
试样5(管管接头) 除了进行弯扭多轴试验以外,还分别进行了纯弯和纯扭单轴试验作为比较 (如图 8所示)。加载时弯矩和扭转大小相等,应力比有-1和0两种情况,试验应力范围在70~450 MPa之间,试验寿命范围在6×103~2×106次内。除纯扭工况外,数据均以弯曲正应力范围的形式给出。通过比较可以看出,焊接接头的多轴疲劳寿命普遍低于单轴疲劳寿命。
|
图 8 接头试样5的疲劳寿命数据 Figure 8 Fatigue test data of specimen 5 |
从图 6~8的焊接接头名义应力数据可以看出,不同的焊接接头缺口等级不同,结果必然呈现较大的分散性,因此很难将其应用于其他接头类型。解决这一问题可以采用缺口分析方法对各组数据进行综合。
4 多轴缺口疲劳分析 4.1 缺口应力集中系数焊接接头的名义应力数据和应力集中系数是进行缺口应力分析的两个基础条件。前者通过疲劳试验获得,后者则需采用数值方法或公式法进行计算。
缺口应力集中系数Kt是描述焊接接头疲劳强度减小量的参数。由于文中的焊接接头均较为复杂,而公式法大多只涉及单轴加载情况下的对接接头和角接头,且准确性较低[12-13]。因此根据文献提供的焊接接头尺寸数据建立了相应的缺口有限元模型。
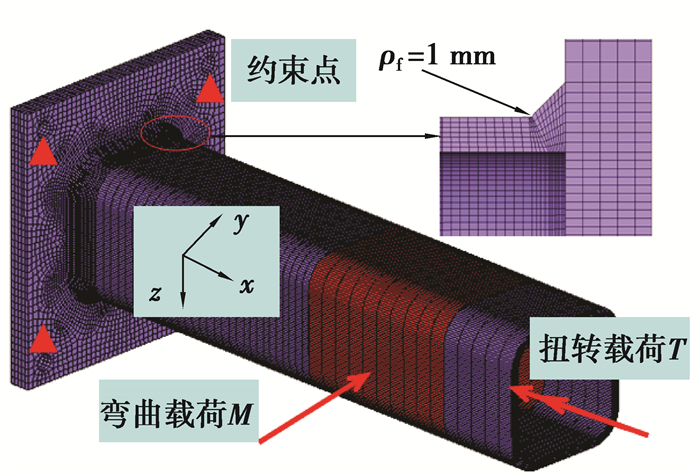
如图 9所示的试样1接头FE模型,根据焊趾角度和焊脚长度建立焊缝,并在焊趾开裂处设置1 mm虚拟缺口半径。实体模型全部采用六面体单元。根据试验中的试样夹紧和加载位置施加约束和载荷。
|
图 9 焊接接头缺口应力集中系数分析模型 Figure 9 The FE model of welded joint for calculating notch stress concentration factor |
根据焊接接头的抗弯和抗扭截面系数,可以换算出加载时所需的单位载荷大小,通过有限元分析,可以直接获得焊接接头缺口点各方向的缺口应力集中系数Kt。在表 2给出的各接头应力集中系数基础上,联合相应方向上的名义应力数据,可以最终确定该方向上缺口应力值
| $ {{\sigma }_{\text{K}}}={{K}_{\text{t}, {{\sigma }_{n}}}}。 $ | (6) |
| 表 2 焊接接头缺口应力集中系数Kt Table 2 The notch stress concentration factors of welded joints |
在确定了焊接接头缺口点各向缺口应力值后,代入多轴疲劳准则公式,可以将试验结果转变为多轴等效缺口应力,从而进行相应的多轴缺口疲劳分析。
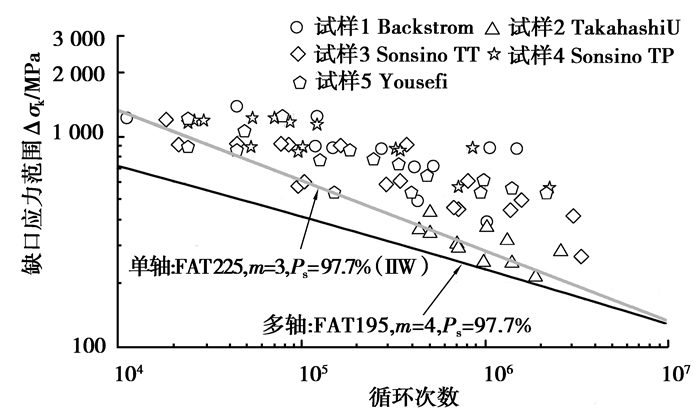
4.2 疲劳曲线拟合图 10~12分别基于Von Mises、IIW和EESH 3种多轴疲劳准则,将计算后的5种焊接接头等效缺口应力数据置于同一坐标系统下。可以看出,缺口应力数据相对于之前的名义应力数据明显具有更小的分散性,这是由于缺口应力的性质所决定的,即缺口等级较高的结构疲劳强度较低,而疲劳强度较高的结构必定缺口等级较低。因此多轴试验数据越多,包括的缺口等级范围越大,其结果越具有可靠性和准确度。
|
图 10 Von Mises准则下的缺口疲劳寿命分析 Figure 10 The notch fatigue life analysis with Von Mises criterion |
|
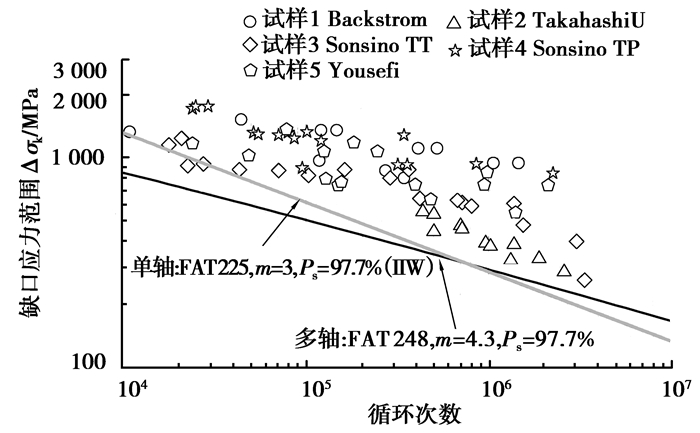
图 11 IIW准则下的缺口疲劳寿命分析 Figure 11 The notch fatigue life analysis with IIW criterion |
|
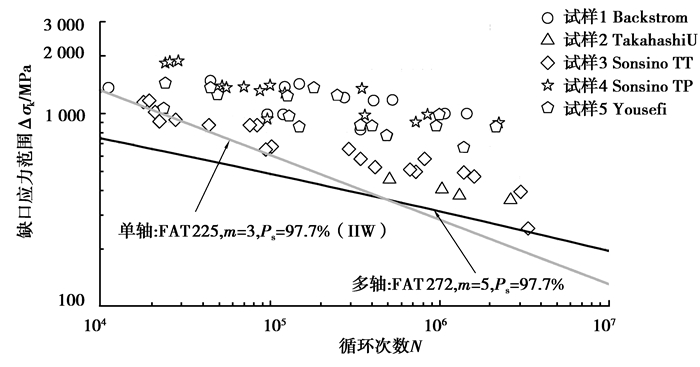
图 12 EESH准则下的缺口疲劳寿命分析 Figure 12 The notch fatigue life analysis with EESH criterion |
由于国际焊接学会IIW的《焊接接头疲劳设计和评估》标准中推荐了单轴标准缺口疲劳曲线FAT225,为了方便进行比较,在进行缺口疲劳曲线拟合时,通过最小二乘法,使其多轴缺口疲劳寿命S-N曲线同样具有97.7%的存活率。
表 3给出了不同多轴准则下所拟合曲线结果参数。在Von Mises准则下,焊接接头多轴缺口疲劳曲线的斜度m=4,疲劳等级值FAT=195;IIW准则下的斜度值为4.3,FAT值为248;EESH准则下的曲线斜度值为5,FAT值272。
| 表 3 多轴缺口疲劳曲线参数 Table 3 The parameters of multiaxial notch S-N curves |
从表 3的疲劳等级值可以看出,3种多轴准则下的FAT值与单轴曲线相差在20%以内,结果在同一等级范围内,表明所拟合的多轴缺口疲劳曲线具有较好的可靠性。
Von Mises多轴准则下的疲劳等级值最小,曲线倾斜度最大;而EESH准则结果FAT值最大,而曲线倾斜度最小。在疲劳评估中,若将103~106次视为中周疲劳范围,106~107次视为高周疲劳范围。Von Mises准则在高周范围更为保守,而EESH准则在中周范围更为保守,IIW准则是在二者之间。
表 4计算了不同循环次数下的曲线所对应的应力范围大小。相对于单轴疲劳,焊接接头多轴加载时在中周范围内疲劳强度更低,在高周范围内则具有相当或则更高的疲劳强度。表明在大载荷作用下,多轴加载明显导致了焊接接头疲劳强度降低;而在小载荷作用时,这种影响程度则不明显。
| 表 4 不同循环次数下的应力范围比较 Table 4 Compare of stress ranges under different cycles |
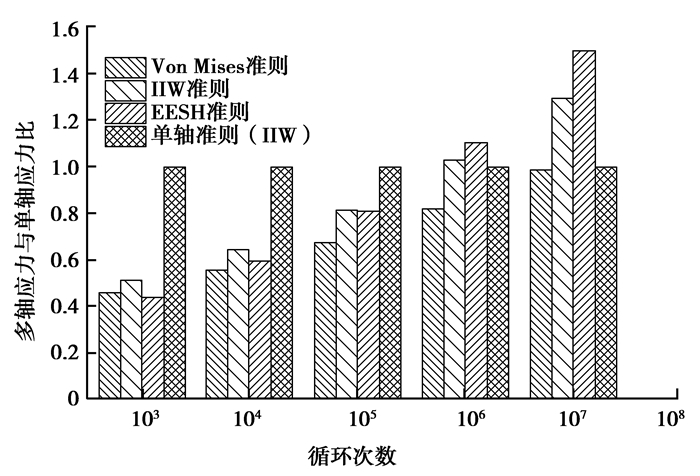
图 13的柱状图直观显示了多轴准则之间以及单轴与多轴准则间的结果异同。随着循环次数的增加,多轴准则结果与单轴准则结果差异在不断减小。相对于其他准则,EESH假设下的多轴S-N曲线在中周范围内允许较小的疲劳载荷,在高周范围内则允许相对较大的疲劳载荷。由于EESH准则的原理更为符合疲劳损伤机理,且得到了相应的试验验证[9],因此在实际的焊接接头多轴缺口疲劳评估中,可以采用该准则的多轴等效应力计算方法及相应的疲劳寿命曲线 (FAT=272,m=5)。
|
图 13 不同应力准则分析结果比较 Figure 13 The results comparison of different stress criterions |
文章在多轴疲劳试验数据的基础上,基于缺口应力分析方法和多轴疲劳准则,对焊接接头进行了多轴缺口疲劳分析。
将多组缺口应力数据统一在同一坐标系统下,通过拟合获得了焊接接头的多轴缺口疲劳寿命曲线。结果表明,相对于单轴情况,多轴缺口疲劳曲线普遍具有较小的倾斜度和较大的疲劳等级值;即多轴加载明显降低了焊接接头在中周范围内的疲劳强度;而对高周疲劳范围的影响则相对较小。
由于等效平衡应力准则 (EESH) 更为符合多轴损伤机理,且得到了相应的试验验证,因此在工程实践中,推荐该方法所拟合的疲劳寿命曲线 (FAT=272,m=5)。
缺口应力分析方法的准确性是建立在对足够多的数据进行综合[14],因此不断增加焊接接头多轴疲劳试验数据于其中,能够有效提高多轴缺口疲劳曲线的准确性。
| [1] |
刘刚, 刘英芳, 黄一.
焊接结构多轴疲劳寿命预测结构应力法[J]. 船舶力学, 2014, 18(10): 1220–1227.
LIU Gang, LIU Yingfang, HUANG Yi. Structural stress approach for multiaxial fatigue life estimation of welded structures[J]. Journal of Ship Mechanics, 2014, 18(10): 1220–1227. DOI:10.3969/j.issn.1007-7294.2014.10.008 (in Chinese) |
| [2] | Sonsino C M, et al. A consideration of allowable equivalent stresses for fatigue design of welded joints according to the notch stress concept with the reference radii ref=1.00 and 0.05 mm[J]. Welding in the World Le Soudage Dans Le Monde, 2009, 53(3-4): 64–75. |
| [3] | Bäckström M. Multiaxial fatigue life assessment of welds based on nominal and hot spot stresses [D]. Finland: Laapeenranta University, 2003. |
| [4] | Takahashi I, Ushijima M, Takada A, et al. Fatigue behaviour of a box-welded joint under biaxial cyclic loads[J]. Fatigue & Fracture of Engineering Materials & Structures, 1999, 22(10): 869–877. |
| [5] | Sonsino C M. Multiaxial fatigue of welded joints under in-phase and out-of-phase local strains and stresses[J]. International Journal of Fatigue, 1995, 17(1): 55–70. DOI:10.1016/0142-1123(95)93051-3 |
| [6] | Yousefi F, Witt M, Zenner H. Fatigue strength of welded joints under multiaxial loading: experiments and calculations[J]. Fatigue & Fracture of Engineering Materials & Structures, 2001, 24(5): 339–355. |
| [7] | Sonsino C M, Fricke W, Bruyne F D, et al. Notch stress concepts for the fatigue assessment of welded joints – Background and applications[J]. International Journal of Fatigue, 2012, 34(1): 1–16. DOI:10.1016/j.ijfatigue.2010.11.013 |
| [8] | Radaj D, Lazzarin P, Berto F. Generalized Neuber concept of fictitious notch rounding[J]. International Journal of Fatigue, 2013, 51: 105–115. DOI:10.1016/j.ijfatigue.2013.01.005 |
| [9] | Sonsino C M, Kueppers M, Eibl M, et al. Fatigue strength of laser beam welded thin steel structures under multiaxial loading[J]. International Journal of Fatigue, 2006, 28(5-6): 657–662. DOI:10.1016/j.ijfatigue.2005.09.013 |
| [10] | Sonsino C M. Multiaxial fatigue assessment of welded joints: Recommendations for design codes[J]. International Journal of Fatigue, 2009, 31(1): 173–187. DOI:10.1016/j.ijfatigue.2008.06.001 |
| [11] | Hobbacher A. Fatigue design of welded joints and components[M]. Cambridge: Abington Publishing, 2007. |
| [12] |
邱宝象, 高增梁, 王效贵, 等.
基于有限元法的16MnR缺口件疲劳寿命预测方法[J]. 工程力学, 2010, 27(8): 21–27.
QIU Baoxiang, GAO Zengliang, WANG Xiaogui, et al. A fatigue life prediction method for 16mnr steel notched components based on the finite element method[J]. Engineering Mechanics, 2010, 27(8): 21–27. (in Chinese) |
| [13] |
吴志荣, 胡绪腾, 宋迎东.
多轴载荷下缺口件的疲劳寿命估算方法[J]. 工程力学, 2014, 31(10): 216–221.
WU Zhirong, HU Xuteng, SONG Yingdong. Estimation method for fatigue life of notched specimen under multi-axial loading[J]. Engineering Mechanics, 2014, 31(10): 216–221. (in Chinese) |
| [14] |
刘旭, 张开林, 姚远, 等.
缺口应力法在机车焊接构架疲劳分析中的应用[J]. 铁道学报, 2015, 37(1): 24–29.
LIU Xu, ZHANG Kailin, YAO Yuan, et al. Application of notch stress method in fatigue analysis of locomotive welded frame[J]. Journal of the China Railway Society, 2015, 37(1): 24–29. (in Chinese) |
 2017, Vol. 40
2017, Vol. 40

