2. 重庆大学 航空航天学院, 重庆 400044
2. Department of Engineering Mechanics, College of Aerospace Engineering, Chongqing University, Chongqing 400044, P. R. China
脉冲电流烧结 (pulse electric current sintering,PECS) 是近年来发展起来的一种快速烧结技术,将脉冲电流通过石墨模具直接加到粉末试样上,在强电流、高温度和高温升率条件下对粉末颗粒进行快速烧结[1-2]。不同学者对其烧结机理进行了分析,对导电粉体,Tokita[3]认为颗粒间放电激发等离子体,在接触部产生瞬时的局部高温,形成烧结颈部,而Zhang[4]在实验中观察到等离子体的产生。Chen[5]研究了温度场和电场耦合作用下导电陶瓷的致密化机理,得到温度场和电场分布的不均匀性。但是颗粒间放电现象不适用于非导电粉体烧结机理的解释,因为非导电粉体中不会有电流通过。Wang和Chen[6-7]分别对导电Cu粉末和非导电Al2O3粉末进行了脉冲电流烧结实验,得出导电粉体的烧结机理为脉冲放电和焦耳热效应,非导电粉体为模具和压头的热传导。
烧结是一个系统自由能降低的热力学不可逆过程,是多种因素作用下的一系列物理、化学变化过程,化学势梯度是烧结的驱动力[8]。化学势梯度影响烧结颈部的空位浓度梯度,从而在颈部产生空位流动,形成颈长。Kuczynski等[9]推导出了表面扩散、体积扩散、蒸发凝聚和晶界扩散机制下的颈长动力学方程。
脉冲大电流作用下非导电颗粒具有烧结时间短、升温速度快和存在较大温度梯度的特点,经典的热弹性理论受到挑战[10]。粉末烧结体具有显著非均匀内结构的特性,使其在极高温升率与温度梯度下的短时程传热中表现出显著的非Fourier特征。Roetzel[11]在15~25 ℃的温度下,对平均粒径为130 nm的Al2O3颗粒的实验测得其延迟时间为5~45 s。因此,在探究脉冲电流烧结机理时需要引入非Fourier定律和相应的广义热弹性理论。Tian等[12]采用直接有限元法,研究了半无限大体受热冲击作用的动态响应问题, 得到了热的波传播形式。Strunin[13]分析了半无限长杆中线性和非线性热弹性波的传播规律,并比较了L-S和G-L (Green and Lindsay) 两种广义热弹性理论。
采用L-S型广义热弹性方程,结合烧结边界条件,对脉冲电流烧结等径两颗粒系统过程,建立无量纲化的三维控制方程。利用Comsol Multiphysics计算烧结过程中颗粒系统内部的温度场和应力场,并给出烧结颈部边缘和中心点化学势和空位浓度差变化规律,初步探究非导电粉体的快速烧结机理。
1 基本控制方程CV (Cattaneo-Vernotte) 型非傅里叶热传导方程[14]:
| $ {{\mathit{\boldsymbol{q}}}_{j}}\left( x, t \right)+\tau {{\mathit{\boldsymbol{\dot{q}}}}_{j}}\left( \mathit{\boldsymbol{x}}, t \right)=-k\theta {{, }_{j}}\left( \mathit{\boldsymbol{x}}, t \right), $ | (1) |
式中:q为热流矢量;k为热扩散率;θ, j为温度梯度;x为位置矢量。与傅里叶热传导方程相比引入了延迟时间τ,并且给出了温度波传播的速度为
| $ {{v}_{t}}=\sqrt{\frac{k}{\rho {{C}_{\varepsilon }}\tau }}, $ | (2) |
式中:ρ为材料密度;Cε为等应变比热。
将颗粒系统看成热弹性虎克介质,不计外力和体热源的L-S型广义热弹性控制方程[15]为
| $ k\theta {{, }_{jj}}=\rho {{C}_{\varepsilon }}\dot{\theta }+\rho {{C}_{\varepsilon }}\tau \ddot{\theta }+{{T}_{0}}\beta ({{{\mathit{\boldsymbol{\dot{u}}}}}_{j}}{{, }_{j}}+\tau {{{\mathit{\boldsymbol{\ddot{u}}}}}_{j}}{{, }_{j}}), $ | (3) |
| $ \left( \lambda +\mathit{\boldsymbol{ }}\!\!\mu\!\!\rm{ } \right){{\mathit{\boldsymbol{u}}}_{j}}{{, }_{jk}}+\mathit{\boldsymbol{ }}\!\!\mu\!\!\rm{ }{{\nabla }^{2}}{{\mathit{\boldsymbol{u}}}_{k}}-\beta \theta {{, }_{k}}-\rho {{{\mathit{\boldsymbol{\ddot{u}}}}}_{k}}=0, $ | (4) |
式中:uj为位移张量;λ和μ为拉梅常数;T0为参考温度;
无量纲分析中令:
在不引起混淆的情况下,略去右上角符号 (*),对方程 (3) 和 (4) 无量纲后的三维方程组为
| $ \begin{align} & \left( 2\mu +\lambda \right)\frac{{{\partial }^{2}}u}{\partial {{x}^{2}}}+\mu \frac{{{\partial }^{2}}u}{\partial {{y}^{2}}}+\mu \frac{{{\partial }^{2}}u}{\partial {{z}^{2}}}+\left( \mu +\lambda \right)\frac{{{\partial }^{2}}v}{\partial x\partial y}+\left( \mu +\lambda \right)\frac{{{\partial }^{2}}w}{\partial x\partial z}-\\ & \ \ \ \ \ \ \ \ \ \ \left( 2\mu +\lambda \right)\frac{{{\partial }^{2}}u}{\partial {{t}^{2}}}-\beta {{T}_{0}}\frac{\partial \theta }{\partial x}=0,\\ \end{align} $ | (5.1) |
| $ \begin{align} & \mu \frac{{{\partial }^{2}}u}{\partial {{x}^{2}}}+\left( 2\mu +\lambda \right)\frac{{{\partial }^{2}}v}{\partial {{y}^{2}}}+\mu \frac{{{\partial }^{2}}v}{\partial {{z}^{2}}}+\left( \mu +\lambda \right)\frac{{{\partial }^{2}}\boldsymbol{u}}{\partial x\partial y}+\left( \mu +\lambda \right)\frac{{{\partial }^{2}}w}{\partial y\partial z}-\\ & \ \ \ \ \ \ \ \ \ \left( 2\mu +\lambda \right)\frac{{{\partial }^{2}}v}{\partial {{t}^{2}}}-\beta {{T}_{0}}\frac{\partial \theta }{\partial y}=0,\\ \end{align} $ | (5.2) |
| $ \begin{align} & \mu \frac{{{\partial }^{2}}w}{\partial {{x}^{2}}}+\mu \frac{{{\partial }^{2}}w}{\partial {{y}^{2}}}+\left( 2\mu +\lambda \right)\frac{{{\partial }^{2}}w}{\partial {{z}^{2}}}+\left( \mu +\lambda \right)\frac{{{\partial }^{2}}\mathit{\boldsymbol{u}}}{\partial x\partial z}+\left( \mu +\lambda \right)\frac{{{\partial }^{2}}v}{\partial y\partial z}-\\ & \ \ \ \ \ \ \ \ \ \left( 2\mu +\lambda \right)\frac{{{\partial }^{2}}w}{\partial {{t}^{2}}}-\beta {{T}_{0}}\frac{\partial \theta }{\partial z}=0, \\ \end{align} $ | (5.3) |
| $ \begin{align} & \frac{{{\partial }^{2}}\theta }{\partial {{x}^{2}}}+\frac{{{\partial }^{2}}\theta }{\partial {{y}^{2}}}+\frac{{{\partial }^{2}}\theta }{\partial {{z}^{2}}}=\frac{\partial \theta }{\partial t}+\tau \frac{{{\partial }^{2}}\theta }{\partial {{t}^{2}}}+\frac{\beta }{\rho {{C}_{\varepsilon }}} \\ & \ \ \ \ \left( \frac{{{\partial }^{2}}\mathit{\boldsymbol{u}}}{\partial x\partial t}+{{\tau }_{0}}\frac{{{\partial }^{3}}\mathit{\boldsymbol{u}}}{\partial x\partial {{t}^{2}}}+\frac{{{\partial }^{2}}v}{\partial y\partial t}+{{\tau }_{0}}\frac{{{\partial }^{3}}v}{\partial y\partial {{t}^{2}}}+\frac{{{\partial }^{2}}w}{\partial z\partial t}+{{\tau }_{0}}\frac{{{\partial }^{3}}w}{\partial z\partial {{t}^{2}}} \right),\\ \end{align}$ | (6) |
由烧结理论可知应力对化学势的影响[16]为
| $ P=-\sigma \cdot \mathit{\Omega }\mathit{。} $ | (7) |
颈部与颗粒中心的空位浓度差[8]为
| $ \Delta C=\sigma \mathit{\Omega }{{C}_{0}}/k\prime \theta , $ | (8) |
式中:P为化学势;Ω为原子体积;C0为无应力区的平衡浓度;k′为玻尔兹曼常数。空位浓度差会使空位源和阱之间产生空位流动,而原子则按相反方向扩散至颈部表面,从而形成烧结颈长大过程。
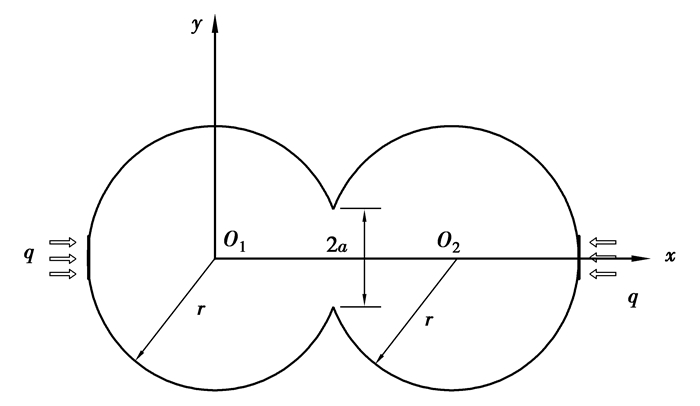
2 模型及参数烧结两颗粒模型如图 1所示。
|
图 1 两颗粒烧结模型 Figure 1 Double equal-sized particles model |
两颗粒半径均为r=0.5,球心距O1O2=0.99,颈部接触部位半径为a。考虑颗粒与模具的接触情况,在两颗粒左右两端距球心距离为l=0.497 5处分别取一平行于Oyz平面的切面,相对应的边界条件为
在左右端面 (xleft=-0.497 5, xright=1.487 5) 受脉冲热流作用且位移分量被约束:
| $ \begin{array}{l} q\left( {x,y,z,t} \right) = \left\{ \begin{array}{l} {q^*}{\rm{sin}}\left( {\omega t} \right),\;\;\;\;\;0 \le t \le 0.02;\\ 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;t > 0.02; \end{array} \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;u = v = w = 0, \end{array} $ |
式中:q*=1 000,ω=50π,其他地方为位移自由且绝热。
初始条件为
| $ {{\boldsymbol{u}}_{j}}\left( t \right)=\theta \left( t \right)=\dot{\theta }\left( t \right)=0, $ |
材料参数[8, 17]取E=340 GPa,ν=0.23,α=8.1×10-6K-1,ρ=3 780kg/m3,k=24 W/(m·K),Cε=1 080 J/(kg·K),Ω=1.4×10-23cm2,k′=1.38×10-23J/K,取无量纲热延迟时间τ=0.05。
3 数值结果及讨论图 2为t=0.06和t=0.316颗粒三维表面的温度场和颗粒内部沿xOy切面温度场分布,由图可知,热在颗粒内部具有明显的波传播形式,热波波前将颗粒分为热传播区域和未传播区域,造成颗粒内部温度场的不均匀分布;随着烧结过程的进行,热波波前在颗粒接触部叠加,产生局部高温。

|
图 2 温度场分布 Figure 2 Temperature field distribution |
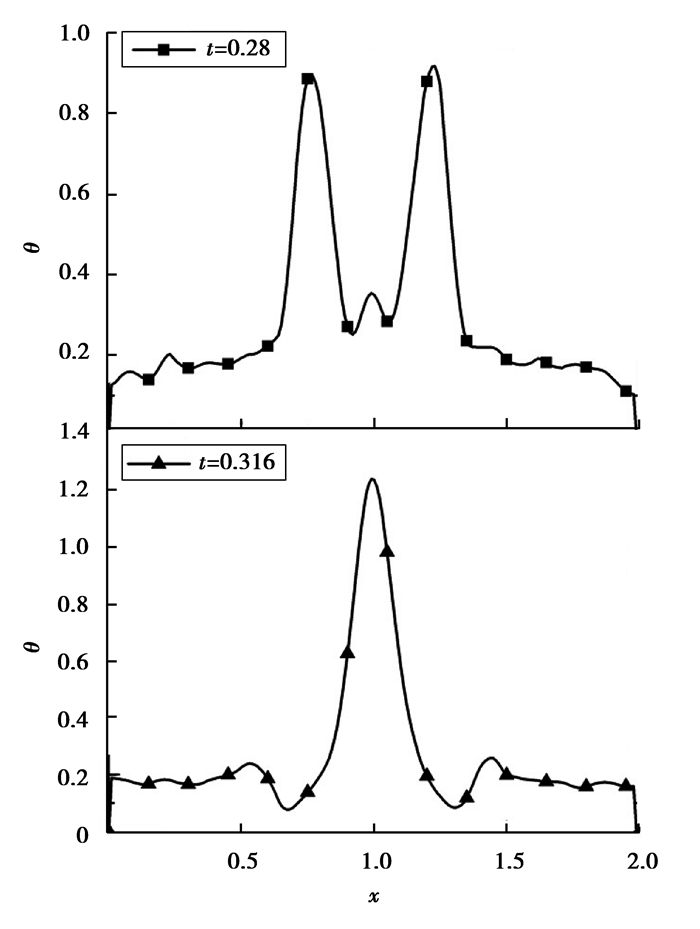
图 3给出了t=0.28和t=0.316两颗粒连心线上的温度分布曲线,热以波的形式从颗粒两端向中心传播。热波在两等径颗粒中传播速度相同,恰好在颗粒接触部位形成叠加,由图 3可知叠加后形成的瞬时温度高于未叠加前的温度值。由叠加时刻结合几何尺寸还可求得热波传播的速度为v=4.7,式 (2) 的理论值为vt=4.472。温度场分布与文献[18]用直接有限元求解结果具有相同的趋势。
|
图 3 两球连心线上温度分布 Figure 3 Temperature distribution on the line of centers |
烧结颈长大的原因是在颈部出现了空位流动,而空位流动取决于空位在颈部附近的浓度分布[8]。化学势作为烧结过程的驱动力,会影响颈部附近的空位浓度分布。
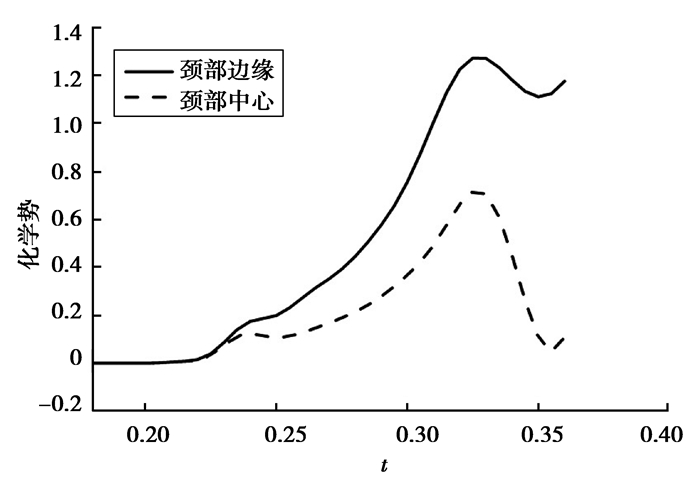
图 4给出了烧结颈部边缘和中心点由热应力 (σy或σz) 产生的无量纲化学势变化规律,温度波到达烧结颈部时,边缘比中心点先产生突变,且突变值大于中心点,这说明在烧结初期表面扩散先于体积扩散,且表面扩散占主要作用,这与实际烧结过程相吻合[19]。
|
图 4 颈部边缘和中心点的化学势变化 Figure 4 The chemical potential curve of neck edge and center |
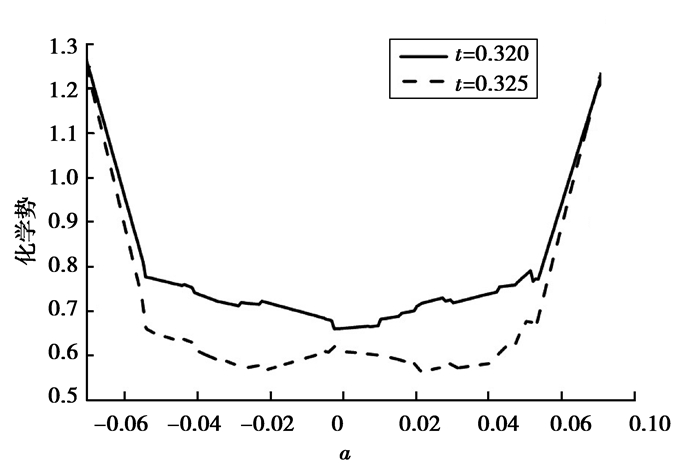
图 5为颈部边缘和中心点化学势产生突变值最大时,沿烧结颈部宽度的化学势分布。在烧结过程中颈部边缘的化学势最大,该结果与文献[16]相一致。这也说明了在烧结初期,物质迁移主要发生在烧结颈边缘。
|
图 5 化学势沿烧结颈部宽度分布 Figure 5 The chemical potential distribution along the sintering neck width |
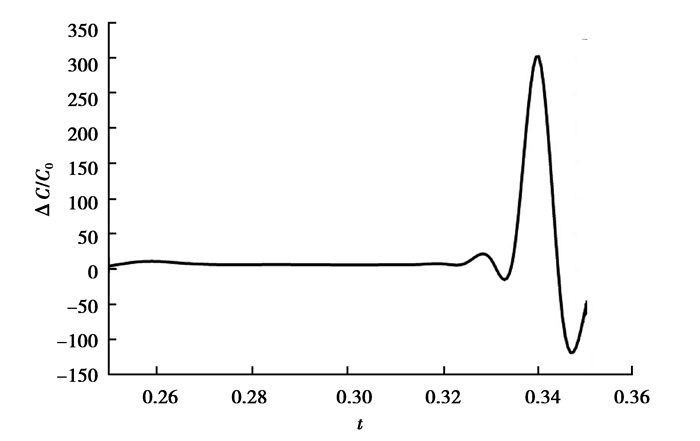
由式 (8) 可得到烧结颈部边缘和中心点的空位浓度差,如图 6所示。空位浓度差在烧结过程中是瞬态变化的,当热波到达时会发生突变,在颗粒边缘产生局部过剩空位,从而产生局部的空位浓度梯度,提高物质迁移驱动力,缩短了烧结时间。
|
图 6 颈部边缘和中心点空位浓度差 Figure 6 Vacancy concentration difference of neck edge and center |
采用L-S型广义热弹性理论,结合相应的初始和边界条件,得到脉冲电流加热作用下非导电Al2O3粉体烧结过程中的温度场、应力场,颈部化学势和空位浓度变化规律。计算结果表明:1) 热的波传播模式使得颗粒内部温度场分布不均匀,存在明显的温度梯度,并且在两球接触部位产生叠加形成了局部高温,促进粉末颗粒的快速烧结。2) 热波到达烧结颈部时,烧结颈部边缘和中心点化学势均产生突变,且边缘的化学势最大,说明在烧结初期,表面扩散占主要作用,这与实际烧结过程相吻合。3) 当热波到达时,在颗粒边缘会产生局部过剩空位,从而产生局部的空位浓度梯度,促进了烧结颈长,提高了颗粒的烧结活性。
| [1] |
白玲, 葛昌纯, 沈卫平.
放电等离子烧结技术[J]. 粉末冶金技术, 2007, 25(3): 217–223.
BAI Ling, GE Changchun, SHEN Weiping. Spark plasma sintering technology[J]. Powder Metallurgy Technology, 2007, 25(3): 217–223. (in Chinese) |
| [2] | Tokita M. Spark plasma sintering (SPS) method, systems, and applications[M]// Handbook of Advanced Ceramics. 2013: 1149-1177. |
| [3] | Tokita M. Development of large-size ceramic/metal bulk FGM fabricated by spark plasma sintering[J]. Materials Seienee Forum, 1999(308/309/310/311): 83–88. |
| [4] | Zhang Z H, Liu Z F, Lu J F, et al. The sintering mechanism in spark plasma sintering-proof of the occurrence of spark discharge[J]. Scripta Materialia, 2014, 81(11): 56–59. |
| [5] | Chen F, Yang S, WU J Y, et al. Spark plasma sintering and densification mechanisms of conductive ceramics under coupled thermal/electric fields[J]. Journal of the American Ceramic Society, 2015, 98(3): 732–740. DOI:10.1111/jace.2015.98.issue-3 |
| [6] | Wang S W, Chen L D, Kang Y S, et al. Effect of plasma activated sintering (PAS) parameters on densification of copper powder[J]. Materials Research Bulletin, 2000, 35(4): 619–628. DOI:10.1016/S0025-5408(00)00246-4 |
| [7] | Wang S W, Chen L D, Hirai T. Densification of Al2O3 powder using spark plasma sintering[J]. Journal of Materials Research, 2000, 15(4): 982–987. DOI:10.1557/JMR.2000.0140 |
| [8] |
果世驹. 粉末烧结理论[M]. 北京: 冶金工业出版社, 2007.
GUO Shiju. Powder metallurgy sintering theory[M]. Beijing: Metallurgical Industry Press, 2007. (in Chinese) |
| [9] |
程远方, 果世驹, 赖和怡.
烧结理论进展-1.烧结单元模型建立方法之比较[J]. 粉末冶金技术, 1999, 17(3): 216–221.
CHENG Yuanfang, GUO Shiju, LAI Heyi. Theoretical modelling progress-1. The comparison of the unit model for the first stage of gravity sintering[J]. Powder Metallurgy Technology, 1999, 17(3): 216–221. (in Chinese) |
| [10] |
田晓耕, 沈亚鹏.
广义热弹性问题研究进展[J]. 力学进展, 2012, 42(1): 18–28.
TIAN Xiaogeng, SHEN Yapeng. Research progress in generalized thermo-elastic problems[J]. Advances in Mechanics, 2012, 42(1): 18–28. DOI:10.6052/1000-0992-2012-1-lxjzJ2011-115 (in Chinese) |
| [11] | Roetzel W, Putra N, Das S K. Experiment and analysis for non-fourier conduction in materials with non-homogeneous inner structure[J]. International Journal of Thermal Sciences, 2003, 42(6): 541–552. DOI:10.1016/S1290-0729(03)00020-6 |
| [12] | Tian X G, Shen Y P, Chen C Q, et al. A direct finite element method study of generalized thermoelastic problems[J]. International Journal of Solids and Structures, 2006, 43: 2050–2063. DOI:10.1016/j.ijsolstr.2005.06.071 |
| [13] | Strunin D V, Melnik R V N, Roberts A J. Coupled thermomechanical waves in hyperbolic thermoelasticity[J]. Journal of Thermal Stresses, 2001, 24(2): 121–140. DOI:10.1080/01495730150500433 |
| [14] | Kumar K, Tamma, Zhou X M. Macroscale and microscale thermal transport and thermo-mechanical interactions:some noteworthy prespectives[J]. Journal of Thermal Stresses, 1998, 21(3/4): 405–449. |
| [15] | Lord H W, Shulman Y. A generalized dynamical theory of thermoelasticity[J]. Journal of Guangxi University for Nationalities, 2007, 15(5): 299–309. |
| [16] |
吴艳青, 黄风雷.
粉末热压扩散与应力场耦合的力学模型[J]. 力学学报, 2008, 40(4): 550–556.
WU Yanqing, HUANG Fenglei. A powder compaction mechanical model for diffusion coupled with stress field[J]. Chinese Journal of Theoretical and Applied Mechanics, 2008, 40(4): 550–556. DOI:10.6052/0459-1879-2008-4-2006-489 (in Chinese) |
| [17] | Taymaz I, Mimaroglu A, Avci E, et al. Comparison of thermal stresses developed in Al2O3±SG, ZrO2±(12%Si+Al) and ZrO2±SG thermal barrier coating systems with NiAl, NiCrAlY and NiCoCrAlY interlayer materials subjected to thermal loading[J]. Surface and Coatings Technology, 1999, 116: 690–693. |
| [18] |
张龙, 张晓敏, 褚钟祥. 基于非Fourier热传导的Al2O3颗粒烧结的三维广义热弹性分析[C]//中国计算力学大会2014暨钱令希计算力学奖颁奖大会, 2014. ZHANG Long, ZHANG Xiaomin, CHU Zhongxiang. Study on Three-dimensional Generalized Thermoelastic Analysis of Al2O3 Powder Sintering Sintering Based on Non-Fourier Heat Conduction[C]//CCCM, 2014. |
| [19] |
程远方, 果世驹, 赖和怡.
烧结理论研究进展-2.烧结初期多种扩散机制耦合作用的烧结模型[J]. 粉末冶金技术, 1999, 17(4): 257–263.
CHENG Yuanfang, GUO Shiju, LAI Heyi. Theoretical modelling progress-2. Coupling model of multiple sintering mechanisms for the initial stage sintering[J]. Powder Metallurgy Technology, 1999, 17(4): 257–263. (in Chinese) |
 2017, Vol. 40
2017, Vol. 40



