2. 中国电力科学研究院, 北京 100192;
3. 重庆大学 输配电装备及系统安全与新技术国家重点实验室, 重庆 400044
2. China Electric Power Research Institute, Beijing 100192, P. R. China;
3. State Key Laboratory of Power Transmission Equipment & System Security and New Technology, Chongqing University, Chongqing 400044, P. R. China
电力系统互联能有效提高系统运行的经济性和可靠性,但规模的扩大也使电力系统可靠性评估遭遇“组合爆炸”问题,计算的高度复杂性严重阻碍了其在实际工程中的应用[1]。鉴于电网可靠性评估实际应用中常常重点关心整个互联电网某一特定区域的可靠性,因此,针对该特定研究区域寻求一个快速高效的可靠性评估方法成为亟待解决的问题。
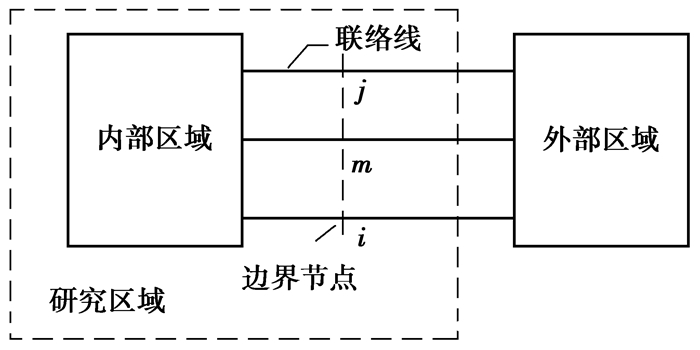
可靠性等值技术的提出为该问题解决提供了思路[2],该思路将整个电网划分为研究区域 (study area,SA) 和外部区域 (external area,EA),如图 1所示,通过外部区域的等值来减少网络规模,且通过合理保留外部等值区域对研究区域的影响来保证计算准确性。现有可靠性等值研究主要集中于充裕度等值模型[3-5],即采用状态枚举法对外部区域进行充裕性建模,其计算时间随网络规模的增大急剧增长。近年来,静态等值技术在电力系统静态安全分析、无功优化以及分布式潮流计算方面取得了较好的成果[6-8]。为缓解电网可靠性的计算复杂性,静态等值技术也被引入可靠性评估领域,文献[9-10]用直流Ward等值法将外网等值为边界节点上的注入功率,文献[11]进一步指出基于静态Ward等值技术的电网可靠性评估随研究区域的增大,计算精度随之增加,文献[12]采用发电转移系数和线路停运分布系数筛选对研究区域有重要影响的外网元件,以此决定缓冲区域的范围。但上述文献的共同不足在于缺乏对等值网络随机不确定性的深入考虑和精确建模。
|
图 1 电网分区示意图 Figure 1 Partitioning a power system into EA and SA |
外部等值区域的运行状态受其内部设备随机故障影响而具有随机不确定性,故对其进行等值建模时,等值参数 (等值注入功率和等值支路阻抗) 也随外网运行状态的变化而具有随机性。现有基于静态等值技术的电网可靠性评估很少考虑外部区域元件故障对等值参数的影响。文献[13]虽然有所考虑,但却采用外网在各种随机故障运行状态下等值参数的期望值作为外网等值参数,外网等值参数本质上是一个随机变量,期望值仅是其众多数字特征的一种,期望值虽然可以大体反映等值参数的平均趋势,但难以反映外网等值参数的分布顾虑和变动幅度,因此,基于外网等值参数期望值的电网可靠性评估结果可能具有较大的误差。如何准确计算外网等值参数不确定性实现电网可靠性的高效准确评估是本文要解决的关键问题。
笔者将外网等值参数看成依赖于外部区域网络拓扑和设备偶发故障的连续型随机变量,基于非参数核密度估计构建外网等值参数的联合概率密度分布,基于静态DC Ward等值技术,开展了外网静态等值模型的随机性建模研究。外网等值参数联合概率密度分布的引入,从根本上提高了等值网络的准确性,在保持较高计算准确性的基础上提高了电网可靠性评估的计算效率。
1 外网静态概率等值模型 1.1 外网状态已知时外网等值参数计算为研究整个电网中感兴趣的子区域,可根据网络特点将整个电网划分为内部区域、边界节点和外部区域,且由内部区域和边界节点组成研究区域,如图 1所示。
大电网可靠性评估通常采用基于直流潮流的最优负荷削减方法,具有较好的精度。当已知外网运行状态时,为计算外网的等值参数,先给出直流Ward等值公式的推导。
以下标I、B、E分别表示研究区域内部节点、边界节点和外部区域节点。根据直流潮流法,除平衡节点外电网中其他节点的注入功率和相角关系为
| $ \left[{\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{B}}_{EE}}}&{{\mathit{\boldsymbol{B}}_{EB}}}&0\\ {{\mathit{\boldsymbol{B}}_{BE}}}&{{\mathit{\boldsymbol{B}}_{BB}}}&{{\mathit{\boldsymbol{B}}_{BI}}}\\ 0&{{\mathit{\boldsymbol{B}}_{IB}}}&{{\mathit{\boldsymbol{B}}_{II}}} \end{array}} \right]\left[\begin{array}{l} {\mathit{\boldsymbol{\theta }}_E}\\ {\mathit{\boldsymbol{\theta }}_B}\\ {\mathit{\boldsymbol{\theta }}_I} \end{array} \right] = \left[\begin{array}{l} {\mathit{\boldsymbol{P}}_E}\\ {\mathit{\boldsymbol{P}}_B}\\ {\mathit{\boldsymbol{P}}_I} \end{array} \right], $ | (1) |
式中:B为节点电纳矩阵。将矩阵形式展开,写成方程组的形式为
| $ {\mathit{\boldsymbol{B}}_{EE}}{\mathit{\boldsymbol{\theta }}_E} + {\mathit{\boldsymbol{B}}_{EB}}{\mathit{\boldsymbol{\theta }}_B} = {\mathit{\boldsymbol{P}}_E}, $ | (2) |
| $ {\mathit{\boldsymbol{B}}_{BE}}{\mathit{\boldsymbol{\theta }}_E} + {\mathit{\boldsymbol{B}}_{BB}}{\mathit{\boldsymbol{\theta }}_B} + {\mathit{\boldsymbol{B}}_{\mathit{\boldsymbol{BI}}}}{\mathit{\boldsymbol{\theta }}_I} = {\mathit{\boldsymbol{P}}_B}, $ | (3) |
| $ {\mathit{\boldsymbol{B}}_{IB}}{\mathit{\boldsymbol{\theta }}_B} + {\mathit{\boldsymbol{B}}_{II}}{\mathit{\boldsymbol{\theta }}_I} = {\mathit{\boldsymbol{P}}_I}。 $ | (4) |
为消去外部区域节点,即消去式 (1) 中的变量θE,将式 (2) 进行变换,可得:
| $ {\mathit{\boldsymbol{\theta }}_E} = \mathit{\boldsymbol{B}}_{EE}^{-1}{\mathit{\boldsymbol{P}}_E}-\mathit{\boldsymbol{B}}_{EE}^{-1}{\mathit{\boldsymbol{B}}_{EB}}{\mathit{\boldsymbol{\theta }}_B}, $ | (5) |
将上式带入式 (3),整理后得到
| $ ({\mathit{\boldsymbol{B}}_{BB}}-{\mathit{\boldsymbol{B}}_{BE}}\mathit{\boldsymbol{B}}_{EE}^{-1}{\mathit{\boldsymbol{B}}_{EB}}){\mathit{\boldsymbol{\theta }}_B} + {\mathit{\boldsymbol{B}}_{BI}}{\mathit{\boldsymbol{\theta }}_I} = {\mathit{\boldsymbol{P}}_B}-{\mathit{\boldsymbol{B}}_{BE}}\mathit{\boldsymbol{B}}_{EE}^{ - 1}{\mathit{\boldsymbol{P}}_E}。 $ | (6) |
合并式 (6) 与式 (4),可得
| $ \left[{\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{B}}_{BB}}-{\mathit{\boldsymbol{B}}_{BE}}\mathit{\boldsymbol{B}}_{EE}^{-1}{\mathit{\boldsymbol{B}}_{EB}}}&{{\mathit{\boldsymbol{B}}_{BI}}}\\ {{\mathit{\boldsymbol{B}}_{IB}}}&{{\mathit{\boldsymbol{B}}_{II}}} \end{array}} \right]\left[\begin{array}{l} {\mathit{\boldsymbol{\theta }}_B}\\ {\mathit{\boldsymbol{\theta }}_I} \end{array} \right] = \left[{\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{P}}_B}-{\mathit{\boldsymbol{B}}_{\mathit{\boldsymbol{BE}}}}\mathit{\boldsymbol{B}}_{EE}^{-1}{\mathit{\boldsymbol{P}}_E}}\\ {{\mathit{\boldsymbol{P}}_I}} \end{array}} \right]。 $ | (7) |
上式表示消去外部区域节点以后的等值网络直流潮流方程式,由式 (7) 可得等值网络边界节点的等效节点电纳矩阵为
| $ {\mathit{\boldsymbol{B}}_{eq}} = {\mathit{\boldsymbol{B}}_{BB}}-{\mathit{\boldsymbol{B}}_{BE}}\mathit{\boldsymbol{B}}_{EE}^{-1}{\mathit{\boldsymbol{B}}_{EB}}。 $ | (8) |
由该等效节点电纳矩阵,可以求出边界节点间等值串联支路的阻抗向量Xeq,等值串联支路ij的阻抗为
| $ {\mathit{\boldsymbol{X}}_{ij}} =-\frac{1}{{{\mathit{\boldsymbol{B}}_{eq\left( {i, j} \right)}}}}, (i, j \in N{B_{eq}}), $ | (9) |
式中:NBeq表示边界节点的集合。
边界节点上的等值注入功率增量为
| $ {\mathit{\boldsymbol{P}}_{eq}} =-{\mathit{\boldsymbol{B}}_{BE}}\mathit{\boldsymbol{B}}_{EE}^{-1}{\mathit{\boldsymbol{P}}_E}。 $ | (10) |
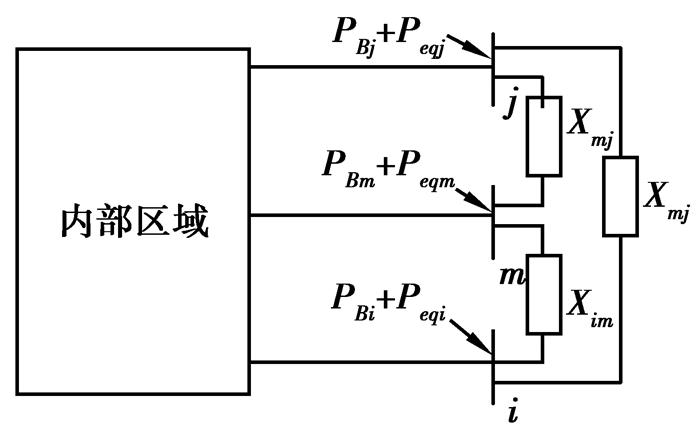
通过上述方法求得的边界节点上等值串联支路阻抗Xeq和等值注入功率增量Peq统称为外网等值参数。可将图 1的等值网络用图 2表示。
|
图 2 等值网络 Figure 2 Equivalent network |
本节计算外网等值参数时假设内网 (即内部区域加边界节点) 元件均正常运行。采用状态枚举法枚举外网 (外部区域) 状态,计算其等值参数, 流程为
1) 枚举外网发电机和线路故障。外网运行状态概率由下式表示:
| $ P\left( s \right) = \prod\limits_{i = 1}^{{N_f}} {{Q_i}} \prod\limits_{i = 1}^{{N_{EA}}-{N_f}} {{P_i}} , $ | (11) |
式中:Pi和Qi分别为外网第i个元件工作和失效的概率;NEA分别为外网元件数;Nf和NEA-Nf分别为外网在状态s中失效和未失效的元件数量。若所有元件均正常,则公式为
| $ P\left( s \right) = \prod\limits_{i = 1}^{{N_{EA}}} {{P_i}} 。 $ | (12) |
2) 对枚举到的外网状态,首先判断由内网和外网构成的整个电网是否可用发电容量不足:
① 如果整个电网可用发电容量大于负荷需求,则对全网进行潮流计算,根据潮流计算结果,如果未出现电网运行约束被违反,则采用公式 (9)-(10) 计算外网的等值注入功率增量向量Peq(s) 和等值串联支路阻抗向量Xeq(s),记录外网等值参数及其状态概率。
② 如果整个电网可用发电容量小于负荷需求或上一步骤中经过潮流计算出现运行约束被违反,则进行最优负荷削减计算,得到该外网状态下的负荷削减量C(s),累计计算研究区域和全网的可靠性指标。对于枚举到的外网状态,如果出现整个电网可用发电容量不足或运行约束被违反而导致负荷削减,通常都是源于外网高阶故障,由于其出现概率很小,在外网静态等值随机建模时可以忽略该类状态。
运用状态枚举法枚举外网状态进行等值参数计算时,外网故障引发系统失效的可靠性指标部分按下式计算。
期望失负荷概率为
| $ LOL{P^1} = \sum\limits_{s \in {G^1}} {P\left( s \right)} , $ | (13) |
期望缺供电量为
| $ EEN{S^1} = \sum\limits_{s \in {G^1}} {C\left( s \right)} P\left( s \right) \times 8{\rm{ }}760, $ | (14) |
式中:G1为外网故障引起的负荷削减状态集合。
1.3 等值参数的联合概率密度分布估计对仅知道实验样本的多个随机变量,可以假设这些随机变量服从多维正态分布,在对样本进行k均值聚类分析后进行联合概率密度估计[14]。但由于这些随机变量服从的概率分布其实事先未知,并不一定服从多维正态分布,其随机变量之间的相关性也无法事先知道,因此,使用任何参数估计方法都无法保证准确刻画多个随机变量的随机变化规律。为准确刻画外网等值参数的随机性和相关性,采用课题组在文献[15]中介绍的非参数核密度估计方法。
设边界系统由m个边界节点组成,则等效串联支路有Cm2条,等值注入功率有m组。设Y表示等效串联支路阻抗向量Xeq和等值注入功率增量Peq的所构成维数为k的等值参数向量Y=[Peq Xeq],令Y=(y1, y2, …, yk)T。通过上一节的计算,可以得到随机向量Y的n个样本,每个样本的权重系数ωi取该样本对应的外网运行状态概率 (见式 (11)) 的归一值。外网等值参数的联合概率密度分布估计为
| $ \hat f\left( \boldsymbol{Y} \right) = {\omega _i}\sum\limits_{i = 1}^n {\frac{1}{{{h_1}{h_2} \ldots {h_k}}}\prod\limits_{j = 1}^k {K(\frac{{{y_j}-{y_{ji}}}}{{{h_j}}})} } , $ | (15) |
式中:hj为第j个等值参数变量的窗宽;K(·) 为核函数,本文采用标准高斯核函数;ωi为样本Yi的权重系数,所有权重系数之和为1。取矩阵中外网等值参数的状态概率P(si) 作为权重系数表示每个样本的重要程度。当样本数n→∞,带宽h→0且nh→∞时,
采用高斯核函数,通常核函数的选择不是密度估计的关键,带宽对模型光滑性的影响很大。通常考虑估计的积分均方误差 (mean integral square error, MISE) 和渐近均方误差 (asymptotic integral mean square error, AMISE) 作为选择最优带宽的标准。但在实际计算中,利用该标准计算出的估计值仅仅是探索最优估计的起点。带宽的计算方法有LSCV法,即基于积分平方误差 (integrated square error, ISE) 最小准则法、直接插入选择法 (plug-in method) 和交叉验证方法 (cross-validation method) 等。为提高计算效率,选择直接插入选择法[16]计算AMISE。
2 等值网络可靠性评估 2.1 评估方法和流程第2节对研究区域正常运行而外部区域处于不同运行状态 (正常或故障) 的情况进行了分析计算,当运用静态概率等值模型评估研究区域和全网可靠性时,由于研究区域正常运行的情况已进行过分析,故只需要分析研究区域出现元件随机故障的情况。
采用非序贯蒙特卡洛仿真法评估等值网络的可靠性,通过对式 (15) 所得到的联合概率密度分布进行抽样,可以得到外网等值参数抽样值。在抽取了内网的运行状态后,按两种不同方式对等值网络进行分析:
方式1:外网等值参数中等值注入功率看成固定不变的出力,即认为不可调整,因此, 在抽取了内网的运行状态后,直接利用等值网络进行潮流和最优负荷削减计算。
方式2:根据等值网络可用发电容量是否充裕按两种情况进行处理,其中等值网络可用发电容量的充裕性可以采用下式进行判断:
| $ \Delta P = \sum\limits_{i \in N{G_{eq}}} {{G_i}}-\sum\limits_{i \in N{D_{eq}}} {{L_i}} + {\rm{ }}\sum\limits_{i \in N{B_{eq}}} {({P_{Bi}} + {P_{eqi}}),} $ | (16) |
式中:Gi和Li分别为研究区域节点i的发电机容量和负荷;Peqi为节点i上的外网等值注入功率增量;NGeq、NDeq和NGeq分别为等值网络内的发电机节点、负荷节点和边界节点。
a) 当等值网络可用发电容量大于等值网络负荷需求,即ΔP大于零时,利用等值网络直接进行潮流和最优负荷削减计算。
b) 当等值网络可用发电容量小于等值网络负荷需求,即ΔP小于零时,考虑到外网发电机通常并没达到出力上限,即外网发电机出力可调,此时不对等值网络进行直接分析,而是对未等值的整个完整电网进行潮流和考虑外网机组可调性进行最优负荷削减计算。
基于非序贯蒙特卡洛仿真的等值网络可靠性评估过程包含以下步骤:
1) 枚举外网状态,求取其等值参数,从而得到外网等值参数样本;
2) 基于外网等值参数样本,采用式 (15) 计算外网等值参数的联合概率密度分布;
3) 通过外网等值参数的联合概率密度分布抽取外网等值参数,通过内网元件的可靠性模型抽取内网元件运行状态;
4) 如果等值网络可用发电容量充裕,则对等值网络进行系统状态分析,否则对全网进行系统状态分析;
5) 判断是否达到蒙特卡洛仿真的模拟次数N,若未达到,返回第3) 步;否则,结束可靠性评估,统计失负荷状态并计算可靠性指标LOLP和EENS。
2.2 可靠性指标计算对等值网络进行可靠性评估得到的期望缺供电量不足指标计算公式为
| $ EEN{S^{2eq}} = \frac{1}{N}\sum\limits_{s \in {G^{2eq}}} {C\left( s \right)} \times 8{\rm{ }}760。 $ | (17) |
期望失负荷概率指标计算公式为
| $ LOL{P^{2eq}} = \frac{{{k_{eq}}}}{N}, $ | (18) |
式中:G2eq是采用等值网络进行计算时,等值网络发生故障引起失效的所有失效状态的集合;keq为失效状态发生的总次数;N为仿真次数。
外网概率等值模型能充分计及外部区域不同运行状态对研究区域的影响。整个电网的失负荷概率和期望缺供电量指标的计算公式如下:
| $ LOLP = LOL{P^1} + LOL{P^2}, $ | (19) |
| $ EENS = EEN{S^1} + EEN{S^2}。 $ | (20) |
用本文方式1进行计算时,由于负荷削减范围为等值网络,式LOLP2和EENS2与LOLP2eq和EENS2eq分别相等,计算公式为式 (17)-(18)。
采用方式2评估网络可靠性,等值网络可用发电容量不足时,需要对整个全网进行分析而不是对等值网络进行分析,对整个全网进行分析时出现负荷削减的系统状态集合为G2al,可靠性指标计算公式为
| $ LOL{P^{2al}} = \frac{{{k^{al}}}}{N}, $ | (21) |
| $ EEN{S^{2al}} = \frac{1}{N}\sum\limits_{s \in {G^{2al}}} {C\left( s \right)} \times 8{\rm{ }}760, $ | (22) |
式中:kal为全网分析时失效状态发生的总次数。
用方式2评估等值网络状态时,评估分析既有等值网络,也有全网分析两种,故计算得到可靠性指标分成两部分,即等值网络可靠性指标计算部分和全网可靠性指标计算部分。全网的可靠性指标计算公式为
| $ LOL{P^2} = LOL{P^{2al}} + LOL{P^{2eq}}, $ | (23) |
| $ EEN{S^2} = EEN{S^{2al}} + EEN{S^{2eq}}。 $ | (24) |
为验证概率等值模型的评估精度,一种有效的方法是检验各指标的相对误差,以EENS指标的相对误差为例,计算公式为
| $ {R_{EENS}} = \frac{{\left| {EEN{S^{{\rm{new}}}}-EEN{S^{{\rm{base}}}}} \right|}}{{EEN{S^{{\rm{base}}}}}}, $ | (25) |
式中:EENSbase为准确值 (基准值);EENSnew为本文方法的计算值。
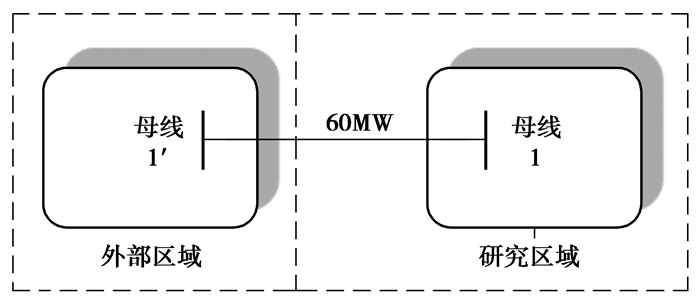
3 算例分析首先,采用网络规模较小的两区域RBTS[17]系统对外网静态概率等值模型进行验证。联络线容量假设为60 MW,故障率为1次/年,修复时间为10 h。如图 3所示,假设左边的RBTS代表外部区域,右边的RBTS代表内部区域,节点1作为边界节点。
|
图 3 两区域RBTS示意图 Figure 3 Symbolic interconnected two-area RBTS |
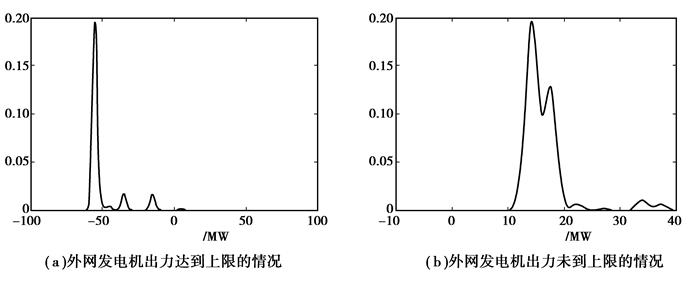
由于仅有一个边界节点,该等值网络只有外网等值注入功率增量参数,无等值串联支路。在全网正常运行情况下,使用直流Ward静态等值方法计算得到外网等值注入功率增量为-55 MW。假设内网正常运行,枚举外网故障,故障阶数取发电机4阶、线路3阶、发电机和线路组合3阶,枚举到的所有外网系统状态的概率累计值达到0.999 996,用于外网等值参数计算的系统状态累积概率为0.998 501,其中外网发电机出力达到上限的系统状态累积概率为0.998 421,未达到上限的累计概率为0.000 080。
节点1等值注入功率增量的概率密度分布如图 4所示,由图可见,外网等值注入功率增量在一定分布范围内随机变化,其概率密度分布不服从任何已知的分布类型。
|
图 4 等值注入功率的概率密度分布 Figure 4 Equivalent power injection of the EA of 2-RBTS |
基于非序贯蒙特卡洛进行仿真分析,负荷采用年峰荷,仿真总次数100万次。按以下情况进行可靠性评估:
Case1:不进行等值,始终对全网进行分析;
Case2:对外网进行概率等值,按本文方式1计算电网的可靠性;
Case3:对外网进行概率等值,按本文方式2计算电网的可靠性;
Case4:对外网采用确定性的静态等值模型。
整个全网的可靠性评估指标见表 1,以Case1计算结果作为基准值。本文方法计算时间相比采用完整电网进行计算大幅下降。由于本文采用外网概率静态等值模型的同时,对等值网络状态进行分类处理,有效计及了外网的影响,因此,本文方式2的全网系统可靠性指标相对误差最小;方式1由于没有考虑外网发电机出力可调节,计算的可靠性指标相对误差稍大;而不考虑外部区域的状态变化,直接采用确定性静态Ward等值对外网进行化简的计算误差最大。由于外部区域发电机出力未达到上限的系统状态累积概率很小,因此,采用本文方式1和2均能得到满意的计算结果。
| 表 1 两区域RBTS系统全网可靠性指标对比 Table 1 Comparison of reliability for 2-RBTS |
表 2为研究区域的可靠性评估指标。通过本文方式2得到的期望负荷概率指标与基准值基本一致。
| 表 2 两区域RBTS研究区域的可靠性指标对比 Table 2 Comparison of reliability for the SA of 2-RBTS |
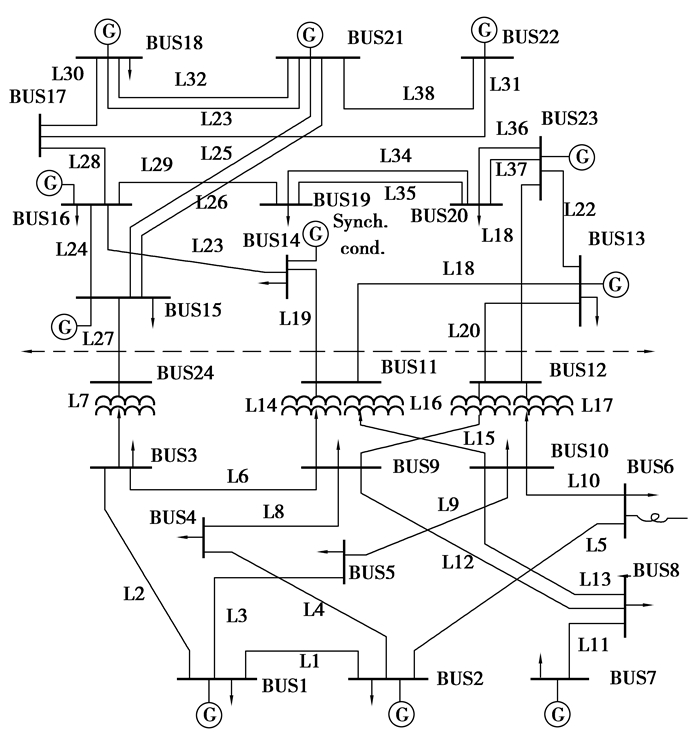
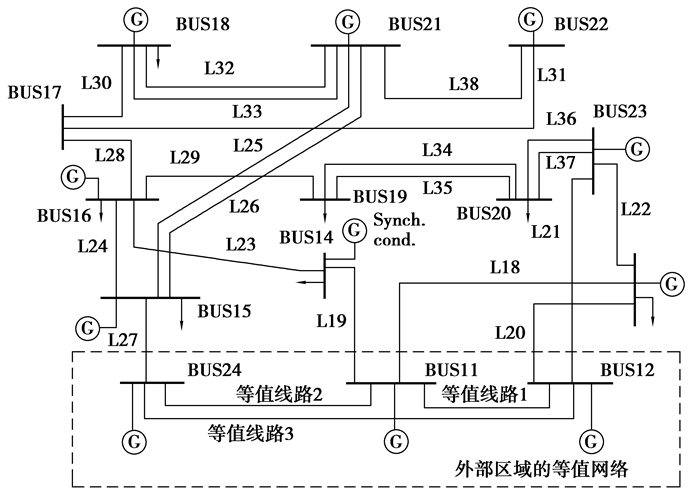
为对具有多个边界节点的网络进行验证,进一步采用IEEE-RTS79系统[18]进行分析。将该网络划分为为两区域,如图 5所示。选取网络上半部分为研究区域,边界节点为BUS11、12、24,下半部分为外部区域。图 6为系统等值后的网络,虚线框里的网络部分表示等值注入功率增量和等值串联支路。
|
图 5 RTS79原始网络 Figure 5 RTS79 original system |
|
图 6 RTS79等值网络图 Figure 6 RTS79 equivalent system |
假设研究区域元件都处于运行状态,枚举外部区域元件状态,发电机失效考虑4阶,线路失效情况考虑3阶,发电机和线路共同失效考虑3阶,状态概率累计值达到0.999 613,得到外部区域发电机出力达到上限和未达到上限的两类用于外网等值参数构建的系统状态,其中外部区域发电机出力达到上限系统状态累计概率为0.471 859,未达到出力上限的系统状态累计概率为0.527 754。
采用非参数核密度估计法求取外网等值参数的概率密度函数,基于直流潮流法采用非序贯蒙特卡洛仿真法对RTS79进行可靠性评估,仿真次数10万次,计算结果见表 3。
| 表 3 RTS79全网系统可靠性指标对比 Table 3 Comparison of reliability for RTS |
① 对比Case2和Case1,采用本文方式1计算结果误差较大,LOLP和EENS指标相对误差均超过10%,这是因为外部区域发电机出力未达到上限的状态累计概率达到0.527 754,当研究区域出现故障导致发电容量不足时,在方式1下无法增加外部区域发电机出力,导致削减负荷过多。可见,当外部区域发电机出力未达到上限的状态概率较大时,不考虑外网发电机出力可调况,会导致可靠性评估结果误差较大。
② 对比Case3和Case1,可知方式2下可靠性评估指标误差很小,LOLP指标相对误差为2.9%,而EENS相对误差为1.8%,计算时间却相比基准值下降了75%左右,可见方式2节约计算时间的同时有效保证了计算精度。
③ 对比Case4和Case1,LOLP指标相对误差达到25%,而EENS相对误差高达51%,可知,对该网络确定性静态等值方法计算得到的可靠性指标误差已经难以接受。
4 结语提出考虑外网等值参数联合概率密度分布的概率等值模型,基于非参数核密度估计技术准确估计外网运行状态对研究区域的影响,并运用蒙特卡洛抽样法进行等值后网络可靠性计算。在两区域RBTS系统和RTS79系统进行了仿真研究,算例结果静态概率等值模型能有效地提高等值精度,对于规模大的复杂网络,能有效提高电网可靠性评估的计算效率。
| [1] |
赵渊, 周家启, 周念成, 等.
大电力系统可靠性评估的解析计算模型[J]. 中国电机工程学报, 2006, 26(5): 19–25.
ZHAO Yuan, ZHOU Jiaqi, ZHOU Niancheng, et al. An analytical approach for bulk power systems reliability assessment[J]. Proceedings of the CSEE, 2006, 26(5): 19–25. (in Chinese) |
| [2] | Sanei H, Asoodeh A, Hamedakbari T S, et al. Review of reduction techniques in the determination of composite system adequacy equivalents[J]. Electric Power Systems Research, 2010, 80(12): 1385–1393. DOI:10.1016/j.epsr.2010.06.002 |
| [3] | Zhang W, Billinton R. Application of an adequacy equivalent method in bulk power system reliability evaluation[J]. IEEE Transactions on Power Systems, 1998, 13(2): 661–666. DOI:10.1109/59.667397 |
| [4] | Billinton R, Zhang W. Adequacy equivalent development of composite generation and transmission systems using a d.c. load flow[J]. Reliability Engineering & System Safety, 1999, 65(3): 295–305. |
| [5] |
汪兴强, 丁明, 韩平平.
互联电力系统可靠性评估的改进等效模型[J]. 电工技术学报, 2011, 26(9): 201–207.
WANG Xingqiang, DING Ming, HAN Pingping. An improved equivalent model for reliability evaluation in interconnected power system[J]. Transactions of China Electrotechnical Society, 2011, 26(9): 201–207. (in Chinese) |
| [6] | Monticelli A, Deckmann S, Garcia A, et al. Real-time external equivalents for static security analysis[J]. IEEE Transactions on Power Apparatus and Systems, 1979, 98(2): 498–508. |
| [7] |
刘志文, 刘明波.
基于Ward等值的多区域无功优化分解协调算法[J]. 电力系统自动化, 2010, 34(14): 63–69.
LIU Zhiwen, LIU Mingbo. A decomposition and coordination algorithm for multi-area reactive power optimization based on Ward equivalent[J]. Automation of Electric Power Systems, 2010, 34(14): 63–69. (in Chinese) |
| [8] |
颜伟, 何宁.
基于ward等值的分布式潮流计算[J]. 重庆大学学报, 2007, 29(11): 36–40.
Yan Wei, He Ning. Distributed power flow method based on ward equivalent[J]. Journal of Chongqing University, 2007, 29(11): 36–40. (in Chinese) |
| [9] | Leite d S A M, Fonseca Manso L A D, Anders G J. Composite reliability evaluation for large-scale power systems[C]//Power Tech Conference Proceedings, 2003 IEEE Bologna.[S.l.]: IEEE, 2003. |
| [10] | Silva A M L D, Resende L C, Manso L A F. Application of Monte Carlo simulation to well-being analysis of large composite power systems[C]//International Conference on Probabilistic Methods Applied to Power Systems.[S.l.]: IEEE, 2006. |
| [11] | Kumar S, Billinton R. Adequacy evaluation of a small area in a large composite power network[J]. IEEE Transactions on Power Systems, 1989, 4(2): 551–558. DOI:10.1109/59.193829 |
| [12] | Akhavein A, Fotuhi-Firuzabad M, Billinton R, et al. Adequacy equivalent development of composite generation and transmission systems using network screening[J]. Iet Generation Transmission & Distribution, 2011, 5(11): 1141–1148. |
| [13] | Audomvongseree K, Eua-Arporn B. Composite system reliability evaluation using AC equivalent network[C]//International Conference on Power System Technology.[S.l.]: IEEE, 2000. |
| [14] |
丁明, 洪梅.
电力系统概率分析中的K均值聚类负荷模型[J]. 电力系统自动化, 1999, 23(19): 51–54.
DING Ming, HONG Mei. The K-means cluster based load model for power system probabilistic analysis[J]. Automation of Electrical Power Systems, 1999, 23(19): 51–54. DOI:10.3321/j.issn:1000-1026.1999.19.011 (in Chinese) |
| [15] |
赵渊, 张夏菲, 周家启.
电网可靠性评估的非参数多变量核密度估计负荷模型研究[J]. 中国电机工程学报, 2009, 29(31): 27–33.
ZHAO Yuan, ZHANG Xiafei, ZHOU Jiaqi. Load modeling utilizing nonparametric and multivariate kernel density estimation in bulk power system reliability evaluation[J]. Proceedings of the CSEE, 2009, 29(31): 27–33. DOI:10.3321/j.issn:0258-8013.2009.31.005 (in Chinese) |
| [16] |
张夏菲.
非参数核密度估计负荷模型在电网可靠性评估中的应用[J]. 重庆:重庆大学, 2010.
ZHANG Xiafei. The application of non-parametric kernel density estimation load model in power system reliability evaluation[J]. Chongqing: Chongqing University, 2010. (in Chinese) |
| [17] | Billinton R, Kumar S N, Chowdhury N, et al. A reliability test system for educational purposes-basic data[J]. IEEE Transactions on Power Systems, 1989, 4(3): 1238–1244. DOI:10.1109/59.32623 |
| [18] | Subcommittee P M. IEEE reliability test system[J]. IEEE Transactions on Power Apparatus and Systems, 1979, 98(6): 2047–2054. |
 2017, Vol. 40
2017, Vol. 40
