人致振动已成为人行桥设计中必须考虑的重要问题[1-2]。当前大多数设计规范中,估算人致激励引起人行桥竖向振动幅值的方法,均把行人对人行桥的作用单纯看作人行荷载[3-4]。这种方法适用于大多数情形,但不同于一般荷载,行人是具有独立反馈系统的动力系统,步行力随着人行桥振动而发生改变,进而再次影响人行桥的振动情况,从而构成所谓的人-桥动力相互作用,对于轻质人行桥,特别是行人步频与结构自振频率接近时,忽略人-桥动力相互作用,估算结果与实测值会偏离很大[5]。
目前人-桥动力相互作用主要局限于侧向相互作用,而关于竖向的动力相互作用研究成果较少。王海等[6]基于具有分布参数的人体动力学模型,分析了人简支梁耦合体系的动力学特征,研究了人对简支梁动力特性的影响。何卫等[7]基于单自由度的人体模型,将分布人群简化成均匀连续分布的质量弹簧阻尼系统,考虑楼板的阻尼,建立了有阻尼的分布人群薄板耦合系统模型,研究了人体等参数对耦合系统动力特性的影响。以上研究关注静态的人或人群对结构竖向动力特性的影响。李红利等[8]基于反映行人步行特征的生物力学模型,从等效的观点研究振动环境下行人平衡控制理论,借用风工程中强迫振动气动导数识别的思想,研究了人-桥竖向动力相互作用效应理论。秦敬伟等[9]基于生物力学中的双足步行模型,通过施加水平控制力的反馈机制保持行走中的步态稳定,采用Lagrange方程推导人体结构相互作用系统的运动方程,探讨了低频结构考虑人体结构相互作用的必要性。对于结构工程师所关注的行人对结构的动力学特性的影响以及考虑人结构相互作用时结构的动力响应而言,以上分析所采用人体动力学模型过于复杂。Kim等[10]提出一种两自由度的人体动力学模型以模拟行走过程中人体竖向动力特征,但是该人体动力学模型参数取自ISO 5982所建议的人站立时的相关动力参数,不能代表实际行走过程中的动力参数。Silva等[11]基于20组行人行走在坚硬地面上的实测加速度数据,提出了模拟行人行走竖向动力特性的单自由度人体动力学模型,模型中质量、刚度和阻尼等参动力数用人体质量和步频表示。文献[5]、[12]和[13]分别基于Silva和Pimentel提出的人体动力学模型,研究了人结构竖向动力相互作用,但在研究中均把结构当作单自由度动力系统处理,关注点都是共振时的动力响应,没有深入探讨行人对结构动力特性的影响。
笔者在已有研究成果基础上,建立人-桥竖向动力相互作用控制方程,由于结构阻尼较低,人体阻尼较高,使得人-桥竖向动力耦合系统是非比例阻尼系统,采用状态空间法进行瞬时模态的求解,得到系统的时变频率和阻尼比;由于行人在人行桥的不断移动,使得人-桥竖向动力相互作用系统是时变系统,利用变步长四阶五级Runge-Kutta-Felhberg算法求解控制方程,对比分析考虑人-桥竖向动力相互作用和只在人行荷载作用下人行桥的动力响应。
1 人-桥竖向动力相互作用控制方程图 1所示为由行人和人行桥组成的耦合动力系统。人行桥假定为均匀截面的Euler-Bernoulli梁,L为人行桥跨度,EI为人行桥的抗弯刚度 (E为弹性模量,I为惯性矩),m为人行桥单位长度的质量。行人模型由弹簧质量阻尼器 (SMD) 的人体动力学模型和人行荷载共同组成,人行荷载用傅立叶级数模拟[11, 14]。mp、kp、cp分别表示人体动力学模型中的质量、刚度和阻尼,Fp表示为人行荷载,v表示为行人步速,一般可取0.9倍的步频,up、u表示行人和人行桥的竖向位移,t为步行时间。假定在步行中,行人与桥面始终处于接触状态。
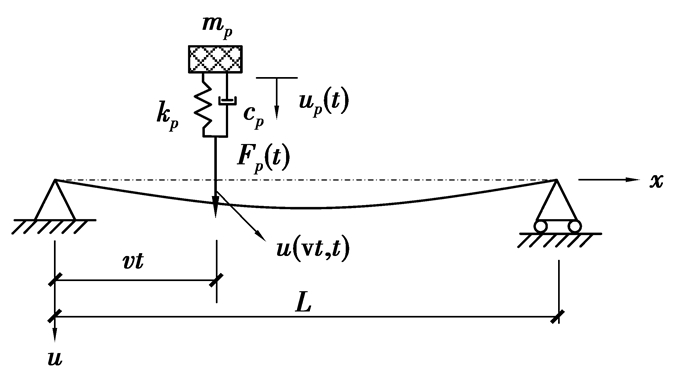
|
图 1 人-桥竖向动力相互作用示意图 Figure 1 Pedestrian-bridge dynamic interaction in the vertical |
行人的受力包括:惯性力FI=mpüp、阻尼力FD=cp(du/dt-
| $ \begin{array}{l} {m_{\rm{p}}}{{\dot u}_{\rm{p}}} + {k_{\rm{p}}}\left( {{u_{\rm{p}}} - u} \right) + {c_{\rm{p}}}\left( {{{\dot u}_{\rm{p}}} - {\rm{d}}u/{\rm{d}}t} \right) = 0,\\ \end{array} $ | (1) |
式中:mp、kp、cp为人体动力参数。Felipe等[11]对20个行人利用加速度传感器对行人的走行情况进行试验研究,将得到的每个行人的加速度以及对应的人行荷载取前三阶幅值,通过求解相应的方程得到每个行人的人体动力参数,将参数进行统计分析得出行人步频、质量与人体动力学参数的相关关系,拟合出关于行人步频、质量的人体参数回归表达式,其中
| $ \left. \begin{array}{l} {m_{\rm{p}}} = 97.082 + 0.275M - 37.518{f_{\rm{p}}},\\ {c_{\rm{p}}} = 29.041m_{\rm{p}}^{0.883},\\ {k_{\rm{p}}} = 30\;351.744 - 50.261{c_{\rm{p}}} + 0.035c_{\rm{p}}^2, \end{array} \right\} $ | (2) |
式中:M为行人实际质量,fp为行走频率。
注意到du/dt=∂u/∂t+v∂u/∂x,第一项表示荷载所在位置梁的振动速度;第二项表示由于荷载的移动,使其在人行桥振动过程中引起了的斜率上移动而产生的附加速度。由于人行走速度较低和一般人行桥在活载作用下变形斜率很小,这一项可忽略不计。式 (1) 可写成
| $ \begin{array}{*{20}{l}} {{m_{\rm{p}}}{{\ddot u}_{\rm{p}}} + {k_{\rm{p}}}\left( {{u_{\rm{p}}} - u} \right) + {c_{\rm{p}}}\left( {{{\dot u}_{\rm{p}}} - \partial u/\partial t} \right) = 0} \end{array}。 $ | (3) |
人行桥的受力包括:行人重力F′G=mpg、惯性力F′I=mpd2/dt2、弹性力F′S=kp(up/u)、阻尼力F′D=cp(
| $ {F_{\rm{p}}} = G\sum\limits_i {{\alpha _i}\sin \left( {2\pi i{f_{\rm{p}}}t - {\theta _i}} \right)} , $ | (4) |
式中:G为行人体重,一般取750 N;αi为动载因子;fp为行走步频;θi为相位角,一般取0。动载因子一般取前三阶,如式 (5) 所示。
| $ \left. \begin{array}{l} {\alpha _1}\left( {{f_{\rm{p}}}} \right) = - 0.27f_{\rm{p}}^3 + 1.32f_{\rm{p}}^2 - 1.76{f_{\rm{p}}} + 0.76,\\ {\alpha _2} = 0.07,\\ {\alpha _3} = 0.06。 \end{array} \right\} $ | (5) |
则人行桥所受的荷载,可表示为
| $ F = \delta \left( {x - vt} \right)\left( {{{F'}_G} - {{F'}_1} + {{F'}_{\rm{S}}} + {{F'}_{\rm{D}}} + {F_{\rm{p}}}} \right)。 $ | (6) |
人行桥动力平衡方程可表示为
| $ m\frac{{{\partial ^2}u}}{{\partial {t^2}}} + c\frac{{\partial u}}{{\partial t}} + EI\frac{{{\partial ^4}u}}{{\partial {x^4}}} = \delta \left( {x - vt} \right)\left[ {{m_{\rm{p}}}g + {k_{\rm{p}}}\left( {{u_{\rm{p}}} - u} \right) + c\left( {{{\dot u}_{\rm{p}}} - \partial u/\partial t} \right) + {F_{\rm{p}}}} \right], $ | (7) |
将
| $ \left. \begin{array}{l} {F_m} = {F_{m1}} + {F_{m2}},\\ {F_{m1}} = \int_0^L {\delta \left( {x - vt} \right)\left( {{m_{\rm{p}}}g + {F_{\rm{p}}}} \right){\varphi _m}{\rm{d}}x,} \\ {F_{m2}} = \int_0^L {\delta \left( {x - vt} \right)\left\{ {{k_{\rm{p}}}{u_{\rm{p}}} + {c_{\rm{p}}}{{\dot u}_{\rm{p}}} - \sum\limits_{n = 1}^\infty {\left[ {{k_{\rm{p}}}{y_n} + {c_{\rm{p}}}{{\dot y}_n}} \right]} {\varphi _n}} \right\}{\varphi _m}{\rm{d}}x。} \end{array} \right\} $ | (8) |
人行桥的动力平衡方程可化为
| $ \begin{array}{l} {m_n}{{\ddot y}_n} + 2{\xi _n}{\omega _n}{m_n}{{\dot y}_n} + {c_{\rm{p}}}\sum\limits_{m = 1}^\infty {{{\dot y}_m}{\varphi _m}{\varphi _n}} + {m_n}\omega _n^2{y_n} + \\ {k_{\rm{p}}}\sum\limits_{m = 1}^\infty {{y_m}{\varphi _m}{\varphi _n}} - {\varphi _n}\left( {{k_{\rm{p}}}{u_{\rm{p}}} + {c_{\rm{p}}}{{\dot u}_{\rm{p}}}} \right) = {\varphi _n}\left( {{m_{\rm{p}}}g + {F_{\rm{p}}}} \right)。 \end{array} $ | (9) |
式中:mn、ξn、ωn=2πfn为模态质量、模态阻尼比和模态圆频率。
1.3 人-桥竖向动力相互作用控制方程行人所在位置人行桥的位移也用振型叠加表示,即
| $ {m_{\rm{p}}}{\ddot u_{\rm{p}}} + {c_{\rm{p}}}{\dot u_{\rm{p}}} + {k_p}{u_{\rm{p}}} - {c_{\rm{p}}}\sum\limits_{n - 1}^\infty {{{\dot y}_n}{\varphi _n}} - {k_{\rm{p}}}\sum\limits_{n - 1}^\infty {{y_n}{\varphi _n}} = 0。 $ | (10) |
将式 (9) 和式 (10) 联立,就得到人-桥竖向动力相互作用控制方程组,该动力系统是时变系统,写成如 (11) 的矩阵形式。
| $ \mathit{\boldsymbol{M\ddot{y}}}+\mathit{\boldsymbol{C\dot{y}}}+\mathit{\boldsymbol{Ky}}=\mathit{\boldsymbol{F}}, $ | (11) |
式中:质量矩阵M、刚度矩阵K和阻尼矩阵C如式 (12) 所示。
| $ \mathit{\boldsymbol{M}} = \left( {\begin{array}{*{20}{c}} {{m_1}}&0& \cdots &0&0\\ 0&{{m_2}}& \cdots &0&0\\ \vdots&\vdots&\vdots&\vdots&\vdots \\ 0&0& \cdots &{{m_N}}&0\\ 0&0&0&0&{{m_{\rm{p}}}} \end{array}} \right), $ | (12a) |
| $ \mathit{\boldsymbol{K = }}\left( {\begin{array}{*{20}{c}} {{K_{11}}}&{{K_{12}}}&{ \cdot \cdot \cdot }&{{K_{1N}}}&{ - {k_{\rm{p}}}{\varphi _1}}\\ {{K_{21}}}&{{K_{22}}}&{ \cdot \cdot \cdot }&{{K_{2N}}}&{ - {k_{\rm{p}}}{\varphi _2}}\\ \vdots&\vdots&\vdots&\vdots&\vdots \\ {{K_{N1}}}&{{K_{N2}}}&{ \cdot \cdot \cdot }&{{K_{NN}}}&{ - {k_{\rm{p}}}{\varphi _N}}\\ { - {k_{\rm{p}}}{\varphi _1}}&{ - {k_{\rm{p}}}{\varphi _2}}& \cdots &{ - {k_{\rm{p}}}{\varphi _N}}&{ - {k_{\rm{p}}}} \end{array}} \right), $ | (12b) |
| $ \mathit{\boldsymbol{C = }}\left( {\begin{array}{*{20}{c}} {{C_{11}}}&{{C_{12}}}&{ \cdot \cdot \cdot }&{{C_{1N}}}&{ - {c_{\rm{p}}}{\varphi _1}}\\ {{C_{21}}}&{{C_{22}}}&{ \cdot \cdot \cdot }&{{C_{2N}}}&{ - {c_{\rm{p}}}{\varphi _2}}\\ \vdots&\vdots&\vdots&\vdots&\vdots \\ {{C_{N1}}}&{{C_{N2}}}&{ \cdot \cdot \cdot }&{{C_{NN}}}&{ - {c_{\rm{p}}}{\varphi _N}}\\ { - {c_{\rm{p}}}{\varphi _1}}&{ - {c_{\rm{p}}}{\varphi _2}}& \cdots &{ - {c_{\rm{p}}}{\varphi _N}}&{ - {c_{\rm{p}}}} \end{array}} \right), $ | (12c) |
式中,Cii=2ξiωimi+cpφiφi,Kii=ωi2mi+kpφiφi,i=1, 2, …N,Cij=cpφiφj,Kij=kpφiφj,i, j=1, 2, …N且i≠j。
式 (11) 中F为广义力向量,y为广义位移向量即
| $ $$\mathit{\boldsymbol{F}} = {\left[ {{\rho _F}{\varphi _1},{\rho _F}{\varphi _2}, \cdots {\rho _F}{\varphi _N},0} \right]^{\rm{T}}},$$ $ | (13) |
| $ $$\mathit{\boldsymbol{y}} = {\left[ {{y_1},\;\;{y_2},\;\; \cdots \;\;{y_N}\;\;{u_{\rm{p}}}} \right]^{\rm{T}}},$$ $ | (14) |
式中,ρF=mpg+Fp(t)。由于行人在人行桥上行走,K、C和F都在不断变化,成为一个时变的微分方程组。对于这样的时变的微分方程组,笔者基于MATLAB计算仿真平台,利用变步长四阶五级Runge-Kutta-Felhberg算法求解。
1.4 人-桥竖向动力相互作用模态分析人-桥竖向动力相互作用耦合系统中,由于结构阻尼较低,人体阻尼较高,使得人-桥耦合系统的阻尼为非比例阻尼,笔者采用状态空间方法进行瞬时模态的求解[15]。定义以下变量:
| $ $$A = \left[ {\matrix{ 0&I \cr { - {M^{ - 1}}K}&{ - {M^{ - 1}}C} \cr } } \right]。$$ $ | (15) |
通过求解特征值,可得到系统的模态特性,见式 (16):
| $ A\varphi = \lambda \varphi 。 $ | (16) |
第i阶频率fi和阻尼比ξi可由式 (17) 确定:
| $ {f_i} = \frac{{\left| {{\lambda _i}} \right|}}{{2\pi }};{\xi _i} = \frac{{{\mathop{\rm Re}\nolimits} \left( {{\lambda _i}} \right)}}{{\left| {{\lambda _i}} \right|}}。 $ | (17) |
本文算例取自文献[16]提供的由FRP材料制作成的斜拉轻质人行桥。该桥全长为113 m,主跨为63 m,该桥全重20 000 kg。在文献[16]中把该人行桥主跨部分近似为简支梁,在本算例中沿用这一做法。该人行桥实测得到的竖向前两阶模态参数为:f1=1.52 Hz, ξ1=0.42%, m1=2 750 kg,f2=1.86 Hz, ξ2=0.70%, m2=3 600 kg。
图 2所示为行人以1.74 Hz的步频通过人行桥时,系统瞬时频率变化情况,可以看出结构瞬时频率与空载时相比略有减少,而人体频率有增大趋势。结构一阶瞬时频率在一阶振型顶点处达到最小值,结构二阶瞬时频率在二阶振型两个顶点处达到最小值,行人的瞬时频率的两个峰值介于结构一阶振型和二阶振型顶点之间。这与早期的研究发现行人行走不改变结构的频率结果不一致[17],而与近期的研究结果吻合[18]。
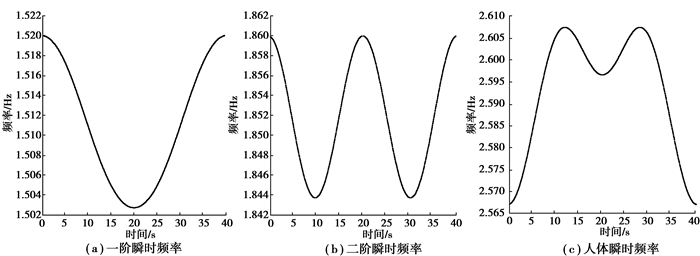
|
图 2 系统瞬时频率 Figure 2 Vibration frequencies of the pedestrian-bridge dynamic interaction system |
图 3所示为行人以1.74 Hz的步频通过人行桥时,系统瞬时阻尼变化情况,可以看出与空载时相比,均呈增大趋势。结构瞬时阻尼均在相应振型峰值点处达到最大值,类似于TMD减振器,放置在相应振型峰值点处,可得到最佳减振效果;人体最大阻尼出现在结构一阶振型峰值点处。
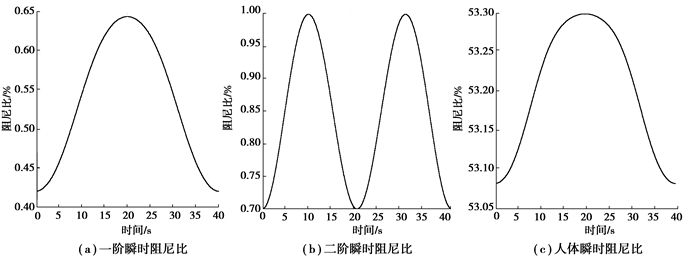
|
图 3 系统瞬时阻尼比 Figure 3 Damping ratio of the pedestrian-bridge dynamic interaction system |
图 4所示为结构动力特性随行人行走步频的变化率,变化率定义为考虑人-桥相互作用时的动力特性 (频率、阻尼比) 极值与空载时值的差值再与空载时值的比值。从图 4中可以看出,考虑人-桥相互作用,人行桥自振频率都有所降低,一阶频率的变化率绝对值要比二阶的值要大,频率变化率的绝对值随着行走步频的增大而减少,但变化率总体很少;考虑人-桥相互作用时结构阻尼比均有显著增加,一阶阻尼比的变化率绝对值要比二阶的值大,变化率也随着行走步频的增大而减少。
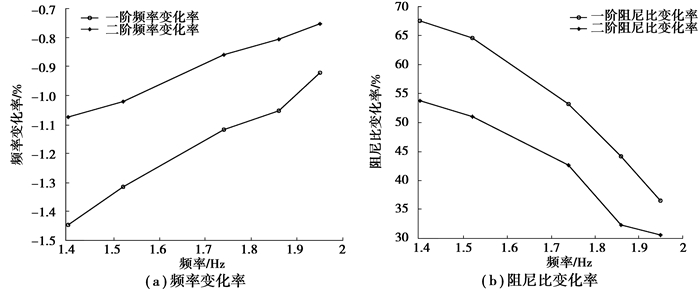
|
图 4 结构频率和阻尼比变化率 Figure 4 Change rate of vibration frequencies and damping ratio |
图 5所示为行人以1.52、1.70、1.86 Hz的步频通过时人行桥的加速度时程曲线。其中当行人以与结构的一阶频率1.52 Hz相等的步频通过该桥时,只是在人行荷载作用下该桥的加速度峰值为3.36 m/s2,考虑人-桥相互作用时的加速度峰值为2.35 m/s2,比只是在人行荷载作用下降低30.7%;当行人以与结构的二阶频率1.86 Hz相等的步频通过该桥时,只是在人行荷载作用下的加速度峰值为2.32 m/s2,考虑人-桥相互作用时的加速度峰值为1.98 m/s2,比只是在人行荷载作用下降低14.7%;当行人以处在结构一阶频率和二阶频率之间的1.70 Hz的步频通过该桥时,只是在人行荷载作用下加速度峰值为0.39 m/s2,考虑人-桥相互作用时的加速度峰值为0.34 m/s2,比只是在人行荷载作用下降低12.4%。根据文献[2],加速度峰值为0.35 m/s2取为振动舒适度限值,可知行人以结构一阶频率和二阶频率相等的步频通过人行桥时,无论是否考虑人-桥相互作用,加速度峰值都远超振动舒适度限值,而当行人以1.70 Hz的步频通过该桥时,只是在人行荷载作用下评估结果会出现振动舒适度问题,考虑人-桥相互作用则不会引起振动舒适度问题。
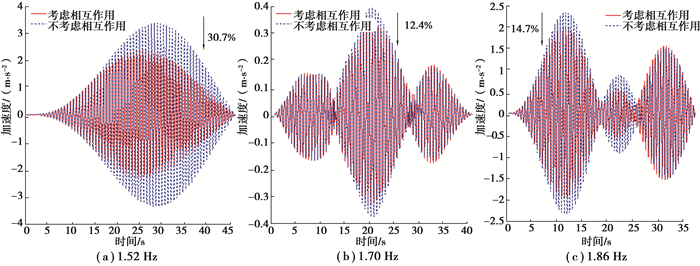
|
图 5 不同行走下步频人行桥的加速度时程曲线 Figure 5 Acceleration of the bridge at different walkingfrequency |
图 6所示为行人以1.52、1.70、1.86 Hz的步频通过,人行桥加速度时程的傅立叶谱曲线。由图 6可以看出,当行人以与结构一阶频率1.52 Hz相等的步频通过该桥时,引起该桥一阶频率共振,在其步频倍频处亦有较小振动;当行人以与结构二阶频率1.86 Hz相等的步频通过该桥时,人行桥的加速度时程的傅立叶谱值在1.807、1.855、1.904 Hz处较大,其中1.855 Hz与行人步频十分接近,而1.807 Hz和1.904 Hz可以看成由行人类似于TMD减振器分解而成,降低了共振时傅立叶谱峰值;当行人以处在结构一阶频率和二阶频率之间的1.70 Hz的步频通过该桥时,激起人行桥一阶频率振动量较小,其步频的倍频处也有一定的振动谱值,
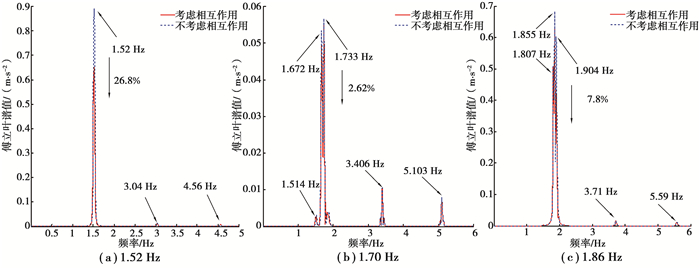
|
图 6 不同行走步频下人行桥加速度时程傅立叶谱曲线 Figure 6 Fourier spectrum of acceleration at different walking frequency |
而傅立叶谱峰值谱的峰值主要出现在1.672 Hz和1.733 Hz处,实际上这是行人类似于TMD减振器把步频1.70 Hz谱峰值分解而成。从图 6中还可以看出考虑人-桥相互作用与不考虑人-桥相互作用傅立叶谱值有不同程度减小。
图 7所示为不同步频下考虑人-桥动力相互作用与只在人行荷载作用下加速度峰值变化率,变化率定义为只在人行荷载作用下结构加速度峰值与考虑相互作用加速度峰值的差值与只在人行荷载作用下加速度峰值的比值。从图 7中可以看出当行人步频与人行桥频率相等时,考虑人-桥相互作用加速度峰值要比不考虑相互作用时显著减小,这与现场测试结果吻合[18];而当行人以其它步频行走时,考虑人-桥相互作用加速度峰值与只在人行荷载作用下的值相比不确定。行人实际上类似与TMD减振器,当TMD的频率与结构频率一致时,有较好的减振效果,若TMD参数取值不合适,非但没有减振效果,反而会增大结构振动。
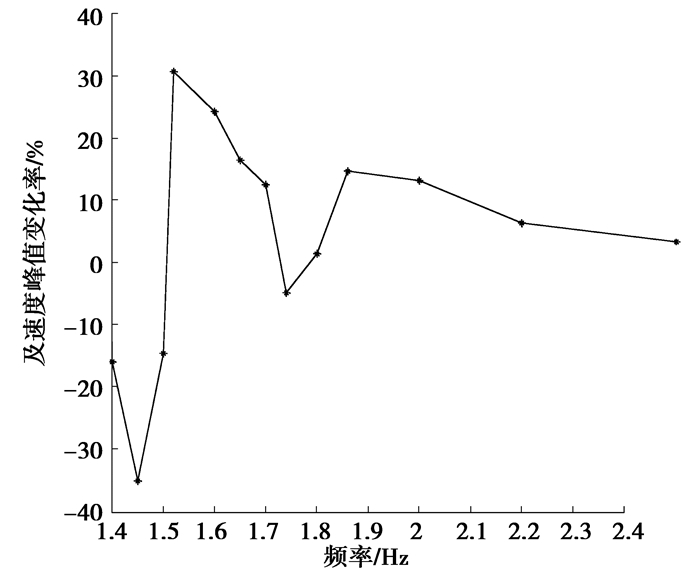
|
图 7 不同步频下人行桥加速度峰值变化率 Figure 7 Acceleration peak change rate of bridge at different walking frequency |
1) 考虑人-桥动力相互作用,行人在通过人行桥过程中,系统的频率和阻尼是时变的,这与早期的研究认为行人行走不改变动力特性结果不一致,而与近期的研究结果一致;由于人体是高阻尼的动力系统,考虑人-桥相互作用后,结构的阻尼比比不考虑人-桥相互作用显著增加,但结构的频率比不考虑人结构相互作用略有降低,变化率均随着行走步频的增大而减少。
2) 在考虑人-桥动力相互作用人行桥的时变频率和阻尼,在行人行至其相应振型顶点处达到极值,这一结论类似把行人看成TMD减振器,把TMD安置到振型顶点处得到较好的减振率。
3) 当行人的行走频率与结构频率一致时,考虑人结构相互作用结构的动力响应比只在人行荷载作用显著降低,与实测结果一致,行人类似于TMD减振器,把共振时的谱值分解成与共振频率相邻两个频率上较小的谱峰值;而当行人以其它步频行走时,考虑人-桥相互作用加速度峰值与只在人行荷载作用的值相比不确定,类似于TMD减振器,如果取的参数不合适,非但没有减振效果,反而会增大结构振动。
4) 这里主要研究了单人-桥竖向动力相互作用,对于随机人群人行桥竖向动力相互作用有待在后续工作中进行。
| [1] | Živanović S, Pavić A, Reynolds P. Probability-based prediction of multi-mode vibration response to walking excitation[J]. Engineering Structures, 2007, 29(6): 942–954. |
| [2] |
冯鹏, 金飞飞, 叶列平, 等.
人行天桥结构振动舒适度定量化与振动特性实测研究[J]. 振动工程学报, 2013, 26(4): 545–553.
FENG Peng, JING Feifei, YE Lieping, et al. Quantification of pedestrian's comfort level and dynamic properties of footbridge vibration based on in-situ measurement[J]. Journal of Vibration Engineering, 2013, 26(4): 545–553. (in Chinese) |
| [3] | Caetano E, CunhaÁ, Moutinho C, et al. Studies for controlling human-induced vibration of the Pedro e Inês footbridge, Portugal. Part 2: Implementation of tuned mass dampers[J]. Engineering Structures, 2010, 32(4): 1082–1091. DOI:10.1016/j.engstruct.2009.12.033 |
| [4] | BS Institute. Steel, concrete and composite bridges. Specification for loads, BS 5400: Part 2[M]. London: British Standard Institution, 1978. |
| [5] | da Silva F T, Brito H M B F, Pimentel R L. Modeling of crowd load in vertical direction using biodynamic model for pedestrians crossing footbridges[J]. Canadian Journal of Civil Engineering, 2013, 40(12): 1196–1204. DOI:10.1139/cjce-2011-0587 |
| [6] |
王海, 周叮, 王曙光.
人-梁相互作用动力学模型研究[J]. 工程力学, 2010, 27(5): 14–20.
WANG Hai, ZHOU Ding, WANG Shuguang. Modeling of the dynamicinteraction of human occupants and beam[J]. Engineering Mechanics, 2010, 27(5): 14–20. (in Chinese) |
| [7] |
何卫, 谢伟平, 刘隆.
人板耦合系统动力特性研究[J]. 工程力学, 2013, 30(1): 295–300.
HE Wei, XIE Weiping, LIU Long. Study on dynamic characteristics of human-floor interaction system[J]. Engineering Mechanics, 2013, 30(1): 295–300. (in Chinese) |
| [8] |
李红利, 陈政清.
人-桥竖向动力相互作用效应理论与试验研究[J]. 土木工程学报, 2014, 47(6): 78–87.
LI Hongli, CHEN Zhengqing. Analytical and experimental study on vertically dynamic interaction between human and bridge[J]. China Civil Engineering Journal, 2014, 47(6): 78–87. (in Chinese) |
| [9] |
秦敬伟, 杨庆山.
基于双足步行模型和反馈机制的人体-结构相互作用[J]. 建筑结构学报, 2014, 35(s1): 18–24.
QIN Jingwei, YANG Qingshan. Human-structure interaction based on bipedal walking model and feedback mecha-nism[J]. Journal of Building Structures, 2014, 35(s1): 18–24. (in Chinese) |
| [10] | Kim S H, Cho K I, Choi M S, et al. Development of human body model for the dynamic analysis of footbridges under pedestrian induced excitation[J]. International Journal of Steel Structures, 2008, 8(4): 333–345. |
| [11] | Silva F T, Pimentel R. Biodynamic walking model for vibration serviceability of footbridges in vertical direction[C]//EURODYN 2011 Proceedings of the 8th International Conference on Structural Dynamics. Leuven, Belgium. 2011: 1090-1096. |
| [12] | Pfeil M, Amador N, Pimentel R, et al. Analytic-numerical model for walking person-footbridge structure interaction[C]//Proceedings of the 9th International Conference on Structural Dynamics, EURODYN 2014, Porto, Portugal. Portugal: [s. n. ], 2014: 1079-1085. |
| [13] | Dang H V, Živanović S. Modellingpedestrian interaction with perceptibly vibrating footbridges[J]. FME Transactions, 2013, 41(4): 271–278. |
| [14] | Kerr S C, Bishop N W M. Human induced loading on flexible staircases[J]. Engineering Structures, 2001, 23(1): 37–45. DOI:10.1016/S0141-0296(00)00020-1 |
| [15] | Juang J N. Applied system identification[M]. Englewood Cliffs, NJ, USA: Prentice Hall, 1994. |
| [16] | Živanović S. Probability-based estimation of vibration for pedestrian structures due to walking[D]. Sheffield, England: The University of Sheffield, 2006. |
| [17] | Ellis B R. Human-structure interaction in vertical vibrations[J]. Proceedings of the ICE-Structures and Buildings, 1997, 122(1): 1–9. |
| [18] | Gomez D, Silva C E, Dyke S J, et al. Interactiveplatform to include human-structure interaction effects in the analysis of footbridges[M]//Caicedo J, Pakzad S. Dynamics of Civil Structures, Volume 2. [S. l. ]: Springer International Publishing, 2015: 59-65. |
 2017, Vol. 40
2017, Vol. 40

