粒子群优化算法(particle swarm optimization, PSO)是1995年由Eberhart和Kennedy提出一种模拟鸟群捕食行为的群智能优化算法[1-2]。PSO具有操作简单,可调参数少的优点,目前已广泛应用于函数优化、神经网络训练、模糊系统控制以及其他相关的工程应用领域[3-4]。关于PSO性能的改进,目前主要有以下几种策略:一是基于算法参数的选择[5-7];二是基于粒子位置及速度的更新规则[8-9];三是与其它算法的融合,如混沌PSO[10]、模糊PSO[11]、多子群PSO[12]、模拟退火PSO[13]等。四是赋予粒子新特性,例如文献[14]提出一种基于非均匀变异和多阶段扰动的粒子群优化算法;文献[15]在改进的算法中建立了一种新的粒子群模型,在该模型中的粒子具有视野受阻且认知自身目标的特性;文献[16]提出一种基于粒子分类和按维动态改变权重的改进粒子群算法。以上这些改进中,比较典型的是对于惯性因子的改进。文献[17]详细考察了惯性因子的各种取值对算法性能的影响,文献[18]研究了动态惯性因子(随迭代步数线性或非线性下降)对性能的影响,这些改进使PSO性能均有不同程度的提高。
为了进一步提高PSO的优化能力,研究从粒子群初始化方法、惯性因子的动态更新策略、粒子的速率更新式、位置的越界处理4个方面,提出相应的改进措施,以期提高传统PSO的优化性能。采用50个不同类型和维度的标准测试函数作为优化对象,并通过与其他同类方法对比,结果验证了提出方法的有效性。
1 基本粒子群算法设在n维空间中的N个粒子组成一个种群。其中,第i个粒子位置Xi、速度Vi、自身搜索到的最优位置PiL、整个种群搜索到的最优位置Pg分别记为:Xi=(xi1, …, xin);Vi=(vi1, …, vin);PiL=(pi1, …, pin);Pg=(pg1, …, pgn)。将Xi代入目标函数可计算其目标值。种群的初始化方法为Xij=Xmin, j+(Xmax, j-Xmin, j)× rand,rand为在区间(0, 1) 均匀分布的随机数,粒子的更新策略为
| ${V_i}\left( {t + 1} \right) = w{V_i}\left( t \right) + {c_1}{r_1}(P_i^L - {X_i}\left( t \right)) + {c_2}{r_2}({P_g} - {X_i}\left( t \right)),$ | (1) |
| ${X_i}\left( {t + 1} \right) = {X_i}\left( t \right) + {V_i}\left( {t + 1} \right),$ | (2) |
其中i=1, 2, …, N;w为惯性因子;c1为自身因子;c2为全局因子;r1、r2是(0, 1) 之间随机数。对种群中每个粒子应用式(1)、(2) 循环迭代,可使整个种群逐步逼近全局最优解。为便于叙述,将式(1) 重写为如下形式
| ${V_i}\left( {t + 1} \right) = w{V_i}\left( t \right) + \left[ \mathit{\Phi } \right]({P_i} - {X_i}\left( t \right)),$ | (3) |
其中
| ${P_i} = {\rm{diag}}\left( {\frac{{{c_1}r_1^1}}{{{c_1}r_1^1 + {c_2}r_1^2}}, \cdots ,\frac{{{c_1}r_n^1}}{{{c_1}r_n^1 + {c_2}r_n^2}}} \right)P_i^L + {\rm{diag}}\left( {\frac{{{c_2}r_1^2}}{{{c_1}r_1^1 + {c_2}r_1^2}}, \cdots ,\frac{{{c_2}r_n^2}}{{{c_1}r_n^1 + {c_2}r_n^2}}} \right){P_g},$ | (4) |
| $\left[ \mathit{\Phi } \right] = {\rm{diag}}({c_1}r_1^1 + {c_2}r_1^2, \ldots ,{c_1}r_n^1 + {c_2}r_n^2),$ | (5) |
为使PSO收敛,所有粒子应逼近式(4) 定义的Pi。
2 改进的粒子群算法笔者提出的改进粒子群优化(improved pso, IPSO),其改进措施主要针对如下4个方面:粒子群初始化、惯性因子、速率更新、位置越界。
2.1 粒子群初始化优化过程,实质上是在解空间搜索最优解的过程,群智能优化的优势在于,群体成员相互协作共同向着最优解逼近,即“围攻”最优解。因此,种群初始位置的设置就在一定程度上影响着搜索的进程,传统的按均匀分布随机生成初始位置的方法,简单易行,但不利于形成对最优解的“包围”。为使初始位置有效包围最优解,提出基于Beta分布的种群初始化方法。
Beta分布函数的定义为
| $\beta \left( x \right) = \frac{{{x^{a - 1}}{{\left( {1 - x} \right)}^{b - 1}}}}{{B\left( {a,b} \right)}},0 < x < 1,$ | (6) |
其中分母是β函数,定义如下
| $B\left( {a,b} \right) = \int_0^1 {{t^{a - 1}}} {\left( {1 - t} \right)^{b - 1}}{\rm{d}}t,$ | (7) |
其中a=b < 1。
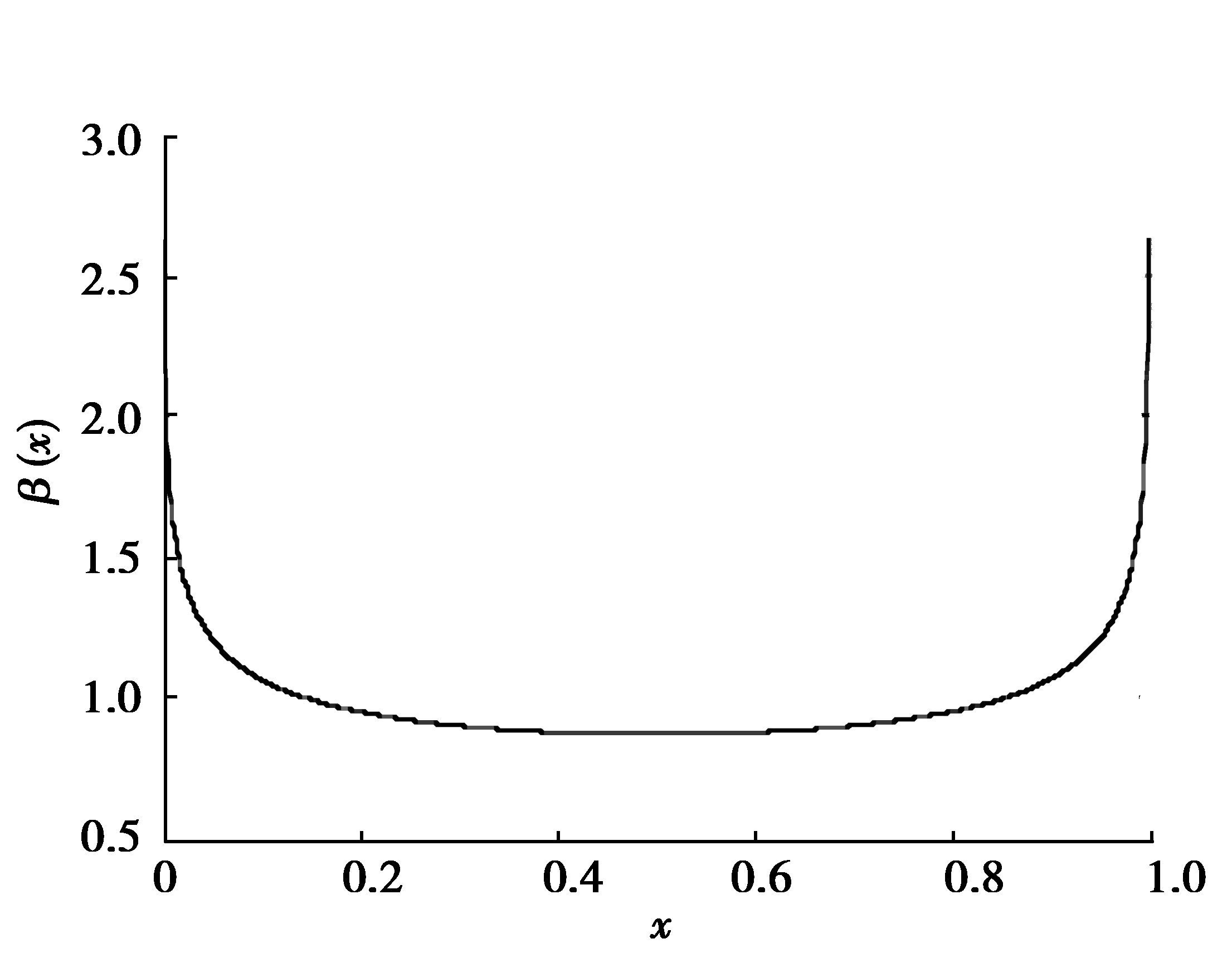
在这种情况下,密度函数的形状是一个对称的U型。此时有这样的结果,候选解最有可能位于搜索空间的边界附近,因此全局最优解被较好的“包围”在初始粒子种群内。大量实验表明,当a=b=0.8时,初始化效果较好,此时该分布在区间(0, 1) 的概率密度函数图像如图 1所示。
|
图 1 Beta分布函数图像(a=b=0.8) Figure 1 Beta distribution function with a=b=0.8 |
令粒子个数为N,优化空间为D维,初始化后的候选解为Xi。根据β概率分布对Xi的每一维按下式赋初值。
| ${X_{ij}} = {X_{min,j}} + ({X_{max,j}} - {X_{min,j}}) \times {\rm{betarnd}}\left( {a,b,1,1} \right),$ | (8) |
其中i=1, 2, …, N; j=1, 2, …, D,betarnd为MATLAB中产生Beta分布随机数的内置函数。
在普通PSO粒子初始化方法中,采用均匀分布的随机数,此时的初始化结果近似在搜索空间中均匀赋初值,不利于形成对最优解的包围,而基于Beta分布的种群初始化方法克服了这一不足。
2.2 惯性因子的设计在PSO中,惯性因子对算法性能具有重要影响,若惯性因子大于1,将很快导致算法发散,若惯性因子小于0,将很快导致算法停滞。通常在算法初期,主要关注全局探索,这时需要使搜索过程迈大步,以实现大范围寻优,因此惯性因子应较大;而在算法后期,主要侧重局部开发,此时需要使搜索过程迈小步,以避免错过全局最优解,此时惯性因子应较小。为合理实现探索和开发两阶段的平衡,提出基于逆不完全伽马函数的惯性因子调整方法。下面首先给出逆不完全伽马函数的定义及特性。
不完全伽马函数
|
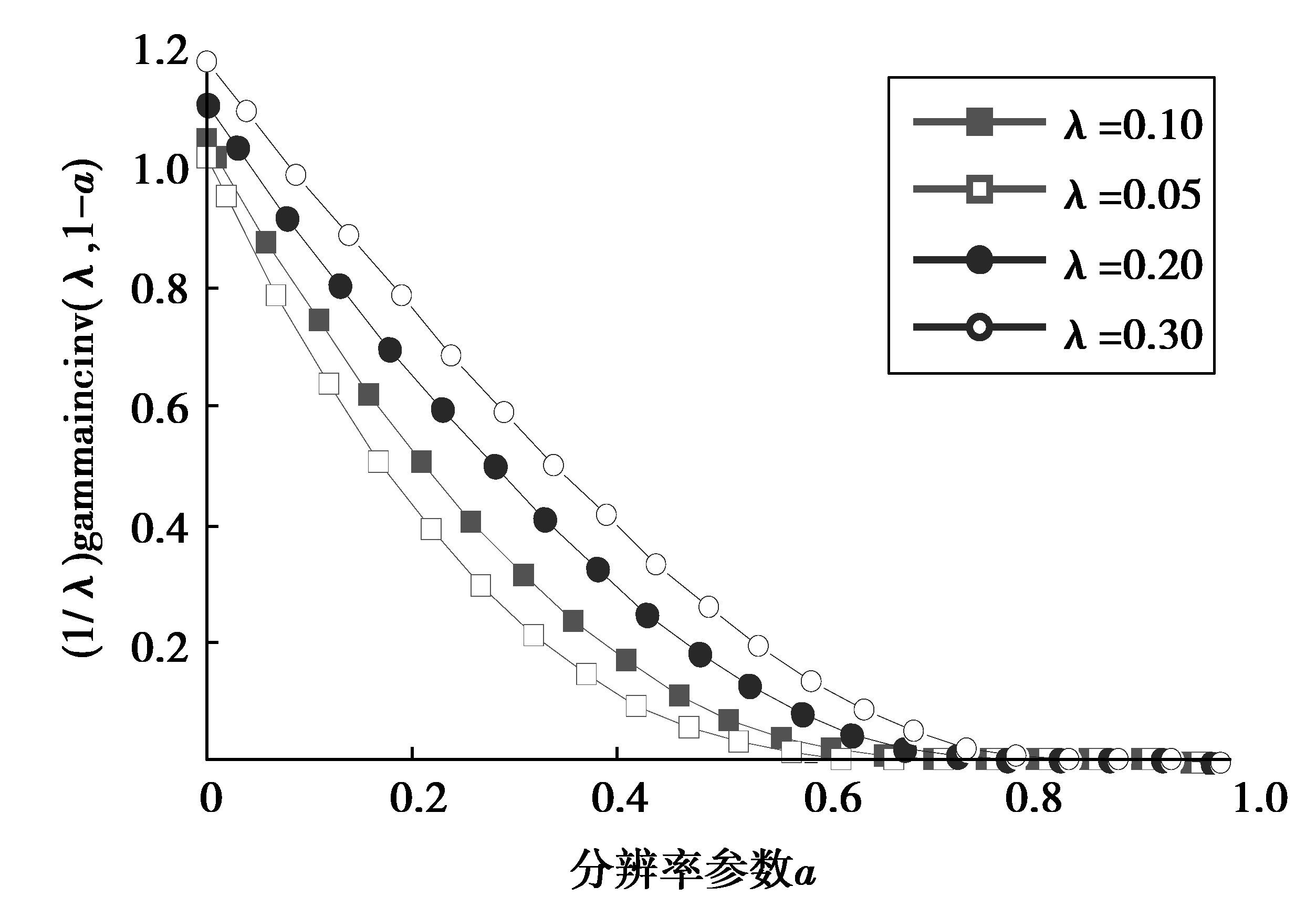
图 2 (1/λ)gammaincinv(λ, 1-a)在a∈(0, 1]时的特性 Figure 2 The characteristics of (1/λ) gammaincinv(λ, 1-a) |
从图 2可以得到这样的启示,若使λ取定值,而使a随迭代步数以等步长Δa从0线性增加到1,则(1/λ)gammaincinv(λ, 1-)具有从略大于1单调下降到接近于0的特性,这恰好符合对于调整惯性因子的要求。
经过初步探索,取λ=0.1,a=t/MaxItr,其中t为当前迭代步数,MaxItr为限定迭代步数。此时逆不完全伽马函数具有这样一个优良特性:在迭代步数的前一半,接近线性下降,而在后一半,接近指数下降。用这样的函数来动态调整惯性因子,能够较好地实现探索与开发之间的平衡,进而有效避免早熟收敛[19]。
根据以上思路,惯性因子的调整方法可表述为下式。
| $w\left( t \right) = {w_{{\rm{min}}}} + \frac{{{w_{{\rm{max}}}} - {w_{{\rm{min}}}}}}{\lambda }{\rm{gammaincinv}}\left( {\lambda ,1 - \frac{t}{{{\rm{MaxItr}}}}} \right),$ | (9) |
式中,wmax, wmin分别为惯性因子最大值和最小值。
在普通粒子群算法速率更新式(1) 中,惯性因子w取定值,或者全程随迭代步数线性下降,就获得探索和开发之间的平衡而言,显然不如基于逆不完全伽马函数的调整方法理想。
2.3 速度更新式的设计对于速率的更新,受差分进化思想启发,引入了一个新算子,该算子可表述为:各自身最优粒子的算术平均值与当前粒子的差,再乘以一个幅度随迭代步数单调下降的随机数,如下式所示。
| ${\delta _i}\left( t \right) = {\left( {1 - \frac{t}{{{\rm{MaxItr}}}}} \right)^\alpha } \times {\rm{rand}} \times \left( {\frac{1}{N}\sum\limits_{i = 1}^N {P_i^L - {X_i}} } \right),$ | (10) |
式中rand为在区间(0, 1) 均匀分布的随机数。
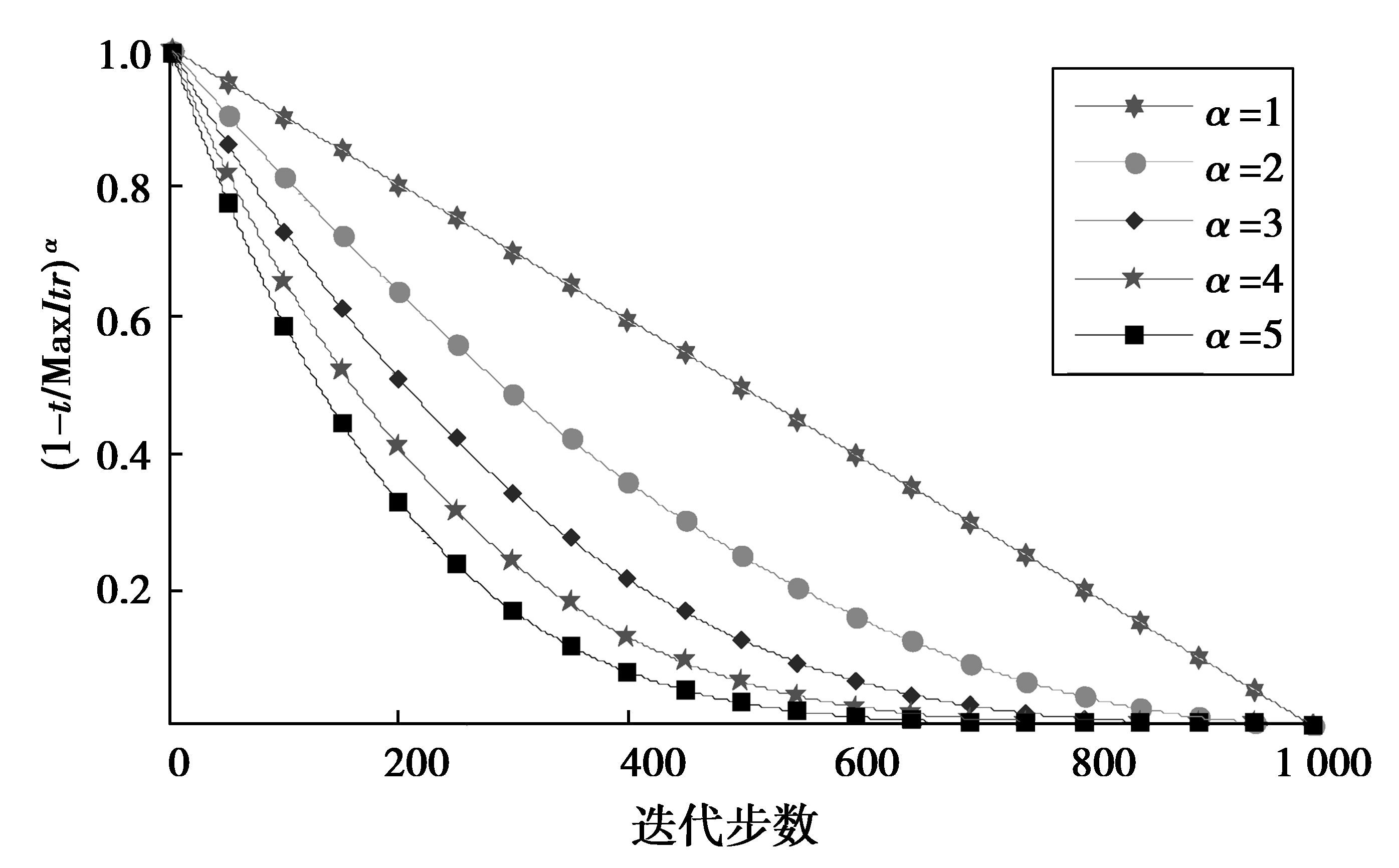
该算子的作用效果与α的取值有关,为便于分析该算子的特性,首先给出(1-t/MaxItr)α在不同α取值下随迭代步数的变化情况,如图 3所示。
|
图 3 不同α取值下(1-t/MaxItr)α的动态特性 Figure 3 The characteristics of (1-t/MaxItr)αunder different α |
由上图可知,在算法的初期,该算子可引领种群向着自身最优粒子的平均值逼近,有利于全局探索;随着迭代步数的增加,该算子的作用指数减小,有利于局部开发,从而可有效实现探索和开发之间的合理平衡。大量实验表明,当α=5时优化性能最佳。因此在后续的数值函数优化中,将该算子的参数固定为α=5。综上所述,改进的速度更新式可表述为下式
| ${V_i}\left( {t + 1} \right) = w\left( t \right){V_i}\left( t \right) + {c_1}{r_1}(P_i^L - {X_i}\left( t \right)) + {c_2}{r_2}({P_g} - {X_i}\left( t \right)) + {\delta _i}\left( t \right)。$ | (11) |
与普通粒子群算法速率更新式(1) 对比可知,改进的速率更新式中增加了一项幅度随迭代步数指数下降的随机项δi(t),该随机项的核心作用在于进一步获得探索和开发之间的合理平衡。
2.4 粒子位置的越界处理目前,在绝大多数群智能优化算法中,个体位置的越界处理均采用“若越出边界,就等于边界”的简单方法,该方法的优点是实现简单,但由于边界点肯定不是全局最优解,因此这种越界处理方式对优化进程不利。
鉴于此,采用了基于边界对称映射的新方法。具体处理方法为:令[Xmin, j, Xmax, j]为第j维寻优区间,若Xij越界,则按下式处理。
| $X{\prime _{ij}} = \left\{ {\begin{array}{*{20}{l}} {{\rm{min}}\left( {{X_{{\rm{max}},j}},2{X_{{\rm{min}},j}} - {X_{ij}}} \right),}&{i{\rm{f}}\;{X_{ij}}{ < _{{\rm{min}},j}},}\\ {{\rm{max}}({X_{{\rm{min}},j}},2{X_{{\rm{max}},j}} - {X_{ij}}),}&{{\rm{if}}\;{X_{ij}} > {X_{{\rm{max}},j}},} \end{array}} \right.$ | (12) |
上述越界处理方法与普通PSO越界处理方法的差别可用图 4直观表示。

|
图 4 基于边界对称映射的越界处理方法 Figure 4 Cross boundary treatment based on symmetry mapping |
尽管对传统PSO进行了多项改进,但就控制参数的个数而言,仅比传统PSO多了2个参数:wmax, wmin。
2.5 终止条件终止条件可设置为精度阈值,即当最优解达到某种精度要求后迭代终止; 也可以设置为限定步数,即当达到限定步数之后,不论是否满足精度要求迭代均终止,研究选择限定步数作为终止条件。
2.6 改进PSO的算法流程笔者提出的改进PSO算法的实施方案如下:
Step1 参数初始化,包括:种群规模,空间维数,全局因子,自身因子,惯性因子的上、下限,限定迭代步数。
Step2 按式(8) 采用Beta分布随机数初始化种群;
Step3 按式(9)、(10) 计算w(t)和δi(t),按式(11) 计算Vi(t+1)),按式(2) 计算Xi(t+1)),按式(12) 执行越界处理,计算目标函数值。
Step4 判断终止条件,若满足则结束,否则转Step3。
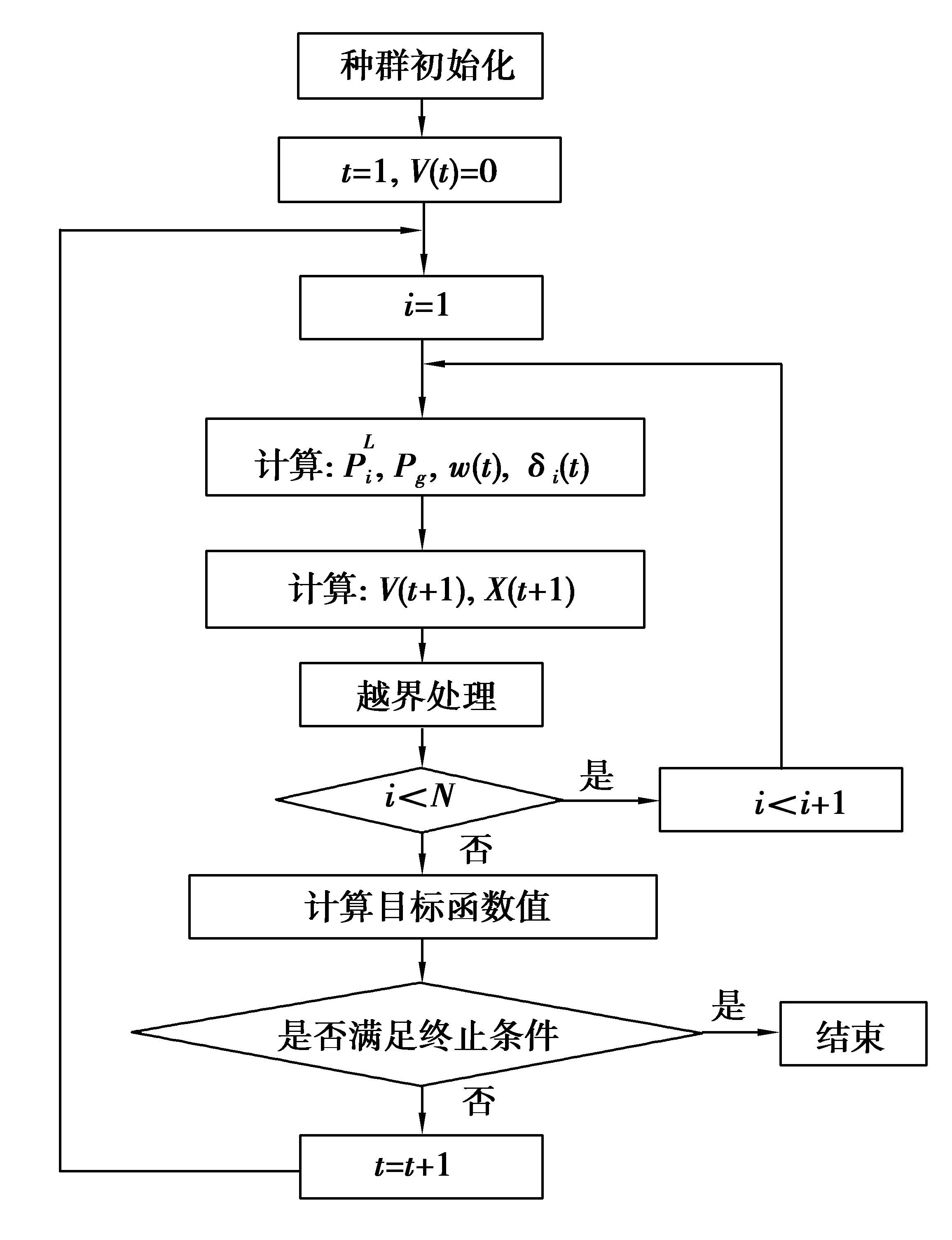
上述流程可用图 5直观描述。
|
图 5 改进PSO的算法流程 Figure 5 Algorithm flow of improved PSO |
为了充分验证提出改进算法的优势,采用了50个标准测试函数,这些测试函数均为极小值优化,每个测试函数的解析表达式、自变量取值范围、参数取值、精确极小值等信息均请参阅文献[20],其中f1-f5为单峰可分离函数(unimodal separable, US);f6-f17为单峰不可分离函数(unimodal non-separable, UN);f18-f26为多峰可分离函数(multimodal separable, MS);f27-f50为多峰不可分离函数(multimodal non-separable, MN)。
3.2 参数设置用上述50个不同类型和维度的标准测试函数作为优化对象,用IPSO与基本PSO、差分进化(DE)、人工蜂群(ABC)和量子行为粒子群(QPSO)算法的优化结果进行对比。为使对比公平,所有算法的种群规模均取50,迭代次数均取1 000。其中基本PSO的控制参数取c1=c2=2.0,惯性因子从0.9到0.4随迭代步数线性减小;IPSO控制参数c1=c2=2.0, 惯性因子最大值wmax=0.9,最小值wmin=0.4;DE的缩放因子取α=0.6,交叉概率取CR=0.8;ABC的控制参数limit=50;QPSO的控制参数取α=0.5。为降低优化结果的随机性,对每个测试函数,分别用5种算法独立优化50次,以50次优化的平均结果作为对比指标。
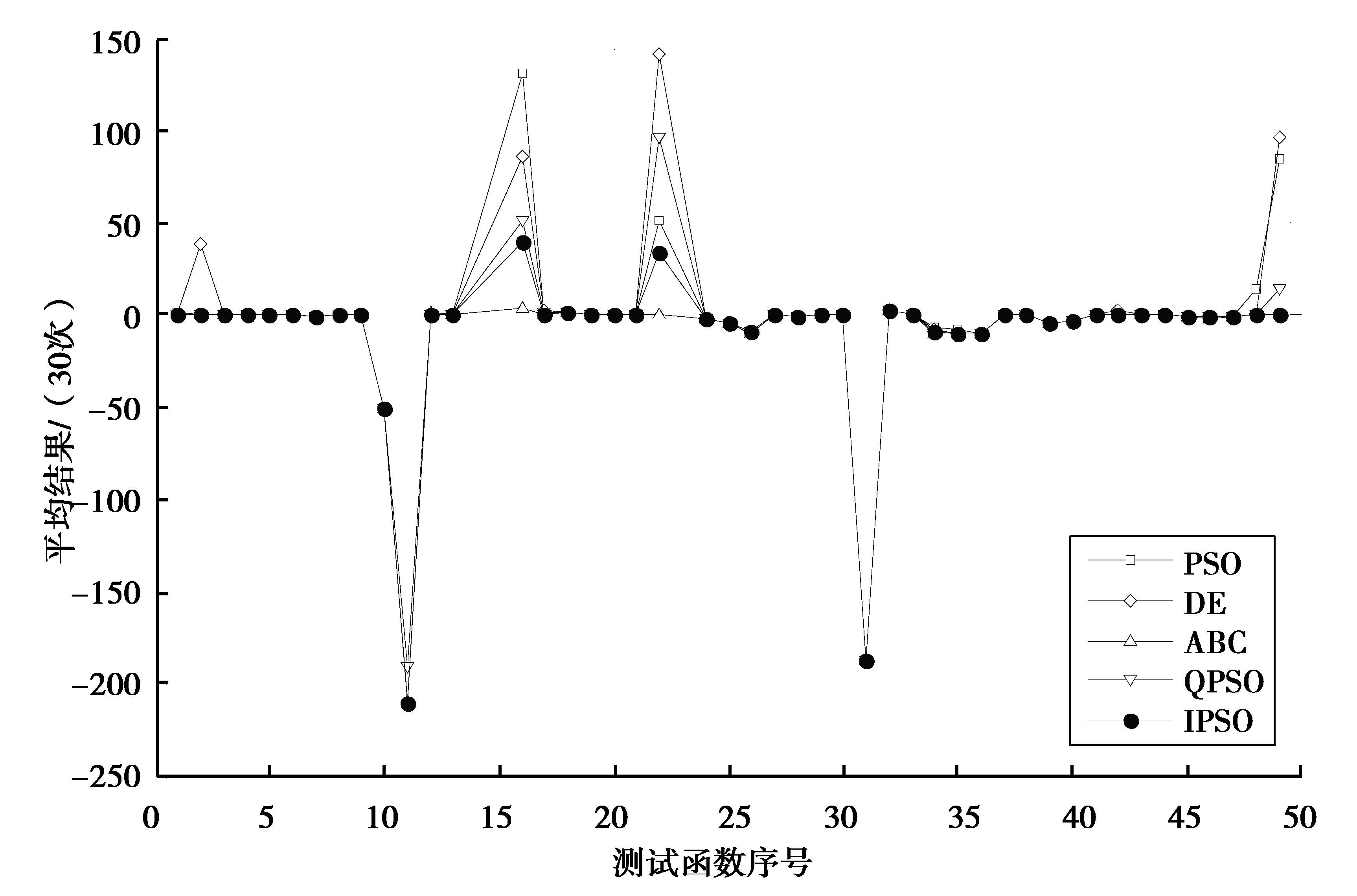
3.3 结果对比以50次独立优化的平均结果、平均时间作为对比指标。就优化的平均结果而言,对于F1~F5,IPSO优于PSO和DE的有4个,优于ABC的有3个,优于QPSO的有2个;对于F6~F17,IPSO优于PSO的有9个,优于DE的有5个,优于ABC的有8个,优于QPSO的有10个;对于F18~F26,IPSO的优化性能不够好,优于PSO的仅有2个,优于DE的仅有4个,优于QPSO的仅有3个,优于ABC的仅有1个;对于F27~F50,IPSO优于PSO的有16个,优于DE的有18个,优于ABC的有9个,优于QPSO的有10个。5种算法优化的平均结果对比如图 6所示,平均时间对比如图 7所示。由于函数14, 15, 23, 50各种方案优化得到的目标函数值相当大,为使图示清晰,图 6中这4个函数没有给出。
|
图 6 五种算法在相同迭代步数下的平均优化结果对比 Figure 6 Comparison of average optimal results of five algorithms under the same number of iteration steps |
|
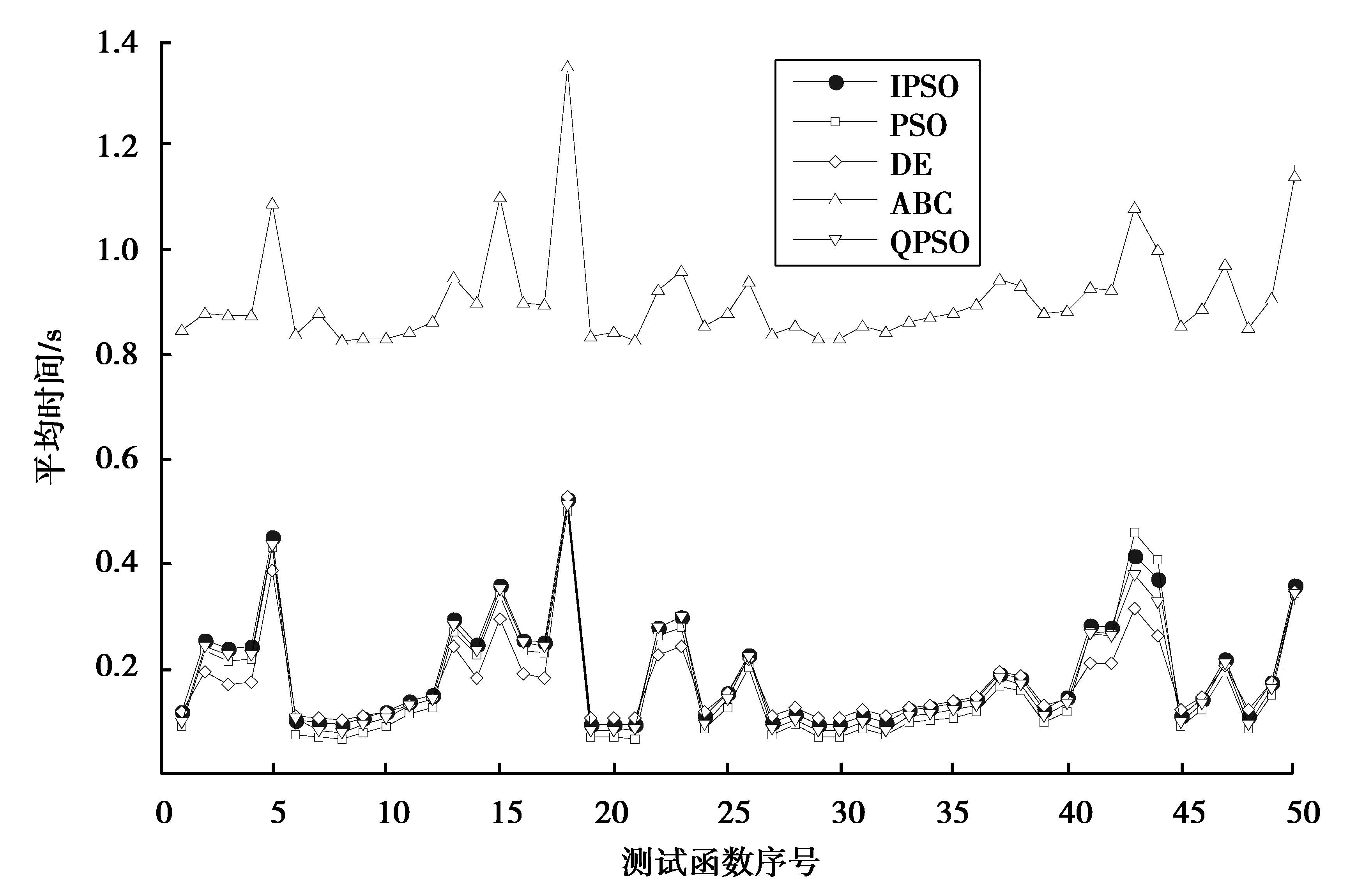
图 7 五种算法在相同迭代步数下的平均运行时间对比 Figure 7 Average running time comparison of five algorithms under the same number of iteration steps |
就平均运行时间而言,IPSO略长于除ABC以外的其他算法,这是由于引入了逆不完全伽马函数和一个基于差分进化的新算子导致了运算量增加的缘故。
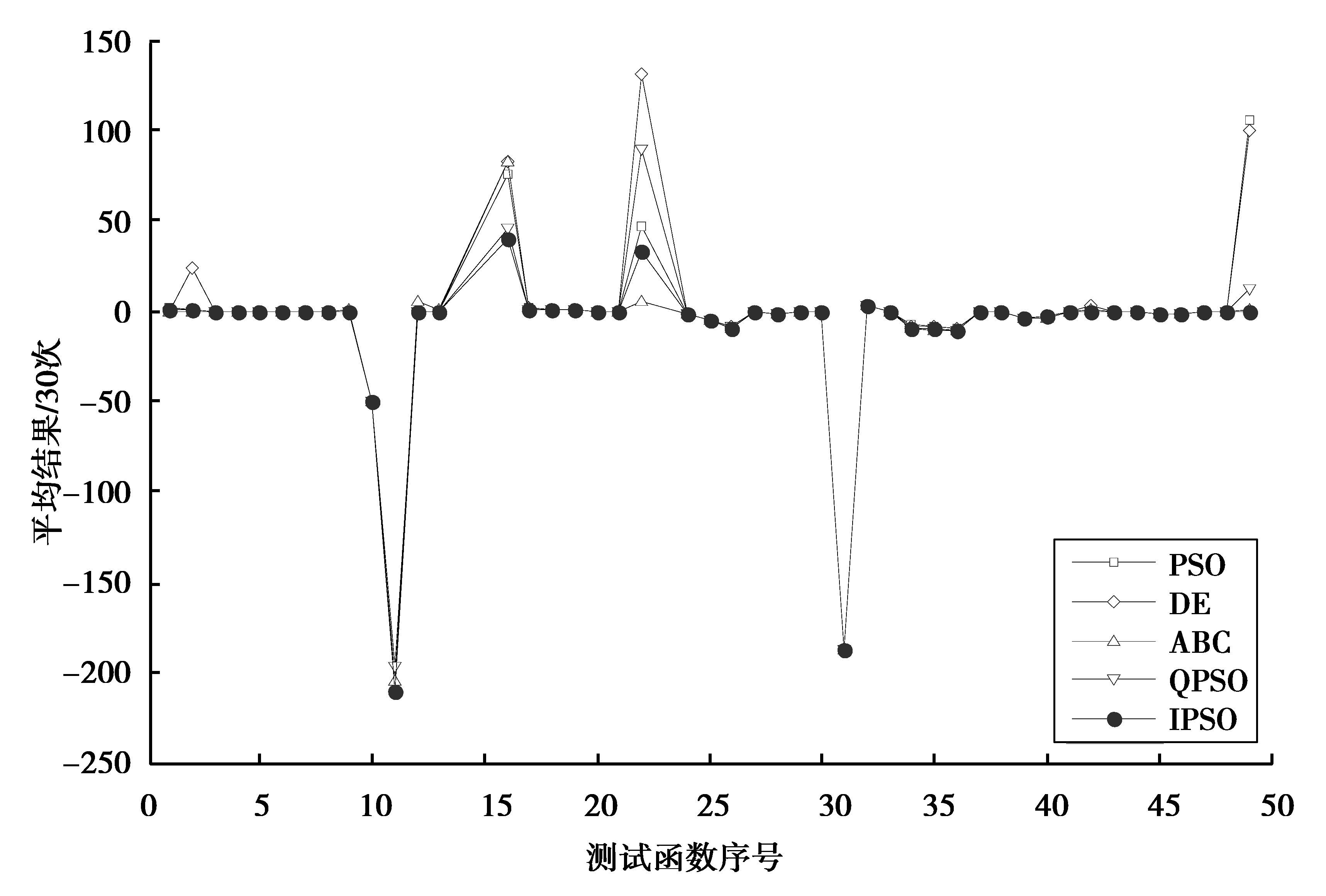
为便于对比平均运行时间,首先将这50个测试函数的平均时间再取平均值,然后将该平均值作为对比的指标。IPSO的平均时间为PSO的1.118 9倍,为DE的1.097 2倍,为ABC的0.212 7倍,为QPSO的1.066 7倍。为充分展示IPSO的优良性能,进一步考察相同运行时间下的对比结果。根据IPSO与其他算法平均时间的比值,首先将PSO、DE、ABC、QPSO的迭代步数分别设置为1 200、1 200、500、1 200,然后对所有函数重新优化,每个测试函数分别用5种算法优化50次,然后取50次优化的平均结果作为对比指标,优化结果对比如图 8所示。实验结果表明,IPSO的性能与图 1中展示的结果区别不大,仍然明显优于其他算法。
|
图 8 5种算法在相同运行时间下的平均优化结果对比 Figure 8 Comparison of average optimal results of five algorithms under the same running time |
为了更加客观公正的展示IPSO的优良性能,下面根据所有测试函数采用IPSO和PSO、DE、ABC、QPSO分别优化50次的结果,利用统计阈值α=0.05进行秩和检验。该检验的原假设是:“对于同一函数,IPSO的优化结果和其它算法的优化结果没有差异”。检验结果如表 1所示,表中w列的“+、=、-”表示对于该行的函数,IPSO在统计意义上分别优于、等于、劣于对比算法,NaN表示2种算法对于该行的函数完全等价,为简洁直观,表中每类函数仅随机选取了2个。基于检验假设的统计结果表明,IPSO有20~40个函数优于对比算法,而劣于对比算法的函数仅有1~11个。
| 表 1 采用秩和检验的算法成对测试显著性结果对比(α=0.05) Table 1 Comparison of pairwise test significance results based on rank sum test(α=0.05) |
从以上三类实验结果看,IPSO表现出了相同的趋势。即对于单峰(变量可分离和不可分离)和多峰变量不可分离函数,IPSO明显优于PSO、DE、ABC和QPSO;而对于多峰变量可分离函数,IPSO的优化性能不够理想。然而任何算法都不是万能的,不可能对于所有类型的问题都适用,这恰与无免费午餐定理的思想是一致的。对于IPSO表现出的优良特性,给出如下理论分析。
首先,从种群的初始化方法看,采用了基于Beta分布的随机数产生初始种群粒子位置的新方法。这种方法的优点在于,利用Beta分布函数的特性,能够以较大概率确保初始种群遍布于最优解周围,从而有利于使种群向着最优解逼近。而其他算法采用的基于均匀分布随机数的种群初始化方法,种群在优化空间的初始分布是随机的,不能呈现出对最优解的“包围”特性,从而在对最优解的逼近上略逊色于IPSO。
第二,在搜索过程中,探索和开发两阶段的合理平衡往往是制约算法性能的关键因素。从IPSO惯性因子的更新方式看,采用了基于逆不完全伽马函数的新方法,逆不完全伽马函数的独特性能使惯性因子的下降趋势,较好的符合了算法在全局探索和局部开发两阶段之间的平衡,从而使优化性能得到进一步提高。
第三,从粒子的速率更新式看,研究在传统PSO速率更新的基础上,受差分进化思想的启发,增加了一个基于所有粒子自身最优平均值与当前粒子之差的新算子。在算法初期的全局探索阶段,该算子的作用幅度较大,有利于发现较好的目标区域;随着迭代步数逐渐减小,其作用幅度逐渐减小,直至为零,有利于在最优解附近局部开发,进一步保证了探索和开发之间的合理平衡。
第四,越界处理是所有群智能优化算法都面临的问题,该问题也对算法性能有较大影响,若不及时处理会使算法迅速发散,若处理不当则会使算法陷入早熟收敛。采用的基于边界点对称映射的粒子越界处理方法,使越界的粒子立即返回寻优空间,而不是停留在边界,这种处理方法也使寻优速度得到了进一步的提高。
4 结论提出了一种改进的粒子群优化算法。该算法主要针对种群初始化方法、惯性因子的更新方法、粒子速率更新式的设计、例子的越界处理方法4个方面进行了改进。改进的目标是有效实现寻优过程中全局探索和局部开发2阶段的合理平衡,采用的主要方法是在惯性因子的更新式中引入了逆不完全伽马函数,在速率更新式中,引入了基于差分进化的新算子。标准函数极值优化的实验结果验证了提出方法的优越性,从而揭示出本文提出的改进措施是有效的可行的。
| [1] | Kennedy J, Eberhart R C. Particle swarms optimization[C]//Proceedings of IEEE international conference on Neural Networks. Perth. WA, USA:IEEE, 1995:1942-1948. |
| [2] | Shi Y H. Eberhart R C. A modified particle swarm optimizer[C]//Proceedings of the 1998 IEEE International Conference on Evolutionary Computation. Piscataway, USA:IEEE, 1998:67-73. |
| [3] | Cui G Z, Li X G, Zhang X C, et al. The optimization of DNA encodings based on modified PSO/GA algorithm[J]. Chinese Journal of Computers, 2010, 33(2): 311–316. DOI:10.3724/SP.J.1016.2010.00311 |
| [4] | Zhand C S, Sun J G, Ouyang D T, et al. A self-adaptive hybrid particle swarm optimization algorithm for flow shop scheduling problem[J]. Chinese Journal of Computers, 2009, 32(11): 2137–2146. |
| [5] | Jiang M, Luo Y P, Yang S Y. Stochastic convergence analysis and parameter selection of the standard particle swarm optimization algorithm[J]. Information Processing Letters, 2007, 102(1): 8–16. DOI:10.1016/j.ipl.2006.10.005 |
| [6] | Bergh F, Engelbrecht A P. A study of particle swarm optimization particle trajectories[J]. Information Science, 2006, 176(8): 937–971. DOI:10.1016/j.ins.2005.02.003 |
| [7] | Cai X J, Cui Z H, Zeng J C, et al. Dispersed particle swarm optimization[J]. Information Processing Letters, 2008, 105(6): 231–235. DOI:10.1016/j.ipl.2007.09.001 |
| [8] | Lu Z S, Hou Z R. Particle swarm optimization with adaptive mutation[J]. Acta Electronica Sinica, 2004, 32(3): 416–420. |
| [9] | Liu Y, Qin Z, Shi Z W, et al. Center particle swarm optimization[J]. Neurocomputing, 2007, 70(4-6): 672–679. DOI:10.1016/j.neucom.2006.10.002 |
| [10] | Liu B, Wang L, Jin Y H, et al. Improved particle swarm optimization combined with chaos[J]. Chaos Solitons & Fractals, 2005, 25(5): 1261–1271. |
| [11] | Luo Q, Yi D Y. A co-evolving framework for robust particle swarm optimization[J]. Applied Mathematics and Computation, 2008, 199(2): 611–622. DOI:10.1016/j.amc.2007.10.017 |
| [12] | Jiang Y, Hu T S, Huang C C, et al. An improved particle swarm optimization algorithm[J]. Applied Mathematics and Computation, 2007, 193(1): 231–239. DOI:10.1016/j.amc.2007.03.047 |
| [13] | Li L L, Wang L, Liu L H. An effective hybrid PSOGA strategy for optimization and its application to parameter estimation[J]. Applied Mathematics and Computation, 2006, 179(1): 135–146. DOI:10.1016/j.amc.2005.11.086 |
| [14] |
赵新超, 刘国莅, 刘虎球, 等.
基于非均匀变异和多阶扰动的粒子群优化算法[J]. 计算机学报, 2014, 37(9): 2058–2070.
ZHAO Xinchao, LIU Guoli, PENG Daogang, et al. Particle swarm optimization algorithm based on non-uniform mutation and multiple stages perturbation[J]. Chinses Journal of Computers, 2014, 37(9): 2058–2070. (in Chinese) |
| [15] |
钱玉良, 张浩, 彭道刚, 等.
基于EMD调制和粒子群模型的发电机组轴心轨迹提纯[J]. 信息与控制, 2013, 42(2): 243–251.
QIAN Yuliang, ZHANG Hao, PENG Daogang, et al. Purifying the orbit of generator unit based on EMD modulation and a particle swarm model[J]. Information and Control, 2013, 42(2): 243–251. (in Chinese) |
| [16] |
白国振, 荆鹏翔.
基于改进粒子群算法的并联机械手运动学参数辨识[J]. 信息与控制, 2015, 44(5): 545–551.
BAI Guozhen, JING Pengxiang. Kinematic parameter identification of parallel manipulator based on improved particle swarm algorithm[J]. Information and Control, 2015, 44(5): 545–551. (in Chinese) |
| [17] | Bergh F, Engelbrecht A P. A study of particle swarm optimization particle trajectories[J]. Information Sciences, 2006, 176(8): 937–971. DOI:10.1016/j.ins.2005.02.003 |
| [18] | Chatterjee A, Siarry P. Nonlinear inertia weight variation for dynamic adaptation in particle swarm optimization[J]. Computers & Operations Research, 2007, 33(3): 859–871. |
| [19] | Kerman. GSA:A gravitational search algorithm[J]. Information Sciences, 2009, 179(1): 2232–2248. |
| [20] | Berat D, Tamer O. A new metaheuristic for numerical function optimization:vortex search algorithm[J]. Information Sciences, 2015, 293(1): 125–145. |
 2017, Vol. 40
2017, Vol. 40

