有限单元法是在上世纪六七十年代发展起来的强有力的数值分析方法,它使许多复杂的工程分析问题迎刃而解,但传统有限单元法中每一种单元都由单一的材料组成,这比利用复合单元经行建模需要更多的工作量。为此,考虑不同材料组合的复合单元法的开发就显得尤为重要。1909年Ritz[1]提出了一个求解连续介质力学[2]中的场问题近似解的方法。这个方法利用未知量的试探函数将势能泛函近似化,根据泛函取极小值的条件,就能导出求解未知量的一组方程。1943年Courant[3]首先尝试应用在一系列三角形区域上定义的分片连续函数和最小位能原理相结合,来求解St.Venant扭转问题。这种方法要求在边界处的函数只须满足有限个点,解决了Ritz的整体试探函数必须满足边界条件的限制,为Clough等人系统的建立有限单元法提供了理论数学基础。1956年Turner等[4]将钢架分析中的位移法推广到弹性力学平面问题,并用于飞机结构的分析,首次给出了用三角形单元求解平面应力问题的正确解答。他们的研究工作开始了利用计算机求解复杂弹性力学问题的新阶段。1960年Clough进一步求解了平面弹性问题[5],并第一次提出了“有限单元法[6]”的名称,使人们更清楚的认识到有限单元法的特性和功效。2003年陈胜宏提出了一种结合了离散模型和等效模型的优点的新的数值计算方法。它汲取了有限单元法、块体单元法和数值流行法等多种计算方法的优点,开始了为复合单元法的研究。2010年吕中荣等[7]利用复合单元法建立了多阶梯变截面和渐变截面梁的有限元分析方程, 并进行了自由振动问题的分析。结果表明:复合单元法具有计算量小、计算精度高的优点。2015年薛娈鸾[8-9]基于复合单元法,建立了裂隙岩体非定常温度场的复合单元算法。结合裂隙岩体水流传热模型试验数据,构建相应的复合单元数值模型进行对比计算分析,验证了裂隙岩体非定常温度场的复合单元算法的有效性和可靠性。
复合单元法是近年来在有限单元法方面的拓展,是一种新的数值计算方法。它采用传统有限元法的求解思路,将同一个复合单元覆盖下的多种类型的分属于不同材料属性的单元进行整合,形成一种新的复合单元后再进行求解。当建筑结构中遇到复杂配筋等情况时,该方法在建模分析方面将明显优于传统有限元。两种不同类型单元进行复合是利用两种不同材料的单元根据虚功原理[10],通过能量守恒[11]的原则,推导出不同材料组成的复合单元下的虚功原理方程与单一材料的普通单元下虚功原理方程的关系,得到形成复合单元单元刚度矩阵的基本理论。
笔者利用针对悬臂梁端部作用集中荷载的简单算例,使用平面矩形单元与线单元进行复合的复合1型单元和平面三角形参单元与线单元进行复合的复合2型单元分别进行划分计算。两种情况得到的位移分别与悬臂梁在同等条件下ANSYS[12-13]计算得到的结果进行对比分析,验证了复合单元构造方法的正确性。
1 复合单元法构造过程 1.1 复合单元虚功原理复合单元的网格划分与普通有限单元法的网格划分一致,只是划分过程不用将不同的材料分开考虑。本次研究方法中的复合单元考虑不同材料之间不存在相对滑动,处于线弹性条件下。
根据能量守恒的原则单元在假设的虚位移上应该有外力做功与内力做功产生的能量相等的关系,设外力做功能量为Q1,内力做功部分分为矩形单元做功Q2和线单元做功Q3。
由Q1=Q2+Q3得:
| $ \mathit{\boldsymbol{\delta }}{^{{{\rm{e}}^{\rm{*}}}{\rm{T}}}} \times \mathit{\boldsymbol{F}}{^{\rm{e}}}{\rm{ = }}\int {\int\limits_\mathit{\Delta } {{{\{ \mathit{\boldsymbol{\varepsilon }}{^{{{\rm{e}}^{\rm{*}}}}}\} }^{\rm{T}}}} } \{ {\sigma ^{\rm{e}}}\} t{\rm{d}}x{\rm{d}}y{\rm{ + }}\int {{F_{\rm{N}}}} {\rm{d}}\mathit{u}\mathit{。} $ | (1) |
引入弹性力学中位移与应变的关系
| $ {\{ {\mathit{\boldsymbol{\delta }}^*}\} ^{\rm{T}}} \times {\mathit{\boldsymbol{F}}^{\rm{e}}} = \int {\int\limits_\mathit{\Delta } {{{\{ {\mathit{\boldsymbol{\delta }}^*}\} }^{\rm{T}}}} } {\mathit{\boldsymbol{B}}^{\rm{T}}}DBt{\rm{d}}x{\rm{d}}y\{ \delta \} {\rm{ + \{ }}{\delta ^{\rm{*}}}{{\rm{\} }}^{\rm{T}}}F。 $ | (2) |
将式(2) 中的虚伪移约掉得:
| $ \mathit{\boldsymbol{F}}{^{\rm{e}}} = \int {\int\limits_\mathit{\Delta } {{\mathit{\boldsymbol{B}}^{\rm{T}}}} } DBt{\rm{d}}x{\rm{d}}y\left\{ \delta \right\} + F{\rm{。}} $ | (3) |
观察式(3) 可以得知复合型单元所受到的节点力由两部分组成,一部分为矩形单元节点所受的力,一部分为线单元所受的力,将等式右边进行数值积分后有:
| $ \boldsymbol{F}{{~}^{\text{e}}}=\text{ }{{\boldsymbol{K}}_{1}}\left\{ \delta \right\}+\text{ }{{\boldsymbol{K}}_{2}}\left\{ \delta \right\}。 $ | (4) |
合并后可以得到:
| $ {{\boldsymbol{F}}^{\text{e}}}=\boldsymbol{K}\left\{ \delta \right\}。 $ | (5) |
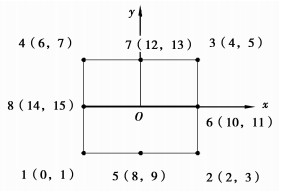
复合1型单元考虑2节点线单元通过8节点等参单元对边节点进行单元复合的一种单元,单元在编程过程中的节点位移编码如图 1所示。
|
图 1 复合3型单元 Figure 1 Composite element of type three |
图 1中标明了每个节点的节点编号和每个节点对应的位移编号用来方便编程的使用,同时复合单元的单元刚度矩阵的形成也需要根据位移编码对应进行刚度矩阵的叠加。
考虑四边形单元的位移模式[14]采用完备多项式的形式:
| $ u={{a}_{1}}+{{a}_{2}}x+{{a}_{3}}y+{{a}_{4}}xy+{{a}_{5}}{{x}^{2}}+{{a}_{6}}{{y}^{2}}+{{a}_{7}}x{{y}^{2}}+{{a}_{8}}{{x}^{2}}y。 $ | (6) |
则有:
| $ \left[{\begin{array}{*{20}{c}} {{u_1}}\\ {{u_2}}\\ {{u_3}}\\ {{u_4}}\\ {{u_5}}\\ {{u_6}}\\ {{u_7}}\\ {{u_8}} \end{array}} \right] = \left[{\begin{array}{*{20}{c}} 1&{{x_1}}&{{y_1}}&{{x_1}{y_1}}&{x_1^2}&{y_1^2}&{{x_1}y_1^2}&{x_1^2y}\\ 1&{{x_2}}&{{y_2}}&{{x_2}{y_2}}&{x_2^2}&{y_2^2}&{{x_2}y_2^2}&{x_2^2y}\\ 1&{{x_3}}&{{y_3}}&{{x_3}{y_3}}&{x_3^2}&{y_3^2}&{{x_3}y_3^2}&{x_3^2y}\\ 1&{{x_4}}&{{y_4}}&{{x_4}{y_4}}&{x_4^2}&{y_4^2}&{{x_4}y_4^2}&{x_4^2y}\\ 1&{{x_5}}&{{y_5}}&{{x_5}{y_5}}&{x_5^2}&{y_5^2}&{{x_5}y_5^2}&{x_5^2y}\\ 1&{{x_6}}&{{y_6}}&{{x_6}{y_6}}&{x_6^2}&{y_6^2}&{{x_6}y_6^2}&{x_6^2y}\\ 1&{{x_7}}&{{y_7}}&{{x_7}{y_7}}&{x_7^2}&{y_7^2}&{{x_7}y_7^2}&{x_7^2y}\\ 1&{{x_8}}&{{y_8}}&{{x_8}{y_8}}&{x_8^2}&{y_8^2}&{{x_8}y_8^2}&{x_8^2y} \end{array}} \right]\left[{\begin{array}{*{20}{c}} {{a_1}}\\ {{a_2}}\\ {{a_3}}\\ {{a_4}}\\ {{a_5}}\\ {{a_6}}\\ {{a_7}}\\ {{a_8}} \end{array}} \right], $ | (7) |
变形后
| $ \left[{\begin{array}{*{20}{c}} {{a_1}}\\ {{a_2}}\\ {{a_3}}\\ {{a_4}}\\ {{a_5}}\\ {{a_6}}\\ {{a_7}}\\ {{a_8}} \end{array}} \right] = {\left[{\begin{array}{*{20}{c}} 1&{{x_1}}&{{y_1}}&{{x_1}{y_1}}&{x_1^2}&{y_1^2}&{{x_1}y_1^2}&{x_1^2y}\\ 1&{{x_2}}&{{y_2}}&{{x_2}{y_2}}&{x_2^2}&{y_2^2}&{{x_2}y_2^2}&{x_2^2y}\\ 1&{{x_3}}&{{y_3}}&{{x_3}{y_3}}&{x_3^2}&{y_3^2}&{{x_3}y_3^2}&{x_3^2y}\\ 1&{{x_4}}&{{y_4}}&{{x_4}{y_4}}&{x_4^2}&{y_4^2}&{{x_4}y_4^2}&{x_4^2y}\\ 1&{{x_5}}&{{y_5}}&{{x_5}{y_5}}&{x_5^2}&{y_5^2}&{{x_5}y_5^2}&{x_5^2y}\\ 1&{{x_6}}&{{y_6}}&{{x_6}{y_6}}&{x_6^2}&{y_6^2}&{{x_6}y_6^2}&{x_6^2y}\\ 1&{{x_7}}&{{y_7}}&{{x_7}{y_7}}&{x_7^2}&{y_7^2}&{{x_7}y_7^2}&{x_7^2y}\\ 1&{{x_8}}&{{y_8}}&{{x_8}{y_8}}&{x_8^2}&{y_8^2}&{{x_8}y_8^2}&{x_8^2y} \end{array}} \right]^{ - 1}}\left[{\begin{array}{*{20}{c}} {{u_1}}\\ {{u_2}}\\ {{u_3}}\\ {{u_4}}\\ {{u_5}}\\ {{u_6}}\\ {{u_7}}\\ {{u_8}} \end{array}} \right]。 $ | (8) |
根据形函数的定义可以得形函数N1~N2为:
| $ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} 1&x&y&{xy}&{{x^2}}&{{y^2}}&{{x^2}y}&{x{y^2}} \end{array}} \right]\\ {\left[ {\begin{array}{*{20}{c}} 1&{{x_1}}&{{y_1}}&{{x_1}{y_1}}&{x_1^2}&{y_1^2}&{{x_1}y_1^2}&{x_1^2y}\\ 1&{{x_2}}&{{y_2}}&{{x_2}{y_2}}&{x_2^2}&{y_2^2}&{{x_2}y_2^2}&{x_2^2y}\\ 1&{{x_3}}&{{y_3}}&{{x_3}{y_3}}&{x_3^2}&{y_3^2}&{{x_3}y_3^2}&{x_3^2y}\\ 1&{{x_4}}&{{y_4}}&{{x_4}{y_4}}&{x_4^2}&{y_4^2}&{{x_4}y_4^2}&{x_4^2y}\\ 1&{{x_5}}&{{y_5}}&{{x_5}{y_5}}&{x_5^2}&{y_5^2}&{{x_5}y_5^2}&{x_5^2y}\\ 1&{{x_6}}&{{y_6}}&{{x_6}{y_6}}&{x_6^2}&{y_6^2}&{{x_6}y_6^2}&{x_6^2y}\\ 1&{{x_7}}&{{y_7}}&{{x_7}{y_7}}&{x_7^2}&{y_7^2}&{{x_7}y_7^2}&{x_7^2y}\\ 1&{{x_8}}&{{y_8}}&{{x_8}{y_8}}&{x_8^2}&{y_8^2}&{{x_8}y_8^2}&{x_8^2y} \end{array}} \right]^{ - 1}}\left[ {\begin{array}{*{20}{c}} {{u_1}}\\ {{u_2}}\\ {{u_3}}\\ {{u_4}}\\ {{u_5}}\\ {{u_6}}\\ {{u_7}}\\ {{u_8}} \end{array}} \right] \end{array}。 $ | (9) |
得到用逆矩阵表达的形函数以后,就可以按照常规有限单元法的推导过程得到单一面单元的刚度矩阵K1。观察式Fe= K 1{δ}+ K 2{δ}和式Fe= K {δ}可以看出复合单元在整体坐标系下的综合单元刚度矩阵为K = K 1+ K 2,(K 2为线单元在整体坐标下的单元刚度矩阵,此处不予赘述)。该综合刚度矩阵是将两种单元下的刚度矩阵进行了整合,注意其中的刚度叠加位置要根据节点编号下的位移编号对号入座。
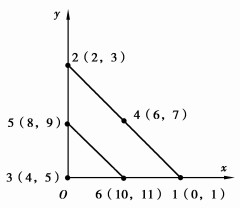
1.3 复合2型单元形成过程三角形6节点等参单元与2节点线单元复合而成的单元命名为复合2型单元,复合3型单元考虑的是2节点线单元穿过三角形6节点等参单元的临边,并且共用临边的节点。具体情况如图 2所示。
|
图 2 复合6型单元 Figure 2 Composite element of type six |
由上述可知要想得到复合单元的综合刚度矩阵,就必须首先得到各个子单元的单元刚度矩阵,因此首先对三角形6节点等参单元的单元刚度矩阵的形成过程进行推导,我们同样用利于编程实现的逆矩阵来构造形函数。
首先设定完备多项式类型的位移模式:
| $ u = {a_1} + {a_2}x + {a_3}y + {a_4}{x^2} + {a_5}xy + {a_6}{y^2}。 $ | (10) |
因为三角形单元中有6个节点,能够提供6个独立的位移方程,因此上式中的6个未知参数理论上是可以求解出来的。根据复合1型单元的形成过程可以推导得到6节点三角形单元的形函数为:
| $ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{N_1}}&{{N_2}}&{{N_3}}&{{N_4}}&{{N_5}}&{{N_6}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1&x&y&{{x^2}}&{xy}&{{y^2}} \end{array}} \right]\\ {\left[ {\begin{array}{*{20}{c}} 1&{{x_1}}&{{y_1}}&{x_1^2}&{{x_1}{y_1}}&{y_1^2}\\ 1&{{x_2}}&{{y_2}}&{x_2^2}&{{x_2}{y_2}}&{y_2^2}\\ 1&{{x_3}}&{{y_3}}&{x_3^2}&{{x_3}{y_3}}&{y_3^2}\\ 1&{{x_4}}&{{y_4}}&{x_4^2}&{{x_4}{y_4}}&{y_4^2}\\ 1&{{x_5}}&{{y_5}}&{x_5^2}&{{x_5}{y_5}}&{y_5^2}\\ 1&{{x_6}}&{{y_6}}&{x_6^2}&{{x_6}{y_6}}&{y_6^2} \end{array}} \right]^{ - 1}}。 \end{array} $ | (11) |
得到用逆矩阵表达的形函数以后,就可以按照常规有限单元法的推导过程得到单一面单元的刚度矩阵K 1。
| $ {K^{- 1}} = \left[{\begin{array}{*{20}{c}} {{k_{0, 0}}}&{{k_{0, 1}}}&{{k_{0, 2}}}& \cdots &{{k_{0, 10}}}&{{k_{0, 11}}}\\ {{k_{1, 0}}}&{{k_{1, 1}}}&{{k_{1, 2}}}& \cdots &{{k_{1, 10}}}&{{k_{1, 11}}}\\ {{k_{2, 0}}}&{{k_{2, 1}}}&{{k_{2, 2}}}& \cdots &{{k_{2, 10}}}&{{k_{2, 11}}}\\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ {{k_{10, 0}}}&{{k_{10, 1}}}&{{k_{10, 2}}}& \cdots &{{k_{10, 10}}}&{{k_{10, 11}}}\\ {{k_{11, 0}}}&{{k_{11, 1}}}&{{k_{11, 2}}}& \cdots &{{k_{11, 10}}}&{{k_{11, 11}}} \end{array}} \right]。 $ | (12) |
根据图中表明的每个节点的节点位移编号,并且运用与复合1型单元相同的方法进行单元刚度矩阵的形成。因此复合刚度矩阵为K = K 1+ K 2。
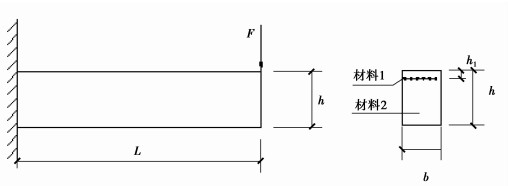
2 算例如图 3所示,矩形截面悬臂梁的高度h=2,长度L=10,厚度b=1,悬臂梁端部受集中荷载F=100 kN。材料1所在位置h1=0.06,弹性模量E=2.0×1011,面积As=3.0×10-3,材料2的弹性模量E=2.0×1010,泊松比为μ=0.25(未标注单位的量均为国际单位制)。
|
图 3 悬臂梁图示 Figure 3 Cantilever beam |
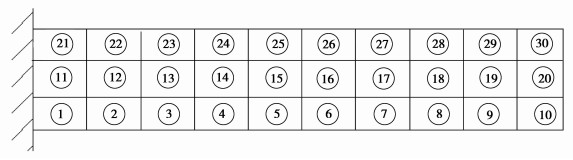
采用以上例题的条件,用复合1型单元进行单元划分计算,悬臂梁的单元划分情况如图 4所示。
|
图 4 复合1型单元网格划分 Figure 4 The grid for composite element of type one |
图 4中21~30号单元的单元类型为1型复合单元,编程过程中的单元类型定义为12,其余单元类型为普通的8节点矩形单元,编程过程中单元类型定义为21。
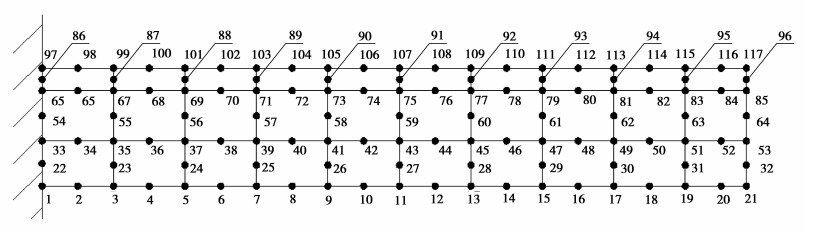
单元节点编号情况如图 5所示,图 5描述了用于程序计算的文本文件的单元节点编号的输入依据。
|
图 5 复合1型单元节点编号 Figure 5 The node number for composite element of type one |
复合1型单元划分下的计算结果如表 1所示。
| 表 1 复合1型单元划分下的计算结果 Table 1 The results of composite element of type one |
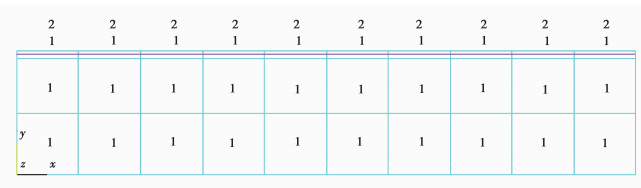
采用PLANE82单元与LINK1单元,并且单元划分按照图 4和图 5的单元位置和节点坐标进行单元划分。单元网格划分如图 6所示。图 6中紫色的单元代表材料1,绿色单元代表材料2。
|
图 6 ANSYS建模过程中梁的单元划分 Figure 6 The grid of ANSYS model |
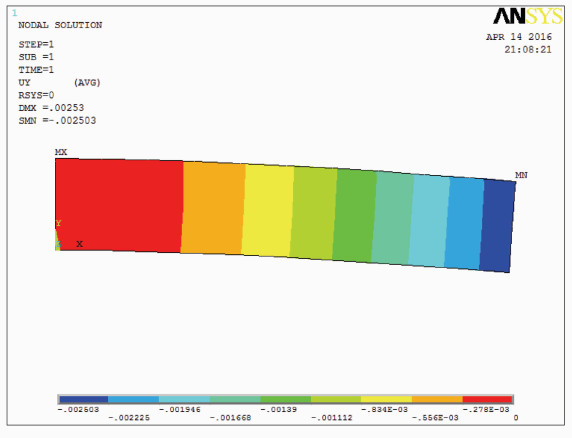
ANSYS计算结果如图 7所示。
|
图 7 ANSYS计算结果 Figure 7 The result of ANSYS model |
| 表 2 复合1型单元划分下的ANSYS计算结果 Table 2 The results of composite element of type one |
ANSYS计算结果与自编程序的对比结果如表 3所示。
| 表 3 两种计算方式结果 Table 3 The results of two computing methods |
通过表 3可知,采用复合单元求解方法和ANSYS在同样条件下的分析得到的结果,显示两种情况结果非常接近。
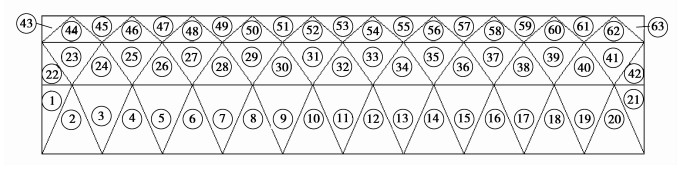
2.3 复合2型单元求解采用例1的条件,用复合2型单元进行单元划分计算,悬臂梁的单元划分情况如图 8所示。
|
图 8 复合2型单元网格划分 Figure 8 The grid for composite element of type two |
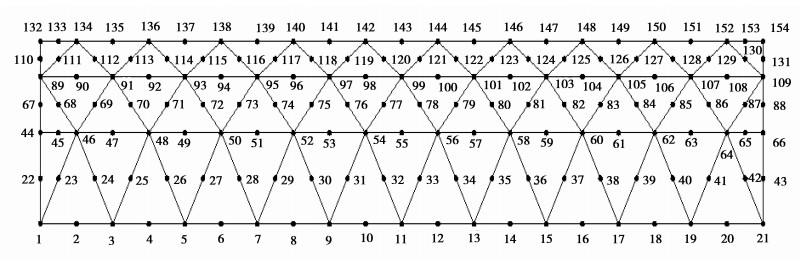
图 8中43~63号单元为复合2型单元,单元在编程过程中的单元类型编码为8。1~42号单元为普通2节点等参单元,单元在编程过程中的单元类型编码为5。单元的节点编号情况如图 9所示。
|
图 9 复合2型单元节点编号 Figure 9 The node number for composite element of type two |
图 9描述了用于程序计算的文本文件的单元节点编号的输入依据。
通过文本文件输入梁的各项条件后得到梁的计算结果如表 4所示。
| 表 4 复合2型单元划分下的计算结果 Table 4 The results of composite element of type two |
为了验证复合2型单元计算的正确性,我们同样采用ANSYS12.0进行结构分析。
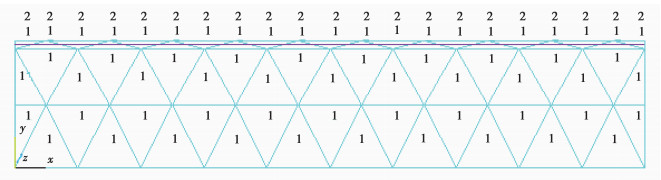
采用PLANE2单元与LINK1单元,并且单元划分按照图 8和图 9的单元位置和节点坐标进行单元划分。单元网格划分如图 10所示。图 10中紫色的单元代表材料1,绿色单元代表材料2。
|
图 10 ANSYS建模过程中梁的单元划分 Figure 10 The grid of ANSYS model |
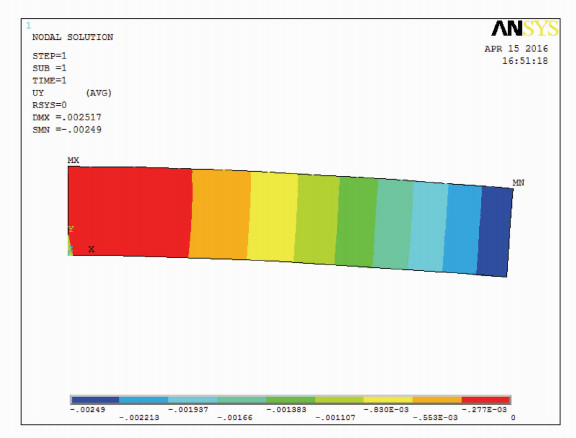
ANSYS计算结果如图 11所示。复合2型单元划分下的ANSYS计算结果如表 5所示。
|
图 11 ANSYS计算结果 Figure 11 The result of ANSYS model |
| 表 5 复合2型单元划分下的ANSYS计算结果 Table 5 The results of composite element of type two |
ANSYS计算结果与自编程序的对比结果如表 6所示。
| 表 6 两种计算方式结果 Table 6 The results of two computing methods |
通过表 3和表 6可以看出,利用复合单元法计算值与有限元数值模拟分析值十分接近,说明本文的理论和编程计算过程是正确的,但是由于在编程过程中采用的是8节点高斯数值积分[15],所以存在相对较小的误差是正常的。
5 结论对复合单元的理论做出推导,通过悬臂梁作用端部集中荷载的简单算例,利用ANSYS和自编程序得到的结果进行对比,可以得到以下结论:
1) 将不同种类的材料属性的单元整合到一起形成新型复合单元的设想是可以实现的,通过单元的复合,使得结构在划分单元时大大减少了单元的个数,而计算结果的精度却不会减小,不同材料的性能都可以在结构中体现。通过对实例的计算,对比采用复合单元求解方法和ANSYS在同样条件下的分析得到的结果,显示两种情况结果非常接近。
2) 不同材料组成的复合单元,在节点相结合的部位位移相同的前提条件下,只需要将两种不同材料的单元在同一个自然坐标系下的单元刚度矩阵按照节点位移编号进行叠加就可以很方便的得到复合单元的单元刚度矩阵。这种方法具有很好的操作性和稳定性。
3) 在使用逆矩阵形函数构造方法时,要特别注意母单元节点的个数和位置,为保证形成形函数的矩阵求逆的顺利进行,矩阵中的母单元局部坐标系下的元素必须保证矩阵是非奇异的。在矩阵非奇异的前提条件下,移动节点位置时,逆矩阵形函数方法能够很好的适应这类问题。
| [1] | Tanaka T, Nodera T. Ritz value of approximate inverse by MR algorithm[J]. IPSJ SIG Notes, 2002, 2002: 19–24. |
| [2] | Chen W Q. The renaissance of continuum mechanics[J]. Univ-Sci A, 2014, 15(4): 231–240. DOI:10.1631/jzus.A1400079 |
| [3] | Courant R. Variational methods for the solution of problems of equilibrium and vibrations[J]. Bulletin of the American Mathematical Society, 1943, 49(1943): 1–23. |
| [4] | Turner M J. Stiffness and deflection analysis of complex structures[J]. Journal of Aerosol Science, 1956, 23(9): 805–823. |
| [5] | Gladwell G M L. On the solution of problems of dynamic plane elasticity[J]. Mathematika, 1957, 4(2): 166–168. DOI:10.1112/S002557930000125X |
| [6] | Clough R W. The finite element method in plane stress analysis[C]//Proceedings of 2nd ASCE Conference on Electronic Computation. Pittsburgh, PA. Pittsburgh:[s.n.], 1960:345-378. |
| [7] |
吕中荣, 谢瑾荣, 刘济科.
复合单元法在变截面梁自由振动分析中的应用[J]. 中山大学学报, 2010, 49(6): 49–52.
LYU Zhongrong, XIE Jinrong, LIU Jike. Composite element method for the free vibration analysis of non-uniform beams[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2010, 49(6): 49–52. (in Chinese) |
| [8] |
薛娈鸾.
裂隙岩体不稳定温度场的复合单元算法研究[J]. 岩土力学, 2015, 36(7): 2088–2093.
XUE Luanluan. Composite element algorithm for transient thermal field in fractured rock mass[J]. Rock and Soil Mechanics, 2015, 36(7): 2088–2093. (in Chinese) |
| [9] |
薛娈鸾.
裂隙岩体渗流传热藕合的复合单元模型[J]. 岩土力学, 2016, 37(1): 264–278.
XUE Luanluan. A composite element model for coupled seepage-heat transfer of fractured rock mass[J]. Rock and Soil Mechanics, 2016, 37(1): 264–278. (in Chinese) |
| [10] |
萧允晖, 张来仪. 结构力学Ⅰ[M]. 北京: 机械工业出版社, 2010: 107-117.
XIAO Yunhui, ZHANG Laiyi. Structural mechanics Ⅰ[M]. Beijing: China Machine Press, 2010: 107-117. (in Chinese) |
| [11] |
潘天林, 吴斌, 郭丽娜, 等.
能量守恒逐步积分方法在工程结构动力分析中的应用[J]. 工程力学, 2014, 31(9): 21–27.
PAN Tianlin, WU Bin, GUO Lina, et al. Application of energy conserving step-by-step integration algorithm in dynamic analysis of engineering structures[J]. Engineering Mechanics, 2014, 31(9): 21–27. (in Chinese) |
| [12] |
王新敏. ANSYS工程结构数值分析[M]. 北京: 人民交通出版社, 2013: 6-10.
WANG Xinmin. ANSYS numerical analysis of engineering structure[M]. Beijing: China Communications Press, 2013: 6-10. (in Chinese) |
| [13] |
沈聚敏, 王传志, 江见鲸. 钢筋混凝土有限元与板壳极限分析[M]. 北京: 清华大学出版社, 1993: 240-246.
SHEN Jumin, WANG Chuanzhi, JIANG Jianjing. Finite element analysis of reinforced concrete and limit analysis of plate and shell[M]. Beijing: Tsinghua University Press, 1993: 240-246. (in Chinese) |
| [14] |
沈琪雯. 有限元逆矩阵形函数构造方法及其编程[D]. 重庆: 重庆大学, 2014. SHEN Qiwen. Inverse matrix shape function of finite element and programming[D]. Chongqing:Chongqing University, 2014. (in Chinese) |
| [15] |
李开泰, 黄艾香, 黄庆怀. 有限元方法及应用[M]. 北京: 科学出版社, 2006: 63-93.
LI Kaitai, HUANG Aixiang, HUANG Qinghuai. Finite element method and its application[M]. Beijing: Science Press, 2006: 63-93. (in Chinese) |
 2017, Vol. 40
2017, Vol. 40


