随着日常工业生产中无功设备的日益增加及广泛应用,无功功率损耗越来越多,使得整个系统的功率因数大大降低[1-2]。并且,无功功率在电力系统中的流动,会产生大量的额外损耗,造成电压幅值的降落,对电力系统的稳定性及安全运行产生严重的威胁。因此无功功率补偿早已成为世界各国发展智能电网,进行电力系统优化的重要研究课题。当前工业生产中常采用的无功补偿系统多以三相电路瞬时无功功率理论为基础,依据p-q或ip-iq方法实现对系统无功电流的检测。当系统负载平衡、三相电压对称时,上述方法均能准确地检测出系统的无功电流分量。但是,当系统三相不对称,电压波形发生畸变的情况下,电压信号中除了正序分量外也包含了负序及零序分量,因此,采用传统的ip-iq检测法对a相电压进行锁相时会产生一定的偏差,从而无法准确检测出系统的无功电流分量[3]。另外,在进行负载电流直流信号地提取时,传统的低通滤波器设计模型增加了系统无功电流检测延迟时间,降低了系统的实时性。依据对称分量法思想将系统分解到正、负、零相序下分别求解其有功及无功电流值,解决了由于系统三相不对称造成的检测误差问题;对各相负载电流进行整定、化简,采用积分滤波法提取直流信号,提高了系统的动态响应速度,保证了无功补偿系统的准确性和实时性。
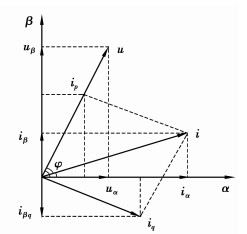
1 经典无功电流检测法分析 1.1 p-q法无功电流检测采用p-q法进行无功电流检测,需要采集系统三相电压与三相电流的瞬时值并将其变换到α-β坐标系下进行研究。图 1所示在α-β坐标系下进行电压、电流矢量变换,uα、uβ和iα、iβ可分别合成电压矢量u和电流矢量i [4]。图 1中ip为瞬时有功电流;iq为瞬时无功电流;p为瞬时有功功率;q为瞬时无功功率;φ为电压矢量u和电流矢量i分别与α轴夹角的差值;p为瞬时有功功率直流分量;q为瞬时无功功率直流分量。
|
图 1 α-β坐标系中的电压、电流矢量图 Figure 1 Voltage and current vector in the α-β coordinates |
| $ p = \boldsymbol{u} \times {i_p}, q = \boldsymbol{u} \times {i_q}。 $ | (1) |
| $ \left[{\begin{array}{*{20}{c}} p\\ q \end{array}} \right] = \left[{\begin{array}{*{20}{c}} {{e_\alpha }\;\;\;{e_\beta }}\\ {{e_\beta }-{e_\alpha }} \end{array}} \right]\left[{\begin{array}{*{20}{c}} {{i_\alpha }}\\ {{i_\beta }} \end{array}} \right] = {\boldsymbol{C}_{pq}}\left[{\begin{array}{*{20}{c}} {{i_\alpha }}\\ {{i_\beta }} \end{array}} \right], $ | (2) |
式中:
当电网电压波形无畸变,通过式(2) 可准确求出系统瞬时功率p、q,经LPF滤波即可得到其基波分量进而求解出系统基波无功电流值。
当电网电压波形畸变,且仍保持三相对称,按照p-q法进行无功电流检测,得到p/q的直流分量为
| $ \left[{\begin{array}{*{20}{c}} {\bar p}\\ {\bar q} \end{array}} \right] = 3\left[{\begin{array}{*{20}{c}} {\sum\limits_{n = 1}^\infty {{E_n}{I_n}\cos ({\theta _n}-{\varphi _n})} }\\ {\sum\limits_{n = 1}^\infty { \pm {E_n}{I_n}\sin ({\theta _n}-{\varphi _n})} } \end{array}} \right]。 $ | (3) |
由于各次谐波电压的存在,p、q中除直流分量外还含有谐波电压、谐波电流相互作用的成分,因此检测出的基波无功电流存在很大的误差。
1.2 ip-iq法无功电流检测采用ip-iq法进行系统无功电流检测,可以减少对系统三相电压信号地采集,选用与a相电压同相位的正弦信号sin ωt和余弦信号cos ωt参与运算,不受畸变电压谐波成分的影响[5]。
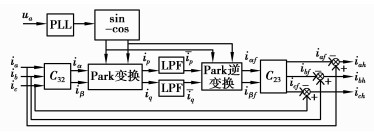
图 2中,首先对a相电压进行锁相获取对应的sin ωt和cos ωt值,然后进行坐标变换获取ip、iq电流值,最终经LPF滤波可以得到其直流分量ip、iq进而计算出系统三相基波电流iaf、ibf、icf和三相谐波电流量iah、ibh、ich。
|
图 2 ip-iq运算方式原理图 Figure 2 Operation schematic diagram of ip-iq |
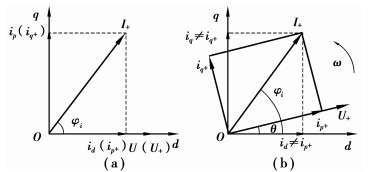
图 3反映了电压、电流在d-q坐标系下的矢量关系。图 3(a)中,系统三相电压对称,正序电流矢量I+在正序电压U+上的投影即为正序有功电流分量ip+,其方向同d轴重合;I+在U+法线上的投影为正序无功电流分量iq+,其方向同q轴重合[6]。
|
图 3 电压、电流在d-q坐标系中矢量关系 Figure 3 The vector relationship between voltage and current in d-q coordinate system |
图 3(b)所示,系统三相电压不对称,电压信号中除正序分量外也包含了负序及零序分量,a相电压锁相角度值与正序电压U+之间存在相位差θ,此时U+与d轴不再重合,即在d-q坐标系下id、iq分量不再对应于系统正序有功电流ip+和无功电流iq+。
针对系统在三相不对称情况下采用传统ip-iq法进行无功电流检测时存在较大误差的问题,提出了一种改进的锁相环节无功电流检测方法。以对称分量法思想把不对称的三相系统分解为正、负、零序3个独立的对称系统地叠加。
Ua、Ub、Uc为系统三相不对称电压;U+、U-、U0为独立对称的正、负、零序分量;Ua(bc)+、Ua(bc)-、Ua(bc)0为a(bc)相电压的正、负、零序分量。
| $ \left\{ \begin{array}{l} {U_a} = {U_a}^ + + {U_a}^-+ {U_a}^0, \\ {U_b} = {U_b}^ + + {U_b}^-+ {U_b}^0, \\ {U_c} = {U_c}^ + + {U_c}^-+ {U_c}^0, \end{array} \right. $ | (4) |
式中:Ua+、Ub+、Uc+构成对称正序系统,并且Ua+=U+,Ub+=a2U+,Uc+=aU+;Ua-、Ub-、Uc-构成对称负序系统,同样满足了Ua-=U-,Ub-=aU-,Uc-=a2U+;Ua0、Ub0、Uc0构成对称零序系统,满足Ua0=Ub0=Uc0=U0。由此,可以得出
| $ \left\{ \begin{array}{l} {U_a} = {U_a}^ + + {U_a}^-+ {U_a}^0 = {U_ + } + {U_-} + {U_0}, \\ {U_b} = {U_b}^ + + {U_b}^-+ {U_b}^0 = {a^2}{U_ + } + a{U_ - } + {U_0}, \\ {U_c} = {U_c}^ + + {U_c}^ - + {U_c}^0 = a{U_ + } + {a^2}{U_ - } + {U_0}。 \end{array} \right. $ | (5) |
进而可求解出系统a相正、负、零序电压分量
| $ \left[{\begin{array}{*{20}{c}} {U_a^ + }\\ {U_a^-}\\ {U_a^0} \end{array}} \right] = \frac{1}{3}\left[{\begin{array}{*{20}{c}} 1&a&{{a^2}}\\ 1&{{a^2}}&a\\ 1&1&1 \end{array}} \right]\left[{\begin{array}{*{20}{c}} {{U_a}}\\ {{U_b}}\\ {{U_c}} \end{array}} \right], $ | (6) |
式中:a=ej2π/3, a2=e-j2π/3, 规定电网电路采用三相三线制接法,因此系统中不存在零序电压分量[7]。由此可以求解出a相的正、负序电压为
| $ \begin{array}{l} {U_a}^ + = \frac{{({U_a} + {{\rm{e}}^{{\rm{j}}2{\rm{\pi }}/3}}{U_b} + {{\rm{e}}^{{\rm{-j2\pi /}}3}}{U_c})}}{3}, \\ {U_a}^-= \frac{{({U_a} + {{\rm{e}}^{{\rm{-j2\pi /3}}}}{U_b} + {{\rm{e}}^{{\rm{j2\pi /3}}}}{U_c})}}{3}{\rm{。}} \end{array} $ | (7) |
根据式(7) 可以看出,要得到a相的正、负序电压,需要240 °的相移,这会给无功电流的检测带来较大的延时,因此我们将正、负序电压表达式转换成
| $ \begin{array}{l} {U_a}^ + = \frac{{({U_a} + {{\rm{e}}^{{\rm{j\pi /3}}}}{U_b}-{U_b}-{{\rm{e}}^{{\rm{j\pi /3}}}}{U_c})}}{3}, \\ {U_a}^-= \frac{{({U_a} - {{\rm{e}}^{{\rm{j\pi /3}}}}{U_b} + {{\rm{e}}^{{\rm{j\pi /3}}}}{U_c} - {U_c})}}{3}{\rm{。}} \end{array} $ | (8) |
转换后电压只需移相60°即可得出正、负序电压矢量,延时1/6个电网电压周期。此时,通过锁相环分别对Ua+、Ua-进行锁相为三相电流的d-q转换提供相应的正弦、余弦值从而求出系统基波正序无功电流和基波负序电流。
2.2 基于ip-iq检测法的积分滤波环节设计采用传统LPF滤波方式进行无功电流检测对系统的动态响应速度以及检测精度都带来很大的影响。实验证明, 选用2阶LPF模块,设定截止频率为15 Hz进行基波的提取时,需要2个电源周期实现直流信号提取,动态响应时间过长。基于积分求平均值思想改进滤波环节,缩短系统延时时间。
系统电流中除了基波分量外主要含有5, 7, 11, 13次高次谐波,坐标变换后可看到,ip、iq中主要的谐波频率为基波6倍频[8]。因此,在1/6个电网周期下分别对ip、iq进行积分求平均值,即可滤除电流中的谐波成分。
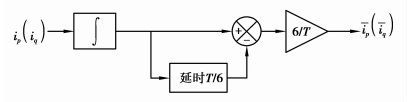
利用简单的积分、延时以及增益模块搭建改进的滤波环节模型,降低系统延时,增强了无功电流提取的实时性,如图 4所示。
|
图 4 积分滤波法原理图 Figure 4 Schematic diagram of integral filtering method |
上述所提出的积分滤波法是以系统三相对称为前。在三相不对称情况下,需要对各相不对称电流进行逐一化简,之后设计积分滤波环节,提取基波分量。以a相负载电流为例进行分析
| $ \begin{array}{l} {i_a}\left( t \right){\rm{ }} = \sum\limits_{k = 0}^\infty {\sum\limits_{n = 1, 5} {\left\{ {\sqrt 2 {I_{6k + n}}{\rm{sin[}}\left( {6k + n} \right)\omega t + {\varphi _{6k + n}}]} \right\}} } \\ \;\;\;\;\;\;\;\; = \sqrt 2 {I_1}{\rm{cos}}{\varphi _1}{\rm{sin}}\omega t + \sqrt 2 {I_1}{\rm{sin }}{\varphi _1}{\rm{cos}}\omega t + {i_h}\left( t \right) = {i_p}\left( t \right) + {i_q}\left( t \right) + {i_h}\left( t \right)。 \end{array} $ | (9) |
式中:ip(t)为负载电流的基波有功分量,与电源电压同频同相的正弦信号;iq(t)为负载电流的基波无功分量;ih(t)负载电流的谐波分量。
Ip、Iq为基波有功、无功电流的最大值
| $ \left\{ \begin{array}{l} {I_p} = \sqrt 2 {I_1}{\rm{cos }}{\varphi _1}, \\ {I_q} = \sqrt 2 {I_1}{\rm{sin }}{\varphi _1}。 \end{array} \right. $ | (10) |
将式(9) 两边同时乘以sin ωt, 得
| $ \begin{array}{l} {i_a}\left( t \right){\rm{sin}}\omega t = {I_p}{\rm{sin}}{^2}\omega t + {I_q}{\rm{cos}}\omega t\;{\rm{sin}}\omega t + {i_h}\left( t \right){\rm{sin}}\omega t, \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \frac{{{I_p}}}{2}\left( {1-{\rm{cos }}2\omega t} \right) + \frac{{{I_q}}}{2}{\rm{sin }}2\omega t + {i_h}\left( t \right)4\omega t。 \end{array} $ | (11) |
对式(11) 采用积分滤波法,可获取基波有功分量Ip;同理,将式(9) 两边同时乘以cos ωt,化简后进行积分滤波处理,可获取基波无功分量Iq。
选取T/2作为积分周期,电流信号直流分量的提取如式(12) 所示:
| $ \left[\begin{array}{l} {I_p}\\ {I_q} \end{array} \right] = 2 \times \frac{2}{T}\left\{ \begin{array}{l} \int_t^{t - T/2} {[{i_a}\left( t \right){\rm{sin}}\left( {\omega t} \right)]{\rm{d}}t} \\ \int_t^{t - T/2} {[{i_a}\left( t \right){\rm{cos}}\left( {\omega t} \right)]{\rm{d}}t} \end{array} \right\}。 $ | (12) |
在MATLAB环境下搭建仿真模型并完成系统实验验证分析。
正序分量和负序分量只是相序相反,因此在进行负序分量的求解过程中,矩阵C32-即可通过将C32矩阵的第二、三列交换得到[9]。
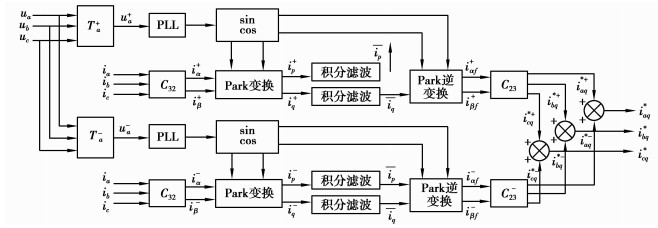
|
图 5 改进的无功电流检测法结构框图 Figure 5 Schematic diagram of improved reactive current detection method |
Ta+、Ta-分别为正、负序分量矩阵系数
| $ T_a^ + = \left[\begin{array}{l} 1\\ {{\rm{e}}^{{\rm{j\pi }}/3}}-1\\ -{{\rm{e}}^{{\rm{j\pi /3}}}} \end{array} \right], T_a^ + = \left[\begin{array}{l} 1\\ -{{\rm{e}}^{{\rm{j\pi /3}}}}\\ {{\rm{e}}^{{\rm{j\pi }}/3}}-1 \end{array} \right]。 $ | (13) |
笔者利用三相异步电机(asynchronous machine)、Series RLC Branch和开关模块(breaker)搭建负载模型[10-11]。由于感应电机的存在,系统启动时电流会产生一定的波动。待电流稳定后通过调整开关模块的导通和关断状态改变三相负载进而调节系统三相电流。通过实验对比可以看到改进后的系统对电流变化的快速响应性能明显增强[12]。
由图 6可见,电机稳定运行后,在0.15 s时刻改变系统三相负载。可以看到:传统检测方式下,a相基波正序电流在近2个电源周期后趋于稳定的正弦电流波形输出,而改进后的检测方法在一个电源周期内即可实现[13-14]。将系统响应时间降低60%左右。
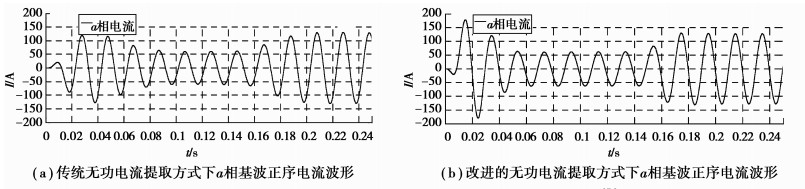
|
图 6 单相基波正序电流波形 Figure 6 Positive sequence current waveform of single-phase wave |
图 7(a)所示,系统独立运行,无外加静止无功补偿电路时,由于感性负载的存在,a相电压超前负载电流一定的相位角。此时系统的功率因数如图 8中曲线所示,约为0.85。图 7(b)所示,在0.2 s时刻加入静止无功补偿部分,补偿后的a相系统电流不再等于a相负载电流,经过0.02 s后,系统电压、电流实现同相位。从图 8中可以看到,补偿后系统的功率因数接近于1[15];在0.4 s时刻改变系统的三相负载,从图 7(c)以及图 8可以看到,由于静止无功补偿系统的存在,a相电流经过短暂的调整后(不到一个电源周期)再次实现了与电压的零相位差,功率因数接近于1[16-17]。
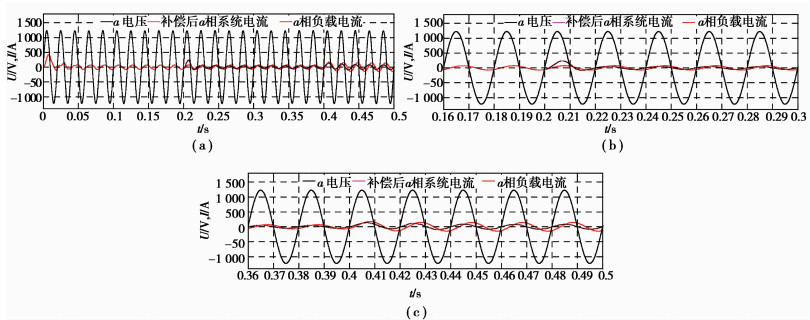
|
图 7 无功补偿前后单相波形图 Figure 7 Single-phase waveforms before and after static var compensation |
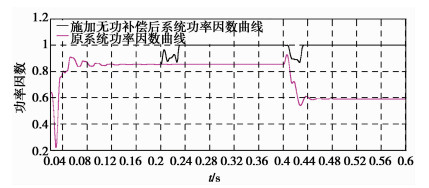
|
图 8 无功补偿前后系统功率因数曲线 Figure 8 System power factor curves before and after static var compensation |
针对传统的静止无功补偿系统在三相电压不对称情况下普遍存在的无功电流检测延时过长及误差较大等问题进行了理论分析和数学模型地改进,并通过仿真实验进行了进一步地验证。改进后系统无功电流检测延迟时间缩短了60%;原系统加入静止无功补偿电路部分后,系统功率因数会在一个电源周期内提升到95%以上,实现系统无功功率地快速、精确补偿。
| [1] | Li B B, Yang R F, Xu D D, et al. Analysis of the phase-shifted carrier modulation for modular multilevel conver-ters[J]. IEEE Transaction on Power Electronics, 2015, 30(1): 297–310. DOI:10.1109/TPEL.2014.2299802 |
| [2] |
朱建玉. 积并联型有源电力滤波器的电流检测和无差拍控制方法的研究分[D]. 无锡: 江南大学, 2014. ZHU Jianyu. Current detection of active power filter with parallel active power filter and the research of the control method of nondifference[D]. Wuxi:Jiangnan University, 2014.(in Chinese) |
| [3] | Milanovic J V, Zhang Y. Modeling of FACTS devices for voltage sag mitigation studies in large power systems[J]. IEEE Transactions on Power Delivery, 2010, 25(4): 3044–3052. DOI:10.1109/TPWRD.2010.2052395 |
| [4] | Cavaliere C A C, Watanabe E H, Aredes M. Multi-pulse STATCOM operation under unbalanced voltages[C]//Power Engineering Society Winter Meeting. New York:IEEE, 2002:567-572. |
| [5] |
王炜煜, 陈阿莲.
一种改进的无功电流:频率正反馈孤岛检测方法[J]. 电源学报, 2016, 14(5): 54–59.
WANG Weiyu, CHEN Alian. An improved reactive current disturbance islanding detection method with fraquency positive feedback[J]. Journal of Power Supply, 2016, 14(5): 54–59. (in Chinese) |
| [6] |
杨华.
无功电流的实时检测研究[J]. 通信电源技术, 2014, 31(1): 57–59.
YANG Hua. Research on real time detection of reactive current[J]. Communication Power Technology, 2014, 31(1): 57–59. (in Chinese) |
| [7] | Zhang D Y, Liu Y Q, Cao J. Application of single neuron adaptive PID control during the process of timber drying[J]. Journal of Forestry Research, 2003, 14(3): 244–248. DOI:10.1007/BF02856839 |
| [8] |
王兆安, 杨君, 刘进军, 等. 谐波抑制和无功功率补偿[M]. 北京: 机械工业出版社, 2005.
WANG Zhaoan, YANG Jun, LIU jinjun, et al. Harmonic suppression and reactive power compensation[M]. Beijing: Mechanical Industry Press, 2005. (in Chinese) |
| [9] | McGrath B P, Holmes D G. Analytical modelling of voltage balance dynamics for a flying capacitor multilevel converter[J]. IEEE Transactions on Power Electronics, 2008, 23(2): 543–550. DOI:10.1109/TPEL.2007.915175 |
| [10] | McGrath B P, Holmes D G. Analytical determination of the capacitor voltage balancing dynamics for three-phase flying capacitor converters[J]. IEEE Transactions on Industry Applications, 2009, 45(4): 1425–1433. DOI:10.1109/TIA.2009.2023480 |
| [11] | Pan Z G, Peng F Z. A sinusoidal PWM method with voltage capability balancing for diode-clamped five-level convert-ers[J]. IEEE Transactions on Industry Applications, 2009, 45(3): 1028–1034. DOI:10.1109/TIA.2009.2018962 |
| [12] | Saeedifard M, Bakhshai A, Joos G. Low switching frequency space vector modulators for high power multimodule converters[J]. IEEE Transactions on Power Electronics, 2005, 20(6): 1310–1318. DOI:10.1109/TPEL.2005.857532 |
| [13] |
黄湘源, 夏向阳, 周云, 等.
一种改进的谐波电流检测方法及其实现[J]. 电力科学与工程, 2010, 26(9): 59–62.
HUANG Xiangyuan, XIA Xiangyang, ZHOU Yun, et al. An improved harmonic current detection method and its realization[J]. Electric Power Science and Engineering, 2010, 26(9): 59–62. (in Chinese) |
| [14] | Shi Y, Liu B, Duan S. Eliminating DC current injection in current-transformer-sensed STATCOMs[J]. IEEE Tran-sactions on Power Electronics, 2013, 28(8): 3760–3767. DOI:10.1109/TPEL.2012.2228883 |
| [15] |
王昊宁. 直接电流控制的静止无功发生器的研究[D]. 济南: 山东大学, 2010. WANG Haoning. Direct current control of static var generator[D]. Jinan:Shandong University, 2010.(in Chinese) |
| [16] | Mohammadi P H, Bina M T. A transformerless medium-voltage STATCOM topology based on extended modular multilevel converters[J]. IEEE Transactions on Power Electronics, 2011, 26(5): 1534–1545. DOI:10.1109/TPEL.2010.2085088 |
| [17] | Hagiwara M, Maeda R, Akagi H. Negative-sequence reactive-power control by a PWM STATCOM based on a modular multilevel cascade converter (MMCC-SDBC)[J]. IEEE Transactions on Industry Applications, 2012, 48(2): 720–729. DOI:10.1109/TIA.2011.2182330 |
 2017, Vol. 40
2017, Vol. 40


