当前对于声振响应预测的数值方法主要包括：基于单元类的方法如有限元法(FEM)、边界元法等^[1-2]，但该类方法由于存在插值误差与污染误差^[3]，对于较高频率问题的仿真需要更小尺寸的单元来获取短波特性，这导致了计算成本的显著增加，因此这类方法主要用于低频问题的预测；而基于模态理论的统计类方法，其理论前提则要求分析的子系统的1/3倍频程模态数大于5^[4]，也即该类方法只能运用于高频的声振响应分析。因而，在低频与高频间缺少了较高效可靠的数值分析方法，即是在20世纪发现的“中频危机”。为此，从欧洲开始了对中频类数值分析方法的探索，如超弱变分公式(UWVF)^[5]、波边界元方法(WBEM)^[6]、自由单元Galerkin法(EFGM)^[7]、复射线变分理论(VTCR)^[8]、混合FE-SEA法^[9]等。其中惟一商用的混合FE-SEA方法就是单元类方法与统计类方法的结合，但该方法也是基于能量的耦合，得到的仍是时间与空间的平均，无法得到模型的确定性细节。而基于间接Treffz理论而建立的波函数法(WBM)则是全局性的确定性方法。自Desmet教授^[10]提出波函数法理论以来，该方法已成功运用于基于Kirchhoff理论^[11-12]与Mindlin理论^[13]的平板振动响应预测，结构声学耦合响应分析^[14]，混合有限元波函数法^[15]耦合等响应预测，都表现出了非常高的计算效率与精度，为中频声振问题的预测提供了很好的手段。

作为工程中对薄板类结构常用的减振方式，板梁耦合结构如加筋薄板也大量应用于汽车、航空等领域，而且该类结构包含薄板短波子系统与梁长波子系统，是典型具有中频特性的结构。因此，以波函数理论实现该类耦合结构的振动响应，更精确地描述其中频振动响应，为后续的改进与优化提供依据都有重要的工程意义。笔者以Kirchhoff薄板与Euler-Bernoulli梁理论为基础，结合波函数法，推导出板梁耦合结构的振动响应预测模型，并进行了数值验证，证明了该方法的有效性。

波函数法是一种间接Trefftz方法，利用精确满足控制方程的波函数来表示场变量，再通过边界残差值积分最小化的方法求取各波函数系数，从而获得结构或声学的响应。

对于各向同性薄板的法向稳态位移w_z在Kirchhoff理论下满足^[16]

式中：${\nabla ^4} = \frac{{{\partial ^4}}}{{\partial {x^4}}} + 2\frac{{{\partial ^4}}}{{\partial {x^2}\partial {y^2}}} + \frac{{{\partial ^4}}}{{\partial {y^4}}}$；δ为Dirac函数；k_b为薄板弯曲波数；D为薄板弯曲刚度。

而根据波函数法理论，将薄板的法向振动位移响应展开成一系列的波函数，

式中：Φ = {φ₁, φ₂, …, φ_i}, 即严格满足控制方程齐次解的波函数^[10]，取Φ=e^{-j(k_xx+k_yy)}, 且(k_x²+k_y²)²=k_b⁴。W = {w₁, w₂, …, w_i}为各波函数的权系数，也为需求解的未知量。${\hat w_{\rm{F}}}$为外界作用的特解, 对于r_F点激励有

对于x向长度为L的细梁，由Euler-Bernoulli可知，在x_F处施加F，在x_T处施加扭矩T时，其弯曲与扭转振动响应控制方程分别为^[17]

式中：k_bl是梁的弯曲波数；k_tl为梁的扭转波数；E为弹性模量；I为截面矩；G为剪切模量, I_p为极惯性矩；J为截面惯性矩。

同样按波函数法理论，梁结构位移与扭转角度的精确解分别由两类波函数来表示

式中：波函数ψ(x)、Γ(x)分别精确满足梁的齐次弯曲与扭转控制方程，定义为

对于位于x_F的单位力和位于x_T的单位扭矩产生的特解${{\hat u}_{\rm{F}}}(x)、{{\hat \theta }_{\rm{T}}}(x)$也分别定义为^[18]

对于板或梁结构，在其各自的边界运用加权余量公式求得各波函数的权系数后即可得到板或梁的振动响应，但对于板梁耦合结构，除了各自的边界外，还需在接合面进行耦合。笔者采用接合边界上的薄板与梁在法向位移与转角上进行耦合，得到耦合边界残差为

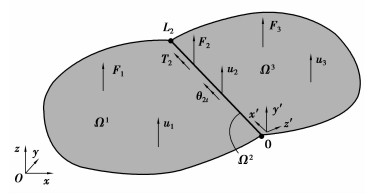
文中e=(1, 3) 分别为图示中1和3区域薄板，γ_e为薄板域内梁的纵向方向。

图 1(Figure 1)

图 1 板梁耦合示意图 Figure 1 Problem domain of plate beam coupling

由于梁在耦合边界上受到两边板对其的作用，耦合系统中梁的弯曲位移响应与扭转响应定义为：

式中：${{\mathit{\boldsymbol{\hat u}}}_{2s3}}、{{\hat u}_{2Fe}}、{{\mathit{\boldsymbol{\hat \theta }}}_{2se}}、{{\hat \theta }_{2Fe}}$分别为板波函数与特解对梁的作用方程。

将耦合边界残差公式(10)(11) 添加到板的加权余量公式中有

算子${L_{{\theta _{\rm{n}}}}}{\rm{ = }}-\frac{\partial }{{\partial {\gamma _{\rm{n}}}}}, {L_{{{\rm{m}}_{\rm{n}}}}} =-D(\frac{{{\partial ^2}}}{{\partial \gamma _{\rm{n}}^2}} + v\frac{{{\partial ^2}}}{{\partial \gamma _{\rm{s}}^2}}), {L_{{{\rm{Q}}_{\rm{n}}}}} =-D\frac{\partial }{{\partial {\gamma _{\rm{n}}}}}(\frac{{{\partial ^2}}}{{\partial \gamma _{\rm{n}}^2}} + (2 - v)\frac{{{\partial ^2}}}{{\partial \gamma _{\rm{s}}^2}})$，γ_n、γ_s分别为平板边界的法线和切线方向。

运用迦辽金法将式(2)(12)(13) 代入式(14) 即可得到系统矩阵

结合实际边界条件求解该矩阵就能获得板波函数的权系数u₁，u₃和梁波函数的权系数u₂，θ_2t，再分别代入各自的波函数展开式就可以得到板、梁的振动响应。

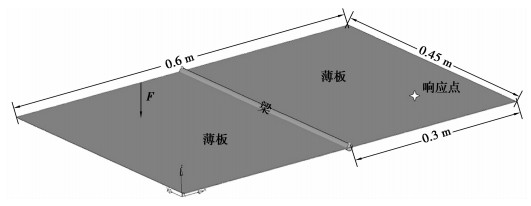
为验证该方法的有效性，引入了加梁矩形薄板，其尺寸形状如图 2所示。板与梁都为钢材，材料密度ρ=7 900 kg/m³, 弹性模量E=2.1×1 011 Pa, 泊松比μ=0.3。板的厚度h=0.001 m。细长梁结构为实心圆截面，其截面参数为：面积为78.54×10^-6 m²，截面矩为490.87×10^-12 m⁴，极惯性矩为981.75×10^-8 m⁴，截面惯性矩为981.75×10^-8 m⁴。耦合模型的周边固支，并在点(0.140 m, 0.320 m)处施加一法向单位力激励，同时选取点(0.480 m, 0.165 m)为频响参考点。

图 2(Figure 2)

图 2 薄板与梁耦合几何域 Figure 2 Coupled plate-beam problem

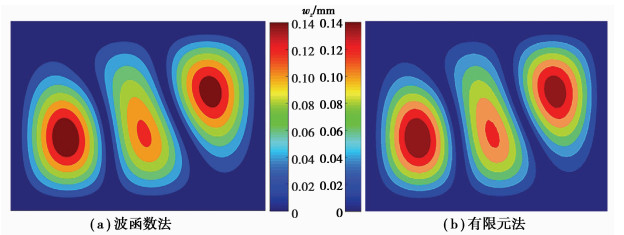
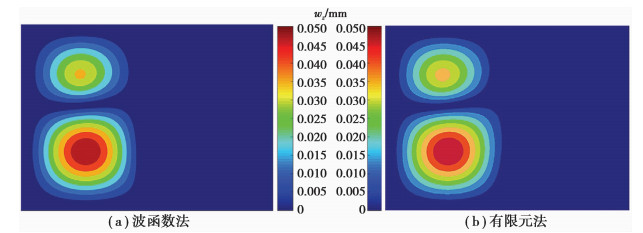
为了与波函数法进行比较，该模型也以有限元法进行计算。有限元模型选取四边形单元，其建立和计算都在MSC/Nastran中完成。而波函数法模型的构建与计算均以matlab2016a平台完成。图 3、图 4分别为100 Hz时薄板和薄板加梁系统的法向振动位移响应。从两云图可以看出，对于纯薄板与添加梁结构后的板梁耦合系统，波函数法计算结果与有限元精细建模的结果很好地吻合。而且相比于图 3，添加梁结构后的耦合系统响应有了明显的变化，除了全局振动幅值降低外，梁右边薄板的振动响应已经被明显抑制，说明梁结构对薄板刚度增加效果明显，也验证了所提方法的正确性。

图 3(Figure 3)

图 3 未添加梁结构的薄板法向振动位移响应对比 Figure 3 Comparison of displacement of plate without beam at 100 Hz

图 4(Figure 4)

图 4 添加梁结构后薄板法向位移响应对比 Figure 4 Comparison of displacement of plate with a beam at 100 Hz

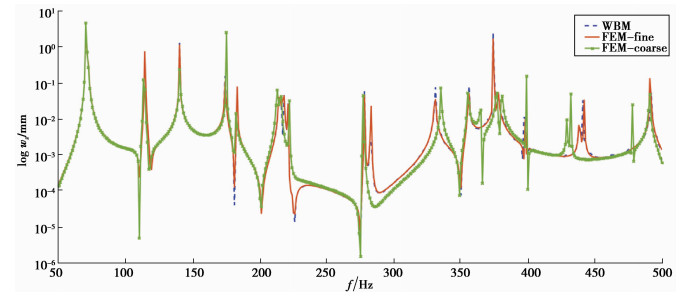
同时，为验证该方法在其他频率下的响应，以及反映有限元方法的频率响特性，选取响应参考点在50~500 Hz的振动位移响应进行了对比分析。图 5为添加梁后薄板选取响应点的频响结果，图中包含了较大单元尺寸(8 mm)和精细单元尺寸(2 mm)两种有限元模型的结果。从对比结果可以看出，波函数法在分析频段内与精细有限元模型的计算一致，而尺寸较大的有限元模型虽在频响趋势与波函数法计算结果相符，但在200 Hz左右开始位移响应出现偏移，而且这种偏移随着频率的增加而变得更加严重。有限元法应用在较高频率且针对较复杂结构时需要大量精细的单元来获取短波细节，造成了计算模型过大、CPU计算时间过长，因此单元类方法主要用于低频类问题的预测分析。

图 5(Figure 5)

图 5 板梁耦合结构参考点频率响应 Figure 5 Bending vibration response with beam

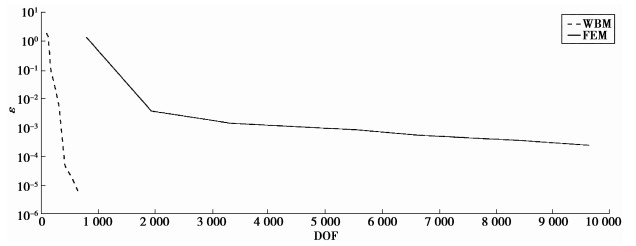
同时，除了精度的保证，收敛性也是评价数值算法优劣的主要指标。图 6为波函数法与有限元法在100 Hz时的收敛曲线，图中横坐标为模型计算自由度DOF(degree of freedom)，即前文论述的波函数数量，纵坐标为相对误差$\varepsilon = \left| {\frac{{w-{w_{{\rm{ref}}}}}}{{{w_{{\rm{ref}}}}}}} \right|$, w_ref为选定参考点在100 Hz时法向振动位移响应，w_ref为100 Hz精细有限元模型的位移响应值。图 7为100 Hz时计算精度与计算时间的对比曲线。从图中可以看出，在相同计算精度的前提下，波函数法的计算成本(模型计算所需自由度与计算时间)较有限元法显著减少。这也是波函数法除了其本身没有单元划分带来的差值误差和污染误差外，能更好地运用于较高频率声振预测的原因。同时，利用波函数法计算的高效性，可以更好地应用于需要大量重复计算的前期设计与改进优化阶段。

图 6(Figure 6)

图 6 100 Hz计算相对误差与自由度曲线对比 Figure 6 Convergence comparisondegree of freedom at 100 Hz

图 7(Figure 7)

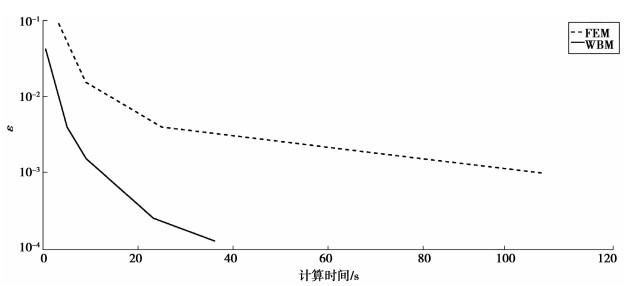
图 7 100 Hz计算相对误差与计算时间曲线对比 Figure 7 Convergence comparison with computational time at 100 Hz

笔者综合Kirchhoff薄板振动理论、Euler-Bernoulli梁理论和波函数理论，以法向位移与扭转角为接合边界的连续性条件，运用迦辽金法推导了耦合系统的加权余量公式，构建了计算板梁耦合结构振动响应的波函数模型。并引入周边固支加梁薄板模型，与有限元法进行了对比，数值验证表明，所提出的基于波函数法计算板梁耦合结构的方法是有效的，而有限元法为保证计算的准确需要精细的模型，且随着频率的提高，单元尺寸要求越小；同时，波函数法在相同计算精度的前提下，相较于有限元法其计算成本显著减少，能更好的预测中频振动响应。在实现对结构振动响应预测的基础上，下一步将研究板梁结构与声腔在波函数法下进行多物理场耦合。