近年来，随着高速公路的快速修建以及物流产业的不断壮大，以重型半挂车为载体的道路运输业蓬勃发展。但重型半挂汽车由于载质量大，质心位置相对较高，车身过长，轮距相对于车身高度过窄等一系列特点，使其侧倾稳定性较差，在转弯或避障的过程中很容易发生侧翻，并且驾驶员对此危险还不易察觉。因此，如何及时告知驾驶员车辆的运行状态，并对车辆的危险状况进行适时的控制，成为解决半挂汽车侧翻问题的关键。

重型车大多数侧翻属于非绊倒型侧翻，目前在侧翻预警及防侧翻控制的研究中，Chen等^[1]基于TTR动态侧翻预警算法，运用神经网络技术提高了预警算法的精度，具有一定的超实时性；和好等^[2]提出基于车身侧倾角估计的TTR侧翻预警算法；朱天军等^[3]采用动态横向载荷转移率作为侧翻预警门限值，结合卡尔曼滤波技术，提出了改进的TTR侧翻预警算法。然而采用神经网络训练，实时性差；预警算法选用汽车的侧倾角作为侧翻指标，因不同车辆的阈值不同，普适性不强，侧翻预警精度不高。金智林等^[4]提出汽车动态侧翻过程稳定性评价指标，提高了侧翻预警实时性及动态侧翻精度；Kenan等^[5]采用线性的车辆动力学模型，开发了实时TTR计算的硬件在环模拟器，然而算法尚未应用到实车侧翻预警系统，且线性模型过于简单，保证了运算速度，却降低了模型精度。Yim等^[6]采用主动防侧倾杆和底盘集成控制相结合的防侧倾控制方法，其中主动防侧倾杆用于控制汽车侧倾运动，底盘集成控制提高侧倾稳定性的同时保证车辆可操控性^[6-7]。相比主动转向、差动制动会改变驾驶员意图，主动、半主动悬架过于复杂，成本较高，采用主动防侧倾杆则弥补了以上不足。综上所述，基于模型反馈的运动预测技术结合状态估计的方法具有其优越性，建立动力学模型超实时预测车辆侧翻危险状态，能预留给驾驶员更多的反应时间。

笔者以TruckSim中自带的车辆模型为真实车辆，考虑汽车运行过程中的过程噪声及量测噪声，利用Kalman滤波技术实时估计半挂汽车的当前运行状态，并建立了基于模型的TTR预警算法和防侧倾控制算法，实现了侧翻危险状态的实时预警和对挂车侧倾的非连续性控制。

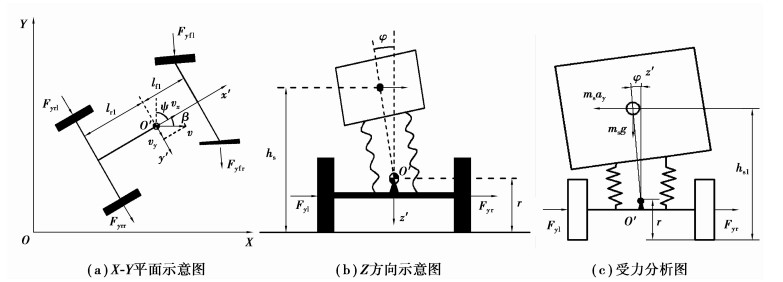
如图 1(a)(b)所示，选取的大地坐标系为XOYZ，车辆坐标系x′o′y′z′固结于车身上，以车辆质心的铅垂线和侧倾轴线的交点为原点o′，以车辆的纵向为x′轴，前进方向为正；y′轴平行于地面，指向驾驶员右侧；过o′点的垂直方向为z′轴，向下为正。

图 1(Figure 1)

图 1 坐标系及受力分析示意图 Figure 1 Coordinate system and force analysis schematic

对于侧倾分析，只需求解侧向力方程F_y、侧倾力矩M_x和横摆力矩M_z。在固结于车身的坐标系中，假设前进速度恒定不变，忽略垂向和俯仰运动，则运动的一般方程为：

式(1)—(3) 中：m为整车质量; v_x为纵向车速; v_y为侧向车速; I_xx为侧倾转动惯量; I_xz为侧倾横摆惯性积; I_zz为横摆转动惯量。

刚性车身的侧倾受力分析如图 1所示，根据刚体运动模型分别建立牵引车和半挂车的数学模型。

沿y′轴力平衡方程式：

其中Y_β1=k_αf1+k_αr1，Y_δf1=－k_αf1，${Y_{\dot \psi 1}} = {k_{\alpha {\rm{f}}1}}\frac{{{l_{{\rm{f}}1}}}}{{{v_x}}}-{k_{\alpha {\rm{r}}1}}\frac{{{l_{{\rm{r}}1}}}}{{{v_x}}}$。

式中：m_s1为牵引车簧载质量；m₁为牵引车整车质量；φ_s1为牵引车簧载质量侧倾角；β₁为牵引车质心侧偏角；ψ₁为牵引车横摆角；δ为转向轮转角；F₅为第5轮处的力；k_αf1、k_αr1分别为牵引车前、后轮胎侧偏刚度；l_f1、l_r1分别为牵引车质心至前后轴的距离。

绕z′轴力矩平衡方程式：

其中N_β1=l_f1k_αf1－l_r1k_αr1，${N_{\dot \psi 1}} = {k_{\alpha {\rm{f}}1}}\frac{{{l_{{\rm{f}}1}}^2}}{{{v_x}}}-{k_{\alpha {\rm{r}}1}}\frac{{{l_{{\rm{r}}1}}^2}}{{{v_x}}}$。

式中：φ_uf1、φ_ur1分别为牵引车前、后非簧载质量侧倾角；I_z′z′1为牵引车横摆转动惯量；I_x′z′s1、I_x′z′uf1、I_x′z′ur1分别为牵引车簧载质量和前、后非簧载质量侧倾横摆惯性积；k_ψ为第5轮处的横摆刚度；ψ₂为挂车横摆角。

簧载质量绕x′轴的力矩平衡方程式：

式中：I_x′x′s1为牵引车簧载质量侧倾转动惯量；k_f1、k_r1分别为牵引车前、后悬架侧倾刚度；c_f1、c_r1分别为牵引车前、后悬架阻尼；k_φ为第5轮处的侧倾刚度；φ_s2为挂车簧载质量侧倾角；h₅为第5轮离地高度。

前非簧载质量绕x′轴的力矩平衡方程式：

其中Y_βf1=k_αf1，${Y_{\dot \psi {\rm{f}}1}}{\rm{ = }}{k_{\alpha {\rm{f}}1}}\frac{{{l_{{\rm{f}}1}}}}{{{v_x}}}$。

式中：I_x′x′uf1为牵引车前非簧载质量侧倾转动惯量；k_tf1为牵引车前轮胎侧倾刚度。

后非簧载质量绕x′轴的力矩平衡方程式:

其中Y_βr1=k_αr1，${Y_{\dot \psi {\rm{f}}1}}{\rm{ = }}-{k_{\alpha {\rm{r}}1}}\frac{{{l_{{\rm{r}}1}}}}{{{v_x}}}$。

式中：I_x′x′ur1为牵引车后非簧载质量侧倾转动惯量；k_tr1为牵引车后轮胎侧倾刚度。

沿y′轴力平衡方程式：

其中Y_βr2=k_αr2，${Y_{\psi {\rm{r2}}}}{\rm{ = }}-{k_{\alpha {\rm{r2}}}}\frac{{{l_{{\rm{r2}}}}}}{{{v_x}}}$。

式中：m_s2为挂车簧载质量；m₂为挂车整车质量；β₂为挂车质心侧偏角；ψ₂为挂车横摆角；k_αr2为挂车轮胎侧偏刚度；l_r2为挂车质心至后轴的距离。

绕z′轴力矩平衡方程式：

其中N_β2=-l_r2k_αr2，${N_{\dot \psi {\rm{2}}}}{\rm{ = }}{k_{\alpha {\rm{r2}}}}\frac{{{l_{{\rm{r2}}}}^2}}{{{v_x}}}$。

簧载质量绕x′轴的力矩平衡方程式：

式中：φ_ur2为挂车非簧载质量侧倾角; I_z′z′2为挂车横摆转动惯量; I_x′z′s2、I_x′z′ur2分别为挂车簧载质量和非簧载质量侧倾横摆惯性积; l_f2为挂车质心至第5轮距离。

非簧载质量绕x′轴的力矩平衡方程式：

式中:I_x′x′s2为挂车簧载质量侧倾转动惯量; k_r2为挂车悬架侧倾刚度; c_r2为挂车悬架阻尼; h₅为第5轮离地高度。

第5轮处的约束方程：

轮胎非线性对车辆的操纵稳定性有重要影响，为了模型的准确性，笔者建立了非线性轮胎模型，其侧偏刚度F_y/α与轮胎垂直载荷F_z之间的关系可用式(14) 来描述：

式中：c₁和c₂的值可以在平板式轮胎测试台上进行低速动态滚动试验，然后将测试数据经过拟合得到^[8]。

半挂汽车的状态空间变量为：

控制输入为：u = [u_f1 u_r1 u_r2]^T，将式(1)—(14) 写成状态空间表达式

其中控制输入量u_f1、u_r1、u_r2分别为牵引车前轴、驱动轴及挂车集中车轴的辅助力矩；δ为转向轮输入转角；A、B₀、B₁为状态矩阵。

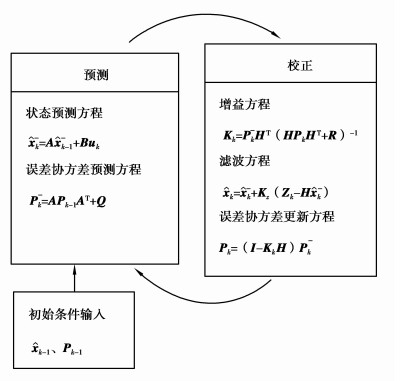
目前常见的侧翻预警算法主要有基于门限值的侧翻预警算法和基于时间的动态侧翻预警算法两种，后者可以实时提醒驾驶员关于车辆在未来一段时间内的侧翻危险程度，所以笔者采用基于时间的TTR侧翻预警算法来预测半挂汽车的侧翻危险状态。但TTR算法中需要的一些状态变量难于或者无法测取，同时为了减少车辆中传感器的布置，所以将Kalman技术融合于其中，实现对实车状态的动态估计。

状态估计就是在系统数学模型已知的前提下，通过某一时刻的已知状态y_k去估计该时刻或下一个时刻的未知状态x_k的过程。Kalman滤波器通过估计过程中某一时刻的状态，然后以(含噪声的)测量变量的方式获得反馈，因此Kalman滤波可分为时间更新过程和测量更新过程两部分^[9-10]。其工作过程如图 2所示。

图 2(Figure 2)

图 2 Kalman滤波算法及其滤波方程的示意图 Figure 2 Kalman filter algorithm and its filtering equation schematic

将笔者建立的九自由度模型写成状态方程的形式并进行离散化，这里假设系统的状态方程和量测方程如下^[10]：

其中w_k、v_k为相互独立的系统过程噪声和传感器测量噪声。

以TruckSim中牵引车和挂车的横摆角速度${\dot \psi _1}、{\dot \psi _2}$以及3个非簧载质量侧倾角φ_uf1、φ_ur1、φ_ur2为测量变量，对牵引车和挂车的簧载质量侧倾角度φ_s1、φ_s2以及质心侧偏角β₁、β₂进行估计，测量值和估计值作为侧翻预警模型进行迭代的初始值。

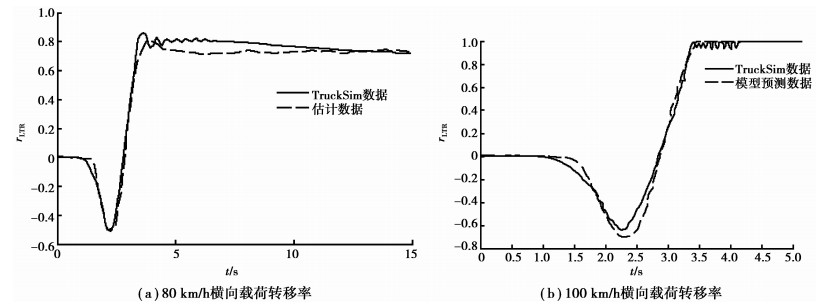
表 1为半挂汽车模型主要参数，图 3(a)、(b)为鱼钩转向工况下通过Kalman滤波得出的半挂汽车横向载荷转移率与TruckSim中实际半挂汽车的横向载荷转移率的对比，可以看出估计值可以较好地跟随实际值，为后续预警算法的准确性提供了保证。

图 3(Figure 3)

图 3 横向载荷转移率对比图 Figure 3 Lateral load transfer ratio comparison

表 1(Table 1)

表 1 半挂汽车模型主要参数 Table 1 Main parameters of semi trailers model 模型 ms/ kg Ix′x′s/ (kg·m2) Iz′z′s/ (kg·m2) Ix′z′s/ (kg·m2) l/m lf/m lsf/m lsr/m r/m hs/m huf/m hur/m 牵引车 6 873 6 234 27 071 2 284 5.07 1.846 2.210 2.01 0.53 1.1 0.51 0.528 半挂车 26 660 30 312 493 663 -1 318 11.30 6.670 3.281 4.25 0.53 1.5 — 0.528

表 1 半挂汽车模型主要参数 Table 1 Main parameters of semi trailers model

侧翻预警时间t_TTR定义为固定当前时刻转向盘转角输入，以当前时刻车辆运动状态为初始条件，汽车运行到发生侧翻(即一侧轮胎离开地面)的剩余时间。

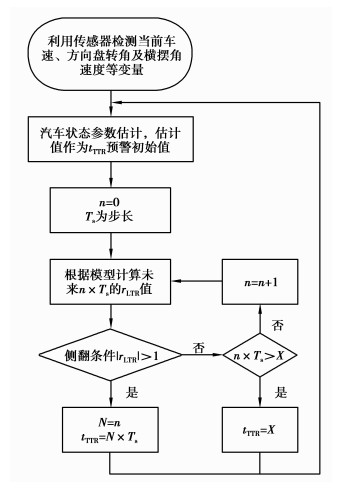
该算法以侧翻预警模型为基础，利用计算机实时计算汽车在未来X秒(为减小计算机运算量和保证算法实时性，本文X=3) 内的侧翻指标值，一旦检测到满足侧翻条件，则记录计算步数N, t_TTR为步数N与步长T_s(这里选取T_s=0.02) 的乘积。侧翻预警算法流程图如图 4所示^[1]。

图 4(Figure 4)

图 4 侧翻预警算法流程图 Figure 4 Rollover warning algorithm flowchart

为了表示汽车侧翻的危险程度，笔者选取具有高可信度的横向载荷转移率r_LTR(lateral load transfer rate, LTR)作为侧翻指标^[11]。r_LTR定义为

式中：F_Li和F_Ri分别为第i根轴左右轮胎的垂直载荷; n为半挂汽车车轴总数; 当r_LTR= ±1时表示有一侧的车轮已离开路面，车辆开始侧翻。

考虑到左右轮胎的横向载荷转移率在汽车行驶过程中难以测量，故结合已建立的半挂车模型及Kalman状态估计算法，在Hyun等^[12]提出的横向载荷转移率的基础上进行扩展：

式中：φ_{u, i}为第i根轴非簧载质量侧倾角；φ_{umax, i}为挂车不翻车情况下第i轴的最大允许侧倾角度；k_t为车轴上轮胎的刚度；m_effg为相应车轴的载荷；d为轮距。

为减少半挂汽车侧翻的发生，笔者采用主动横向稳定器(又称主动防侧倾杆)对车辆的侧倾危险状况进行控制。它在车轴两端各安装一个液压作动器，当车辆出现侧翻危险时通过提供主动辅助侧倾力矩来控制车辆的横向载荷转移，从而防止侧翻的发生。

由于建立的半挂汽车输出状态变量多于输入控制变量个数，系统输入不足，导致系统不可控。由此看出，单独靠主动横向稳定器不可能对所有的目标变量进行有效的控制。因此，为了能够有效控制半挂汽车的侧翻，选取以平衡各个车轴的横向载荷转移率以及控制各非簧载质量的侧倾角度为控制目标，既要尽量降低车辆各轴的横向载荷转移率，又要保证由于主动横向稳定器所施加的辅助防侧倾力矩不会使非簧载质量侧倾角度过大而导致侧翻的发生^[13]。

线性二次最优控制以线性系统为控制对象，以包含系统状态和控制输入的二次型函数为控制目标，本质是用较小的控制输入保持系统较小的误差，使控制能量和输出误差综合最优。

笔者设计线性二次型最优调节器LQR(linear quadratic regulator)控制车辆侧翻。

对于完全可控离散系统的状态方程为：

离散线性二次型最优控制的目标就是寻求最优控制向量u(k)，使二次型性能指标值达到最小^[8]：

式中: Q与R分别为性能输出z以及控制输入u的加权矩阵。

最优控制规律为：

式中：K为最优反馈增益矩阵；P为常值正定矩阵并且满足黎卡提(Riccati)代数方程

最优控制的关键是反复调节加权矩阵Q和R，以使横向载荷转移以及非簧载质量侧倾角度达到所需要的设计目标^[14]。

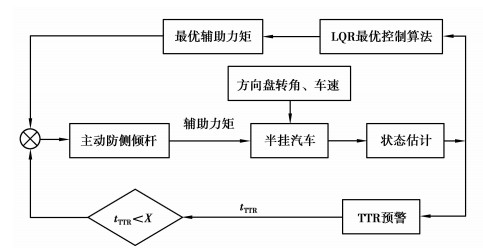
在matlab中搭建半挂汽车的预警和控制模型，然后在TruckSim中定义模型的输入输出接口，通过联合仿真的形式验证预警及控制算法的有效性。为实现挂车的间断性控制, 将t_TTR值作为控制器触发的门限值。其原理是当t_TTR值开始倒计时时(即t_TTR < 3 s)，接通LQR控制器；当t_TTR≥3 s时，说明汽车在未来3 s内不会发生侧翻危险，故防侧翻装置不工作，不对车辆进行控制。其防侧翻控制策略如图 5所示。

图 5(Figure 5)

图 5 基于tTTR预警的侧翻控制框图 Figure 5 Rollover control block diagram based on tTTR warning

选择车辆的速度为80 km/h，反复选择验证加权矩阵Q和R，得到的结果如下：

根据选取的Q与R矩阵经计算生成全状态反馈控制器。最优反馈矩阵为：

笔者采用角阶跃仿真工况对所提出的侧翻预警算法和防侧翻控制方法进行仿真分析。仿真车速设定为80 km/h，在2 s时刻对牵引车转向轴转向输入一阶跃信号，经过0.5 s之后达到最大转角11°，得到的仿真结果如下。

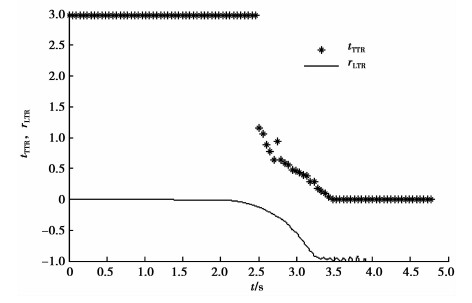
通过图 6可以看出，半挂汽车在3.4s时横向载荷转移率达到-1，从仿真动画中可以看到半挂汽车开始侧翻，预警系统从2.5 s时开始检测到侧翻危险，并进行TTR倒计时，到3.48 s时t_TTR变为0，即半挂汽车发生侧翻，说明建立的TTR侧翻预警算法具有较高的可信度，可以准确提醒驾驶员未来时刻侧翻危险的发生，为驾驶员采取防侧翻措施赢得时间。

图 6(Figure 6)

图 6 横向载荷转移率与TTR对比 Figure 6 Lateral load transfer rate compared with TTR

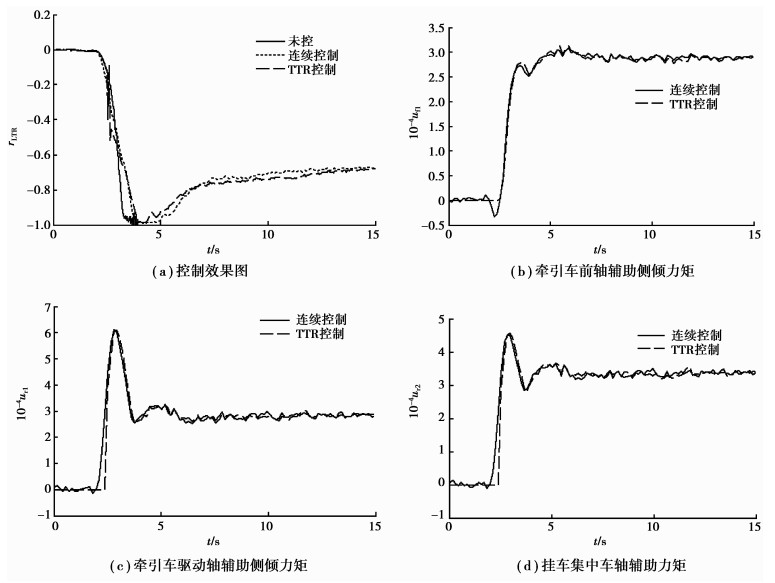
由图 7(a)—(d)可知，与连续控制系统相比，基于TTR预警的防侧翻控制也可以降低半挂汽车在危险工况下的横向载荷转移率，有效防止车辆侧翻危险的发生。且基于TTR预警的防侧翻控制只有检测到侧翻危险发生时其控制装置才进行工作，有效减少了主动防侧倾装置的工作时间，实现了间断性控制，进而降低了主动防侧倾装置的功率消耗，提高其使用寿命。

图 7(Figure 7)

图 7 控制效果及各辅助力矩对比图 Figure 7 The comparison of control effect and auxiliary overturning moment

虽然主动防侧倾装置可以提高半挂汽车的侧倾稳定性，但是从图 7中可以看出控制后的横向载荷转移率r_LTR也已接近-1，如果此时驾驶员继续增大方向盘转角或提高车速，侧翻的发生将不可避免。所以通过预警系统及时提醒驾驶员车辆的侧翻危险状态，进而使驾驶员采取相应措施(如降低车速、减小方向盘转角等)来降低侧翻风险尤为重要。

1) 将预警与防侧翻控制进行有效结合，建立了基于模型预测的侧翻预警算法。仿真结果分析表明TTR预警系统可以超实时地预测车辆的侧倾稳定性，为驾驶员反应并采取相应操作避免侧翻危险赢得时间。

2) 通过LQR最优控制算法并结合TTR预警不仅可以有效提高半挂汽车的侧倾稳定性，还可以减少能量消耗，并提高主动防侧倾稳定装置的寿命。

3) 由于半挂汽车运动较为复杂, 为了更加精确地获得车辆动态状态, 可以考虑建立更加复杂的非线性模型, 利用扩展kalman滤波或者无迹kalman滤波进行状态估计。

4) 驾驶员作为“人—车—路”系统中不可或缺的因素，如果可以对驾驶员行为进行研究，并根据不同的驾驶风格动态地改变TTR门限值，从而改变防侧翻控制系统介入的时间，将会进一步提高防侧翻控制效果。