b. 重庆大学 软件学院, 重庆 400044
b. School of Software Engineering, Chongqing University, Chongqing 400044, P. R. China
密码技术是保证现代通信安全的重要工具。目前,实际应用中广泛使用的密码方案主要有:RSA、DSA以及ECC。这些密码方案的理论基础几乎都是数论难题,如:大整数的因子分解问题、离散对数问题等。随着量子计算机的实现,这些方案将变得不再安全。在量子计算机上利用Shor算法[1],可以在多项式时间内完成大整数分解和离散对数求解。因此,设计能够抵抗量子计算攻击的公钥密码方案,来取代这些传统的密码方案,显得尤为重要。
多变量公钥密码方案是一种业界公认的能抵抗量子计算攻击的备选方案,具有执行速度快,且仅需要模块化的计算资源的特性。可以将其应用到低功耗的设备中,如RFID、IC卡[2]、传感网络等[3-5]。现在已经有许多能应用于实际应用的多变量公钥签名方案[6-10]。但是,高效且安全的多变量公钥加密方案却很少。
在2013年的后量子密码会议上,Tao等人提出了一种新的多变量公钥加密方案:简单矩阵加密方案(simple matrix scheme)[11]。该方案具有较高的效率,同时还能抵抗所有已知的针对多变量公钥密码方案的攻击算法。随后,Ding与Petzoldt对该方案的安全性做了进一步加强,提出3次简单矩阵加密方案(cubic simple matrix scheme)[12]。之后,Tao与Xiang[13]、Petzoldt与Ding[14]对该方案的解密失败概率进行改进。除此之外,针对简单矩阵原始方案中密文明文长度比固定为2的情况,Petzoldt提出了一种改进方案:ABCD加密方案[14],使得密文明文长度比不再固定为2。但是,ABCD方案的密文明文长度比值,可选范围很小,只有2个值。
针对ABCD加密方案提出进行改进,设计Cubic AB加密方案。利用Cubic AB加密方案,可增大密文明文长度比值可取范围。除此之外,Cubic AB加密方案借鉴三次简单矩阵加密方案的思想,使用随机二次多项式构造公钥来提高安全性。使得Cubic AB加密方案除了能抵抗求解随机二次方程组的代数攻击,还能抵抗秩攻击。
1 简单矩阵加密方案介绍多变量公钥密码体系的主要思想和简单矩阵加密方案。
1.1 多变量公钥密码体系多变量公钥密码体系的核心部分在于构建了一组二次多项式
| $ \begin{array}{l} {p^{\left( 1 \right)}}\left( {{x_1}, ..., {x_n}} \right) = \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {p_{ij}^{\left( 1 \right)}} } \cdot {x_i}{x_j} + \sum\limits_{i = 1}^n {p_i^{\left( 1 \right)}} \cdot {x_i}, \\ {p^{\left( 2 \right)}}\left( {{x_1}, ..., {x_n}} \right) = \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {p_{ij}^{\left( 2 \right)}} } \cdot {x_i}{x_j} + \sum\limits_{i = 1}^n {p_i^{\left( 2 \right)}} \cdot {x_i}, \\ {p^{\left( m \right)}}\left( {{x_1}, ..., {x_n}} \right) = \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {p_{ij}^{\left( m \right)}} } \cdot {x_i}{x_j} + \sum\limits_{i = 1}^n {p_i^{\left( m \right)}} \cdot {x_i}, \end{array} $ | (1) |
该类密码方案的安全性依赖于MQ(multivariate quadratic)问题。即:在公式(1) 中的个m二次多项式p(1)(x), …, p(m)(x)中,找出一个n维向量X(x1, x2, …, xn),使得p(1)(x)=…=p(m)(x)=0。而MQ问题的困难性已经被证明:当m≈n时,即便在有限域GF(2) 上,MQ问题也是一个NP难题[15]。
通过MQ问题构建公钥密码方案,需要:1) 找到一个很容易进行逆运算的二次映射F:Fn→Fn。通常这个映射F也被称为中心映射。2) 对外提供公钥时,中心映射需要被隐藏起来。因此将中心映射,与另外2个可逆线性仿射S:Fm→Fm和T:Fn→Fn复合。容易看出,通过这种方式构建的公钥密码系统,其安全性不仅只依赖MQ问题,还依赖于EIP(extended isomorphism of polynomials)问题。3) 最终对外提供的公钥为:P=SoFoT:Fn→Fm。而私钥则包括:中心映射F,以及2个线性仿射S、T。
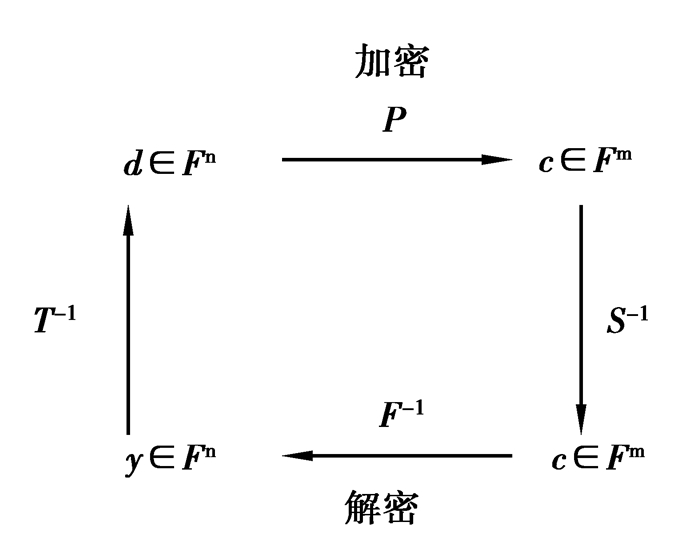
多变量公钥加密方案的标准加密、解密过程如图 1所示。
|
图 1 多变量加密方案标准加密解密流程 Figure 1 Encrgption and decryotion process of multivariate |
加密:对明文d∈Fn进行加密,只需要简单地用公钥,计算c=P(d),便得到密文c∈fm。
解密:对密文c∈fm进行解密,需要进行3次计算,即:x=S-1(c),y=F-1(x)和d=T-1(y)。由此,得到密文c对应的明文d∈fn。
对于多变量公钥加密方案,通常有m>n,因此通过解密过程得到的明文是唯一的。
1.2 简单矩阵加密方案由Tao提出的简单矩阵加密方案的结构如下:
密钥生成:有参数s∈N,且存在关系s2=n,2n=m。并定义3个维度为s×s的矩阵A,B与C。形如
| $ \begin{array}{l} \boldsymbol{A = }\left( \begin{array}{l} \;\;\;\;{x_1}\;\;\;\;\;\; \cdots \;\;\;\;\;{x_s}\\ \;\;\;\;\; \vdots \;\;\;\;\;\;\; \ddots \;\;\;\;\;\; \vdots \\ {x_{\left( {s-1} \right) \cdot s + 1}}\;\;\; \cdots \;\;\;\;\;{x_n} \end{array} \right), \;\boldsymbol{B = }\left( \begin{array}{l} \;\;\;\;{b_1}\;\;\;\;\;\; \cdots \;\;\;\;\;{b_s}\\ \;\;\;\;\; \vdots \;\;\;\;\;\;\; \ddots \;\;\;\;\;\; \vdots \\ {b_{\left( {s-1} \right) \cdot s + 1}}\;\;\; \cdots \;\;\;\;\;{b_n} \end{array} \right), \\ \;\;\;\;\;\;\;\;\;\;\;\;\boldsymbol{C = }\left( \begin{array}{l} \;\;\;\;{c_1}\;\;\;\;\;\; \cdots \;\;\;\;\;{c_s}\\ \;\;\;\;\; \vdots \;\;\;\;\;\;\; \ddots \;\;\;\;\;\; \vdots \\ {c_{\left( {s-1} \right) \cdot s + 1}}\;\;\; \cdots \;\;\;\;\;{c_n} \end{array} \right), \end{array} $ |
其中,矩阵B、C的各元素是变量x1, x2, …, xn的随机线性组合。
由矩阵A,B与C计算出矩阵E1=A·B、E2=A·C。容易看出,矩阵E1、E2的维度也为s×s。其元素便是关于变量x1, x2, …, xn的二次多项式。由这m(即:2·s2)个二次多项式构成了中心映射F:Fn→Fm。
然后,随机构造2个可逆线性仿射S:Fm→Fm和T:Fn→Fn,与中心映射F复合,得到公钥P=SoFoT:Fn→Fm。而私钥则包含S,T与F。
加密:与标准过程一样,只需要对明文d∈Fn,进行一次c=P(d)运算即可。
解密:要对密文c∈Fm进行解密,要经过3个步骤进行:
1) 计算x=S-1(c),得到一个m维向量x∈Fm。由简单矩阵加密方案的构造过程得知,将向量x转换为矩阵形式,便可得到矩阵E1和E2,形如
| $ \begin{array}{l} {\boldsymbol{E}_1}\boldsymbol{ = }\left( \begin{array}{l} \;\;\;\;{x_1}\;\;\;\;\;\; \cdots \;\;\;\;\;{x_s}\\ \;\;\;\;\; \vdots \;\;\;\;\;\;\; \ddots \;\;\;\;\;\; \vdots \\ {x_{\left( {s-1} \right) \cdot s + 1}}\;\;\; \cdots \;\;\;\;\;{x_n} \end{array} \right), \\ {\boldsymbol{E}_2}\boldsymbol{ = }\left( \begin{array}{l} \;\;\;\;{x_{n + 1}}\;\;\;\;\;\; \cdots \;\;\;\;\;{x_{n + s}}\\ \;\;\;\;\; \vdots \;\;\;\;\;\;\; \ddots \;\;\;\;\;\; \vdots \\ {x_{n + \left( {s-1} \right) \cdot s + 1}}\;\;\; \cdots \;\;\;\;\;{x_m} \end{array} \right)。\end{array} $ |
2) 参考标准过程,需要求出n维向量y∈Fn,使得F(y)=x。而根据具体情况的不同,有3种不同的方式来求出向量y。
a.若矩阵E1可逆,则由B·E1-1·E2=C得到n个关于y1, y2, …, yn的线性方程。由此,便可求出向量y。
b.若矩阵E1不可逆,但矩阵E2可逆。类似的,有C·E2-1·E1=B。也可得到n个关于y1, y2, …, yn的线性方程。由此,求出向量y。
c.若矩阵E1、E2均不可逆,但矩阵A可逆。将矩阵A-1的元素视为新的未知变量。同时,有A-1E1=B,A-1E2=C。由此,可以得到m个关于y1, y2, …, yn与A-1的各元素的线性方程。
d.若矩阵E1、E2和A均不可逆,则解密失败。
3) 最后,通过线性仿射T,计算出明文d=T-1(y)。
解密失败的概率决定于矩阵A是否可逆,其概率又取决于有限域的元素个数q。所以解密失败的概率大约为1/q。
在进行第二步时,可能会求出多个满足条件的向量y。只需要将求得的结果代入中心映射,判断是否与原密文相同即可。
2 Cubic AB加密方案 2.1 方案结构在所有的简单矩阵加密方案及其变种方案中,其密文明文长度比都为2。即使是ABCD加密方案,其密文明文长度比值,也只能是1.5和1.33其中之一,并不能更灵活地改变密文明文长度之比。笔者提出Cubic AB加密方案,通过使用一个扁长的矩阵B来取代简单矩阵加密方案中的矩阵B和C。并用变量x1, x2, …, xn的二次多项式来充当矩阵A的各元素,以此提高方案的安全性。其结构如下:
密钥生成:参数s, u∈N,且s < u。令m=s·u,n=m-s2=s·(u-s)。由此,定义一个维度为s×s的矩阵A,以及维度为s×u的矩阵B,形如
| $ \begin{array}{l} \boldsymbol{A = }\left( \begin{array}{l} {a_{11}}\;\;\;\;{a_{12}}\;\;\; \cdots \;\;\;\;{a_{1s}}\\ {a_{21}}\;\;\;\;{a_{22}}\;\;\; \cdots \;\;\;\;{a_{2s}}\\ \vdots \;\;\;\;\;\;\;\; \vdots \;\;\;\;\;\; \ddots \;\;\;\;\; \vdots \\ {a_{s1}}\;\;\;\;{a_{s2}}\;\;\; \cdots \;\;\;\;{a_{ss}} \end{array} \right), \\ \boldsymbol{B = }\left( \begin{array}{l} {b_{11}}\;\;\;{b_{12}}\;\; \cdots \;\;{b_{1s}}\;\; \cdots \;\;{b_{1u}}\\ {b_{21}}\;\;\;{b_{22}}\;\; \cdots \;\;{b_{2s}}\;\; \cdots \;\;{b_{2u}}\\ \vdots \;\;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\;\; \vdots \\ {b_{s1}}\;\;\;\;{b_{s2}}\; \cdots \;\;{b_{ss}}\;\;\; \cdots \;\;\;{b_{su}} \end{array} \right)。\end{array} $ |
与简单矩阵加密方案不同的是,矩阵A的各元素是变量x1, x2, …, xn的随机二次多项式;而矩阵B的各元素依然是变量x1, x2, …, xn的随机线性组合。
由矩阵A与B计算出矩阵E=A·B。容易看出,矩阵E的维度也为s×u,其元素便是关于变量x1, x2, …, xn的3次多项式。这m(即:s·u)个3次多项式便构成了中心映射F:Fn→Fm。
然后,将中心映射与2个随机生成的可逆线性仿射S:Fm→Fm、T:Fn→Fn,进行复合,得到公钥P=SoFoT:Fn→Fm。私钥则包含S,T与F。
加密:用公钥P对明文d∈Fn进行c=P(d)计算,即可得到密文c∈Fm。
解密:对密文进行解密需要经过3个步骤:
1) 计算x=S-1(c),得到一个m维向量x∈Fm。并用向量x的分量作为矩阵E的元素,即
| $ E = \left( \begin{array}{l} \;\;\;{x_1}\;\;\;\;\;\;\;\;{x_2}\;\;\;\; \cdots \;\;\;\;\;{x_u}\\ \;\;{x_{u + 1}}\;\;\;\;\;{x_{u + 2}}\;\;\; \cdots \;\;\;\;{x_{2 \cdot u}}\\ \;\;\; \vdots \;\;\;\;\;\;\;\;\;\;\; \vdots \;\;\;\;\;\;\; \ddots \;\;\;\; \vdots \\ {x_{\left( {s-1} \right) \cdot u + 1}}\;{x_{\left( {s-1} \right) \cdot u + 2}}\;\; \cdots \;\;{x_{s \cdot u}} \end{array} \right)。$ |
2) 需要对向量x进行中心映射F的逆运算,得到n维向量y∈Fn。与简单矩阵加密方案不同,此处只讨论2种情况:
a.若矩阵A可逆,将矩阵A-1的各元素视为新的未知量。同时,需要对向量y进行求解。因此,一共有s2+n、即m个未知量。而矩阵A可逆,还存在关系A-1·E=B。由此,可得到m个关于y1, y2, …, yn与A-1各元素的线性方程。便可使用高斯消元法对方程组进行求解。
b.若矩阵A不可逆,则解密失败。
3) 再由d=T-1(y),计算出明文。
与简单矩阵加密方案类似,在解密过程执行第二步时,有可能求出多个满足条件的向量y。同样,也只需要将求出的向量y,代入中心映射F,确保计算出的结果与向量x相同。
从解密过程的第二步中,可以看到,由于需要为A-1矩阵保留s2个未知量,以保证方程组能够求解。因此,需要将明文的长度设计为:n=m-s2。故,密文明文长度之比为
| $ \alpha = \frac{m}{n} = \frac{{s \cdot u}}{{s \cdot u-{s^2}}} = 1 + \frac{s}{{u-s}}。$ | (2) |
容易看出,比值通过参数s、u控制,使得取值范围大大增加,较于ABCD加密方案,粒度更细。
2.2 安全性分析 2.2.1 秩攻击秩攻击是针对多变量密码方案的一种主要攻击方法。秩攻击主要分为2种:小秩攻击(minrank attack)、高秩攻击(highrank attack)。针对不同的多变量密码方案,利用小秩攻击和高秩攻击,攻击者可以还原出私钥中的可逆线性仿射T和S。
对于Cubic AB加密方案而言,其矩阵A的各元素是变量x1, x2, …, xn的随机二次多项式。所以,秩都接近n,并且变量x1, x2, …, xn在中心映射中出现的次数基本相同。因此,针对Cubic AB加密方案,并不能利用秩攻击来进行攻击。
2.2.2 直接攻击直接攻击即,直接对公钥所构成的非线性方程组P(d)=c进行求解,最终求得明文d。
对于Cubic AB加密方案而言,其矩阵A的元素是关于变量x1, x2, …, xn的随机二次多项式;矩阵B的元素是关于变量x1, x2, …, xn的随机线性组合。
即便简化方案,攻击者只需要对中心映射进行求解,即:F(x)=y。由于中心映射是通过A·B=E而来。所以,即便攻击者还被告知了矩阵B的值,依然有A=E·B-1(矩阵B的广义逆矩阵)。此时,攻击者还是需要求解一个二次方程组。并且,这个方程组的系数是随机的(矩阵A的元素是变量x1, x2, …, xn的随机二次多项式)。
因此,针对Cubic AB加密方案,使用直接攻击,其难度比求解一个随机二次方程组更大。
2.3 建议参数如果选定Cubic AB加密方案在有限域GF(28)上进行计算,则该方案解密失败概率的上限定可确定为:2-8。相对于3次简单矩阵加密方案,Cubic AB加密方案并没有使得安全性降低。相反,在固定密文长度时,增加明文长度(增加变量数目),还会提高方案的安全性。因此,参考3次简单矩阵加密方案的密文长度。由公式(2) 可以看出密文明文长度之比,根据参数s、u的不同,可以变得很灵活。
在表 1中列举了六组,在满足不同安全级别,选择不同的s、u参数,对应的明文、密文长度及其比值,以及生成的公钥、私钥大小。
| 表 1 Cubic AB加密方案的参数选择 Table 1 Parameter settings of Cubic AB Scheme |
比较Cubic AB加密方案和简单矩阵加密方案的解密过程,第一步与第三步仅仅是矩阵与向量之间相乘,运算量相差不多。在第二步中,对线性方程组进行求解,要执行的运算较多,性能消耗主要在此。线性方程的系数矩阵的维度为m×n时,通过高斯消元法对方程组进行求解,在有限域上进行乘法操作的次数为
| $ \frac{{n \cdot \left( {n + 1} \right) \cdot \left( {3m-n + 1} \right)}}{6} + \frac{{n\left( {n-1} \right)}}{2}。$ |
在同样的安全级别下,Cubic AB方案的m、n参数取值都比简单矩阵方案的取值更小。容易得出,Cubic AB方案在第二步执行的有限域乘法的次数更少。在表 2中列举了在不同安全级别下,两种方案在解密过程第二步中执行有限域乘法操作的次数。
| 表 2 2种方案的乘法操作次数 Table 2 Multiplications of the two cryptography schemes |
容易得出,Cubic AB加密方案的解密过程,比简单矩阵加密方案更快。
3 结论研究对ABCD加密方案的思想进行扩展,通过使用一个扁长的矩阵B来取代ABCD方案中的一组方阵,设计了Cubic AB多变量公钥加密方案,使得该方案的密文明文之比取值更灵活。同时,借鉴3次简单矩阵加密方案来提高新方案的安全性,相应的明文、密文可以更短,从而降低解密过程的计算量。
| [1] | Shor P W. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer[J]. Siam Review, 1997, 41(2): 1484–1509. |
| [2] | Hwajeong S, Jihyun K, Jongseok C, et al. Small private key mqpks on an embedded microprocessorg[J]. Sensors, 2014, 14(3): 5441–5458. DOI:10.3390/s140305441 |
| [3] | Singaravelu P, Verma S. Feasibility of rainbow signature for broadcast authentication in sensor networks[C]//Vehicular Technology Conference (VTC Spring).[S.L.]:IEEE, 2011:1-5. |
| [4] | Singaravelu P, Verma S. Practicability of HFE scheme for wireless sensor network[C]//Transactions on Computational Science XVⅡ. Berlin:IEEE, 2013:116-132. |
| [5] | Sundar D S, Narayan N. A novel voting scheme using quantum cryptography[C]//Open Systems (ICOS), 2014 IEEE Conference on.[S.L.]:IEEE, ,2014:66-71. |
| [6] | Ding J, Schmidt D. Rainbow, a new multivariable polynomial signature scheme[C]//Applied Cryptography and Network Security. Berlin:Springer, 2005:164-175. |
| [7] | Petzoldt A, Bulygin S, Buchmann J. Linear recurring sequences for the UOV key generation revisited[C]//Information Security and Cryptology-ICISC 2012. Berlin:Springer, 2013:441-455. |
| [8] | Porras J, Baena J, Ding J. ZHFE, a new multivariate public key encryption scheme[C]//Post-Quantum crypto-graphy.[S.L.]:Springer International Publishing, 2014:229-245. |
| [9] | Petzoldt A, Bulygin S, Buchmann J. Fast verification for improved versions of the UOV and rainbow signature sche-mes[C]//Post-Quantum Cryptography. Berlin:Springer, 2013:188-202. |
| [10] | Petzoldt A, Thomae E, Bulygin S, et al. Small public keys and fast verification for multivariate quadratic public key systems[J]. Cryptographic Hardware & Embedded System, 2011: 475–490. |
| [11] | Tao C, Diene A, Tang S, et al. Simple matrix scheme for encryption[C]//Post-Quantum Cryptography. Berlin:Springer, 2013:231-242. |
| [12] | Ding J, Petzoldt A, Wang L C. The cubic simple matrix encryption scheme[C]//Post-Quantum Cryptography.[S.L.]:Springer International Publishing, 2014:76-87. |
| [13] | Tao C, Xiang H, Petzoldt A, et al. Simple matrix-a multivariate public key cryptosystem(MPKC)for encryption[J]. Finite Fields & Their Applications, 2015, 35: 352–368. |
| [14] | Petzoldt A. Eliminating Decryption Failures from the Simple Matrix Encryption Scheme. http://eprint.iacr.org/2016/010.pdf, 2016. |
 2017, Vol. 40
2017, Vol. 40

