符号有向图SDG(signed directed graph, SDG)主要应用于工业过程的安全评价和复杂系统的故障诊断上,最初研究的目的是进行故障溯源[1]。SDG是描述复杂系统的一种方式,为研究故障溯源及故障传播提供了模型依据[2]。
Iri等[3-5]的研究工作奠定了对故障进行定性分析的基础,主要应用在化工过程和液压设备流量控制等复杂系统故障分析上,但将该方法应用到复杂机电产品可靠性研究的成果相对较少。刘伟等[6]通过分析故障频谱对故障进行定量和分类,能够有效诊断发电机组励磁系统的故障。杨帆等[1]给出了SDG图的定义,SDG是由若干个节点和若干条支路组成,节点表示变量,支路表示变量之间的关系。当被测节点的变量值为正常时,节点的值取为“0”,偏大记为“+”,偏小记为“-”。
姜洪权等[7]基于系统层和设备层来对机电系统故障溯源集成模型进行研究,最后将两层之间通过设备功能状态变量进行关联集成。谢志江等[8]和胡芳霞等[9]运用模糊数学理论对机械故障进行了诊断,提高了机械故障诊断的准确率。文献[10]将状态关联概率和模糊信息引入SDG中,解决复杂系统中的关联关系。Maurya等[11]将定性趋势分析(QTA)与SDG结合进行故障诊断,提高了故障诊断的准确性与效率。Bushan等[12]运用SDG故障诊断时对传感器进行优化配置,提高了故障诊断的精度,为传感器的使用提供了重要的依据。Umeda等[13-14]运用SDG模型描述变量和变量自身随时间变化的故障传递关系,使不同的时刻出现了不同的节点。研究复杂系统特征行为时,一般是以静态结构变量为节点建模。但对于复杂机电系统来说,具有将系统作为一个动态过程进行研究的特征,更适用于复杂机电产品的可靠性研究。因此笔者首先对复杂机电产品进行结构化分解,利用元动作层面的信息属性建立SDG符号有向图可靠性模型,然后再进行故障的定量分析。
1 基于元动作的结构化分解笔者研究的复杂机电产品主要是指实现机电产品的功能时运动复杂,且运动涉及的零部件较多的机电产品。一些复杂机电产品如机床、机器人等,整体功能(一般是运动功能)的实现是由一些部件的子功能(一般也是运动)来完成的。而部件的运动子功能最终是由基本的“元动作”来实现的,产品的故障也最终体现在“元动作”上。也就是说,正是因为元动作出现故障,才影响到部件的子功能不能实现,并最终影响整个产品的功能。以数控机床为例,为实现数控机床的运动功能(刀具和工件的相对运动),机床的进给、工作台的回转、刀架的回转、从刀库抓取刀具、主轴的回转等功能必须保证正常。而刀架部件的子功能是刀架的移动和转动,这两个运动功能又是由其内部的元动作机构来保障的。在机电系统功能实现的过程中元动作之间会相互影响,而这种影响也会根据动作的属性而不相同,元动作之间存在相互耦合的关系和顺序关系。所以在研究元动作较多的复杂机电产品时,系统存在较多的耦合关系,而不是化工或液压等系统存在较多的是顺序关系。因此,可以以“功能—运动—动作”作为主线对数控机床的整体功能进行分解,得到最基本的元动作层(称为元动作单元),作为可靠性分析的基础,这种分解方式称为基于FMA的结构化分解[15]。其分解原则[16]为:
1) 元动作单元的独立性原则。为了减少元动作单元之间的耦合,将实现同一元动作的零件分配到一个元动作单元。
2) 元动作单元物理结构的完整性原则。在进行分解时对每一个元动作都要有完整的结构,否则元动作无法实现,也无法建立完整的分析模型。
3) 元动作单元结构的最小性原则。为保证合理的分解粒度,要确保分解的功能、运动、动作与机床硬件结构相对应,以便在元动作层面独立的进行可靠性分析、试验和控制。
4) 元动作单元的结构层次性原则。FMA分解要体现明显的层次性,按层次分解会降低元动作故障之间的耦合度,也便于从元动作故障预计整机的可靠性。
5) 元动作单元的重点突出性原则。事实上,在分解到元动作层面后,单元之间的可靠性、单元故障的重要程度都不相同,在建模和分析时要抓住重点。
实践中,由于机电产品的复杂性,有些动作又可以分为一级动作、二级动作甚至三级动作等,这里将最后一级不能再被分解的动作定义为“元动作”[17]。例如,蜗轮蜗杆传动在运动分析层面是一个整体,但它又可以分解为蜗杆转动和蜗轮转动两个元动作。FMA结构化分解的示意图[16]如图 1所示。
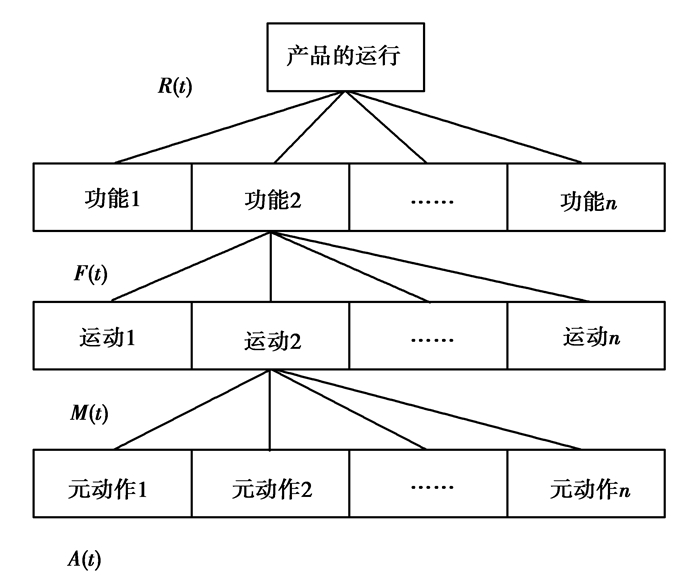
|
图 1 基于功能的机电产品结构化分解 Figure 1 Electromechanical products structural decomposition base on function |
复杂机电产品的整体功能是以各个子功能之间相互协调实现的,而动作完成是实现功能的基础。因此,每一个动作都会有相应的设计要求,这些设计要求实际上是一些参数,系统在正常运转时这些参数是在一个阈值内波动,当出现故障时这些变量就会超出正常阈值。
在研究故障的模式时,如果仅从结构层进行遍历再去查找相应的参数变化会使得遍历不完全,或效率较低。如果建立完整的运动结构层与信息属性层,在故障发生的位置运动层会出现状态偏离,然后遍历相关信息属性层。化工系统和液压系统等存在顺序关系较多的系统,仅仅去找一个结构或几个结构。
对大规模复杂系统,构建的SDG一般比较庞大,可以采用分层的方法来对模型进行描述,逐层细化。这就不仅需要定义节点和支路,还要解决层与层之间的关系表达。在对功能进行结构化分解后,高层次的功能失效一般是由低层次的功能故障引起的,而低层次的功能失效必会引起高层次的功能失效。将结构化分解后的功能与运动分别建立不同的关系层:
1) 运动关系层,根据机电产品结构运动关系分解出的运动作为运动关系层。例如,刀架的转动和移动,蜗轮蜗杆的转动等同属运动关系层。
2) 元动作关系层,在分解出运动层后分解出的元动作作为元动作关系层。例如,蜗轮蜗杆的转动运动又可以分解为:蜗轮的转动和蜗杆的转动,与轴承的转动元动作。分解得到的元动作同属元动作层。
将运动关系层与元动作关系层根据分解顺序放在同一层内作为运动层。针对以上描述,笔者在复杂机电产品“功能—运动—动作”结构化分解的基础上提出一种面向复杂机电系统故障诊断的运动分解网络图(Movement Decomposition Graph-MDG)的建模方法。
2.2 面向故障诊断的MDG-SDG建模对于元动作较多的复杂机电产品,由于设备的运行是个动态的变化过程,而不是一个静态的系统,每一部分的信息属性都会处于不断的变化中。所以从元动作层面分析系统设备故障之间的复杂关联关系更适用于以运动功能为主的复杂机电产品。
根据系统层的元动作的信息属性映射,建立信息属性层,这些信息属性是元动作的设计要求。以液压回转工作台的移动为例,液压缸最小启动压力,液压缸最小工作稳定压力,活塞在移动过程的活塞杆的直线度等,将这些元动作的设计要求作为信息属性。元动作每一个信息属性为一个节点,信息属性的状态变量为节点间的支路。
在进行故障诊断时,计算机或人工排除故障时,首先从系统层,根据结构化分解的运动关系从高层次到底层次进行故障诊断,在每一个元动作的信息属性存在一些状态变量,这些状态变量可以构成SDG的节点。根据2.1节,故障诊断的模型如图 2所示,可以由两部分构成:1) 系统层MDG,根据“功能—运动—动作”原则建立运动关系层。2) 元动作信息属性层SDG,在信息属性层内的信息属性作为节点建立SDG。
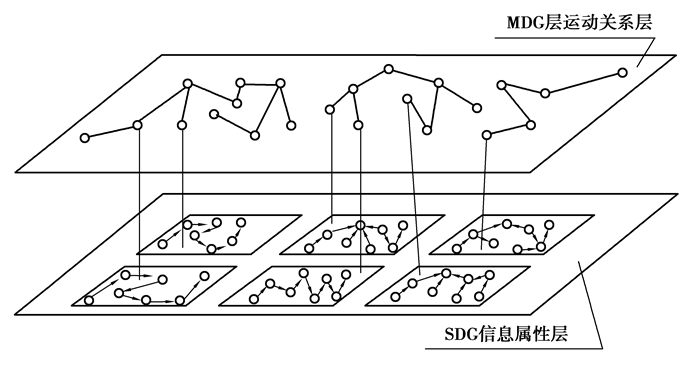
|
图 2 MDG-SDG模型 Figure 2 MDG-SDG model |
根据系统层与信息属性层的映射关系建立多维MDG-SDG模型,这种映射属于一对一或一对多的类型。为了更方便研究根据元动作的故障诊断,下面定义元动作故障与元动作故障节点。
定义1 元动作故障:根据FMA的结构化分解的元动作,在产品运行时,元动作所涉及的控制参数超出允许范围,称为元动作故障。
由于运动的连续性,定义元动作故障将区别于一般的故障定义。根据设计的运动参数作为控制指标可以便于判定故障。
定义2 元动作故障节点:当元动作故障发生时,故障所涉及的零件称为元动作故障节点。
3 基于SDG模型的定量故障诊断在使用SDG模型进行定性分析时,模型中存在的冗余较多,为了提高分析的准确性,在建模时加入更多的定量信息是现在研究SDG的重要方向[18]。
Yu等[19]将稳态增益的知识引入SDG模型,可以计算出相容通路的相容度(SDG所有支路最小相容数值)。这样将一定的定量信息和定性信息集合在符号有向图中,形成SDG半定量的故障诊断模型。采用的方法是用被影响因素和影响因素变化的比率(增益)来代替图中分支正负符号,并计算故障模式的隶属度[18]。由于所使用的定量信息是从起始节点通过不同的途径到终端节点的净影响,因此在测量参数所构建的SDG基础上形成的模型必须是树状结构[19]。在简单SDG中仅仅是定性模型:Fa±Fb;Fa为影响因素,Fb为被影响因素。在半定量模型中变量Fa与Fb的增益为ΔFa/ΔFb,根据故障信息分别计算增益。在一种故障模式中构造隶属度函数S(ΔFa/ΔFb),涉及到几个测量状态变量,这些参数之间构成树状子SDG。
| 表 1 故障模式测量参数表 Table 1 Failure mode measurement parameter list |
从根节点出来的支路符号保持原来的正负号,其他节点的支路符号用隶属函数来代替。如在故障T1中根节点为正,下一个节点的支路符号用ΔF1/ΔF2=(a21-a11)/(a31-a21)代替,如图 3所示。
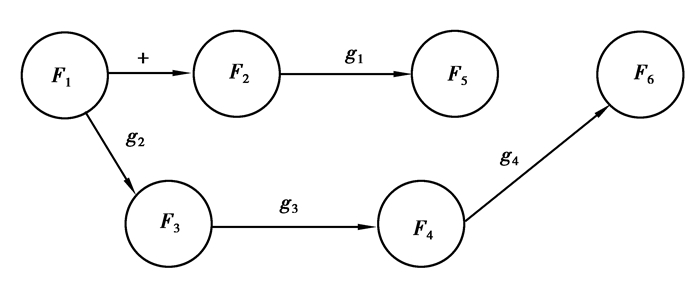
|
图 3 故障T1的SDG模型 Figure 3 SDG model of the fault T1 |
1) 从故障测量参数的根节点到与下一个直接连接节点的隶属度函数:
| $ 支路符号为正\;\;\;\;\;\;\;S\left( g \right) = \left\{ \begin{array}{l} 1, g > 0;\\ 0, g \le 0。\end{array} \right. $ | (1) |
| $ 支路符号为负\;\;\;\;\;\;\;S\left( g \right) = \left\{ \begin{array}{l} 1, g > 0;\\ 0, g \le 0。\end{array} \right. $ | (2) |
2) 其他节点间定量关系的隶属函数。令相对变化率T=(g-g*)/g*,其中g*为典型已知故障类型的被影响与影响的增益,g为待诊断模式相应节点值变化比率,节点的隶属度函数:
| $ S\left( g \right) = \left\{ \begin{array}{l} 0, \;\;\;T \ge 0.3;\\ 1.5-5T, \;\;0.1 \le T \le 0.3;\\ 1, \;\;-0.1 \le T \le 0.1;\\ 1.5 + 5T, \;\;\;-0.3 \le T \le - 0.1;\\ 0, \;\;\;T \le - 0.3。\end{array} \right. $ | (3) |
先确定被诊断模式对一只故障类型的模式隶属度,根据最大隶属度原则来确定该故障模式下的故障类型[18]:
| $ {S_\tau } = \min \left[{S\left( {{g_{\tau 1}}} \right), S\left( {{g_{\tau 2}}} \right), \cdots, S\left( {{g_{\tau j}}} \right)} \right], $ | (4) |
得出Sτ,求得的最大隶属度所对应的故障类型τ为诊断结果。式中τ为已知故障模式(τ=1, 2, …, n);n为已知故障种类;j为该故障模式的分支j=1, 2, …, j。
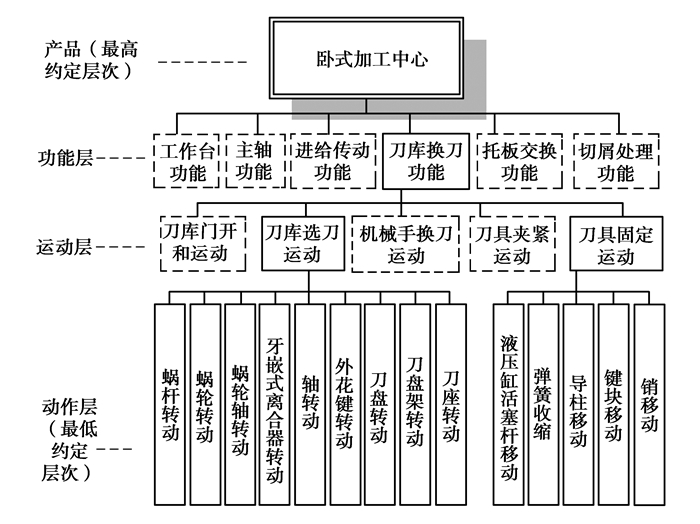
4 实例分析以某种型号的卧式加工中心刀库选刀运动和刀具固定运动为例,图 4所示为刀库部件结构简图。加工中心的各个子系统及单元部件中,自动换刀系统故障率占整机的比重约为1/5[22]。所以在对加工中心进行故障分析时,刀库换刀功能的故障分析尤为重要。由于篇幅原因现仅以刀库选刀运动和刀具固定运动为实例进行研究,这两个运动包含了机械结构的两种基本运动形式:直线移动和转动。根据图 1所示的FMA结构分解原则对卧式加工中心进行结构化分解,得到图 5所示的刀库选刀运动和刀具固定运动结构化分解图。
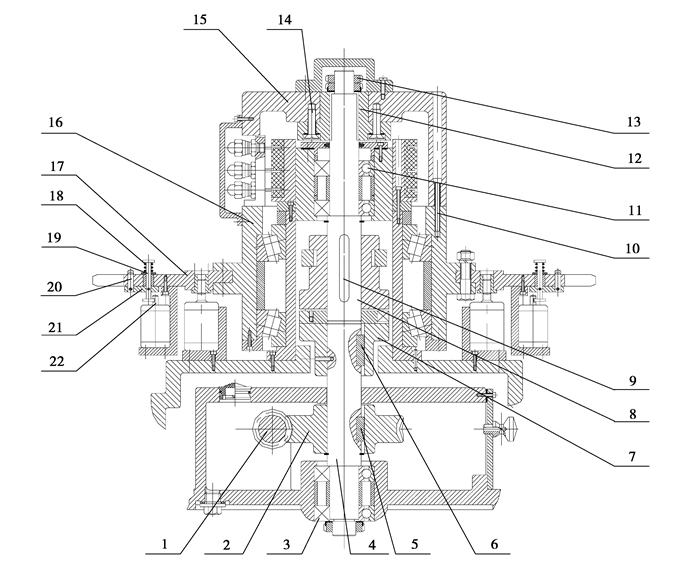
|
图 4 刀库部件结构简图 Figure 4 Tool magazine components structure diagram 1.蜗杆;2.蜗轮;3.蜗轮键;4.蜗轮轴;5.角接触球轴承;6.键;7.牙嵌离合器;8.轴;9.轴键;10.螺钉;11.轴承;12.外花键;13.圆螺母;14.沉头螺钉;15.刀盘;16.刀盘架;17.刀座;18.弹簧;19.导柱;20.销;21.键块;22.液压杆 |
|
图 5 刀库运动结构化分解 Figure 5 Tool magazine structural decomposition |
图 5中刀库选刀运动和刀具固定运动可以分解为如下几个元动作,包括:M1蜗杆转动,M2蜗轮转动,M3蜗轮轴转动,M4牙嵌式离合器转动,M5轴转动,M6外花键转动,M7刀盘转动,M8刀盘架转动,M9刀座转动,M10液压缸的活塞杆直线移动,M11弹簧的收缩,M12导柱直线移动,M13键块直线移动,M14销直线移动。根据结构设计要求在刀库选刀运动和刀具固定运动时元动作所映射出信息属性层I包括:(F1, F2, F3, F4, F5, F6, F7, F8, F9, F10, F11, F12, F13, F14)=(蜗杆的转动角度,蜗轮的转动角度,蜗轮轴的转动角度,牙嵌式离合器的转动角度,轴的转动角度,外花键的转动角度,刀盘的转动角度,刀盘架的转动角度,刀座的转动角度,液压缸活塞杆的直线位移,弹簧收缩的长度,导柱直线位移,键块直线位移,销的直线位移)。由这些刀库选刀运动和刀具固定运动结构设计指标建立MDG-SDG模型。
在实验环境下用传感器采集在选择3号刀具时的2组设计指标参数,如表 2所示。
| 表 2 采集的设计指标 Table 2 Collection of design index |
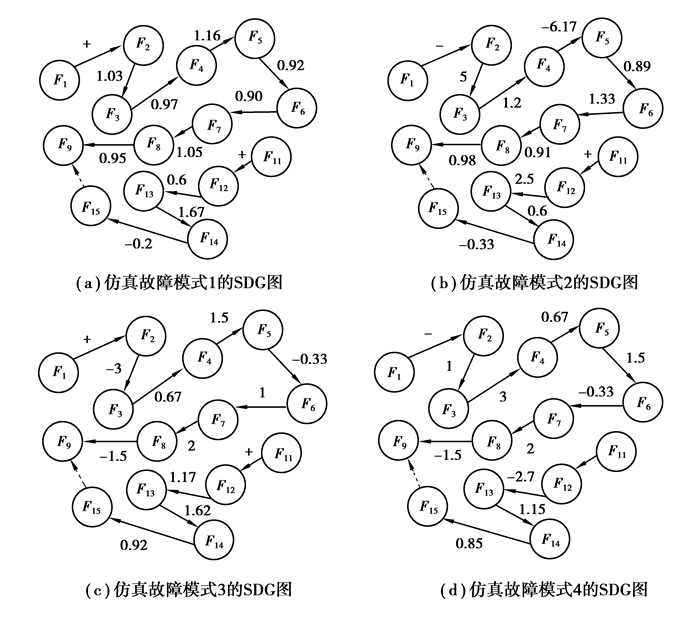
根据以上数据建立故障1和故障2的SDG图如图 6所示,首先将符号有向图根据经验去掉图中的次要分支,再利用数据计算出各个分支的被影响因素与影响因素的变化比率。由于两个动作的时间顺序有时间间隔,导致两个元动作影响较小,所以节点F15至F9支路标记为虚线。
|
图 6 仿真故障模式的SDG图 Figure 6 Simulation SDG of fault mode |
从图 6可以看出,4种故障的g值是不同的。通过传感器的对运行的状态检测可以解决在故障诊断时不用拆卸检查故障。可以通过计算隶属度来确定该模式下在哪一个元动作的故障模式更接近,由此判断出该元动作故障节点。
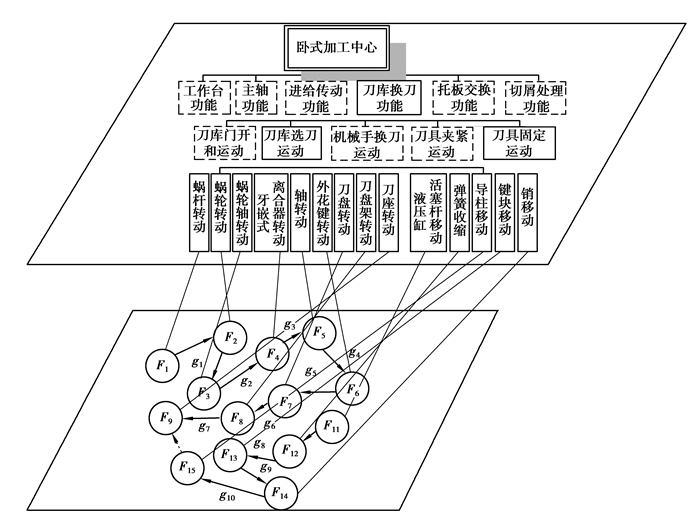
在故障诊断时,由复杂机电产品的结构属性与信息属性所建立起的MDG-SDG图,方便了在故障诊断与仿真时遍历效率。图 7是根据多维MDG-SDG模型对刀库选刀运动和刀具固定运动进行的故障诊断模型。
|
图 7 刀具固定运动的MDG-SDG模型 Figure 7 Cutter fixed movement MDG-SDG model |
通过第3节给出的隶属度计算方法,计算4种模式下的隶属度,进行对比确定该模式的故障节点。
| 表 3 故障模式的隶属度 Table 3 Subordination degree of failure mode |
根据最大隶属度原则,从表中可以得出故障的节点是F1、F4、F10、F11处。通过传感器的状态监测得出元动作故障,然后根据元动作故障节点进行维修。
5 结论1) 构建了一种新型的复杂机电产品的故障诊断模型。MDG-SDG模型与SDG定量诊断相结合能够较为准确地判断出以运动功能型机电产品的故障诊断结果,将元动作应用于故障诊断。
2) 可以通过对系统的参数监测,能够更有效地查找出元动作故障节点,然后根据元动作节点进行维修。这样可以根据复杂机电产品的特点进行故障诊断,为计算机故障诊断提供了理论基础。
3) 为复杂机电产品故障诊断提供了更多的定量信息。通过FMA结构化分解,对元动作信息属性进行映射,并对映射的变量进行监测,更准确得到定量信息。
| [1] |
杨帆, 萧德云.
SDG建模及其应用进展[J]. 控制理论及应用, 2005, 22(5): 767–774.
YANG Fan, XIAO Deyun. Review of SDG modeling and its application[J]. Control Theory and Application, 2005, 22(5): 767–774. (in Chinese) |
| [2] | Yang F, Sirish L S, Xiao D Y. Signed directed graph modeling of industrial processes and their validation by data-based methods[C]//2010 Conference on Control and Fault Tolerant Systems, October 6-8, 2010, Nice, France. IEEE, 2010:387-392. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=5676059 |
| [3] | Iri M, Aoki K, O'Shima E, et al. An Algorithm for diagnosis of system failures in the chemical process[J]. Computers and Chemical Engineering, 1979, 3(1/2/3/4): 489–493. |
| [4] | Bauer M, Cox J M, Caveness M H, et al. Finding the direction of disturbance propagation in a chemical process using transfer entropy[J]. IEEE Transaction on Control Systems Technology, 2007, 15(1): 12–21. DOI:10.1109/TCST.2006.883234 |
| [5] | Bauer M, Thornhill N F. A practical method for identifying the propagation path of plant-wide disturbances[J]. Journal of Process Control, 2008, 18(7/8): 707–719. |
| [6] |
刘伟, 张朕滔, 梁康有, 等.
励磁功率单元主回路快速故障诊断策略[J]. 重庆大学学报, 2015, 38(4): 137–158.
LIU Wei, ZHANG Zhentao, LIANG Kangyou, et al. Fast fault diagnosis strategy for the main loop of excitation power unit[J]. Journal of Chongqing University, 2015, 38(4): 137–158. DOI:10.11835/j.issn.1000-582X.2015.04.019 (in Chinese) |
| [7] |
姜洪权, 王金宇, 高建民, 等.
面向复杂系统故障溯源的SDG-FG模型建模方法[J]. 计算机集成制造系统, 2015, 21(3): 749–757.
JIANG Hongquan, WANG Jinyu, GAO Jianmin, et al. Modeling method for SDG-FG model oriented to fault root causes tracing analysis of complex electromechanical system[J]. Computer Integrated Manufacturing Systems, 2015, 21(3): 749–757. (in Chinese) |
| [8] |
谢志江, 谢长贵, 陈平.
自学习模糊脉冲神经网络的旋转机械诊断[J]. 重庆大学学报, 2013, 36(2): 18–22.
XIE Zhijiang, XIE Changgui, CHEN Ping. Fault diagnosis of rotating machinery based on self-learning fuzzy spiking neural networking[J]. Journal of Chongqing University, 2013, 36(2): 18–22. DOI:10.11835/j.issn.1000-582X.2013.02.004 (in Chinese) |
| [9] |
胡芳霞, 谢志江, 岳茂雄.
混沌粒子群优化模糊聚类的旋转机械故障诊断[J]. 重庆大学学报, 2011, 34(6): 26–30.
HU Fangxia, XIE Zhijiang, YUE Maoxiong. Fault diagnosis of machinery based on fuzzy clustering optimized by chaos embedded particle swarm optimization[J]. Journal of Chongqing University, 2011, 34(6): 26–30. DOI:10.11835/j.issn.1000-582X.2011.06.005 (in Chinese) |
| [10] |
朱琳, 陈杰, 陈文颉, 等.
基于模糊概率符号有向图的复杂系统故障诊断[J]. 北京理工大学学报, 2007, 27(11): 969–973.
ZHU Lin, CHEN Jie, CHEN Wenjie, et al. Fault diagnosis based on fuzzy probability signed directed graph in complex system[J]. Transactions of Beijing Institute of Technology, 2007, 27(11): 969–973. DOI:10.3969/j.issn.1001-0645.2007.11.008 (in Chinese) |
| [11] | Maurya M R, Rendaswamy R, VenkatasubramanianV, et al. Incipient fault diagnosis of ennessee eastman flowsheet using signed directed graph and trend analysis[C]//12th European Symosium on Computer Aided Process Engineering-12(ESCAPE-12) (Supplementary proceedings), The Hague, The Netherlands, 2002. |
| [12] | Bhushan M, Rengaswamy R. Comprehensive design of a sensor network for chemical plants based on various diagnosability and reliability criteria.1.Framework[J]. Industrial and Engineering Chemistry Research,, 2002, 41(7): 1826–1839. DOI:10.1021/ie0104363 |
| [13] | Umelda T, Kuriyama T, O'Shima E, et al. A graphical approach to cause and effect analysis of chemical processing systems[J]. Computer and Chemical Engineering, 1980, 35(12): 2379–2388. |
| [14] | Li A F, Xia T, Zhang B K, et al. SDG modelling approach for chemical engineering process[J]. Acta Simulata Systematica Sinica, 2003, 15: 1364–1368. |
| [15] | Zhang G B, Lou J H, Li D Y, et al. Fault diagnosis study of complex mechanism based on FMA function decomposition model[J]. Procedia Cirp, 2015, 27: 176–180. DOI:10.1016/j.procir.2015.04.062 |
| [16] |
李冬英. 数控机床装配质量建模与诊断技术研究[D]. 重庆: 重庆大学, 2014. LI Dongying. Research on modeling and diagnosis technology for the assembly process of CNC machine tool[D]. Chongqing:Chongqing University, 2014. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10611-1015016987.htm |
| [17] | Li D Y, Zhang G B, Li M Q. Assembly reliability modeling technology based on meta-action[J]. Procedia Cirp, 2015, 27: 207–215. DOI:10.1016/j.procir.2015.04.068 |
| [18] |
晏政. 航天器推进系统基于有向图的故障诊断方法研究[D]. 长沙: 国防科技大学, 2007. YAN Zheng. Research of fault diagnostic method for spacecraft propulsion system based on directed graph[D]. Changsha:National University of Defense Technology, 2007. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-90002-2008098019.htm |
| [19] | Yu C C, Lee C. Fault diagnosis based on qualitative/quantitative process knowledge[J]. Aiche Journal, 1991, 37(4): 617–628. DOI:10.1002/(ISSN)1547-5905 |
| [20] |
黄卫东, 王克昌.
基于定性和定量关系的液体火箭发动机故障诊断[J]. 航空动力学报, 1996, 11(3): 281–284.
HUANG Weidong, WANG Kechang. Liquid rocket engine fault diagnosis based on qualitative/quantitative model[J]. Journal of Aerospace power, 1996, 11(3): 281–284. (in Chinese) |
| [21] |
曹文亮, 王兵树, 马良玉, 等.
基于SDG推理规则和定量分析的故障诊断技术[J]. 热能动力工程, 2005, 20(6): 619–623.
CAO Wenliang, WANG Bingshu, MA Liangyu, et al. Fault diagnosis technology based on the reasoning rules of SDG (Sign directed Graph) and a quantitative analysis[J]. Journal of Engineering for Thermal and power, 2005, 20(6): 619–623. (in Chinese) |
| [22] |
涂林. 卧式加工中心可靠性试验技术研究[D]. 重庆: 重庆大学, 2012. TU Lin. Research on reliability test technology of horizontal machining center. Chongqing:Chongqing University, 2012. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10611-1012049039.htm |
 2017, Vol. 40
2017, Vol. 40


