精确而高效率地测量信号的频率、幅值和相位是工程信号处理中一个基本的课题，它在雷达测距、通信信号处理、机床振动信号分析、电力谐波分析、流量计信号分析等领域有重要的作用^[1-4]。利用快速傅里叶变换(FFT)，通过离散频谱分析进行参数估计是目前较为常用的方法。然而，由于很难实现信号的同步采样，时域的非整周期截断将导致频谱泄漏效应，同时信号频谱的离散化将导致栅栏效应^[5-6]，这使得利用频谱分析进行信号的参数估计时将存在一定程度的误差。因此，如何在频谱分析的基础之上通过额外的算法从而获得精确的频谱参数成为工程信号处理领域一个重要课题，离散频谱校正技术正是为了解决这一问题而提出的。目前，离散频谱校正方法依据算法原理主要可以分为插值法^[7-9]、相位差法^[10-12]、能量重心法^[13-16]三大类。其中插值法是当前研究最多、运用最广、相对比较成熟的一种离散频谱校正方法^[17]。

一般来讲，通过在有效信号后补零对谱线进行插值可以使频谱谱线更密，能在一定程度上达到减小栅栏效应的目的，但补零后数据量增大，导致处理时间长、实时性不好。而插值法在增加较小计算量的前提下，通过简单的算法可以减小栅栏效应。此方法的基本原理是利用离散频谱中的最大两条或者更多的谱线的比值(幅值谱比值或者直接FFT变换后的复数谱值)，建立一个以频率校正量为变量的函数关系，通过比值求解出校正频率，进而得到更加精确的信号频率。为了减小频谱泄漏效应，提高校正的精度，通常需要对原始信号进行加窗处理。加窗将显著地改变频谱谱线幅值大小，这使得不同的窗函数具有不同的插值公式。

插值法的另外一个重要的影响因素是随机噪声的干扰。随机噪声不但会改变谱线的数值大小，而且会干扰谱线定位位置。因此，强噪声干扰下算法稳定性研究是目前算法研究的热点。Schoukens等^[18]定性地研究了噪声干扰下算法的稳定性问题，Offelli等^[19]定量得分析了噪声对算法的影响。柏林等^[20]讨论了信噪比、采样序列含有的波数以及频率偏移量对插值算法精度的影响。齐国清和贾欣乐^[21-22]研究了校正极性错误的问题，指出了当信号频率接近整周期采样时由插值的方向错误对频率估计精度的影响。需要指出的是对于不同的算法，插值的方向错误的原因和结果迥异，而且目前的研究也仅限于少数几种插值算法。各种算法在强噪声下的性能，特别是强噪声下产生校正极性错误这一问题，尚未进行深入而广泛的研究。

笔者首先总结了目前文献中所提出的各种插值法，提出了影响影响插值法校正精度的各种因素，通过计算机仿真重点考察了目前算法在随机噪声干扰下的性能以及对谱线定位错误的敏感性，研究了插值法校正极性错误的两种不同情况，即因谱线定位错误而导致的校正极性错误和因谱线数值大小改变而导致的校正极性错误。在此基础之上，深入分析了随机噪声对各种算法的影响，比较了不同算法的优缺点，为实际工程应用提供了理论依据，最后指出了现有插值法的不足之处和亟待解决的问题，对插值校正算法的发展进行了探讨和展望。

1 基于幅值谱比值的插值法 1.1 两谱线幅值插值算法

1979年Jain等^[23]提出了适用于矩形窗函数的两谱线幅值插值法，其原理是利用两条最大谱线与幅值比，建立其与频率校正量$\hat \delta $的函数关系，表达式为

$ \hat \delta = \pm \frac{\alpha }{{\alpha + 1}}, $

(1)

其中$\hat \delta $的正负号由最大幅值谱线与次大幅值谱线的相对位置决定，若前者处于后者左边，则取正号，反之取负号。式中α表示次大谱线与最大谱线的幅值比值，即

$ \alpha = \frac{{\left| {X\left( {l \pm 1} \right)} \right|}}{{X\left( l \right)}}。$

(2)

Grandke^[24]在Jain的启示下，提出了适用于汉宁窗的最大两条谱线幅值插值校正方法，频率校正量的表达式为

$ \hat \delta = \pm \frac{{2\alpha-1}}{{\alpha + 1}}。$

(3)

国内研究者谢明等^[7-8]在研究了矩形窗和汉宁窗窗波特性基础之上，利用最大两条谱线重心特点，提出了相同的校正公式，并命名为比值法。

Belega等^[25]在Jain和Grandke算法的基础上，进一步将两谱线幅值插值法推广到适用于最大旁瓣衰减窗，提出了通用的插值公式

$ \hat \delta = \pm \frac{{H\alpha-H + 1}}{{\alpha + 1}}, $

(4)

式中H(H≥1) 表示最大旁瓣衰减窗的项数。

1.2 Agrez算法

2002年Agrez^[26]提出利用幅值最大的3条谱线的校正方法以减少相邻频率成分泄露干扰影响，其校正精度有了一定程度的提高。适用于矩形窗的归一化频率校正量的表达式为

$ \hat \delta = \mu \frac{{\left| {X\left( {l + 1} \right)} \right| + \left| {X\left( {l-1} \right)} \right|}}{{2\left| {X\left( l \right)} \right| + \left| {\left| {X\left( {l + 1} \right)} \right|-\left| {X\left( {l-1} \right)} \right|} \right|}}, $

(5)

其中μ=sign|X(l+1)|-|X(l-1))|。

重新定义谱线的比值为

$ \alpha = \frac{{\left| {X\left( l \right)} \right| + \left| {X\left( {l-1} \right)} \right|}}{{\left| {X\left( l \right)} \right| + \left| {X\left( {l + 1} \right)} \right|}}。$

(6)

Agrez^[26]还提出了适用于汉宁窗的三谱线算法，得到归一化频率校正量的表达式为

$ \hat \delta = 2\frac{{1-\alpha }}{{1 + \alpha }}。$

(7)

Belega^[25]在Agrez算法的基础上，对最大旁瓣衰减窗进行了研究，推导出了利用幅值最大三条谱线的频率校正通式

$ \hat \delta = H\frac{{1-\alpha }}{{1 + \alpha }}, $

(8)

式中H(H≥2) 表示最大旁瓣衰减窗的项数。

1.3 基于幅值比值的Jacobsen算法

2007年，Jacobsen等^[27]提出了一种不同于Agrez算法的三谱线校正算法，其中适用于矩形窗的归一化校正频率表达式为

$ \hat \delta = \frac{{\left| {X\left( {l + 1} \right)} \right| - \left| {X\left( {l-1} \right)} \right|}}{{4\left| {X\left( l \right)} \right|-2\left| {X\left( {l + 1} \right)} \right|-2\left| {X\left( {l - 1} \right)} \right|}}。$

(9)

与此同时也给出了可适用于汉宁窗、海明窗、布莱克曼窗和布莱克曼哈里斯窗的经验校正公式

$ \hat \delta = \frac{{P\left( {\left| {X\left( {l + 1} \right)} \right|-X\left( {l-1} \right)} \right)}}{{\left| {X\left( l \right)} \right| + \left| {X\left( {l + 1} \right)} \right| + \left| {X\left( {l-1} \right)} \right|}}, $

(10)

其中P=1.22(海明窗)，P=1.36(汉宁窗)，P=1.75(布莱克曼窗)，P=1.72(布莱克曼哈里斯窗)。该算法进一步将插值法推广到更多的窗函数，同时提高了传统插值法的抗噪声性能。

1.4 基于补零和窗函数主瓣拟合的Luo算法

无论是两谱线插值法还是三谱线插值法，不同窗函数具有不同的校正公式。更重要的是，仅仅某些窗函数具有频率校正量$ {\hat \delta }$与幅值比值α的简单显式表达式。然而，目前绝大部分窗函数的频率校正量的显式表达式尚未推导出^[28]。针对这一问题，Luo等^[6]在研究汉宁窗窗波特性的基础上，提出了基于补零和窗函数主瓣拟合的三谱线幅值插值法，解决了一般窗函数的离散频谱插值算法的问题。

引入变量γ₁, γ₂，定义为

$ {\gamma _1} = \frac{{\left| {X\left( {{l_{{\rm{ap}}}}-1} \right)} \right|}}{{\left| {X\left( {{l_{{\rm{ap}}}}} \right)} \right|}}, $

(11)

$ {\gamma _2} = \frac{{\left| {X\left( {{l_{{\rm{ap}}}} + 1} \right)} \right|}}{{\left| {X\left( {{l_{{\rm{ap}}}}} \right)} \right|}}, $

(12)

式中：|X_ap(l_ap)|、|X_ap(l_ap+1)|和|X_ap(l_ap-1)|代表补零后信号的频谱中的3条最大谱线。令

$ g\left( \delta \right)a{\delta ^3} + b{\delta ^2} + c\delta + d, $

(13)

其中

$ \begin{array}{l} a = 2\cos \;{\rm{\pi }}\varepsilon-\left( {{\gamma _1} + {\gamma _2}} \right), \\ b =-3\left( {{\gamma _1}-{\gamma _2}} \right)\varepsilon, \\ c = \left( {{\gamma _1} + {\gamma _2} - \frac{{2\cos \;{\rm{\pi }}\varepsilon }}{{1 - 3{\varepsilon ^2}}}} \right)\left( {1 - 3{\varepsilon ^2}} \right), \\ d = \left( {{\gamma _1} - {\gamma _2}} \right)\left( {\varepsilon - {\varepsilon ^3}} \right), \end{array} $

ε=1/M代表补零因子，M表示补零后的数据为原始信号M倍，其中补零数目为原始信号M-1倍。

可以证明归一化频率校正量${\hat \delta }$是方程

$ g\left( \delta \right) = 0 $

(14)

的一个根。根据Dorf的研究，${\hat \delta }$可表示为

$ \hat \delta = \bar \delta + 2\sigma \cos \left( {2{\rm{\pi /3}}-\varphi } \right), $

(15)

其中$\bar \delta = \frac{{-b}}{{3a}}, \sigma = \sqrt {\frac{{{b^2}-3ac}}{{9{a^2}}}}, \cos \;3\varphi =-g\left( {\bar \delta } \right)/p $和p=2aδ³。

研究表明该算法具有突出的抗噪声性能，但其计算量也相对较大。

2 基于复数谱比值的插值法

除了基于幅值比值的插值法，一些学者还提出了直接利用快速傅里叶变换后的复数谱比值，构造校正频率关于复比值的显示函数表达式。这类比值法统称为基于复数谱比值的插值法。

2.1 Quinn1算法

Quinn^[29]在1994年提出了一种适用于矩形窗的复数谱插值法。定义

$ {\delta _\varepsilon } = \frac{{\varepsilon {\beta _\varepsilon }}}{{{\beta _\varepsilon }-1}}, \varepsilon = \pm 1, $

(16)

其中

$ {\beta _\varepsilon } = {\rm{Re}}\left[{X\left( {l + \varepsilon } \right)/X\left( l \right)} \right], $

(17)

Re[·]表示取复数的实部。归一化频率校正量${\hat \delta }$表示为

$ \hat \delta = \left\{ \begin{array}{l} {\delta _1}, {\delta _{-1}} > 0且{\delta _1} > 0;\\ {\delta _{-1}}, 其他。\end{array} \right. $

(18)

类似地，Quinn^[30]于2006年提出了适用汉宁窗的复数谱的插值法，只需将式(16) 替换为

$ {\delta _\varepsilon } = \frac{{\varepsilon \left( {2{\beta _\varepsilon } + 1} \right)}}{{{\beta _\varepsilon }-1}}, \varepsilon = \pm 1。$

(19)

该算法在δ=0处有最大的渐进方差，在δ=0.5取得最小渐进方差。当采用矩形窗时，其最大和最小渐进方差约为频率估计的克拉美罗下界(Cramér-Rao low bound，CRLB)的π²/3≈3.289 9倍和π⁴/96≈1.014 7倍。Quinn1算法利用复数谱的相位信息来判断插值方向，从而在一定程度上降低了在δ≈0时两谱线幅值插值法校正极性错误这一问题，因此明显地提高了算法的抗噪声性能。

2.2 Quinn2算法

为了在δ≈0附近取得更好统计性能，Quinn等^[31-32]提出了改进的Quinn1算法。归一化频率校正量${\hat \delta }$不是简单的按照式(18) 取δ₁或δ_-1，而是由二者的函数表达式来表示

$ \hat \delta = \frac{{{\delta _1} + {\delta _{-1}}}}{2} + \kappa \left( {\delta _1^2} \right)-\kappa \left( {\delta _{-1}^2} \right), $

(20)

其中函数κ(v)由所采用的窗函数决定。适用于矩形窗的κ(v)函数为

$ \kappa \left( v \right) = \frac{1}{4}\log q\left( v \right)-\frac{{\sqrt 6 }}{{24}}\log \frac{{p\left( {v, -1} \right)}}{{p\left( {v, + 1} \right)}}, $

(21)

式中q(v)=3v²+6v+1和$p\left( {v, r} \right) = v + 1 + \sqrt {2/3} r $。

适用于汉宁窗的κ(v)函数为

$ \kappa \left( v \right) = \frac{5}{{14}}\log q\left( v \right)-\frac{{\sqrt {155} }}{{140}}\log \frac{{p\left( {v, -1} \right)}}{{p\left( {v, + 1} \right)}}, $

(22)

式中q(v)=35v²+120v+32和$ q\left( {v, r} \right) = 7v + 12 + 4\sqrt {31/5} r$。

与Quinn1不同的是，Quinn2算法在δ=0处有最小的渐进方差而在δ=0.5取得最大渐进方差。

2.3 Quinn3算法

该算法先采用Quinn1算法，首先得到频率校正量的中间量${\tilde \delta }$

$ \tilde \delta = \left\{ \begin{array}{l} {\delta _1}, {\delta _{-1}} > 0且{\delta _1} > 0;\\ {\delta _{-1}}, 其他。\end{array} \right. $

(23)

而归一化频率校正量由式(24) 函数得到^[32]

$ \hat \delta = \frac{{{\delta _1} + {\delta _{-1}}}}{2} + \left( {{\delta _1}-{\delta _{-1}}} \right)\frac{{3{{\tilde \delta }^3} + 2\tilde \delta }}{{3{{\tilde \delta }^4} + 6{{\tilde \delta }^2} + 1}}。$

(24)

当采用矩形窗时，该算法在δ=0和δ=0.5处分别取得最大和最小渐进方差，约为克拉美罗下界的π²/6≈1.644 9和171π⁴/16 512≈1.008 8倍。与Quinn1算法相比，在δ≈0附近的渐进方差大大减小。

2.4 Quinn-MacLeod算法

MacLeod在研究了校正极性错误对校正结果影响的基础之上，提出了Quinn3算法的改进方案^[32-33]。改进的算法将Quinn算法3中的中间量${\tilde \delta }$计算由式(18) 替换为

$ \tilde \delta = \left\{ \begin{array}{l} {\delta _{-1}}, {\beta _{-1}} > {\beta _1};\\ {\delta _{-1}}, 其他。\end{array} \right. $

(25)

而归一化频率校正量仍然由函数式(24) 得到。MacLeod指出，在Quinn1算法中尽管采用了比较δ₁, δ_-1的方式来避免校正极性错误的问题，然而在强噪声干扰下，当|δ|足够小时算法方差依然较大，因此，建议采用通过直接比较β_-1，β₁的实部大小来判断插值方向。研究表明，这种改进算法进一步提高了抗噪声干扰能力。

2.5 MacLeod算法

MacLeod^[33]提出一种利用最高谱线和其左右两条次高谱线来得到归一化频率校正量的方法。定义

$ \gamma = {\rm{Re}}\left[{X\left( l \right){X^*}\left( l \right)} \right], $

(26)

$ {\gamma _{\rm{L}}} = {\rm{Re}}\left[{X\left( {l-1} \right){X^*}\left( l \right)} \right], $

(27)

$ {\gamma _R} = {\rm{Re}}\left[{X\left( {l + 1} \right){X^*}\left( l \right)} \right], $

(28)

其中X^*(l)表示为X(l)的共轭复数，X(l)为最大谱线幅值。对于矩形窗，归一化频率校正量可由式(29) 求得

$ \hat \delta = \frac{{\sqrt {1 + 8{{\bar \gamma }^2}}-1}}{{4\bar \gamma }}, $

(29)

其中中间变量γ定义为

$ \bar \gamma = \frac{{{\gamma _{\rm{L}}}-{\gamma _{\rm{R}}}}}{{2\gamma + {\gamma _{\rm{L}}} + {\gamma _{\rm{R}}}}}。$

(30)

则适用于汉宁窗的归一化频率校正量为

$ \hat \delta = 2\frac{{{\gamma _{\rm{L}}}-{\gamma _{\rm{R}}}}}{{2\gamma-{\gamma _{\rm{L}}}-{\gamma _{\rm{R}}}}}。$

(31)

2.6 Li算法

2007年，Li等^[34]提出了一种新的可适用于矩形窗和汉宁窗的复数谱比值的插值法，其频率校正量表达式分别为

$ \hat \delta = {\rm{Re}}\left( {\frac{\beta }{{\beta-1}}} \right), $

(32)

$ \hat \delta = {\rm{Re}}\left( {\frac{{2\beta + 1}}{{\beta-1}}} \right), $

(33)

其中

$ \beta = \left\{ \begin{array}{l} X\left( {l-1} \right)/X\left( l \right), \left| {X\left( {l-1} \right)} \right| \ge \left| {X\left( {l + 1} \right)} \right|;\\ X\left( l \right)/X\left( {l + 1} \right), \left| {X\left( {l-1} \right)} \right| < \left| {X\left( {l + 1} \right)} \right|。\end{array} \right. $

即幅值最大的两条谱线的复比值。

2.7 基于复数谱比值的Jacobsen算法

Jacobsen等^[27]在给出基于幅值的比值法的同时，也总结了若干复数谱比值的插值法的算法，其中适用于矩形窗的校正公式为

$ \delta =- {\rm{Re}}\left[{\frac{{X\left( {l + 1} \right)-X\left( {l-1} \right)}}{{2X\left( l \right)-X\left( {l + 1} \right) - X\left( {l - 1} \right)}}} \right]。$

(34)

而适用于汉宁窗、海明窗和布莱克曼窗、布莱克曼和哈尔斯窗的经验校正公式为

$ \delta = {\rm{Re}}\left[{\frac{{Q\left[{X\left( {l + 1} \right)-X\left( {l-1} \right)} \right]}}{{2X\left( l \right) -X\left( {l + 1} \right) -X\left( {l -1} \right)}}} \right], $

(35)

其中Q=0.60(海明窗)，Q=0.55(汉宁窗)，Q=0.55(布莱克曼窗)，Q=0.56(布莱克曼哈里斯窗)。

3 插值法精度的若干影响因素

插值法是通过建立若干谱线比值与归一化频率校正量的对应关系来实现的。而谱线比值大小与采用的窗函数密切相关。因此，窗函数的选择很大程度上影响着频率校正的精度。一方面，由于比值大小不同，归一化频率校正的表达式因为窗函数的不同而不同。另一方面，不同窗函数的主瓣宽度和旁瓣电平大小以及旁瓣衰减速度不一样，这导致对于同一种插值法，选择不同窗函数下校正精度也不同。总的来看，窗函数主瓣宽度越大，旁瓣电平越小衰减越快；主瓣宽度越小，旁瓣电平相对越小衰减相对越慢；部分窗函数是以上两情况的折中。若信号中存在多种相隔较远的频率成分，在没有噪声干扰的情况下，相同的校正算法，一般来讲采用的窗函数旁瓣电平越低或旁瓣衰减越快，精度越高。当存在相隔较近的频率成分时，若窗函数主瓣太宽可能导致主瓣干涉，此时宜选择主瓣宽度窄的窗函数。

插值法精度的另一个影响因素为选用谱线的数量。目前常用的插值法都是运用离散频谱幅值最大的两条或者3条谱线。由于3谱线利用的信息较两谱线多，在噪声干扰较小情况下，前者较后者有更高的校正精度。然而需要指出的是，较多的谱线在噪声情况下可能导致其抗噪声性能降低。

在实际的工程应用中，不可避免地存在各种噪声的干扰，因此算法抗噪声性能是评价一种算法优劣的重要指标。在强噪声干扰下，算法的精度决定于窗函数选择，谱线的选择以及算法校正原理。需要特别指出的是噪声的存在易导致谱线定位错误，对校正精度有极大的影响，此问题称为插值极性错误。当信号接近整周期采样时(即归一化校正频率接近零)，此时容易产生次高谱线定位错误。此时由于最高谱线左右的两条次高谱线大小相近，在噪声或者因素的干扰之下，次高谱线定位错误都非常明显，其概率高达0.5，这将明显影响两谱线插值法的校正精度。同样，当信号接近最大非整周期采样时，最高谱线会有很大的误选几率，此时可能对三谱线插值法有较大影响。可见克服谱线定位错误是大噪声下插值算法的一个关键问题^[35-36]。

4 仿真研究

为了比较不同算法在强噪声下的性能，通过计算机产生余弦信号并采用高斯白噪声进行干扰。仿真信号如式(36) 所示：

$ x\left( n \right) = A\cos \left( {2{\rm{\pi }}n\frac{f}{{{f_s}}} + \theta } \right) + s\left( n \right)。$

(36)

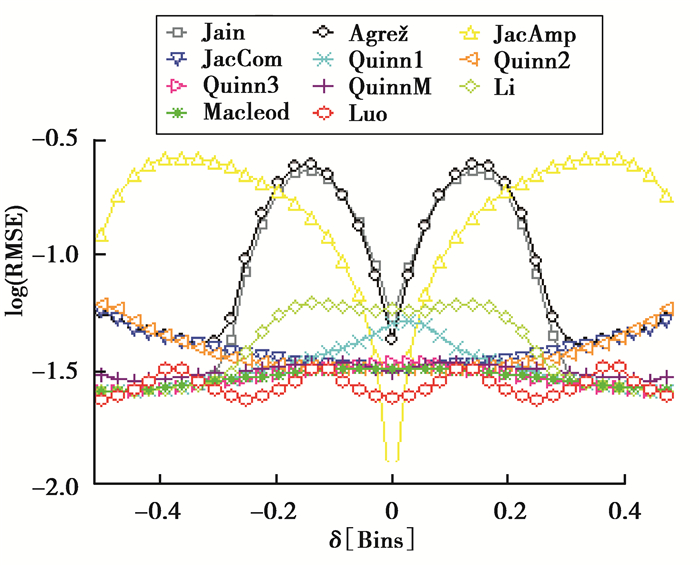
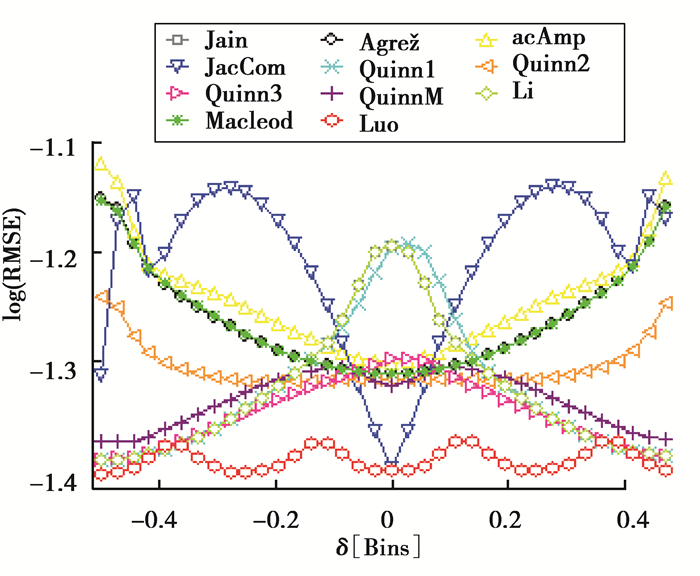
不失一般性，采样频率f_s设为1 000 Hz，仿真信号幅值A为1，采样点数N为1 000，信号频率f在[249.5, 250.5]连续内变化，步距0.01。每个频率下相位θ在(-π, π)内以π/16步长扫描，选择在一次噪声干扰下误差最大值作为该次的误差。对每一频率f考察10 000次噪声干扰下的均方根值(root mean squire error, RMSE)，其信噪比(signal-to-noise ratio, SNR)设为零。图 1和图 2分别显示了矩形窗和汉宁窗下各算法的结果。

4.1 采用矩形窗时各种算法性能比较

插值法的校正精度由${\hat \delta }$数值的大小与符号共同决定。在${\hat \delta }$符号正确的情况下，校正后的频率将趋近真实频率，即频率误差变小；若${\hat \delta }$符号取错，即出现插值方向错误，校正后的频率将会远离真实频率，导致比未校正前的频率误差更大^[6-7]。

由图 1可以看出当采用矩形窗时各种算法的RMSE有明显的区别，当|δ|位于零附近时，次大谱线与最大谱线的幅值相差最大。由式(3) 可知，若α非常小，${\hat \delta }$亦非常小；主瓣内次大谱线幅值和旁瓣内的第三大谱线幅值都非常小，其抗噪干扰性能非常差，噪声极易导致主瓣内次大值谱线的幅值小于旁瓣内最大谱线的幅值，从而发生次大谱线定位错误现象。因此，当|δ|位于零附近时，Jain算法具有较大的RMSE。当|δ|逐渐增大时，最大谱线与次大谱线的幅值大小差距减小，α变大，|δ|变大，此时主瓣内次大谱线幅值增大，谱线定位错误概率相对减小。然而相对于|δ|接近零时，此时归一化校正量${\hat \delta }$的数值变大，尽管错误定位概率减小，却使得RMSE增大，从仿真图可以看出δ的绝对值从0到0.15时，逐渐增大至最大。当δ绝对值超过0.15后，由于主瓣内的次大谱线幅值远大于旁瓣内谱线幅值，噪声的干扰导致次大谱线定位错误概率大大降低，因此RMSE越来越小。

对于Agrez算法，最大幅值谱线定位错误对其有重要的影响。|δ|在零附近时，尽管不会出现谱线定位错误，但依然容易出现了校正极性错误。这是由于${\hat \delta }$的符号由幅值次大谱线和幅值第三大谱线决定，而此时二者幅值都较小，谱线抗噪声能力较弱，极易造成符号反向。与Jain算法类似，随着|δ|增大尽管符号错误的概率减小，但由于误差的绝对数值增大，使得RMSE增大。当RMSE一直增大到最大值，随着符号错误的概率大大降低，RMSE逐渐减小，|δ|超过0.3以后，RMSE又逐渐变大。需要指出的是当|δ|在0.5附近时，RMSE并未剧增，这是因为尽管此时容易出现最大谱线定位错误，但根据式(5) 可知其符号相应也随着反向，从而保证校正极性的正确。

对于JacAmp算法，通过其校正公式可以看出，${\hat \delta }$的符号也是由幅值次大谱线和幅值第三大谱线决定。当|δ|在零附近时，由于最高谱线旁边的两条谱线幅值都较小，而最大谱线的系数为4，导致RMSE误差较小。随着|δ|增大，RMSE也快速增大，一直递增至0.35左右开始下降。这是由于|X(l+1)|或|X(l-1)|增大，分子的值越来越大，分母的值越来越小，进而使得${\hat \delta }$幅值数值大小的误差剧增。δ的绝对值在0.35以后，随着符号错误的概率大大降低，算法RMSE减小。与Agrez算法相比，在δ接近0.5时，该算法效果较差。

JacCom算法和Quinn2算法较为接近，二者都是在|δ|=0时具有较小的RMSE，随着|δ|增大RMSE增大，在0.3以后几乎和Agrez算法保持一致，这表明这两种算法对谱线定位错误有较强的抗性。而Quinn1算法与Li算法在|δ|=0.5时具有较小的RMSE。随着|δ|的减小，Quinn1算法的RMSE逐渐增大，并在|δ|=0时达到了最大，而li算法|δ|=0.2附近增长迅速，并在达到最大值后RMSE保持相对稳定。Quinn3算法、QuinnM算法和Macload算法也具有非常接近的结果，三者随着|δ|的变化其结果基本稳定，且相对其他算法RMSE保持较低水平。Luo算法除了在|δ|=0.38附近外，与以上其他所有算法相比具有较低的RMSE，随着|δ|的变化该算法的RMSE有一定程度的波动，但总体控制在-1.5左右。

综合上述，就校正精度而言，当|δ|≈0附近时可选择JacAmp算法，当|δ|≈0.5附近时，Jain算法、Quinn1算法、Li算法、Quinn3算法、QuinnM算法和Macload算法都可以取得较好的结果。而Luo算法是在无法预先判定|δ|范围情况下的最佳选择。

4.2 采用汉宁窗时各种算法性能比较

总体上看，当采用汉宁窗时的RMSE比采用矩形窗时的RMSE波动幅度小，稳定性得到较大提升。Grandke算法、Quinn1算法和Li算法结果十分接近，特别是Grandke算法和Li算法的RMSE几乎完全重合。而Quinn3算法与QuinnM算法结果相差不大。除了在|δ|=0附近QuinnM算法的RMSE略小外，Quinn3算法在绝大部分区域都稍比QuinnM算法好。由于以上5种方法都是基于两谱线的插值法，在|δ|=0.5附近时都取得了较小的RMSE，而在|δ|=0附近时RMSE较大。与采用矩形窗时相比，Grandke算法改善较为明显，这是由于不同于矩形窗主瓣内只有两条谱线，汉宁窗主瓣内有4条谱线，次大幅值谱线和第三大幅值谱线都在主瓣内，而且相对于矩形窗，其幅值都较大，抗噪声性能较强，噪声的干扰导致次大谱线定位错误的概率相对小很多。

Agrez算法与Macload算法的RMSE一致性较好，二者在|δ|的整个区域都略比JacAmp算法好。Quinn2在|δ|＜0.35区域都保持了较小的RMSE，且十分稳定。JacCom算法变化十分剧烈，但在|δ|≈0附近时有非常好的效果。以上5种算法都是采用了3条谱线的校正法，因此在|δ|≈0.5时结果都不甚理想。除了JacCom外，其他4种算法的RMSE都增长较快。尽管JacCom的RMSE在|δ|≈0.5附近急剧下降，但与两谱线插值法相比仍然维持在一个较高水平。当采用汉宁窗时候Luo算法与以上10种算法相比具有绝对优势。首先，其RMSE在|δ|的整个区域都是较低的。其次，Luo算法随着|δ|的变化波动较小，保持了较好的稳定性。

5 结论与展望

1) 无论是基于幅值比值还是基于复数比值的插值法都会受到谱线定位错误的影响，但是不同算法之间对谱线定位错误的敏感度差异性较大，且目前插值算法的RMSE值与归一化校正频率密切相关。因此，如何避免插值算法受谱线定位错误影响以及如何解决算法的噪声性依赖于归一化校正频率，进一步提高算法的抗噪声性能等问题是未来研究的重点。

2) 插值公式与窗函数选择密切相关，且仅仅极少部分窗函数有简单的解析表达式，因此提出一种对各种窗函数通用的插值算法是目前研究的难点，是解决插值法普适性和工程应用的基础。

3) 在信噪比非常低的情况下，所有的插值校正方法都不稳定，校正误差将会非常大。通常为了降低噪声干扰，突出信号的特征，工程中多采用多段平均的频谱。然而，目前的各种算法均不能对多段平均后的频谱进行校正，因此研究适用于多段平均后的频谱的插值算法，对推广插值法应用于工程领域的具有重要的价值。

4) 受随机噪声干扰的影响，各种校正算法的结果都成一定的随机性。而工程应用中需要尽可能降低这种随机性。因此，在多次测量下研究各种算法校正结果的概率分布特性并在此基础之上进一步研究如何取得较为精确的频率是插值算法发展的重要方向。