2. 吉林大学 汽车仿真与控制国家重点实验室, 长春 130022
2. State Key Laboratory of Automobile Dynamic Simulation, Jilin University, Changchun 130022, P. R. China
重型半挂车具备营运成本低、节油性好和运输效率高等优势,因此在公路长途货运车辆中,重型半挂车比例最高,获得广泛的运用[1]。但因重型半挂车质心高、尺寸大、载重量重,且牵引车和挂车之间相互作用,容易发生摆振、折叠和侧翻等事故[2]。同时,重型半挂车大多数事故发生在高速路上,易造成多车连环相撞,造成巨大的人员伤亡、环境损害和经济损失,成为重大安全事故[3]。加拿大大多数事故与重型半挂车相关,2004年度共造成212 347人受伤、2 730人死亡[4]。鉴于此,针对重型半挂车易发生重大危险事故的中高速工况进行重型半挂车包括侧翻控制在内的稳定性控制研究具有重要现实意义。
主动转向系统具备控制车辆稳定和减小轮胎与地面磨损的能力,并且对车辆速度和驾驶员干扰较小,尤其是挂车主动转向系统。因此,国外高校和企业进行了基于挂车主动转向系统的重型半挂车控制策略研究[4-7]。Islam等[8]和Ding等[9]基于简化模型和挂车主动转向系统,运用LQR方法,提出了重型多挂列车控制策略。Cheng等[10]以挂车后端与第5轮轨迹的偏差量为控制目标,提出了重型半挂车侧翻控制策略。仿真结果表明:挂车主动转向控制策略提高了重型半挂车抗侧翻能力。Jujnovich等[11]基于挂车主动转向系统且考虑侧向风干扰基础上,提出了重型半挂车路径跟随控制策略,实现了重型半挂车良好的路径跟随。Kim等[12]提出了主动转向控制策略,保证了铰接车辆侧向位移偏移量在允许范围之内。Wang等[13]以路径偏移量为控制目标,提出了挂车主动转向控制策略,提高了车辆操纵稳定性。Oreh等[14]基于挂车主动转向系统,运用模糊PID算法,提出了重型半挂车控制策略。该策略减少了路径偏移量和保证了铰接角跟随期望值,并提高了重型半挂车操纵稳定性。为提高重型半挂车汽车的横摆稳定性,Kharrazi等[15]在考虑车辆参数不确定性基础上,提出了挂车主动转向控制策略,并验证了高速工况下控制策略有效性和鲁棒性。
综上所述,大多数挂车主动转向控制策略针对工况为普通工况,未对极限工况进行重型半挂车稳定性控制研究。同时,考虑到重型半挂车工况复杂多变和车辆状态变化较大,为实现各工况下重型半挂车控制策略最优控制,需要最优的控制权重系数。
针对以往研究不足,在建立线性变参数实时简化模型的基础上,笔者提出了模式切换的中高速重型半挂车挂车主动转向控制策略。该策略基于挂车主动转向系统,并通过模式切换实现重型半挂车从低附到高附,从普通工况到极限工况的中高速工况良好地控制。由于遗传粒子群优化算法具有全局最优和寻优速度快等优势,采用遗传粒子群优化算法优化模式切换的中高速挂车主动转向控制策略的控制权重系数,从而实现重型半挂车中高速各工况最优控制。
1 线性变参数三自由度实时简化模型根据模式切换的中高速重型半挂车挂车主动转向控制策略的需要,建立了重型半挂车线性变参数实时简化模型,其三自由度分别为牵引车质心侧偏角、牵引车横摆和挂车横摆[1]。
牵引车运动学方程为
| $ {m_1}{u_1}\left( {{{\dot \beta }_1} + {{\dot \psi }_1}} \right) = {F_1}\cos \left( {{\delta _{\rm{f}}}} \right) + {F_2} + {F_4}, $ | (1) |
| $ {I_{1zz}}{{\ddot \psi }_1} = {F_1}a\cos \left( {{\delta _{\rm{f}}}} \right) - {F_2}b - {F_4}c, $ | (2) |
式中:u1为牵引车纵向速度;F2为牵引车驱动轴侧向力;
挂车运动学方程为
| $ {m_2}{u_2}\left( {{{\dot \beta }_2} + {{\dot \psi }_2}} \right) = {F_3}\cos \left( {{\delta _r}} \right) + {F_4}cos\mathit{\Gamma }, $ | (3) |
| $ {I_{2zz}}{{\ddot \psi }_2} = - {F_3}d\cos \left( {{\delta _r}} \right) - {F_4}e\cos \mathit{\Gamma }, $ | (4) |
式中:m2为挂车质量;
牵引车和挂车的约束方程为
| $ {{\dot \beta }_2} = {{\dot \beta }_1} - \frac{c}{{{u_1}}}{{\ddot \psi }_1} - \frac{c}{{{u_2}}}{{\ddot \psi }_2} + {{\dot \psi }_1} - {{\dot \psi }_2}。$ | (5) |
文中采用线性轮胎模型,具体公式为
| $ {F_1} = {k_1}\left( {{\beta _1} + \frac{{a{{\dot \psi }_1}}}{{{u_1}}} - {\delta _{\rm{f}}}} \right),\;\;\;\;\;\;\;\;{F_2} = {k_2}\left( {{\beta _1} - \frac{{b{{\dot \psi }_1}}}{{{u_1}}}} \right),\;\;\;\;\;\;\;\;{F_3} = {k_3}\left( {{\beta _2} - \frac{{d{{\dot \psi }_2}}}{{{u_2}}} + {\delta _{\rm{r}}}} \right)。$ | (6) |
由于重型半挂车工作地域广,工况复杂多变,因此重型半挂车精确控制依赖于以车辆实时状态相匹配的实时准确简化模型。鉴于此,在建立简化模型基础上,辨识出与重型半挂车实时工况匹配的具有非线性特性的简化模型关键参数,成为准确控制重型半挂车稳定性的关键。文献[16]运用提出的离线参数辨识方法辨识了简化模型关键参数,并将辨识后的简化模型关键参数值形成了关键参数MAP图。利用线性变参数实时简化模型结合关键参数MAP图,获得了与车辆实际状态相匹配的线性变参数三自由度实时简化模型,为重型半挂车稳定性控制奠定了必要的基础。考虑到文章长度问题,详细过程参考文献[16],此处不累述。
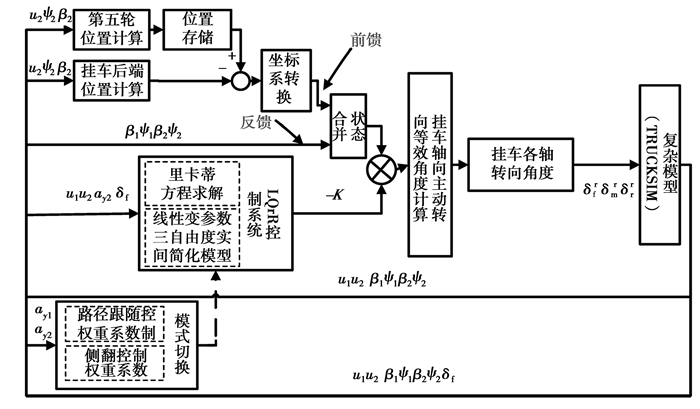
2 模式切换的中高速重型半挂车挂车主动转向控制策略针对重型半挂车极易发生危险事故的中高速工况,提出了模式切换的中高速重型半挂车挂车主动转向控制策略,此策略控制框图详见图 2。
|
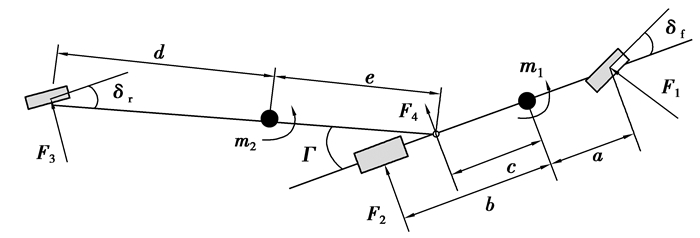
图 1 重型半挂车横摆运动示意图 Figure 1 The sketch map of articulated heavy vehicles yaw motion |
|
图 2 模式切换的中高速重型半挂车挂车主动转向控制策略框图 Figure 2 The sketch map of the active trailer steering control strategy for articulated heavy vehicles based on modes switching in medium/high speed conditions |
模式切换的中高速重型半挂车挂车主动转向控制策略在建立虚拟驾驶员的基础上,基于挂车主动转向系统,运用LQR最优控制方法。此策略由侧翻控制和路径跟随控制2个控制模式组成,根据车辆实时状态变换控制权重系数,实现2个控制模式切换。针对普通工况,控制策略采用路径跟随模式,实现重型半挂车横摆、折叠和路径跟随控制;针对极限工况,控制策略采用侧翻控制模式,实现重型半挂车侧翻控制。因此,提出的控制策略能够充分利用不同控制模式优势,实现重型半挂车中高速从普通工况到极限工况良好地控制。
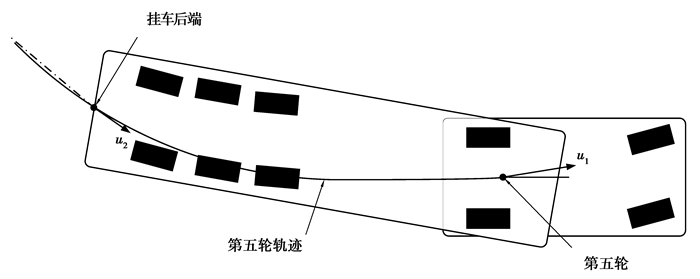
2.1 控制算法 2.1.1 增强型状态方程挂车主动转向控制策略基本准则为挂车后端跟随第5轮的轨迹,即假设有一虚拟驾驶员根据第5轮轨迹操纵重型半挂车挂车主动转向,从而实现挂车后端与第5轮轨迹偏差值最小,具体见图 3。
|
图 3 挂车虚拟驾驶员示意图 Figure 3 The sketch map of trailer virtual driver model |
控制策略状态方程在线性变参数实时简化模型基础上,增加了挂车主动转向而成,详见式(7)。
| $ \mathit{\boldsymbol{\dot x}} = \mathit{\boldsymbol{Ax}} + {\mathit{\boldsymbol{B}}_0}\mathit{\boldsymbol{u}} + {\mathit{\boldsymbol{B}}_1}{\delta _{\rm{f}}}, $ | (7) |
式(7) 中:
| $ \mathit{\boldsymbol{A}} = {\mathit{\boldsymbol{M}}^{ - 1}}\\ \left[ {\begin{array}{*{20}{c}} 0&{\begin{array}{*{20}{c}} {\left( {c + a} \right){k_1} + \left( {c - b} \right){k_2}}&{\frac{{a\left( {c + a} \right){k_1}}}{{{u_1}}} - \frac{{b\left( {c - b} \right){k_2}}}{{{u_1}}} - {m_1}{u_1}c}&0&0&0&0\\ {{k_1} + {k_2}}&{\frac{{a{k_1}}}{{{u_1}}} - \frac{{b{k_2}}}{{{u_1}}} - {m_1}{u_1}}&{{k_3}}&{ - \frac{{d{k_3}}}{{{u_2}}} - {m_2}{u_2}}&0&0\\ 0&0&{\left( {e + d} \right){k_3}}&{ - \frac{{d\left( {e + d} \right){k_3}}}{{{u_2}}} - {m_2}{u_2}e}&0&0\\ 0&1&0&{ - 1}&0&0\\ 0&0&{{u_2}}&0&0&{{u_2}}\\ 0&0&0&1&0&0 \end{array}} \end{array}} \right], $ |
| $ \mathit{\boldsymbol{M = }}\left[ {\begin{array}{*{20}{c}} {{m_1}{u_1}c}&{{I_{1zz}}}&0&0&0&0\\ {{m_1}{u_1}}&0&{{m_2}{u_2}}&0&0&0\\ 0&0&{{m_2}{u_2}e}&{ - {I_{2zz}}}&0&0\\ { - 1}&{ - \frac{c}{{{u_1}}}}&1&{\frac{e}{{{u_2}}}}&0&0\\ 0&0&0&0&1&0\\ 0&0&0&0&0&1 \end{array}} \right], $ |
| $ \begin{array}{l} {\mathit{\boldsymbol{B}}_1} = {\mathit{\boldsymbol{M}}^{ - 1}}{\left[ {\begin{array}{*{20}{c}} { - \left( {c + a} \right){k_1}}&{ - {k_1}}&0&0&0&0 \end{array}} \right]^{\rm{T}}},\mathit{\boldsymbol{u = }}\left[ {{\delta _{\rm{r}}}} \right],\\ {\mathit{\boldsymbol{B}}_0} = {\left[ {\begin{array}{*{20}{c}} 0&{ - {k_3}}&{ - \left( {e + d} \right) * {k_3}}&0&0&0 \end{array}} \right]^{\rm{T}}},\mathit{\boldsymbol{x = }} {\left[ {\begin{array}{*{20}{c}} {{\beta _1}}&{{{\dot \psi }_1}}&{{\beta _2}}&{{{\dot \psi }_2}}&{{{\dot Y}_2}}&{{\psi _2}} \end{array}} \right]^{\rm{T}}}。\end{array} $ |
状态方程离散化:
| $ \mathit{\boldsymbol{x}}\left( {k + 1} \right) = {\mathit{\boldsymbol{A}}_d}\mathit{\boldsymbol{x}}\left( k \right) + {\mathit{\boldsymbol{B}}_{0d}}u\left( k \right) + {\mathit{\boldsymbol{B}}_{1d}}{\delta _{\rm{f}}}\left( k \right)。$ | (8) |
第5轮轨迹侧向位移滚动模型为
| $ {\mathit{\boldsymbol{Y}}_r}\left( {k + 1} \right) = \mathit{\boldsymbol{D}}{\mathit{\boldsymbol{Y}}_r}\left( k \right) + \mathit{\boldsymbol{E}}{\mathit{\boldsymbol{Y}}_{\left( {r + 1} \right)}}\left( k \right), $ | (9) |
式中:
控制策略的增强型状态方程由离散的状态方程和路径滚动模型组成,为重型半挂车中高速控制策略提供了必要的基础,此增强型状态方程为
| $ \underbrace {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{x}}_d}\left( {k + 1} \right)}\\ {{\mathit{\boldsymbol{Y}}_r}\left( {k + 1} \right)} \end{array}} \right]}_{\mathit{\boldsymbol{Z}}\left( {k + 1} \right)} = \underbrace {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{A}}_d}}&0\\ 0&\mathit{\boldsymbol{D}} \end{array}} \right]}_{\mathit{\boldsymbol{A}}Z}\underbrace {\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{x}}\left( k \right)}\\ {{\mathit{\boldsymbol{Y}}_r}\left( k \right)} \end{array}} \right]}_{\mathit{\boldsymbol{Z}}\left( k \right)} + \underbrace {\left[ {\begin{array}{*{20}{c}} 0\\ \mathit{\boldsymbol{E}} \end{array}} \right]}_{{\mathit{\boldsymbol{E}}_z}}{Y_{\left( {r + 1} \right)}}\left( k \right) + \underbrace {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{B}}_{0d}}}\\ 0 \end{array}} \right]}_{{\mathit{\boldsymbol{B}}_{Z0}}}u\left( k \right) + \underbrace {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{B}}_{1d}}}\\ 0 \end{array}} \right]}_{{\mathit{\boldsymbol{B}}_{Z1}}}{\delta _{\rm{f}}}\left( k \right), $ | (10) |
式中,
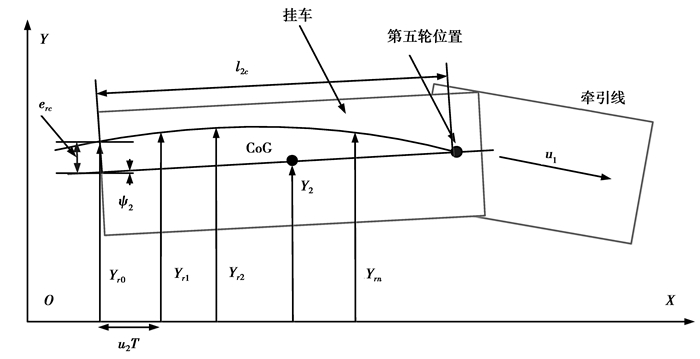
计算挂车后端与第5轮轨迹的路径偏移量首先需要获得大地坐标系下第5轮轨迹坐标值。大地坐标系下路径偏移量如图 4所示。
|
图 4 大地坐标系下路径偏移量示意图 Figure 4 The sketch map of path deviation at global coordinate system |
第5轮航向角为
| $ {\gamma _5} = {\mathit{\Psi }_2} + \beta _2^5。$ | (11) |
挂车横摆角为
| $ {\mathit{\Psi }_2} = \int {{\mathit{\Psi }_2}{\rm{d}}t} 。$ | (12) |
第5轮质心侧偏角为
| $ \beta _2^5 = {\tan ^{ - 1}}\left( {\tan \left( {{\beta _2}} \right) + \frac{e}{{{u_2}}}{\mathit{\Psi }_2}} \right)。$ | (13) |
大地坐标下,第5轮横纵坐标为
| $ {X_5} = {l_{2{\rm{e}}}} + \int_0^l {\frac{{{u_2}}}{{\cos \left( {\beta _2^5} \right)}}\cos \left( {{\gamma _5}} \right){\rm{d}}t} , $ | (14) |
| $ {Y_5} = \int_0^l {\frac{{{u_2}}}{{\cos \left( {\beta _2^5} \right)\sin \left( {{\gamma _5}} \right)}}{\rm{d}}t} 。$ | (15) |
第5轮坐标存储的长度由采样时间和车速确定。
挂车后端坐标值为
| $ {X_{{\rm{rc}}}} = {X_5} - {l_{2{\rm{e}}}}\cos \left( {{\mathit{\Psi }_2}} \right), $ | (16) |
| $ {Y_{{\rm{rc}}}} = {Y_5} - {l_{2{\rm{e}}}}\sin \left( {{\mathit{\Psi }_2}} \right)。$ | (17) |
第5轮挂车坐标系下坐标值为
| $ {x_5} = \left( {{X_5} - {X_{{\rm{rc}}}}} \right)\cos \left( {{\mathit{\Psi }_2}} \right) + \left( {{Y_5} - {y_{{\rm{rc}}}}} \right)\sin \left( {{\psi _2}} \right), $ | (18) |
| $ {y_5} = \left( {{X_5} - {X_{{\rm{rc}}}}} \right)\sin \left( {{\mathit{\Psi }_2}} \right) + \left( {{Y_5} - {y_{{\rm{rc}}}}} \right)\cos \left( {{\psi _2}} \right), $ | (19) |
此时挂车后端与第5轮轨迹的路径偏移量为
| $ {y_{{\rm{t}}\left( i \right)}} = {y_{5\left( i \right)}}, $ | (20) |
| $ {e_{{\rm{rc}}}} = {y_{{\rm{t}}\left( 0 \right)}}。$ | (21) |
式中:β25为第5轮质心侧偏角挂车坐标系下值;Γ为铰接角;Y5为第5轮大地坐标系y轴值;γ5为第5轮航向角;Yrc为挂车后端大地坐标系y轴值;X5为第5轮大地坐标系x轴值;Xrc为挂车后端大地坐标系x轴值;x5为第5轮挂车坐标系x轴向量;y5为挂车坐标系第5轮y轴向量;yt为挂车后端与第5轮轨迹差值y轴向量值;erc为挂车后端与第5轮轨迹偏差值。
2.1.3 控制策略目标函数挂车侧向加速度是引起重型半挂车侧翻重要因素,通过控制挂车侧向加速度大小,即可实现重型半挂车侧翻控制。
挂车侧向加速度为
| $ {a_{y2}} = \left( {\mathit{\boldsymbol{E}}{\mathit{\boldsymbol{E}}_1}A + \mathit{\boldsymbol{E}}{\mathit{\boldsymbol{E}}_2}} \right)\dot x + \mathit{\boldsymbol{E}}{\mathit{\boldsymbol{E}}_1}{B_0}u + \mathit{\boldsymbol{E}}{\mathit{\boldsymbol{E}}_1}{B_1}{\delta _{\rm{f}}}, $ | (22) |
式中:
挂车侧向加速度离散化
| $ {a_{y2}}\left( k \right) = \mathit{\boldsymbol{HH}}x\left( k \right) + \mathit{\boldsymbol{KK}}u\left( k \right), $ | (23) |
式中:
挂车侧向加速度和路径偏移量结合成增强型状态空间的输出矩阵,为重型半挂车路径跟随控制和侧翻控制提供必要基础。
| $ \left\{ \begin{array}{l} {e_{rc}}\left( k \right)\\ {a_{y2}}\left( k \right) \end{array} \right\} = {\mathit{\boldsymbol{H}}_d}{\mathit{\boldsymbol{Z}}_t}\left( k \right) + {\mathit{\boldsymbol{K}}_d}u\left( k \right), $ | (24) |
式中:
| $ J = \sum\limits_{k = 0}^\infty {\left\{ {{q_1}{{\left( {{e_{{\rm{rc}}}}\left( k \right)} \right)}^2} + {q_2}{{\left( {{a_{y2}}\left( k \right)} \right)}^2} + {r_1}{{\left( {{\delta _{\rm{r}}}\left( k \right)} \right)}^2}} \right\}} , $ | (25) |
式中:r1为挂车转向角度权重系数,q1为路径偏移量权重系数,q2为挂车侧向加速度权重系数。
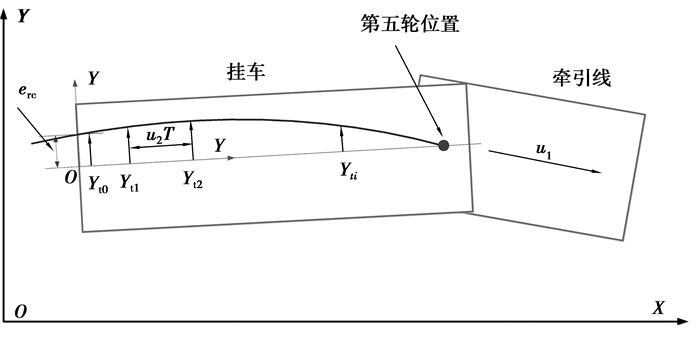
2.1.4 坐标系转换在大地坐标系下,若横摆角较大时,计算路径跟随偏差量将产生很大的误差。因此,大地坐标系仅适合于横摆角较小的工况。鉴于此,为了克服大横摆角工况偏差量计算大的误差,需要将第5轮轨迹坐标值从大地坐标下的绝对坐标转换成挂车坐标系下的相对坐标,坐标系转换示意图详见图 5。
|
图 5 第5轮轨迹坐标计算示意图 Figure 5 The fifth wheel trajectory coordinate at trailer coordinate system |
第5轮轨迹侧向位移
| $ {Y_{ri}} = \left( {{Y_2} - {l_{2c}}{\mathit{\Psi }_2}} \right) + i{u_2}T{\mathit{\Psi }_2} + {Y_{ti}}。$ | (26) |
大地坐标系转换到挂车坐标系的中间矩阵详见式(27),具体推导过程参考文献[17-18]。
| $ \mathit{\boldsymbol{W = }}\left[ {\begin{array}{*{20}{c}} 0&0&0&0&0&0&1&{1 \times {u_2} \times T - {l_{2{\rm{e}}}}}\\ 0&0&0&0&0&0&1&{2 \times {u_2} \times T - {l_{2{\rm{e}}}}}\\ 0&0&0&0&0&0&1&{3 \times {u_2} \times T - {l_{2{\rm{e}}}}}\\ \vdots &{}&{}& \vdots &{}&{}& \vdots & \vdots \\ 0&0&0&0&0&0&1&{k \times {u_2} \times T - {l_{2{\rm{e}}}}} \end{array}} \right]。$ | (27) |
增强型状态空间状态量
| $ \mathit{\boldsymbol{Z = }}\left[ {\begin{array}{*{20}{c}} 1&0\\ W&I \end{array}} \right]{\mathit{\boldsymbol{Z}}_t}。$ | (28) |
控制策略控制量
| $ \mathit{\boldsymbol{u = }} - K\left[ {\begin{array}{*{20}{c}} 1&0\\ W&I \end{array}} \right], $ | (29) |
式中:
若挂车轴各轴侧向力不相等,将对车辆轮胎力控制产生负面影响。由于挂车各轴轮胎为同一类型轮胎,保证挂车各轴侧偏角相等即可保证挂车各轴侧向力相等。
| $ a_{\rm{f}}^{\rm{r}} = a_{\rm{m}}^{\rm{r}} = a_{\rm{r}}^{\rm{r}}。$ | (30) |
将控制策略决策出的后轴主动等效转向角度赋值给挂车中间轴
| $ \delta _{\rm{m}}^{\rm{r}} = {\delta _{\rm{r}}}, $ | (31) |
式中,δmr为挂车中间轴主动转向角度。
挂车轴前轴和后轴转向角度为
| $ \delta _{\rm{f}}^{\rm{r}} = {\tan ^{ - 1}}\left( {\tan \left( {\delta _{\rm{m}}^{\rm{r}}} \right) + \frac{{{l_{{\rm{we}}}}}}{{{u_2}}}{{\mathit{\dot \Psi }}_2}} \right), $ | (32) |
| $ \delta _{\rm{r}}^{\rm{r}} = {\tan ^{ - 1}}\left( {\tan \left( {\delta _{\rm{m}}^{\rm{r}}} \right) + \frac{{{l_{{\rm{we}}}}}}{{{u_2}}}{{\mathit{\dot \Psi }}_2}} \right), $ | (33) |
式中:lwe为挂车轴两轴之间的距离。
2.2 挂车主动转向控制策略权重系数优化控制策略控制效果由控制策略权重系数决定,控制策略权重系数表征了目标函数对各控制量和状态量重视程度。选择最优控制策略权重系数将获得最优控制效果;而选择的控制策略权重系数不合适,将使控制策略的控制效果达不到预期效果;若控制策略权重系数与控制策略不匹配,可能造成控制系统不收敛,反而加剧车辆稳定性恶化。
通常情况下,研发人员根据实践经验确定调整控制策略权重系数。通过这种方式确定控制策略权重系数需要研发人员对控制策略和控制效果有充分理解,同时调试过程费时又单调,并且不能够保证控制效果全局最优。文献[8]采用遗传算法优化了控制策略权重系数,控制策略控制效果良好。但考虑到遗传粒子群的优化算法具有更快更好优化的优势和重型半挂车控制策略复杂性,笔者采用遗传粒子算法进行控制策略权重系数优化。
模式切换的中高速重型半挂车挂车主动转向控制策略分为路径跟随控制和侧翻控制两个控制模式。针对普通工况,采用路径跟随控制模式来实现重型半挂车良好的横摆、折叠和路径跟随;针对极限工况,采用侧翻控制模式,实现重型半挂车侧翻控制。不同优化指标针对不同控制模式,以达到各个工况最优控制。
路径跟随控制模式的优化指标为:挂车后端跟随第5轮轨迹运动,即挂车后端与第5轮轨迹路径偏差最小。
| $ obj\left( x \right) = \sum\limits_{k = 0}^l {{{\left( {{e_{{\rm{rc}}}}\left( k \right)} \right)}^2}} 。$ | (34) |
由于重型半挂车侧翻与后端放大率存在直接的关系,因此侧翻控制模式的优化指标为:后端放大率最小。
| $ obj\left( x \right) = \frac{{\max \left| {{a_{y2}}} \right|}}{{\max \left| {{a_{y1}}} \right|}}。$ | (35) |
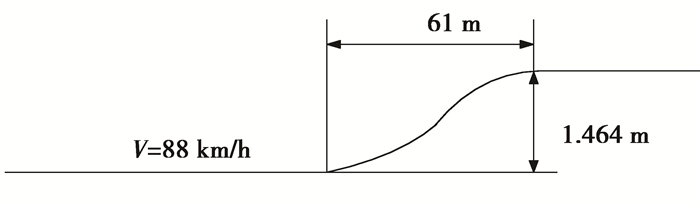
SAE J2179单移线工况能够良好体现后端放大率,成为测试重型半挂车中高速特性的重要工况,此工况设置见图 6[10]。因此,这里采用此工况进行挂车主动控制策略权重系数优化。
|
图 6 车速88 km/h,侧向位移1.464 m单移线工况 Figure 6 Lateral displacement 1.464m, 88km/h, single lane change condition |
重型半挂车挂车主动转向中高速控制策略两个控制模式的优化权重系数结果为:路径跟随控制模式最优权重系数q1=1, q2=0.01, r1=1.503;侧翻控制模式最优权重系数q1=1, q2=334, r1=162 7。
2.3 模式切换的中高速重型半挂车挂车主动转向控制策略切换条件通过Trucksim软件仿真研究表明,挂车一侧车轮全部离地的挂车侧向加速度为0.35 g,此时重型半挂车开始进入极限工况。鉴于此,中高速控制策略从路径跟随控制模式向侧翻控制模式切换条件为0.35 g。由于侧翻控制模式针对极限工况,若控制策略采用侧翻控制模式,表明重型半挂车已经进入极限工况。若控制不佳和模式切换不合适,将造成不可挽回的事故。鉴于此,为了确保侧翻控制模式退出后,重型半挂车一定处于稳定性状态,侧翻控制模式退出的条件不是挂车侧向加速度小于0.35g就立即切换到路径跟随控制模式,具体切换条件为
| $ \left[ {\left( {\left| {{a_{y1}}} \right| < 0.01g} \right)\& \left( {\left| {{a_{y2}}} \right| < 0.01g} \right)\& \left( {\left| {{{\dot a}_{y2}}} \right| < 0.002g/{\rm{s}}} \right)\\ \& \left( {\left| {{{\dot a}_{y2}}} \right| < 0.002g/{\rm{s}}} \right)\& \left( {{u_2} > 20{\rm{km/h}}} \right)} \right] = {\rm{True}}{\rm{。}} $ | (36) |
为了充分验证提出的重型半挂车控制策略,设计了88 km/h,3.9 m低附单移线工况和85 km/h,3.5 m高附双移线工况两个工况。设计工况覆盖了低附到高附,普通工况到极限工况。
3.1 88 km/h,3.9 m,低附单移线工况此工况设置为:车速88 km/h,侧向偏移位移3.9 m的单移线,测试路面为附着系数0.3低附着路面。此工况主要测试模式切换的中高速重型半挂车挂车主动转向控制策略的低附着横摆,路径跟随和折叠控制能力。
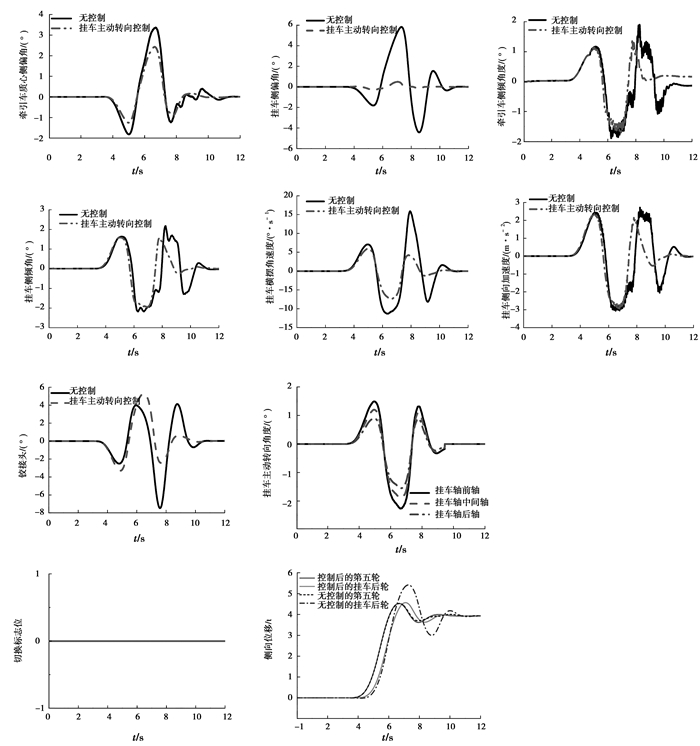
由于此工况下侧向加速度未超过0.35g,因此,此工况为普通工况。在此工况下,挂车主动转向控制策略采用的控制模式为路径跟随控制模式。由图 7和表 1可知,模式切换的中高速重型半挂车挂车主动转向控制策略控制相对于无控制,重型半挂车牵引车质心侧偏角,挂车质心侧偏角,挂车横摆角速度分别提高了27.6%,91.6%和53.2%。这3个指标与车辆横摆稳定性有直接的关系。因此,挂车主动转向控制策略极大提高了车辆横摆稳定性。挂车主动转向控制相对于无控制的铰接角提高了29.1%。铰接角与重型半挂车折叠稳定性有直接关系,因此,挂车主动转向控制策略提高了车辆折叠稳定性。挂车主动转向控制相对于无控制的挂车后端与第5轮轨迹路径偏差提高了95.5%。由此可见,挂车主动转向控制策略极大提高了重型半挂车路径跟随能力。挂车主动转向控制相对于无控制的牵引车侧倾角,挂车侧倾角和挂车侧向加速度分别提高了11.2%,10.3%和4.1%。因此,挂车主动转向控制策略的路径跟随控制模式间接提高了重型半挂车侧倾稳定性。
|
图 7 88 km/h,3.9 m低附单移线工况仿真结果 Figure 7 Simulation results under 88 km/h, low adhesion coefficient, 3.9 m single lane change condition |
| 表 1 此工况下仿真结果 Table 1 Simulation results under the condition |
85 km/h,3.5 m, 高附双移线工况设置为:车速85 km/h,侧向偏移3.5 m,附着系数0.85。此工况为极限工况,重型半挂车不进行控制将很快发生侧翻。
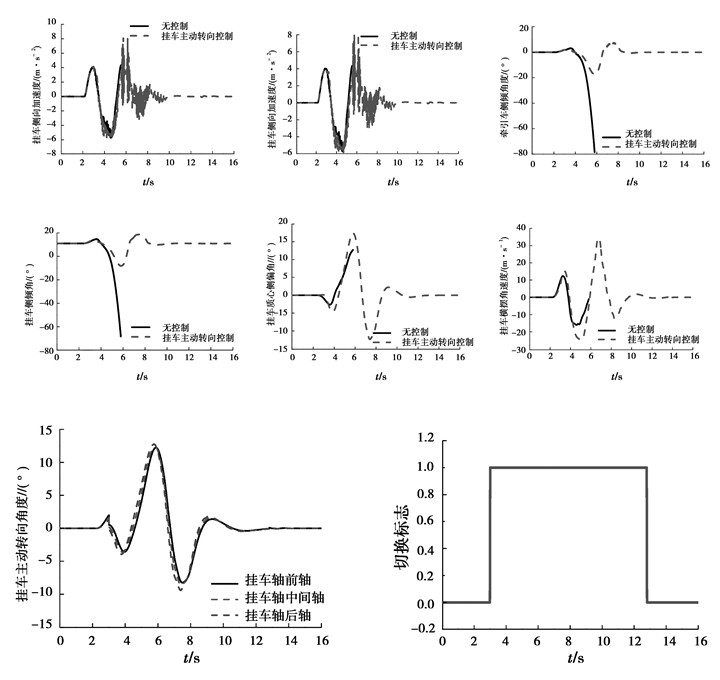
由图 8可知,在此工况下,无控制的重型半挂车很快发生了侧翻。但是,模式切换的中高速重型半挂车挂车主动转向控制策略避免了车辆侧翻并使重型半挂车最终平稳运行。因此,本文提出挂车主动转向控制策略实现了重型半挂车极限工况的侧翻控制。图 8切换标识记录了控制策略随着车辆状态变化从路径跟随模式切换到侧翻控制模式,再从侧翻控制模式切换到路径跟随模式的过程。
|
图 8 85 km/h,3.5 m高附双移线工况仿真结果 Figure 8 Simulation results under 85 km/h, high adhesion coefficient, 3.5m double lane change condition |
综上所述,提出的挂车主动转向控制策略实现了普通工况下的路径跟随,横摆和折叠控制;并且实现了极限工况下的侧翻控制。同时,仿真结果表明:遗传粒子群算法优化的控制策略权重系数能够满足模式切换的中高速重型半挂车挂车主动转向控制策略最优控制的要求。
4 结论1) 针对重型半挂车中高速不同工况,提出了模式切换的中高速重型半挂车挂车主动转向控制策略。此策略分为路径跟随控制和侧翻控制两个控制模式。路径跟随控制模式利用路径跟随权重系数,实现了重型半挂车普通工况的路径跟随,横摆和折叠控制;侧翻控制模式利用侧翻控制权重系数,实现了重型半挂车极限工况的侧翻控制。因此,提出的重型半挂车中高速挂车主动转向控制策略通过控制模式切换,适应了重型半挂车工况变化,从而实现了从低附到高附,从普通工况到极限工况中高速各个工况良好地控制。
2) 针对重型半挂车不同工况,运用遗传粒子群算法获得了控制策略最优控制权重系数。仿真实验结果表明:遗传粒子群算法满足模式切换的中高速重型半挂车挂车主动转向控制策略权重系数优化的要求;利用优化控制权重系数,提出的控制策略实现了重型半挂车中高速各工况最优控制。
| [1] |
宗长富, 聂枝根, 张振.
厢式半挂车简化模型参数辨识研究[J]. 中国公路学报, 2014, 27(4): 112–120.
ZONG Changfu, NIE Zhigen, ZHANG Zhen. Parameters identification for simplified model of container semi-trailer[J]. China Journal of Highway and Transport, 2014, 27(4): 112–120. (in Chinese) |
| [2] | Kamnik R, Boettiger F, Hunt K. Roll dynamics and lateral load transfer estimation in articulated heavy freight vehicles[J]. Proceedings of the Institution of Mechanical Engineers, Part D:Journal of Automobile Engineering, 2003, 217(11): 985–997. DOI:10.1243/095440703770383884 |
| [3] | Kusters L J J. Increasing rollover safety of commercial vehicles by application of electronic strategies. Netherland:Swets and Zeitlinger, 1995. https://link.springer.com/article/10.1631/FITEE.1500211 |
| [4] | Islam M M, Mikaric S, He Y, et al. Rollover parallel design optimization of multi-trailer articulated heavy vehicles with active safety systems. Canada:University of Ontario Institute of Technology, 2013. http://link.springer.com/content/pdf/10.1007/978-3-642-33738-3_53.pdf |
| [5] | Hata N, Hasegawa S, Takahashi S, et al. A control method for 4WS truck to suppress excursion of a body rear overhang//SAE International Truck & Bus Meeting & Exposition, 1989, 892521:754-760. http://papers.sae.org/gsdownload/?prodCd=892521 |
| [6] | Jujnovich B A. Active steering of articulated vehicles. England:University of Cambridge, 2005. https://link.springer.com/article/10.1007/s12239-017-0030-8 |
| [7] | Poggetto V F D, Serpa A L. Vehicle rollover avoidance by application of gain-scheduled LQR controllers using state observers[J]. Vehicle System Dynamics, 2016, 54(2): 191–209. DOI:10.1080/00423114.2015.1125005 |
| [8] | Islam M M, Ding X J, He Y P. A closed-loop dynamic simulation-based design method for articulated heavy vehicles with active trailer steering systems[J]. Vehicle System Dynamics, 2012, 50(5): 675–697. DOI:10.1080/00423114.2011.622904 |
| [9] | Ding X J, Mikaric S, He Y P. Design of an active trailer-steering strategy for multi-trailer articulated heavy vehicles using real-time simulations[J]. Proceedings of the Institution of Mechanical Engineers Part D:Journal of Automobile Engineering, 2013, 227(5): 643–655. DOI:10.1177/0954407012461223 |
| [10] | Cheng C, Cebon D. Improving roll stability of articulated heavy vehicles using active semi-trailer steering[J]. Vehicle System Dynamics, 2008, 46(suppl1): 373–388. |
| [11] | Jujnovich B A, Cebon D. Path-following steering control for articulated vehicles[J]. Journal of Dynamic Systems Measurement & Control, 2013, 135(5): 1–15. |
| [12] | Kim Y C, Yun K H, Min K D. Automatic guidance control of an articulated-all wheel steered vehicle[J]. Vehicle System Dynamics, 2014, 52(4): 456–474. DOI:10.1080/00423114.2013.831458 |
| [13] | Wang Q S, He Y P. A study on single lane-change manoeuvres for determining rearward amplification of multi-trailer articulated heavy vehicles with active trailer steering systems[J]. Vehicle System Dynamics, 2016, 54(1): 102–123. DOI:10.1080/00423114.2015.1123280 |
| [14] | Oreh S H T, Kazemi R, Azadi S. A new method for off-tracking eliminating in a tractor semi-trailer[J]. International Journal of Heavy Vehicle Systems, 2016, 23(2): 107–130. DOI:10.1504/IJHVS.2016.075490 |
| [15] | Kharrazi S, Lidberg M, Fredriksson J. Robustness analysis of a steering-based control strategy for improved lateral performance of a truck-dolly-semitrailer[J]. International Journal of Heavy Vehicle Systems, 2015, 22(1): 1–20. DOI:10.1504/IJHVS.2015.070414 |
| [16] |
聂枝根, 宗长富.
重型半挂车简化模型参数辨识研究[J]. 汽车工程, 2015, 37(6): 622–630.
NIE Zhigen, ZONG Changfu. A study on the parameters identification of simplified models for articulated heavy vehicles[J]. Automotive Engineering, 2015, 37(6): 622–630. (in Chinese) |
| [17] | Sharp R S, Valtetsiotis V. Optimal Preview car steering control[J]. Vehicle System Dynamics, 2001, 35(suppl): 101–117. |
| [18] | Tamaddoni S H, Taheri S, Ahmadian M. Optimal preview game theory approach to vehicle stability controller design[J]. Vehicle System Dynamics, 2011, 49(12): 1967–1979. DOI:10.1080/00423114.2011.565778 |
 2017, Vol. 40
2017, Vol. 40

