1b. 重庆大学 土木工程学院, 重庆 400045;
2. 上海市隧道 工程轨道交通设计研究院, 上海 200235
1b. School of Civil Engineering, Chongqing University, Chongqing 400045, P. R. China;
2. Shanghai Tunnel Engineering and Rail Transit Design and Research Institute, Shanghai 200235, P. R. China
20世纪60年代以来,中国在各类岩土工程中使用了大量锚杆、锚索和土钉,其总数当以亿计。中国是一个多山的国家,随着城市化进程和经济建设的快速发展,在山区公路、铁路、水利工程和工业与民用建筑的修建过程中,出现大量需要支护的边坡以及隧道、隧洞,这些工程中使用了大量的锚固类结构。然而,由于锚杆耐久性不足而失效的情况时常发生,轻则产生巨大的经济损失,重则产生重大的人员伤亡。
总参工程兵科研第三研究所于1985年7月到1987年7月,以“砂浆锚固体腐蚀及防护研究”为题,深入地研究了锚固体保护层的使用寿命问题[1]。陈庆玉等[2]采用浸烘循环加速的方法,测试了硫酸作用下3种水灰比的锚固砂浆整个劣化损伤过程的单轴抗压强度。王桂林等[3]从理论上推导一般大气环条件下钢筋的锈蚀速度以及不同服役时间钢筋各部位的锈蚀深度和体积变化规律,得到了钢筋非均匀锈蚀轮廓线的理论计算模型。徐洪等[4]研究了围岩作用下砂浆锚固体的锈胀开裂过程,得出锚固系统的锈蚀而导致保护层开裂以及后续的开裂过程均与围岩性质密切相关。Schneide等[5]将水灰比为0.5的纯水泥试样、普通混凝土试样、高强混凝土试样浸泡到硫酸氨和饱和石灰水溶液中,并且施加应力水平为0.3的弯曲荷载,测定了试样强度随着时间的变化曲线。
由于砂浆锚固体多处于地下工程中,环境中难免会存在腐蚀因素,这将导致砂浆锚杆宏观力学性能退化,而导致宏观力学性能退化的根本原因是腐蚀导致了砂浆锚固体微观结构的变化,微观结构发生了怎样的变化,如何去衡量这些变化,这是一个亟待解决的问题。
要获取砂浆锚固体微观结构特征,基于扫描电镜技术的岩体微观孔隙结构研究是当前岩土工程中最有效和最直接的方法[6]。目前,国内外学者采用扫描电镜(SEM)从不同角度研究了岩、土等微观表面结构变化情况,同时借助于专业图像处理技术和分形理论来间接研究了岩土体孔隙、裂隙、矿物质以及显微构造等特征[6-14]。
笔者运用图像处理技术对砂浆锚固体腐蚀实验过程的SEM图像进行处理,采用分形理论对提取的腐蚀形貌微观特征进行分形研究,并采用压汞试验进行验证。
1 砂浆锚固体腐蚀SEM图像处理及分形 1.1 砂浆锚固体腐蚀试验砂浆锚固体腐蚀试验分锚杆未受力和受力(受拉)2种工况,为模拟锚固体受力的工作状态,这里采用高精度、高适应性不锈钢弹簧加载装置系统模拟锚固体受拉状态下的腐蚀过程。水泥砂浆锚固体在工作时会承受各种荷载,其内部的剪应力比一般为砂浆锚固体强度的0.25~0.5,随着时间的增长,砂浆锚固体抗剪强度将逐年下降,采用了0(未受力)、0.3(受拉)2组应力比进行试验。该试验装置应用虎克定理,预先测量弹簧弹性模量,通过控制压缩距离,从而控制对砂浆锚固体施加的应力。该加载系统装置的试件尺寸如图 1所示。

|
图 1 加载装置系统试件尺寸 Figure 1 Specimen dimension and loading testing equipment |
砂浆锚固体采用重庆拉法基水泥厂生产的42.5R级普通水泥;砂采用岳阳产中砂,其细度模数为3.0;砂浆配合比为水泥:砂:水=1:1:0.6。试件制备好以后放入标准养护室养护28 d,对试件进行编号,放入质量分数为15%的Na2SO4和MgSO4的混合溶液进行腐蚀。在试验中选取的干湿循环制度为:试件在室温下浸泡16 h,然后再放入温度为70 ℃的烘箱中烘8 h为一个循环。
1.2 图像获取随着腐蚀的进行,砂浆锚固体的孔隙特征将越来越明显。腐蚀离子主要通过孔隙进行砂浆锚固体内部,并与其发生反应,致使砂浆锚杆的宏观力学性能逐渐退化,而这正是由于微观孔隙的存在而导致的,不同腐蚀时间下砂浆锚固体微观孔隙率一定程度上决定了宏观力学性能。本次SEM图像的获取是采用VEG A 3 LMH扫描电子显微镜,主要技术指标:1) 钨灯丝电子枪,最大加速电压30 kV;2) 点分辨率3.0 nm@30 kV;3) 可扫描直径为260 mm大样品,可用于金属、非金属、生物等各种物品微观形貌分析。

|
图 2 未受力工况腐蚀不同天数微观形貌图 Figure 2 Microscopic images of unstressed corrosion for different days |

|
图 3 受力工况腐蚀不同天数微观形貌图 Figure 3 Microscopic images of stressed corrosion for different days |
扫描电镜成像的原理是通过向物质表面发射高能电子束,激发物质产生反射电子束而成像。某些情况下图像亮度不均匀的现象比较严重,而亮度不均匀将为后续对砂浆锚杆孔隙率的测量带来麻烦,致使测量误差偏大。光照不均匀校正一般按以下步骤进行:
1) 首先估计图像背景的灰度,一般是取图像中每个32×32大小的图形块中的最小值作为图像背景的灰度;
2) 然后将粗略估计出的背景灰度矩阵扩展成和原始图像大小相同的矩阵;
3) 从原始图像中减去前两步计算出的背景灰度矩阵,校正光照的不均匀,但是此操作同时也会导致前景图像变暗,所以需要对其进行对比度增强。
1.3.2 图像对比度增强图像的对比度可以理解为颗粒区域和孔隙区域的亮度差问题,增强对比度的目的是使二者的亮度差增大,以便后续二值化处理过程中将二者更好的分割出来。对比度增强常用方法为增强目标区域、抑制背景区域,让原来模糊的图像变得清晰。采用灰度线性变换增强、直方图均衡化增强、直方图规定化增强、有限对比自适应直方图均衡化等方法对砂浆锚固体的SEM图像进行对比度增强。
1.3.3 图像去噪图像的噪声是在拍摄图像以及图像转换和传输过程中各种随机信号对图像造成的干扰。噪声的存在又会使图像质量下降,影响对图像的分析,所以要对图像进行降噪处理。对于砂浆锚固体SEM图像而言,噪声表现为图像表面棱刺和麻点较多,在二值化过程中,就有可能将这些麻点误当成孔隙,使孔隙参数的测量精度降低。在降噪过程中往往会引起图像所含信息发生一定程度上的损失,降噪和保留图像信息是一对矛盾体,因此降噪方法和参数的选取要合理。图像去噪的主要方法有均值滤波、中值滤波、自适应维纳滤波等,这里采用使用较为普遍的中值滤波。
1.3.4 图像二值化图像二值化简单说就是将灰度图像转为黑白图像,转换后图像的像素只有两个值0或1,0表示黑色,1表示白色。对于砂浆锚固体SEM图像,0表示孔隙区域,1表示颗粒区域。图像分割后,由于灰度值只有0和1,原图所携带的信息大幅度减小。不同的二值化方法分割阀值不同,可使孔隙和颗粒区域相对面积也不同,因此,合理选取一种二值化分割方法对后续孔隙特征的提取尤为重要。二值化方法主要有最佳阀值法、最大类间方差法和最大熵阀值法,通过对比处理结果,最大类间方差法对本文的SEM图像分割效果较好,最终二值化图像如图 4所示。

|
图 4 未腐蚀时二值图 Figure 4 Binary images of corrosion for 0 day |
图像经过二值化后,总有少数毛刺和孤立的点存在,这些点的存在对孔隙特征提取是不利的,会加大定量统计的误差。基本的形态学方法经笔者多次试算后,误差较大,不适用于对空隙孤立点的去除。查阅相关文献,发现bwareaopen函数可删除二值图像中面积小于一定值的对象,经过大量试算,面积阀值取为5。以图 4(a)为例进行说明,其他图像做同样处理。为与孔隙特征的测定联系起来,先将图像进行反转,即白色变为黑色,黑色变为白色。
从图像反转的结果来看,存在大量的孤立的点,通过bwareaopen函数可消除面积小于5个像素平方的孤立的点。结果如图 5所示,大部分孤立的点被去除,而孔隙没有受到影响。

|
图 5 图像反转及形态学处理结果 Figure 5 The results of image reversal and morphological processing |
利用扫描电镜对砂浆锚固体表面进行扫描,经过图像预处理操作处理后,得到了SEM图像的二值黑白图像,其中黑色代表孔隙区域,白色代表固体颗粒区域。在MATLAB图像处理工具箱中,可以通过bwlabel函数来对二值图像中的对象进行标记。该函数能返回前景(像素值为1) 中对象的个数,即可统计出孔隙的数目。同时,可以通过regionprops函数测量图像区域的几何属性,例如每个孔洞的面积、平均面积、孔洞的直径等,这些测量结果在MATLAB中都是以像素为单位的[14]。二值化图像中黑色代表的是孔洞区域,而bwlabel和regionprops函数统计的是图像中白色区域的属性,故使用这两个函数前需要将图像进行颜色反转。孔隙率可以通过得到的孔隙像素点的个数除以整个图像总像素点的个数得到。
从表 1可以看出,未腐蚀情况下,受力工况与未受力工况孔洞数量差别不大,受力工况下孔隙率较大;腐蚀情况下,腐蚀前期受力与未受力工况下孔隙数量和孔隙面积差别不大,腐蚀后期受力工况下孔洞数量大概为未受力工况下的一半,这说明腐蚀后期受力情况下会加速砂浆锚固体的腐蚀,更快地使小孔隙连通成大孔隙,使腐蚀离子更易进入锚固体内部;受力工况下和未受力工况下的孔隙率均随着腐蚀时间的增加而增加。
| 表 1 孔隙特征统计表 Table 1 The statistic table of pore characteristics |
分形几何作为自然界中复杂、无序现象的一种定量描述的手段,已经在诸多研究领域得到广泛的应用。自然界中孔隙介质中孔隙结构的空间分布均可以用分形几何的方法进行描述[14]。研究分形,分形维数也就成为了衡量的标准,分形维数是对分形对象特征的定量描述。
用边长为r立方体去覆盖线段的长度的单位,需要1/r个立方体;覆盖单位长度的正方形,总共需要有1/r2这样的小立方体;覆盖单位边长的正方体,需要1/r3个小正方体。注意指数r和覆盖对象的尺寸是一样的,这决不是偶然的。一般的,可以用“盒子”来覆盖任意形状的图形,盒计数维数是这样定义:设A是任意的n维欧式空间的非空有界子集,对任意的r≥0,Nr(A)表示用来覆盖A所需边长为r的n维立方体(盒子)的最小数目。如果存在数d使得当r→0,Nr(A)∝1/rd,那么称d为A的盒子计数维数(简称盒维数)。需要注意:盒维数为d若存在k使得
| $ \mathop {\lim }\limits_{r \to 0}\, \frac{{{N}_{r}}\left( A \right)}{1/{{r}^{d}}}=k。$ | (1) |
两边同时去对数,得
| $ \mathop {\lim }\limits_{r \to 0}\, \left( \log {{N}_{r}}\left( A \right)+d\ \log \ r \right)=\log \ k。$ | (2) |
进一步求得
| $ d=-\mathop {\lim }\limits_{r \to 0}\, \frac{\log \ {{N}_{r}}\left( A \right)}{\log \ r}。$ | (3) |
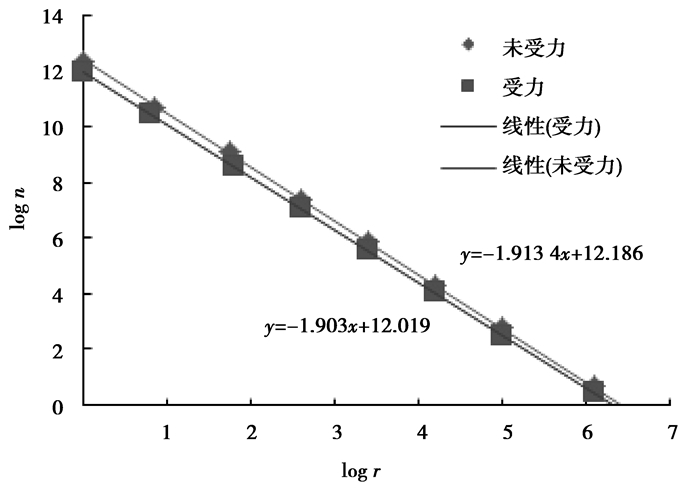
这里去掉log k,因为它是常数项。当r→0时,分母会趋于无穷大。另外,由于0≤r≤1,log r < 0,因此,d为需要的正数,一般用Db表示盒维数。通过计算,腐蚀120 d时孔隙的盒维数如图 6所示。
|
图 6 腐蚀120 d时孔隙的分形维数 Figure 6 Pore fractal dimension when corroded for 120 days |
从图 6可以看出,盒子的大小和覆盖孔隙的盒子数目的双对数关系具有明显的线性特征,由计盒维数的定义可知,盒子大小的对数和盒子数目的对数线性拟合的直线方程斜率的相反数即为此时孔隙的分形维数。其他腐蚀时间的分形维数由同样的方法得到,如表 2所示。
| 表 2 分形维数统计表 Table 2 The statistic table of fractal dimension |
从所得结果可以看出,未受力工况下和受力工况下,孔隙分形维数均随着腐蚀时间的增加而降低;同一腐蚀时期,受力工况下的分形维数略小于未受力工况下的分形维数。
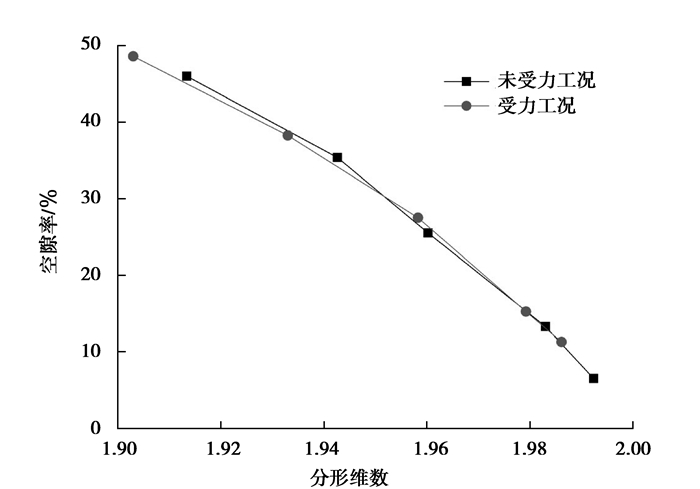
1.6 分形维数与孔隙率、粘结强度之间的关系从图 7可以看出,分形维数与孔隙率近似成负线性关系,随着分形维数的减小,孔隙率几乎线性增加,这可以解释为随着分形维数的减小,孔隙的空间分布复杂程度降低,孔隙数量减少,孔径增大,砂浆锚固体孔隙率增加。
|
图 7 分形维数与孔隙率之间的关系 Figure 7 The relationship between the fractal dimension and porosity |
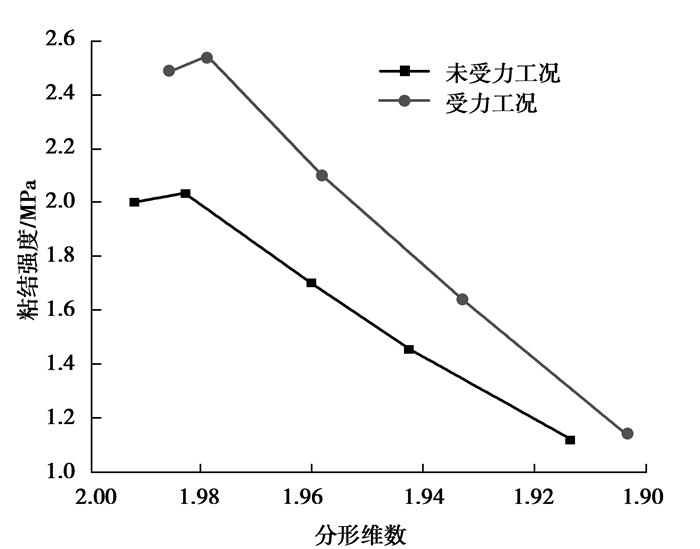
从团队所做物理实验以及文献[15]可知,未受力工况下腐蚀0, 30, 60, 90, 120 d砂浆锚杆的粘结强度依次为2.02, 2.055, 1.72, 1.475, 1.14 MPa;受力工况下腐蚀0, 30, 60, 90, 120 d砂浆锚杆的粘结强度依次为2.51, 2.565, 2.12, 1.66, 1.16 MPa,进而得到分形维数与粘结强度之间的关系,如图 8所示。
|
图 8 分形维数与粘结强度之间的关系 Figure 8 The relationship between the fractal dimension and the bond strength |
从图 8看出,随着砂浆微观孔隙分形维数的减小,其粘结强度先升后降。受力与不受力2种不同工况下的粘结强度曲线变化趋势相似,都可以分为2段:第一段为上升段,第二段为下降段。腐蚀时间到一个月左右粘结强度有所增加,是因为锚固体内部硫酸盐和水泥水化产物的反应,使得锚固体膨胀,锚固体受到约束,膨胀相当与增加了围压,提高了界面的极限粘结强度[17],随着腐蚀的进行,砂浆锚固体孔隙率增加,分形维数的降低,腐蚀介质更易进入锚固体内部,故粘结强度降低。
受力工况的粘结强度下降速率要明显快于未受力工况,是由于拉应力的存在使得锚固体与钢筋界面存在应力,加快腐蚀溶液的侵蚀。
2 压汞试验与扫描电镜对比分析为验证图像处理的准确性,通过压汞试验的方法进行对比分析,首先选取未腐蚀及腐蚀后的砂浆锚固体进行压汞试验,测得其孔隙率,然后通过电镜扫描获得其微观SEM图像,利用图像处理技术测算其孔隙率,并与压汞试验测的孔隙率进行对比。
2.1 压汞试验分析 2.1.1 试验设备及试样制备本试验采用PoreMaster 33全自动压汞仪进行测量,该圧汞仪主要用于分析粉末或块状固体的孔隙率、孔尺寸、总孔体积、总孔面积、孔曲率、样品表观密度等物理性质,可测量孔径范围为0.006~1 080 μm。取腐蚀和未腐蚀条件下的两个试样进行测试。
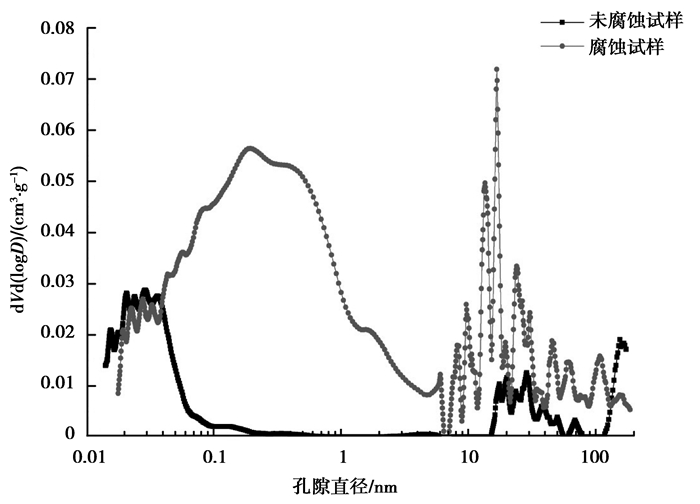
2.1.2 试验结果与分析关于孔径分布,图 9表示进汞体积对孔径微分曲线,横坐标表示孔隙直径,纵坐标表示进汞量对孔隙直径的微分,其值越大,表示该点所对应直径的孔隙进汞量就越大,孔隙数量就越多。从图中可以看出,随着腐蚀的进行,孔隙直径分布逐渐从小孔向大孔方向发展,且大孔数量逐渐增多,而小孔数量逐渐减少。
|
图 9 孔径分布图 Figure 9 Image of pore size distribution |
关于孔隙率,总的孔隙率等于总的进汞体积除以试样的体积,试样的质量试验前已测量出,其中M未腐蚀=0.829 8 g,M腐蚀=0.406 5 g,查阅相关文献可知,水泥砂浆密度大约为ρ=1.9 g/cm3,故试样总的体积为
| $ {{V}_{\text{未腐蚀}}}=\frac{{{M}_{\text{未腐蚀}}}}{\rho }=0.436\ 7\ \text{c}{{\text{m}}^{3}}, $ | (4) |
| $ {{V}_{\text{腐蚀}}}=\frac{{{M}_{\text{腐蚀}}}}{\rho }=0.213\ 9\ \text{c}{{\text{m}}^{3}}。$ | (5) |
未腐蚀试样和腐蚀试样压汞试验结果所得到的孔容分别为0.020 9 cm3/g和0.107 0 cm3/g,进而可求得两试样的进汞量和孔隙率。
未腐蚀试样进汞量:V1=0.020 9 cm3/g×0.829 8 g=0.017 3cm3;腐蚀试样进汞量:V2=0.107 0 cm3/g×0.406 5 g=0.043 5 cm3;未腐蚀试样孔隙率:
分别各取a、b试样未腐蚀与腐蚀后微观SEM图像,采用本文方法对其进行孔隙特征提取,计算结果如表 3所示。
| 表 3 对比试样孔隙特征统计表 Table 3 The statistic table of samples' pore characteristics |
从表 3可以看出,试样从未腐蚀到腐蚀,孔隙数量逐渐减少,而孔隙平均面积、平均直径均增大,说明孔隙逐渐从小孔隙向大孔隙转变,这与压汞试验得出的结论是相符的。
同时,未腐蚀试样图像分析得到的平均孔隙率为10.42%,比压汞试验测的孔隙率3.97%偏大6.45%;腐蚀试样分析得到的平均孔隙率为26.15%,比压汞试验测的孔隙率20.3%偏大5.85%。可能有以下几方面的原因:1) 通过压汞法测得的孔隙率是开口孔隙率,即与外界连通的孔隙率,在砂浆内部,还含有与外界不连通的闭口孔,这些孔是压汞法无法测量的,而图像处理却可以测得到;2) 由于孔隙直径较小,通过图像处理技术测得孔隙率就不得不采用高倍显微镜将其形貌特征放大,但这样会使视域变小,使获得的图像不具有代表性从而产生误差。3) 图像预处理过程中方法不当,图像分割时阀值太大或太小都将影响孔隙率的测定。
综上所述,与压汞试验测试相比,图像处理技术测量孔隙率虽然存在一定误差,但其结果仍在可接受范围内。
3 结论1) 通过提取不同腐蚀时间下的微观孔隙特征,发现随着腐蚀时间的增加,受力和未受力工况下锚固体的孔隙率均成线性增大,孔隙数量随着腐蚀时间的增加逐渐减少,孔隙平均面积随腐蚀时间的增加而增大。腐蚀后期受力工况下的锚固体与未受力工况的锚固体相比,孔隙数量更少,孔隙面积和孔隙率更大。
2) 分形维数和孔隙率成负线性关系,分形维数越小,孔隙率越大;随着分形维数降低,未受力与受力工况下砂浆锚固体的粘结强度都是先增大后减小的趋势,受力工况的砂浆锚固体粘结强度下降速度快于未受力工况。
3) 过压汞试验,发现随着腐蚀的进行,孔隙直径分布逐渐从小孔向大孔方向发展,且大孔数量逐渐增多,而小孔数量逐渐减少,与SEM图像处理结果基本一致。由于压汞试验测得的是开口孔的孔隙率,所测得的孔隙率较SEM图像处理得到的孔隙率偏低。
| [1] |
赵健, 冀文政, 肖玲, 等.
锚杆耐久性现场试验研究[J]. 岩石力学与工程学报, 2006, 25(7): 1377–1385.
ZHAO Jian, JI Wenzheng, XIAO Lin, et al. In-situ experimental study on anchor durability[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(7): 1377–1385. (in Chinese) |
| [2] |
陈庆玉, 王桂林, 徐洪, 等.
锚固砂浆硫酸盐腐蚀损伤试验研究[J]. 地下空间与工程学报, 2011, 7(2): 291–295.
CHEN Qingyu, WANG Guilin, XU Hong, et al. Experimental research on sulfate attacking damage of anchor mortar[J]. Chinese Journal of Underground Space and Engineering, 2011, 7(2): 291–295. (in Chinese) |
| [3] |
王桂林, 陈庆玉, 徐洪, 等.
钢筋非均匀锈蚀轮廓线理论解[J]. 重庆大学学报, 2010, 32(2): 87–91.
WANG Guilin, CHEN Qingyu, XU Hong. Theoretical contour line of reinforcement bar of non-uniform corrosion[J]. Journal of Chongqing University, 2010, 32(2): 87–91. DOI:10.11835/j.issn.1674-4764.2010.02.017 (in Chinese) |
| [4] |
徐洪, 张永兴, 王桂林.
围岩作用下锚杆砂浆锈胀开裂过程分析[J]. 岩土力学, 2010, 31(4): 1193–1198.
XU Hong, ZHANG Yongxing, WANG Guilin. Analysis of corrosion cracking model of anchorage body in consideration of rock actions[J]. Rock and Soil Mechanics, 2010, 31(4): 1193–1198. (in Chinese) |
| [5] | Schneider U, Chen S W. The chemomechanical effect and the mechanochemical effect on high-performance concrete subjected to stress corrosion[J]. Cement and Concrete Research, 1998, 28(4): 509–522. DOI:10.1016/S0008-8846(98)00015-5 |
| [6] |
綦建峰, 隋旺华, 张改玲, 等.
基于SEM图像处理红层砂岩孔隙度及分维数计算分析[J]. 工程地质学报, 2014, 22(suppl1): 339–345.
QI Jianfeng, SUI Wanghua, ZHANG Gai-ing, et al. Calculation and analysis of the porosity and fractal dimention of red stratum sandstone based on SEM images processing[J]. Journal of Engineering Geology, 2014, 22(suppl1): 339–345. (in Chinese) |
| [7] | Kata A J, Thompson A H. Fractal sandstone pores:implication for conductivity and formation[J]. Physical Review Letters, 1985, 54(3): 1325–1328. |
| [8] | Wang L B, Lai J S, Frost J D. Fourier morphological descriptors of aggregate profiles[C/OL]//Imaging Technologies:Techniques and Applications in Civil Engineering. Second International Conference. 1998[2016-07-03]. http://worldcat.org/isbn/0784403252. |
| [9] | Lian T L, Radhakrishnan P, Sagar B S D. Morphological decomposition of sandstone pore-space:fractal power-laws[J]. Chaos Solitons and Fractals, 2004, 19(2): 339–346. DOI:10.1016/S0960-0779(03)00046-8 |
| [10] | Hood S D, Nelson C S, Kamp P J J. Modification of fracture porosity by multiphase vein mineralization in an Oligocene nontropical carbonate reservoir, Taranaki Basin, New Zealand[J]. Aapg Bulletin, 2003, 87(10): 1575–1597. DOI:10.1306/06040301103 |
| [11] |
刘凤和, 李二娜, 李丽, 等.
于SEM图像处理法的冻干马铃薯内部孔隙率表征[J]. 干燥技术与设备, 2013, 11(4): 51–56.
LIU Fenghe, LI Erna, LI Li, et al. Porosity determination of freeze-dried potato by image processing method[J]. Drying Technology and Equipment, 2013, 11(4): 51–56. (in Chinese) |
| [12] |
连会青, 夏向学, 王世东, 等.
含水层微观孔隙分形特征与渗透性关联研究[J]. 工程勘察, 2014, 42(1): 36–41.
LIAN Huiqing, XIA Xiangxue, WANG Shidong, et al. Association study of fractal characteristics of microscopic pore with permeability of aquifer[J]. Geotechnical Investigation and Surveying, 2014, 42(1): 36–41. (in Chinese) |
| [13] |
于华伟. 单颗粒煤孔隙结构的数值模拟研究[D]. 包头: 内蒙古科技大学, 2014. YU Huawei. Numerical simulation of single-partical pore structure of caol[D]. Baotou:Inner Mongolia University of Science and Technology, 2014. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-11973-1014080533.htm |
| [14] |
朱华, 姬翠翠. 分形理论及其应用[M]. 北京: 科学出版社, 2011.
ZHU Hua, JI Cuicui. Ractal theory and its applications[M]. Beijing: Science Press, 2011. (in Chinese) |
| [15] |
周金飞. 砂浆锚固体腐蚀后结构微观分析及力学性能研究[D]. 重庆: 重庆大学, 2012. ZHOU Jinfei. Structure microstructure analysis and mechanical properties of mortar anchor solid under sulfate attack[D]. Chongqing:Chongqing University, 2012. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10611-1012048023.htm |
 2017, Vol. 40
2017, Vol. 40

