b. 重庆大学土木工程学院, 重庆 400045;
c. 重庆大学建筑城规学院, 重庆 400045
b. College of Civil Engineer, Chongqing University, Chongqing 400045, P. R. China;
c. Faculty of Architecture and Urban Planning, Chongqing University, Chongqing 400045, P. R. China
几何非线性和材料非线性并存是钢筋混凝土构件在受荷过程中的基本特征[1]。几何非线性主要指轴向压力对受压构件的侧移和挠曲产生附加弯矩和附加曲率,即二阶效应问题;材料非线性主要指构件材料自身所表现出来的非线性弯矩轴力曲率关系,由自身本构关系所决定,同时还受裂缝、钢筋滑移等因素的影响。为在结构设计中能同时考虑这两类非线性问题,中国《混凝土结构设计规范》(GB 50010—2010)[1]参考国外先进规范而引入了考虑构件刚度折减的弹性二阶分析法,该方法的关键在于对其折减系数取值的合理性。目前所查的国内外规范对柱的刚度折减系数取值仅针对框架结构[2-5],尚缺乏对排架结构柱刚度折减系数的研究。且现行《混凝土结构设计规范》[1]中对排架结构的二阶效应设计方法仍采用具有理论瑕疵且缺乏有效分析验证的η-l0法,该方法只考虑了几何非线性而没有考虑材料非线性[6];另外,对比框架结构,排架结构的特殊性还在于承受荷载形式的复杂性和冗余度较小,因此有必要对排架结构的二阶效应进行深入研究,提出适用于整个排架结构的刚度折减系数,完善规范对排架结构在同时考虑材料非线性和几何非线性时存在的问题。
1 排架结构折减刚度的基本原理和分析程序 1.1 排架结构折减刚度的基本原理考虑刚度折减系数的弹性二阶分析方法的设计思想主要来自美国认证协会(ACI)的规范[3],《ACI 318》对考虑材料非线性后结构构件的刚度有2个重要的概念:被用于强度设计的刚度EI[7]能够代表该构件将要破坏时的刚度;EI值应符合构件整体的弯矩端部转角关系,而不是构件最危险截面的弯矩曲率关系。
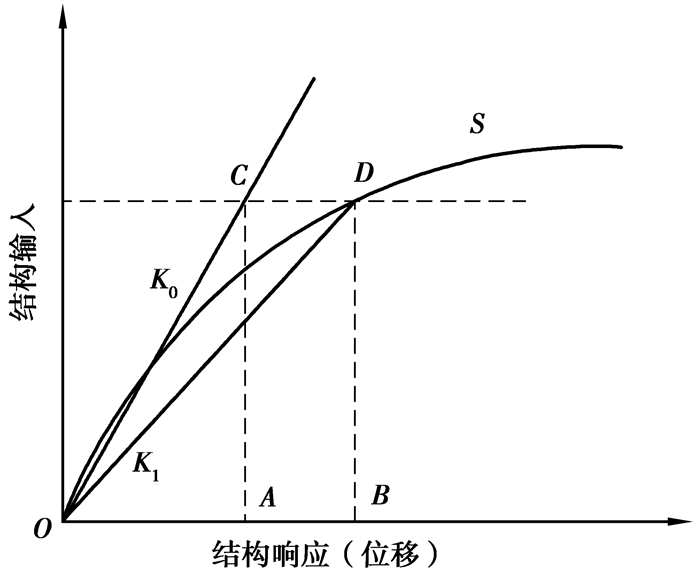
结构刚度折减系数基本原理如图 1所示[6]。结构处于弹性状态的本构关系如直线OC,非线性状态的本构关系如曲线OS。在进行非线性分析时,可以通过引入一个刚度折减系数α,将弹性刚度K0折减为K1,使结构在原有的荷载水平下,弹性分析与非线性分析产生近似相同的结构响应[8]。运用此原理,同一非线性本构模型S在不同的结构输入水平下均可对应不同的折减系数,但鉴于工程实用性,只需找出一个具有普遍适用的折减系数,将其用于弹性二阶分析法,弹性二阶法计算出的层间位移角和层间位移与非线性有限元法计算出的结果等效,而不是仅拘泥于某个状态的刚度折减系数α[8]。
|
图 1 结构的非线性反应 Figure 1 The non-liner response of structure |
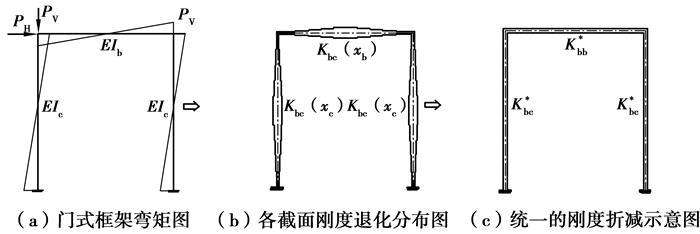
如图 2(a)所示的门式框架,在承载能力极限状态下,梁柱沿长度方向每个截面的刚度退化程度不相同,表现为从中部沿两端退化不断增大,如图 2(b)所示;为能得到在工程设计中实用的方法,以柱顶位移和变形等效作为控制条件,通过一个统一的刚度折减系数模拟非线性状态下结构的内力和变形,而不是针对不同刚度退化截面均给出不同的折减系数;这种统一的折减系数被称之为综合刚度折减系数[3],如图 2(c)所示。
|
图 2 弹性刚度折减的等代思想 Figure 2 The equivalent procedure of elastic stiffness reduction |
根据单层工业厂房标准设计图集[9],运用以上原理可设计出具有代表性的排架结构算例,以结构整体二阶效应等效为控制条件,对其进行非线性有限元分析和基于刚度折减的弹性二阶分析,对比计算结果,寻找出仅针对排架结构的综合刚度折减系数。
1.2 分析程序简介采用较为成熟的商业软件SAP2000进行静力非线性分析。在SAP2000中,非线性二阶分析是考虑了构件曲率、层间位移和材料的非线性等共同因素的影响[3];即构件曲率和层间位移主要是通过P-Δ效应和大位移效应考虑[10-11],材料的非线性主要通过布置在杆件上离散的塑性点铰进行分析,结构的塑性变形均发生在此点铰内[12],沿构件不同位置布置多个塑性铰来模拟构件的塑性特征。由于设计图集中采用的截面形式和配筋较为规则,塑性铰通常采用自动铰进行分析,本研究采用基于FEMA-356准则[13]中形成的五阶段本构自动P-M-M铰,沿构件长度方向0.05, 0.15, 0.25, …, 0.95[12]的相对位置处均匀布置,程序将根据实际的截面和配筋情况获得自动铰属性。
2 双跨排架结构刚度折减系数的分析过程 2.1 有关荷载的分析方案排架柱设计是通过弹性二阶分析方法找出承载能力状态下的最不利工况[14],确定最不利截面和截面配筋;其非线性分析是指在非线性状态下求出结构的内力及变形。当进行排架设计和非线性分析时,荷载取值均取用更加符合设计思想的荷载设计值,一方面,在进行结构非线性分析时,刚度对结构计算结果更加不利;另一方面,在承载能力极限状态下结构能得到稳定性较好的刚度折减系数。
2.2 分析过程关键点概述 2.2.1 分析模型当采用忽略空间效应的单层双跨有侧移排架结构进行静力非线性分析时,排架结构下柱均分为10个单元,吊车梁牛腿部分分为2个单元,剩余部分均分为4个单元。
2.2.2 荷载分析结构的荷载分析[14]主要是确定在结构设计中用于最危险截面设计和非线性分析时所采用的荷载工况和最不利荷载组合,根据不用荷载工况作用下的荷载组合,利用Mu-Nu求出最危险截面及其对应的最不利荷载组合。对于单层双跨排架结构进行非线性分析时,主要对边柱下柱进行荷载分析,经计算其最不利荷载组合如下[15]:
| $ \begin{array}{l} {\rm{A}}:1.0 \times {G_{{\rm{DEAD}}}} + 1.4 \times {W_{\rm{L}}} + 1.4 \times (0.7 \times {Q_{{\rm{CVC}}}} + 0.7 \times {T_{\rm{B}}}), {\rm{ }}\\ {\rm{B}}:1.0 \times {G_{{\rm{DEAD}}}}-1.4 \times {T_{\rm{A}}} + 1.4 \times (0.6 \times {W_{\rm{R}}} + 0.7 \times {Q_{{\rm{DC}}}}), \\ {\rm{C}}:1.0 \times {G_{{\rm{DEAD}}}} + 1.4 \times {W_{\rm{R}}} + 1.4 \times (0.7 \times {Q_{{\rm{DC}}}}-0.7 \times {T_{\rm{A}}}), \end{array} $ |
式中:GDEAD为恒载;WL为迎风面在左侧的风载;WR迎风面在右侧的风载;TA为小车在第一跨时的横向水平荷载;TB小车在第二跨时的横向水平荷载;QCVC为当仅有2台吊车作用于同一跨时,第二跨左侧产生最大轮压,另一侧产生最小轮压;QDC为当每跨均有2台吊车同时作用时,第一跨右侧和第二跨左侧产生最大轮压,另一侧产生最小轮压;“+”表示荷载方向向右,“-”表示荷载方向向左。
2.2.3 加载方式采用SAP2000有限元程序分析时,荷载的加载顺序直接影响到计算结果的正确性,于是为更好地模拟实际受力情况,通常首先加竖向荷载和弯矩,再施加水平荷载,加载方式均采取荷载控制的方式进行逐级加载,并控制水平位移直至设计控制的限值,同时确定刚度折减系数的最终非线性状态。
2.3 计算刚度折减系数的方法参考框架结构中对刚度折减系数的研究方法,在进行弹性二阶分析时,以结构的整体位移作为宏观控制指标,使结构的整体位移和沿长度方向的层间位移与实际非线性二阶分析等效,从而引入一个能反应整体刚度退化的综合刚度折减系数[16-18],其理论公式可表示为
| $ EI = \alpha {E_{\rm{c}}}I, $ |
式中:α为综合刚度折减系数;Ec为混凝土刚度;E为折减后刚度。
通过大量具有代表性的单层双跨排架算例,提出针对所有柱段均适用的单层双跨排架的统一刚度折减系数α。
3 双跨排架结构刚度折减系数的取值建议根据单层工业厂房设计图集[9],选取了综合考虑排架结构特征和受荷情况的34个单层双跨排架结构作为研究算例;在最不利荷载组合下,对排架结构进行弹性二阶分析和非线性二阶分析,当最不利截面达到承载能力极限状态时,以结构整体位移等效作为控制目标,对比分析此时的二阶内力和位移,综合确定刚度折减系数。
3.1 计算结果与分析根据国家建筑建筑标准设计图集[9],可通过吊车吨位确定上下柱的截面尺寸,选取吊车吨位为10 t,20 t,32/5 t,50/10 t 4种类型,对应的边柱上柱截面尺寸分别为400 mm×400 mm,400 mm×400 mm,400 mm×500 mm,400 mm×500 mm;中柱上柱截面尺寸均为400 mm×600 mm;下柱截面尺寸分别均为400 mm×800 mm,400 mm×800 mm,400 mm×1 000 mm,400 mm×1 000 mm。根据排架结构承受的基本风压、跨度、吊车吨位和上下柱高比等因素设计算例,其编号汇总如表 1所示,各算例采用的荷载组合类型汇总如表 2所示,计算结果汇总如表 3所示。
| 表 1 双跨排架结构算例编号 Table 1 The example number of double-span bent frames |
| 表 2 算例采用的荷载组合类型 Table 2 The loading combination types of the example adopted |
| 表 3 排架结构位移比较及刚度折减系数 Table 3 The displacement comparison of bent frames and stiffness reduction factors |
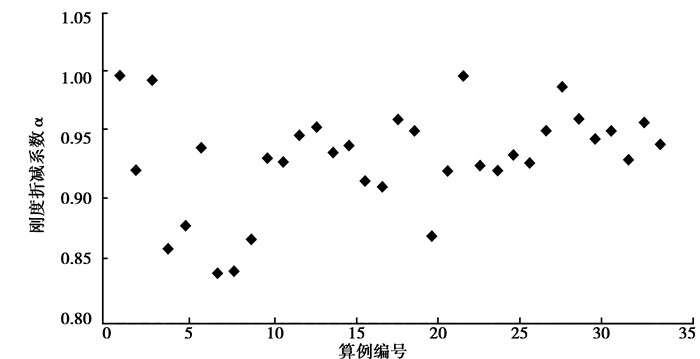
为更直观地观察和分析刚度折减系数的变化规律,将表 3中计算出的结果绘制成二维坐标散点图,如图 3所示。根据图 3刚度折减系数散点图的分布情况,为使排架结构具备足够的安全储备和考虑最不利情况下最大的刚度退化程度,给出所有柱段统一的刚度折减系数取值建议:α=0.85。
|
图 3 刚度折减系数散点图 Figure 3 The scatter diagram of stiffness reduction factors |
为了验证刚度折减系数α=0.85的合理性,选取4个具有代表性的排架结构进行基于刚度折减的弹性二阶分析和非线性二阶分析,分别计算出各柱段的弯矩、剪力、位移,将其值汇总如表 4所示。
| 表 4 刚度折减系数建议值的验证 Table 4 Checking the suggested value of stiffness reduction factor |
通过表 4可看出,考虑刚度折减后的截面内力有所增加,这是由于构件刚度的折减致使结构整体位移增加,增加的位移将放大截面弯矩从而表现为截面内力的增加,同时也间接证明了可通过引入刚度折减系数来考虑构件的材料非线性;但总体来说两种方法的计算结果较为接近,吻合程度较好,甚至采用刚度折减的弹性二阶方法更偏于安全,证明排架结构采用α=0.85的刚度折减系数是合理的且可方便运用于工程设计中。
4 结论参考美国ACI318关于考虑刚度折减的弹性二阶分析方法的理念,选取34个具有代表性的单层双跨等高排架结构对其进行非线性反应分析和弹性二阶分析,对比两种分析方法的结果,以排架结构整体二阶效应等效为准,提出具有工程实用性的刚度折减系数为0.85的取值建议。通过多个典型算例的对比分析,表明只要选取了合适的排架柱刚度折减系数,将考虑刚度折减的弹性二阶分析法运用于荷载组合非常复杂的排架结构的内力分析中,直接得到既考虑几何非线性又考虑材料非线性的排架结构内力是高效且合理的。
| [1] | Macgregor J G, Hage S E. Stability analysis and design of concrete frames[J]. Journal of the Structural Division, 1970, 103(10): 1953–1970. |
| [2] |
中华人民共和国住房和城乡建设部.混凝土结构设计规范:GB 50010-2010[S].北京:中国建筑工业出版社, 2010. Ministry of Housing and Urban-Rural Construction of the People's Republic of China. Code for design of concrete structures: GB 50010-2010[S]. Beijing: China Building Industry Press, 2010. (in Chinese) |
| [3] | American Concrete Institute. ACI 318-14. Building code requirements for structural concrete and commentary[S]. Farmington Hills, MI48331: American Concrete Institute, 2014. https://www.concrete.org/store/productdetail.aspx?ItemID=31814 |
| [4] | New Zealand Concrete Design Committee.NZS3101-2006. Standard concrete structure standard[S].New Zealand Concrete Design Committee, 2006. |
| [5] | Fafitis A, Kadam A N. Elasto-plastic Analysis and Design of Concrete Frames[C]// Computing in Civil Engineering and Symposium on Data Bases.[S.l.]:ASCE, 2010:402-411. |
| [6] |
刘毅, 朱占友, 魏巍, 等.
排架柱抗弯刚度折减系数探讨[J]. 重庆大学学报:自然科学版, 2007, 30(4): 61–66.
LIU Yi, ZHU Zhanyou, WEI Wei, et al. Discussion of the stiffness factor of bent-columns[J]. Journal of Chongqing University(Natual Science Edition), 2007, 30(4): 61–66. (in Chinese) |
| [7] | Tikka T K, Mirza S A. Nonlinear EI equation for slender reinforced concrete columns[J]. Aci Structural Journal, 2005, 102(6): 839–848. |
| [8] | Feng X, Shen M, Sun C, et al. Research on flexural stiffness reduction factor of reinforced concrete column with equiaxial+ shaped section[J]. Procedia-Social and Behavioral Sciences, 2013, 96(2): 168–174. |
| [9] |
国家建筑标准设计图集. 单层工业厂房钢筋混凝土柱: 05G335 [S]. 北京: 中国建筑标准设计研究院, 2005. National building standard design drawings. Reinforced concrete column of single storey industrial building: 05G335[S]. Beijing: China building standard design and Research Institute, 2005.(in Chinese) |
| [10] | Scholz H. P-delta effect in elastic analysis of sway frames[J]. Journal of Structural Engineering, 1987, 113(3): 534–545. DOI:10.1061/(ASCE)0733-9445(1987)113:3(534) |
| [11] | Kijania M, Seruga T, Rewers I. Effect of some factors on second order effects in reinforced concrete columns[J]. 2013, 168(3-4):289-293. http://yadda.icm.edu.pl/yadda/element/bwmeta1.element.baztech-a8990c13-33a4-4695-a1c4-0124764fcff5 |
| [12] |
北京金土木软件技术有限公司. CSI分析参考手册[M]. 北京: 中国建筑标准设计研究院, 2009.
Beijing Civil King Software Technology Co.Ltd. CSI analysis reference manual[M]. Beijing: China Institute of Building Standard Design and Research, 2009. (in Chinese) |
| [13] | Emergency F, Agency M.FEMA 356.Prestandard and commentary for the seismic rehabilitation of buildings[S].Washington, D.C:Federal Emergency Management Agency, 2000. |
| [14] |
中华人民共和国国家标准. 建筑结构荷载规范: GB50009-2012[S]. 北京: 中国建筑工业出版社, 2012. People's Republic of China national standard. Load code for the design of building structures: GB50009-2012[S]. Beijing: China Building Industry Press, 2010.(in Chinese) |
| [15] |
潘斯. 钢筋混凝土两跨排架柱二阶效应规律及等效长度研究[D]. 重庆: 重庆大学, 2014. PAN Si. Research on the second-order effect of two cress reinforced concrete bent-frames and the effective length of bentcolumns[D]. Chongqing: Chongqing University, 2014. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10611-1014044179.htm |
| [16] |
刘毅, 魏巍, 白绍良.
考虑非弹性特征的钢筋混凝土框架杆件刚度折减系数[J]. 重庆建筑大学学报, 2000, 22(1): 25–32.
LIU Yi, WEI Wei, BAI Shaoliang. RC frame component's stiffness reduction factor considering non-elastic characteristics[J]. Journal Chongqing Jianzhu University, 2000, 22(1): 25–32. (in Chinese) |
| [17] | Paulay T. Seismic displacement capacity of ductile reinforced concrete building systems[J]. Bulletin NZ Society for Earthquake Engineering, 2003, 36(1): 47–65. |
| [18] | Li B, Xiang W. Effective stiffness of squat structural walls[J]. Journal of Structural Engineering, 2011, 137(12): 1470–1479. DOI:10.1061/(ASCE)ST.1943-541X.0000386 |
 2017, Vol. 40
2017, Vol. 40

